
2022第24卷第4期
2.山东财经大学 经济研究中心, 山东 济南 250014
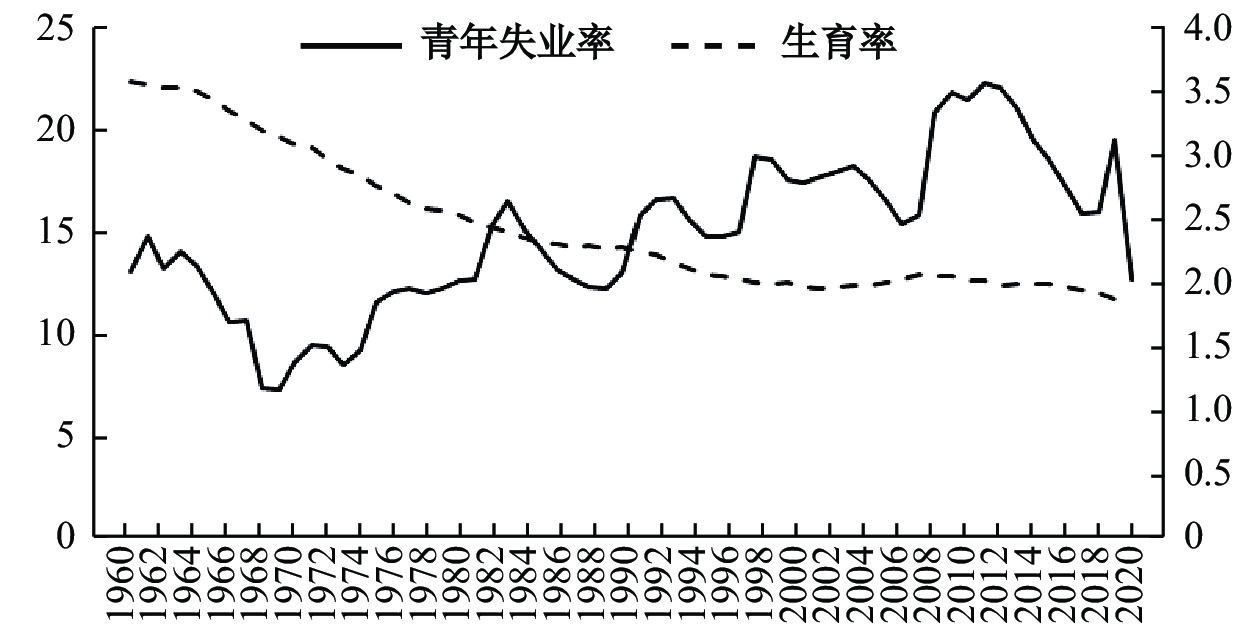
青年群体就业困难一直是全球性问题,中国亦然。在当前需求收缩、供给冲击和预期转弱的三重压力冲击下,我国青年群体进一步面临就业规模扩大和失业问题严重的两难局面。2022年5月份,16–24岁青年人口城镇调查失业率攀升至历史新高的18.4%,相当于全国城镇调查失业率的3倍之多。为确保就业形势稳定,《“十四五”就业促进规划》首次明确提出了促进青年就业,并作出了单独的部署安排。从国际上看,初次就业市场不景气不仅是就业数量上失业率高企的问题,还会连带造成就业质量下降,引发青年就业者持久收入损失,扩大不同就业队列的内部收入差距和组间收入差距,进而影响青年群体婚姻和生育决策(Choi等,2020)。值得注意的是,近年来中国生育率也逐渐回落。根据《中国统计年鉴》统计数据,中国人口自然增长率从2016年开始出现了五连降,到2021年仅为0.34‰。由于中国缺少青年失业率的历史统计数据,我们统计了世界各国平均青年失业率和生育率的变化趋势(见图1)。图1显示,青年失业率总体在波动中上升,而生育率则缓慢下降,二者之间呈现十字交叉的相反趋势。那么,我们思考一个问题:不断升高的青年失业率是否会对一国生育率产生负面影响?
|
| 图 1 青年失业率与生育率变化趋势 |
失业率对生育率的影响已经在国外有丰富的研究,但针对青年失业率影响生育决策的研究依然匮乏。一方面,失业率对生育行为的影响随着年龄段递进而依次递减,中老年阶段越来越接近育龄末期,该年龄段失业率对生育行为的影响从权重上并不显著;另一方面,青年失业率在整体失业率中最为突出,在全球范围内都是最高的失业年龄段,平均达到了中年失业率的2.6倍,老年失业率的3.5倍。青年失业除了推迟结婚生育决策,造成晚婚晚育(Wood和Neels,2017),还会在多个维度上影响就业质量,从而降低个体生育意愿(Vignoli等,2020)。青年失业造成长期的低质量就业状态,形成社会学领域所说的青年就业的“疤痕效应”(Oreopoulos等,2012),此时生育率的影响已经不再局限于一个狭小的年龄段,而是对总和生育率产生全局性和长期性影响。基于此,本文认为,当前对生育意愿的研究要体现整体性和前瞻性思维,不能仅从当前群体的就业状态推定当前群体的生育意愿,还要溯源而上,探讨初次就业市场不景气对生育率的长期和整体影响,即研究“疤痕效应”在生育意愿上的体现。
本文可能的边际贡献为:首先,首次探及了青年失业率与生育率之间的负向关系,验证了青年失业率存在生育抑制效应,且在长期内持续发生作用,将初次就业市场不景气对收入的“疤痕效应”研究延伸到生育层面,指出了促进青年更充分和高质量就业的人口学意义。其次,检验了青年失业率抑制生育率的中间作用机制,否定了晚婚晚育、收入质量下降和收入波动增大三个渠道,证明了工作压力加大在其中的完全中介效应,使青年失业的生育抑制效应研究结论更加完备。最后,基于OECD统计数据验证了就业数量向就业质量的传导效应,为我国未来协同推进青年群体充分就业和高质量就业提供了学理基础。
二、文献评述与理论假说 (一) 青年失业率的影响研究已就业的存量劳动者存在工资粘性和劳动管制,不易被灵活调整,故而受到经济冲击的影响较小。相较而言,青年群体往往属于新的增量就业者,对宏微观经济环境变化的敏感度最高。一方面,企业在经济增速放缓时期解雇青年员工比解雇老员工的机会成本更小(谭永生,2016);另一方面,企业往往通过灵活调整新人招聘而非裁减存量员工来应对经济冲击(戴觅等,2013)。青年个体不会长期失业,但失业却会给青年个体带来长期偏低的就业质量,从而导致持续影响。针对美国、加拿大、日本、韩国等多个国家的实证研究均显示,与经济冲击时期的青年就业者相比,经济平稳时期就业者的相对收入差距需要6–25年不等的时间才可能逐渐消弭(Kahn,2010;Oreopoulos等,2012;Hamaaki等,2013;Choi等,2020)。青年就业影响的长期性由多重原因造成:一是更差的初次就业机会意味着低效的专用人力资本积累,让就业者很难在未来获得好的内部晋升和外部跳槽机会(Oyer,2006);二是初次就业和学历教育一样释放了个体能力信号,雇主为了廉价获得信号,会异常重视上一任雇主给予的雇佣机会质量高低,以快速判断该员工的工作能力(Genda等,2010)。因此,在不同时期就业的劳动者之间产生了从雇主质量到起薪高低等就业结果差距明显的“队列效应(cohort effect)”(Hamaaki等,2013)。经济冲击下青年就业影响的路径往往是从高失业率向低就业质量的传导,包括相对收入水平、收入稳定性和工作环境等多方面都受到持续的负面影响。青年就业质量的下降造成了工作贫困群体,有大量初次就业人员虽然有工作,但却处于极度贫困状态,2019年东亚地区工作贫困青年占比达到了1.4%(ILO,2020)。青年失业率的升高也造成了工作的不稳定预期,给就业者带来了随时可能失去工作、被迫换工作的不确定性,这种不确定性对女性生育第一胎的时机选择产生了显著影响(Liepmann,2018)。与此同时,青年失业率高企还会恶化工作岗位环境,降低工作相关的不易直接度量的便利性条件,如尊严性、工作生活的平衡、福利保障的供给等因素,造成员工工作压力加大,主观幸福感降低,进而会推迟或者取消生育计划(Vignoli等,2020)。青年失业率对个体就业质量多方面的长期影响被称为“疤痕效应”(Oreopoulos等,2012;Huckfeldt,2022),更缓慢的财富积累过程和更差的收入状态也连带影响了青年群体的结婚生育决策,降低了其婚育概率(Maclean等,2016;Choi等,2020)。
(二) 生育率的影响因素研究从生育经济动机来看,有消费动机和投资动机两种。前者是将孩子看作是“消费品”,孩子能够为父母直接带来效用(Becker,1960);后者是将孩子看作是“投资品”,希望未来能够从孩子那里得到回报(Ehrlich和Lui,1991)。无论是消费动机还是投资动机,父母在作出生育决策时都要考虑生育成本问题(特别是机会成本的影响很大)。收入是在微观层面影响个体生育行为的关键因素,关于收入对生育决策的影响尚未达成一致结论。Bongaarts和Watkins(1996)认为收入与生育之间存在负相关关系;Galor(2005)的统一增长模型将人口与经济增长内生化,认为收入增加会引起生育率的增长。近年来,实证研究发现,生育意愿随家庭人均收入水平呈先下降后上升的U形关系(李子联,2016;何明帅和于淼,2017),故而与高收入和低收入群体相比中等收入群体具有更高的生育率。收入对生育的非线性影响源自其本身的二元性:一方面,收入越高,家庭融资约束越小,生育成本显得相对越低;另一方面,收入越高,意味着一旦生育行为需要牺牲工作,其所引致的生育机会成本也就越大。特别是女性,作为生育一方,其就业受到生育行为的影响更为直接,更容易面临失业、收入减少、失去晋升机会等诸多直接成本,其生育决策对劳动力市场的敏感度更高,也更为负面。来自众多国家同一样本的研究结论经常会出现男性生育效应为正、女性生育效应为负的割裂结论(Choi等,2020)。究其根源,还是在于家庭内部性别间收入差距的错位分布,往往当女性家庭内部收入偏低时,女性生育机会成本和家庭内部协调成本较小,容易达成生育子女的决策;反之,则容易作出推迟或者减少生育的家庭决策(Galor和Weil,1996;Prettner和Strulik,2017)。除了相对收入水平以外,劳动力市场不确定性也会影响微观层面个人收入的不确定性,导致婚龄个体作出推迟婚配和生育的决策(Kohler H P和Kohler I,2002)。相对于高收入阶层,低收入阶层的收入脆弱性程度更高,收入不确定性显著抑制其生育意愿(徐巧玲,2019)。劳动力市场不景气下就业岗位的低质量还体现在工作环境恶劣带来的工作压力加大、主观幸福感降低,从而降低生育意愿(Vignoli等,2020)。无论是收入水平、收入不确定性还是工作压力,低质量就业都容易成为生育孩子的机会成本和阻碍因素。
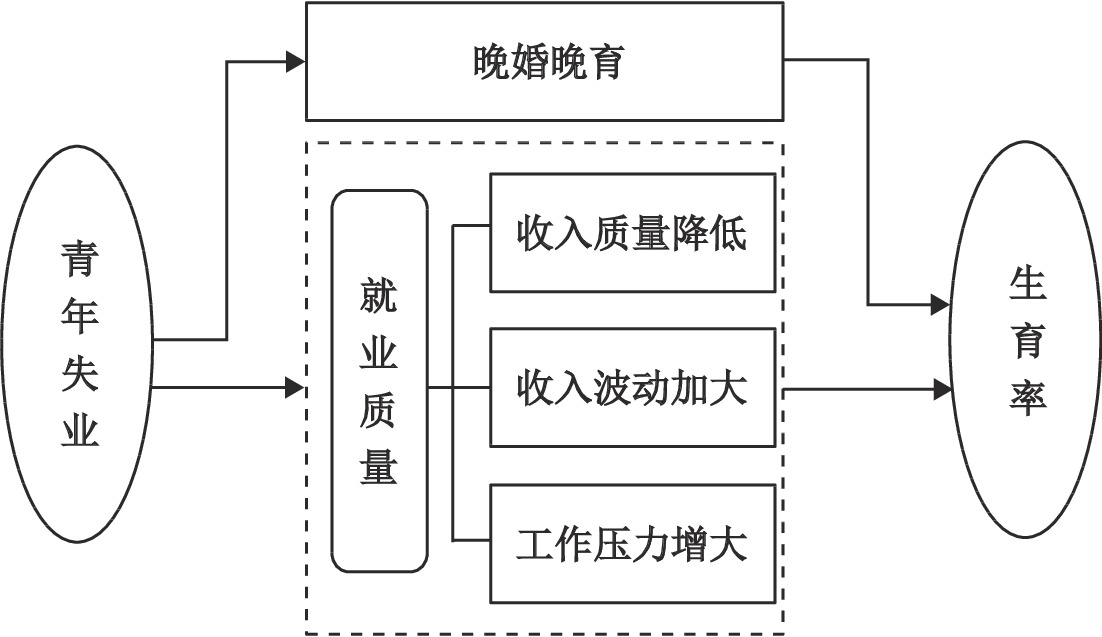
(三) 研究假说的提出青年失业率可能通过多个渠道影响生育率(见图2)。首先是晚婚晚育效应。失业状态让青年群体短时间内无法成为脱离原生家庭的独立经济个体,无形中推迟了婚恋和生育的时间安排。这一效应也取决于失业时间的长短,青年失业往往是一种动态失业状态,一般表现为“慢就业”特征(靳卫东等,2022),在就业等待时间较短的情况下,其对生育率产生的影响可能是短期而有限的。相对而言,青年失业率更可能是通过降低劳动力市场就业质量间接影响青年群体的生育意愿,即青年失业率会向就业质量传导,造成收入匹配程度、收入稳定程度、工作压力等不同维度就业质量的总体下降,且这种影响具有长期可持续性。从婚姻市场来看,受到失业率冲击、收入质量下降的就业者婚姻价值降低,从而造成生育率下降(Autor等,2019)。从自身决策来看,失业率冲击会带来收入的不确定性,造成未来收入波动幅度和概率加大,这种不确定性预期也会降低婚姻和生育倾向(Chevalier和Marie,2017;徐巧玲,2019)。高失业率也降低了人力资本潜在价格,造成合同保障、福利待遇不完善等诸多问题,工作环境的压力增大也会降低适龄就业者的生育意愿(褚湜婧,2015)。高失业率下就业质量下降影响生育率的本质是让就业者生育机会成本更大,从事健康行为的可能性更小,从而对生育率产生了不利影响。基于以上文献梳理,提出如下两个研究假说:
|
| 图 2 青年失业率影响生育率的作用机制 |
假说1:青年失业率存在显著的生育抑制效应。
假说2:就业质量下降在青年失业率的生育抑制效应中发挥了中介效应。
三、研究设计 (一) 数据来源由于国内青年失业率的官方统计刚刚开始,本文以数据更为齐全的OECD国际面板数据为研究对象,实证检验各国青年失业率对生育率的影响,以更具有参考意义的国际经验为中国未来决策提供参考。本文的数据来源于OECD数据库和世界银行数据库,鉴于数据指标的可得性,最终整理的面板数据涵盖澳大利亚、奥地利、比利时、加拿大、智利、哥伦比亚、哥斯达黎加、捷克共和国、丹麦、爱沙尼亚、芬兰、法国、德国、希腊、匈牙利、冰岛、爱尔兰、以色列、日本、韩国、拉脱维亚、立陶宛、卢森堡、美国、墨西哥、荷兰、新西兰、挪威、波兰、葡萄牙、斯洛伐克共和国、斯洛文尼亚、西班牙、瑞典、瑞士、土耳其、意大利、英国总计38个OECD成员国家,时间则涵盖1960—2020年长达61年的历史长度。需要说明的是,本文涉及的数据变量指标较多,各指标的缺失程度不一,故而在使用不同面板数据时为非平衡面板,样本量会出现一定差异。
(二) 模型构建本文要通过实证回归验证青年失业率是否存在生育抑制效应。核心解释变量是各国青年失业率(OECD统计标准为15–24岁,与国内略有差异);被解释变量则是各国生育率,以统计更为齐全的总和生育率指标来衡量,该指标衡量的是按照当期生育水平育龄妇女一生能生育几个孩子。构建基准的面板回归方程表示如下:
| $ {ferte}_{it}=\alpha +\beta {unempr}_{it}+\lambda {\Theta }_{it}+{\mu }_{i}+{\mu }_{t}+{\varepsilon }_{it} $ | (1) |
其中,下标
在机制分析部分,我们采用了中介效应检验方法,在上述式(1)以外,加入就业质量的中介变量,同时进行了另外两个方程的回归:
| $ {quality}_{it}=\alpha +\beta {unempr}_{it}+\lambda {\Theta }_{it}+{\mu }_{i}+{\mu }_{t}+{\varepsilon }_{it} $ | (2) |
| $ {ferte}_{it}=\alpha +\beta {unempr}_{it}+\gamma {quality}_{it}+\lambda {\Theta }_{it}+{\mu }_{i}+{\mu }_{t}+{\varepsilon }_{it} $ | (3) |
其中,
在控制变量集中,我们选取了如下国家层面对生育率可能有影响的变量,包括经济增长率(gdpg)、居民消费价格指数(cpi)、人口增长率(popug)、城镇化率(urbr)、抚养比(depr)、对外开放程度(trade)、人均居民消费支出(perconep)、每万人申请专利技术数量(techq)、有工资男性占比(salrm)、有工资女性占比(salrf)。其中,城镇化率以城镇人口占总人口之比表示,抚养比以非劳动年龄人口(15岁以下及64 岁以上)占劳动年龄人口(15–64岁)之比表示,对外开放程度以进出口总额与国内生产总值(GDP)的比值表示。
考虑到下文影响机制分析部分中介效应检验的需要,本文也从OECD数据库收集了衡量晚婚晚育效应的女性平均生育年龄(meabr)和三个维度的就业质量指标作为中介变量。OECD详细制定了衡量和评估就业质量的框架,该框架考虑了三个客观和可测量的维度,三者综合刻画了就业质量高低,且为精确划分不同年龄群体提供了三类评估指标:(1)青年收入质量指标(earqlty)。收入质量指标是通过考虑整个劳动力的收入水平和分布形态来综合衡量的,前者是收入的算数平均值,衡量市场上青年群体相对收入高低;后者借鉴了Atkinson不平等厌恶指数,衡量不同参数选择下总体和算术平均值之间的相对楔形,即收入的总体差异程度。该指标为正向指标,指标越大,意味着青年收入质量越高。(2)青年收入波动指标(lmrkt)。该指标基于失业概率、预期失业持续时间以及政府发放失业救济金数额测算了预期失业收入损失占平均薪酬的百分比,以此衡量劳动力市场的不稳定程度,代表了就业者的不安全感。该指标越大,意味着收入的不稳定程度越高。(3)青年工作压力指标(qwenvir)。工作压力指标是OECD基于欧洲工作条件调查(EWCS)和国际社会调查计划(ISSP)统计指标测算得出的,一般是以工作压力事件的发生率来衡量。一旦工人面临的工作需求超过他们可支配的工作资源,即可界定为工作压力事件。该指标越大,意味着青年工作压力越大。
此外,考虑到控制内生性的需要,我们还收集了相应的工具变量,包括中年(25–54岁)和老年(55–64岁)失业率、收入质量、收入波动性、工作压力等指标。需要指出的是,OECD统计就业质量的年龄划分与统计失业率的年龄划分略有不同,分别以15–29岁、30–49岁、50–64岁来界定青年、中年和老年。按照阳义南和谢予昭(2014)、李成友等(2020)的研究,老年就业表现可能会对青年就业有溢出效应,从而满足相关性假设;同时,老年就业表现无法直接影响本文的被解释变量(生育率),只能通过影响青年就业间接影响生育率,从而满足工具变量的外生性假设。全部变量的描述统计如表1所示。
| 变量 | 单位 | 样本数 | 平均值 | 标准差 | 最小值 | 最大值 |
| ferte | 个 | 2 291 | 2.161 | 0.954 | 0.920 | 6.830 |
| unempr | % | 907 | 16.209 | 8.714 | 1.808 | 59.250 |
| earqlty | 原始值 | 272 | 12.565 | 5.249 | 3.211 | 31.875 |
| lmrkt | 原始值 | 311 | 9.782 | 6.922 | 1.004 | 44.179 |
| qwenvir | 原始值 | 91 | 34.661 | 9.484 | 18.214 | 59.468 |
| meabr | 岁 | 1 857 | 28.397 | 1.690 | 24.500 | 32.600 |
| gdpg | % | 1 986 | 3.254 | 3.454 | −14.839 | 25.176 |
| cpi | % | 2 036 | 10.902 | 50.595 | −4.478 | 1281.444 |
| popug | % | 2 307 | 0.817 | 0.858 | −2.574 | 6.017 |
| urbr | % | 2 257 | 71.175 | 13.489 | 28.204 | 98.079 |
| depr | % | 2 257 | 55.238 | 10.109 | 38.457 | 101.577 |
| trade | 原始值 | 1 859 | 0.534 | 0.332 | 0.056 | 1.821 |
| perconep | 美元/年 | 1 751 | 14580.070 | 8736.922 | 1447.251 | 44877.030 |
| techq | 个/万人 | 1 362 | 2.673 | 8.371 | 0.000 | 62.145 |
| salrm | % | 1 073 | 78.958 | 9.722 | 45.680 | 93.300 |
| salrf | % | 1 073 | 84.627 | 11.514 | 36.600 | 96.160 |
表2第(1)、(2)列为OLS回归,第(3)列为面板固定效应模型(FE)回归,回归结果均显示,一国的青年失业率对生育率有显著抑制效应。以第(3)列加入控制变量后的面板固定效应回归结果为例,青年失业率(unempr)的系数估计值为–0.004,意味着青年失业率每提高1个百分点,则该国总和生育率降低0.004个单位,即一个育龄妇女终其一生平均生育子女的数量减少0.004个。这一影响不容忽视,我们以38个OECD样本国家1968—2012年这一历史阶段来看,总和生育率下降1.24个单位,青年失业率上升15.694个单位,按照0.004的边际影响来看,青年失业率上升大约能解释同一时期内总和生育率下降的5.06%(15.694×0.004/1.24≈5.06%)。虽然中国与OECD成员国在经济社会和人口结构上没有直接可比性,但反观国内生育政策净效应也能反映基准回归系数估计值的影响程度:按照我国2010年第六次人口普查和2020年第七次人口普查数据,从“双独二孩”到“单独二孩”到“全面二孩”再到“全面三孩”政策的持续宽松政策刺激下,总和生育率在十年间仅从1.18上升到1.30,平均每年涨幅仅为0.012。由此可见,青年失业率的生育抑制效应从经济社会意义上是一个值得警惕的重要现实问题。
| (1) | (2) | (3) | (4) | |
| OLS | OLS | FE | IV回归 | |
| unempr | −0.011***(−7.99) | −0.004***(−3.50) | −0.004***(−4.88) | −0.005***(−4.34) |
| gdpg | 0.001(0.47) | −0.007***(−4.12) | −0.007***(−3.91) | |
| cpi | 0.017***(4.50) | −0.001(−0.63) | −0.002(−0.90) | |
| popug | 0.243***(17.11) | 0.029***(2.95) | 0.027**(2.13) | |
| urbr | 0.004***(4.38) | −0.018***(−7.79) | −0.020***(−9.92) | |
| depr | 0.032***(16.96) | 0.011***(7.95) | 0.012***(7.69) | |
| trade | −0.028(−0.99) | 0.241***(7.80) | 0.240***(7.08) | |
| perconep | −0.000***(−8.68) | −0.000(−0.20) | −0.000(−0.74) | |
| techq | 0.000(0.08) | −0.003***(−2.98) | −0.002**(−2.31) | |
| salrm | 0.003(0.84) | 0.002(0.77) | 0.003(0.98) | |
| salrf | 0.002(0.96) | 0.001(0.37) | 0.003(1.01) | |
| Constant | 1.887***(71.74) | −0.601***(−4.57) | 2.229***(9.64) | 2.570***(10.49) |
| 国家固定效应 | No | No | Yes | Yes |
| 年份固定效应 | No | No | Yes | Yes |
| Observations | 875 | 730 | 730 | 689 |
| R-squared | 0.068 | 0.653 | 0.494 | 0.963 |
| 注:(1)括弧内为t统计值或z统计值;(2)***、**、*分别表示在1%、5%、10%的水平上显著;(3)个别系数估计值为零是小数点后保留四位四舍五入的结果。下同。 | ||||
考虑到核心解释变量青年失业率(unempr)的内生性问题,我们同时使用了工具变量法(IV)回归,以本国老年失业率为工具变量。Cragg-Donald Wald F统计值为945.138,超出了Stock-Yogo临界值,通过了弱工具变量检验。同时,Kleibergen-Paap rk LM统计值为157.321,通过了不可识别检验。在控制了内生性后,第(4)列回归结果显示,青年失业率依然对生育率有显著的抑制效应,且数值在经济学意义上更为显著,达到了−0.005。因此,研究假说1得到证实。
(二) 长期影响检验考虑到青年失业率本身存在波动性,其对生育率的影响可能是短期波动关系的结果,而非长期影响。为了验证青年失业率对生育率的影响是否具有长期可持续性,我们参考马光荣等(2016)的做法,对被解释变量生育率和核心解释变量青年失业率分别进行了N年期移动平均以平滑短期波动成分,然后进行面板固定效应模型回归。表3面板固定效应回归结果显示,在3年期、4年期、5年期、8年期移动平均处理后,青年失业率(unempr)的回归系数依然显著为负,直到10年期移动平均处理后才逐渐失去显著性,表明青年失业率对生育率具有长期持续性影响,而非仅仅是短期效应。相对于短期效应,青年失业率长期影响的系数估计值在数值上偏小一些,表明短期视野内由于波动的存在,青年失业率的生育抑制效应在一定程度上被高估和放大。同时,随着移动平均的窗口期延长,生育抑制效应逐渐趋于微弱,表明其影响虽然具有持续性,但影响力度随着时间的拉长而逐渐衰减。
| (1) | (2) | (3) | (4) | (5) | |
| 3年期 | 4年期 | 5年期 | 8年期 | 10年期 | |
| unempr | −0.003***(−4.12) | −0.003***(−4.06) | −0.003***(−3.93) | −0.002**(−2.09) | −0.001(−1.07) |
| 控制变量 | YES | YES | YES | YES | YES |
| 国家固定效应 | YES | YES | YES | YES | YES |
| 年份固定效应 | YES | YES | YES | YES | YES |
| Observations | 666 | 634 | 602 | 504 | 440 |
| R-squared | 0.507 | 0.509 | 0.515 | 0.530 | 0.552 |
| 注:篇幅所限,控制变量回归结果不再一一呈现,留存备索,下同。 | |||||
按照新古典经济学理论,就业周期和经济周期是一致的,但这与现实并不相符。来自各国的事实显示,就业存在“回滞”现象,即就业波动易跌难升,在经济繁荣期和萧条期的变化是非对称的。之所以出现这种反差,是因为新古典理论中劳动可变要素假定太过理想化,现实中由于存在长期合同关系和严格的劳动力市场管制,劳动成本向下调整的成本偏大,存在工资向下粘性和扩招容易裁员难(都阳,2013;Abbritti和Fahr,2013),造成雇主对扩大雇佣规模的招聘决策更加谨慎(钟宁桦等,2021),从而就业调整无论是对经济复苏还是政策刺激的反应都较为滞后,表现出弱周期性特征(黄赜琳和朱保华,2015)。基于此,我们思考一个问题:是否青年失业率对生育率的影响也存在非对称性特征,存在易跌难升的不利局面?为了检验这一问题,我们参考刘金东等(2019)的做法,构建如下面板固定效应的非对称反应模型:
| $ {ferte}_{it}=\alpha +\beta {dum}_{it}\times {unempr}_{it}+\gamma (1-{dum}_{it})\times {unempr}_{it}+\lambda {\Theta }_{it}+{\mu }_{i}+{\mu }_{t}+{\varepsilon }_{it} $ | (4) |
其中,
| (1) | (2) | (3) | (4) | (5) | |
| 当期 | 3年期移动均值 | 4年期移动均值 | 5年期移动均值 | 8年期移动均值 | |
| dum
|
−0.004***(−4.75) | −0.003***(−3.99) | −0.003***(−4.01) | −0.003***(−3.89) | −0.002**(−2.06) |
| (1-dum)
|
−0.004***(−4.84) | −0.004***(−4.36) | −0.003***(−4.15) | −0.003***(−3.89) | −0.002**(−2.28) |
| 控制变量 | YES | YES | YES | YES | YES |
| 国家固定效应 | YES | YES | YES | YES | YES |
| 年份固定效应 | YES | YES | YES | YES | YES |
| Observations | 730 | 666 | 634 | 602 | 504 |
| R-squared | 0.495 | 0.508 | 0.510 | 0.516 | 0.532 |
老龄化程度越高的国家,其“少子化”倾向越强,故而青年失业率的生育抑制效应可能也越强。我们首先针对老龄化程度进行异质性分析,即采用OECD数据库提供的65岁以上老年人口占总人口数的比值来测度老龄化程度,并根据中位数将总样本划分为低老龄化组和高老龄化组两个子样本进行回归分析。考虑到稳健性,我们也在基准回归方程(1)的基础上加入老龄化程度(paging)及其与青年失业率的交互项(ue_pag)到解释变量中,进行异质性检验。
表5第(1)、(2)列的面板固定效应回归结果显示,在高老龄化组的样本中,青年失业率的系数估计值为−0.005且在1%的水平上显著为负,而在低老龄化组的样本中青年失业率系数估计值不显著。第(3)列报告了加入交互项的全样本回归结果,交互项系数估计值为−0.025,在10%的水平上显著为负。两种异质性分析结果均表明,青年失业率对生育意愿的影响因老龄化程度不同而异,老龄化程度越高的国家,则青年失业率影响生育率的抑制作用越明显。对中国而言,虽然老龄化程度比欧美发达国家低,但老龄化趋势却越来越明显,故而青年失业率的生育抑制效应也将会越来越显著,应当引起政策层面的足够重视。
| (1) | (2) | (3) | |
| 低老龄化组 | 高老龄化组 | 交互项回归 | |
| unempr | −0.003 | −0.005*** | −0.001 |
| (−1.58) | (−6.07) | (−0.39) | |
| paging | −4.756*** | ||
| (−8.09) | |||
| ue_pag | −0.025* | ||
| (−1.69) | |||
| 控制变量 | YES | YES | YES |
| 国家固定效应 | YES | YES | YES |
| 年份固定效应 | YES | YES | YES |
| Observations | 154 | 576 | 730 |
| R−squared | 0.783 | 0.553 | 0.545 |
此外,失业持续时间代表了失业率对个体的影响程度。青年失业很多是结构性和摩擦性失业,“慢就业”“缓就业”特征明显,如果等待就业时间较短,则青年失业率的生育抑制效应可能偏低一些。反之,如果失业持续时间较长,则对青年生育意愿的影响将更为凸显。基于此,我们针对失业持续时间进行必要的异质性分析。首先,按照国际标准,将OECD数据库中失业持续时间少于6个月的样本划分为短期失业样本组,其他则归入长期失业样本组,进行分子样本回归。同时,稳健性起见,将失业持续时间的对数(lavgu)及其与青年失业率的交互项(ue_lavgu)作为解释变量加入基准回归方程(1)进行异质性检验。
表6的第(1)、(2)列显示了划分子样本回归的实证结果,可以发现:短期失业样本中青年失业率的系数估计值为0.017,在1%的水平上显著为正,而在长期失业样本组的样本中青年失业率的系数估计值为−0.004,在1%的水平上显著为负。第(3)列加入交互项的检验结果显示,交互项估计系数为−0.011,在1%的水平上显著为负,与子样本回归结果一致。以上结果表明,青年失业率对生育率的影响因失业持续时间长短不同而异,在长期失业的样本中,青年失业率对生育率有显著抑制效应,而且失业等待时间越长,抑制效应越强。为什么当失业等待时间较短时青年失业率反而会促进生育呢?这是一个有意思的问题。已有文献探及了失业影响生育行为的性别差异,认为男性失业必然会降低婚配价值,从而降低已婚率和生育率,但女性却不同,一旦陷入失业状态反而容易作出生育决策(Maclean等,2016;Choi等,2020)。本文推测,当失业等待时间较长时,失业成本更为高昂,此时对男性女性的影响相对一致,均不会轻易作出生育决策;而当失业等待时间偏短时,性别间的影响差异开始显现,女性可能会考虑及时生育孩子。从全社会来看,男性参与工作能够提高生育率,女性参与工作则会降低生育率,这既是性别规范使然,也是“母职惩罚”所致(Albanesi和Kim,2021)。与其因为生育而受到就业惩罚,不如趁着失业而主动进行生育安排,故而造成当失业等待时间较短时青年失业率反而促进生育的反差结果。Hofmann和Hohmeyer(2016)针对德国40年追踪数据的微观实证分析也佐证了我们的观点,其研究发现,当因为毕业季遭遇经济萧条时,男性生育率不受影响,女性生育率则受到显著的正向激励,但该正向激励仅仅发生在毕业后一年之内,随着时间推移而迅速消失。
| (1) | (2) | (3) | |
| 短期失业组 | 长期失业组 | 交互项回归 | |
| unempr | 0.017*** | −0.004*** | 0.027*** |
| (6.03) | (−4.99) | (2.92) | |
| lavgu | 0.011 | ||
| (0.20) | |||
| ue_lavgu | −0.011*** | ||
| (−3.52) | |||
| 控制变量 | YES | YES | YES |
| 国家固定效应 | YES | YES | YES |
| 年份固定效应 | YES | YES | YES |
| Observations | 68 | 662 | 210 |
| R-squared | 0.985 | 0.487 | 0.666 |
正如本文第二部分所述,青年失业率可能通过收入质量下降、收入波动加大、工作压力增大三个就业质量渠道影响生育率,三个就业质量渠道主要通过影响个体生育意愿进而影响生育率结果。当然,我们也不排除青年失业率造成晚婚晚育而作用于生育率的客观影响。这一部分依次求证四个渠道中哪个是青年失业率生育抑制效应的主要作用机制。
(一) 晚婚晚育的渠道检验首先,在检验三个就业质量渠道之前,先行排除生育率通过晚婚晚育效应产生影响的可能性。我们以各国女性平均生育年龄(meabr)作为中介代理变量,检验了青年失业率对其是否存在显著影响。考虑到女性平均生育年龄已经部分超出了青年时期(15–24岁),均值达到28.397,故而此处额外加入中年失业率(unempr_m)作为控制变量。表7第(1)、(2)列回归结果显示,无论是面板固定效应模型(FE)回归还是工具变量法回归(IV),青年失业率均未对女性平均生育年龄产生显著影响,证明青年失业率并没有通过促使个体晚婚晚育进而影响生育率。
| (1) | (2) | (3) | (4) | |
| FE | IV | FE | IV | |
| 被解释变量 | meabr | earqlty | ||
| unempr | −0.004 | 0.037 | 0.013 | 0.001 |
| (−0.63) | (0.05) | (0.90) | (0.05) | |
| unempr_m | −0.004 | −0.085 | ||
| (−0.34) | (−0.06) | |||
| 控制变量 | Yes | Yes | Yes | Yes |
| 国家固定效应 | Yes | Yes | Yes | Yes |
| 年份固定效应 | Yes | Yes | Yes | Yes |
| Observations | 652 | 647 | 248 | 235 |
| R−squared | 0.877 | 0.964 | 0.457 | 0.989 |
| 注:IV回归均以老年失业率为工具变量,各项检验均通过。 | ||||
接下来,我们进一步检验青年失业率是否会显著降低个体就业质量,从而让个体在相对收入水平下降、收入分配差距拉大的情况下降低生育意愿。前文已经回归检验了青年失业率对生育率的显著影响,接下来我们要进行方程(2)的回归以检验青年失业率对青年收入质量是否产生显著影响。我们以青年收入质量指标(earqlty)为中介变量,表7第(3)、(4)列回归结果和晚婚晚育的渠道检验一样,此处中介效应检验的第二步回归同样没有得到满足,证明青年失业率也没有显著降低青年收入质量,故而这一中介渠道也不能得到实证支持。
(三) 收入波动加大的渠道检验我们以青年收入波动指标(lmrkt)为中介变量,表8第(1)、(2)列首先检验青年失业率(unempr)对青年收入波动的影响,显示系数估计值均显著为负。需要说明的是,工具变量法(IV)回归的过度识别检验并没有通过,即以老年失业率作为工具变量的外生性(排他性)假设没有通过。参考Conley等(2012),放宽外生性约束,允许工具变量对被解释变量存在一定的影响,其参数具有某个取值范围或先验分布,然后根据参数的先验信息构造出回归系数的置信区间,以检验在工具变量非完全外生时估计结果的稳健性。基于置信区间集合法(UCI)估计得到的青年失业率(unempr)系数估计95%置信区间为[0.608,0.930],均显著区别于零,故而可以认定青年失业率能够显著增大青年收入波动。进一步,对方程(3)进行回归,同时使用面板固定效应回归和工具变量法回归,其中工具变量法回归将青年失业率(unempr)和青年收入波动指标(lmrkt)均看作内生变量,以老年失业率和老年员工收入波动指标为工具变量,均通过不可识别检验、过度识别检验和弱工具变量检验。表8第(3)、(4)列显示,无论是面板固定效应(FE)还是工具变量法(IV)回归,按照中介效应检验程序进行第三步加入中介变量(lmrkt)的全方程(3)回归时,中介变量系数估计值均不显著,而青年失业率(unempr)的系数仍然显著,且系数大小未受到明显影响。这表明,虽然青年失业率会显著提高青年收入波动程度(降低青年收入稳定性),青年收入波动却并没有进一步传导至生育率,故而该作用渠道没有发挥作用。
| (1) | (2) | (3) | (4) | |
| FE | IV | FE | IV | |
| 被解释变量 | lmrkt | ferte | ||
| unempr | 0.592*** | 0.769*** | −0.005*** | −0.007* |
| (12.93) | (9.71) | (−3.11) | (−1.78) | |
| lmrkt | 0.000 | 0.002 | ||
| (0.02) | (0.41) | |||
| 控制变量 | Yes | Yes | Yes | Yes |
| 国家固定效应 | Yes | Yes | Yes | Yes |
| 年份固定效应 | Yes | Yes | Yes | Yes |
| Observations | 286 | 275 | 286 | 272 |
| R−squared | 0.652 | 0.915 | 0.477 | 0.964 |
我们以青年工作压力指标(qwenvir)为中介变量,同时进行面板固定效应回归和工具变量法回归,以老年失业率和老年员工工作压力指标为相应的工具变量,由于弱工具变量检验未能通过,故而额外加入了低技能员工工作压力指标作为工具变量。表9第(1)、(2)列显示,青年失业率显著加大了工作压力。表9第(3)、(4)列按照中介效应检验程序进行第三步加入中介变量(lmrkt)的全方程(3)回归,由于内生性偏误,造成面板固定效应回归结果与工具变量法回归结果有差异。我们以控制内生性的工具变量法(IV)回归结果为准:中介变量系数估计值显著为负(–0.006),与此同时,青年失业率(unempr)的系数为0.002且不再显著。这表明,青年失业率会显著加大青年就业者的工作压力,而工作压力会显著降低生育率,从而发挥了青年失业率→青年工作压力→生育意愿的传导机制,且青年工作压力在其中发挥了100%的完全中介效应。换言之,青年失业率并不存在对生育率的直接影响,完全是通过加大青年工作压力间接降低生育率。总体来看,在就业质量三个维度的细分指标上,虽然收入质量和收入波动没有充当青年失业率影响生育率的中介渠道,但工作压力发挥了完全中介效应,是青年失业率影响生育率的主要传导路径,从而验证了假说2。这一结论与Liepmann(2018)、Vignoli等(2020)的结论类似,前者基于东西德合并事件的研究发现,失业与否本身没有直接影响生育率,主要是通过影响个人预期进而影响生育决策;后者基于欧洲两轮社会调查数据的研究认为,工作压力及其带来的主观幸福感降低是抑制生育意愿的重要原因,越是已育的高龄者,受到这种影响的程度越高,这也表明青年失业率通过影响就业质量有可能给个体生育意愿带来长期的负面影响。
| (1) | (2) | (3) | (4) | |
| FE | IV | FE | IV | |
| 被解释变量 | qwenvir | ferte | ||
| unempr | 0.420* | 0.565** | −0.000 | 0.002 |
| (1.82) | (2.57) | (−0.01) | (0.88) | |
| qwenvir | −0.001 | −0.006** | ||
| (−0.59) | (−2.35) | |||
| 控制变量 | Yes | Yes | Yes | Yes |
| 国家固定效应 | Yes | Yes | Yes | Yes |
| 年份固定效应 | Yes | Yes | Yes | Yes |
| Observations | 85 | 81 | 85 | 85 |
| R-squared | 0.433 | 0.786 | 0.628 | 0.972 |
由于青年工作压力指标是OECD基于欧洲工作条件调查(EWCS)计算得来,EWCS每隔5年统计一次,目前OECD统计数据库只有2005、2010、2015三个年度的统计数据,造成表9中有效观测值太少,使得回归结果的可信度受到影响。基于稳健性考量,我们在此处作两部分补充论证:首先,根据Acemoglu等(2003)的渠道识别检验方法,由于就业质量共计三个维度,前两个维度均没有承担传导渠道的角色,故而反推第三个维度就业压力是青年失业率影响生育率的主要渠道。与此同时,我们也另辟蹊径,利用统计数据更为齐全的2005年工作压力指标按照均值为分界线将所有样本国家划分为工作压力偏低组国家和工作压力偏高组国家进行分子样本回归,结果如表10所示。表10显示,工作压力偏低组国家青年失业率对生育率的抑制效应不显著,而工作压力偏高组国家青年失业率对生育率的抑制效应显著,意味着工作压力指标发挥调节效应的幅度之大,可以使青年失业率对生育率的影响从无到有,从而表明工作压力确实是青年失业率产生生育抑制效应的关键因素。上文虽然论证了青年失业率没有显著影响平均生育年龄,但平均生育年龄仍可能对生育率产生直接影响,故而在表10的稳健性检验中也将女性平均生育年龄(meabr)加入控制变量集合,考察对比是否加入女性平均生育年龄对结果的影响,结果显示,无论加入该控制变量与否,子样本回归结论均没有发生变化,结论稳健。
这一结论对中国当前的青年就业现状具有启示意义。根据中山大学社会科学调查中心发布的《中国劳动力动态调查:2021年报告》统计显示,国内就业者的加班时长有显著上升,然而加班工资增长的幅度并没有相应跟上。2019年,从互联网行业开始,全国兴起了“996工作制”的大讨论,表明随着人民生活水平的提高,劳动者的关注点也开始从收入结果向获得收入的过程转移,这也符合高质量发展阶段马斯洛需求层次理论的认知规律。在收入一定的情况下,获得收入的过程更加符合“体面劳动”,更能满足尊严感,能够给劳动者带来更高的效用水平,对生育也会有直接影响:随着工作压力的加大,年轻的婚龄人群存在不良的健康行为,在重压之下很难创造合适的生育子女的身心条件,生育意愿也随之降低。由此可见,为青年劳动者创造更加宽松的工作环境,不仅关乎青年群体劳动者权益保护,还关乎生育意愿和劳动力人口长期可持续性问题,对中国劳动力市场发展有着更加深远的影响。
| (1) | (2) | (3) | (4) | |
| FE | FE | FE | FE | |
| 分组 | 工作压力偏低组 | 工作压力偏高组 | ||
| unempr | −0.001 | −0.001 | −0.009*** | −0.007*** |
| (−1.20) | (−0.80) | (−5.55) | (−4.37) | |
| 控制变量 | Yes | Yes | Yes | Yes |
| 国家固定效应 | Yes | Yes | Yes | Yes |
| 年份固定效应 | Yes | Yes | Yes | Yes |
| Observations | 254 | 249 | 401 | 368 |
| R-squared | 0.691 | 0.693 | 0.644 | 0.628 |
青年失业率高企在全球范围内备受关注,也对就业者长期收入状态、财产积累等产生持久性影响。在青年失业问题突显的背景下,无论是在世界各国还是在我国均出现了生育率逐年下降的趋势。青年失业率上升和生育率下降同时发生,这是相同因素作用下的巧合现象还是二者之间存在某种因果关联?针对这一现实问题,本文收集1960—2020年38个OECD国家的长期历史面板数据进行了系统性实证分析,发现青年失业率会显著抑制生育率,且生育抑制效应存在长期可持续性特征。青年失业的生育抑制效应是可逆的,未来控制青年失业率依然能够让生育率恢复到原有状态。同时,青年失业率的生育抑制效应存在不同老龄化程度、不同失业持续时间的差异化表现,老龄化程度越高、失业持续时间越长的国家,其生育抑制效应越显著。进一步的机制分析发现,在青年失业率高企的背景下,工作压力加大发挥了完全中介效应,收入质量下降、收入波动加大以及晚婚晚育效应均没有得到实证支持。
本研究对未来政策选择具有多重启示:其一,要协同推进青年更加充分和更高质量就业。就业数量充分程度和就业质量高低之间存在传导效应,特别是在经济增速放缓的情况下,青年失业率更容易向就业质量传导,而给就业者收入状态带来持久的负面影响。因此,要持续压实“六稳”“六保”政策责任,特别是“保岗位”“稳岗位”,只有保证就业者的收入质量不明显下降,保证收入稳定性和工作压力不明显恶化,才能从根本上稳住就业的基本盘,为进一步改善消费疲软、生育低迷等一系列经济社会问题创造空间。其二,提高生育意愿的政策取向不能聚焦于短期视野,还要具有长期性和前瞻性。根据本文的研究结论,如果仅仅关注当前适龄家庭的生育意愿,则容易陷入“头痛医头脚痛医脚”的困境,因而还需要体现前瞻性,关注就业待业的青年群体。青年失业问题存在长期持续的“疤痕效应”,对个体婚育意愿有滞后影响,一旦不能及时扶正纠偏,其生育抑制效应将成为难以克服的长期痼疾。其三,要特别关注青年就业者的非经济性待遇问题,持续减轻工作压力。高失业率下青年群体往往会调低预期、接受更加低薪的工作岗位,时间精力投入和个体工资报酬之间的匹配程度被拉低,从而增大了工作压力。关于“996”工作制的大讨论也体现了青年群体工作压力之大,其本质是我们日益增长的美好生活需要和不平衡不充分的发展之间存在矛盾。未来从政策上不仅要保障收入水平,还要保障工作环境,引入工会和社会监督,有效维护劳动者特别是青年女性劳动者的合法权益不受损害。
| [1] | 褚湜婧. “单独二孩”政策与青年生育[J].中国青年研究,2015(2). |
| [2] | 戴觅, 徐建炜, 施炳展. 人民币汇率冲击与制造业就业——来自企业数据的经验证据[J].管理世界,2013(11). |
| [3] | 都阳. 制造业企业对劳动力市场变化的反应: 基于微观数据的观察[J].经济研究,2013(1). |
| [4] | 何明帅, 于淼. 家庭人均收入、代际社会流动与生育意愿[J].劳动经济研究,2017(5). |
| [5] | 黄赜琳, 朱保华. 中国的实际经济周期与税收政策效应[J].经济研究,2015(3). |
| [6] | 靳卫东, 李淑玥, 何丽. “慢就业”的职业损失: 工资收入和工作职位[J].财经研究,2022(7). |
| [7] | 李成友, 刘安然, 袁洛琪, 等. 养老依赖、非农就业与中老年农户耕地租出——基于CHARLS三期面板数据分析[J].中国软科学,2020(7). |
| [8] | 李子联. 收入与生育: 中国生育率变动的解释[J].经济学动态,2016(5). |
| [9] | 刘金东, 薛一帆, 管星华. 财政信息公开为何陷入“低水平陷阱”?——基于地方标杆竞争视角的研究[J].公共行政评论,2019(5). |
| [10] | 马光荣, 郭庆旺, 刘畅. 财政转移支付结构与地区经济增长[J].中国社会科学,2016(9). |
| [11] | 温忠麟, 张雷, 侯杰泰, 等. 中介效应检验程序及其应用[J].心理学报,2004(5). |
| [12] | 徐巧玲. 收入不确定与生育意愿——基于阶层流动的调节效应[J].经济与管理研究,2019(5). |
| [13] | 阳义南, 谢予昭. 推迟退休年龄对青年失业率的影响——来自OECD国家的经验证据[J].中国人口科学,2014(4). |
| [14] | 钟宁桦, 解咪, 钱一蕾, 等. 全球经济危机后中国的信贷配置与稳就业成效[J].经济研究,2021(9). |
| [15] | Abbritti M, Fahr S. Downward wage rigidity and business cycle asymmetries[J].Journal of Monetary Economics,2013,60(7):871–886. |
| [16] | Acemoglu D, Johnson S, Robinson J, et al. Institutional causes, macroeconomic symptoms: Volatility, crises and growth[J].Journal of Monetary Economics,2003,50(1):49–123. |
| [17] | Albanesi S, Kim J. Effects of the COVID-19 recession on the US labor market: Occupation, family, and gender[J].Journal of Economic Perspectives,2021,35(3):3–24. |
| [18] | Autor D, Dorn D, Hanson G. When work disappears: Manufacturing decline and the falling marriage market value of young men[J].American Economic Review:Insights,2019,1(2):161–178. |
| [19] | Becker G S. An economic analysis of fertility[A]. Roberts G B. Demographic and economic change in developed countries[C]. New York: Columbia University Press, 1960: 209–240. |
| [20] | Bongaarts J, Watkins S C. Social interactions and contemporary fertility transitions[J].Population and Development Review,1996,22(4):639–682. |
| [21] | Chevalier A, Marie O. Economic uncertainty, parental selection, and children’s educational outcomes[J].Journal of Political Economy,2017,125(2):393–430. |
| [22] | Choi E J, Choi J, Son H. The long-term effects of labor market entry in a recession: Evidence from the Asian financial crisis[J].Labour Economics,2020,67:101926. |
| [23] | Conley T G, Hansen C B, Rossi P E. Plausibly exogenous[J].The Review of Economics and Statistics,2012,94(1):260–272. |
| [24] | Ehrlich I, Lui F T, Francis T. Intergenerational trade, longevity, and economic growth[J].Journal of Political Economy,1991,99(5):1029–1059. |
| [25] | Galor O. From stagnation to growth: Unified growth theory[J]. Handbook of Economic Growth,2005,1:171–293. |
| [26] | Galor O, Weil D N. The gender gap, fertility, and growth[J]. The American Economic Review,1996,86(3):374–387. |
| [27] | Genda Y, Kondo A, Ohta S. Long-term effects of a recession at labor market entry in Japan and the United States[J].Journal of Human Resources,2010,45(1):157–196. |
| [28] | Hamaaki J, Hori M, Maeda S, et al. How does the first job matter for an individual's career life in Japan?[J].Journal of the Japanese and International Economies,2013,29:154–169. |
| [29] | Hofmann B, Hohmeyer K. The effect of the business cycle at college graduation on fertility[J].Economics of Education Review,2016,55:88–102. |
| [30] | Huckfeldt C. Understanding the scarring effect of recessions[J].American Economic Review,2022,112(4):1273–1310. |
| [31] | International Labour Organization (ILO). Global employment trends for youth 2020: Technology and the future of jobs[R]. Geneva: International Labour Organization, 2020: 160–161. |
| [32] | Kahn L B. The long-term labor market consequences of graduating from college in a bad economy[J].Labour Economics,2010,17(2):303–316. |
| [33] | Kohler H P, Kohler I. Fertility decline in Russia in the early and mid 1990s: The role of economic uncertainty and labour market crises[J].European Journal of Population,2002,18(3):233–262. |
| [34] | Liepmann H. The impact of a negative labor demand shock on fertility - evidence from the fall of the Berlin Wall[J].Labour Economics,2018,54:210–224. |
| [35] | Maclean J C, Covington R, Kessler A S. Labor market conditions at school-leaving: Long-run effects on marriage and fertility[J].Contemporary Economic Policy,2016,34(1):63–88. |
| [36] | Oreopoulos P, von Wachter T, Heisz A. The short- and long-term career effects of graduating in a recession[J].American Economic Journal:Applied Economics,2012,4(1):1–29. |
| [37] | Oyer P. Initial labor market conditions and long-term outcomes for economists[J].Journal of Economic Perspectives,2006,20(3):143–160. |
| [38] | Prettner K, Strulik H. Gender equity and the escape from poverty[J].Oxford Economic Papers,2017,69(1):55–74. |
| [39] | Vignoli D, Mencarini L, Alderotti G. Is the effect of job uncertainty on fertility intentions channeled by subjective well-being?[J].Advances in Life Course Research,2020,46:100343. |
| [40] | Wood J, Neels K. First a job, then a child? Subgroup variation in women’s employment-fertility link[J].Advances in Life Course Research,2017,33:38–52. |
2.Center of Economic Research, Shandong University of Finance and Economics, Shandong Jinan 250014, China

