一、引言和文献综述

改革开放后，中国的扶贫工作取得的成就令人称羡，但不必讳言的是，社会中仍有一部分低收入群体出现了贫困代际传递现象。如果贫困代际传递持续存在，这部分群体就会难以共享发展成果并影响社会公平。中国政府高度重视贫困人口的代际传递问题，习近平总书记指出：“阻止贫困现象代际传递，是功在当代、利在千秋的大事。”传统的贫困代际传递研究大多是从静态视角展开，忽视了个体未来的福利特征。随着反贫困理论的发展，贫困治理尤其是贫困脆弱性问题成为公共政策制定者关注的重点。因此，从微观和宏观相结合的视角解读贫困脆弱性代际传递，把握其与财政政策之间的关系，不仅有利于揭示贫困的发生和传递机制，而且有利于制定预防贫困及阻断长期贫困的公共财政政策，从而保证精准扶贫、精准脱贫工作的顺利进行。

代际间贫困传递的经济学文献通常侧重于对父母及其后代的代际收入弹性、收入流动性估计（Becker和Tomes，1979；Solon，1992、2004）。Mayer和Lopoo（2008）利用PSID数据测算了美国代际收入弹性（Intergenerational Income Elasticity，IGE），并比较了不同地区之间代际收入的流动差异。国内学者基于微观数据的分析表明中国存在较明显的收入代际传递现象（王海港，2005；方鸣和应瑞瑶，2010；张立冬，2013；卢盛峰和潘星宇，2016；谷晓然和刘维娜，2016）。贫困脆弱性是一种事前测度，具有前瞻性特点，它克服了传统贫困的静态性、事后性的不足。贫困脆弱性的测度方法包括期望贫困的脆弱性（VEP）、期望效用的脆弱性（VEU）和风险暴露的脆弱性（VER），学界普遍使用Chaudhuri等（2002）提出的VEP方法（Dutta等，2011）。基于期望贫困的脆弱性（VEP）方法，邹薇和方迎风（2011）利用中国健康与营养调查（CHNS）数据测算了中国农户的贫困脆弱性，聂荣和张志国（2014）研究了1993–2011年中国农村家庭贫困脆弱性的动态特征。

现存文献强调了财政教育政策在影响贫困代际传递中的重要作用。比如，Alkire和Santos（2014）认为，教育不平等会导致一个国家或地区进入持续性贫困状态且易陷入贫困代际传递，实施均衡的教育政策可以减轻教育不平等程度进而影响代际收入流动性。Ihori等（2017）研究发现父代对子代的人力资本投资，并不能自动实现最优水平，需要财政教育政策的干预。国内学者认为财政教育政策在提高代际收入流动性方面有着不可替代的作用（周波和苏佳，2012；李力行和周广肃，2015；徐俊武和易祥瑞，2014；杨娟等，2015；郭熙保和周强，2017；宋旭光和何宗樾，2018；潘星宇和卢盛峰，2018）。影响贫困脆弱性的因素则包括地区发展不均衡（Gloede等，2015）、人力资本较低（Imai等，2013）、公共转移支付瞄准偏误（Celidoni，2013；樊丽明和解垩，2014）等。

从已有文献可以看出，国内外学者对财政政策与贫困代际传递、财政政策与贫困脆弱性进行了分析，但缺乏阻断贫困脆弱性代际传递的财政政策研究。基于此，本文立足于父子两代的未来贫困，对财政教育政策是否能阻断长期贫困进行了分析，以期为扶贫攻坚提供新的研究视角。本文的主要贡献在于：（1）建立了加入财政教育政策变量后的两期世代交叠模型，发现财政教育支出增加对子代未来收入存在积极影响，丰富了世代交叠理论。（2）从前瞻性视角出发，考查了贫困脆弱性代际传递的分布特征、动态特征。（3）结合微观层面父子配对数据及宏观层面省级财政教育支出数据，实证评估了财政教育政策阻断贫困脆弱性代际传递的效应，探讨财政教育政策是否能缓解长期贫困。

本文其他内容如下：第二部分为理论分析与实证设计，第三部分为数据来源和描述性分析，第四部分利用Beta回归分析财政教育政策对贫困脆弱性的影响，第五部分为门槛效应和分位数回归的稳健性检验，最后为结论和政策性建议。

二、理论分析与实证设计 (一) 理论分析

首先，本文构建一个父子两期模型，父代为t-1期，子代为t期。家庭决策目标是父代收入分配于消费、储蓄以及对子代的教育投入，以期实现效用最大化。其中，父代的收入表述如下：

$Y_{i, t - 1}{{ = }}C_{i, t - 1} + E_{i, t - 1}{{ + }}S_{i, t - 1}$

(1)

其中， $C_{i, t - 1}$ 为父代的消费， $E_{i, t - 1}$ 为父代对子代的教育投入， $S_{i, t - 1}$ 为父代的储蓄。

子代的人力资本为：

$h_{i, t} = \theta \ln (E_{i, t - 1} + G_{i, t - 1}) + e_{it}$

(2)

其中， $\theta > 0$ ， $E_{i, t - 1}$ 为父代对子代的教育投入， $G_{i, t - 1}$ 为财政教育政策支出， $e_{it}$ 表示子代的禀赋。

子代的收入为：

$\ln Y_{i, t} = \mu + ph_{i, t}$

(3)

其中， $p$ 为教育回报率， $\mu $ 为常数。

假设父代的效用函数为Cobb-Douglas形式：

$U_i = (1 - \alpha )\ln C_{i, t - 1 }+ \alpha \ln \left[ {Y_{i, t} + (1 + r)S_{i, t - 1}} \right]$

(4)

其中， ${{0<}}\alpha {{<1}}$ ， $\alpha $ 表示父代在当期投资与未来期收入之间的选择偏好系数。联立式（1）至式（4），效用方程为：

$U_i = (1 - \alpha )\ln (Y_{i, t - 1} - E_{i, t - 1} - S_{i, t - 1}) + \alpha \theta p\ln (E_{i, t - 1 }+ G_{i, t - 1}) + \alpha \ln (1 + r)S_{i, t - 1} + \alpha \left( {\mu + pe_{it}} \right)$

(5)

父代对子代投资的最大化效用条件为：

$\frac{{\partial U_i}}{{\partial E_{i, t - 1}}} = \alpha \theta p/(E_{i, t - 1} + G_{i, t - 1}) - (1 - \alpha )/(Y_{i, t - 1 }- E_{i, t - 1} - S_{i, t - 1})$

(6)

于是可得父代对子代投资的教育投入的最优水平为：

$E_{i, t - 1} = \left[ {\frac{{\alpha p\theta }}{{1 - \alpha (1 - \theta )}}} \right](Y_{i, t - 1} - S_{i, t - 1}) - \left[ {\frac{{1 - \alpha }}{{1 - \alpha (1 - \theta )}}} \right]G_{i, t - 1}$

(7)

式（7）中，当教育的收益回报率 $p\theta $ 越高时，父代对子代的教育投入也越高；父代收入越高，其对子女的教育投入也越多。由于 ${{0<}}\alpha {{<1}}$ ，那么 $[1 - \alpha /1 - \alpha (1 - \theta )]G_{i, t - 1} > 0$ ，表明财政教育支出可以弥补低收入父代对子代教育投入的不足。为分析政府财政教育支出与后代收入的关系，将式（2）代入式（3）得到：

$\ln Y_{i, t }= \mu + p\left[ {\theta \ln (E_{i, t - 1} + G_{i, t - 1}) + e_{it}} \right]$

(8)

其中，

$\frac{{\partial Y_{i, t}}}{{\partial G_{i, t - 1}}} = \frac{{p\theta Y_{i, t}}}{{E_{i, t - 1} + G_{i, t - 1}}} > 0$

(9)

即财政教育支出投入的增加会促进子代未来收入的提高，从而阻断贫困的代际传递。

(二) 实证设计

1. 基于Chaudhuri等（2002）脆弱性估计方法

测量贫困脆弱性的三阶段最小二乘基本方程为：

$VU{L_{ht}} = \Pr ({Y_{h, t + 1}} \leqslant poor)$

(10)

其中， $VU{L_{ht}}$ 代表第h个家庭在t时期的脆弱性，指家庭未来期收入（ ${Y_{h, t + 1}}$ ）低于某个门槛值（即贫困线 $poor$ ）的概率。利用Chaudhuri等（2002）的估计步骤，第一步首先估计收入方程，即存在下式：

$ln{Y_{h, t}} = {\alpha _h}{X_{h, t}} + {e_h}$

(11)

其中， ${Y_{h, t}}$ 代表个体h在t时期的收入， ${X_{h, t}}$ 为个体或家庭特征变量，在本文中分别纳入个体年龄、年龄平方、教育、职业、婚姻、医疗保险等变量，对子代贫困脆弱值、父代贫困脆弱值分别进行计算。假设分布为对数正态分布，贫困脆弱性可以表示为：

$\hat VU{L_h} = \hat {\rm{Pr}}(ln{Y_h} \leqslant lnpoor) = \phi (\frac{{lnpoor - {X_h}\hat \alpha }}{{\sqrt {{X_h}\hat \beta } }})$

(12)

2.Beta回归模型

Beta回归模型是由Ferrari和Cribari-Neto （2004）提出的，Smithson和Verkuilen（2006）、Rocha和Simas（2011）又进一步扩展并发展了Beta回归模型。Beta回归模型是专门用于分析被解释变量为连续型变量且严格位于（0，1）的模型，可将混合分布的参数建模为回归参数函数。

令Beta分布为： $\mu = \alpha /\left( {\alpha + \beta } \right)$ ， $\phi = \left( {\alpha + \beta } \right)$ 。此时密度函数为：

$f(y;\mu , \phi ) = \frac{{\Gamma (\phi )}}{{\Gamma (\mu \phi )\Gamma ((1 - \mu )\phi }}{y^{\mu , \phi - 1}}{(1 - y)^{(1 - \mu )\phi - 1}}, 0<y<1$

(13)

均值和方差分别为： $E(y) = \mu {\text{和}} \operatorname{var} (y) = V(\mu )/(1 + \phi )$ 。

Beta分布具有不同的概率分布形式，对拟合贫困脆弱值的各种可能分布形式有比较大的灵活性。在Beta回归模型中，要求被解释变量在（0，1）内取值，子代的贫困脆弱值满足此条件，因此Beta回归模型适用于本文贫困脆弱值的统计建模。

与线性模型不同，Beta回归模型的系数仅表示自变量对因变量影响的方向及是否显著，但是并不能得到影响效应的大小。本文在实证分析中使用平均半弹性（ASE）来度量效应大小，ASE表示x变化1%时对y的影响。对不同条件均值函数的AIC进行计算，得到logit（−8345.29），probit（−8320.96），clog-log（−8352.37），loglog（−8316.19），根据AIC最小准则，选择clog-log形式的均值函数。

3. 实证策略

利用Beta回归模型对子代、父代的贫困脆弱值进行统计建模：

$g(y_s) = \beta _0 + \beta_ 1y_f + \gamma z_x + \mu_ x$

(14)

其中， $y_s$ 和 $y_f$ 分别表示根据子代、父代的收入计算得到的子代贫困脆弱值和父代贫困脆弱值， $\beta _1$ 为父代的贫困脆弱值对子代的贫困脆弱值的弹性系数。在本文的控制变量 $z_x$ 中引入子代工作状况、性别、婚姻状况、家庭劳动人数、城乡等因素。

为分析政府财政教育政策对贫困代际传递的影响，将式（14）进一步扩展为：

$g(y_s) = \beta_ 0 + \beta _1y_f + \beta _2\ln G + \gamma z_x + \mu _x$

(15)

其中G为财政教育支出。引入财政教育支出与父代收入的交互项，对式（15）进行再扩展：

$g(y_s) = \beta_ 0 + \beta_ 1y_f + \beta_ 2\ln G + \beta _3\ln Y_f \times \ln G + \gamma z_x + \mu _x$

(16)

其中 $\ln Y_f$ 为父代的收入对数值。

三、数据来源和描述性分析 (一) 数据来源

本文使用中国健康和营养调查数据（China Health and Nutrition Survey，CHNS）的9次调查数据（1991年、1993年、1997年、2000年、2004年、2006年、2009年、2011年、2015年），本文对父代和子代相关信息进行配对以期研究贫困脆弱性代际传递的分布特征及动态趋势。省级层面的财政教育支出数据来源于《中国教育经费统计年鉴》、《中国教育统计年鉴》及《中国统计年鉴》。

1. 收入变量。参考卢盛峰和潘星宇（2016）的做法，分别取1991年至2015年子代、父代的多年收入均值进行回归，使得代际弹性系数的估计更准确。选取子代和父代年龄在16岁到60岁的男性作为研究对象，剔除在学阶段的个体，剔除收入为0的个体。考虑到异常值的存在，对子代、父代的收入分别进行缩尾处理。

2. 财政教育支出。以预算内生均教育经费作为衡量财政教育政策的代理变量，为区分城乡教育投入水平，分别计算城镇和农村各级各类生均教育经费支出，缺失的数据按照统一增长比例补齐。由于财政教育支出为省级层面变量，可能导致残差在省内部存在相关性，因而参照标准的处理方法，将稳健标准误聚类到省一级。考虑到人力资本积累阶段存在时间不匹配问题，对财政教育政策的代理变量生均教育经费进行滞后一期处理，以捕捉财政教育政策的长期影响。

3. 个人特征变量。本文控制其他有可能影响子代贫困脆弱值的变量，包括子代年龄、性别、婚姻状态、工作状况、职业层次^①、有无参加医疗保险、教育程度、家庭规模、居住地等变量。按照国际贫困线的标准为人均2美元，利用CHNS数据库提供的不同地区城乡生活成本调整，并结合汇率通过购买力平价（PPP）折算处理到2015年，得到以人民币衡量的新贫困线为2790元。描述性分析如表1所示。

(二) 贫困脆弱性测度

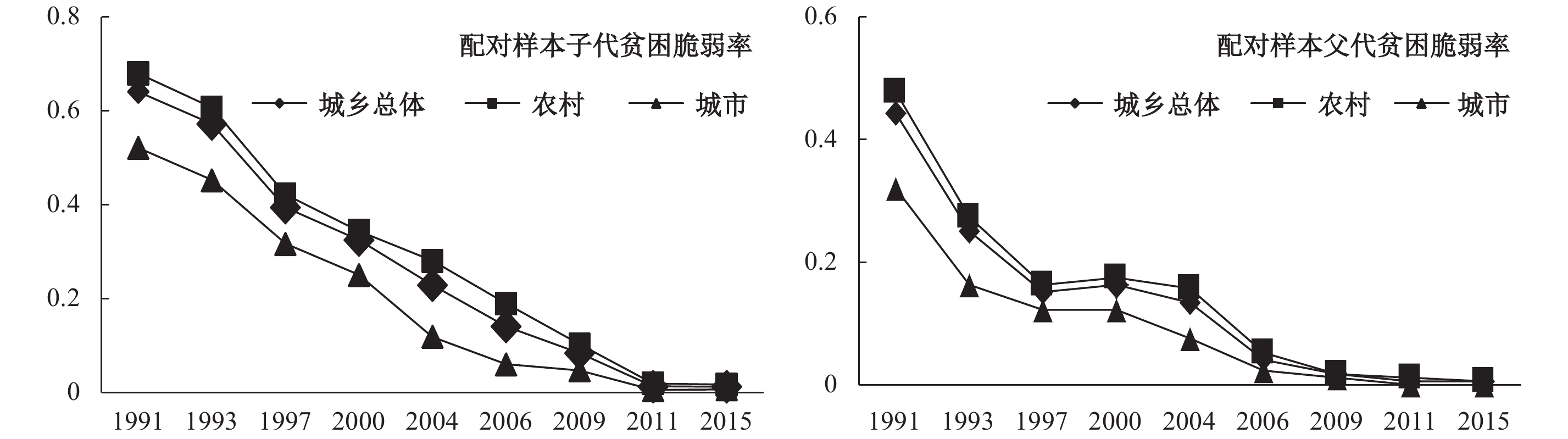
基于VEP估计方法，分别对配对样本的子代、父代的贫困脆弱值进行估计，结果如图1所示。图1中子代、父代的贫困脆弱性从1991年到2015年整体呈下降的趋势；农村的贫困脆弱性始终高于城市的贫困脆弱性，农村更容易陷入贫困脆弱性；贫困脆弱性初期下降较快，后期趋于稳定，呈现“厚尾”的趋势并维持在较低的贫困脆弱率水平。

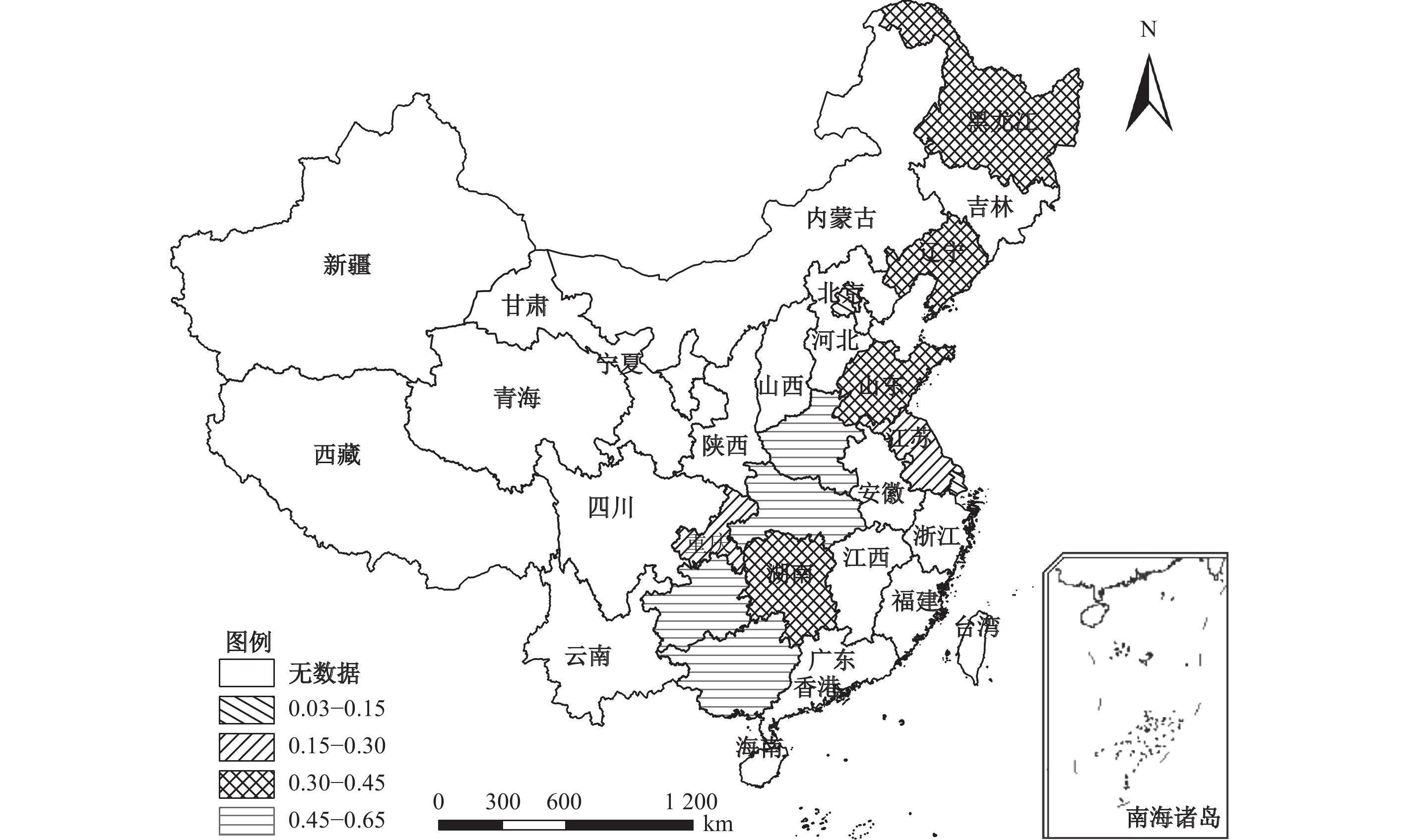
根据样本数据调查情况采用ArcGIS10.2绘制专题地图，以呈现子代、父代的贫困脆弱性地理分布（见图2和图3）。

图2和图3显示：经济发展水平较高的地区伴随着更低的贫困脆弱性。如北京、上海、江苏，其贫困脆弱性较低，而经济发展水平较低的省份如贵州、广西等地具有较高的贫困脆弱性，说明贫困脆弱性存在地区异质性特征。其原因可能在于，经济发展水平较高的地区其对教育的财政支出也较高，这些地区的高人力资本积累减弱了贫困脆弱性。

为分析贫困脆弱性代际传递动态趋势，我们将样本分为1991–1997年、2000–2006年、2009–2015年三个时间区间，两代人的贫困状况将形成三种状态组合，这三组分别为父代与子代同样陷入贫困脆弱为贫困脆弱性代际传递组，父代陷入贫困脆弱而子代非贫困脆弱则为逃离贫困脆弱组，父代非贫困脆弱而子代陷入贫困脆弱则为落入贫困脆弱组。基于此，计算出三种状态的概率，这一概率可以较为准确地反映脆弱性代际流动的情况，如表2所示。

贫困脆弱性代际传递概率在三个阶段均有所下降，陷入贫困脆弱的概率也呈现下降趋势，而脱离贫困脆弱的概率则有较大幅度的上升。下文将进一步通过实证分析论证财政教育政策对阻断代际间贫困脆弱性传递的效应。

四、实证分析 (一) 财政教育政策对阻断代际间贫困脆弱性传递的影响

首先，对贫困脆弱性的代际传递进行基准回归分析。在基准回归基础上，将财政教育支出、财政教育支出与父代收入的交互项逐步加入回归模型来实证检验财政教育政策对贫困脆弱性代际传递的阻断效果。为稳健起见，将标准误聚类到省级层面。

表3显示，父代的贫困脆弱性对子代的贫困脆弱性影响极为显著，父代脆弱值较高时其子代脆弱值也较高，即来自贫困家庭的子代未来将有很大概率陷入贫困；反之，父代脆弱值较低时其子代脆弱值也较低，来自背景良好家庭的子代未来获得高收入的可能性也较高，贫困脆弱性存在代际传递现象。可能的原因在于家庭背景良好的父代有较高的收入，保证其子代拥有更好的教育机会和生活条件，其子代具有未来保持较高收入的可能，而贫困家庭子代教育机会的获得处于劣势，贫困家庭的子代未来仍难以逃离贫困，而陷入贫困代际传递的陷阱中。性别变量系数显著为负，说明女性更容易陷入贫困脆弱性，这可能是由于一部分家庭更倾向于对男孩投资。家庭规模增大会使得子代贫困脆弱性增加，一方面，可能是大家庭中抚养人口占比较高所致，如Pezzin和Schone（1999）、Bhaumik等（2006）认为有老年人和儿童的家庭中家庭成员赚取收入的能力较弱，家庭的总劳动供给降低，进而会对收入有负向影响；另一方面，家庭规模的增大可能会导致父代对子代的人力资本投资减少，这将为子代收入带来负面影响，进而会增大子代陷入贫困和其贫困脆弱性的概率。子代有工作状态会显著降低子代陷入贫困脆弱性的概率。城市地区的子代陷入贫困脆弱性的概率要明显小于农村地区的子代。

在表3（1）栏的基础上分别加入小学阶段的财政教育支出和初中阶段的财政教育支出得到（2）、（3）、（4）、（5）栏的结果，父代贫困脆弱性对子代的影响系数从（1）栏中的0.1791分别降为（2）栏中的0.1024和（4）栏中的0.1042，说明财政教育支出的增加可以减弱贫困脆弱性的代际传递。这可能是因为贫困家庭的子代获得更多的财政支持后，其可能选择在完成义务教育后继续读书，由此降低其未来陷入贫困脆弱的可能性。这说明财政教育政策投资是阻断贫困代际传递的重要途径。引入父亲收入与教育支出的交互项，交互项的系数显著为负，说明财政教育支出的增加在一定程度上可以弥补父代对子代的教育投入不足，进而降低贫困脆弱性的代际传递。

(二) 异质性分析

本部分将探讨不同地区、父代教育水平不同情况下财政教育支出对子代的影响。将生均教育经费分别对应城市样本的小学、初中阶段^③及农村样本的小学、初中阶段，分组回归结果参见表4。表4显示，城乡父代的贫困脆弱性均显著影响了子代的贫困脆弱性，其中农村家庭的贫困脆弱性代际传递系数高于城市家庭的代际传递系数，说明农村家庭贫困脆弱性代际传递效应较城市家庭更强。这可能是因为农村家庭的子代在教育机会的获得和就业选择中处于明显的弱势地位，其更容易继承父代的不利因素，故其收入与父代收入的关联性更强。农村家庭女孩更容易陷入贫困脆弱性，因此在制定相应的财政教育政策时，应更多地向农村女孩倾斜，从而弥补农村家庭父代对女孩教育投入的不足。财政教育支出增加能降低子代陷入贫困脆弱性的概率，其对农村家庭子代的贫困脆弱性的降低效果更大，说明财政教育支出对农村家庭的子代产生了更加积极的影响。比较小学阶段和初中阶段的教育支出增加对贫困脆弱性的影响，发现小学阶段教育支出增加对贫困脆弱性代际传递的改善效果更强。财政教育支出通过影响父代收入，间接影响其对子代人力资本的投资，从而影响子代的收入水平，这一效果对于城市家庭更显著，这可能与制度性因素和城乡经济发展水平差距有关，城乡财政教育支出经费投入在城乡间存在很大差距，城市家庭拥有更多的优势教育资源使得子代贫困脆弱性降低。

基于父代的受教育水平划分为高学历家庭样本和低学历家庭样本，父代为小学毕业及以下和初中毕业的家庭为低学历家庭，父代为高中毕业、大学毕业及以上的家庭为高学历家庭。分样本估计结果参见表5。

表5中高学历家庭和低学历家庭背景的贫困脆弱性代际传递系数分别为0.0551、0.1982，说明低学历家庭比高学历家庭有着更为严重的贫困脆弱性代际传递现象，反映了贫困存在自加强的趋势，低学历家庭更容易陷入贫困代际传递状态，阶层固化现象有所凸显。低学历家庭中的女孩更容易陷入贫困脆弱，反映了在低学历家庭的教育决策中，女孩受教育机会比高学历家庭要少。其他控制变量如有工作、已婚、居住地为城市均对贫困脆弱性起到了降低作用。加入财政教育支出的回归结果显示，财政教育支出的增加对子代贫困脆弱性的降低起着非常显著的作用，其中对低学历家庭子代贫困的降低作用更大。引入财政教育支出与父代收入交互项，发现此交互项对低学历家庭影响显著为负，说明财政教育政策可以通过间接影响低学历家庭父代收入的方式影响其对子代的教育投入，从而提高子代教育机会的获得水平，促进其人力资本的积累，进而影响贫困脆弱性的代际传递。财政教育支出增加对高学历家庭的影响不显著，可能的原因是高学历家庭在进行教育投资时通常受到较少的预算约束，教育投入已经达到了较高的水平，财政政策对其子代的补偿作用效果较小。为财政支出效益计，财政教育投入应有所侧重，更多地投向家庭教育背景较差的子代。

五、稳健性分析 (一) 门槛效应检验

为验证不同的财政教育支出水平下贫困脆弱性的代际传递是否存在差异，本文以财政教育支出作为门槛变量，父代收入作为门槛协变量，将教育支出分为低水平支出和高水平支出。通过模拟得出小学阶段和初中阶段的门槛值分别为5.302和6.360，结果参见表6。

表6的回归结果表明，财政教育支出水平较低的地区相对于财政教育支出水平较高的地区贫困代际传递系数大，说明在较低教育支出水平的地区，子代未来有更大概率陷入贫困脆弱性，贫困存在自加强的趋势，以致陷入贫困代际传递的困境。而财政教育水平较高的地区，代际传递系数小，说明财政教育支出增加可以促进代际流动，降低其子代未来陷入贫困的概率，进而阻断贫困脆弱性的代际传递，弱化贫困的自加强趋势。其他控制变量的结果与上文基本一致。

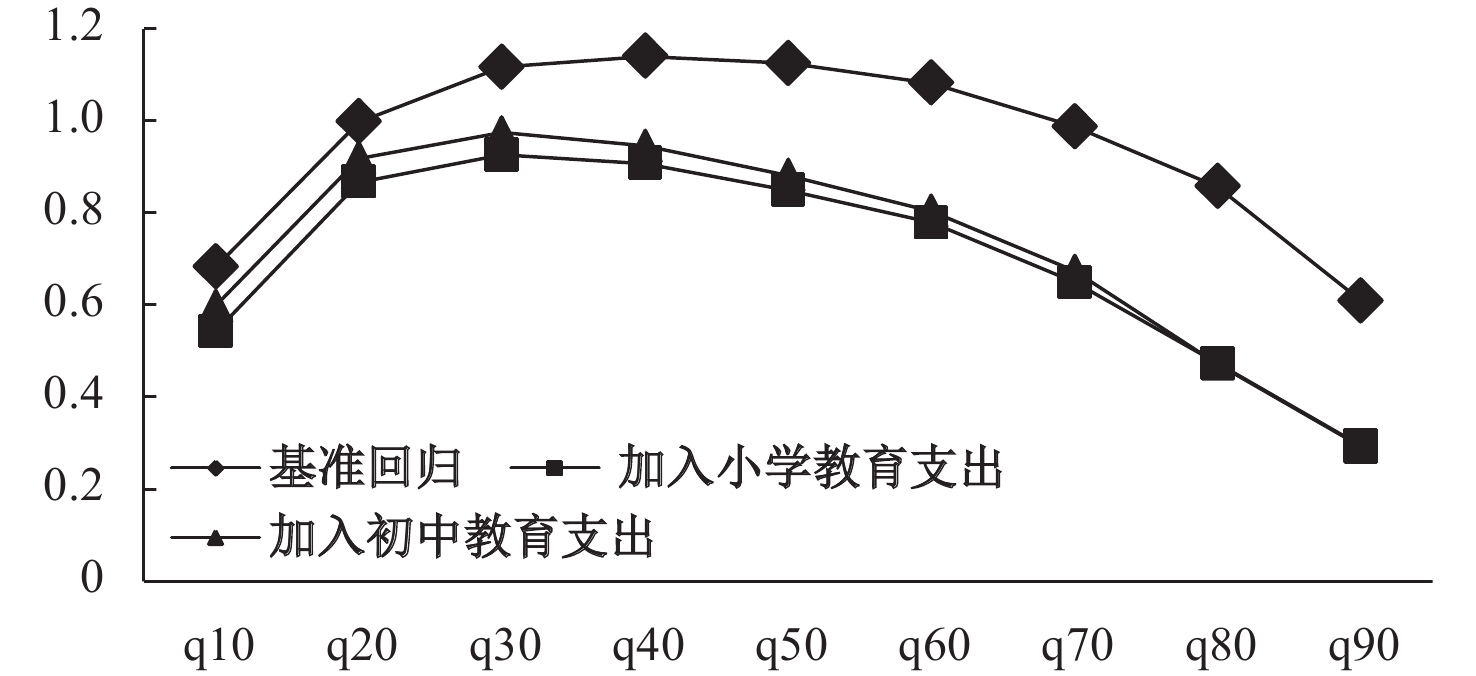
(二) 分位数回归

以父代贫困脆弱值划分父代阶层，本文借助分位数回归方法验证财政教育政策对不同阶层子代的贫困脆弱性是否有降低作用，具体回归结果参见图4。

父代脆弱值处于两端时，其代际传递系数较低，子代更有可能保持在当前阶层。即当父代脆弱性较高时，贫困传递效果较强，其子代更倾向于陷入贫困脆弱，说明低阶层存在持续贫困及代际贫困现象。加入财政教育政策后，曲线向下移动，说明财政教育支出的增加可以显著降低贫困脆弱性在代际间的传递，财政教育支出的增加，对减弱高脆弱值家庭贫困代际传递的效果强于对低脆弱值家庭的效果，即对于贫困家庭而言，财政教育政策通过影响父代收入进而减弱子代贫困脆弱性的作用效果非常显著，财政教育政策更多地影响贫困家庭。贫困家庭能从教育政策中获益更多，意味着财政教育支出的增加有助于减轻不平等程度和阻断贫困代际传递。相对于初中阶段，小学阶段的财政教育支出对贫困代际传递的减弱作用更明显。这说明前文分析是比较稳健的。

六、结论及政策建议

“寒门出贵子”“穷不过三代”反映了人们对破解贫困代际传递实现良性、纵向阶层流动的希冀。传统的贫困测度更多的具有静态性和事后性，反贫困实践中应关注体现前瞻性的贫困脆弱性代际传递问题，以便对贫困进行有效预防。本文首先建立了加入财政教育政策变量的两期世代交叠模型，然后基于中国健康与营养调查（CHNS）的调查数据，使用三阶段最小二乘法对子代、父代的贫困脆弱性进行测算，并通过Beta回归探讨财政教育政策对代际间的贫困脆弱性传递的长期影响。结果表明，子代、父代的贫困脆弱性在1991年到2015年均呈现下降趋势；农村地区的贫困脆弱性始终高于城市的贫困脆弱性；东部地区人群陷入贫困脆弱性的概率低于中西部地区人群；贫困脆弱性具有显著的代际传递特征，子代的性别、工作状态、婚姻状况等变量会影响贫困脆弱性；财政教育支出的增加会显著降低子代的贫困脆弱性，从而阻断贫困的代际传递。父代教育水平较低的子代能从财政教育政策中获益更多，财政投资于小学阶段的减贫效果大于其对初中阶段的减贫效果，分位数回归和门槛回归的结果也验证了上述结论。

结论的相应政策含义为：第一，在当前的反贫困背景下，靶向父代、子代贫困脆弱性人群是精准扶贫和精准脱贫的重要一环，制定贫困脆弱性群体的识别标准，剖析贫困脆弱性代际传递模式及成因，是有效预防贫困首要解决的问题。第二，贫困脆弱性家庭能从财政教育政策中获益更多的结论说明，在推进教育公共服务均等化过程中，财政支出应适当向贫困脆弱性人群倾斜。财政投资于小学阶段的减贫效果大于其对初中阶段的减贫效果说明，财政支出在义务教育阶段中应实行差异化的支出政策，更多地投向小学阶段。第三，针对影响贫困脆弱性的特定因素，扶贫进程中对这些因素设定相应受益条件，比如参加某种工作作为受益条件，抑或限定扶贫款（项目）优先用于某一用途的行为。当然，平衡地区、城乡资源也是减贫的题中应有之意。

① 调查问卷中，01高级专业/技术工作者（医生、教授、律师、建筑师、工程师等）、03管理者/行政官员/经理（厂长、政府官员、处长、司局长、行政干部及村干部等）、08军官与警官归类为脑力劳动职业（higher）；02一般专业/技术工作者（助产士、护士、教师、编辑、摄影师等）、04办公室一般工作人员（秘书、办事员）、06技术工人（领班、车间班长、工艺工人等）、07非技术工人（普通工人、伐木工等）、09士兵与警察、10司机、12运动员、演员、演奏员归类为中度体力劳动职业（middle）；05农民、渔民、猎人、13其他或者由于“正在找工作”、“残疾”、其他原因以及回答不知道什么原因等4类“被迫性”失业类型视为非固定职业，这一职业地位从事重体力劳动或者被动失业状态，并且收入存在不确定性（lower）。

② 为计算父代的贫困脆弱值，表1中也列出了父代的变量情况。

③ 城镇小学（初中）生均教育经费=[全国小学（初中）生均教育经费×全国小学（初中）在校人数−农村小学（初中）生均教育经费×农村小学（初中）在校人数]/[全国小学（初中）在校人数−农村小学（初中）在校人数]。