文章信息
 | 上海财经大学 2018年20卷第5期 |
- 苑德宇, 宋小宁, 李德刚
- Yuan Deyu, Song Xiaoning, Li Degang
- 中央投资项目跨区配置的决定因素:经济准则还是政治影响力
- Determinants of Central Investment Across Chinese Regions: Economic Normative Criteria or Political Clout
- 上海财经大学学报, 2018, 20(5): 30-43.
- Journal of Shanghai University of Finance and Economics, 2018, 20(5): 30-43.
-
文章历史
- 收稿日期:2018-01-02

2018第20卷第5期
2.中山大学管理学院/现代会计与财务研究中心,广东 广州 510275;
3.北京第二外国语学院 经贸与会展学院,北京 100024
政府投资在我国经济40年持续快速增长中发挥了十分重要的作用。其中,中央投资引导了地方投资方向和规模,发挥着“四两拨千斤”的作用。从理论上讲,中央投资作为中央政府的一种资金支出安排,除了要讲求产出效率外,还应兼顾统筹区域经济发展、公共服务均等化等公平准则(Yamano等,2000)。那么,长期以来,我国中央投资在省区间分配更重视效率因素还是公平因素?厘清这一问题,可为中央制定更好地促进我国经济稳定、协调、可持续性发展的投资策略提供理论依据和决策参考。
然而,从另一角度而言,中央政府投资项目通常被地方政府作为一种“公共利益”而竞相追逐,不可避免地会受到政治影响力、游说等因素的影响(Oates,1999;Kemmerling和Stephan,2015)。当前,我国中央投资项目分配并无明确的制度依据,通常由中央部委(主要为国家发改委)直接作出,具有相当的任意性。在以经济增长作为最重要“竞争目标”的背景下,地方政府利用其官员的政治影响力来干预中央投资项目分配就成为一个自然的做法,而这一做法通常却会对中央投资公平和效率目标的实现产生“干扰”。由此,明确政治影响力对中央投资项目分配的影响效应,是中央政府充分把握投资政策机制的必然要求。
目前,国外学者已沿着效率与公平因素、政治因素等视角对中央投资的决定因素进行了大量的实证研究。从效率与公平因素决定方面,Lambrinidis等(2005)利用希腊地区面板数据对中央基础设施的决定进行了实证研究,结果发现中央基础设施投资集中于欠发达地区,主要目的是为了缩小地区间的贫富差距。从政治因素决定方面,Cadot等(2006)利用法国地区面板数据对基础设施支出的区域分布进行了研究,发现分肥政治(Pork-Barrel Politics)是跨区交通基础设施投资的显著决定因素;Sturm(2001)基于非OECD国家数据研究认为,政治制度变量,比如意识形态、政治稳定性、政治经济周期等并未显著影响政府资本的形成;Wallis(1998)、Boyle和Matheson(2009)基于美国数据实证研究发现,一个州要获得更多的联邦政府投资,通常需要有更多的人均立法机关代表和国会议员,或者参议员具有更深资格、与总统同属于一个党派等;Duchin和Sosyura(2012)对美国地方企业政治关联与政府之间的关系进行了研究,认为一个地区从联邦获得的政府投资资金与这个地区企业—政治关联度正相关。此外,Worthington和Dollery(1998)、Arulampalam等(2009)均针对中央投资的政治决定问题进行了实证研究。在政治和经济综合因素决定方面,Castells和Solé-Ollé(2005)利用西班牙地区面板数据对中央投资的影响因素进行了研究,发现效率与公平的权衡因素的影响有限,相反政治因素则是主要的影响因素;Kemmerling和Stephan(2015)对影响法国、德国、意大利和西班牙四国基础设施区域分布的政治因素和经济准则因素的重要性进行了实证研究,发现各个国家因政治制度不同导致了经济准则因素在影响各自国家的基础设施投资分布的作用不同,但总体上党派政治下的经济准则因素的影响作用要比其他政治制度大。在国内,虽有部分学者对中国政府投资决定问题进行了探讨,但鲜有中央投资相关主题的研究。例如,张军(2007)基于中国省际面板数据探索了决定基础设施投资变动的因素,认为地方政府之间的标尺竞争和政治治理的转型是解释中国基础设施投资决定的重要因素;何庆光(2010)实证研究了财政分权对政府投资的影响,认为财政分权与政府投资间存在着长期均衡的正向关系。尽管Zheng等(2013)就中央基础设施投资的影响因素进行了实证研究,发现中央政府在分配投资时将公平和效率均衡作为突出的考虑因素,但是并未关注政治影响力因素的影响。
综上,国内外学者从多个视角研究了政府投资的决定问题,并得到了一些重要结论,这为本文提供了重要的研究基础。本文基于中央投资决定的理论模型,就效率、公平及政治影响力等因素提出相关理论假说,构建空间面板数据模型,并利用中国转型期1998–2015年省级面板数据进行经验检验,厘定中央投资项目跨省区配置的依据,以期为中央投资政策完善提供支撑。本文可能的创新在于:(1)基于中国制度背景,扩展出一个反映中央政府投资与多个影响因素之间关系的经济政治理论模型。(2)构建“基础设施综合指数”,以其为基础,进一步衡量地区基础设施的公平、效率状况,避免以某一种或某一类基础设施的公平和效率代替基础设施总体公平和效率所造成的研究结论偏颇。在实证模型中,我们用“基础设施综合指数”平减中央政府投资水平,以剥离不同地区已有基础设施水平的差异对中央政府投资跨区配置决策产生的影响。(3)除了总体研究外,本文还考察了中央政府投资决定因素的时序差异,以获得更为准确和翔实的研究结果。
本文余下部分安排如下:第二部分构建了中央投资的决定模型并提出了相关理论假说;第三部分构建实证模型,并对回归方法和数据选取进行了说明;第四部分展示了实证回归结果并对其进行分析;第五部分是对基准回归结果的稳健性检验;第六部分给出了本文结论和政策启示。
二、理论模型及研究假说本部分基于地区生产函数及中央政府效用函数构建反映中央投资决定的理论模型,提出研究假说,并以此作为下文实证研究的理论基础。
(一) 代表性地区的生产函数假设一个国家由N个辖区组成,每个地区的私人部门均利用其拥有的私人资本、劳动力及获得的本辖区基础设施所提供的生产性公共服务,以同样的方式组织生产。依据Barro(1990)和Alonso-Carrera等(2009)的做法,将代表性地区的生产函数设定为如下形式:
| ${Y_{it}} = {A_i}K_{it}^\alpha L_{it}^{1 - \alpha }S_{it}^\gamma \quad\alpha ,\gamma \in \left( {0,1} \right)$ | (1) |
其中,Yit、Kit、Lit和Sit分别为地区i第t期的产出水平、私人资本存量、劳动力水平以及生产性公共服务;Ai为仅具有地区特征的技术进步参数。
假设生产性公共服务Sit仅取决于地区i的公共基础设施水平Git以及地理特征
| ${S_{it}} = {{{G_{it}}}/{{\xi _i}}}$ | (2) |
在此,假设兴建基础设施Git的资金来源于中央对地区i的政府投资
| ${G_{it}} = I_{it}^C + (1 - \delta ){G_{it - 1}}$ | (3) |
国家在分配中央投资资金或项目时,除了考虑中央层面的社会福利外,还要顾及中央投资资金给地方带来的社会福利水平的变化。①依据Cadot等(2006)、Behrman和Craig(1987)、Castells和Solé-Ollé(2005)的做法,我们将中央投资的社会福利目标函数设定为:
| ${{\rm{W}}_t} = {\sum\nolimits_i {{L_{it}}\left( {{Y_{it}}/{L_{it}}} \right)} ^\varphi }{\rm{ + }}1/\eta \ln \left[ {\sum\nolimits_i {{L_{it}}\Theta _{it}^{}{{\left( {{Y_{it}}/{L_{it}}} \right)}^\eta }} } \right]$ | (4) |
在式(4)等号右边,前一项表示地方层面社会福利之和,后一项表示中央层面的社会福利。对于前者,
假设中央政府通过产品税筹集财政资金,并用于各辖区基础设施投资,这样有:
| $\sum\nolimits_i {I_{it}^C} \leqslant \sum\nolimits_i {\tau {Y_{it}}} $ | (5) |
其中,
| $LAG = {\sum\nolimits_i {{L_{it}}\left( {{Y_{it}}/{L_{it}}} \right)} ^\varphi }{\rm{ + }}(1/\eta )\ln \left[ {\sum\nolimits_i {{L_{it}}\Theta _{it}^{}{{\left( {{Y_{it}}/{L_{it}}} \right)}^\eta }} } \right] - {\lambda _t}(\sum\nolimits_i {I_{it}^C} - \sum\nolimits_i {\tau {Y_{it}}} )$ | (6) |
其中,
| $\left[ {\varphi \times {{\left( {\frac{{{Y_{it}}}}{{{L_{{\rm{it}}}}}}} \right)}^{\varphi - 1}}{\rm{ + }}\frac{{\Theta _{it}^{}}}{{{e^{\eta {U_t}}}}} \times {{\left( {\frac{{{Y_{it}}}}{{{L_{it}}}}} \right)}^{\eta - 1}}{\rm{ + }}\tau {\lambda _{\rm{t}}}} \right] \times \frac{{{Y_{it}}}}{{{G_{it}}}} \times \frac{{\partial {G_{it}}}}{{\partial I_{it}^C}} = \frac{{{\lambda _t}}}{\gamma }$ | (7) |
其中,
| $G_{it}^* = \frac{\gamma }{{{\lambda _t}}} \times \left[ {\varphi \times {{\left( {\frac{{{Y_{it}}}}{{{L_{it}}}}} \right)}^{\varphi - 1}} + \frac{{\Theta _{it}^{}}}{{{e^{\eta {U_t}}}}} \times {{\left( {\frac{{{Y_{it}}}}{{{L_{it}}}}} \right)}^{\eta - 1}} + \tau {\lambda _t}} \right] \times {Y_{it}}$ | (8) |
由式(8)可知,一个地区基础设施的最优水平G*由该地区的总产出、人均产出以及政治影响力决定。
为了进一步明确中央投资与公平、效率、政治影响力等因素之间的关系,我们设定中央政府根据上期地方基础设施水平(
| ${G_{it}} - {G_{it - 1}} = \pi (G_{it - 1}^* - {G_{it - 1}})$ | (9) |
其中,
| $\frac{{I_{it}^C}}{{{G_{it - 1}}}} = \frac{{\pi \gamma }}{{{\lambda _{t - 1}}}} \times \left[ {\varphi \times {{\left( {\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}}} \right)}^{\varphi {\rm{ - }}1}} + \frac{{\Theta _{it - 1}^{}}}{{{e^{\eta {U_{t - 1}}}}}} \times {{\left( {\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}}} \right)}^{\eta {\rm{ - }}1}} + \tau {\lambda _{t - 1}}} \right] \times \frac{{{Y_{it - 1}}}}{{{G_{it - 1}}}} + (\delta - \pi )$ | (10) |
其中,
由式(10)分别对
| ${{\partial \frac{{I_{it}^C}}{{{G_{it - 1}}}}}/\partial }\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}} = \frac{{\pi \gamma }}{{{\lambda _{t - 1}}}} \times \left[ {\varphi (\varphi - 1) \times {{\left( {\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}}} \right)}^{\varphi {\rm{ - 2}}}} + (\eta - 1) \times \frac{{\Theta _{it - 1}^{}}}{{{e^{\eta {U_{t - 1}}}}}} \times {{\left( {\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}}} \right)}^{\eta {\rm{ - 2}}}}} \right] \times \frac{{{Y_{it - 1}}}}{{{G_{it - 1}}}} < 0$ | (11) |
| ${{\partial \frac{{I_{it}^C}}{{{G_{it - 1}}}}}/\partial }\frac{{{Y_{it - 1}}}}{{{G_{it - 1}}}} = \frac{{\pi \gamma }}{{{\lambda _{t - 1}}}} \times \left[ {\varphi \times {{\left( {\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}}} \right)}^{\varphi {\rm{ - }}1}} + \frac{{\Theta _{it - 1}^{}}}{{{e^{\eta {U_{t - 1}}}}}} \times {{\left( {\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}}} \right)}^{\eta {\rm{ - }}1}} + \tau {\lambda _{t - 1}}} \right] > 0$ | (12) |
| ${{\partial \frac{{I_{it}^C}}{{{G_{it - 1}}}}}/\partial }{\Theta _{it - 1}} = \frac{{\pi \gamma }}{{{\lambda _{t - 1}}{e^{\eta {U_{t - 1}}}}}} \times {\left( {\frac{{{Y_{it - 1}}}}{{{L_{it - 1}}}}} \right)^{\eta {\rm{ - }}1}} \times \frac{{{Y_{it - 1}}}}{{{G_{it - 1}}}} > 0$ | (13) |
由此,得到关于中央投资决定的3个假说:
假说1(效率假说):一个地区单位基础设施的产出水平越高(效率越高),中央越倾向于投资于该地区,即中央投资与单位基础设施的产出水平正相关。
假说2(公平假说):一个地区的人均产出水平越低(越不公平),中央政府越注重加强对这个地区的投资,以实现经济上再分配,即中央投资与人均产出水平负相关。
假说3(政治假说):地方的政治影响力也是中央分配投资项目的一个重要影响因素。一个地区拥有的政治影响力越大,其获得中央投资项目会越多。
三、实证模型及数据 (一) 计量模型设定根据上文式(11)至式(13),我们将计量模型设定为如下线性形式:
| $\begin{aligned} {{I_{it}^C}/{{G_{it - 1}}}} = &{\beta _0} + {\beta _1} \times \ln ({Y_{it - 1}}/{G_{it - 1}}) + {\beta _2} \times \ln ({Y_{it - 1}}/{L_{it - 1}}) + {\beta _3} \times {\Theta _{it - 1}} \\ &{\rm{ }} + {{ Z}^{\bf{'}}}{ X} + {{ H}^{\bf{'}}}{ D} + {\mu _i} + {\varepsilon _{it}} \\ \end{aligned} $ | (14) |
在此,
中央投资项目落户于地方,通常会因为两个方面的原因产生空间关联性:一是由中央投资的大型基础设施项目本身的性质决定的。像高速公路、铁路、管道等建设项目不太可能只局限于某一省区,通常会贯穿或者覆盖多个地区,因此中央投资在不同地区之间分配就产生相关关系。二是地方政府的相互攀比引起的。在相邻或相近地区之间,通常存在着较多相似特征,比如经济发展水平、地理状况等,当一个地区从中央获取了一笔投资资金时,相邻或相近地区可能因为攀比也会努力向中央争取一定数量的投资资金,由此中央投资资金分配会在地区之间产生相关关系(Zheng等,2013)。基于上述考虑,我们将实证模型式(14)扩展为如下空间自回归模型(SAR)的形式:
| $\begin{aligned} {{I_{it}^C}/{{G_{it - 1}}}} =& {\beta _0} + \beta \sum\nolimits_j {{{{w_{ij}}(I_{jt}^C}/{{G_{jt - 1}})}}} + {\beta _1} \times \ln ({Y_{it - 1}}/{G_{it - 1}}) + {\beta _2} \times \ln ({Y_{it - 1}}/{L_{it - 1}}) + {\beta _3} \times {\Theta _{it - 1}} \\ &{\rm{ }} + {{Z}}^{\bf{'}}{{X}} + {{H}^{\bf{'}}}{{D}}+ {\mu _i} + {\varepsilon _{it}} \\ \end{aligned} $ | (15) |
其中,
为了保证实证结果的可靠性,本文通过不断放松实证模型式(15)中误差项的假设,并选择合理的估计方法进行回归。首先,假设误差项
(1)中央投资(
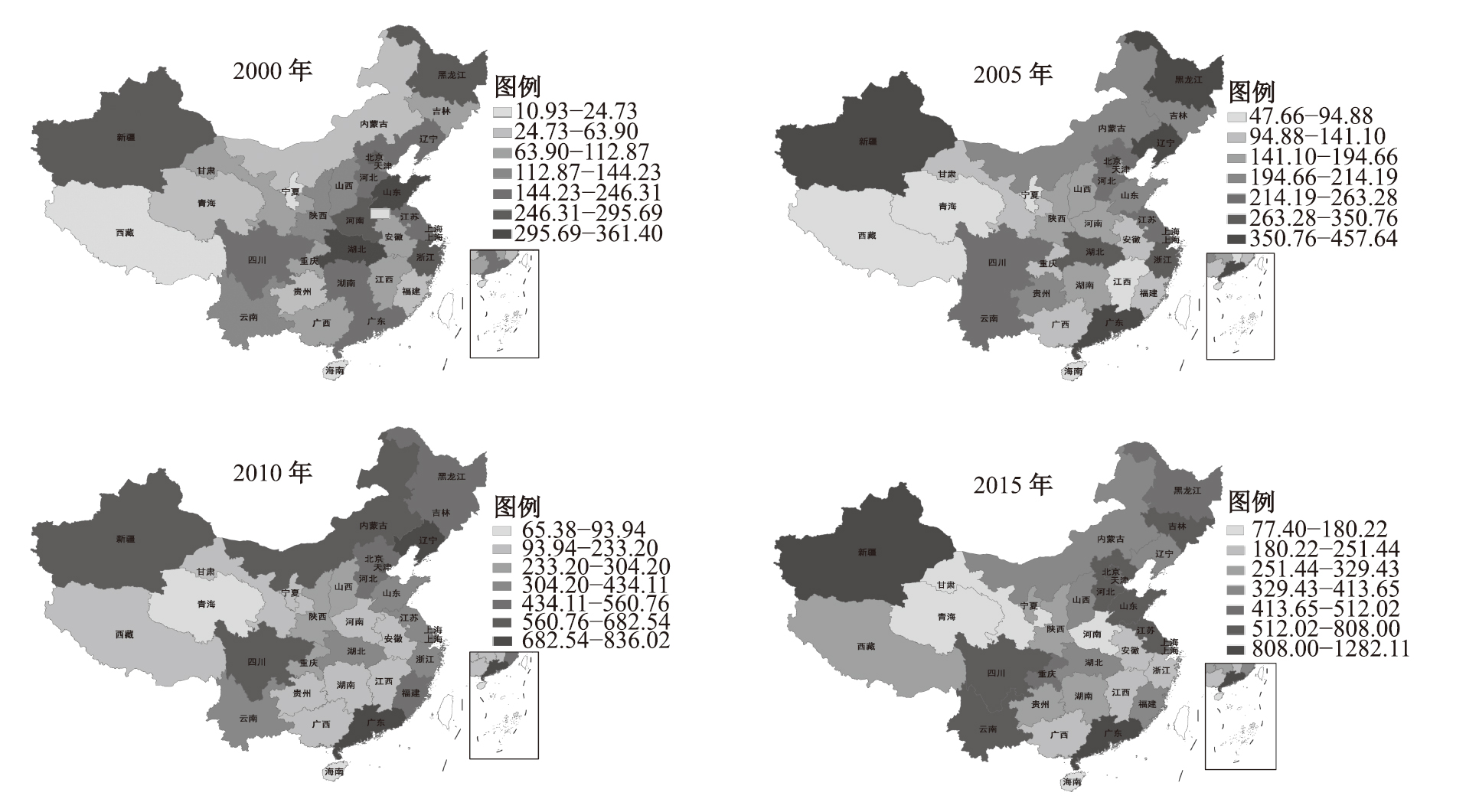
|
| 图 1 中央投资项目的空间分布情况 数据来源:相关年份的《中国统计年鉴》。 |
不同基础设施实物存量的衡量有着不同单位,无法进行简单的算术相加,因此为了获得一个能够综合衡量基础设施水平的指标,需对基础设施实物存量指标做一定的技术处理。本文选用全局主成分分析法(Global Principal Component Analysis)来克服上述指标加总问题,同时获得一个能够反映多指标绝大部分有用信息且这些信息互不重叠的综合指标。参照张军等(2007)的做法,并考虑数据的可得性,我们主要选取了五个方面的基础设施实物存量指标进行处理:一是交通基础设施,包括公路里程(公里)、内河航道长度(公里)、铁路营业里程(公里)、航空运输业就业人员数(人);二是能源基础设施,包括焦炭生产量(万吨)、能源消耗总量(万吨标准煤)、发电量(亿千瓦时);三是通讯基础设施,包括邮路总长度(公里)、邮政局所数量(处)、长途电话交换机容量(路端)、长途光缆线路长度(公里)、移动电话用户数量(万户)、本地电话局用交换机容量(万门);四是城市基础设施,包括城市供水管道长度(公里)、城市环卫机械台数(台)、城市公园面积(公顷)、城市拥有城市公共汽电车辆(辆)、城市供气管道长度(公里)、城市供水综合生产能力(万立方米/日)、城市污水处理能力(万立方米/日)、城市排水管道长度(公里);五是社会基础设施,包括普通中学学校数(所)、卫生机构数(所)、卫生机构床位数(万张)、公共图书馆数(个)、艺术表演单位数(个)。因为利用上述方法处理所得的“基础设施水平综合指数”可能为负值,因此我们通过一致取自然指数的方法对它们进行了“正化”处理。图2列示了1998–2015年省级基础设施水平综合指数的变化情况,从中可以看到,1998–2015年间,全国各省份基础设施总体水平基本保持上升态势,而省际间基础设施水平差异呈现平稳—扩大—下降的变化趋势。
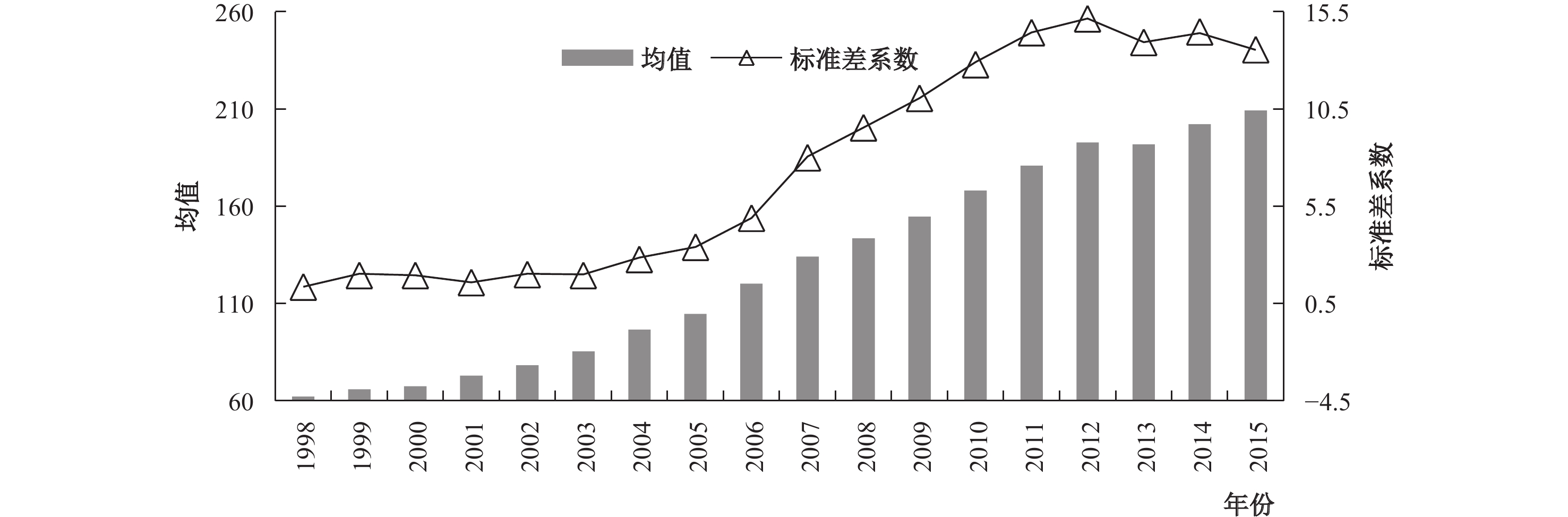
|
| 图 2 1998–2015年省级基础设施水平综合指数的变化 数据来源:各年份《中国统计年鉴》以及作者计算。 |
(2)单位基础设施产出水平(Yit/Git)和人均产出水平(Yit/Lit)。与上文理论模型中设定涵义相一致,这两个指标分别用于描述中央投资对于效率因素和公平(再分配)因素的考虑。其中,Y用“省级地区GDP水平”进行衡量;L用“省级地区的年初和年末常住人口数的算术平均值”来衡量。
(3)政治影响力。此指标被界定为一个地区对中央的影响力或者在中央决策层的代表性(李明和李慧中,2010),我们通过构建“政治影响力”指标对其进行衡量。在中国的政治体制下,考虑到中共中央委员会在国家经济和社会资源配置中的重要作用,我们选用各省份拥有的中央委员(包括政治局委员和中央候补委员)来构建地方的“政治影响力”指标。参照吴凤武等(2013)的做法,我们计算某年在某地任职的地方官员同时位居中央政治局委员、中央委员、中央候补委员的人数,按每人10分、2分和1分的标准分别赋予任职地相应的政治影响力得分,并逐年加总各省(自治区或直辖市)的得分,得到来自地方的政治影响力指标,即“地方政治影响力”(local)。另外,考虑到一个地区的政治影响力还可能来源于与这个地区有一定关联但目前在中央任职的官员,因此,我们还按照“籍贯地”(或“出生地”)和“任现职前主要任职地”两个标准分别对在中央任职的中央委员按省份进行人数归并⑥,同样按照“地方政治影响力”指标对中央政治局委员、中央委员和中央候补委员的赋分标准,构建两个来自中央的政治影响力指标,即“籍贯地政治影响力”(jgd)和“任职地政治影响力”(rzd)。此外,考虑到国家发展与改革委员会对中央投资具有重要的配置权力,我们还将此部门当年在任的主任和副主任分别参照中央委员和中央候补委员的标准赋分,计入上述两个中央政治影响力指标的分值中。需要指出的是,我们在统计中央委员人数时,并未把军队系统考虑在内,这是因为军队系统通常是独立封闭运行的,与地方的经济社会发展并无太多直接利益关系。
此外,我们还选择如下控制变量用于实证模型回归以及稳健性检验:(1)地方社会投资水平(locin),具体用“省级地方项目金额与基础设施水平综合指数的比值”表示,用于控制省级地方社会投资水平。(2)城市化水平(urb)。具体用“城镇人口占辖区人口总数的比重”表示,用于控制一个地区的城市化进程对中央投资决策的影响。(3)人口密度(popden)。即辖区单位面积的人口数,具体用“辖区人口总数与辖区地域面积的比值”表示,用于控制地区人口数以及地域面积构成的综合因素对中央投资决策的影响。(4)工业化水平(indus)。具体用“工业总产值占GDP的比重”来表示,用于控制工业化进程对中央投资的影响。(5)财政分权(fce)。具体用“一省的地方预算财政支出占该省中央和地方预算财政支出总和的比重”来表示,用于控制财政分权因素对中央投资的影响。
另外,我们还在回归模型中加入一些政策和地区虚拟变量,用于控制重要政策变化和地区特征可能对中央投资决策产生的影响。第一,2002年中国进行了所得税收入分享制度改革,这致使中央税收收入在2002年前后发生了结构性变化,进而可能影响中央投资的决策,对此我们设置政策虚拟变量policy02加以控制。第二,2008年美国“次贷”危机后中央政府均推行了以政府投资为主要手段的扩张性财政政策以刺激经济,而这可能使得政策前后中央投资的决策发生结构性变化,我们用虚拟变量policy08加以控制。这两个政策变量的设定方法均为:政策变动之前年份为0,政策变动年份及之后年份为1。第三,考虑到中央对少数民族地区的投资政策可能有别于其他地区,我们还在实证模型中加入民族地区虚拟变量(minority),即设定属于民族地区省份为1,其他省份为0⑦。
以上各指标的时间跨度为1998–2015年,横截面涉及中国31个省(自治区和直辖市)。构建各指标的所用的原始数据和资料,除中央委员名单和简历来源于《新华网》和《人民网》,其余均来自于《中国统计年鉴》、《中经网统计数据库》和《中国区域经济统计年鉴》。计算“中央投资”和“地方社会投资水平”所用的“中央项目”金额和“地方项目”金额,均利用固定资产投资价格指数调整为以1998年为基期不变的价格水平。主要变量的描述性统计如表1所示。
| 变量 | 样本数 | 均值 | 标准差 | 最小值 | 最大值 |
| 中央投资(
|
496 | 2.618 | 1.690 | 0.255 | 12.856 |
| 单位基础设施产出水平(
|
496 | 58.224 | 32.454 | 2.651 | 184.698 |
| 人均产出水平(
|
496 | 2.012 | 1.463 | 0.271 | 8.232 |
| 地方政治影响力(
|
496 | 7.397 | 3.964 | 2.000 | 20.000 |
| 地方社会投资水平(
|
496 | 13.554 | 8.832 | 0.208 | 57.553 |
| 城镇化水平(
|
496 | 46.382 | 14.785 | 18.204 | 89.600 |
| 人口密度(
|
496 | 4.087 | 5.869 | 0.021 3 | 38.384 |
| 工业化水平(
|
496 | 39.682 | 9.927 | 7.026 | 57.319 |
| 财政分权(
|
496 | 77.600 | 11.033 | 31.831 | 95.671 |
依据前文对回归方法的说明和选择,我们在运用STATA软件时执行了相关实证模型的回归,在估计时均使用了robust命令选项对模型可能存在的组间异方差进行修正,以获得稳健的回归结果。基本回归结果如表2所示。
| 静态模型 | 动态模型 | |||
| (ⅰ)MLE | (ⅱ)MLE | (ⅲ)SYS-GMM | (ⅳ)SYS-GMM | |
| 因变量一阶滞后项 | 0.718***(7.17) | 0.811***(6.07) | ||
|
|
2.670***(21.00) | 2.452***(18.19) | 0.203**(2.06) | 0.220*(1.67) |
|
|
–0.229(–0.73) | –0.016 4(–0.13) | 0.531(0.50) | 0.490(1.35) |
|
|
0.089 4***(4.46) | 0.060 6***(3.21) | 0.045 0***(3.22) | 0.018 3**(2.16) |
|
|
0.003 58(0.58) | 0.011 2*(1.73) | 0.061 0***(3.99) | 0.096 8***(2.87) |
|
|
0.007 40(0.88) | –0.036 4*(–1.95) | ||
|
|
0.003 10(0.59) | 0.016 1(1.16) | ||
|
|
–0.006 24(–1.10) | 0.016 8**(2.53) | ||
|
|
–0.011 5(–1.19) | 0.013 8(0.86) | ||
|
|
0.005 56*(1.68) | –0.013 9*(–1.69) | ||
|
|
0.534 | 0.630 | 0.775 | 0.847 |
| LogL | –659.7 | –677.5 | –448.97 | –489.3 |
| Robust LM_LAG | 3. 105** | 4. 050** | 40.42*** | 13.87*** |
| Robust LM_ERROR | 0.170 | 0.294 | 17.591*** | 0.137 |
| 观察值数 | 496 | 496 | 465 | 465 |
| 注:(1)***、**和*分别表示1%、5%和10%的显著性水平。(2)圆括号中数据为异方差稳健的t统计量,表3和表4同。(3)Robust LM_LAG是空间滞后效应拉格朗日乘子稳健统计量(服从卡方分布),而Robust LM_ERROR是空间误差效应拉格朗日乘子稳健统计量(服从卡方分布)。这两个指标用于检验实证模型中加入空间变量的必要性和合理性,其检验的原假设为:空间滞后因变量或误差项不存在空间自相关。 | ||||
在表2中,第(ⅱ)列给出了静态回归模型式(15)基于极大似然估计法(MLE)下的回归结果,以及第(ⅳ)列给出了引入因变量一阶滞后项后的空间动态面板模型基于SYS-GMM的回归结果,其余两列分别为相应对照回归结果。由第(ⅱ)列和第(ⅳ)列对比发现,在这两列回归结果中的空间滞后项系数均至少在10%的水平上显著,并且Robust LM_LAG检验统计量均至少在5%显著性水平上拒绝原假设,而Robust LM_ERROR在10%显著性水平上均不显著,说明前文将实证模型设定为空间自回归形式(SAR)具有一定的合理性。由表2后两列发现,因变量一阶滞后项系数均高度显著且动态模型的拟合优度相对于静态模型有明显提高,表明中央投资具有明显的跨期效应,将实证模型设定为动态形式可以相对更好地解释因变量。
基于上述对实证方法的对比考察与判断,我们以表2最后一列的回归结果为基准进行分析。第一,单位基础设施产出水平显著正向影响了中央投资。这证实了前文关于中央投资分配的效率决定假说。总体上来说,这与中国自改革开放以来长期贯彻的效率优先的经济政策导向是相吻合的。第二,人均产出水平系数的回归结果为正且不显著,上文公平假说并未得到充分证实。这可能因为,中央在安排投资项目时,特别是安排地区性投资项目时,通常要求“落户地”进行一定比例的资金配套(这个比例通常为1∶1),并且要求优先保障。这样,落后地区可能会因为配套资金“门槛”的存在,被排除在很多中央投资项目的承接地范围之外,相反发达地区可能会因为配套能力相对较强而成为这些中央投资项目的落户地,这在一定程度上加剧了中央投资的地区不公平性。第三,政治影响力显著正向影响了中央投资,这证实了前文的政治假说。根据前文对政治影响力指标的界定,local表示的政治影响力来源于地方任职的高级官员(中央政治局委员、中央委员和中央候补委员通常在地方都身居要职),这就说明了地方政府在争取中央投资项目上,政治影响力的确起到了重要的影响作用。1994年之后,中国建立起了社会主义市场经济体系并推行了分税制改革,地方政府获得了更大的自主发展经济的权力。与此同时,中央强化了GDP在地方政绩考核中的核心地位,这使得地方政府官员的政治利益(主要为晋升机会)很大程度上内生化为地方经济利益,即地方官员通过提速GDP来获得更大的晋升机会(Yang,2006),而中央投资作为推动地方经济快速增长最重要的力量之一,正是地方政府竞相追逐的对象,这对近些年来一直盛行的地方官员“跑步进京”现象作了充分说明。
此外,地方社会投资水平对中央投资产生了显著的负面影响。这说明中央在安排区域性投资项目时,出于均衡财力的考虑,与地方政府之间通常形成了一种互补关系,即当地方社会投资水平较高时,中央就会有意识地减少对该地区的投资,而当地方社会投资水平较低时,中央又会加大对该地区的投资力度,这样就形成了中央投资与地方社会投资之间的负向关系。工业化水平和财政分权分别对中央投资产生了显著正向和负向的影响,而城市化水平和人口密度对中央投资的影响并不显著。
(二) 分时段考察在上文的基本回归中,我们考察的样本期间是1998–2015年。在此期间,国家社会经济发展战略发生了重大变化,特别是在中共十六大后,中央明确要求政策导向要从原来的效率优先向更加注重公平转变,这很可能引起影响中央投资的因素发生时序上的变化。为了进一步厘定中央投资与其影响因素之间的实证关系,我们将上文的实证过程按1998–2007年和2008–2015年两个时段分别重新进行,相关结果如表3所示。
在表3中,我们给出了这两个时段样本基于SYS-GMM的回归结果,分别列于第(ⅰ)列和第(ⅱ)列以及第(ⅲ)列和第(ⅳ)列。其中,第(ⅱ)列和第(ⅳ)列是分时段基准回归结果,另外两列为相应对照结果。
| 1998–2007年 | 2008–2015年 | |||
| SYS(ⅰ) | SYS(ⅱ) | SYS(ⅲ) | SYS(ⅳ) | |
| 因变量一阶滞后项 | 0.943***(10.32) | 0.917***(6.61) | 0.618***(5.83) | 0.650***(3.18) |
|
|
–0.709(–0.80) | 0.184(0.55) | 0.267**(2.42) | 0.429**(2.00) |
|
|
0.632***(4.08) | 0.462**(2.33) | 0.640**(2.04) | –0.029 3(–1.05) |
|
|
0.012 6***(2.77) | 0.024 3**(2.27) | 0.050 3(1.54) | 0.060 0(1.34) |
|
|
0.037 5***(2.82) | 0.035 2***(2.95) | 0.035 6**(2.18) | 0.022 4*(1.80) |
| 控制变量 | NO | YES | NO | YES |
|
|
0.892 | 0.930 | 0.745 | 0.876 |
| LogL | –83.6 | –74.0 | –235.5 | –231.2 |
| 观察值数 | 217 | 217 | 217 | 217 |
通过对比表3中第(ⅱ)列和第(ⅳ)列的回归结果可以发现:第一,利用1998–2007年样本回归得到的中央投资一阶滞后项系数明显高于利用2008–2015年样本回归所得的结果,说明中央投资跨期效应的大小随时序显著下降。这与近年来国家不断完善中央财政预算制度,在编制中央财政预算和分配中央投资项目时更多地考虑经济发展真实需要的现实是相吻合的。第二,在前一时段样本回归中,单位基础设施产出水平对中央投资的影响虽然为正但不显著,而在后一时段样本的回归中,这一效应表现为正向显著;人均产出水平在前一时段显著地正向影响了中央投资,但在后一时段样本回归中这一系数变为负向且不显著。这说明在1998–2007年中央投资配置不仅没有充分考虑效率因素,而且显著违背了前文的公平假说。然而,随着国家社会经济发展战略的调整,在2008–2015年中央投资不仅更显著地关注效率,而且之前有违公平假说的配置模式也得到一定程度的扭转。第三,政治影响力在前一时段中显著正向影响了中央投资,而在后一时段中此效应却不显著。地方政治影响力对中央投资的影响作用之所以出现上述弱化趋势,可能与近年来中国的财政预算、政府项目审批制度不断完善,逐渐挤压中央政府分配投资项目的可操作空间密切相关。
五、稳健性检验为了进一步验证上文总体回归结果的稳健性,我们将模型式(15)作如下三个方面的变换,并分别重新进行回归:一是将地方政治影响力(local)分别替换为来自中央的籍贯地政治影响力指标(jgd)和任职地政治影响力指标(rzd);二是将中央政治局委员、中央委员和中央候补委员的分值分别设置为20分、2分和1分以及10分、2分和2分,计算两个新的地方政治影响力指标loca和locb,用于替换原来政治影响力指标;三是利用距离衰减权重矩阵⑧和经济相邻权重矩阵⑨分别生成距离衰减空间溢出项(
| 使用中央政治影响力变量 | 改变地方政治影响力赋值 | 扩展空间权重矩阵 | ||||
|
|
|
local1 | local2 |
|
|
|
| SYS(ⅰ) | SYS(ⅱ) | SYS(ⅲ) | SYS(ⅳ) | SYS(ⅴ) | SYS(ⅵ) | |
| 因变量一阶滞后项 | 0.799***(9.87) | 0.817***(10.72) | 0.785***(10.26) | 0.782***(10.24) | 0.836***(5.73) | 0.797***(5.71) |
|
|
0.401***(3.24) | 0.354***(2.87) | 0.419***(3.46) | 0.437***(3.63) | 0.256*(1.72) | 0.157(1.49) |
|
|
0.250(1.52) | 0.212(1.16) | 0.199(1.02) | 0.216(1.22) | 0.322(1.55) | 0.276(1.07) |
|
|
0.017 7**(2.40) | 0.016 8**(1.98) | 0.022 6***(3.03) | 0.030 1***(2.76) | ||
|
|
–0.004 23(–0.60) | 0.006 33**(2.04) | ||||
|
|
0.020 1**(2.21) | 0.017 3*(1.82) | 0.013 3**(2.41) | 0.018 3*(1.94) | ||
|
|
12.117*(1.76) | 0.068 6***(3.42) | ||||
| 控制变量 | YES | YES | YES | YES | YES | YES |
|
|
0.802 | 0.799 | 0.800 | 0.796 | 0.859 | 0.868 |
| LogL | –441.8 | –441.0 | –439.3 | –440.2 | –469.8 | –473.7 |
| 观察值数 | 465 | 465 | 465 | 465 | 465 | 465 |
如表4的前两列所示,无论将政治影响力变量(local)替换为籍贯地政治影响力变量(jgd)还是任职地政治影响力变量(rzd),与表2第(ⅳ)列相比,回归模型中其他主要变量回归系数的正负方向和显著性均未发生显著变化。两个中央政治影响力回归系数的方向和显著性之间存在较大差异,即任职地政治影响力显著促进了中央投资,而籍贯地政治影响力对中央投资的影响并不显著。这一结果表明,相对于籍贯地,中央政府官员更倾向于将中央投资项目分配给其曾经长期任职的地区。
从表4的第(ⅲ)列和第(ⅳ)列可以看到,在地方政治影响力变换赋分后,并未引起此变量本身以及其他主要变量回归系数的方向和显著性发生变化,说明前文基准回归结果具有较好的稳健性。从表4最后两列的回归结果可以看到,距离衰减、空间溢出项和经济相邻空间溢出项均显著地正向影响了中央投资。这说明中央投资确实存在着跨省份之间的关联性,而且这种关联性不仅受到省份间距离的影响,而且还受到相邻地区间经济发展水平差异的影响,这也充分验证了前文关于“中央投资具有空间溢出效应”的判断。表4后两列与表2第(ⅳ)列相同自变量的回归系数无论从方向还是显著性上均无较大差别,进一步证明了前文基准回归结果的稳健性。
六、结论与政策启示自社会主义市场经济建立以来,中央投资在政策上被赋予经济、社会甚至政治等诸多方面的功能和责任。然而,在现实中,中央在跨省份对投资项目进行配置时究竟受到哪些因素的影响尚不清晰,本文厘清了这些因素的影响作用。本文利用1998–2015年中国转型期省级面板数据进行了实证分析后发现:第一,效率因素在总体上显著正向影响了中央投资,而公平因素则不显著。从跨时对比来看,两个因素的影响均发生了时序变化,即效率因素对中央投资的影响由1998–2007年间的正向不显著变为2008–2015年间的正向显著,而公平因素的影响效应则由前一时段的正向显著变为后一时段的负向不显著。第二,政治影响力在总体上显著正向影响了中央投资,但从时序上显著正向效应仅存在于1998–2007年间。
基于以上结论,当前经济和社会背景下,为使中央投资项目能在促增长、调结构、惠民生等方面更有效地发挥作用,中央可以从以下两个方面进行政策把握:第一,减少政治干预,强化中央投资资金的预算管理和审批。既要通过严格审核资金是否符合预算管理制度来减少政治干预,还要通过对预算资金使用的事中监督和事后评估等方式来保证预算资金的使用效率。第二,调整和优化中央投资的规模和结构,将更多的中央项目投向公共服务和协调区域经济发展等方面,更有效地促进中央投资从效率单一目标向公平与效率并重的目标转变。
尽管本文研究得到了一系列重要结论,但近年来随着中央投资监督评价机制的完善、中央高层反腐力度的加大等经济政治制度变化,均可能决定性地改变中央投资的分配机制,而本文并未能将其纳入理论和实证考察,这也是未来进一步完善相关主题研究的重点方向。
① 在中国,地方政府为中央社会经济政策的执行机构,相应地,“中央政府”实质性地成为了“国家政府”。因此,中央政府在安排投资时通常会从国家整体考虑,其不仅要从中央层面去关注投资对其本身产生的福利,而且还要关注国家投资项目落地后为其辖区带来的社会福利情况。
② 也有文献使用Y/G和Y/L两个指标衡量影响政府投资的效率因素和公平因素,如Kemmerling等(2015)。我们知道,政府投资通常形成基础设施,在其他条件一定的情况下,单位基础设施所带来的产出越多,表示之前的政府投资就越有效率;政府投资可以直接或间接促进经济发展,如果一个相对较发达的地区,中央政府仍加强对其进行投资而减少对欠发达地区投资,那么无疑会加剧地区之间的经济发展不平衡或不公平程度。
③ 海南省与其他省份并无陆域邻接,但考虑到该省地理位置及与其他地区的经济往来情况,本文设定其与广东省、广西壮族自治区具有共同边界。
④ 政府投资项目特别是中央项目的周期通常超过1年,并且当前我国政府预算的编制采用的方法仍是基数法,当年预算是以上年度的预决算为基础进行预测、调整而编制完成的,因此假定中央投资跨期性有理论上的合理性。
⑤ 国内文献对“政府投资”数据的处理主要采用加总法,即加总财政支出中 “基本建设费”“企业挖潜改造”“科技三项费用”“城市维护建设费”“支援不发达地区建设费”等具有投资性支出项目的决算额,如张卫国等(2010)、苑德宇(2014)等。这种方法虽然有针对性地反映了中国政府投资性支出情况,但是因为1998年后至今官方财政支出统计口径和国民经济行业口径均发生了变化,这严重地影响了利用上述方法获得“政府投资”数据的连贯性甚至可得性。本文之所以借鉴王曦等(2014)的做法,利用固定资产投资中“中央项目”(主要包括中央预算内投资资金、专项建设基金、国家主权外债资金等中央财政投资性资金项目)表示“中央对地方的政府投资”主要出于数据可得性考虑,尽管用于“中央项目”的固定资产投资资金并不完全来源于公共部门,但因项目由政府主导,所建设施通常具有公共性,我们把其中使用的民间资金也视为政府投资,具有一定的合理性。
⑥ 在处理“政治影响力”指标时,如果遇到中央委员的“籍贯地”和“出生地”不同时,我们综合考虑该官员背景,将其适当地归入“籍贯地”或“出生地”。“任现职前主要任职地”的界定标准为:如果官员擢升为现职前最近地方任职的年限超过1年(包括1年),我们以该最近任职所在地作为其“任职地”;如果上述任职年限低于1年,我们则以该官员最长地方任职地作为“任职地”。当然如果一个官员没有地方任职经历,我们不对其进行“任职地”归并处理,仅将其规定到“籍贯地”(“出生地”)中。
⑦ 本文按照少数民族人口数占全省人口数的比例超过15%的标准划定某一省份是否为少数民族地区。本文利用1998–2015年全国各省的人口数据进行综合计算,选定内蒙古、辽宁、广西、海南、贵州、云南、西藏、青海、宁夏和新疆10省份为少数民族地区。
⑧ 设定矩阵元素wij为两省份距离(省会城市之间公路里程)的倒数。
⑨ 我们将经济发展水平纳入影响相邻地区间中央投资空间联系的因素中,构建了此空间权重矩阵。具体设定为:
| [1] | 何庆光. 财政分权对地方公共投资的长期和短期影响效应研究——基于省级面板数据的实证分析[J].经济理论与经济管理,2010(7). |
| [2] | 金戈. 中国基础设施资本存量估算[J].经济研究,2012(4). |
| [3] | 李明, 李慧中. 政治资本与中国的地区收入差异[J].世界经济文汇,2010(5). |
| [4] | 王曦, 杨扬, 余壮雄, 等. 中央投资对中国区域资本流动的影响[J].中国工业经济,2014(4). |
| [5] | 吴凤武, 刘琦, 胡祖铨. 中央对地方转移支付影响因素分析——地方政府政治力量的作用研究[J].经济研究参考,2013(67). |
| [6] | 苑德宇. 地方政府投资的决定因素研究: 基于税收预决算偏离的视角[J].世界经济,2014(8). |
| [7] | 张军, 高远, 傅勇, 等. 中国为什么拥有了良好的基础设施?[J].经济研究,2007(3). |
| [8] | 张卫国, 任燕燕, 花小安. 地方政府投资行为、地区性行政垄断与经济增长——基于转型期中国省级面板数据的分析[J].经济研究,2011(8). |
| [9] | Alonso-Carrera J, Freire-Serén M J, Manzano B. Macroeconomic effects of the regional allocation of public capital formation[J]. Regional Science and Urban Economics,2009,139(5):563–574. |
| [10] | Anselin L, Moreno R. Properties of tests for spatial error components[J].Regional Science and Urban Economics,2003,33(5):595–618. |
| [11] | Arulampalam W, Dasgupta S, Dhillon A, et al. Electoral goals and center-state transfers: A theoretical model and empirical evidence from India[J].Journal of Development Economics,2009,88(1):103–119. |
| [12] | Barro R J. Government spending in a simple model of endogeneous growth[J]. Journal of Political Economy,1990,198(5):103–125. |
| [13] | Behrman J, Craig S. The distribution of public services: An exploration of local governmental preferences[J]. American Economic Review,1987,177(1):37–49. |
| [14] | Blundell R, Bond S. Initial conditions and moment restrictions in dynamic panel data models[J].Journal of Econometrics,1998,87(1):115–143. |
| [15] | Boyle M A, Matheson V A. Determinants of the distribution of congressional earmarks across states[J].Economics Letters,2009,104(2):63–65. |
| [16] | Cadot O, Röller L H, Stephan A. Contribution to productivity or pork barrel? The two faces of infrastructure investment[J].Journal of Public Economics,2006,90(6-7):1133–1153. |
| [17] | Castells A, Solé-Ollé A. The regional allocation of infrastructure investment: The role of equity, efficiency and political factors[J].European Economic Review,2005,49(5):1165–1205. |
| [18] | Duchin R, Sosyura D. The politics of government investment[J].Journal of Financial Economics,2012,106(1):24–48. |
| [19] | Kemmerling A, Stephan A. Comparative political economy of regional transport infrastructure investment in Europe[J]. Journal of Comparative Economics,2015,143(1):227–239. |
| [20] | Lambrinidis M, Psycharis Y, Rovolis A. Regional allocation of public infrastructure investment: The case of Greece[J].Regional Studies,2005,39(9):1231–1244. |
| [21] | Oates W E. An essay on fiscal federalism[J].Journal of Economic Literature,1999,37(3):1120–1149. |
| [22] | Sturm J. Determinants of public capital spending in less-developed countries[R]. University of Groningen &CESifo Munich Working Paper, 2001. |
| [23] | Wallis J J. The political economy of new deal spending revisited, again: With and without Nevada[J].Explorations in Economic History,1998,35(2):140–170. |
| [24] | Worthington A C, Dollery B E. The political determination of intergovernmental grants in Australia[J]. Public Choice,1998,94(3-4):299–315. |
| [25] | Yang D L L. Economic transformation and its political discontents in China: Authoritarianism, unequal growth, and the dilemmas of political development[J].Annual Review of Political Science,2006,9:143–164. |
| [26] | Zheng X Y, Li H, Song F, et al. Central government’s infrastructure investment across Chinese regions: A dynamic spatial panel data approach[J].China Economic Review,2013,27:264–276. |
2.Sun Yet-sen University,Guangdong Guangzhou 510275,China;
3.Beijing International Studies University,Beijing 100024,China
 2018, Vol. 20
2018, Vol. 20



