
2024第50卷第10期
一、引 言
高质量发展的核心是通过技术创新获得持续的内生动力,从而降低资源等要素投入,使经济发展进入创新驱动的质量增长型模式(钟春平,2021)。然而,中国制造业部门主要依赖渐进式的增量创新,缺乏基于基础研究的突变型创新,关键领域的核心技术受制于人的局面还未从根本上得到改变(简泽等,2017)。那么,创新和技术进步的引擎是什么?这个引擎能否促进企业提高全要素生产率?又是什么因素制约着这个引擎发挥作用呢?
作为创新理论的奠基人,熊彼特主张创新的精髓在于创造性破坏,这是推动经济增长的核心动力。他关于创造性破坏的观点可以归纳为三个方面:首先,经济增长的源泉在于创新;其次,创新诞生于创业投资的过程中,企业家在竞争中寻求垄断利润或利益,这成为他们推动创新的主要动力;最后,创新的成果,如新产品或新技术的出现会全面替代旧有的产品和技术,并最终将它们逐出市场,这一过程本质上就是创造性的破坏。在新古典框架下,Segerstrom等(1990)最早尝试把熊彼特的创造性破坏思想纳入增长理论并形式化(刘志铭和郭惠武,2008)。自Aghion和Howitt(1992)构建了一个通过创造性破坏实现经济增长的内生增长模型开始,熊彼特增长范式已衍生出众多基于创造性破坏的模型,这些模型从竞争、失业、市场结构、企业动态变化、制度等方面重新阐释增长和发展。
与本文相关的文献主要分为创造性破坏测度和创造性破坏经济效应分析两大类。已有文献主要从国家层面(Peters和Zilibotti,2021)、产业层面(Becker和Ivashina,2023)和企业层面(Acemoglu等,2018)对创造性破坏进行测度。Haltiwanger等(2013)通过深入观察新企业的生命周期,从进入、成长到退出市场来测算创造性破坏,发现每一代新创企业都会创造大量新就业岗位,其中许多企业会在成立不久后消失,很多岗位也随之被摧毁。Decker等(2014)用企业创造率与企业破坏率之间的平均值来测算创造性破坏,发现创造性破坏平均水平更高的地区,其人均GDP的年均增长率也更高。
国内外学者对创造性破坏与生产率之间相关关系的研究结论并不一致,既有文献发现,创造性破坏能促进生产率的提高,在创造性破坏驱动的经济增长中,质量提升是增长的核心,创造性破坏的增强能带来更高的质量提升与创新,进而推动经济快速增长(钟春平和徐长生,2011;鄢萍等,2022)。随着增长模式从投入型向创新型转变,生产率提升的动力也发生转变,从过去主要依赖产业间的资源重新配置,转向如今经营主体间的优胜劣汰,在此过程中,创造性破坏机制的作用将更加凸显(蔡昉,2021)。但也有学者指出创造性破坏造成的真正意义上的破坏体现在两个方面:其一是当实体资产供过于求时,这些资产会被彻底销毁;其二是当传统的工作岗位不再被需要时,这些岗位上的工人会失业(Greenspan和Wooldridge,2018)。没有人知道未来哪些资产能成为具备生产效率的资产,哪些资产在未来不具备生产效率。新技术总是能诱发投机性泡沫,只要是泡沫就会有破灭的一天,有的泡沫破灭会造成极大的危害(McCloskey,2016)。创造性破坏会产生抑制效应,类似于产品市场竞争的熊彼特可挪用效应,从而阻碍生产率的提高(马红旗和申广军,2021),这提示创造性破坏可能对生产率产生非线性影响。企业在其增长潜力方面是异质性的(Acemoglu等,2018),不同企业类型的存在突出了创造性破坏在选择过程中的作用(Peters和Zilibotti,2021)。Freeman和Nelson认为,制度是影响创新进入市场的重要因素之一。制度创新能为技术创新以及经济增长提供激励和秩序(吴静,2018)。企业研发投入偏好创新数量还是质量,会直接影响其创新策略的选择(王志阁,2023)。创新策略选择是企业能否长期运行的关键(应千伟和何思怡,2022)。Acemoglu等(2006)认为,企业到技术前沿的距离取决于企业创造性破坏的速度,而企业创造性破坏的速度又取决于进入企业的质量以及进入的壁垒程度。可见,现有文献多数关注创造性破坏对生产率的线性影响,但对非线性影响的关注不足;多数研究聚焦创造性破坏对生产率的直接效应,但缺少对影响机制的深度分析;多数研究从理论上解释了创造性破坏对生产率影响的异质性,较少从实证层面上进行论证。
基于一个包含企业动力学的理论框架,本文提出创造性破坏与企业生产率之间存在倒U形关系的研究假说,即创造性破坏不足和过度都可能不利于企业生产率的提高。利用中国工业企业数据库中包含的新进入企业信息,匹配专利数据和城市面板数据,本文在制造业行业大类(二位码)层面系统检验了创造性破坏对企业生产率的影响,并从创新投资选择和成本约束两个角度分析了制约创造性破坏作用效果的内在原因。此外,鉴于企业异质性特点,本文进一步考察创造性破坏对企业生产率作用效果的差异性。与已有文献相比,本文可能的边际贡献主要体现在以下几点:(1)系统考察了创造性破坏对企业生产率的影响。近年来,不少文献认为,创造性破坏的增强能带来更高的质量提升与创新(钟春平和徐长生,2011;鄢萍等,2022)。蔡昉(2021)强调随着增长模式从投入型向创新型转变,创造性破坏机制的作用将更加凸显。简泽等(2017)认为,现有文献的注意力主要集中在创造性破坏过程“创造性”的一面,很大程度上忽略了“破坏性”的一面。本文将创造性破坏的两面性进行综合性分析,发现创造性破坏与生产率之间并不是简单的线性关系,而是存在倒U形的非线性关系,并从创新投资选择和成本约束两个视角分析了制约创造性破坏作用效果的内在原因。(2)拓展了企业全要素生产率领域的研究文献。以往文献研究对全要素生产率的分解主要从不同生产率企业进入、退出市场的行为以及生产要素在不同生产率企业间的再配置入手(乔小乐等,2020),而没有给出导致企业进出市场和生产要素再配置的具体原因。本文模型化了企业根据预期的租金来选择创新类型,推导出新企业通过创造性破坏进入市场,而被创造性破坏的企业则可能会退出市场,进而引致生产要素跨企业的再配置。(3)具有明确的政策含义。作为培育发展新质生产力的重要因素,创造性破坏一直是政府、业界和学术界共同关注的问题。本文研究发现,创造性破坏对企业生产率的影响呈现倒U形,且影响效果因创造性破坏主体、行业竞争程度和企业特性不同而呈现出差异性,这可以为政府制定更具有针对性的行业创新发展政策提供一定参考。
二、理论模型与研究假说
本文借鉴Peters和Zilibotti(2021)的方法,通过建立一个包含企业动力学的理论框架,将现有企业根据预期租金进行创新选择的过程进行模型化构建。
(一)劳动力数量与产品质量之间的关系。消费者有影响企业创新决策的力量(Aghion和Howitt,1992)。假定消费者偏向购买最高质量水平的产品j,产品j市场上的激烈竞争会促使企业开展更多的创新,即竞争促使企业通过创新来提升产品价值,以取得领先地位。假设代表性家庭的总效用函数为:
| $ U=\int_0^{\infty}e^{-\rho t}\mathrm{ln}C_t\mathrm{d}t $ | (1) |
| $ \mathrm{ln}C_t=\int_0^1\mathrm{l}\mathrm{n}\left[x_t\left(j\right)z_t\left(j\right)\right]\mathrm{d}j $ | (2) |
其中,
借鉴Garcia-Macia等(2019)的做法,假设在决定价格和产出之前,企业需先承担一项固定的生产成本。因此,仅有那些可以制造出最高质量产品
| $ Y={\left[\sum _{j=1}^{M}{\left({q}_{j}{y}_{j}\right)}^{1-\frac{1}{\sigma }}\right]}^{\frac{\sigma }{\sigma -1}} $ | (3) |
其中,
| $ {l}_{j}={\left(\frac{\sigma -1}{\sigma }\right)}^{\sigma -1}L{W}^{1-\sigma }{q}_{j}^{\sigma -1} $ | (4) |
其中,
| $ L_j=\sum_{j=1}^{M_f}l_j=\left(\frac{\sigma-1}{\sigma}\right)^{\sigma-1}LW^{1-\sigma}\sum_{j=1}^{M_f}q_j^{\sigma-1} $ | (5) |
由式(5)可以看出,一家企业的总劳动力需求完全取决于其生产产品的质量特性。换言之,劳动力在不同企业之间的分配与产品质量的分布紧密对应,呈现出一一映射的关系。
(二)创造性破坏对企业生产率的影响。借鉴Klette和Kortum(2004)的分析方法,将企业定义为其生产的产品组合,企业拥有多个产品线,这些产品线在创新和创造性破坏作用的基础上被增加或丢失。在任意时点,在位企业对产品生产存在两种状态,即创新或不创新。记
| $ g={\omega }_{0}I(1-\tau )-{\omega }_{1}\left(1-I\right)\tau $ | (6) |
假定在位企业生产率的期望增长率
| $ E\left(\frac{{V}_{t+1}-{V}_{t}}{{V}_{t}}|{V}_{t}=[{V}_{t}^{{\stackrel-{q}}_{k}},{V}_{t}^{{q}_{k}}]\right)=I\left(\zeta -1\right)=g $ | (7) |
其中,
| $ I=\frac{{\omega }_{1}\tau }{{\omega }_{1}\tau +{\omega }_{0}(1-\tau )-\left(\zeta -1\right)} $ | (8) |
由式(8)可得:
| $ \frac{\mathrm{\mathrm{\partial}}I}{\mathrm{\partial}\tau}=\frac{\omega_1(\omega_0-\zeta+1+\tau\dfrac{\partial\zeta}{\partial\tau})}{\left[\omega_1\tau+\omega_0\left(1-\tau\right)-\zeta+1\right]^2} $ | (9) |
定义
在创造性破坏程度较低时,在位企业有较强的动力加大产品研发力度,会将要素资源更多分配给研发创新。一旦研发成功,在位企业就可以垄断生产这一新产品,从而提升全要素生产率。然而对全新产品研发的投入会随着创造性破坏程度的提高而逐渐减少,当创造性破坏达到一定程度后,随着在位企业产品类型的增加,所需的固定成本会超比例上升,由于时间约束,在位企业不得不把其经营的产品类型限制在一定数量内,加上原有产品市场竞争愈发激烈,在位企业分配给原有产品创新的要素资源较少,可能无法与其他企业竞争,当其他企业推出质量更高的产品替代这一产品时,在位企业则会逐渐退出原有产品市场,全要素生产率下降。在某个创造性破坏程度之下,创造性破坏的正面效应超出负面效应,超出该创造性破坏程度后,负面效应将占据主导地位。由此,提出假说1:适度的创造性破坏会促进企业生产率的提升,但过度的创造性破坏又会抑制企业生产率的提升,即创造性破坏与企业生产率之间呈倒U形关系。
(三)在位企业创新投资策略选择。假设在位企业希望继续获得产品
| $ {I}_{j}=\gamma {\lambda }_{j}{R}_{j} $ | (10) |
其中,
根据在位企业的创新能力与技术前沿的距离,在位企业创新投资策略选择存在以下两种情形:
情形一:若在位企业的创新能力落后技术前沿,只有当产品
| $ \underset{{R}_{j}}{\mathrm{max}}\left\{\gamma {\lambda }_{j}{R}_{j}\left(1-{\tau }_{j}\right){V}_{t}^{{\stackrel-{q}}_{k}}-{\frac{1}{2}\phi_{I} }{R}_{j}^{2}{V}_{t}^{{q}_{k}}\right\} $ | (11) |
其中,
| $ {R}_{j}=\frac{\gamma {\lambda }_{j}}{{\phi }_{I}}\left(1-{\tau }_{j}\right)\zeta ={R}_{j1} $ | (12) |
由式(12)可知,
情形二:若在位企业的创新能力靠近技术前沿,当在位企业对产品
| $ \underset{{R}_{j}}{\mathrm{max}}\left\{\gamma {\lambda }_{j}{[{R}_{j}{V}_{t+1}^{{\stackrel-{q}}_{k+1}}+(1-R}_{j})(1-{\tau }_{j}){V}_{t}^{{\stackrel-{q}}_{k}}]-{\frac{1}{2}\phi }_{I}{R}_{j}^{2}{V}_{t}^{{\stackrel-{q}}_{k}}\right\} $ | (13) |
其中,
| $ {R}_{j}=\frac{\gamma {\lambda }_{j}}{{\phi }_{I}}\left(\zeta -1+{\tau }_{j}\right)={R}_{j2} $ | (14) |
由式(14)可知,
根据式(10),式(7)可表示为:
| $ E\left(\frac{{V}_{t+1}-{V}_{t}}{{V}_{t}}|{V}_{t}=[{V}_{t}^{{\stackrel-{q}}_{k}},{V}_{t}^{{q}_{k}}]\right)=\gamma {\lambda }_{j}{R}_{j\mathrm{1,2}}\left(\zeta -1\right)=g $ | (15) |
分别将式(12)和式(14)代入式(15)中,可得到:
| $ {g}_{1}=\frac{{\gamma }^{2}{\lambda }_{j}^{2}}{{\phi }_{I}}\left(1-{\tau }_{j}\right)(\zeta -1)\zeta $ | (16) |
| $ {g}_{2}=\frac{{\gamma }^{2}{\lambda }_{j}^{2}}{{\phi }_{I}}\left(\zeta -1+{\tau }_{j}\right)(\zeta -1) $ | (17) |
由式(16)和式(17)可知,
假说2a:创造性破坏将会通过创新投资赋能机制影响企业生产率提升;
假说2b:企业的创新能力对创新投资赋能效应有调节作用,倒U形曲线在创新能力较强的企业中更加陡峭。
(四)其他企业创新选择。其他企业不可能无条件获取产品
| $ \frac{\partial {g}_{1}}{\partial c}=-\frac{{\gamma }^{2}{\lambda }_{j}^{2}}{\theta {\phi }_{I}}{\tau }_{j}^{'}\left(c\right)\left(\zeta -1\right)\zeta > 0 $ | (18) |
| $ \frac{\partial {g}_{2}}{\partial c}=\frac{{\gamma }^{2}{\lambda }_{j}^{2}}{\theta {\phi }_{I}}{\tau }_{j}^{'}\left(c\right)\left(\zeta -1\right) < 0 $ | (19) |
进入成本降低会阻碍创新能力低的在位企业的自我创新,激发创新能力强的在位企业生产率的提升。因为进入成本降低时,其他企业更倾向对产品
在同一行业内,不同企业在创新资源的拥有情况上以及将资源转化为创新成果的能力上均表现出明显的不同。拥有更多创新资源的企业意味着更具有创新的能力,经过“循环累积因果”效应将初始的创新优势越积越大,从而通过研究与开发活动实现产品创新和工艺创新,最终促进企业生产率的提升。根据假定条件
三、研究设计
(一)样本数据。本文以中国工业企业数据库中制造业行业为研究样本。已有研究指出,中国工业企业数据库中2009年和2010年缺失法人代码、应付工资总额和折旧数据,样本统计质量难以保证研究的可靠性(余淼杰等,2018)。因此,本文采用2011—2013年数据作为研究样本,并用1998—2007年数据进行稳健性检验。为保证数据的准确性,剔除了缺失关键变量或明显违反会计准则的样本。为避免异常值的干扰,对连续变量进行上下1%的缩尾处理。
(二)变量定义。
1. 企业全要素生产率(tfp)。综合比较企业全要素生产率估算方法,LP法相较于其他测算方法更具合理性,该方法以中间产品投入作为企业全要素生产率的代理变量,而不是使用投资额作为代理变量,样本损失量较少,并在一定程度上有助于避免可能出现的内生性问题。为了获得投入要素的一致性和有效性估计,本文选择采用LP法来估算企业的全要素生产率,并对得到的tfp进行对数化处理。
2. 创造性破坏率(creative)。关于创造性破坏率的测算,现有研究主要形成了两类方法。一类是以Klette和Kortum(2004)、Peters和Zilibotti(2021)为代表,根据企业的研发创新强度来测算创造性破坏率;另一类是以Aghion等(2009)、Garcia-Macia等(2019)为代表的研究,利用结构模型间接地将企业创新活动与雇佣人数变动联系起来,构建了二者之间的映射关系,从而估计创造性破坏率。根据本文式(5)可推导出生产产品
(三)模型设计。为检验创造性破坏对企业全要素生产率的影响,本文构建如下基准回归模型:
| $ {tfp}_{it}={\beta }_{0}+{\beta }_{1}{creative}_{jt}+{\beta }_{2}{creative}_{jt}^{2}+\alpha {\mathit{C}}_{it}+{\mu }_{i}+{\sigma }_{t}+{\delta }_{j}{+\varepsilon }_{it} $ | (20) |
其中,i、j和t分别代表企业、行业和年份,被解释变量为企业
四、实证结果与分析
(一)描述性统计。本文以2011—2013年期间
(二)基准回归检验。由表1可知,在依次加入年份、行业和企业个体固定效应后,创造性破坏及其平方项均在1%的显著性水平下显著,创造性破坏(creative)的系数为正,而其平方项(creative2)系数为负。
| (1) | (2) | (3) | |
| creative | 0.2164***(5.54) | 0.5704***(10.05) | 0.1770**(2.39) |
| creative2 | −7.4741***(−7.72) | −13.5631***(−8.98) | −4.5887**(−2.47) |
| 控制变量 | 控制 | 控制 | 控制 |
| 年份固定效应 | 控制 | 控制 | 控制 |
| 行业固定效应 | 不控制 | 控制 | 控制 |
| 企业固定效应 | 不控制 | 不控制 | 控制 |
| 观测值 | 606 905 | 606 905 | 606 905 |
| R2 | 0.131 | 0.129 | 0.171 |
| 注:*** 、**、*分别代表1%、5%、10%的显著性水平,括号内为t值。限于篇幅,控制变量和常数项的估计结果未予列出,感兴趣的读者可以向作者索取,下表统同。 | |||
根据列(3),可画出创造性破坏与企业全要素生产率的关系图,见图1。该倒U形关系的表达式为Y = −
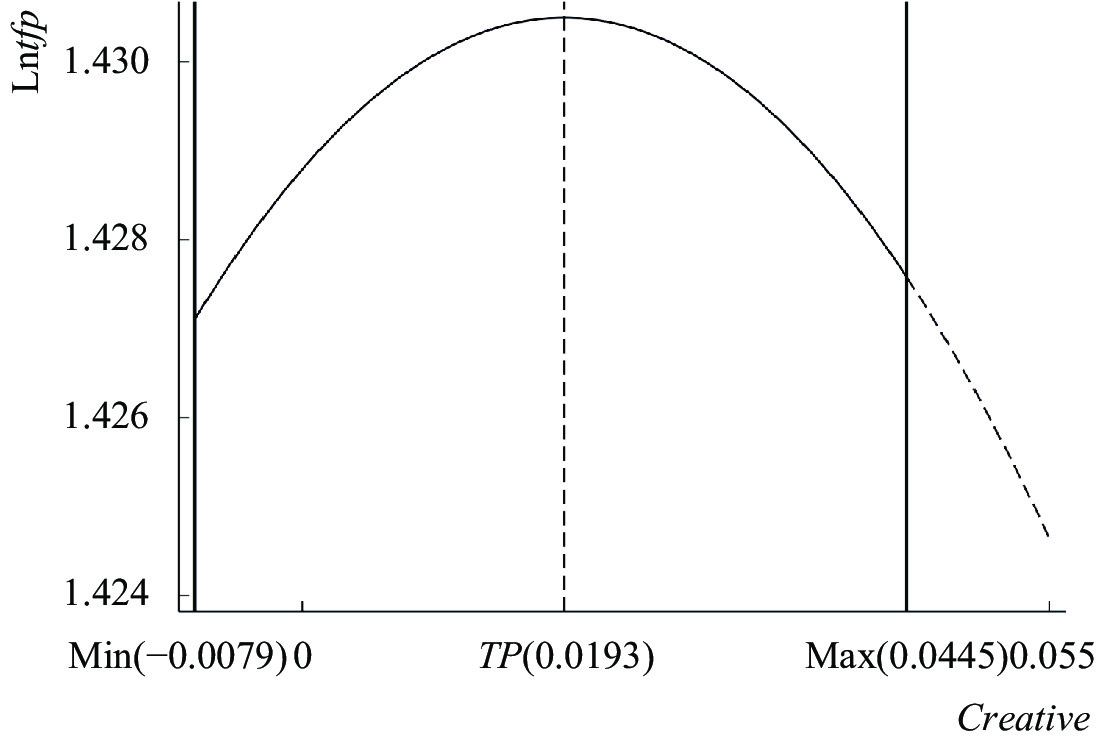
|
| 图 1 创造性破坏与企业生产率的倒U形关系 |
(三)作用机制检验。
1. 创新投资赋能机制。创造性破坏对企业创新活动会产生两种效应(张杰等,2014)。一是“熊彼特效应”。由于原生产企业创新研发投入的资金主要以内源融资为主,创造性破坏的增加会降低企业的超额利润。因此,创造性破坏会抑制企业的创新投资。二是“逃离竞争效应”。原生产企业为保持产品领先地位,会通过创新提升原有产品价值,当产品自我创新成功后,该产品的质量有所上升,从而继续垄断这一特定产品的生产。因此,创造性破坏会激励企业进行创新投资。本文选取专利申请数量(patent)作为企业创新活动的代理变量。根据创造性破坏对企业创新活动产生的两种效应,构建如下模型:
| $ {patent}_{it}={\beta }_{0}+{\beta }_{1}{creative}_{jt}+{\beta }_{2}{creative}_{jt}^{2}+\alpha {\mathit{C}}_{it}+{\mu }_{i}+{\sigma }_{t}+{\delta }_{j}{+\varepsilon }_{it} $ | (21) |
用模型(21)检验创造性破坏和企业创新活动之间存在的非线性关系。在此基础上,为了进一步检验创造性破坏对企业创新投资策略选择(invest)的影响,本文将研究样本缩小,仅保留专利申请数量不为零的企业样本。由于企业的创新投资主要发挥两大作用:一方面,通过过程创新引入足以提高生产效率的新工艺,从而降低生产成本;另一方面,通过产品创新提升产品质量,进而增加新产品在企业销售收入中的份额。所以,过往研究通常利用专利申请的具体情况来刻画企业的创新投资策略选择(黎文靖和郑曼妮,2016)。根据企业专利申请类型,本文把企业申请发明专利的行为界定为产品创新策略选择,而将企业申请实用新型专利和外观设计专利的行为视作过程创新策略选择(闫静波等,2023)。若企业选择进行产品创新,则invest赋值为1,进行过程创新则赋值为0。为此,本文构建如下模型:
| $ {invest}_{it}{=\beta }_{0}+{\beta }_{1}{creative}_{jt}+{\beta }_{2}{creative}_{jt}^{2}+\alpha {\mathit{C}}_{it}+{\mu }_{i}+{\sigma }_{t}+{\delta }_{j}{+\varepsilon }_{it} $ | (22) |
根据假说2b,本文认为创新能力较强的企业在面临创造性破坏时,更倾向于选择自有产品创新。对此,在模型(22)的基础上加入企业创新能力与创造性破坏的交互项,具体模型如下:
| $ \begin{aligned} {invest}_{it}=&{\beta }_{0}+{\beta }_{1}{creative}_{jt}+{\beta }_{2}{creative}_{jt}^{2}+{\beta }_{3}{dist}_{it}{+\beta }_{4}{creative}_{jt}\times {dist}_{it}\\ &+{\beta }_{5}{creative}_{jt}^{2}\times {dist}_{it}+\alpha {\mathit{C}}_{it}+{\mu }_{i}+{\sigma }_{t}+{\delta }_{j}+{\varepsilon }_{it} \end{aligned}$ | (23) |
其中,调节变量
表2显示了创造性破坏创新投资赋能效应的检验结果。其中,列(1)用全样本,以企业专利申请数量作为被解释变量对模型(21)进行回归的结果。列(2)和列(3)使用仅保留有专利申请数量的企业样本,以企业创造投资决策为被解释变量对模型(22)和模型(23)进行回归的结果。从列(1)可以看出,创造性破坏系数显著为正,而创造性破坏平方项系数显著为负,这表明创造性破坏对企业创新活动的影响是倒U形。因为当创造性破坏程度较低时,“逃离竞争效应”占主流,在位企业有较强的动力加大产品研发力度,会将要素资源更多地分配给研发创新,一旦全新产品研发成功,在位企业可以垄断生产这一新产品,从而提升全要素生产率;但当创造性破坏达到一定程度后,随着创造性破坏程度的增加,“熊彼特效应”占主流,在位企业的创新动力减小,从而抑制全要素生产率。
| (1) patent | (2) invest | (3) invest | |
| creative | 0.3112***(3.61) | 0.0683**(2.48) | 0.0381***(2.76) |
| creative2 | −0.0361*(−1.74) | −0.0305***(−4.03) | −0.0129***(−3.41) |
| creative | 0.0360***(−3.25) | ||
| creative2 | −0.0155***(5.18) | ||
| dist | 1.0972***(167.53) | ||
| 控制变量 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 |
| 观测值 | 606 905 | 94 803 | 94 803 |
| R2 | 0.005 | ||
| sigma_u | 2.5224*** | 2.5135*** | |
| 注:本表和后文实证结果均对年份、行业和企业个体固定效应进行了控制,下表统同。 | |||
从列(2)可以看出,创造性破坏与企业创新策略选择之间呈倒U形关系。在创造性破坏程度较低时,企业实施产品创新的动力会随着创造性破坏的增加而逐渐变强。因为当其他企业对在位企业原有产品创造性破坏的成功率较低时,在位企业一方面会选择产品创新策略中的原有产品创新,若原有产品创新成功,则该产品的质量得到实质性提升,从而能保持领先地位;另一方面,企业也会选择研发全新产品,若研发成功,该在位企业可以垄断生产这一新产品,从而获得该产品的垄断利润。但当创造性破坏程度较高时,这对在位企业原有产品市场份额的冲击较大,考虑到自身的创新能力,在位企业可能会对原产品进行结构和外观的重新设计,从而选择过程创新策略。由此可知,创造性破坏具有创新投资赋能的功能,适度的创造性破坏会促进在位企业进行产品创新,但过度的创造性破坏则会抑制在位企业进行产品创新。
列(3)为模型(23)的检验结果,在加入创造性破坏与企业创新能力的交互项后,交互项的系数都非常显著,这说明创造性破坏对创造投资策略选择的影响不仅与创造性破坏本身有关,还与企业创新能力有关。企业创造性破坏的二次项系数以及创新能力与创造性破坏二次项交互项的系数均显著为负,这说明企业创新能力对创造性破坏与企业创新投资策略选择之间的倒U形关系起到了正向的强化作用,因此,倒U形曲线在创新能力较强的企业中更加陡峭。假说2b得到了支持。当初期创造性破坏力度较弱时,位居前沿之下的企业有较强的动力追赶前沿,因为如果赶上,其利润将显著增加。于是初期远离前沿的大多数企业将很快变成前沿企业,随着创造性破坏程度提高,企业选择产品创新的倾向会逐渐增强。当初期创造性破坏程度较高时,高度的创造性破坏成功率将刺激前沿企业创新,以压倒其他企业。于是技术前沿将迅速推进,这会将大多数企业甩到前沿后面。位居前沿之下的原生产企业没有希望战胜潜在的进入者,随着创造性破坏程度进一步加剧,其选择产品创新的倾向就会逐渐减弱。
2. 成本约束机制。基于理论分析,创造性破坏对企业全要素生产率的影响会受到企业进入成本的约束。本文从人力和物力两个角度出发,分别检验了人力资本成本和物质资本成本对创造性破坏作用的边际效果。借鉴陈建伟等(2021)的研究,本文以每单位主营业务成本所获得的工业销售产值测度企业资本成本;参考董亚宁等(2021)的研究,用主营业务收入与从业人员数比值刻画企业劳动力成本。基于此,在式(20)中加入企业进入成本的交互项,具体模型如下:
| $ {t f p}_{it}={\beta }_{0}+{\beta }_{1}{creative}_{jt}+{\beta }_{2}{creative}_{jt}^{2}+{\beta }_{3}{\mathit{D}}_{it}{+\beta }_{4}{creative}_{jt}\times {\mathit{D}}_{it}+{\beta }_{5}{creative}_{jt}^{2}\times {\mathit{D}}_{it}+\alpha {\mathit{X}}_{it}+{\mu }_{i}+{\sigma }_{t}+{\varepsilon }_{it} $ | (24) |
其中,
表3报告了调节效应检验结果。在企业进入成本上,劳动力成本和资本成本对企业的全要素生产率有显著的正影响。当进入成本较高时,如果其他企业想要进入某一产品市场,那么这些企业需要付出较高的时间和货币成本搜寻产品的相关信息及攻克研发技术,这在一定程度上限制了其他企业的进入,巩固了在位企业生产产品的市场份额,有助于在位企业全要素生产率的提升。由列(1)发现,企业劳动力成本与创造性破坏一次项的交互作用显著为正,与创造性破坏平方项的交互作用显著为负,这说明创造性破坏与企业全要素生产率之间的倒U形关系随着劳动力成本的提升而迅速增加,直至转折点,之后快速下降。因此,在劳动力成本较高的企业,倒U形曲线更加陡峭。由列(2)可以发现,企业资本成本与创造性破坏一次项的交互作用显著为正,与创造性破坏平方项的交互作用显著为负,这意味着在资本成本较高的情况下,创造性破坏在倒U形曲线拐点前的正效应和拐点后的负效应增强。因此,验证了创造性破坏对企业生产率的作用效果会受到成本约束机制的调节。
| 变量 | (1) lntfp | (2) lntfp |
| creative | 0.1437**(2.07) | 0.1659**(2.34) |
| creative2 | −0.0251(−1.45) | −0.0233(−1.30) |
| creative | 0.1229***(4.48) | |
| creative2 | −0.0253***(−3.40) | |
| c_incrd | 4.8995***(48.47) | |
| creative | 0.1501***(5.91) | |
| creative2 | −0.0273***(−3.94) | |
| c_zycb | 6.3090***(26.24) | |
| 控制变量 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 |
| 观测值 | 606 905 | 606 905 |
| R2 | 0.290 | 0.241 |
(四)内生性与稳健性检验。
1. 内生性检验。上述基准回归已初步证实理论分析的结论,即创造性破坏对企业全要素生产率的作用呈倒U形,但基准回归中自变量与因变量可能互为因果,导致出现内生性问题。为解决内生性问题,本文采用工具变量法来缓解内生性。参考马嘉楠等(2018)的研究,以地方政府的科创偏好作为工具变量。一般来说,地方政府的科创偏好越强,其所在地区的企业为了获得财政补贴越有可能进行创新。对于生产某一产品的企业来说,由于财政补贴的加持,其他企业进入这一产品市场的成本相对降低,这在一定程度上激励了其他企业进入该产品市场,导致创造性破坏程度增强。而地方政府的科创偏好与单个企业的创新能力、管理能力均无关。从这个意义来看,使用地方政府科学技术支出与公共财政支出总额的比值作为地方政府的科创偏好(creative_iv)满足工具变量的要求。此外,参考王莉静等(2024)的工具变量构建方法,本文也将解释变量滞后一期(即创造性破坏的一次项和二次项滞后一期)作为工具变量进行回归。
表4列(1)展示了工具变量的第一阶段回归结果,结果显示工具变量与自变量正相关,且第一阶段弱工具变量检验F统计量大于10,满足工具变量的相关性要求。列(2)将创造性破坏与工具变量同时作为解释变量,发现创造性破坏的一次项和二次项系数仍显著,而工具变量的系数却不显著,表明工具变量满足排他性约束。列(3)报告了将解释变量滞后一期作为工具变量进行回归的结果,结果依然支持创造性破坏与企业全要素生产率之间呈倒U形的关系。
| 变量 | (1) creative | (2) lntfp | (3) lntfp |
| creative | 0.1520**(2.04) | ||
| creative_iv | 0.0056***(8.16) | 0.0899(0.96) | |
| creative2 | −0.0375**(−2.01) | ||
| L.creative | 0.8484*(1.78) | ||
| L.creative2 | −0.7883**(−2.13) | ||
| 控制变量 | 控制 | 控制 | 控制 |
| 年份固定效应 | 控制 | 控制 | 控制 |
| 行业固定效应 | 控制 | 控制 | 控制 |
| 企业固定效应 | 控制 | 控制 | 控制 |
| 观测值 | 593 750 | 593 750 | 317 179 |
| F值 | 66.587 |
2. 稳健性检验。第一,为了进一步检验创造性破坏与企业全要素生产率之间的倒U形关系,这里使用utest命令进行检验。结果表明,创造性破坏对企业全要素生产率作用的曲线斜率呈先正后负的特点,极值点为
五、进一步分析
(一)基于创造性破坏类型差异的分析。不同的创造性破坏主体可能对企业全要素生产率产生不同的影响。为此,本文进一步从产品市场竞争的视角出发,将企业定义为其生产的产品组合,并将企业分为原有生产的在位企业、扩展进入该产品市场的其他在位企业和新进入企业。依照理论分析可知,创造性破坏既源于在位企业,也源于新进入企业。这里本文借鉴陈建伟等(2021)的研究,将成立两年的企业定义为新进入企业,则可通过计算新进入企业创造性破坏率得到在位企业创造性破坏率。
为了验证假说4,本文根据创造性破坏的组成结构,分别对新进入企业创造性破坏和其他在位企业创造性破坏与企业全要素生产率之间的关系进行检验。表5的列(1)和列(2)结果表明,不同类型的创造性破坏对企业全要素生产率的影响并不相同。其他在位企业创造性破坏对企业全要素生产率的影响呈倒U形,这与总创造性破坏的变化趋势一致。而新进入企业创造性破坏对企业全要素生产率的影响呈U形。每一代新创企业都会创造大量新就业岗位,由于其中许多企业会在成立不久后消失,很多岗位也随之被破坏,但幸存的企业则继续创造就业并发展壮大。新企业刚进入某一产品市场时,企业规模一般较小,且拥有不需要承担新旧技术转型成本的优势,使得新进入企业的创新更为激进,所带来的创造性破坏力度更强。随着新进入企业规模的扩张,其创新概率会下降,从而对某一产品市场的创造性破坏程度会减弱。
| (1)其他在位企业 | (2)新进入企业 | (3)行业竞争强 | (4)行业竞争弱 | |
| creative | − | |||
| creative2 | − | − | − | |
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 观测值 | 606 905 | 606 905 | 303 453 | 303 452 |
| R2 | 0.171 | 0.172 | 0.169 | 0.163 |
(二)基于行业竞争程度差异的分析。竞争加剧会使靠近技术前沿的企业加强创新,以超越竞争,从而提高企业全要素生产率;相反,远离技术前沿的企业所进行的创新活动则会受到抑制。本文参考连燕玲等(2023)的做法,以企业营业收入占其所在行业比重的赫芬达尔指数表示行业竞争程度。按照行业竞争程度的中位数将样本分为两组,高于等于中位数划分为强竞争组,反之则为弱竞争组。从表5列(3)和列(4)可知,在行业竞争强样本中,创造性破坏与企业全要素生产率之间存在倒U形关系,这与基准结果是一致的,说明处于强竞争行业的企业全要素生产率对创造性破坏变化的反应较敏感。而在行业竞争弱样本中,只有creative2的系数在5%的水平上显著为负,这表明创造性破坏与企业全要素生产率的倒U形关系在弱竞争组中不明显。
(三)基于企业规模和产权性质差异的分析。不同规模的企业在面对创造性破坏时,可能会采取不同的策略和应对方式,从而产生不同的影响和结果。按照企业总资产对数值的中位数将样本分为两组,高于中位数的为大规模企业,反之为小规模企业。由表6列(1)和列(2)可知,创造性破坏与企业全要素生产率的倒U形关系在大规模企业中更明显,而在小规模企业中不显著,这表明创造性破坏有效影响了大型企业全要素生产率水平。与非国有企业相比,国有企业更容易受到政策上的保护,可能缺乏创新激励,进而存在创新效率损失(安同良等,2020)。列(3)和列(4)结果表明,在非国有企业中,创造性破坏对企业全要素生产率的影响更明显,但在国有企业中不显著。这说明非国有企业在面临创造性破坏时会有更高的创新意愿,而国有企业则相对保守,这与近年来我国国有企业处于资源获取优势地位却创新意愿低下的现象相一致。
| (1)大规模企业 | (2)小规模企业 | (3)国有企业 | (4)非国有企业 | |
| creative | ||||
| creative2 | − | − | − | − |
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 观测值 | 303 455 | 303 450 | 22 122 | 584 783 |
| R2 | 0.228 | 0.250 | 0.121 | 0.177 |
六、主要结论与政策建议
创造性破坏是极其强大的“变革发动机”,其不仅能用新技术取代旧技术,而且能开辟生产工艺深刻变革的通路。文章对创造性破坏与企业生产率的关系进行了推导和验证,从创新投资选择和成本约束两个角度分析了制约创造性破坏作用效果的内在原因,并进一步考察了创造性破坏对企业生产率作用效果的异质性,得出以下结论:(1)制造业行业的创造性破坏与企业生产率存在显著倒U形关系。当行业创造性破坏程度小于
本文研究结论可为科技创新引领高质量发展提供有益的政策启示。首先,创新动力源于创新租金激励的投资决策,特别是研发投资。政府需有效干预和监管以保障租金,尤其是知识产权。但补贴在位企业可能阻碍更具创新活力的新企业进入市场,因为补贴可能导致在位企业抬高技能劳动力和其他生产要素的成本,产生资源再配置效应。因此,政府在扶持产业时,应协调产业政策与竞争政策,确保不阻碍新企业进入。其次,初期创造性破坏较弱时,落后企业有追赶动力,一旦赶上,利润大增,多数企业能迅速跻身前沿。而接近前沿的企业则要积极应对创造性破坏加剧的情形。此时,政府应控制破坏力度,因为适度破坏能促进经济创新,此时“超越竞争”效应为主。然而,当初期创造性破坏较强时,高强度破坏会刺激创新能力强的企业进行创新,技术前沿迅速推进,多数企业落后,且远离前沿的企业对此反应消极。此时“打击效应”凸显,政府需警惕过度破坏可能对创新产生抑制作用。最后,政府在制定产业政策时,应优先关注气候变化、可再生能源、医疗和国防等议题。还应鼓励利用高技能劳动力,并特别关注竞争激烈的产业,因为对技能密集型产业的公共投资能更有效地促进生产率增长。
| [1] | 安同良, 魏婕, 舒欣. 中国制造业企业创新测度——基于微观创新调查的跨期比较[J]. 中国社会科学, 2020(3): 99–122. |
| [2] | 蔡昉. 中国经济:实践探索与学理解说[M]. 四川:四川人民出版社,2021:67−70. |
| [3] | 陈建伟, 苏丽锋, 郭思文. 进口渗透、需求异质性与企业进入[J]. 中国工业经济, 2021(7): 175–192. DOI:10.3969/j.issn.1006-480X.2021.07.014 |
| [4] | 董亚宁, 杨开忠, 顾芸. 创新成本、空间分割与创新增长分异研究——基于空间经济增长理论[J]. 中国软科学, 2021(7): 87–96. DOI:10.3969/j.issn.1002-9753.2021.07.009 |
| [5] | 黄勃, 李海彤, 刘俊岐, 等. 数字技术创新与中国企业高质量发展——来自企业数字专利的证据[J]. 经济研究, 2023(3): 97–115. |
| [6] | 简泽, 谭利萍, 吕大国, 等. 市场竞争的创造性、破坏性与技术升级[J]. 中国工业经济, 2017(5): 16–34. |
| [7] | 黎文靖, 郑曼妮. 实质性创新还是策略性创新?——宏观产业政策对微观企业创新的影响[J]. 经济研究, 2016(4): 60–73. |
| [8] | 连燕玲, 郑伟伟, 高皓. 创新困境下的制造业企业战略响应——基于创新绩效期望落差与响应式搜索行为的研究[J]. 中国工业经济, 2023(8): 174–192. DOI:10.3969/j.issn.1006-480X.2023.08.011 |
| [9] | 刘志铭, 郭惠武. 创新、创造性破坏与内生经济变迁——熊彼特主义经济理论的发展[J]. 财经研究, 2008(2): 18–30. DOI:10.3969/j.issn.1001-9952.2008.02.002 |
| [10] | 马红旗, 申广军. 规模扩张、“创造性破坏”与产能过剩——基于钢铁企业微观数据的实证分析[J]. 经济学(季刊), 2021(1): 71–92. |
| [11] | 马嘉楠, 翟海燕, 董静. 财政科技补贴及其类别对企业研发投入影响的实证研究[J]. 财政研究, 2018(2): 77–87. |
| [12] | 乔小乐, 宋林, 戴小勇. 僵尸企业与产能利用率的动态演化——来自中国制造业企业的经验证据[J]. 南开经济研究, 2020(4): 206–225. |
| [13] | 孙浦阳, 宋灿. 贸易网络、市场可达性与企业生产率提升[J]. 世界经济, 2023(3): 125–153. |
| [14] | 王莉静, 徐梦杰, 徐莹莹, 等. 企业数字化转型对服务化价值共创绩效的影响研究: 基于合作网络视角[J]. 中国软科学, 2024(6): 165–176. DOI:10.3969/j.issn.1002-9753.2024.06.016 |
| [15] | 王志阁. 企业研发投入如何影响创新策略选择——基于政府扶持与市场竞争视角[J]. 华东经济管理, 2023(6): 54–65. |
| [16] | 吴静. 环境规制能否促进工业“创造性破坏”——新熊彼特主义的理论视角[J]. 财经科学, 2018(5): 67–78. |
| [17] | 闫静波, 贺小刚, 陈元, 等. 困境企业价值再造: 实质性创新还是策略性创新?[J]. 管理评论, 2023(6): 92–110. |
| [18] | 鄢萍, 殷戈, 袁锡林, 等. 创造性破坏、开发全新产品还是产品质量提升?——中国出口企业的创新维度核算[J]. 经济科学, 2022(4): 34–49. |
| [19] | 应千伟, 何思怡. 政府研发补贴下的企业创新策略: “滥竽充数”还是“精益求精”[J]. 南开管理评论, 2022(2): 57–67. DOI:10.3969/j.issn.1008-3448.2022.02.007 |
| [20] | 余淼杰, 金洋, 张睿. 工业企业产能利用率衡量与生产率估算[J]. 经济研究, 2018(5): 56–71. |
| [21] | 余明桂, 马林, 王空. 商业银行数字化转型与劳动力需求: 创造还是破坏?[J]. 管理世界, 2022(10): 212–225. |
| [22] | 张杰, 郑文平, 翟福昕. 竞争如何影响创新: 中国情景的新检验[J]. 中国工业经济, 2014(11): 56–68. |
| [23] | 钟春平, 徐长生. 产品种类扩大、质量提升及创造性破坏[J]. 经济学(季刊), 2011(2): 493–522. |
| [24] | 钟春平. 高质量发展需要有创造性破坏思路: 理论基础与最优政策[J]. 经济纵横, 2021(3): 72–77. |
| [25] | 朱沛华, 陈林. 工业增加值与全要素生产率估计——基于中国制造业的拟蒙特卡洛实验[J]. 中国工业经济, 2020(7): 24–42. |
| [26] | Acemoglu D, Aghion P, Zilibotti F. Distance to frontier, selection, and economic growth[J]. Journal of the European Economic Association, 2006, 4(1): 37–74. DOI:10.1162/jeea.2006.4.1.37 |
| [27] | Acemoglu D, Akcigit U, Alp H, et al. Innovation, reallocation, and growth[J]. American Economic Review, 2018, 108(11): 3450–3491. DOI:10.1257/aer.20130470 |
| [28] | Aghion P, Howitt P. A model of growth through creative destruction[J]. Econometrica, 1992, 60(2): 323–351. DOI:10.2307/2951599 |
| [29] | Aghion P, Blundell R, Griffith R, et al. The effects of entry on incumbent innovation and productivity[J]. The Review of Economics and Statistics, 2009, 91(1): 20–32. DOI:10.1162/rest.91.1.20 |
| [30] | Becker B, Ivashina V. Disruption and credit markets[J]. The Journal of Finance, 2023, 78(1): 105–139. DOI:10.1111/jofi.13187 |
| [31] | Decker R, Haltiwanger J, Jarmin R, et al. The role of entrepreneurship in US job creation and economic dynamism[J]. Journal of Economic Perspectives, 2014, 28(3): 3–24. DOI:10.1257/jep.28.3.3 |
| [32] | Garcia−Macia D, Hsieh C T, Klenow P J. How destructive is innovation?[J]. Econometrica, 2019, 87(5): 1507–1541. DOI:10.3982/ECTA14930 |
| [33] | Greenspan A,Wooldridge A. Capitalism in America:A history[M]. Penguin:Penguin Press,2018. |
| [34] | Haltiwanger J, Jarmin R S, Miranda J. Who creates jobs? Small versus large versus young[J]. Review of Economics and Statistics, 2013, 95(2): 347–361. DOI:10.1162/REST_a_00288 |
| [35] | Klette T J, Kortum S. Innovating firms and aggregate innovation[J]. Journal of Political Economy, 2004, 112(5): 986–1018. DOI:10.1086/422563 |
| [36] | McCloskey D N. Bourgeois equality:How ideas,not capital or institutions,enriched the world[M]. Chicago:University of Chicago Press,2016. |
| [37] | Peters M,Zilibotti F. Creative destruction,distance to frontier,and economic development[R]. Working Paper 29333,2021. |
| [38] | Segerstrom P S,Anant T C A,Dinopoulos E. A Schumpeterian model of the product life cycle[J]. The American Economic Review,1990,80(5):1077−1091. |

