一、引　言

技能偏向性技术进步（SBTC）在促进发达国家创新型经济发展过程中发挥了重要作用（Eicher和Turnovsky，1999），但与发达国家SBTC迅速发展并在各行业快速扩散不同，中国总体SBTC发展相对缓慢（Shen和Zheng，2020）。其原因在于，技术进步方向由要素禀赋结构所决定，只有与要素禀赋结构相匹配的适宜技术进步才能充分释放技术进步的生产率促进效应（Antonelli和Quatraro，2010），因此，要素禀赋差异内生决定了技术进步的类型。

改革开放初期，中国低技能劳动力相对丰富的要素禀赋和中国制造低端嵌入产品内分工的现实发展路径，使中国经济高速增长主要由低技能偏向性技术进步推动（沈春苗和郑江淮，2022）。虽然低技能偏向性技术进步为中国制造的高速增长做出了重要贡献，但显然无法为高质量发展阶段的经济增长提供持久动力。近年来中美经贸摩擦的常态化与国内劳动力市场出现的结构性难题等都是典型例证。在此背景下，以推动SBTC为抓手，充分发挥高技能要素在中国新动能重塑过程中的支撑和引领作用成为新发展阶段的重要议题。

在市场机制作用下，SBTC的发生和发展是高、低技能劳动力工资相对水平（技能溢价）变动引致企业投资和个体教育投资决策自发调整的内生决定过程（Acemoglu，2002b），而技能溢价的变化趋势是劳动力市场供求关系和劳动力市场规制政策共同作用的结果。已有文献主要从前者出发，基于高技能劳动力供给增加引致技能溢价大幅下降视角，对技术进步偏向成因和机制展开了丰富研究（Krusell等，2000；Acemoglu，2002a），但关于劳动力市场规制尤其是最低工资制度如何通过技能溢价变化影响技术进步偏向这一问题，现有文献较少涉及。

最低工资标准是政府为了维护劳动者取得劳动报酬的合法权益而制定的政策，在中国薪酬体系中主要发挥托底作用。自2004年劳动和社会保障部出台《最低工资规定》和2008年《劳动合同法》实施以来，覆盖全国范围内不同行政区域的多层级、差异化的最低工资标准不断形成，且每两年至少调整一次的制度要求在加强对低技能劳动者保护的同时，也进一步强化了低技能工资上涨的刚性趋势（卿陶和黄先海，2022）。对此，一个很自然的疑问是，最低工资标准上涨推动的低技能劳动力成本上升和短期内的技能溢价下降的趋势，将如何通过微观市场机制作用于总体层面SBTC？如果最低工资标准上涨能够促进SBTC，促进机制又将受到哪些外部条件的影响?对这些问题的思考不仅可以深化我们对劳动力市场规制效应的认识，对认识劳动力市场变化所产生的深远影响以及经济结构调整和转型升级也具有启示意义。

本文将最低工资标准上涨引致的短期内技能溢价下降纳入包含非中性技术进步的一般均衡增长模型，基于资本技能互补和技能投资内生化假说，从微观层面揭示了最低工资标准上涨促进SBTC的作用机理。在手动收集2003—2020年280个地级市最低工资标准并对地级市SBTC进行合理估算的基础上，利用地级市面板数据对理论假说进行了实证检验。结果表明，最低工资标准上涨显著促进了地级市SBTC的发展；最低工资标准上涨通过资本深化和消费升级两个机制合力促进了技术进步的技能偏向水平；最低工资标准上涨的SBTC促进效应存在显著的地区异质性特征。

与本文相关的文献主要有两类：一类是有关SBTC的影响因素研究，从供需两端分别强调了技能供给增加和消费结构升级的积极作用。前者研究表明，资本品价格持续下降和劳动工资刚性上涨，以及以机器设备为载体的物质资本与高技能劳动力的高度互补特征，合力推动了发达国家技术进步的技能劳动偏向（Krusell等，2000），蕴含前沿技术的新增设备投资也在一定程度上促进了中国SBTC的发展（宋冬林等，2010）。后者研究表明，政府或居民的高技能产品需求偏好是引导私人投资流向的重要机制（Cozzi和Impullitti，2010），进而可以通过产业内和产业间的技术偏向变化合力推动经济总体的SBTC发展（姚毓春等，2014）；开放经济背景下，发达国家的技能投资偏向还会因其与发展中国家的进出口贸易（Freeman和Kleiner，2005）和离岸外包（Chu等，2015）等外部需求而被进一步强化。另一类文献是有关最低工资政策经济效应的研究。最低工资对低收入群体的增收机制有助于扩大内需（邹红等，2023）。最低工资标准是对低收入劳动者工资权益的保障，而技能差异又是造成劳动力工资差距的主要因素（洪银兴，2022），所以首当其冲受到影响的是低技能劳动的用工成本和低技能密集型企业。研究发现，最低工资标准上涨导致了低收入劳动者工资的直接上升（马双等，2012），低技能员工更易因最低工资标准提高而被企业辞退，而高能力员工则不存在这一现象（蔡伟贤等，2021），这在自动化程度高的行业更为明显（谢杰等，2022）。低技能成本上升在激励企业资本深化动机（Harasztosi和Lindner，2019；李磊等，2023）的同时，也会影响企业对技术进步方向的选择（魏下海等，2023），进而其能通过企业内或企业间的资源再配置效应作用于经济增长、收入分配和结构转型（杜鹏程等，2022；王文春等，2022）。

相对于已有文献，本文创新之处在于：第一，把最低工资标准上涨引致的短期内技能溢价下降纳入包含非中性技术进步的一般均衡增长模型，基于资本技能互补和技能投资内生化假说，从微观层面揭示了最低工资标准上涨促进SBTC的作用机理；第二，基于手动收集的2003—2020年280个地级市最低工资标准，利用地级市面板数据对理论假说进行了实证检验，为合理评估最低工资政策效应提供了来自转型发展中国家的经验证据；第三，研究发现在资本技能互补和技能投资内生化情境下，最低工资上涨会通过资本深化和消费升级机制促进技术进步的技能偏向，这为政府部门引导技能偏向性技术进步提供了政策制定的依据。

二、典型化事实

（一）总体SBTC、低技能劳动成本与最低工资标准

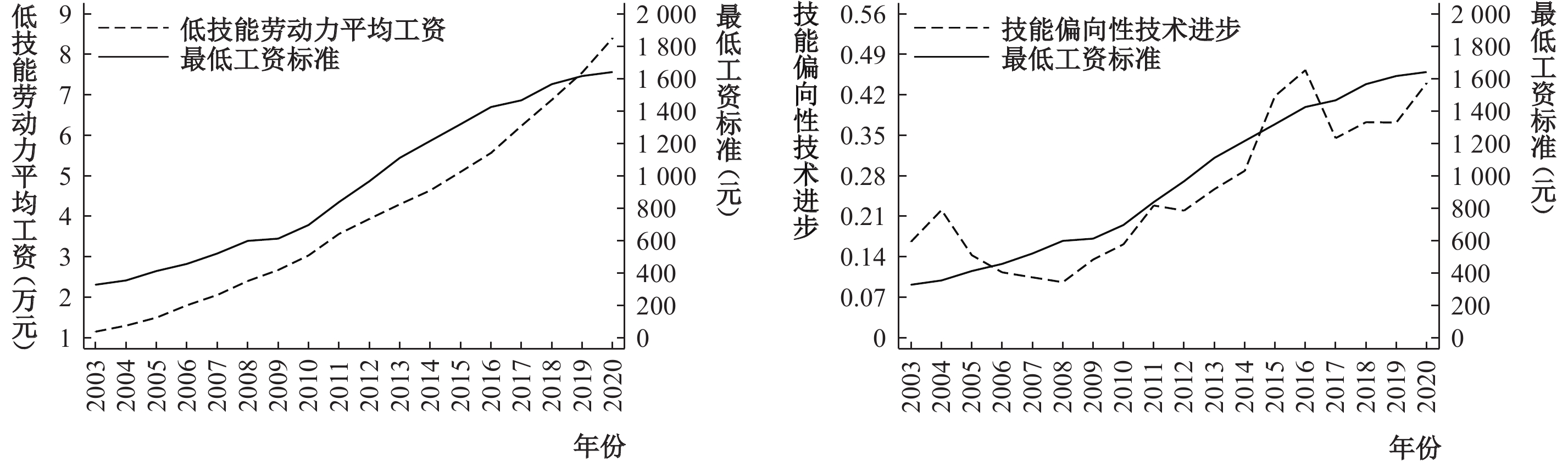
最低工资标准是政府调控劳动市场的主要手段，其实施和调整不仅直接影响低收入群体的工资水平，也是推动企业劳动力成本上升的外部力量，还可能是SBTC的重要诱因。图1描述了2003—2020年全国总体SBTC、低技能劳动成本与最低工资标准的变动趋势，其中，全国平均最低工资标准通过280个地级市最低工资标准的算数平均得到，全国总体SBTC水平通过280个地级市的技能溢价算数均值和技能供给算数均值结合下文式（29）计算得到。从图1可以看出：（1）最低工资标准呈现逐年上涨态势，样本期内全国平均最低工资标准从2003年的320元上涨到2020年的1650元，年均几何平均增速达10.13个百分点；（2）低技能劳动力平均工资与最低工资标准呈现出较为同步的正向变动关系；（3）伴随最低工资标准的不断上涨，全国层面SBTC水平呈现出总体上涨态势。

（二）资本深化、消费升级与最低工资标准

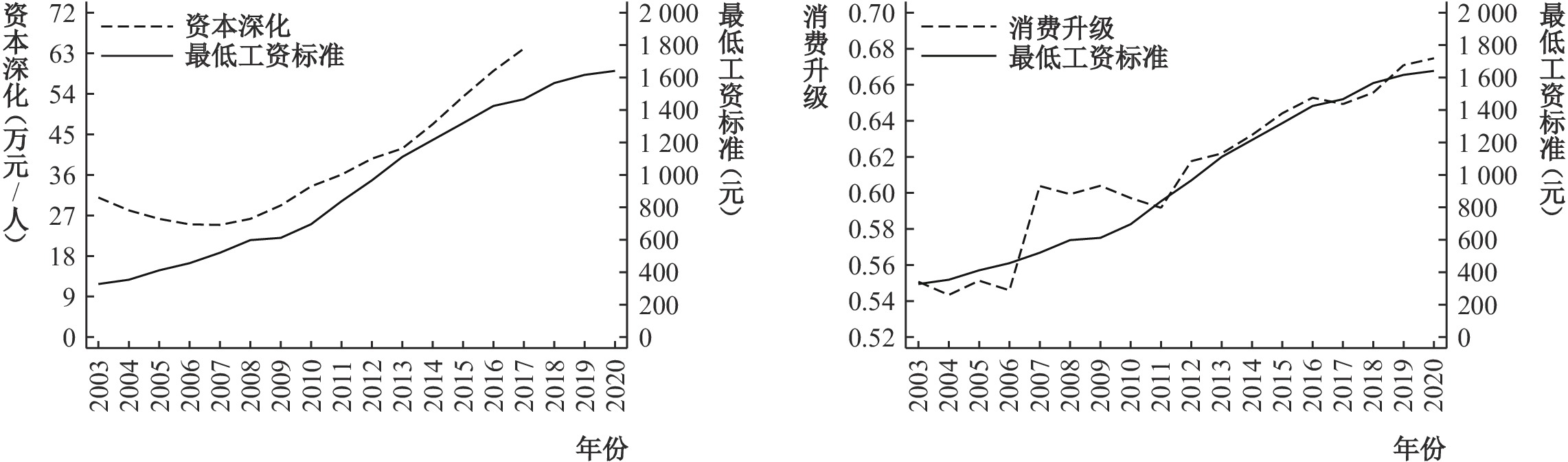
最低工资标准上涨推动了低技能劳动成本上涨，一方面会激励企业用资本替代低技能劳动，由此呈现资本劳动比不断上升的资本深化特征；另一方面，资本和技能互补带来的技能溢价上升以及低技能劳动力的技能投资激励，又会带来人均收入水平的提升，进而呈现高技能产品消费比重不断上升的消费升级特征。图2刻画了2003—2020年我国资本深化、消费升级与最低工资标准的变动关系，可以看出三者呈现较为同步的上涨态势。

三、理论模型

（一）模型构建

1. 消费部门。家庭部门既是劳动力的供给者，又是最终品的需求者，设代表性家庭的效用函数为$ {U_t} = \ln {C_t} $，$ {C_t} $为最终品消费，家庭收入来自劳动供给和资本收入，家庭各部门每期提供高技能劳动力${H_t}$单位和低技能劳动力${L_t}$单位。在把最终品价格作为计价物的条件下，各时期代表性家庭的最优决策函数可设为：

进一步把家庭部门的高、低技能劳动供给数量内生化。假设$ t $时期家庭拥有的总人口数为$ {N_t} $，人口增长率$ n $由各时期的人口出生率$ \beta $和人口死亡率$ \mu $共同决定。每个个体的存活年限为$ T $，教育年限为$ D $，个体出生时拥有的能力禀赋为$ a\in(0,1) $，个体根据自身能力禀赋以及未来各时期市场条件下高、低技能劳动的工资水平来决定是否接受高等教育，进而内生地决定了各时期劳动力市场的技能结构。用$r$表示利率，则$ t $时期个体的教育决策可以表示为：

对式（2）进行求解，得到均衡状态下接受高等教育与否无差异的劳动力禀赋为：

由$ n = \beta - \mu $和$ \beta {N_t} = \mu {N_{t + T}} $得到各时期的出生率和死亡率满足：

由式（3）、式（4）和式（5）得到各时期高、低技能劳动力供给数量为：

2. 最终品部门。设代表性企业的最终品生产函数满足双层嵌套不变替代弹性（CES）生产函数特征，生产过程需要资本（$ {K_t} $）、高技能密集型产品（$ {Y_{ht}} $）和低技能密集型产品（$ {Y_{lt}} $），具体函数形式为：$ {Y}_{t}={[{\left({Y}_{ht}^{\rho }+{K}_{t}^{\rho }\right)}^{\tfrac{\sigma }{\rho }}+{\left({Y}_{lt}-\overline{r}\right)}^{\sigma }]}^{\tfrac{1}{\sigma }}，$其中，$ 0 < \rho < \sigma < 1 $， ¹$ \overline r = \xi ({I_t}){Y_{lt}} $，$ 0 \leqslant \xi ({I_t}) \leqslant 1 $，$ \xi '({I_t}) > 0 $，$ \xi ''({I_t}) < 0 $，$ {I_t} $表示最终品厂商的总支出，反映最终品生产过程中对低技能产品需求的非位似偏好特征。 ²用$ {P_t} $表示最终品价格，$ {P_{ht}} $表示高技能产品价格，$ {P_{lt}} $表示低技能产品价格，$ {R_t} $表示资本价格，最终品厂商的利润最大化问题表示为：

由式（8）的一阶条件可得：

式（9）除以式（11）得：

式（9）除以式（10）得：

式（13）除以式（12）得：

3. 高、低技能产品部门。设高（低）技能厂商分别在给定的技术水平下用高（低）技能中间投入品生产高（低）技能产品，生产函数为$ Y_{jt}=\left(\int_0^{A_{jt}}x_{ijt}^{\alpha}\mathrm{d}i\right)^{\frac{1}{\alpha}} $，其中，$ j=h、j=l $分别表示高、低技能产品，${A_{ht}}$、${A_{lt}}$分别表示高、低技能偏向性技术水平，${x_{ijt}}$表示高（低）技能产品生产所需的中间投入，一单位高（低）技能产品生产需要一单位高（低）技能劳动力投入。静态均衡下，高、低技能产品生产厂商的成本最小化函数可以表示为：

由式（15）得高、低技能最终品厂商对中间投入品的需求函数分别为：

由式（16）需求函数可知，高（低）技能产品分别对高（低）技能中间品投入的需求价格弹性为$1/(1 - \alpha )$，结合中间投入品生产函数${x_{iht}} = {h_{it}}$和${x_{ilt}} = {l_{it}}$，可以得到：

（二）一般均衡求解

由劳动力市场出清得：

由高、低技能中间品厂商零利润条件得：

把式（19）—式（22）代入式（14）并化简得：

把高技能劳动力工资作为计价物，即${w_{ht}} = 1$，由式（6）、式（7）、式（21）和式（23）得到${A_{ht}}/{A_{lt}}$关于${w_{lt}}$的关系式。由参数和变量的取值范围可知，式（23）等号右边第①部分的值恒大于零，因此${A_{ht}}/{A_{lt}}$和${w_{lt}}$的关系主要取决于第②部分，令$ \Phi(w_{lt})=(\dfrac{H_t}{L_t})^{\frac{\sigma-1}{\sigma}\cdot\frac{\alpha}{\alpha-1}}\cdot(\dfrac{w_{lt}}{w_{ht}})^{\frac{1}{\sigma}\cdot\frac{\alpha}{\alpha-1}} $，$ \eta = \dfrac{{{e^{ - rT}} - 1}}{{{e^{ - rT}} - {e^{ - rD}}}} $，$ \upsilon = \dfrac{{{e^{n\left( {T - D} \right)}} - 1}}{{{e^{nT}} - 1}} $，把式（6）和式（7）代入并化简得：

进一步对式（24）两边同时取对数并对$ {w_{lt}} $求导得：

由式（25）可以看出，只要$ \dfrac{\mathrm{d}\ln\Phi(w_{lt})}{\mathrm{d}w_{lt}} > 0 $，那么$ \text{d}\dfrac{A_{ht}}{A_{lt}}/\mathrm{d}w_{lt} > 0 $。为表述方便，令$ F(w_l)=\dfrac{\mathrm{d}\ln\Phi(w_{lt})}{\mathrm{d}w_{lt}} $，由于无法直接求出$F({w_l})$的显示解，所以我们先对式（25）中的模型参数进行校准（见表1），再对函数关系式进行数值模拟。

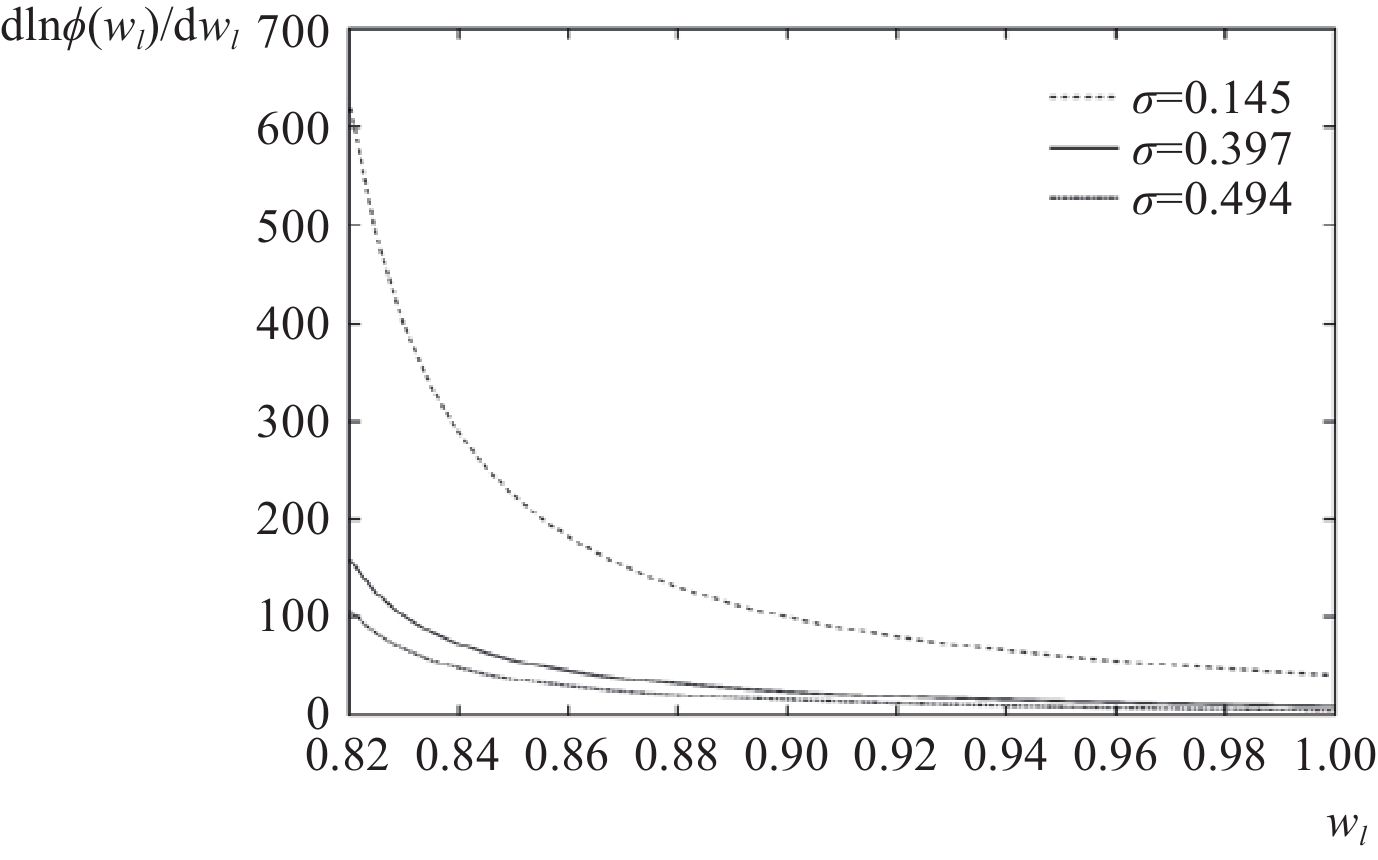
为保证模拟结果的稳健性，根据参数取值范围$ 0 < \sigma < 1 $，结合已有文献的替代弹性估计结果，分别取$ \sigma $为0.145、0.397和0.494，利用MATLAB模拟的$ \sigma $不同取值情形下的$F({w_l})$和$ {w_{lt}} $变动关系如图3所示，可以看出，$F({w_l})$取值始终大于零， ³即$ \dfrac{\mathrm{d}\ln\Phi(w_{lt})}{\mathrm{d}w_{lt}} > 0 $，由此$ \text{d}(A_{ht}/A_{lt})/\mathrm{d}w_{lt} > 0 $得证。据此得到命题1。

命题1：最低工资标准上涨引致的短期内技能溢价缩小，有助于促进长期技能偏向性技术进步的发生和发展。

进一步由式（23）可知，反映非位似消费偏好的参数$ \xi $和反映资本技能互补特征的参数关系$ \rho < \sigma $进入式（23），并且呈现出以下两点特征：一是资本技能互补关系越强，即$ \sigma - \rho $越大，$ \text{d}(A_{ht}/A_{lt})/\mathrm{d}w_{lt} > 0 $值越大，结合低技能劳动工资上涨引致资本对低技能劳动的微观替代关系，这意味着资本对低技能劳动的替代程度越强，资本与高技能劳动的互补程度越高，低技能工资上涨对技能偏向性技术进步的促进效果越强；二是最终消费中的高技能密集型产品比重越高，即$ \xi $越大，$ \text{d}(A_{ht}/A_{lt})/\mathrm{d}w_{lt} > 0 $且值越大，结合低技能工资上涨引致的人均收入水平提高和消费升级特征，这意味着人均收入水平提高引致的消费结构越高级化，低技能劳动工资上涨对SBTC的促进效果越强。据此，我们得到推论1。

推论1：资本技能互补和技能投资内生化情境下，最低工资标准上涨通过供给侧的资本替代劳动（资本深化）机制和需求侧的消费升级机制合力促进了技能偏向性技术进步。

四、计量模型设定、变量测度与数据说明

（一）计量模型设定

本文选取2003年至2020年中国280个地级市面板数据，首先对理论模型部分提出的命题1展开实证检验，计量模型如式（26）所示；其次分别从资本深化和消费升级两个机制对推论1展开实证检验，计量模型如式（27）和式（28）所示。延续Nunn和Qian（2011）的做法，对计量模型中连续数值变量取对数处理，比例变量不取对数处理。

其中，i和t表示地级市和年份，sbtc表示技能偏向性技术进步，mwage表示最低工资标准，klrat表示资本深化，cosm表示消费升级，分别用人均消费支出cosm_pe和技能消费结构cosm_up衡量，X为控制变量集合，${\mu _i}$、${\eta _t}$为城市、时间固定效应，$\varepsilon $为随机扰动项。

（二）变量测度及数据说明

1. 被解释变量：技能偏向性技术进步（sbtc）。采用Acemoglu（2002b）方法计算历年地级市的SBTC水平，测度的方法如下：

其中，$ {\tilde w_{it}} = {w_{iht}}/{w_{ilt}} $表示高、低技能劳动相对工资（技能溢价），$ {w_{iht}} $为高技能劳动的名义工资水平，$ {w_{ilt}} $为低技能劳动的名义工资水平；$ {\tilde h_{it}} = {H_{it}}/{L_{it}} $为高、低技能劳动力的相对供给，$ {H_{it}} $为高技能劳动力数量，$ {L_{it}} $为低技能劳动力数量；$\delta $为高、低技能劳动力间的替代弹性。计算所需变量数据的详细估算方法如下：

首先，用地级市所属省份总就业中的大专及以上学历就业人员比重作为省内各地级市总就业中高技能劳动力比重的替代，结合地级市总就业数，分别计算出各地级市的高、低技能劳动力数，其中，地级市总就业数通过城镇单位就业人数、城镇私营和个体就业人数加总得到。地级市总就业数来自《中国城市统计年鉴》，其余数据来自《中国劳动力统计年鉴》。

其次，用地级市所属省份总就业中的科技人员比重作为地级市总就业中科技人员比重的替代，结合地级市总就业数，分别计算出各地级市的科技人员数，再用地级市GDP占所属省份GDP比重乘以所属省份的科技人员劳务支出，得到各地级市的科技人员总劳务支出； ⁴再用地级市科技人员总劳务支出除以科技人员数，得到科技人员平均劳务支出，用来作为地级市高技能劳动力平均工资水平的替代。各省份科技人员数和劳务支出来自《中国科技统计年鉴》，各省份GDP来自《中国统计年鉴》，各地级市GDP来自《中国城市统计年鉴》。

再次，通过地级市在岗职工平均工资乘以地级市就业人数，得到地级市就业人员的工资总额，再减去高技能劳动的工资总额，得到地级市低技能劳动的工资总额，结合低技能劳动数，得到地级市低技能劳动平均工资。地级市在岗职工工资数据来自《中国城市统计年鉴》。

最后，根据估算得到的高、低技能劳动数量和高、低技能劳动平均工资，计算各地区的技能溢价和技能相对供给，再分别计算替代弹性取值为1.4和2.0时的地级市SBTC水平。

2. 解释变量：最低工资标准（mwage）。本文通过北大法宝等法律法规数据库、各省市人民政府网站以及人力资源和社会保障厅等政府官网，手动搜集并整理各个地级市的月最低工资标准数据。考虑到同一地级市不同区或县的月最低工资标准存在差异，加之并非所有地级市都公布县区层面的月最低工资标准数据，为保证统计口径的一致性，统一采用地级市市区层面的月最低工资标准数据来计算历年各地级市最低工资标准；考虑到不同地级市月最低工资标准的调整时间并不统一，为消除月最低工资标准调整时点（月份）差异对地级市年度最低工资标准的影响，参考许和连和王海成（2016）的做法，使用加权平均法来计算年度平均最低工资标准，具体而言，如果新的最低工资标准调整月份为8月，则地级市年度平均最低工资标准=[（5×新的月最低工资标准数据+7×旧的月最低工资标准数据）]/12，再通过地级市所属省份的居民消费价格指数，将历年名义最低工资标准平减为以2003年为基期的实际最低工资标准。

3. 机制变量。（1）资本深化（klrat）：用地级市资本存量与低技能劳动力的比值来反映资本对低技能劳动的替代，历年实际资本存量通过永续盘存法$ {K}_{t}={K}_{t-1}\left(1-\delta \right)+{I}_{t} $计算得到。其中，$ {I}_{t} $表示经各省份固定资产投资价格指数平减到以2003年为基期的地级市实际投资额，$ \delta $是采用柯善咨和向娟（2012）计算的建筑安装工程和设备工具器具购置两类资本品的折旧率，经地级市所在省份的这两类资本品在城镇及城镇集体单位固定资产投资中的投资比重进行加权平均后的综合折旧率，2003年（基期）实际资本存量通过前一年投资流量和资本存量计算得到，参考Young（2003）和张军等（2004）的做法，2002年末资本存量通过当年实际投资流量的10倍得到。（2）消费升级（cosm）：分别用人均消费支出（人均社会消费品零售总额）和技能消费结构（总消费中的高技能消费支出比重）衡量。 ⁵前者通过地级市社会消费品零售总额除以地级市总人口数得到，其中，社会消费品零售总额是经省份居民消费价格指数处理得到的以2003年为基期的实际值，地级市人口通过地级市GDP除以地级市人均GDP得到。后者利用2002年、2007年、2012年和2017年31个省份的投入产出（IO）表，结合历年地级市三次产业增加值估算得到。具体估算方法为：首先，利用124个（4年×31个省）IO表分别计算各省高、低技能密集型制造业（简称高、低技能制造业）的最终消费率和高、低技能密集型服务业（简称高、低技能服务业）的最终消费率，其最终消费率用最终消费支出除以增加值得到；其次，利用省级高、低技能制造业（服务业）最终消费率乘以省内各地级市历年制造业（服务业）增加值，得到地级市层面历年高、低技能制造业（服务业）最终消费支出，其中，2003—2006年各省历年最终消费率用2002年IO表计算得到，2007—2011年各省历年最终消费率用2007年IO表计算得到，2012—2016年各省历年最终消费率用2012年IO表计算得到，2017—2020年各省历年最终消费率用2017年IO表计算得到；最后，参考鲁桐和党印（2014）的做法，将地级市历年高（低）技能制造业和高（低）技能服务业的最终消费支出进行加总得到高（低）技能最终消费支出，进而用地级市高技能最终消费支出占最终消费总支出的比值来反映居民的技能消费结构。

4. 控制变量。（1）劳动力技能结构（skill）：技能劳动大幅供给引致了发达国家SBTC的发生，用地级市所在省份大专及以上学历的就业人数占总就业人数的比值衡量；（2）所有制结构（own）：城市经济的所有制结构是影响劳动力就业岗位和区域间流向的重要因素，用地级市城镇私营和个体就业数占地级市总就业数的比值衡量；（3）研发补贴强度（rd）：研发补贴是各国政府支持科技创新的重要政策工具，用地级市的地方科学事业经费支出占地方财政一般预算内支出的比重衡量；（4）外资利用度（fdi）：外商直接投资是后发国家获取国际技术溢出的重要途径，用地级市实际外商投资总额占地级市实际增加值的比值衡量；（5）产业结构（ind）：技能偏向性结构变迁是促进SBTC的重要机制，用地级市GDP中的服务业增加值比重衡量；（6）城市化进程（city）：城市化进程是影响要素流动的重要因素，用城镇单位就业人数占地级市总人口的比重衡量；（7）金融深化（fina）：地区金融发展水平是影响地区资本积累和技术创新的重要因素，用城市年末金融机构存贷款总额占地区GDP的比重衡量。劳动力技能结构计算所需数据来自《中国劳动统计年鉴》，其余控制变量计算所需数据均来自《中国城市统计年鉴》。

五、实证结果和分析

（一）最低工资标准上涨影响SBTC的基准回归

表2报告了对命题1的验证。为控制不可观测因素对实证结果稳健性的影响，表2列（1）—列（4）分别报告了逐步控制个体和时间固定效应的回归结果。考虑到同一地级市在不同时间上观测值的相关性，所有回归模型中的残差都聚类到地级市层面，综合表2结果可以发现，样本期内最低工资标准上涨显著促进了SBTC的发展，无论是否控制个体或时间效应，最低工资标准的回归系数始终显著为正。列（4）结果表明，在其他条件不变情形下，最低工资标准每上涨1个百分点，技能偏向性技术进步水平提升0.774个百分点，这意味着，最低工资标准调整的确对微观主体行为进而对总体层面的技术进步方向产生了深刻影响。

（二）资本深化和消费升级机制检验

表3报告了最低工资标准上涨引致企业决策和家庭决策适应性调整进而通过资本深化和消费升级影响SBTC的作用机理，即对推论1的验证。其中，表3列（1）—列（3）报告了最低工资标准上涨促进资本深化的作用机制，列（4）—列（9）分别从人均消费支出上升和技能消费结构变动两个方面报告了最低工资标准上涨促进消费升级的作用机制。回归结果显示了最低工资标准上涨对资本深化和消费升级的显著促进效果。表3列（3）结果表明，在其他条件不变情形下，最低工资标准每上涨1个百分点，资本深化提升0.226个百分点，结合资本和高技能劳动力互补的特征，这意味着最低工资标准上涨引致的资本对低技能劳动力的替代是促进技能偏向性技术进步的重要机制。表3列（6）和列（9）结果则表明，在其他条件不变情形下，最低工资标准每上涨1个百分点，人均消费支出上升0.271个百分点，技能消费比重上升7.900个百分点。这意味着最低工资标准上涨对提高居民消费能力进而促进消费升级发挥了显著促进作用。

（三）工具变量法检验

本文核心变量间的反向因果关系可能会造成严重的估计偏误。为此，对最低工资标准和SBTC的关系重新进行2SLS估计。分别采用三种不同的构造思路设计工具变量（IV）：

1. 参考Mayneris等（2018）做法，以各地级市平均工资预测值（$ prewag{e_{i,t}} $）的40%作为当期最低工资标准的IV（$awage_{it}^P$）。依据主要有两个：一是中国的最低工资标准是从中央到地方政府自上而下制定的，并规定各地区的最低工资标准应不低于当地社会平均工资的40%，故以各地区平均工资的40%作为最低工资标准的IV是相对客观的；二是考虑到地级市平均工资会受到同时期最低工资标准的影响，同时由于相关部门并未公布地级市细分行业平均工资数据，故采用地级市所在省份之外的其他省份的细分行业平均工资数据的增长路径信息来估算当期各地级市平均工资的预测值，计算公式为：

其中，下标i、j和t分别表示地级市、行业和年份，–p（i）表示不包含地级市i所在省份p（i）之外的其他所有省份；$ prewag{e_{i,t}} $表示平均工资水平的预测值；$ L $表示就业，$ {L_{i,j,t - 2}}/{L_{i,t - 2}} $表示滞后2期的地级市细分行业的就业份额；$ wag{e_{ - p(i),j,t - 1}}/wag{e_{ - p(i),j,t - 2}} = 1 + {g_{_{ - p(i),j,t - 1}}} $，$ {g_{_{ - p(i),j,t - 1}}} $是通过–p（i）细分行业j平均工资的算数平均值计算得到的增速；$ wag{e_{ - p(i),j,t - 1}} $为滞后1期的平均工资水平。为确保计算结果的稳健，本文还通过–p（i）细分行业工资总额的加总值除以就业人数加总值，计算得到 –p（i）的各期平均工资水平，进而重新计算得到各地级市平均工资的预测值$ prewage_{_{i,t}}^{new} $和工具变量$awage_{it}^{PN}$。实证结果见表4列（1）和列（2）。

2. 参考邹红等（2023）做法，以最低工资标准预测值作为当期最低工资标准的IV（$mwage_{i,t}^P$）。因该方法使用的是省内其他地级市最低工资增长路径的历史信息，与当期最低工资标准相关且不受地级市劳动市场需求冲击的影响，所以IV外生性更强。用$ mwag{e_{i,t - 2}} $表示滞后两期的地级市最低工资标准，$ g_{-i}^{t - 2 \sim t} $是通过地级市所在省份内其他地级市平均最低工资标准计算的两期几何增长率，详见式（31）。实证结果见表4列（3）。

3. 参考赵瑞丽等（2016）和刘贯春等（2017）的做法，采用同一省份除该地级市外的其他地级市的平均最低工资标准作为对应的IV（$mwag{e_{\_ave}}$）。同一省份内地理位置、要素禀赋和历史文化等经济社会因素较为类似，政府制定的最低工资标准相关性较强，同时理论上看，省内其他城市最低工资标准制定对本地SBTC的直接影响并不大。实证结果见表4列（4）。

（四）稳健性检验

1. 更换解释变量测度方法。基准回归中使用的地级市最低工资标准是通过最低工资标准调整月份进行加权平均计算得到，为确保测度结果的稳健性，本文对最低工资标准调整月份在8月（不含）之后的地级市，统一采用调整前的最低工资标准。即当地级市最低工资标准调整月份大于8月时，地级市当期最低工资标准水平采用调整月份之前的最低工资水平；当地级市最低工资标准调整月份小于等于8月时，地级市当期最低工资标准水平采用调整月份之后的最低工资水平，重新检验最低工资标准上涨的SBTC效应，实证结果见表5列（1）。

2. 重新测度被解释变量。①参考Acemoglu（2002b）的做法，测度替代弹性为2.0情形下的SBTC水平并重新进行实证检验，实证结果如表5列（2）所示。②重新测度不同地区替代弹性水平下的被解释变量。参照郑江淮和荆晶（2021）做法，对东中西部地区替代弹性进行分类估计，得到异质性替代弹性下的地级市SBTC水平，实证结果如表5列（3）所示。

3. 控制异质性时间趋势。为控制地区层面随时间变化的不可观测因素可能引致的估计偏误，进一步引入东中西部地区—年份交互固定效应，实证结果如表5列（4）和列（5）所示。

4. 自然实验检验。基于异质性替代弹性下的地级市SBTC水平，本文进一步利用2008年《劳动合同法》出台引致最低工资标准水平实质性上涨的外生冲击来检验最低工资标准上涨对SBTC的作用方向。用2003年城市平均工资水平的40%与当年最低工资标准的差额反映《劳动合同法》出台对地级市最低工资水平的处理强度，当地级市处理强度大于样本中位数处理强度时，处理组虚拟变量Treat取1；当年份为2008年及之后时，时间虚拟变量Post取1。双重差分的估计结果如表5列（6）所示。

（五）异质性检验

前文实证检验得到了最低工资标准上涨对SBTC的平均效应，然而不同地级市的经济发展水平、最低工资标准和技能密集型产业结构等存在很大差异，可能会导致最低工资标准上涨对处于不同经济环境下的SBTC产生不同的效果，为此需要进一步考察最低工资标准上涨对SBTC的异质性影响。

本文分别利用地级市面板数据最低工资标准的中位数值、人均GDP中位数值和高技能密集型产业比重的中位数值，将样本按照三个类别分别分为两组，以此为基础分别考察最低工资标准的SBTC效应，实证结果如表6所示。其中，列（1）—列（4）显示，最低工资标准上涨对最低工资标准较高地区、经济发展水平较高地区SBTC的促进效果更强，这与经济学直觉相符。一方面，一般来说经济发展水平较高地区的其最低工资标准水平也较高；另一方面，这意味着当且仅当最低工资标准处于较高水平时，最低工资标准持续上涨引致的短期内技能溢价显著下降才会对微观主体的生产和消费决策行为产生实质性影响，进而作用于地区层面的技术进步方向。列（5）—列（6）显示，最低工资标准上涨对高（低）技能密集型产业比重较低（高）地区的SBTC促进效果更强，反映了低技能劳动密集型企业对低技能劳动成本上升更为敏感的生产技术特征，在最低工资标准上涨进而推动低技能劳动成本上升的条件下，会激励低技能密集型企业采用资本替代劳动。

六、结论和启示

技能偏向性技术进步是创新型经济发展的基本动力。在要素偏向技术进步不断发展和低技能劳动成本不断上升的双重背景下，研究最低工资标准刚性上涨对技术进步方向的作用机理，对充分理解中国劳动力市场变化的深层次影响、劳动力市场规制的政策效应和实体经济转型发展具有重要的启示意义。

基于最低工资标准上涨推动的低技能劳动成本上升，进而引致资本深化和消费升级的典型事实，本文研究了最低工资标准上涨对技术进步技能偏向的作用机制。首先，把最低工资标准上涨引致的短期内技能溢价下降纳入包含非中性技术进步的一般均衡增长模型，基于资本技能互补和技能投资内生化假说，从微观层面揭示了最低工资标准上涨促进SBTC的作用机理。其次，在手动收集2003—2020年280个地级市最低工资标准及对地级市SBTC进行合理估算的基础上，利用地级市面板数据对理论假说进行了实证检验。研究发现，最低工资标准上涨显著促进了地级市SBTC的发展。其通过资本深化和消费升级两个机制合力促进了技术进步的技能偏向水平，最低工资标准上涨对SBTC的促进效应存在显著的地区异质性特征。

本文研究具有重要的政策含义。第一，健全最低工资标准调整机制。相关部门应结合所在地区的产业结构、经济发展水平和最低工资标准，因地制宜地推动最低工资标准的动态化和差异化调整，以充分释放最低工资标准上涨对技能偏向性技术进步发展的促进效果。第二，加大对技能培训的支持力度。为克服技术进步技能方向调整引致的结构性失业等负面影响和满足资本深化对高技能劳动需求增加的自然要求，政府部门应加大对高等教育和技能培训的政策支持，通过技能投资决策的内生化机制促进高技能劳动力供给的持续增加。第三，促进劳动力跨地区跨部门自由流动。劳动要素市场化配置是企业资本深化和技能结构升级的应有之义，为此应逐步放开户籍限制并通过地区间交通基础设施和信息基础设施的互联互通，有效降低劳动力空间流动的交易成本。

1$ \rho<\sigma $，意味着资本和高技能密集型产品的替代弹性$ 1 /(1-\rho) $小于资本和低技能密集型产品的替代弹性$ 1 /(1-\sigma) $，由此反映了资本和技能的相对互补特征。

2由于一般均衡状态下，最终品部门的总支出、总产值和总收入与家庭部门的总支出相等，因此，$ \bar{r}=\xi\left(I_{t}\right) Y_{l t} $本质上反映了经济体内居民消费的非位似偏好特征。

3当我们用$ {w}_{h} $作为计价物时，$ {w}_{l} $实则反映了技能溢价的倒数，图3横轴取值范围由2003—2020年地级市面板数据中技能溢价水平的倒数值得到。

4由于《中国科技统计年鉴》统计口径变更，2008年及以前采用科技活动人员数口径，2009年以来采用R&D人员数口径。

5由于统计口径的变更，2011年至2013年人均消费支出用人均消费现金支出替代。