
2024第50卷第3期
2. 兰州大学 经济学院, 甘肃 兰州 730000;
3. 南开大学 经济研究所, 天津 300071
2. School of Economics, Lanzhou University, Lanzhou 730000, China;
3. Institute of Economics, Nankai University, Tianjin 300071, China
一、引 言
“双循环”战略是中国对外开放战略重心的重大调整,内陆地区相对于沿海地区的区位劣势将趋于弱化,这不可避免地对中国的区域经济格局产生影响。改革开放至今,中国沿海和内陆的经济发展差距经历了由拉大到缩小的过程,南北差距则经历了由拉大到短暂缩小再到拉大的过程。这是否预示着中国区域经济发展会出现第三次转折?是否被一股强大的经济力量所驱动?这股力量的来源是什么?为了解开这些疑问,本文尝试弄清“双循环”背景下空间经济理论的思想来源。
“双循环”战略本身即蕴含着经济活动的空间分布问题,从更大范围讲其涉及经济活动的国内与国际循环问题,从次级范围讲其涉及经济活动的国内区域间循环问题。自“双循环”战略提出后,国内学者从不同角度对其进行了解读。钱学锋和裴婷(2021)从大国经济角度进行分析,基于欧阳峣(2012)研究,将大国经济研究范式提炼为从市场范围到分工深化的斯密大国经济研究范式,从规模效应到竞争优势的马歇尔规模经济研究范式,以及从二元结构到经济转型的刘易斯二元经济研究范式。裴长洪和刘洪愧(2021)从马克思的经济循环思想出发,认为构建新发展格局重要论述的思想只能从马克思主义理论中探寻,具体涉及马克思的剩余价值理论和经济循环理论。此外,安虎森和汤小银(2021)分析了新发展格局下的区域协调发展路径,提出区域协调发展要多元开放联动和多元协调。但是,目前“双循环”视角下的区域协调发展研究多为政策解读或是逻辑推理,缺乏更为深入的微观基础方面的研究。
区域经济是空间经济的基本表现形式之一,其主要特征就是块状经济,即经济活动在空间上的非连续性。马歇尔尝试从外部性角度解释经济活动的空间分布不平衡问题,指出投入产出关联、劳动力市场共享、知识溢出导致了经济活动的空间集聚(马歇尔,2019)。胡佛在《区域经济学导论》中则将形成经济活动区位结构的基本因素概括为自然资源优势、集聚经济和交通运输成本,并进一步用专业性的语言将其表述为生产要素的不完全流动性、生产要素的不完全可分性、产品和服务的不完全流动性,同时指出集聚经济可能来源于特定产业的规模经济(胡佛,1990)。比照马歇尔和胡佛的观点,我们会发现投入产出关联本质上反映了规模经济,它与生产要素的不完全可分性对应,劳动力市场共享和知识溢出反映广义生产要素的不完全流动性。而生产要素的不完全流动性、生产要素的不完全可分性、产品和服务的不完全流动性最终又与空间障碍导致的空间成本相关联。鉴于此,安虎森(2020)将块状经济形成的客观基础提炼为这几个方面:生产要素的不完全流动性、经济活动的不完全可分性、商品交易和提供服务的空间障碍、创新能力的区位锁定作用和知识溢出的局域性。
其实,早在1776年亚当·斯密就注意到了自然资源、交易成本、规模经济和技术溢出的作用(亚当·斯密,2015)。他指出,劳动生产力上的最大增进似乎都是分工的结果,而分工水平受交换能力的限制,也即受市场广狭的限制。
综上所述,斯密分工思想不仅是分析“双循环”战略的重要理论范式,也是空间经济理论的主要思想来源。而经济活动要依托于特定的地理空间,根据空间不可能定理,当加入空间因素后经济理论需以规模收益递增为基础。因此,交易成本和规模收益递增是分析空间经济活动时必须考虑的两个基本要素,这与斯密分工思想的理论内涵相一致。因此,本研究将以斯密分工思想为指引,参考杨小凯(2019)对分工的研究,借鉴Lucas(1988)、杨立岩和王新丽(2004)对人力资本的处理技巧,吸收Fujita等(1999)以及Fujita和Thisse(2012)对中间投入品的建模方法,将规模收益递增的工业部门、规模收益递减的农业部门和土地要素加入到中间投入品模型中,建立开放条件下的区域经济模型,并在此基础上深入剖析中国区域经济格局演变的驱动力,探究“双循环”战略实施对中国区域经济格局的影响。
研究结果表明,中国区域经济格局的形成是市场竞争下地域分工演化的结果,是斯密分工思想在区域经济中的体现。沿海地区和内陆地区的发展差距与它们的对外交易效率差异和区域内部的交易效率差异密切相关。在分工原理的作用下,这将演化出不同的区域产业结构,并最终导致区际经济发展差距,并且这种差距在理论上将经历“快速增加—较快下降—缓慢上升”的演变过程。在中期差距虽会收敛但不会消失,在后期甚至还有拉大的风险,而“双循环”战略的实施将影响国内区域间的交易效率和不同区域的对外交易效率,进而影响中国的区域经济格局。因此,要想缩小区域发展差距,可从交易效率入手,借助产业链和产业集群,充分利用分工的作用来实现区域间的协调发展。
本文的边际贡献和创新点主要有:(1)以斯密分工思想为指引,借助于新兴古典理论、新经济地理学理论和新增长理论,加入人力资本累积、规模经济、交易效率、生产迂回和技术扩散等因素,构建开放条件下的区域经济模型,巩固了区域经济关系分析的微观基础;(2)在构建区域经济模型基础上,剖析了中国区域经济格局演变的驱动力,并在其指引下探究了“双循环”战略的实施对中国区域经济格局的影响,最后提出实现区域协调发展的应对策略;(3)从数理和实证两方面证明了斯密分工思想的合理性,并弄清了其确切形式,即劳动生产力上的最大增进大都是分工的结果,而分工水平同时受交换能力和市场范围的限制。
二、理论模型
本部分将基于亚当·斯密的分工思想来构建理论模型。斯密将分工促进经济增长的原因归结为劳动熟练程度的提高、工作转换时间的节约和机器的发明与使用(亚当·斯密,2015)。对斯密分工思想进行模型化的技术路径主要有两条,即专业化报酬递增路径和规模报酬递增路径。前者以杨小凯开创的新兴古典主义为代表,将报酬递增与劳动力的专业化联系起来,假设随着劳动力专业化水平的提升,单位劳动力生产的产品数量会增加。当劳动力完全专业化时,生产的产品数量达到最大值,相应加总的生产率也达到上限,经济增长将陷入停滞。为了解决这一问题,杨小凯(2019)利用干中学思想,假定存在对累积经验的报酬递增,那么经济的持续增长最终源于人力资本的积累。所以由专业化导致加总的生产率的提升最终被人力资本积累所覆盖。
杨小凯的研究思路比较好地解决了斯密提到的劳动分工促进经济增长三个因素中的前两个,即劳动熟练程度的提高和工作转换时间的节约。由于这两个因素在提升生产能力方面存在上限,因此第三个因素才是核心,即机器的发明和使用。机器的使用不可避免地使企业具有规模报酬递增的特性,这需要广阔的市场来提供支撑。由此引出了斯密分工思想模型化的第二条技术路径,即规模报酬递增路径,那么分工将不可避免地导致生产的专业化。由此可见,分工是专业化报酬递增和规模报酬递增共同作用的结果。
对于分工表现出的经济特征,杨格提出了迂回生产的概念(Young,1928),即其与产业链相关的投入产出关联是分工的重要特征之一。投入产出关联本质上反映了分工中的规模经济,而分工的存在将衍生出交换问题,由于时空的不可克服性,这不可避免地增加交易的频次和成本。为了获得分工带来的好处就需降低交易费用,这样规模经济和交易成本成为分工的又一重要特征。由于分工是专业化报酬递增和规模报酬递增共同作用的结果,因此除了规模经济和交易成本,专业化报酬递增也是分工的重要特征,而根据杨小凯对分工的处理,专业化导致加总的生产率的提升最终被人力资本的积累所覆盖,因此需引入人力资本的累积。
因此,本部分基于新经济地理学的中间投入品模型,引入人力资本开发部门,并将分工表现出的迂回生产及其包含的规模收益递增与交易成本加入进来,建立两国家三地区的开放区域经济系统。其中,国家1包括内陆地区1和沿海地区2,国家2为地区3。假设每个地区都存在规模收益递增的工业部门
假设存在土地和劳动两种基本的生产要素,土地要素由农业用地和非农业用地构成。其中,地区
假设每个地区劳动力是同质的,劳动力可以在国家内流动,但不能在国家间流动。如果假定地区1流向地区2的劳动力数量为
假设农产品没有交易成本;工业产品为“冰山型”交易成本,记为
(一)人力资本开发部门
综合Lucas(1988)、杨立岩和王新丽(2004)与杨小凯(2019)的研究,假定人均人力资本决定个体投入劳动的生产率,这样经济系统有效劳动数量受人均人力资本数量的影响。将人力资本开发函数设定为:
| $ h_r{{'}}\left(t\right)=\delta\text{,}h_r\left(0\right)=1 $ | (1) |
其中,
(二)消费者跨期最优
假定地区
| $ \mathrm{Max}\mathit{{U}}=\int_{t=0}^{\infty}e^{-\rho t}\mathrm{l}\mathrm{n}\left[\left(C_{Ar}\right)^{\mu_{Ar}}\left(C_{Mr}^2\right)^{\mu_{Mr}}\left(C_{Lr}\right)^{\mu_{Lr}}\right]\mathrm{d}t $ | (2) |
| $ {D}_{r}{'}\left(t\right)=\varsigma {D}_{r}\left(t\right)+{Y}_{r}\left(t\right)-{E}_{r}\left(t\right) \text{,} {D}_{r}\left(0\right)=0 $ | (3) |
| $ {h}_{r}{'}\left(t\right)=\delta \text{,} {h}_{r}\left(0\right)=1 $ | (4) |
其中,后续变量均为时间
| $ E_r=P_{Ar}C_{Ar}+P_{Mr}^2C_{Mr}^2+P_{Lr}C_{Lr}\text{;}C_{Mr}^2=\left(\int_0^{n_1^2+n_2^2+n_3^2}c_i^{1-1/\sigma}\mathrm{d}i\right)^{1/(1-1/\sigma)} $ | (5) |
式(5)中,
| $ H\left({D}_{r},{h}_{r},{C}_{Ar},{C}_{Mr}^{2},{C}_{Lr}\right)={e}^{-\rho t}\mathrm{l}\mathrm{n}\left[{\left({C}_{Ar}\right)}^{{\mu }_{Ar}}{\left({C}_{Mr}^{2}\right)}^{{\mu }_{Mr}}{\left({C}_{Lr}\right)}^{{\mu }_{Lr}}\right]+{\lambda }_{1}\left[\varsigma {D}_{r}+{Y}_{r}-{E}_{r}\right]+{\lambda }_{2}\delta $ | (6) |
式(6)中
| $ {P}_{Ar}{C}_{Ar}={\mu }_{Ar}{E}_{r} \text{;} {P}_{Mr}^{2}{C}_{Mr}^{2}={\mu }_{Mr}{E}_{r} \text{;} {P}_{Lr}{C}_{Lr}={\mu }_{Lr}{E}_{r} $ | (7) |
这里不考虑储蓄,由
| $ {Y}_{r}\left(t\right)={E}_{r}\left(t\right) \text{;} {D}_{r}\left(t\right)=0 \text{;} {h}_{r}\left(t\right)=\delta t+1 $ | (8) |
结合式(7),给出进一步求解消费者均衡的目标函数和约束方程:
| $ {\rm{Max}} \;\; C_{Mr}^2=(\int_0^{n_1^2+n_2^2+n_3^2}c_i^{1-1/\sigma}\mathrm{d}i)^{\frac{1}{1-1/\sigma}} \quad {\rm{s.t.}}\;\; P_{Mr}^2C_{Mr}^2=\mu_{Mr}E_r $ | (9) |
通过构造拉格朗日函数,并根据最优条件,可求出第
| $ {c}_{i}={\mu }_{Mr}{E}_{r}{{p}_{i}}^{-\sigma }/({P}_{Mr}^{2}{)}^{(1-\sigma )} \text{;} {P}_{Mr}^{2}=({\int }_{0}^{{n}_{1}^{2}+{n}_{2}^{2}+{n}_{3}^{2}}{{p}_{i}}^{1-\sigma }{\mathrm{d}}i)^{1/(1-\sigma )} $ | (10) |
(三)生产者行为
1. 农业部门。设农业部门生产函数
2. 工业部门。根据前文的分析,专业化与分工将导致迂回生产,为此需将这种迂回生产引入进来,假设企业生产过程中需要中间投入品。
(1)中间投入品部门。假定中间投入品部门生产的产品只用于企业生产过程,生产中使用的固定投入和可变投入均为由劳动和中间投入品构成的组合要素,组合要素的函数形式为C-D型。其中,中间投入品和劳动所占份额分别为
| $ {p}_{r}^{1}={P}_{Pr}^{1}{a}_{mr}^{1}/(1-1/\sigma ) \text{;} {\bar{x}}_{r}^{1}=F(\sigma -1)/{a}_{mr}^{1} \text{;} ({P}_{Mr}^{1}{)}^{1-\sigma }={\sum }_{s=1}^{3}{n}_{s}^{1}({T}_{sr}^{1}{p}_{s}^{1}{)}^{1-\sigma } $ | (11) |
(2)最终消费品部门。假定最终消费品部门生产的产品只能用于最终消费。生产中使用的固定投入和可变投入均为由劳动和中间投入品组合构成的组合要素,组合要素的函数形式为C-D型。其中,中间投入品和劳动所占份额分别为
| $ {p}_{r}^{2}={P}_{Pr}^{2}{a}_{mr}^{2}/(1-1/\sigma ) \text{;} {\bar{x}}_{r}^{2}=F(\sigma -1)/{a}_{mr}^{2} \text{;} ({P}_{Mr}^{2}{)}^{1-\sigma }={\sum }_{s=1}^{3}{n}_{s}^{2}({T}_{sr}^{2}{p}_{s}^{2}{)}^{1-\sigma } $ | (12) |
经计算可知,
根据《国富论》中关于对外开放与技术交流的论述,
(四)短期均衡
1. 农业部门。当农业部门达到短期均衡时,农产品需求量
| $ {\sum }_{r=1}^{3}{S}_{r}={\sum }_{r=1}^{3}{Q}_{r} $ | (13) |
其中,
2. 工业部门。在考虑运输损耗情况下,根据式(9),能够求出地区
| $ {c}_{r,s}^{i}=\left({p}_{r}^{i}{)}^{-\sigma }\right({T}_{rs}^{i}/{P}_{Ms}^{i}{)}^{(1-\sigma )}{E}_{s}^{i} $ | (14) |
在式(14)中,
| $ {c}_{r}^{i}\equiv {\sum }_{s=1}^{3}{c}_{r,s}^{i}={\sum }_{s=1}^{3}\left({p}_{r}^{i}{)}^{-\sigma }\right({T}_{rs}^{i}/{P}_{Ms}^{i}{)}^{(1-\sigma )}{E}_{s}^{i}={\bar{x}}_{r}^{i} \text{;} {\bar{x}}_{r}^{i}=F(\sigma -1)/{a}_{mr}^{i} $ | (15) |
根据式(9)、式(10)和式(11),地区
| $ ({P}_{Mr}^{i}{)}^{1-\sigma }={\sum }_{s=1}^{3}{n}_{s}^{i}({p}_{s}^{i}{T}_{sr}^{i}{)}^{(1-\sigma )} \text{;} {p}_{s}^{i}=\frac{({w}_{s}^{i}{)}^{1-{\alpha }_{s}^{i}}({P}_{Ms}^{1}{)}^{{\alpha }_{s}^{i}}{a}_{ms}^{i}/(1-1/\sigma )}{[({\alpha }_{s}^{i}{)}^{{\alpha }_{s}^{i}}(1-{\alpha }_{s}^{i}{)}^{1-{\alpha }_{s}^{i}}]} $ | (16) |
地区
| $ {Y}_{r}={h}_{r}({\lambda }_{Mr}^{1}+{\lambda }_{Mr}^{2}){w}_{r}+A\left({\lambda }_{Ar}{h}_{r}\right)+{P}_{Lr}{L}_{cr} $ | (17) |
在式(17)中,等号右边三项依次为工业部门工人的工资收入、农业部门的总收入和土地收益。
根据定义,地区
| $ {E}_{r}^{1}={\sum }_{i=1}^{2}{\alpha }_{r}^{i}\times {n}_{r}^{i}{p}_{r}^{i}{\bar{x}}_{r}^{i} $ | (18) |
地区
| $ {E}_{r}^{2}={\mu }_{Mr}({Y}_{r}-{\mathrm{\Omega }}_{r}\bar{Y}) $ | (19) |
由于各地区第
| $ {h}_{r}{\lambda }_{Mr}^{i}{w}_{r}^{i}=(1-{\alpha }_{r}^{i})\times {n}_{r}^{i}{p}_{r}^{i}{\bar{x}}_{r}^{i} $ | (20) |
各地区的土地租金等于消费者的收入中用于土地支出的部分,则地区
| $ {\mu }_{Lr}({Y}_{r}-{\mathrm{\Omega }}_{r}\bar{Y})={P}_{Lr}{L}_{cr} $ | (21) |
地区
| $ {G}_{r}^{1}={n}_{r}^{1}{p}_{r}^{1}{\bar{x}}_{r}^{1} \text{;} {G}_{r}^{2}={n}_{r}^{2}{p}_{r}^{2}{\bar{x}}_{r}^{2} $ | (22) |
地区
| $ GD{P}_{r}=A\left({\lambda }_{Ar}{h}_{r}\right)+(1-{\alpha }_{r}^{1}){n}_{r}^{1}{p}_{r}^{1}{\bar{x}}_{r}^{1}+(1-{\alpha }_{r}^{2}){n}_{r}^{2}{p}_{r}^{2}{\bar{x}}_{r}^{2} $ | (23) |
上式中,后两项的和为工业部门的产值,记为
(五)长期均衡条件
当经济系统实现长期均衡时,流动要素在部门间和区域间都要达到稳定状态,此时要满足两个条件。
当人口在部门间流动均衡时,各地区的工业部门和农业部门的工资水平相等:
| $ {w}_{A1}={w}_{1}^{1}={w}_{1}^{2} \text{;} {w}_{A2}={w}_{2}^{1}={w}_{2}^{2} \text{;} {w}_{A3}={w}_{3}^{1}={w}_{3}^{2} $ | (24) |
当人口在区域间流动均衡时,地区1和地区2的实际工资相等:
| $ {\omega }_{1}={\omega }_{2} $ | (25) |
上式中,
三、中国区域经济格局演变的驱动力分析
为了弄清地区交易效率差异对分工的影响,这里假设三个地区间除交易效率不同之外,其它方面均相同。由于所得方程多为非线性隐函数形式,需借助Matlab软件进行数值模拟。
(一)参数校准
(二)均衡存在的稳定性与唯一性分析
在进行驱动力分析之前,需弄清模型均衡解的特征,避免因多种均衡共存而出现模拟结果遗漏问题,为此需探讨均衡存在的稳定性与唯一性问题。Allen等(2020)曾对此做过系统分析。由于模型中所得方程大多为非线性隐函数形式,通过数理分析来证明均衡存在的稳定性与唯一性比较困难。我们这里采取数值模拟这一更为直观的方法来进行论证,具体如下:
首先,将校准后的参数代入方程系统,通过数值模拟求出方程组的一组均衡解
图1中,给出了
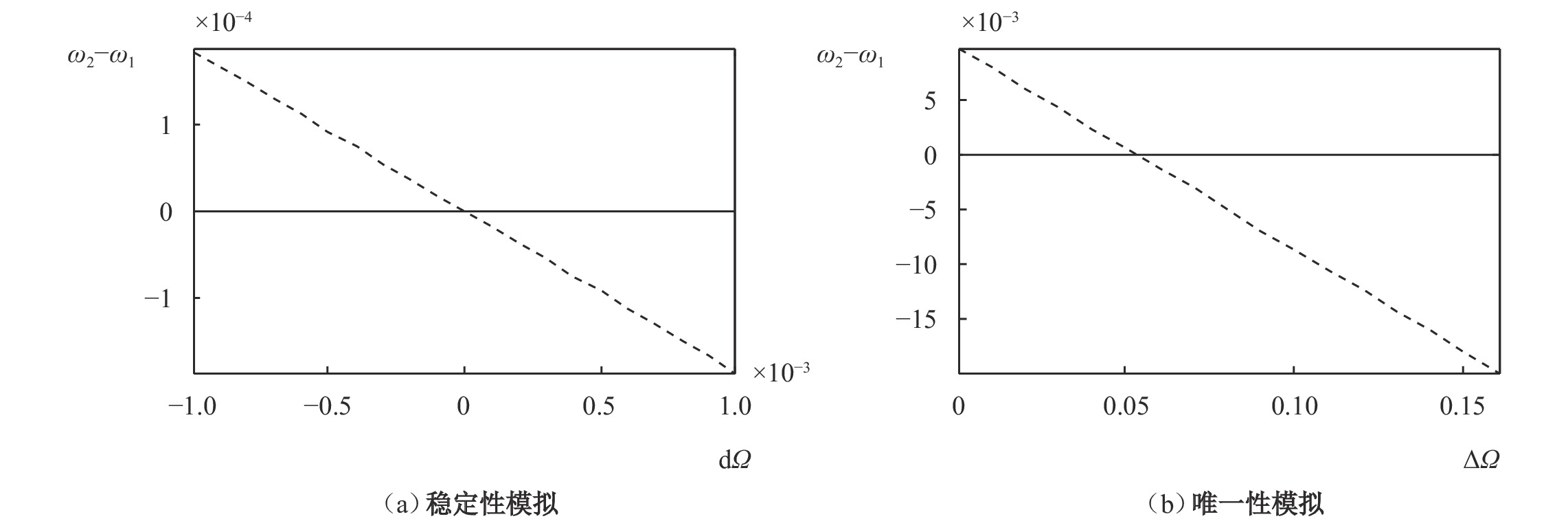
|
| 图 1 均衡存在的稳定性与唯一性模拟 |
(三)中国区域经济格局演变的理论模拟
图2和图3为上述给定参数校准值时的模拟结果。此时,内陆地区对外贸易成本要高于沿海地区,其他都相同。从图2中模拟结果可以看出,随着经济发展,沿海地区和内陆地区的发展差距经历了“快速增加—较快下降—缓慢上升”的演变过程,并且在第三阶段区域间发展差距虽会收敛但不会消失。这与区域经济发展的趋同理论和区际差距演化的“倒U形”学说存在一定的差异。
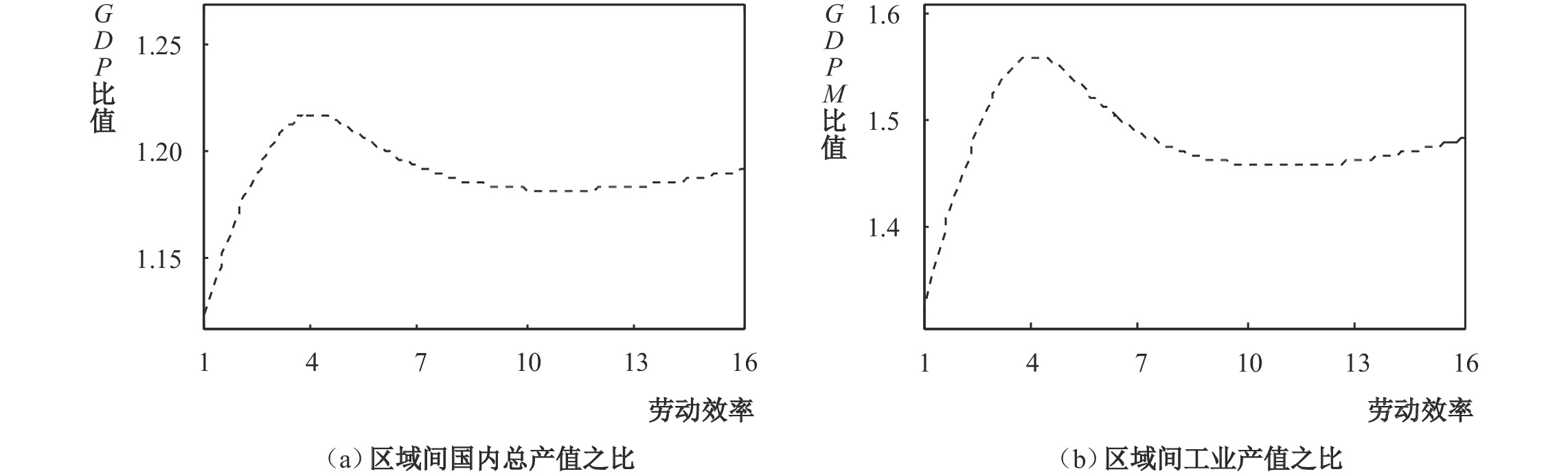
|
| 图 2 对外交易效率差异对区际经济发展差距的影响 |
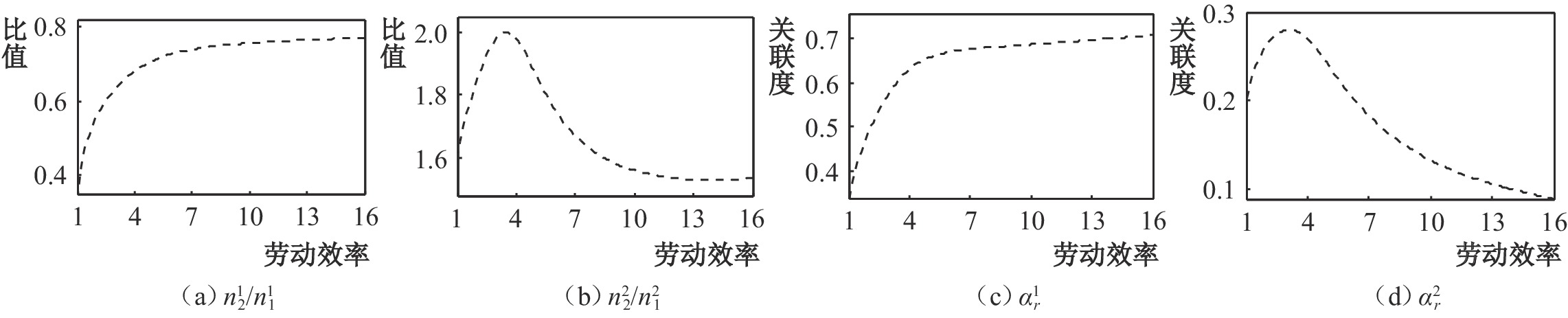
|
| 图 3 沿海地区和内陆地区的产业结构对比 |
图2中模拟结果表明,沿海地区和内陆地区的地理区位差异会导致区域间的经济发展差距,其作用机制为:在第一阶段,沿海地区相对于内陆地区的天然区位优势导致了二者的对外交易效率差异,加上起步阶段国家的政策倾斜和沿海地区的自身努力,这种优势逐渐显现。根据斯密分工思想,交换能力和市场范围会影响分工水平,而分工水平又是促进劳动生产力的最大增进力量。而随着分工发展,投入产出关联与劳动力流动进一步放大沿海地区的市场规模,在循环累积因果效应的作用下,区际发展差距在改革开放后迅速拉大。在第二阶段,随着经济发展,沿海地区面临经济结构调整的“阵痛期”,沿海地区内部的拥塞效应比较明显,此时,区际发展差距进入缩小期。在第三阶段,随着沿海地区经济结构转换的完成,以技术密集和知识密集为代表的生产性服务产业开始壮大,沿海地区经济发展将进入新阶段,这时区际发展差距存在进一步拉大的风险。
由于区域间的国民收入分配取决于各地区拥有的产业份额,接下来进一步从区际产业结构差异方面进行分析。图3(a)和图3(b)分别给出了地区1和地区2的中间投入品部门的企业数量之比和最终消费品部门的企业数量之比,图3(c)和图3(d)则分别给出了中间投入品部门和最终消费品部门的产业关联系数,即组合要素中中间投入品所占比例
从图3(a)和图3(b)可以看出,沿海地区和内陆地区出现了产业的区际分工,沿海地区主要从事最终消费品的生产,内陆地区则更多地从事中间投入品的生产,并且两个地区的最终消费品部门企业数量比值的变化趋势与GDP比值的变化趋势更为接近。这表明,区际经济差距主要源于最终消费品部门。由此可以推断,沿海地区与内陆地区经济发展差距的形成源于初始的区位差异导致的区际产业结构差异,而区际产业结构是区际产业分工的表现。由于分工水平受交换能力和市场范围的影响,沿海地区由于拥有天然的海港,这使其在开展海外贸易和利用海外市场方面存在优势,内陆地区则更多地选择了能弱化其劣势的中间投入品部门。进一步观察图3(c)和图3(d)发现,中间投入品部门的产业关联度大于最终消费品部门,这意味着两个产业部门的要素投入结构存在差异,随着经济发展,最终形成了包括部门分工和区域分工的区际分工模式。
图4呈现了沿海地区和内陆地区的对外交易效率差异对区际经济发展差距的影响。此外,各地区还可以通过建设发达的基础设施和营造良好的营商环境来提升区域内部的交易效率,这同样也会提升本地区的分工水平,进而促进经济发展。这里将探讨区域内部的交易效率差异对区域发展差距的影响。图4中细线的模拟参数与图2中相同,且有
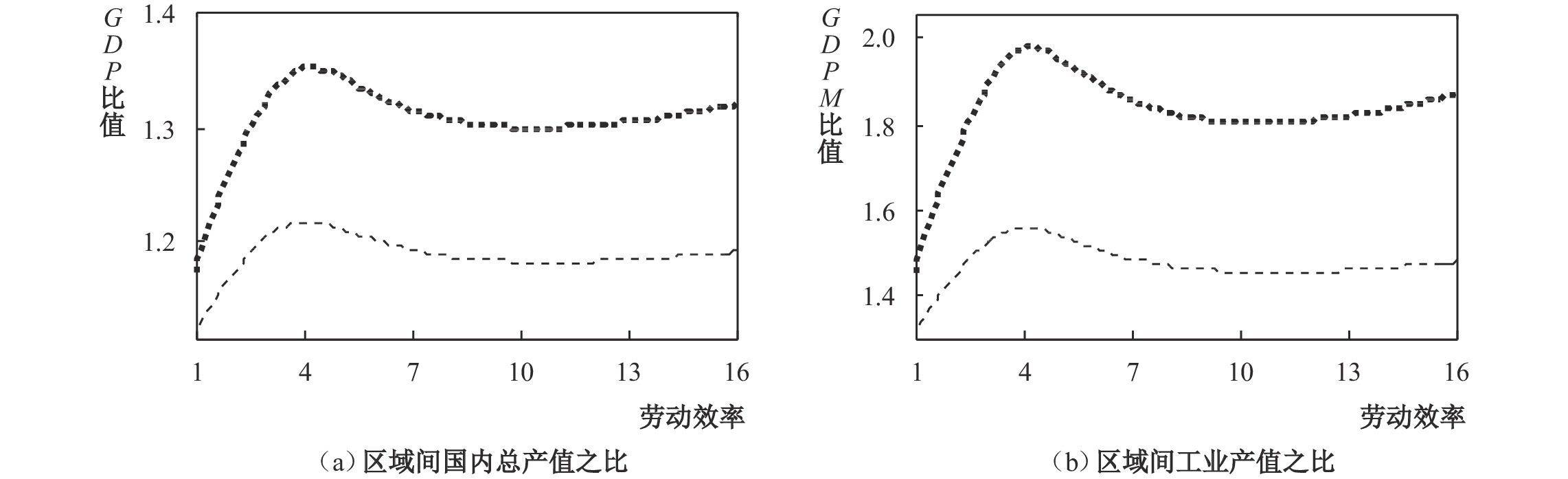
|
| 图 4 区域内部的交易效率差异对区际经济发展差距的影响 |
假设1:分工是提升劳动生产力的最大增长力量,因此各地区的经济发展水平与其分工水平相关。
假设2:分工水平受交换能力,即市场范围的限制,因此各地区的分工水平与其交换能力和市场规模相关。
四、经验事实与实证检验
(一)中国区域经济格局演变的经验事实
本部分将中国大陆地区的31个省级行政区划分为“沿海—内陆”和“南部—北部”。
(二)中国区域经济格局演变的实证分析
这里将通过实证分析对假设1和假设2进行验证。为此,选取面板数据模型,并结合所构建的数理模型,将计量模型的基本形式设定为:
| $ \mathrm{ln}pgd{p}_{i,t}={\beta }_{0}+{\beta }_{1}divisio{n}_{i,t}+{\beta }_{J}{\overrightarrow{J}}_{i,t}+{\beta }_{X}{\overrightarrow{X}}_{i,t}+{\alpha }_{i}+{\gamma }_{t}+{u}_{it} $ | (26) |
式(26)基于假设1,用来检验劳动生产力与分工的关系。其中,
| $ divisio{n}_{i,t}={\beta }_{0}+{\beta }_{1}\mathrm{ln}marke{t}_{i,t}+{\beta }_{J}{\overrightarrow{J}}_{i,t}+{\beta }_{X}{\overrightarrow{X}}_{i,t}+{\alpha }_{i}+{\gamma }_{t}+{u}_{it} $ | (27) |
式(27)基于假设2,用来检验分工与市场规模的关系。式(27)中,
1. 变量说明与数据来源。劳动生产力水平(
本文数据来源于《中国统计年鉴》《中国交通统计年鉴》《国家知识产权统计年报》《各省投入产出表》(1997年、2002年、2007年、2012年和2017年),以中国大陆地区的31个省级行政区已有的5年中间投入产出表数据为基础构建面板数据模型。由于西藏数据缺失较多,将其剔除。少部分缺失数据采用线性插值方法补齐,并对GDP、市场规模和fdi数据取对数。
2. 回归结果。表1以式(26)为基础,用来验证各省级行政区的劳动生产力与分工水平的关系。在式(26)中,分工水平division为核心解释变量,需对其进行内生性检验。由于目前很难找到分工水平的合适工具变量,这里用division的上一期作为工具变量对其进行内生性检验。观察表1中给出的内生性检验的显著性水平,发现式(1)的p值为0.0186,不能通过5%显著性水平检验,这可能是由遗漏变量所致。在模型中加入pcapital、infai和outfai变量后,检验结果得到显著改善,通过了5%显著性水平检验。
| (1) | (2) | (3) | (4) | (5) | |
| lnpgdp | lnpgdp | lnpgdp | lnpgdp | lnpgdp | |
| division | 0.0709***(2.68) | 0.0781***(2.98) | 0.0762***(2.87) | 0.0788***(3.02) | 0.0771***(2.92) |
| pcapital | 0.0990**(2.11) | 0.101**(2.14) | 0.0928**(1.98) | 0.0945**(2.01) | |
| infai | 0.0460(0.63) | 0.0384(0.53) | |||
| outfai | −140.5(−1.50) | −137.0(−1.45) | |||
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 个体与时间效应 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 观测值 | 150 | 150 | 150 | 150 | 150 |
| R2 | 0.9886 | 0.9891 | 0.9891 | 0.9893 | 0.9894 |
| 内生性检验p值 | 0.0186 | 0.0512 | 0.0520 | 0.0652 | 0.0762 |
| 注:括号内为t统计量值;*、**和***分别表示10%、5%和1%的显著性水平,下表同。 | |||||
观察表1可知,列(2)—列(5)中分工水平division的系数均显著为正,这证实了分工能够提高劳动生产力这一结论。列(2)—列(5)中人均人力资本的系数均显著为正,这也与理论分析一致,而infai和outfai的系数不显著,这可能意味着二者并不直接影响劳动生产力。
本文以式(27)为基础,而根据经济理论,市场规模lnmarket通常具有较强的内生性。为此,采用工具变量法进行回归。季鹏等(2021)用夜间灯光数据作为市场规模的工具变量,这里也采用这种处理方法,具体以各省级行政区的夜间灯光总亮度lnlight作为市场规模lnmarket的工具变量。由于夜间灯光数据为非统计数据,并且能够反映经济活动强度,因此是lnmarket的理想工具变量。
根据回归结果,核心解释变量lnmarket的回归系数均显著为正,这证实了分工水平受市场规模限制这一结论。infai的系数显著为正,这表明区域内部交易效率的提升能够促进分工的发展,而outfai的系数却不显著。lnmarket×infai和lnmarket×outfai的系数均不显著,这可能意味着infai和outfai并非直接通过市场规模来影响分工水平。
outfai的回归结果不能与理论分析保持一致,却能够与现实情况一致。在理论上如何解释这种现象?我们回到outfai的计算方法上来,用各省级行政区到最近港口距离的倒数来衡量,各省级行政区的对外交易效率几乎完全取决于地理区位,没有考虑到其后天努力。为此,我们将先天的地理距离与后天的对外经济交往结合起来,构造一个新变量outfaid,令outfaid=outfai×dtrade,并将dtrade从式(27)的控制变量中剔除,用工具变量法再次回归。
根据回归结果,outfaid的回归系数变得显著为正,这表明外因还要通过内因起作用。此外,lnmarket×infai和lnmarket×outfaid总体上均不显著,这表明交易效率直接影响分工水平,而非通过市场规模来发挥作用。这从理论上弄清了斯密分工思想的确切表述形式,即劳动生产力的最大增进大都是分工的结果,而分工水平同时受交换能力和市场范围的限制。
五、“双循环”战略的实施对中国区域发展差距的影响
本部分将探究“双循环”战略的实施对中国区域发展差距的影响。近年来,中央提出“双循环”战略,这将在一定程度上改变沿海地区和内陆地区的内部交易效率、对外交易效率和相互交易效率,进而影响中国的区域经济格局。因此,下面重点从交易效率角度进行分析。
国外贸易保护主义会同时影响中国沿海地区和内陆地区的对外交易效率,这里通过改变两个地区的对外交易成本的方式来模拟这一过程。根据图表分析结果,国外的贸易保护缩小了沿海地区和内陆地区的发展差距,这是因为国家间的贸易冲突对沿海地区影响要大于内陆地区,在一定程度上削弱了沿海地区的区位优势,使得原本的区际分工格局出现调整,沿海地区和内陆地区的发展差距缩小。当然,这种缩小区际经济发展差距的方式一定程度上要付出经济增长的代价。
“双循环”战略的主要抓手之一就是要打破区域市场分割,构建国内统一大市场。从理论上讲,国内统一大市场的建设会提升国内区际一体化水平,这里通过改变沿海地区与内陆地区间交易成本方式来模拟这一过程。根据图表分析结果,在开放环境下,国内区际一体化水平的适当提升能够缩小内陆地区与沿海地区的发展差距。这是因为随着区域内部一体化水平的提升,海外市场相对国内市场的地位出现相对下降,使得内陆地区相对沿海地区的区位劣势有所减弱,最终促使区际经济发展差距缩小。同时,根据分工原理,国内区际交易效率的提高有利于国内分工水平的提升,这在缩小区际经济发展差距的同时也将促进国家的经济发展。
“双循环”战略不仅要求构建国内统一大市场,还要求尽可能利用海外市场。中欧班列开通和“一带一路”倡议改善了内陆地区的对外贸易条件。根据2021年《中欧班列发展报告》,中欧班列运输费用约为空运的1/5,运输时间是海运的1/4,与传统的海铁联运相比,可节约8%至20%的综合物流成本。这里通过改变内陆地区对外交易成本方式来模拟这一过程。根据图表分析结果,内陆地区对外贸易成本的下降有效地缩小了其与沿海地区的发展差距。这是因为“一带一路”倡议及中欧班列的开通弱化了内陆地区相对于沿海地区的区位劣势,在分工原理作用下,缩小了内陆地区与沿海地区经济发展的差距。
六、总 结
本文研究表明,中国区域经济格局的形成是市场竞争下地域分工演化的结果,是斯密分工思想在区域经济中的体现,而“双循环”战略的实施通过改变国内区域间的交易效率和不同区域的对外交易效率的方式来影响各地区的分工水平,进而影响地区经济发展。本文认为可从以下几方面着手来缩小区域发展差距:
第一,要完善国内交通信息基础设施,缩小内陆地区与沿海地区的基础设施差距。随着沿海地区经济发展,其财政实力变得十分雄厚,提升基础设施质量的愿望也更容易实现,以高铁、地铁、高速等为代表的基础设施密度远高于内陆地区,这极大地提升了沿海地区的区内交易效率。因此,内陆地区要打造有利于提升其交易效率的硬件设施,将工作重心放在构建发达的陆运和空运系统上来,借此与沿海地区的海运优势进行错位发展。
第二,要营造有利于提升交易效率的环境,内陆地区可以通过更好地提升其对经济主体的服务意识和服务质量来降低区域内部的交易成本。这里的交易成本是广义的,它包括运输成本、制度成本和信息传递成本等。沿海地区由于地处对外开放的前沿,在对外交往过程中更容易接触到先进的管理经验和管理理念。此外,国家可对当前的转移支付政策进行优化,将部分转移支付资金用于补贴内陆地区企业对外出口时的运输成本,借此缩小内陆地区相对于沿海地区的区位劣势。
第三,要改善国内收入分配状况,提高整体边际消费倾向。根据理论分析,国内市场地位的上升会弱化海外市场对国内区域经济格局的影响,这在理论模拟中也得到了证实。因此,要落实按劳分配为主体、多种分配方式并存的制度。同时,应认识到中国的制度优势和国有经济的作用,更好地发挥国有经济在收入分配中的调节功能。
第四,本文在讨论如何缩小区域经济发展差距时,并没有重点从产业结构的角度进行论述,这是因为区际产业结构是市场竞争下地域分工演化的结果。如果只是围绕着产业结构来缩小区域发展差距,可能达不到预期效果。可行路径应该是从交易效率入手,依赖产业链和产业集群,充分利用分工的力量来实现区域间协调发展。
| [1] | 安虎森, 汤小银. 新发展格局下实现区域协调发展的路径探析[J]. 南京社会科学, 2021(8): 29–37. |
| [2] | 安虎森 等. 高级区域经济学[M]. 第4版. 大连:东北财经大学出版社,2020. |
| [3] | 黄玖立, 李坤望. 出口开放、地区市场规模和经济增长[J]. 经济研究, 2006(6): 27–38. |
| [4] | 季鹏, 袁莉琳, 李荣林. 市场规模、竞争和出口产品结构——基于中国多产品出口企业的微观证据[J]. 国际贸易问题, 2021(10): 73–89. |
| [5] | 马歇尔. 经济学原理[M]. 朱志泰,陈良璧译. 北京:商务印书馆,2019. |
| [6] | 欧阳峣. 大国经济发展理论的研究范式[J]. 经济学动态, 2012(12): 48–53. |
| [7] | 裴长洪, 刘洪愧. 构建新发展格局科学内涵研究[J]. 中国工业经济, 2021(6): 5–22. |
| [8] | 钱学锋, 裴婷. 国内国际双循环新发展格局: 理论逻辑与内生动力[J]. 重庆大学学报(社会科学版), 2021(1): 14–26. |
| [9] | 许统生, 陈瑾, 薛智韵. 中国制造业贸易成本的测度[J]. 中国工业经济, 2011(7): 15–25. |
| [10] | 亚当·斯密. 国富论[M]. 郭大力,王亚南译. 北京:商务印书馆,2015. |
| [11] | 杨立岩, 王新丽. 人力资本、技术进步与内生经济增长[J]. 经济学(季刊), 2004(4): 905–918. |
| [12] | 杨小凯. 基于专业化递增报酬的分工理论:一种微观经济学方法[M]. 苏良,姚顺添译. 北京:社会科学文献出版社,2019. |
| [13] | Anderson J E, van Wincoop E. Trade costs[J]. Journal of Economic Literature, 2004, 42(3): 691–751. DOI:10.1257/0022051042177649 |
| [14] | Brakman S, Garretsen H, Schramm M. The spatial distribution of wages: Estimating the helpman-hanson model for Germany[J]. Journal of Regional Science, 2004, 44(3): 437–466. DOI:10.1111/j.0022-4146.2004.00344.x |
| [15] | Combes P P ,Mayer T,Thisse J F . Economic geography:the integration of regions and nations[M]. Princeton:Princeton University Press,2008. |
| [16] | Fujita M,Krugman P,Venables A J. The Spatial economy:cities,regions,and international trade[M]. Cambridge:MIT Press,1999. |
| [17] | Fujita M,Thisse J F. Economics of Agglomeration:Cities,industrial location,and globalization[M]. Cambridge:Cambridge University Press,2012. |
| [18] | Lucas R E Jr. On the mechanics of economic development[J]. Journal of Monetary Economics, 1988, 22(1): 3–42. DOI:10.1016/0304-3932(88)90168-7 |
| [19] | Mion G. Spatial externalities and empirical analysis: The case of Italy[J]. Journal of Urban Economics, 2004, 56(1): 97–118. DOI:10.1016/j.jue.2004.03.004 |
| [20] | Young A A. Increasing returns and economic progress[J]. The Economic Journal, 1928, 38(152): 527–542. DOI:10.2307/2224097 |

