一、引　言

近年来我国农业经济与农业产出快速发展。伴随农业经济总量的增长，收入分配就成为影响农民福利、农民满足感与获得感的重要问题。但是由于农户内部存在贫富差距，不同财富水平的农户抗风险能力不同，农业生产快速发展造成了不平等问题（万广华等，2005）。农业保险作为一项重要的农业生产保障制度，可以对冲自然灾害带来的风险，保障农民在发生灾害风险冲击时及时获得保险补偿，从而保障农民收入的持续与稳定。然而，农业风险会不会加剧农民收入不平等？农业保险会不会缓和收入不平等？其能在多大程度上缓和不平等？这些都是值得关注的话题。虽然国内已有部分学者对农业保险与收入不平等之间的关系展开研究，但是研究的对象大多是城乡之间的收入不平等，对农民内部的收入分配关注不足（万广华，2013）。此外，已有研究的结论并不一致，本文认为这是由于已往文献只选取农业保险保费收入、赔付等单一指标进行研究，并且受限于样本以及计量方法选择，从而产生了不同结论。因此，全面考察农业风险、农业保险以及农业保险市场结构对于农民收入不平等的影响就显得十分必要。

本文研究发现：（1）在数值模拟中，灾害损失概率和程度、农业保险保障、补贴以及农险市场结构对农村家庭收入的洛伦兹曲线和基尼系数存在线性影响，灾害损失概率和程度的上升会提高农村家庭收入不平等，农业保险免赔率、农业保险补贴的提高和事前异质性的降低可以减轻农村家庭收入不平等。（2）在实证研究中，农业灾害损失会增加农民收入不平等，农险保费收入、赔付与补贴会在灾害损失存在的基础上减缓收入不平等，同时，农业保险市场竞争度的提高有利于促进农民收入平等化。联立方程回归和面板门槛回归发现上述指标对农民收入不平等的影响会伴随不平等程度的不同而发生变化，即存在异质性问题。面板分位数回归发现事前收入越公平，保险越发达，越有利于降低收入不平等。

针对现有研究，本文有以下创新：（1）在理论模型和数值模拟方面，首先，引入了风险乘子与保险乘子，目的在于将Sargent和Stachurski（2023）关于收入的一般化模型改造为能够用于研究农业风险、农业保险对中国农村家庭收入影响的模型。其优越性是在收入不平等的一般化模型基础上，纳入影响农业风险的外生因素（损失概率和损失程度）、保险保障与补贴因素（免赔率和补贴）以及农业保险市场势力，并进行比较静态分析。其次，将农民收入的标准差内生化。主观设定的处理方式是将农业生产收入序列的标准差作为某一确定常数，而由风险概率和风险损失内生决定标准差的方式则充分考虑了农业风险的影响因素，更加符合现实。相对于将标准差设定为风险概率和风险损失的一个线性组合的内生化方式，设定为二次函数可以进一步研究风险概率和风险损失对标准差具有不同影响程度时的情形，更加符合现实且更具优越性。最后，将农民的储蓄函数设置为一个示性函数。储蓄不是在每一期都发生，只有当农民财富超过一定水平之后才会发生。这是因为当财富水平高于某一临界值时，家庭按正常储蓄率储蓄；当财富水平低于该临界值时，家庭不储蓄。基于上述设定的数值模拟更为全面，从农业风险、农业保险及补贴、农业保险市场结构三个方面对农业保险进行衡量，并且考虑了农业保险市场结构和事前异质性对农民收入不平等的影响。（2）在实证研究方面，一是在指标构建上利用了Dagum基尼系数，克服传统指标的不足；二是综合利用多种计量方法，如单方程回归、联立方程回归、面板门槛回归以及面板分位数回归进行实证分析，确保回归结果的稳健有效；三是选取农业风险、农业保险保费收入等指标，全面考察了农业保险对于农民收入分配的影响。（3）在实践层面，利用分析得出的结论可以有针对性地指导农业保险“扶贫攻坚”，改善分配工作，帮助农业保险更好地发挥保险保障和金融服务实体的功效。

本文接下来的结构安排如下：第二部分对已有农业保险和农民收入的文献进行回顾；第三部分构建理论模型并进行数值模拟；第四部分介绍本文计量模型设定并进行变量说明；第五部分对计量结果进行解释；第六部分总结全文结论并给出相关政策建议。

二、文献综述

（一） 农民收入差距影响因素相关研究

在国外学者中，Khan（1993）利用1988年中国农户调查数据，通过计量分解的方法发现地理位置、劳动力禀赋、劳动力性别构成、家庭固定资产等是农户收入的主要来源，也是造成收入差距的主要因素。Scott（1994）则指出鼓励农民进行农业生产的政策会促进农民收入平等化。国内对农民收入差距影响因素的研究大概可分为三个方面：第一，按照收入构成进行研究。李实和赵人伟（1999）通过将农民收入划分为农业收入与非农收入进行考察，发现非农收入差距是收入不平等的主要来源。杜鑫（2021）将农民收入划分为工资性收入、非农经营净收入、农业经营净收入与转移性收入，实证研究发现工资收入差距和非农经营收入差距是构成不平等的主要来源。第二，通过经济政策、经济制度进行研究。研究发现分配政策、财政政策、土地制度等均会影响农民内部的收入分配情况。其中，农村税费（陈斌开和李银银，2020）、财政资金的偏向分配（万海远等，2015）会扩大收入差距，合理土地制度下的土地细碎化（许庆等，2008）与土地流转（陈斌开和马宁宁，2020）则会缩小农民收入差距。第三，基于自然环境、要素禀赋进行研究。要素禀赋又可进一步划分为自然资源、物质资本与人力资本。万广华等（2005）通过回归分解发现地理位置、种植结构与资本投入是影响农民收入不平等的最主要因素，而加大教育投入和促进人力资本积累可以帮助落后地区缩小收入差距。韩菡和钟甫宁（2011）指出土地要素在经济发展程度不同的地区对促进收入的公平化有不同作用。

已有研究表明，影响农民收入差距的因素较多，那么农业风险与农业保险该如何分类呢？农业风险大多以自然灾害方式出现，与当地自然环境有关。同时，风险的发生势必会影响农民收入和改变农民收入结构，而国家对于高风险地区往往采取财政扶持政策，因而风险和经济政策也息息相关，所以农业风险对于农民收入差距的影响不能简单分类。另外，农业保险也和自然环境、经济环境密不可分，保险保障也会影响农民收入。综上所述，农业风险、农业保险与农民收入差距的关系需要进一步考察。

（二）农业保险影响收入差距的相关研究

国外已有大量研究关注农业保险的收入分配作用。Mosley和Krishnamurthy（1995）利用印度数据发现购买保险的农民收入水平更高，Goodwin（2001）运用美国数据进一步证明农业保险可以改善国民收入再分配。国内对于农业保险收入分配作用的研究较少，孙香玉和钟甫宁（2009）在理论层面分析了农业保险可以改善城乡居民的收入分配，缩小收入差距。在实证层面，已有研究大多利用省级面板数据，采用GMM等估计方法来研究农业保险对缩小城乡收入差距的作用。

通过梳理文献可以发现，目前国内针对农业保险保障与农村居民收入差距的研究较少，已有研究也大多集中在城乡收入差距，并且作者往往只选用农业保险的一两个指标，比如保费收入、保费赔付等，很少从农业风险、农业保险、农险市场的一体化角度全面审视农业保险对收入差距的影响。并且，关于农业保险与收入差距关系之间的结论也不尽相同。此外，农业保险通过何种途径来影响收入差距？现有研究也没有给出答案。为此，本文通过理论和实证分析，对于这些问题进行处理和解决，从而得到更加符合现实的研究结论。

三、理论模型与数值模拟

（一）理论模型

基于Benhabib等（2015）以及Benhabib和Bisin（2018）的研究，很多国家关于收入的波动序列以及收入的横截面都符合厚尾分布的特点。Sargent和Stachurski（2023）指出Kesten分布产生的多样本动态过程的横截面分布可以出现厚尾分布，因此本文理论模型基于Kesten过程构建。

假设一个农村家庭t期的收入分为消费和储蓄，按固定储蓄率s储蓄，1−s用于消费。t+1期收入W_t+1由基于t期的储蓄产生的资产回报收入和t+1期从事农业生产的收入y_t+1构成，y_t+1为非金融资产收入，这里主要指农村家庭来自农业生产的收入，如从事农业活动产生的劳务收入或通过销售农产品产生的非劳务收入等。设R_t+1为总资产回报率，如果式（1）中R_t+1和y_t+1都是独立同分布，则式（1）服从Kesten分布。

在此构造有风险、保险与补贴的完整理论模型，将农业保险乘子作用于农业生产带来的收入y_t+1，并同时引入农险保费与补贴，农村家庭收入更新规则如式（1）所示。

其中，p为农业保险损失概率，d为农业保险损失程度，m为农业保险免赔率，相应的1−m为农业保险保障覆盖率，pd（1−m）E（y_t+1）为精算公平保费，保险标的价值基于农业生产带来的收入y_t+1的期望值，λ为农险市场势力的度量参数且λ≥1，sub表示政府对农业保险保费的补贴比例。采用Sargent和Stachurski（2023）的有关设定，设{Z_t}为一个相关状态过程，其形式为：

其中，ε_t、ξ_t、ζ_t为三个独立同分布的标准正态分布，μ、σ分别表示相应序列的期望与标准差，a、b、c_r和c_y为参数。

在式（1）中，当m=1时，式（1）就转化为有风险、无保险模型；当sub=0时，式（1）就转化为有风险、有保险、无补贴模型。因此这些模型都可以统一采用式（1）来进行表示，有风险、无保险模型与有风险、有保险、无补贴模型都是有风险、有保险、有补贴模型的特例。 ¹ 相对于现有研究，式（1）的主要扩展包括：

第一，借鉴邵全权等（2017）的研究，引入农业风险乘子、农业保险乘子 ² 以及农业保险保障、农业保险补贴，基于此构造三类模型：有风险、无保险模型；有风险、有保险、无补贴模型；有风险、有保险、有补贴模型。接下来，本文对三类模型进行比较，研究不同模型对收入不平等的影响差异。

第二，关于农业生产的收入序列y_t的标准差。考虑到在不同的农业风险环境下，收入风险对p和d的依赖情况有所差异，为了能够体现这种区别，设定σ_y为p和d的二次函数σ_y=q₂[q₁p+（1−q₁）d]²，q₁∈（0，1），q₂>0。其中，q₁为损失概率与损失程度的权重系数，q₁越大则表示农业收入风险与损失概率p的联系越紧密，q₁越小则表示农业收入风险与损失程度d的联系越紧密。q₂为此二次函数整体对σ_y影响程度的系数，q₂越大则表示该二次函数对σ_y的影响越强，反之则越弱。农业风险引起的损失在经济理论上主要由损失概率p和损失程度d决定，农业风险导致的实际损失主要取决于损失概率和损失程度的乘积。引入由p和d内生决定σ_y的方式则充分考虑了农业风险的影响因素，更加符合现实，并且具有一定的优越性。将σ_y设定为p和d的二次函数可以进一步研究p和d对σ_y具有不同影响程度时的模拟，这种设定与中国现阶段农业风险主要受损失概率和损失程度影响的现实情况相符合，并且可以将度量农业生产收入风险的产出标准差与农业风险变量损失概率p和损失程度d相结合。

第三，设定储蓄函数为sw_tl{w_t≥ $\overline{w}$ }，l{w_t≥ $\overline{w}$ }为一个示性函数。当w_t≥ $\overline{w}$ 时，l{w_t≥ $\overline{w}$ }=1，家庭按储蓄率正常数s储蓄；当w_t< $\overline{w}$ 时，l{w_t≥ $\overline{w}$ }=0，家庭不储蓄。这种设定储蓄率的方式类似于固定储蓄率模型，并且对于中国农村家庭而言，每一期的储蓄决策依赖于其财富水平，如果家庭财富水平较低，则其收入都会花费完，从而不进行储蓄。

（二）参数校准

本部分对前文中理论模型的参数进行校准。对储蓄函数而言，结合模拟农村家庭收入序列的取值范围，将 $\overline{w}$ 校准为1。根据近年来中国农村家庭储蓄率的事实，将储蓄率校准为20%。参考Sargent和Stachurski（2023）的研究，{Z_t}、{R_t}、{y_t}中有关参数校准如下：对{Z_t}而言，a校准为0.5，b校准为0，σ_z校准为0.1；在{R_t}中，考虑到资产回报率并不具有较大的趋势，c_r应趋近于0，将c_r校准为0.05，μ_r为0.1，σ_r为0.5；在{y_t}中，同时考虑简洁性和合理性，将c_y校准为1，μ_y为1，结合本文假设σ_y由p和d内生决定的处理方式，即σ_y=q₂[q₁p+（1−q₁）d]²，将q₁校准为0.5，即损失概率与损失程度对农业收入风险的影响具有同等效力，将q₂校准为1.5。

在农业风险、农业保险、补贴、农险市场势力的参数方面，考虑到后文数值模拟中对上述参数取值范围进行比较静态分析，因此这部分参数校准主要基于各参数定义域中比较符合现实的数据。借鉴邵全权和刘宇（2022）的研究，农业风险损失概率p校准为0.5，损失程度d校准为0.3，结合我国财产保险和农业保险经营实践，将农险免赔率m校准为0.2。考虑到我国中央、省级、地方三级政府对农险都有补贴的实际情况，将补贴比例sub设定为0.7。由于农险经营具有较强的公益性，农险公司的市场势力受到控制，将λ设定为1。每个个体收入动态模拟500期，计算洛伦兹曲线与基尼系数的横截面分布包含100000个个体。模拟的初值涉及到w₀和z₀，分别设定为y_t和Z_t序列的均值，同时假设模拟样本分布中所有个体初值是一样的。具体参数校准汇总于表1。

（三）数值模拟

本文数值模拟部分的逻辑与安排如下：首先，构造单个农村家庭收入的一期更新规则，研究收入如何从t期更新到t+1期；其次，通过设定农村家庭收入的初值，并将该规则在一定时间区间T内进行递归计算，可以得到该农村家庭在模拟时间区间结束后的收入水平；最后，将研究样本扩展到N个个体，设定其当前初始分布并对每一个个体反复运用更新规则至T期， ³ 得到N个个体T期后的分布，由此可以计算相应分布的洛伦兹曲线和基尼系数，实现度量农村家庭收入不平等的目的。本文主要模拟研究包括三种情况：有风险、无保险（m=1）模型；有风险、有保险、无补贴（sub=0）模型；有风险、有保险、有补贴（正常情况）模型。本文研究外生农业风险因素损失概率和损失程度、可控因素农险免赔率和补贴比例、农险市场势力参数改变对收入不平等的影响。另外，本文也探究事前同质性与事前异质性对收入不平等的影响差异。

1. 几种情形的对比

本文接下来对比上文所述的三种模型。 ⁴ 可以发现有风险、无保险的基准模型的基尼系数最低，有风险、有保险、无补贴模型的基尼系数最高，说明在没有补贴时，农业保险保障会提高农村家庭的收入不平等。同时，有风险、有保险、有补贴模型的基尼系数介于前述两种情形之间，表明补贴的存在相对于只有农业保险保障而无补贴情形可以使得农村家庭收入不平等程度降低。

2. 比较静态分析

（1）外生风险因素对收入不平等的影响

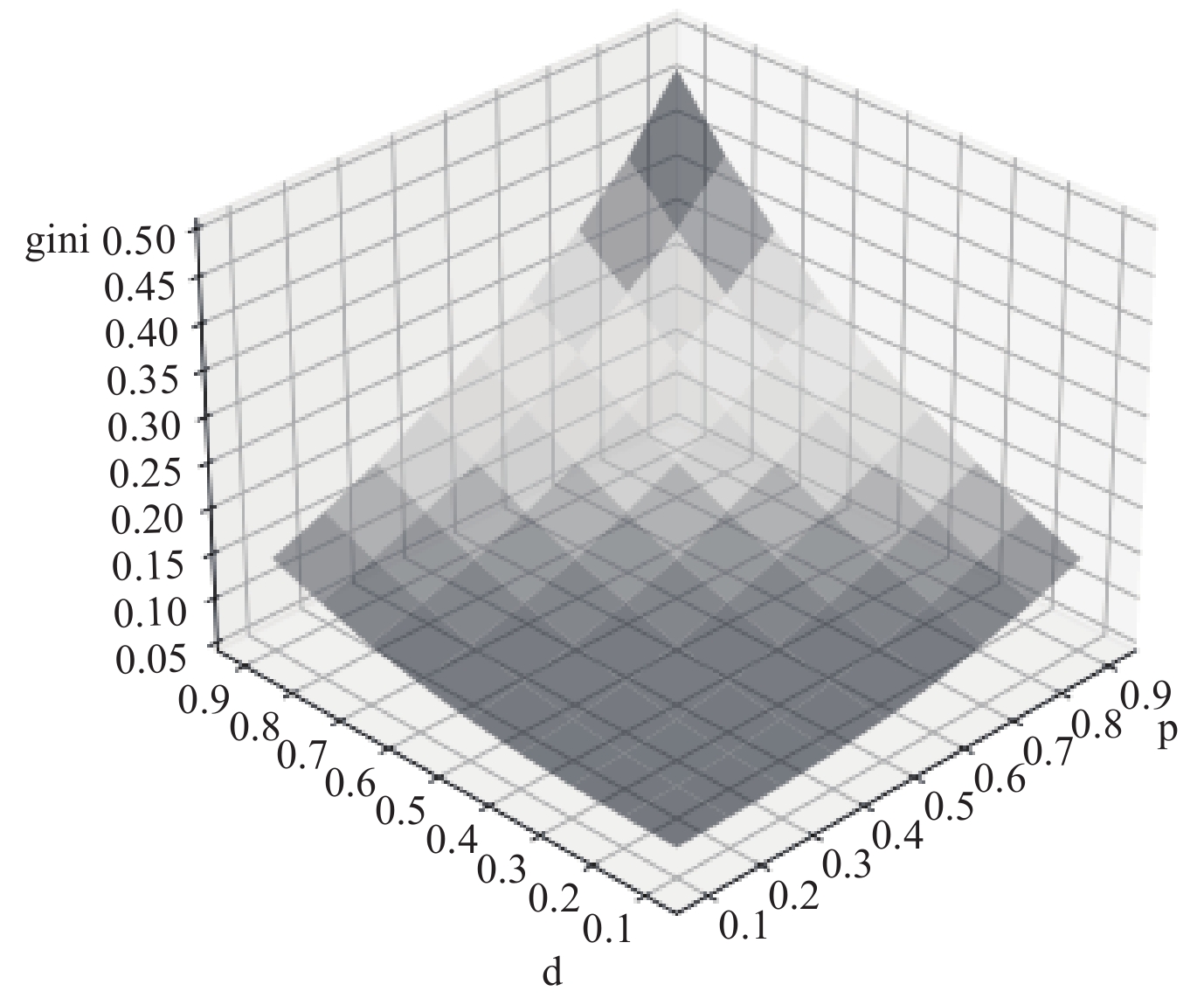
基于有风险、无保险模型，引入农业风险的损失概率p和损失程度d，并且将其作为一种外生冲击。之所以将其称为外生是因为损失概率与损失程度是根据一定的自然规律发生的，我们无法对其进行控制。图1表明，农业风险损失概率变化对农村家庭收入不平等呈现出线性影响。随着损失概率提高，基尼系数不断上升。农业风险损失程度对收入不平等的影响也呈现出线性规律，随着损失程度提高，基尼系数一直上升。因此，农业风险损失概率和损失程度的增加会提高基尼系数，扩大农村家庭收入不平等程度。

（2）保险保障与补贴因素对收入不平等的影响

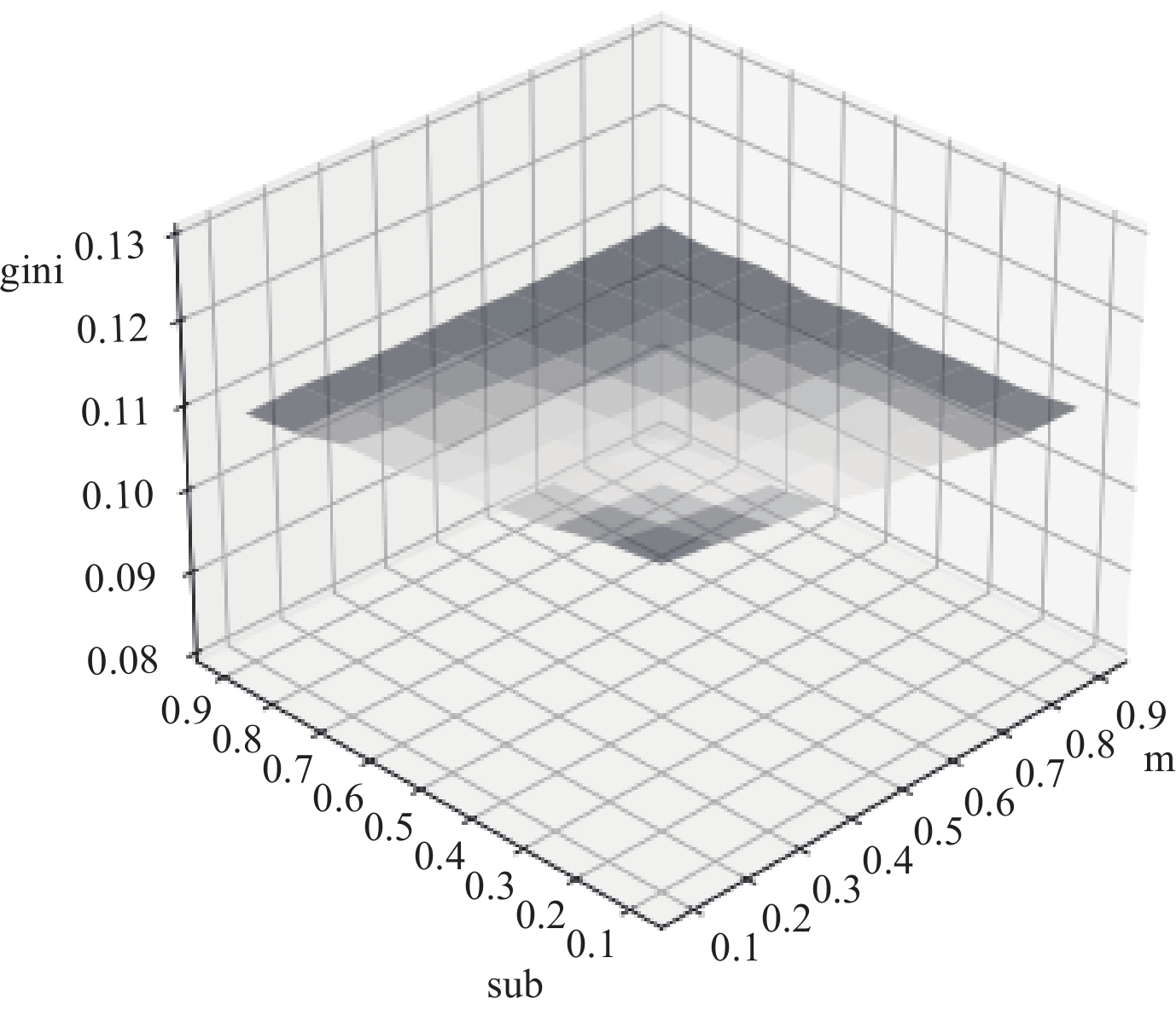
基于有风险、有保险、有补贴模型，引入农业风险的保障程度m和补贴比例sub作为一种可控的政策措施，保障程度和补贴比例分别是农业保险公司提供的农险产品和政府行为。图2表明，农业保险保障程度变化对农村家庭收入不平等的影响存在线性关系，随着保障程度降低（农险免赔率m提高），基尼系数降低。补贴比例对收入不平等的影响也呈现出线性规律，随着补贴比例提高，基尼系数也降低。因此，较高的补贴比例和免赔率对应较低的基尼系数，并由此降低农村家庭收入不平等程度。

（3）农业保险市场势力对收入不平等的影响

将农业保险市场的市场势力λ引入模型，并且进行数值模拟。市场势力λ比较特殊，一方面，λ取决于农业保险市场各公司竞争与垄断相互影响的结果；另一方面，农业保险监管制度和农业保险市场竞争政策也会对λ产生相应的影响。基于此，我们认为λ介于内生与外生之间，既具有一定程度的可控性，同时也受到来自农业保险市场自身发展的影响。市场势力λ对农村家庭收入不平等的影响也呈现出一种明显的线性影响。随着市场势力提高，基尼系数也随之上升，即农险市场较高的竞争度和较低的集中度可以降低农村家庭收入不平等程度。 ⁵

我们认为，参数变化影响农民收入不平等的内在作用机制在于参数对农民单个家庭收入的影响向洛伦兹曲线和基尼系数传导。由基尼系数的界定可知，当计算基尼系数的收入分布时，如果不同个体之间区别较大则会倾向于提高基尼系数；反之，如果收入分布个体之间区别较小则会降低基尼系数。在进行比较静态分析时，参数改变会提高个体的收入变动程度还是会降低个体的收入变动程度？这个问题就显得尤为重要。考虑到现阶段我国已基本实现全面脱贫，但从经济理论角度分析仍在一定程度上存在农村家庭财富脆弱性问题。农村家庭在相同的政策环境下提高收入对其相对收入变动程度影响较小，而因为重大自然灾害等风险因素致贫或返贫，将极大提高其收入变动程度。如果参数变动造成样本中个体收入变动程度较高，则会提高基尼系数；如果参数变动造成样本中个体收入变动程度较低，则会降低基尼系数。

由式（1）可知，p、d、λ都与农村家庭收入负相关。由于我国农村家庭存在财富脆弱性问题，当p、d、λ提高造成家庭收入降低时，很可能会出现致贫或返贫的情况，导致农村家庭收入降低，从而进入收入损失的恶性循环，收入大幅下降，这会加强农村家庭的收入变化程度，造成不同农村家庭之间的收入和财富差距进一步扩大，基于此计算的基尼系数会有所提高。另外，sub与农村家庭收入正相关，sub的提高有助于降低我国农村家庭财富脆弱性，可以提高农村家庭收入，同时使得农村家庭不会处于恶性循环的低收入状态。由于sub在一定时期和一定区域内对所有农村家庭都是相同的，这会降低农村家庭收入变化的程度，使得不同农村家庭之间的收入差距进一步缩小，并由此降低基尼系数。m的情况较为复杂，由式（1）可知既存在降低收入的部分，也存在提高收入的部分，因此m对收入的影响取决于上述两种力量对比的结果。如果降低的收入效应超过提高的收入效应，m提高会导致收入下降，导致一些家庭陷入贫困状态，由此拉大不同家庭的收入差距，并最终提高基尼系数。反之，如果提高的收入效应超过降低的收入效应，那么m提高也可以造成收入提高，使得很多农村家庭缓解财富脆弱性问题，在相似的农业保险制度环境下，不同农村家庭的收入差距缩小，从而降低基尼系数。

3. 事前同质性与事前异质性

本文关注农村家庭收入的事前同质性与事前异质性对其收入不平等的差异化影响。事前同质性的模拟基础来自有风险、有保险、有补贴的设定。与前述模拟相似，在此将时间t=0时刻所有农村家庭的初始收入统一设定为收入的期望值。在事前异质性方面，为体现异质性，需要体现t=0时刻所有农村家庭的初始收入存在区别。因此，将所有家庭事前同质性模拟500期后的收入分布作为事前异质性的收入分布。模拟显示，事前同质性分布的基尼系数低于事前异质性分布的基尼系数，体现出同质性的个体收入分布产生的收入不平等要低于异质性的个体收入分布产生的收入不平等。 ⁶ 原因在于模拟2个分布的所有农村家庭初始收入不同，相对于事前同质性家庭相同的初始收入，事前异质性家庭初始收入不相同。在相同的模拟期间以及收入演化规律下，不同的初始收入具有更大的收入变化，由此计算的洛伦兹曲线和基尼系数更高。基于上述模拟结果以及中国农业保险领域的实际情况，提出以下研究假说：

假说1：以损失概率p和损失程度d为代表的农业灾害损失增加会提高基尼系数。

假说2：以保费、赔付为代表的农险保障程度降低（m提高）以及农险补贴sub的提高可以降低基尼系数。

假说3：农业保险市场集中度降低和竞争度提高可以降低基尼系数。

四、计量模型设定及变量说明

（一）计量模型设定

计量模型设定的目的是考察多种因素对农村居民收入不平等的影响。本文的因变量为各省农村地区的基尼系数，自变量包括农业灾害损失、农业保险保费收入、农业保险保费赔付、农业保险保费补贴、农险市场集中度和竞争度以及其他控制因素对基尼系数的影响。基本计量方程设计如下：

其中，gini_it为i省t年的农村基尼系数。X为本文的核心自变量，包括农业灾害损失占GDP的比重ded，并且本文在计算各省农作物因为自然灾害造成经济损失时，借鉴了灾害学理论，根据各省农作物受灾面积以及农作物单位面积产值估算了农作物因自然灾害造成的经济损失。 ⁷ 其他核心自变量为：农业保险保费收入占GDP的比重nbfzb；农业保险赔付占GDP的比重npfzb；农业保险补贴占GDP的比重nbtzb； ⁸ 农险市场集中特征CR₄；农险市场竞争特征HHI。Y表示控制变量：各省人均生产总值的对数lgdp；城乡居民基本社会养老保险基金支出占GDP比重si；经营单位所在地进出口总额占GDP比重open；农林牧渔业全社会固定资产投资占GDP比重k；死亡率倒数dr；地方财政预算支出占GDP的比重fs；高中及以上在校生占总人口比重edu。本文在基尼系数的计算上采用Dagum基尼系数对2011—2020年中国各省农村地区的经济差异进行测度和分解。与传统基尼系数不同，Dagum基尼系数可以弥补传统研究方法存在的小样本、异方差以及分布不对称的不足。本文利用VIIRS和DMSP网站提供的中国2011—2020年各省的区县夜间灯光数据来计算本文使用的基尼系数。

（二）估计方法

1. 单方程回归

单方程回归选取的方法包括面板固定效应模型、差分GMM模型以及面板工具变量模型。具体说明如下：本文针对农业灾害损失ded、农业保险保费nbfzb、农业保险赔付npfzb、农业保险补贴nbtzb四个核心自变量，选择了当地对应年份的财险深度pp以及城市降雨量rain作为工具变量。一方面，农业保险作为财产保险的组成部分，农险保费、赔付、补贴与财险深度存在直接的相关性。同时，农业保险主要针对农业灾害损失进行补偿，所以当地的自然环境与农业保险息息相关。降雨量作为农业生产的最重要因素之一，必然影响到最终的农业产出进而影响保险赔付，所以城市降雨量rain同样满足工具变量相关性的要求。另一方面，基尼系数主要受样本内个体收入分布影响，较少有研究表明财险深度会直接影响地区内居民的收入分布，而降雨量是地区自然环境的表现，并不会直接影响地区内居民的收入差距。综上所述，财险深度pp以及城市降雨量 rain并不直接影响农户的收入不平等，因而满足工具变量外生性的要求。

本文针对农业保险市场集中度CR₄、竞争度HHI两个核心自变量，选择了因变量gini的滞后项、大中型企业产值占GDP的比重big、国有企业产值占GDP的比重soe三个变量作为工具变量。因变量滞后项的选择参考了邵全权等（2017）的研究。另外，大中型企业产值占GDP的比重big、国有企业产值占GDP的比重soe参考了林毅夫和孙希芳（2008）的研究。一方面，这两个变量代表了当地的金融结构，而金融结构必然会影响保险市场结构，所以满足工具变量相关性的要求；另一方面，金融结构对于农村居民的收入难以产生直接显著的影响，因而总体上满足外生性的要求。

2. 解决内生性的面板门槛回归

农业灾害损失、农业保险和农险市场结构与农村收入不平等之间可能存在非线性关系，从而出现异质性。为此本文采取面板门槛回归进行实证检验，但是传统的门槛回归在估计固定效应估计量时，要求协变量必须是强外生的，这在许多实际应用中会受到限制。Caner和Hansen（2004）在传统门槛回归的基础上进一步提出了克服内生性的面板门槛模型。本文借鉴这一方法，估计了面板门槛回归的系数。

3. 联立方程回归

考虑到单方程设计中可能会存在双向因果关系，而且农业灾害损失、农业保险和农险市场结构和农村收入不平等之间往往存在复杂的双向因果关系。仅依靠单方程回归难以进行因果识别，为此本文选择联立方程回归进行稳健性检验。以农业灾害损失对农村收入不平等的影响为例，联立的两个方程依次是农村收入不平等方程和农业灾害损失方程。其中，农村收入不平等方程与单方程设定相同。而农业灾害损失方程描述农村收入不平等与农业灾害损失之间的关系。控制变量主要为各地自然环境变量，包括城市降水量rain、城市年日照时数sun、二氧化硫排放SO2、城市相对湿度sd。另外，还可以得到农业保险、农险市场结构和农村收入不平等之间的联立方程模型。

4. 面板分位数回归

我国不同地区农村家庭的收入存在较大差异，本文利用面板分位数回归检验在不同初始收入水平的条件下，农业灾害损失、农业保险和农险市场结构对农村收入不平等影响的差异性，为相关部门的政策制定提供一些参考。

（三）变量说明及描述性统计

实证分析的变量界定及数据来源如下：本文使用的所有变量时间跨度为2011—2020年，均为省级层面面板数据；表2中因变量gini为各省市每年农村地区的基尼系数；核心自变量农业灾害损失占GDP的比重ded数据来自国家统计局；农业保险保费、赔付数据来自《中国保险年鉴》；农业保险补贴数据来自中国银保监会；农险市场集中特征CR₄、农险市场竞争特征HHI计算所用的原始数据来自《中国保险年鉴》。表2中除上述变量以外的所有变量的数据均来自国家统计局。

五、计量结果及解释

（一）单方程回归

本部分对我国各省市农业灾害损失、农业保险和农险市场结构对农村收入不平等的影响进行计量检验。选取的方法包括固定效应、差分GMM以及面板工具变量。这么做的理由是：第一，这符合样本的面板数据特征。本文在选取方法时对比了混合OLS、固定效应以及随机效应模型，最终利用F检验、豪斯曼检验确定了固定效应模型为最优模型，同时考虑到回归中仍然存在遗漏变量带来内生偏误的可能，继续使用了面板工具变量模型。此外，个体当期收入差距可能受到过去行为的影响，本文利用差分GMM进行检验。第二，为了保证结果的稳健性，当三种不同的计量方法得出的结论相同或相近时，可以进一步证明回归结果的稳健性。

表3中，ded的回归系数分别为0.0750、0.0707和0.353，均在1%的显著性水平下显著，说明农业灾害不利于促进农村地区的收入平等，同时三种回归方法得到了相同结论，这进一步说明了回归结果的稳健性。农业灾害会加剧农民收入不平等主要是由于农户收入脆弱性不同。根据已有文献结论，当农业灾害发生时，小农户更易受到冲击，而高收入农户具备更强的抗风险能力，所以低收入水平和高收入水平农户的收入差距变大，农民内部的收入不平等程度提高。在前文的数值模拟中，损失概率和损失程度上升会提高样本中个体收入变动程度，进而提高基尼系数，同样也是由于上述原因，低收入农户的收入水平在遭受风险冲击时变动更为剧烈，这提高了样本整体的变动程度，进而提升了整体收入差距，实证结果与数值模拟一致。因此，假说1得到了证明。

nbfzb、npfzb、nbtzb总体上与gini存在显著的负相关关系，说明农业保险发展有利于促进农村地区的收入平等。农业保险之所以能够缩小收入差距，其中的机制如下：杜鑫（2021）研究了全国10个省份、50个县（市、区）粮食主产区、产销平衡区和主销区的农户收入数据，发现不同分区内农户收入差距主要由非农经营净收入导致，农业经营收入可以在一定程度上缓解收入不平等程度。因此，当农业保险保障程度变高时，农户的农业经营收入占比上升，缓解了农民内部的收入不平等。由于从农业生产中获得收入的确定性增强，农户会将应对不确定性风险的储蓄用于资本积累，更新农业技术，从而提高生产效率，这进一步提高了农业经营收入占比，促进收入平等。这一机制与前文的数值模拟也形成了对应：第一，在数值模拟中农户当期收入由上期储蓄产生的资产回报以及本期农业生产的收入组成，本质上同样是利用农业收入与非农收入这一收入结构的视角考察不平等。第二，数值模拟将农业生产收入序列标准差看作风险损失概率和损失程度的函数，同时引入农业保险乘子，考察在风险与保险共同作用下农业收入的动态变化。而在上述的机制过程中，同样解释了当农业风险存在时，农业保险保障程度的提高对农业经营收入变化以及对收入不平等的影响。第三，在数值模拟中储蓄函数设定为示性函数，只有在当期收入高于阈值时农户才进行储蓄，进而产生资产回报。而在上述机制分析中，我们解释了伴随农业保险保障程度的上升，农户进行农业生产的不确定性大大降低，从而可能产生相应的储蓄并进行投资，促进农业资本积累，进而提高农业产出。在数值模拟中，免赔率m对于收入的影响存在降低收入和提高收入两种效应，最终的结果取决于净效应，虽然模拟结果显示保障程度降低（m提高）会降低基尼系数，但与实证结论并不冲突，在数值模拟中给出了提高收入效应小于降低收入效应时的情形，而实证结果则对应相反的情况，这在理论上同样是存在的。因此，农业保险保障与农民收入不平等之间的关系不能简单概述，需要进一步考察。

CR₄、HHI与gini显著正相关，即提高农险市场竞争度、降低集中度有利于改善收入不平等。已有研究表明，市场集中度下降和竞争度提高有利于农业保险市场规模扩大，更好发挥保险保障作用，而农业保险市场竞争度上升和集中度下降可以促进农民收入公平，这与数值模拟的结果相一致，假说3得到验证。

上述回归结果表明，农业灾害损失会加重农村居民收入不平等，农业保险保费、赔付与补贴以及农险市场竞争度的上升都会促进收入平等。对于回归的结果，需要进一步作出以下解释：第一，单方程回归中的农业灾害损失ded、农业保险相关变量nbfzb、npfzb、nbtzb以及农险市场结构变量CR₄、HHI均被认为是外生的，但是它们也有可能与因变量gini之间存在相关性，即有可能是内生变量，与gini存在双向因果关系；第二，在计量回归中经常出现换用计量方法而结果失效的现象，为了进一步检验结果的稳健性，考虑自变量内生的可能性，下面将使用联立方程回归进行分析。

（二）联立方程回归

根据表4列（1）—（6）的结果，ded、nbfzb、npfzb、nbtzb、CR₄和HHI对于基尼系数均在1%的显著性水平下显著，并且与前文单方程回归的符号相同，说明考虑回归中的双向因果关系后，本文结论依然具有稳健性。

在不同的基尼系数水平下，农业灾害损失、农业保险和农险市场结构对农村收入不平等的影响可能是不同的。尤其是农业保险保费收入、赔付以及补贴同收入不平等之间可能存在复杂的异质性联系，前文的基准回归和数值模拟已经证实这一点。为发现异质性，本文接下来进行面板门槛回归。同时在面板门槛回归中对于内生解释变量使用工具变量以克服内生性问题。

（三）面板门槛回归

表5是解决内生性的面板门槛回归结果。当以基尼系数作为门槛变量，核心自变量为被门槛变量时，所有回归均具有显著的单门槛效应，门槛值均在1%的显著性水平下显著。当gini小于0.564时，ded的系数为−0.018；当gini大于0.564时，ded的系数为−0.036，但上述回归系数均不显著。考虑到一种回归方式可能存在局限性，需要更换回归方法再次检验。对于nbfzb、npfzb、nbtzb三个变量，当gini位于不同的门槛区间时，nbfzb、npfzb、nbtzb与收入不平等之间的关系也不相同。这也证明了在保险免赔率机制作用下，农业保险保障和收入不平等之间存在复杂关系。事实上，在不同收入差距情形下，样本的收入分布存在差异，因而农业保险保障降低收入变动与提高收入变动的净效应也会随之变化。单方程回归显示农业保险保障程度的提高可以降低基尼系数，但这只说明农业保险保障降低了基尼系数的条件期望，需要进一步考察不同条件分位数下，农业保险保障与基尼系数的关系。本文接下来将进行面板分位数回归。对于CR₄、HHI两个变量，当gini小于0.618时，CR₄的系数为−0.343，在5%的水平下显著；当gini大于0.618时，CR₄的系数为0.500；当gini小于0.445时，HHI的系数为0.113，在1%的水平下显著；当gini大于0.445时，HHI的系数为−0.0245。出现这一结果的原因有：一方面，我国农业保险起步晚，市场尚不够完善。2011—2020年，在我国大部分省份的财险市场中，少数几家公司独占绝大部分农险业务，形成了高度寡头的局面，市场竞争度与农民收入不平等之间的关系未能充分体现。另一方面，我国农业保险市场的发展存在显著的空间差异，可能影响了保险的普惠性本质。事实上，我国不同省份的农业保险发展水平存在较大差别，保险对农民收入不平等的影响程度也不同。因此，区域性农业保险市场结构差异最终影响了保险市场结构与农民收入不平等之间的关系。

（四）面板分位数回归 ⁹

当农民内部的事前收入差距处于不同水平时，农业灾害损失、农业保险对农村居民收入不平等的影响往往不同。为了研究这种事前效应的影响，本文选择面板分位数回归进行检验。

根据分析结果，从静态角度来看，2011—2020年各省基尼系数存在明显的水平区域差异，东部省份的基尼系数普遍偏小，说明东部相比于西部总体上农民收入差距更小。从动态角度看，基尼系数在不同地区的发展趋势同样存在差异，部分省份如福建、贵州、四川2011—2020年基尼系数的下降趋势明显，但是另一些省份如云南、内蒙古、甘肃等收入不平等的下降程度则并不显著。因此，省份之间在收入不平等程度上存在明显的区域差异。

根据国际标准，基尼系数大于0.4被认为存在明显的收入分配不公。本文对基尼系数进行分位数处理，可以更好地体现事前异质性：当基尼系数较小时，农民内部的收入比较平等，事前异质性较低；当基尼系数较大时，农民内部的收入差距较大，事前异质性较高。根据分析结果，总体上，当基尼系数小于0.4时，灾害损失、保险收入、保险赔付、保险补贴以及市场集中度对于基尼系数均有负向作用；当基尼系数大于0.4时，上述因素提高会促进基尼系数上升。根据回归结果，当基尼系数小于0.42时，农业灾害损失会缩小收入差距；当基尼系数大于0.42时，农业灾害损失会加剧收入不平等程度，这是由于当农户内部收入差距较大时，低收入农户家庭财富更为脆弱，从而进一步扩大其和中高收入群体差距。农业保险对于收入不平等的影响同样存在事前异质性，相应机制如下：第一，低收入农户的保险保障意识比较落后，同时保险消费倾向较低，商业性农业保险资源更多向中高收入群体倾斜。第二，已有研究发现，对于低收入群体来说，农业保险保障存在“失效区间”，只有当保障程度越过“失效区间”后，才能较好地改善贫困农户的收入情况。当农户内部事前收入差距过大时，拥有农业保险的低收入群体的收入状况可能难以改善，而中高收入群体则可以获得有效保障，从而农户内部的收入差距逐步变大。

面板分位数回归的结果也证实了在数值模拟中免赔率与基尼系数之间的复杂机制。当农户内部的收入差距较小时，保险保障程度的上升（免赔率降低）会导致减小收入变动的效应大于提高收入变动的效应，最终的净效应促进了农民的收入更加平等；当农户内部的收入差距较大时，保险保障程度的上升（免赔率降低）会导致提高收入变动的效应大于减小收入变动的效应，最终的净效应导致农民的收入差距进一步扩大，原因是低收入群体可能难以获得有效的保险保障。因此，假说2得以验证。同时，实证结果与机制分析表明，当事前农民内部收入差距较大时，农险保障程度上升会提高基尼系数，增加收入不平等；当事前农民内部收入差距较小时，农险保障程度上升会降低基尼系数，促进收入平等。

六、结论与建议

首先，本文建立农业灾害损失、农业保险发展对于农村居民收入不平等影响的理论模型，运用数值模拟的方法研究了农业灾害损失、农业保险保障、补贴以及农险市场结构对农民收入不平等的影响，结果发现：农业风险损失概率和损失程度上升会提高基尼系数，农险补贴的提高可以降低基尼系数。而农险保障程度与基尼系数的关系取决于保险保障对农民收入变动影响的净效应。当保障程度的净效应降低收入变动时，会促进收入平等；当保障程度的净效应增加收入变动时，会加剧收入不平等。农民个体间的初始差异越低，越有利于促进收入平等。其次，本文运用2011—2020年的省级面板数据进行了检验。实证的主要结论在于：第一，农业灾害损失会增加农民收入不平等程度，农险保费收入、赔付与补贴会减缓收入不平等，同时，农险市场竞争度的提高、集中度的下降有利于促进农民收入平等。第二，联立方程回归和面板门槛回归证实了结果的稳健性，同时发现农业灾害损失、农业保险保费、赔付、补贴以及农险市场结构对农民收入不平等的影响会因为不平等程度的不同而发生变化。第三，面板分位数回归发现事前收入越公平，保险市场越发达，越有利于降低收入不平等。

基于此，本文提出以下建议：第一，政府利用财政积极支持农业公共设施建设，例如兴修水利、加强防灾防损宣传等，同时，针对灾害频发地区积极筹备灾后抢救措施，尽力减少自然灾害给农业带来的不利影响，保证农民收入。第二，大力发展农业保险，重视农业保险补贴。政府应当与保险公司积极配合，加强政策性农业保险与商业性农业保险互动。政府要做好宣传，提升农民参保意识。第三，关注农民内部差异，对于收入差距较大的地区，农业保险的改善作用较小，此时应当配合农业信贷等其他手段来改善收入分配。对于收入差距较小的地区，可以将资金更多地用于农业保险，这样能够更好地促进收入平等。第四，政府应当利用财政积极培育农险市场主体活力，促进更多农业保险参与方加入市场，对已有的农业保险公司进行监督，防止垄断。政府应通过提高农业保险市场竞争度来更好地发挥保险作用，维护农民收入平等。

1限于篇幅，在此不报告有风险、无保险模型与有风险、有保险、无补贴模型形式。

2根据邵全权等（2017b）的研究，风险乘子为p(1−d)+1−p=1−pd，反映不发生风险与发生风险造成损失的按概率进行计算的加权平均。保险乘子为p(1−d)+1−p+pd(1−m)=1−pdm，体现不发生风险与发生风险造成损失并获得农业保险公司扣除免赔后的赔付的加权平均。

3一般情形下设定初始状态相同，对应事前同质性状态，后文中将改变这一设定，研究事前异质性的影响。

4限于篇幅，在此不报告三种情况对比的洛伦兹曲线和基尼系数，感兴趣的读者可以向作者索取。

5限于篇幅，在此不报告市场势力影响的洛伦兹曲线和基尼系数，感兴趣的读者可以向作者索取。

6限于篇幅，在此不报告事前同质性与事前异质性对比的洛伦兹曲线和基尼系数，感兴趣的读者可以向作者索取。

7限于篇幅，不介绍具体计算过程，感兴趣的读者可以向作者索取。

8农业保险补贴的原始数据来自中国银保监会。本文对于中央、省级以及地方县市三级补贴进行了加总处理。

9限于篇幅，图表分析省略，感兴趣的读者可向作者索取。