一、引　言

中国经济步入新常态以来，经济结构性问题日益凸显。党的十九大报告提出“深化供给侧结构性改革”，而民营企业“融资难、融资贵”一直是中国经济面临的重要结构性问题。为了应对这一问题，自2013年起，中国人民银行陆续推出了一系列结构性货币政策工具，如中期借贷便利（MLF）、信贷政策支持再贷款（如支农、支小、扶贫再贷款）等，引导金融机构加大对民营企业的支持力度，为民营企业和小微企业营造良好的金融环境。

党的十九届四中全会提出“建设现代中央银行制度”，而维护央行资产安全、防范道德风险也是建设现代中央银行制度的应有之义。为此，中国人民银行创设的结构性货币政策工具大多需要高质量担保品的支持，如国债、央行票据等。然而，随着中国新型货币政策实施的常态化和规模化，由于国债、央行票据等高等级债券资产的有限性，部分金融机构逐渐出现担保品短缺问题。这限制了金融机构充分获取流动性，严重影响了民营企业和小微企业的正常融资和稳步发展。

为了解决金融机构高等级担保品不足的问题，加大对民营企业和小微企业的支持力度，2018年6月中国人民银行决定扩大中期借贷便利及信贷政策支持再贷款担保品范围。在原有基础上，加入不低于AA级的小微企业、绿色和“三农”金融债券，AA+和AA级公司信用类债券（优先接受涉及小微企业、绿色经济的债券），以及优质的小微企业贷款和绿色贷款。可以看出，此次担保品扩容着重突出了小微企业债券及信贷资产，这相当于以国家信用为小微企业背书，以缓解小微企业“融资难、融资贵”问题。

事实上，将小微企业债券及信贷资产纳入央行担保品范围相当于提高这类资产的抵押率（从0提高到特定抵押率），而提高相应资产的抵押率对宏观经济波动和货币政策有效性的影响是本文探讨的主要问题。本文研究表明，提高信贷资产抵押率会产生银行贷款的违约风险外移效应，即央行通过将小微企业信贷资产纳入担保品范围，可以增强其对相关企业的信用背书，分散借款企业的部分信用风险，从而缓解企业信贷约束。提高信贷资产抵押率将通过银行贷款的违约风险外移效应影响宏观经济波动和货币政策有效性。

一系列理论文献论证了国外央行担保品框架政策的有效性。有研究认为央行扩大担保品范围能够降低信贷利差，缓解信贷紧张，增加产出（Ashcraft等，2011；Koulischer和Struyven，2014）。Ashcraft等（2011）通过构建代际交叠（OLG）模型研究了新型货币政策对经济的影响，发现与调节利率的传统货币政策相比，提高抵押率的货币政策能更有效地降低相应资产的必要回报率和企业融资成本，刺激相关部门的经济活动。部分文献认为央行实施宽松的担保品政策虽然会激励银行将低质量资产抵押给央行，使央行面临潜在损失，但其提高了私人市场的担保品质量，激活了信贷市场（Choi等，2021）。还有文献认为非传统货币政策（如借贷便利、流动性便利等）可以通过放松银行融资约束，增加市场流动性，从而缓解金融危机（Gertler和Kiyotaki，2010）。上述理论得到了实证文献的验证（Ashcraft等，2010；Van Bekkum等，2018；Pelizzon等，2020）。Pelizzon等（2020）研究了欧洲央行担保品框架中企业债券对货币政策的影响，发现企业债券的引入能够放松担保品供给限制，扩大企业债券融资规模。

关于担保品抵押率对货币政策有效性的影响，现有研究大多集中于探讨企业（或家庭）与银行抵押贷款合约中的实物资产抵押率如何影响货币政策作用效果（Iacoviello，2005；Calza等，2013），而目前鲜有文献探讨央行担保品抵押率对传统货币政策规则有效性的影响。此外，相关文献大多旨在比较央行担保品抵押率与传统货币政策规则对经济作用效果的差异，但对两种工具的相互影响研究却较少（Ashcraft等，2010；Schabert，2015）。本文将重点探讨央行担保品抵押率对传统货币政策规则实施效果的影响。

关于中国人民银行扩大担保品范围的研究，大多数文献从实证角度探讨了MLF担保品扩容政策所产生的影响。部分文献集中探讨了央行担保品扩容政策对相关债券信用利差的影响，如王永钦和吴娴（2019）、黄振和郭晔（2021）。部分文献侧重于央行担保品框架的绿色效应，如陈国进等（2021）、郭晔和房芳（2021）。还有文献研究了央行担保品框架对货币政策传导效率的影响，如邓伟等（2021）、刘冲等（2022）。

然而，上述研究都是从实证角度考察担保品扩容的影响。如何从动态随机一般均衡的角度分析信贷资产抵押率的上升对借款企业融资成本、宏观经济波动以及货币政策有效性的影响是本文重点探讨的问题。鉴于此，本文对传统金融加速器模型进行拓展，构建了包含央行担保品框架的动态随机一般均衡模型。本文的主要工作与结论如下：第一，通过稳态分析探讨了信贷资产抵押率对企业融资成本、违约风险和社会福利的影响。研究发现，提高信贷资产抵押率虽然可以通过违约风险外移效应而降低借款企业的融资成本，但也会提高借款企业的违约风险，降低社会福利。第二，本文通过比较不同的信贷资产抵押率下风险冲击和技术冲击对宏观经济的影响，分析了信贷资产抵押率与宏观经济波动的关系。结果表明，当经济面临负面冲击时，提高信贷资产抵押率所产生的违约风险外移效应可以抑制金融加速器效应，从而稳定宏观经济。第三，本文通过比较不同的稳态抵押率下货币政策冲击对经济的作用，探讨了信贷资产抵押率对货币政策有效性的影响。研究发现，信贷资产抵押率与总量型货币政策有效性的关系取决于政策工具，提高信贷资产抵押率在数量型货币政策规则下有助于增强货币政策有效性，但在价格型货币政策规则下对货币政策传导效率的影响较小。第四，本文将单部门模型扩展成包含国企和私企的两部门模型，并探讨了信贷资产抵押率对借贷便利工具有效性的影响。结果显示，担保品扩容之后，扩张性借贷便利操作对经济的刺激作用显著增大，并使通胀率显著下降。

本文的主要贡献如下：第一，首次将央行担保品框架引入金融加速器模型中，为分析这一政策对金融摩擦、宏观经济波动和货币政策有效性的影响提供了模型框架；第二，与以往的经验分析不同，本文从理论上分析了央行将小微企业信贷资产纳入担保品范围所产生的银行贷款违约风险外移效应，并发现了信贷资产抵押率在稳定宏观经济方面的作用；第三，本文从理论上探讨了央行担保品扩容政策对货币政策有效性和借贷便利工具有效性的影响，这对央行货币政策实践具有指导意义。

二、理论模型

本文在传统金融加速器模型的基础上，构建了包含央行担保品框架的动态随机一般均衡。模型涉及的经济主体包括家庭、零售品部门、批发品部门、企业家、资本品生产商、商业银行以及中央银行。^①

（一）最优债务合约

本文假定经济中存在代表性企业家，其在t期末通过自有资金 $ N $ 和银行贷款 $ {B}_{t}^{N} $ 购买下期所需的资本 ${\bar{K}_{t}^{N}}$ 。假定资本品的名义价格为 $ {Q}_{t} $ ，则有：

企业家买入资本品后会立即遭遇异质性冲击 $ {\omega }_{t} $ ，将1单位资本转化为 $ {\omega }_{t} $ 单位有效资本，由此可知企业家的有效资本持有量为 ${\omega }_{t}{\bar{K}}_{t}^{N}$ 。为了引入风险冲击，假定 $ {\omega }_{t} $ 服从期望为1的时变对数正态分布，即 $ \mathrm{l}\mathrm{n}{\omega }_{t} \sim N(-{\sigma }_{t}^{2}/2,{\sigma }_{t}^{2}) $ ，其中 $ {\sigma }_{t} $ 为 $ \mathrm{l}\mathrm{n}{\omega }_{t} $ 的标准差，且服从如下AR（1）过程：

其中， $ {\rho }_{\sigma }\in (-\mathrm{1,1}) $ ， ${\varepsilon }_{\sigma t} \sim N(0,{\sigma }_{\sigma }^{2})$ 。进一步地，企业家将有效资本租给批发商，其预期收益率为：

其中， $ {r}_{t+1}^{k} $ 为资本租金率， $ {P}_{t+1} $ 为价格水平， $ (1-\delta ){Q}_{t+1} $ 为1单位的资本剩余价值。

假定银行贷款利率为 $ {Z}_{t+1} $ （状态或有利率），企业家 $ t+1 $ 期的平均收益率为 $ {{R}}_{t+1}^{k} $ ，异质性收益率为 $ {\omega }_{t+1} $ ，可得企业家总收益为 $ {\omega }_{t+1}{{R}}_{t+1}^{k}(N+{B}_{t}^{N}) $ 。当 $ {\omega }_{t+1} $ 高于还款阀值 $ {\bar{\omega }}_{1,t+1} $ 时，企业家到期偿还贷款；当 $ {\omega }_{t+1} $ 低于还款阀值 $ {\bar{\omega }}_{1,t+1} $ 时，企业家选择违约。还款阀值 $ {\bar{\omega }}_{1,t+1} $ 与贷款利率 $ {Z}_{t+1} $ 存在如下关系：

当企业家违约时，银行需要支付 $ {\mu }_{1}{\omega }_{t+1}{{R}}_{t+1}^{k}(N+{B}_{t}^{N}) $ 的清算成本， $ {\mu }_{1}\in \left(\mathrm{0,1}\right) $ ，并将全部剩余价值拿走，进而可得企业家的利润函数：

其中， $ F\left({\omega }_{t}\right) $ 表示 $ {\omega }_{t} $ 的累积分布函数， $ F\left({\bar{\omega }}_{1,t+1}\right) $ 表示企业违约概率。

银行向企业家发放贷款后将该贷款作为中期借贷便利或再贷款工具的担保品，以一定抵押率获得相应流动性，随后将这部分流动性贷给企业家，最终银行向企业家发放的贷款总额为 $ {B}_{t}^{N} $ ，从央行获得的流动性为 $ {\tau }_{t}{B}_{t}^{N} $ ，其中 $ {\tau }_{t} $ 为信贷资产抵押率。在代表性企业模型中，抵押率 $ {\tau }_{t} $ 能够方便地刻画央行担保品扩容政策，其不仅反映了信贷资产抵押率的大小，还反映了商业银行从央行获得的借贷便利占银行信贷资产的比例。将小微企业信贷资产纳入担保品范围意味着小微企业信贷资产抵押率从0上升到特定水平。

本文进一步假定央行借贷便利操作利率为 $ {R}_{lt} $ ，用 $ {M}_{lt}={\tau }_{t}{B}_{t}^{N} $ 表示借贷便利操作规模。为了体现央行对担保品的信用背书，本文将银行参与约束设定为：

其中， $ {R}_{t} $ 为存款利率， $ {\bar{\omega }}_{2,t+1} < {\bar{\omega }}_{1,t+1} $ ，当 $ {\omega }_{t+1} $ 大于还款阀值 $ {\bar{\omega }}_{1,t+1} $ 时，企业不违约，银行按期从央行赎回担保品，银行需归还借贷便利额 $ {R}_{lt}{\tau }_{t}{B}_{t}^{N} $ ；当 $ {\bar{\omega }}_{2,t+1} < {\omega }_{t+1} < {\bar{\omega }}_{1,t+1} $ 时，企业违约，但此时银行从企业获得的清算价值仍大于借贷便利额，银行会按期赎回担保品并归还借贷便利额 $ {R}_{lt}{\tau }_{t}{B}_{t}^{N} $ ；当 $ {\omega }_{t+1} < {\bar{\omega }}_{2,t+1} $ 时，企业违约，银行获得的清算价值小于借贷便利额，此时银行将把企业清算价值归还央行用以抵扣借贷便利成本，缺口部分视作央行发放借贷便利时的损失。^②可见，当 $ {\omega }_{t+1}={\bar{\omega }}_{2,t+1} $ 时，企业清算价值等于银行借贷便利成本，则有：

进一步地，当企业清算价值不足以支付央行利息时，银行将把企业清算价值归还央行，此时央行损失（即央行承担的信用风险）为：

式（8）也可反映央行对担保品的信用背书。将式（7）代入式（8），整理可得：

其中， $ F\left({\bar{\omega }}_{2,t+1}\right)-{\int }_{0}^{{\bar{\omega }}_{2,t+1}}{\omega }_{t+1}/{\bar{\omega }}_{2,t+1}dF\left({\omega }_{t+1}\right) > 0 $ 。可见，信贷资产抵押率 $ {\tau }_{t} $ 越高，央行对担保品的信用背书越强，其承担的信用风险也越多，从而越有助于缓解银行与企业之间的金融摩擦。虽然央行分散了银行贷款的信用风险，但同时提高了商业银行的风险偏好程度，使得银行愿意接受信用风险更高的企业，从而提高了经济体的潜在金融风险。

本文将单个企业家行为加总，假定净资产 $ N $ 的密度函数为 $ f\left(N\right) $ ，则企业家总体净资产为 $ {N}_{t}={\int }_{0}^{\infty }Nf\left(N\right)dN $ 。类似地，可加总得到总负债 $ {B}_{t} $ 和总资本 $ {K}_{t} $ 。

（二）中央银行与货币政策

在本文基准模型中，央行的资产端包括在公开市场上买入的国债 $ {B}_{gt} $ 以及向商业银行投放的借贷便利额 $ {M}_{lt} $ ，负债端为货币供给量 $ {M}_{t} $ ，进而可得其资产负债表约束：

其中，等式左边表示货币供给增加量，等式右边表示央行净支出。可以发现，借贷便利操作变化会对央行资产负债表约束产生两方面影响。一方面，借贷便利操作规模 $ {M}_{lt} $ 直接出现在央行资产负债表约束中，央行借贷便利操作规模 $ {M}_{lt} $ 越大，央行货币供给量 $ {M}_{t} $ 越大。另一方面，央行借贷便利操作利率 $ {R}_{lt} $ 会影响央行面临的潜在损失。央行下调借贷便利操作利率 $ {R}_{lt} $ ，则企业融资成本下降，导致反映企业和银行违约风险的 $ {\bar{\omega }}_{2,t+1} $ 下降，央行可收回的借贷便利额增加，其在借贷便利操作上面临的潜在损失减小。

担保品抵押率 $ {\tau }_{t} $ 由央行外生决定，且给定借贷便利操作利率 $ {R}_{lt} $ ，企业贷款量 $ {B}_{t} $ 由最优债务合约决定，此时货币供给量 $ {M}_{t} $ 的变化直接决定了央行国债持有量 $ {B}_{gt} $ 的变化。当异质性收益率大于 $ {\bar{\omega }}_{2t} $ 时，央行收回的借贷便利额为 $ {\int }_{{\bar{\omega }}_{2t}}^{\mathrm{\infty }}{R}_{t-1}{\tau }_{t-1}{B}_{t-1}dF\left({\omega }_{t}\right) $ ；而当异质性收益率小于 $ {\bar{\omega }}_{2t} $ 时，央行收回的借贷便利额为 $ {\int }_{0}^{{\bar{\omega }}_{2t}}\left(1-{\mu }_{1}\right){\omega }_{t}{{R}}_{t}^{k}\left({N}_{t-1}+{B}_{t-1}\right)dF\left({\omega }_{t}\right) $ 。可以发现，收回的借贷便利额越小，央行因担保品扩容而承担信用风险所造成的损失越大，这部分损失将由货币供给来抵补。

根据Chen等（2018）的研究，中国人民银行目前仍以数量型货币政策规则为主。鉴于此，本文假定央行根据通货膨胀缺口和产出缺口实施数量型货币政策规则，并借鉴Chen等（2018）的研究，将货币政策规则设置如下：

其中， ${\varepsilon }_{mt} \sim N(0,{\sigma }_{m}^{2})$ 为货币政策冲击， $ {g}_{mt}={M}_{t}/{M}_{t-1} $ 为货币供给增长率， $ {M}_{t} $ 为货币供给量， $ {g}_{m} $ 为稳态货币供给增长率， $ {\rho }_{m}\in (-\mathrm{1,1}) $ 反映上期货币政策对当期的影响程度， $ {g}_{yt}=GD{P}_{t}/GD{P}_{t-1} $ 为实际GDP增长率， $ {g}_{y} $ 为稳态GDP增长率， $ {\pi }_{t} $ 为通货膨胀率， $ \pi $ 为稳态通胀率， $ {\psi }_{mp} < 0 $ 为通胀缺口系数， $ {\psi }_{my} $ 为产出缺口系数，产出上升时 $ {\psi }_{my} > 0 $ ，产出下降时 $ {\psi }_{my} < 0 $ 。这一设定表明中国实施抑通胀、促增长的货币政策。

（三）市场出清

经济均衡时，最终品、零售品、批发品、资本、劳动和货币均实现市场出清，进而可得资源约束方程：

其中， $ {Y}_{t}^{f} $ 为总产出， $ {C}_{t} $ 为消费， $ {I}_{t} $ 为投资， $ {\Omega }_{p} $ 为价格调整成本参数， $ {\mu }_{1} $ 和 $ {\mu }_{2} $ 分别为商业银行和央行清算成本占企业总收益的比例。当 $ {\bar{\omega }}_{2t} < {\omega }_{t} < {\bar{\omega }}_{1t} $ 时，银行清算成本为 $ {\mu }_{1} $ ；而当 $ {\omega }_{t} < {\bar{\omega }}_{2t} $ 时，银行将企业清算价值归还央行，央行需要再次检查以防止银行瞒报，此时总清算成本为 $ {\mu }_{2} $ ，且 $ {\mu }_{2} > {\mu }_{1} $ 。

此外，假定本文经济体为封闭经济体且无政府支出，则GDP只包含消费和投资，即：

根据本文模型设定，银行资产端为企业贷款 $ {B}_{t} $ ，负债端为家庭存款 $ {D}_{t} $ 和央行借贷便利 $ {\tau }_{t}{B}_{t} $ ，则银行资产负债表约束为：

本文将货币供给定义为广义货币供给量，故市场出清时货币供给等于流通中的现金 $ {M}_{t}^{H} $ 和银行存款 $ {D}_{t} $ 之和，即：

三、参数校准

本文共有六类参数需要校准，分别为家庭部门参数、最终品与零售品部门参数、批发品部门参数、资本品生产部门参数、债务合约参数以及货币政策参数。此外，模型中的1期代表现实经济中的1个季度。

在家庭部门参数中，主观折现因子 $ \beta $ 被校准为0.995，以匹配年化稳态市场利率4%。根据王国静和田国强（2014）的估计，本文将 $ \eta $ 设定为2，表明劳动供给弹性为0.5。由于现实经济中家庭劳动时间约占总时间禀赋的1/3，劳动效用损失权重 $ \Psi $ 被设定为17.31。鉴于现实经济中流通现金约占M2的5%，实际货币余额效用权重 $ {\Psi }_{m} $ 被校准为0.0024。

在最终品与零售品部门参数中，借鉴Chang等（2019）的设定，本文将零售品替代弹性 $ \varepsilon $ 校准为10，价格调整成本系数 $ {\Omega }_{p} $ 校准为22。在批发品部门参数中，本文将劳动份额 $ \alpha $ 校准为0.5，这与Zhu（2012）的研究一致。Chang等（2019）将家庭劳动份额 $ \theta $ 设定为0.94，企业家劳动份额设定为0.06，本文也采用这种设定。在资本品生产部门参数中，本文将资本折旧率校准为0.035，表明年度资本折旧率为5%，这与中国实际数据相符；将投资调整成本参数 $ {\Omega }_{K} $ 设定为5，这一数值落在经典DSGE文献估计范围内（Smets和Wouters，2007）。

在债务合约参数中，本文将企业家存活率 $ \xi $ 设定为0.9605，以匹配2.5%的银行贷款违约率，这意味着企业存活期限约为8年。根据Bernanke等（1999），本文将银行清算成本 $ {\mu }_{1} $ 校准为0.12。由于央行监管成本高于银行监管成本，本文假定央行清算成本是银行清算成本的两倍，将其设定为0.24。^③对于异质性冲击标准差 $ \sigma $ ，根据Hsieh和Klenow（2009）的估计，2005年中国企业对数TFP标准差为0.63（年度值），故本文将 $ \sigma $ 校准为0.315。借鉴Christiano等（2014），本文将风险冲击持续性 $ {\rho }_{\sigma } $ 设定为0.97，风险冲击标准差 $ {\sigma }_{\sigma } $ 设定为0.01。

在货币政策参数中，根据中国人民银行对抵押品基础抵押率的规定，本文将担保品扩容后的小微企业信贷资产抵押率校准为0.5。^④本文将稳态通货膨胀率 $ \pi $ 校准为1.005，表明年化通货膨胀率为2%。本文基于2016年第一季度至2020年第四季度中期借贷便利操作规模和利率数据，将借贷便利操作规模的持续性参数 $ {\rho }_{g} $ 校准为0.34，将借贷便利操作利率的持续性参数 $ {\rho }_{l} $ 校准为0.9。对于货币政策规则，根据Chen等（2018）的估计，本文将货币供给持续性参数 $ {\rho }_{m} $ 校准为0.4，通胀缺口系数 $ {\psi }_{mp} $ 校准为−0.4，产出缺口系数 $ {\psi }_{my} $ 校准为−1.3。

四、稳态分析

为了探讨央行担保品扩容政策对经济的长期影响及其传导机制，这部分将进行稳态分析。由理论模型可知，央行担保品框架与信贷资产抵押率 $ {\tau }_{t} $ 存在对应关系，将小微企业信贷资产纳入央行担保品范围意味着小微企业信贷资产抵押率从0上升到特定水平。

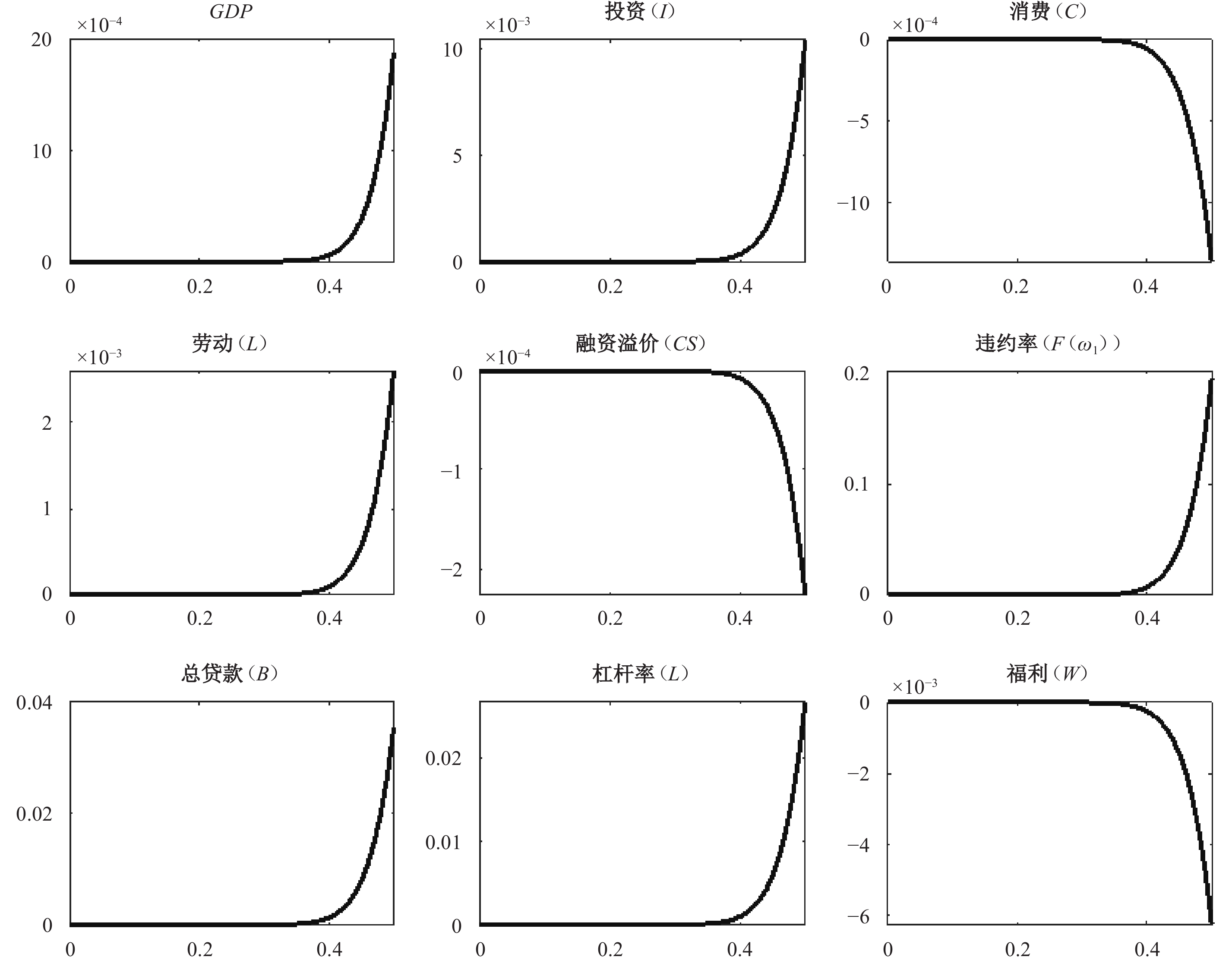
图1展示了信贷资产稳态抵押率与关键经济变量稳态值的关系。可以发现，当稳态抵押率较低时，关键经济变量受信贷资产抵押率的影响较小。这是因为当抵押率较低时，央行对相关企业的信用担保较弱，从而无法有效缓解金融摩擦、降低企业融资成本。随着稳态抵押率的逐渐提高，其对经济体的影响愈加显著。具体而言，当抵押率较高时，央行提高信贷资产抵押率所产生的银行贷款违约风险外移效应增强（央行对企业的信用背书增强，借款企业的信用风险更加分散）。这有助于缓解企业融资约束和信贷摩擦，最终降低企业融资溢价和融资成本。信贷摩擦的减少使银行贷款总量上升，企业投资增加，劳动需求上升，总产出上升。尽管央行扩大担保品范围有助于缓解金融摩擦，降低企业融资成本，但由于银行贷款违约风险外移效应的存在，央行外生化银行贷款的部分信用风险将会提高银行的风险偏好程度。随着时间的推移，较高的银行风险偏好程度使银行贷款增加，企业杠杆率上升，而杠杆率上升又使企业违约风险上升。随着企业违约风险的上升，违约清算成本上升，消费被挤出，使得家庭消费随抵押率上升而下降。又由于家庭劳动随着抵押率的上升而上升，社会福利随抵押率的上升而下降。

综上可知，一方面，央行提高信贷资产抵押率可以通过银行贷款违约风险外移效应而缓解企业信贷约束，降低企业融资溢价，提高企业投资和产出；但另一方面，信贷资产抵押率的提高也会使企业违约风险上升，家庭消费和社会福利下降。

五、宏观经济波动分析

为了探讨信贷资产抵押率对宏观经济波动的影响，这部分比较了不同的信贷资产抵押率在风险冲击和技术冲击下对经济周期的平滑作用，并重点探讨了担保品抵押率对金融加速器效应及宏观变量波动率的影响。^⑤

本文采用波动率指标来反映宏观经济波动情况。本文发现在风险冲击下，GDP、投资、企业违约率、杠杆率、融资溢价以及资本价格的波动率均随稳态抵押率的上升而下降。这表明提高信贷资产抵押率有助于稳定宏观经济。

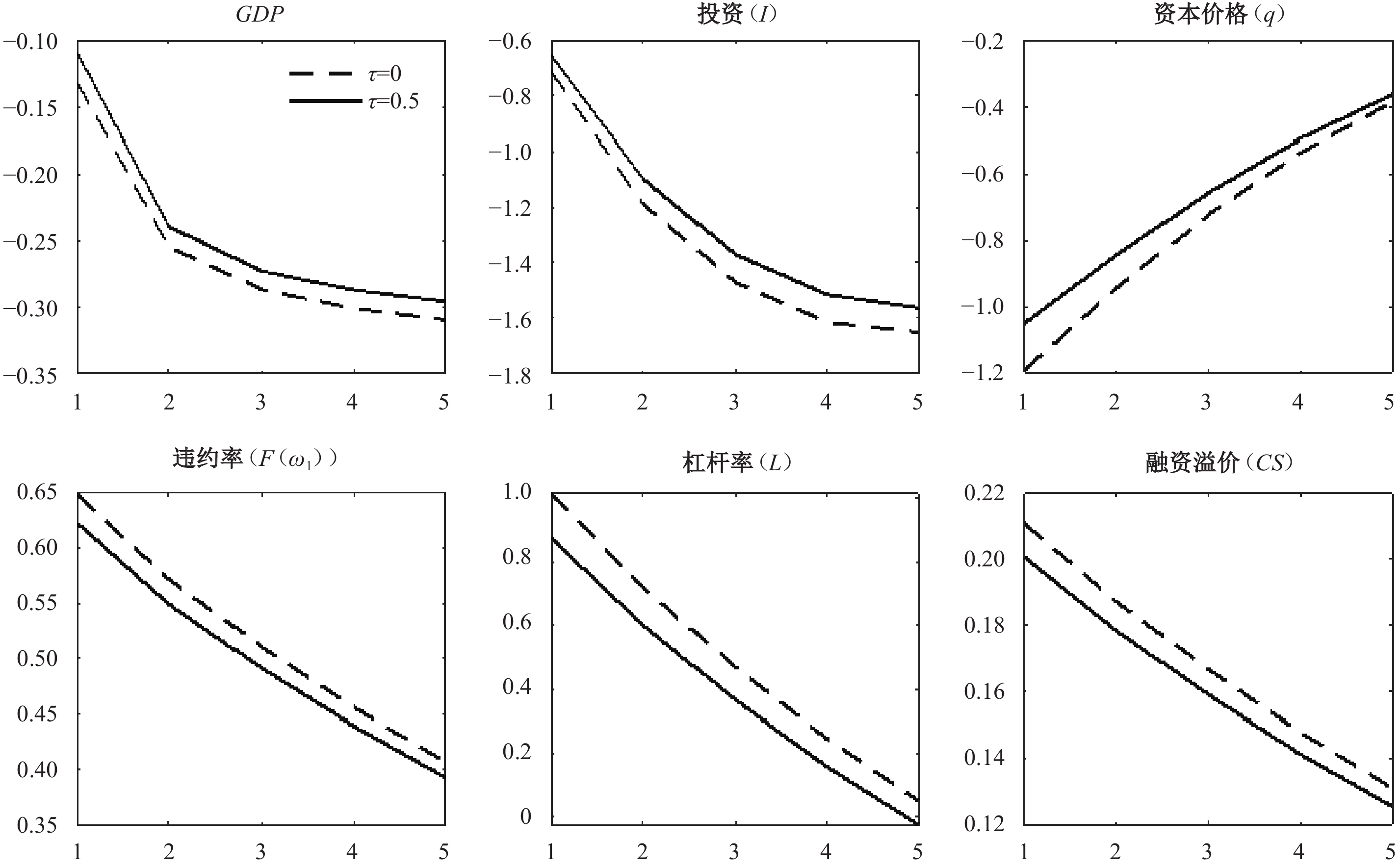
为了进一步理解信贷资产抵押率对宏观经济的影响机制，本文通过脉冲响应分析比较不同的稳态抵押率下风险冲击对经济的影响。图2展示了当稳态抵押率分别为0和0.5时（分别对应信贷资产不可抵押和可抵押的情形），风险冲击上升1%的脉冲响应图。可以发现，风险冲击上升使GDP、投资和资本价格下降，企业杠杆率、违约率和融资溢价上升。这是因为风险冲击使企业经营风险加大，违约风险上升，从而金融摩擦加剧，企业融资溢价上升。融资溢价上升使企业减少贷款并缩减投资，从而资本品需求下降，资本价格下降。而资本价格下降又使企业净资产下降，企业融资溢价上升，投资需求下降，从而形成金融加速器效应，最终使产出下降。

由图2进一步可知，风险冲击使GDP、投资和资本价格的下降幅度随稳态抵押率的上升而下降，企业杠杆率、违约率和融资溢价的上升幅度随稳态抵押率的上升而下降。可见，主要经济变量对风险冲击的敏感性随担保品范围的扩大而下降。这是因为虽然风险冲击使企业违约率上升，并使银行紧缩贷款，但是央行通过将小微企业信贷资产纳入担保品范围，增强了其对相关企业的信用背书，分散了借款企业的部分信用风险（银行贷款的违约风险外移效应），从而在一定程度上减少了金融摩擦，稳定了银行信贷，缓解了企业融资约束，从而抑制了金融加速器效应，起到了稳定经济的作用。

六、货币政策有效性分析

为了探讨信贷资产抵押率对货币政策有效性的影响，这部分将通过脉冲响应函数分析不同稳态抵押率下货币政策冲击对经济的影响。图3展示了不同稳态抵押率下货币供给正向冲击对经济的影响。可以发现，增加货币供给可以刺激投资，提高产出，降低企业违约风险和融资溢价。这是因为央行增加货币供给使市场利率下降，企业融资成本随之下降。企业融资成本下降会刺激投资需求，使资本品价格上升，企业净资产增加。而企业净资产增加又会降低企业违约风险，缓解企业融资约束，降低企业融资溢价。这又进一步刺激投资，形成金融加速器效应，最终使产出增加。

由图3进一步可知，随着信贷资产抵押率的上升，货币政策对主要经济变量的作用效果更加显著。由上文宏观经济波动分析可知，信贷资产抵押率的提高会降低银行对外部冲击的敏感度，从而使银行对利率变化的敏感性下降。在货币数量规则下，央行以货币供给量为中介目标，当央行确定货币供给目标时，信贷供给目标也相应确定。由于较高的信贷资产抵押率会降低银行对利率的敏感度，为了满足央行设定的信贷供给目标，此时实际利率需下降较大幅度。^⑥而实际利率的大幅下降又使企业投资增加，资本品需求增加，从而资本品价格上升，企业净资产上升，杠杆率下降，最终企业违约率下降，融资溢价下降。

为了探讨价格型和数量型货币政策的差异，本文假设中国人民银行不再采取数量型货币政策规则，而是采用价格型货币政策工具，执行如下的标准Taylor规则：

其中， ${\varepsilon }_{rt} \sim N(0,{\sigma }_{r}^{2})$ 为利率冲击， $ {R}_{t} $ 为名义利率，R为其稳态值， $ {\rho }_{r}\in (-\mathrm{1,1}) $ 反映了上期货币政策对当期的影响程度， $ {\psi }_{rp} > 1 $ 为通胀缺口系数， $ {\psi }_{ry} > 0 $ 为产出缺口系数。参照范从来和高洁超（2018），本文将 $ {\rho }_{r} $ 设为0.8， $ {\psi }_{rp} $ 设为1.5， $ {\psi }_{ry} $ 设为0.5。

图4展示了在上述价格型货币政策规则下，不同稳态抵押率下降息冲击对经济的影响。可以发现，不同抵押率下利率冲击对关键变量的影响差异极小，这主要是因为信贷资产抵押率的提高降低了银行对利率变化的敏感性，从而削弱了货币政策传导效率。可见，信贷资产抵押率无法增强价格型货币政策规则（Taylor规则）的作用效果。

综上可知，信贷资产抵押率与总量型货币政策有效性的关系取决于政策工具，提高信贷资产抵押率在数量型货币政策规则下有助于增强货币政策有效性，但在价格型货币政策规则下对货币政策传导效率的影响较小。

七、多企业部门模型中担保品扩容的影响效果

上文基于代表性企业模型探讨了央行担保品扩容所产生的违约风险外移效应，这部分将通过构建包含私有企业和国有企业的多企业部门模型对上述结论作出检验，并对借贷便利工具的有效性进行分析。^⑦

（一）多企业部门模型

在2018年6月央行担保品扩容之前，担保品框架已包含AAA级公司信用类债券，此次扩容加入了不低于AA级的公司信用类债券及优质的小微企业贷款等信贷资产。基于这一背景，假定模型经济中包含两类企业：国有企业（s）和私有企业（p）；同时，国有企业的信贷资产一直在担保品范围内，而私有企业的信贷资产则新进入担保品范围内（抵押率从0上升到特定水平）。与代表性企业模型类似，两企业部门模型中企业最优债务合约问题为：

其中， $ i=s,p $ 表示企业类型， $ {\bar{N}}_{it} $ 表示企业净资产， $ {\bar{B}}_{it} $ 表示企业贷款额， $ {\tau }_{s} $ 表示国企信贷资产抵押率， $ {\tau }_{p} $ 表示私企信贷资产抵押率，其他符号的含义与代表性企业模型一致。根据中国人民银行对信贷资产抵押率的规定，本文将国企信贷资产抵押率 $ {\tau }_{s} $ 校准为0.7，私企信贷资产抵押率 $ {\tau }_{p} $ 校准为0.5。下文将重点探讨私企信贷资产抵押率 $ {\tau }_{p} $ 从0上升到0.5对经济产生的影响。

（二）宏观经济波动分析

由代表性企业模型可知，提高信贷资产抵押率可以通过银行贷款的违约风险外移效应而稳定宏观经济。在多企业部门模型中，提高私企信贷资产抵押率会通过贷款违约风险外移效应和资源配置效应共同影响宏观经济波动。^⑧

当经济面临负面冲击时，一方面，提高私企信贷资产抵押率可通过贷款违约风险外移效应缓解私企信贷约束，抑制金融加速器效应，从而稳定私企产出与经济总产出；另一方面，提高私企信贷资产抵押率会使信贷资源更多地流向私有企业，而私有企业面临相对较严重的融资约束，其金融加速器效应较大，对外生冲击的反应较大，从而造成较大的宏观经济波动。在本文参数校准下，提高私企信贷资产抵押率所产生的风险外移效应大于资源配置效应，最终起到稳定宏观经济的作用。

（三）借贷便利工具有效性分析

基于担保品的借贷便利工具已成为央行调节货币供应量和市场利率的主导方式，这里将在不同担保品抵押率下对借贷便利操作规模和操作利率的政策效果进行分析。

本文将借贷便利操作规模和操作利率分别记为 $ {M}_{lt} $ 和 $ {R}_{lt} $ 。其中，操作规模 $ {M}_{lt} $ 定义如下：

其中， $ {B}_{pt} $ 表示私企信贷资产， $ {\tau }_{p} $ 表示私企信贷资产抵押率， $ {B}_{st} $ 表示国企信贷资产， $ {\tau }_{s} $ 表示国企信贷资产抵押率。可见，信贷资产规模及其抵押率共同决定了借贷便利操作规模。

如果中央银行的借贷便利操作以数量型为主，则以操作规模增长率 $ {g}_{lt}={M}_{lt}/{M}_{l,t-1} $ 为政策工具。为了分析操作规模变动的政策效果，假定 $ {g}_{lt} $ 服从如下AR（1）过程：

其中， $ {\rho }_{g}\in (-\mathrm{1,1}) $ 表示借贷便利操作规模的持续性参数， $ {\varepsilon }_{gt} \sim N(0,{\sigma }_{g}^{2}) $ 表示借贷便利操作规模的随机冲击。

如果中央银行的借贷便利操作以价格型为主，则以操作利率 $ {R}_{lt} $ 为政策工具。为了分析操作利率变动的政策效果，假定 $ {R}_{lt} $ 服从如下AR（1）过程：

其中， $ {\rho }_{l}\in (-\mathrm{1,1}) $ 表示借贷便利操作利率的持续性参数， $ {\varepsilon }_{lt} \sim N(0,{\sigma }_{l}^{2}) $ 表示借贷便利操作利率的随机冲击。

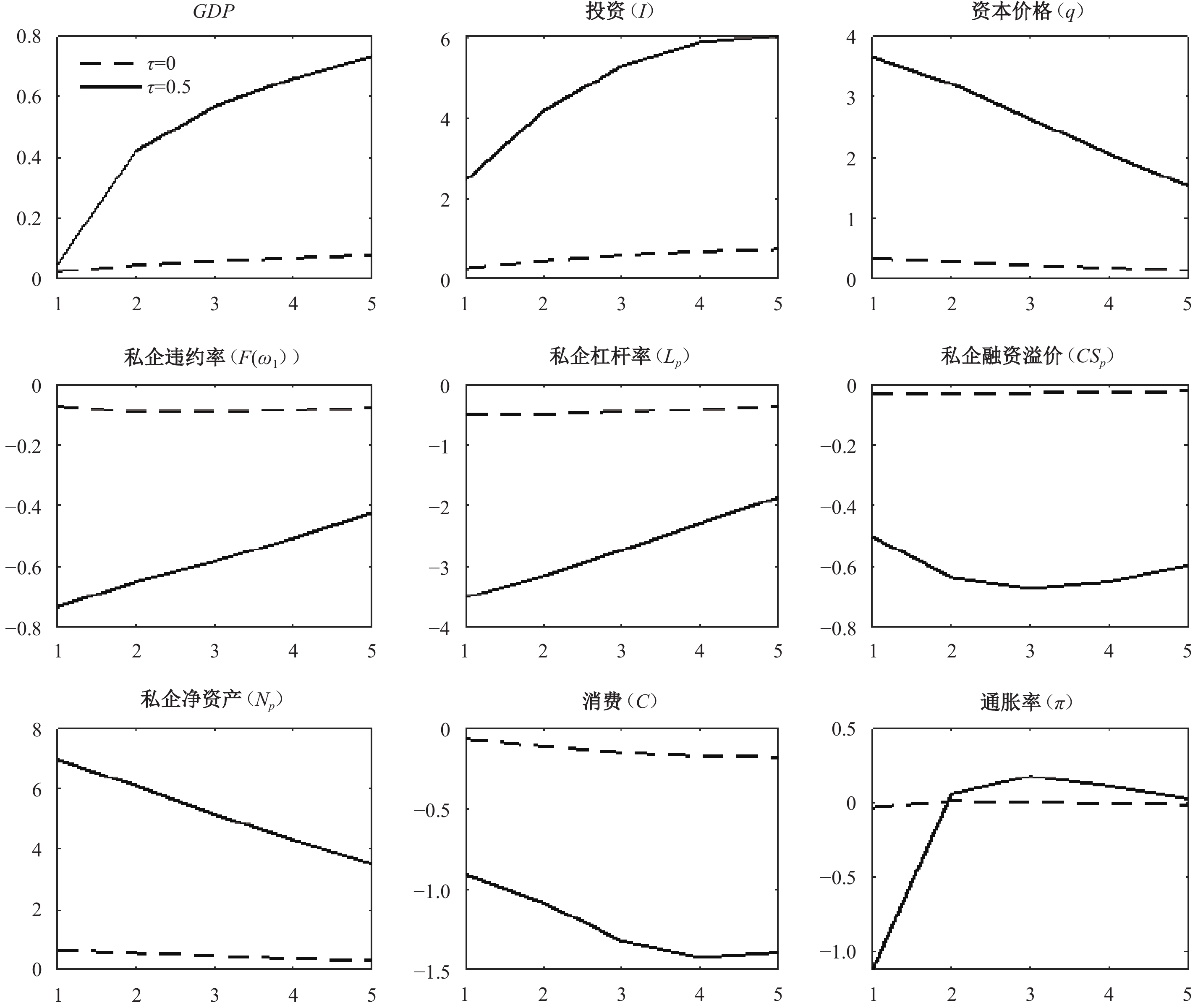
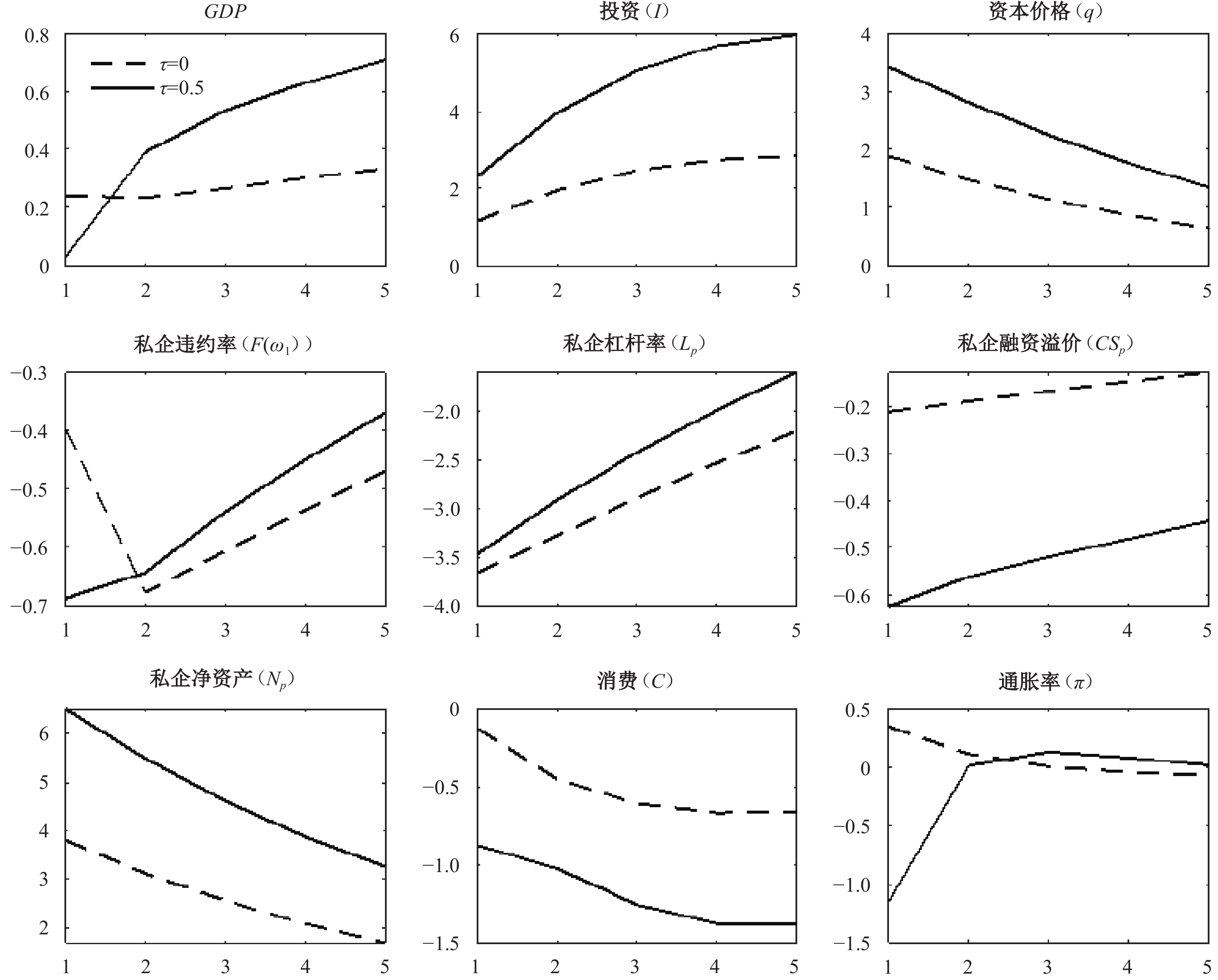
图5和图6分别展示了当私企信贷资产抵押率为0和0.5时，借贷便利操作规模扩张（ $ {\varepsilon }_{gt}=0.01 $ ）和借贷便利操作利率下降（ $ {\varepsilon }_{lt}=-0.01 $ ）对经济的影响。借贷便利操作规模扩张和操作利率下降均会降低银行资金成本，从而降低企业融资成本。而企业融资成本下降会增加企业投资需求，使得资本品价格上升，企业净资产上升。企业净资产上升又会使企业融资溢价下降，从而形成金融加速器效应，最终使产出上升。这一传导机制与传统货币政策比较一致。值得注意的是，与传统货币政策不同，借贷便利工具并不会直接影响储蓄利率，从而不会直接刺激消费。事实上，投资的大幅扩张对消费会产生挤出效应，从而削弱扩张性借贷便利操作对总需求的刺激作用。

本文进一步对比了图5和图6中担保品扩容前后借贷便利操作的政策效果。总体而言，担保品扩容后，扩张性借贷便利操作对经济的刺激作用显著增大。究其原因，提高私企信贷资产抵押率可以通过银行贷款的风险外移效应缓解私有企业信贷约束，提高私有企业信贷可得性，从而产生资源配置效应。可以发现，担保品扩容后，借贷便利工具对私企的刺激作用显著增大。鉴于私有企业比国有企业面临更严重的融资约束，其金融加速器效应更大。因此，担保品扩容后，扩张性借贷便利操作规模和操作利率均会产生更大的金融加速器效应。在图5和图6中，无论操作工具为操作规模还是操作利率，担保品扩容后扩张性借贷便利操作对投资需求的刺激作用均明显增大。

图5和图6还展示了借贷便利操作规模和操作利率冲击对通胀率的影响。可以发现，担保品扩容前，扩张性借贷便利操作使通胀率小幅下降甚至上升；而担保品扩容后，扩张性借贷便利操作使通胀率显著下降。对于通胀率的变化，可以从供给和需求两个方面进行解释。从需求端看，与传统货币政策类似，扩张性借贷便利操作会刺激投资需求，对通胀产生上升压力。从供给端看，担保品扩容前，扩张性借贷便利操作使更多资源流向国企，虽然国企产出上升，但资源配置状况恶化，从而在一定程度上抑制总供给的上升。基于模型模拟结果，担保品扩容前，投资需求扩大所带来的通胀上升压力与总供给上升所带来的通胀下降压力旗鼓相当，相互抵消，此时扩张性借贷便利操作对通胀率的影响较小。而担保品扩容后，扩张性借贷便利操作使更多资源流向私企，资源配置状况得到改善，总供给大幅上升，从而通胀率显著下降。

八、结论与政策建议

2018年6月中国人民银行决定将小微企业信贷资产纳入央行担保品范围，以缓解中国经济结构性矛盾，加大对小微企业的支持力度。从理论上分析信贷资产抵押率的上升对宏观经济波动和货币政策有效性的影响及其机制是本文的主要工作。本文对传统金融加速器模型进行拓展，构建了包含央行担保品框架的动态随机一般均衡模型。

本文得出以下主要结论：第一，提高信贷资产抵押率可以通过违约风险外移效应降低借款企业的融资成本，但也会提高借款企业的违约风险，降低社会福利；第二，当经济面临负面冲击时，提高信贷资产抵押率所产生的违约风险外移效应可以抑制金融加速器效应，从而稳定宏观经济；第三，信贷资产抵押率与总量型货币政策有效性的关系取决于政策工具，提高信贷资产抵押率在数量型货币政策规则下有助于增强货币政策有效性，但在价格型货币政策规则下对货币政策传导效率的影响较小；第四，担保品扩容后，扩张性借贷便利操作对经济的刺激作用显著增大，通胀率显著下降。产生上述结果的核心机制在于，提高信贷资产抵押率可以产生银行贷款的违约风险外移效应，即央行通过将小微企业信贷资产纳入担保品范围，可以增强其对相关企业的信用背书，分散借款企业的部分信用风险，从而缓解企业信贷约束。

基于上述结论，本文提出以下政策建议：第一，央行在调整担保品范围时应充分权衡这一政策的利弊影响，不仅要关注其在缓解金融摩擦、降低企业融资成本以及促进资源有效配置方面的作用，还应注重防范企业违约风险，从而完善和优化担保品管理框架；第二，当经济面临负面冲击（如风险冲击、负向技术冲击等）时，央行可以通过提高信贷资产抵押率来抑制金融加速器效应，稳定银行信贷，熨平经济周期；第三，当企业和商业银行对利率的反应不敏感时，央行应实行以货币供给为中介目标的数量型货币政策规则，以提高货币政策作用效果；第四，鉴于贷款基准利率（LPR）是由中期借贷便利（MLF）操作利率加点形成，MLF利率已被赋予中期政策利率的地位。实行扩张性中期借贷便利操作可以直接影响企业融资成本，而且不会对存款利率产生直接影响。因此，当央行需要实行扩张性货币政策时，应重点进行扩张性借贷便利操作。这一政策既可以提高总产出，又不会对通胀产生压力。

① 本文对家庭部门、零售品部门、批发品部门和资本品部门的设定为常规设定，受篇幅限制，在此不再赘述，感兴趣的读者可向作者索取。

② 欧洲央行实行与我国类似的担保品框架政策，部分文献对欧洲央行因担保品框架政策而产生的资产负债表风险做出说明。例如，Nyborg（2017）以及Choi等（2021）认为担保品框架政策会激励银行将劣质担保品抵押给央行，而劣质担保品将增加央行的资产负债表风险，造成潜在巨大损失。此外，根据担保品法律属性，当担保品价值低于债务价值时，债务人选择违约，此时债权人清算担保品价值，而债务价值与担保品价值缺口便是债权人的损失。因此，本文对银行参与约束的设定具有合理性。

③ 本文尝试将央行清算成本 $ {\mu }_{2} $ 设定为不同数值，发现模型结果具有稳健性。

④ 《中国人民银行再贷款与常备借贷便利抵押品管理指引（试行）》规定，企业信贷资产基础抵押率为50%—70%。鉴于小微企业信贷资产风险等级较高，本文选取这一抵押率区间的下限，将担保品扩容后的小微企业信贷资产抵押率校准为0.5。

⑤ 负向技术冲击对经济的影响与风险冲击相似，且受篇幅限制，相关分析结果未展示，感兴趣的读者可向作者索取。

⑥ 若从商业银行负债端统计，货币供给由流通中现金及银行存款组成；而若从商业银行资产端统计，货币供给由流通中现金及银行贷款组成。因此，央行设定货币供给目标相当于设定银行信贷目标。

⑦ 在多企业部门模型中，代表性企业模型中的核心结论依然成立。受篇幅限制，这里只展示了宏观经济波动与借贷便利工具有效性的相关内容。

⑧ 受篇幅限制，分析结果未展示，感兴趣的读者可向作者索取。