
2023第49卷第5期
2. 南开大学 经济学院, 天津 300071
2. School of Economics, Nankai University, Tianjin 300071, China
一、引言和文献综述
近年来,劳动力在职业选择上越来越倾向于国家机关和以金融机构为代表的垄断国有企业,导致这些部门和企业人力资本高度集中,而以制造业为代表的实体企业人才短缺问题比较严重。2003年国家公务员考试报录比例为23∶1,到2020年该数据上升至 60∶1。①同时,金融机构招聘要求越来越高,在学历及毕业院校等方面都设定了非常苛刻的条件,即便如此,大量毕业生仍对此趋之若鹜;与之形成鲜明对比的是,制造业人才吸引力正在下降,2018年《人民日报》关于三省六市100家企业的调查显示,企业集中反映高水平人才和优秀毕业生“找不到、招不来和留不住”。②在经济增速放缓和国际环境多变的背景下,这种现象更为明显。据智联招聘的数据显示,相对于国有企业和大型企业,民营企业和中小微企业的人才吸引力显著下降。③
这种现象会导致公共部门以及金融部门(以下简称“体制内部门”)与实体部门的人力资本鸿沟不断加深,进而产生人力资本错配。一方面,劳动力职业选择偏好于体制内变相抬高了这些部门的准入门槛,强化了其对高技能劳动力的“虹吸效应”。另一方面,体制内汇集了大量高技能劳动力,造成了了人力资本过剩,同时实体生产部门却出现人力资本不足。那些本可以在生产部门创造更高价值的高技能劳动力进入了体制内从事简单重复的工作,没有充分发挥其应有的作用,这种错配不仅会导致资源浪费,更重要的是会抑制实体部门的创新发展。因此有必要厘清上述问题产生的根源和影响机制,以便为中国经济由高速增长向高质量发展转变,实现建设制造强国和发展先进制造业的目标提供人力资源方面的解决方案。
从已有研究来看,针对劳动力职业选择问题的文献主要从劳动报酬角度展开讨论。Murphy等(1991)认为,当劳动力进入政府部门所获得的预期收益较低时,他们会进入生产部门进行生产活动,这对于经济增长有利;反之,则不利于经济增长。也有研究从职业获得收益多寡(King,1974;Paglin和Rufolo,1990)、匹配效率(Miller,1984;Schuetze和Wood,2013)和最优职业规划(Antonovics和Golan,2012)的角度解释了劳动力职业选择影响因素。但从劳动报酬角度无法解释劳动力对体制内部门和实体部门的偏好差异,因为公务员与其他行业的收入差距在最近几年并没有显著持续性的变化,而 “国考” 的热度却有增无减。关于国内就业倾向于金融行业的问题,相关文献认为其根源在于,垄断行业改革不彻底(任重和周云波,2009)、行业垄断和所有制共同作用(叶林祥等,2011)以及权力的设租寻租行为(桂林等,2012)等因素带来的垄断势力形成了行业高工资吸引劳动力流入,导致以金融为代表的垄断行业对其他行业高技能劳动力产生“虹吸”效应(毛毅,2020)。随着改革深化,垄断和权力寻租等现象不断被削弱,并且对比金融行业与制造业工资水平,如果剔除学历影响,两个行业的工资差距并未出现持续扩大。但动态来看,近年来劳动力在就业时对金融行业的偏好却越来越强。
综上,当前文献的结论都无法解释劳动力对于体制内的偏好持续上升,有必要继续剖析这一现象背后的深层次动因。通过观察可以发现,劳动力对于体制内的偏好持续上升始于21世纪初,与之同步的是 2000年以后地方政府财政收入越来越依赖于土地出让(张双长和李稻葵,2010;梅冬州和温兴春,2020),并基于土地财政开启了债务扩张的过程。那么这两者之间是否有内在的联系呢?
地方政府基于土地财政的债务扩张对劳动力职业选择倾向的影响可分为直接和间接效应。一方面,土地作为地方政府“债务规模扩张的助推器和催化剂”(梅冬州和温兴春,2020)推动了其债务扩张,进而扩大了体制内部门的规模,导致这些部门对劳动力需求增加,产生直接效应;另一方面,债务扩张会形成挤出效应,挤压了私有部门(所有制维度)和制造业(行业维度)的利润和生存空间,导致这些部门对劳动力吸引力下降,产生间接效应。体制内部门招聘“门槛效应”的作用会引发高技能劳动力集中到体制内,形成“虹吸效应”。同时,体制内部门工资制订的市场化程度④较低,这会使得很多低技能劳动力就能承担的岗位实际上是由高技能劳动力承担。
首先,地方政府基于土地财政的债务扩张使得公共部门规模扩大,并通过信贷配置和杠杆效应导致金融行业规模扩张,使公共部门和金融行业劳动力需求增加。1994年分税制改革以后地方财政对土地的依赖越来越强,不仅财政收入依靠土地出让,还通过土地储备进行一系列债务融资(范剑勇和莫家伟,2014)。在政府主导的投融资体系和软预算约束下,会出现地方政府、国有企业和商业银行三方共谋贷款扩张的现象(江曙霞等,2006;张晓晶等,2019)。一方面,在地方政府债务与国有资产捆绑的过程中,平台公司和其他国有企业将债务与土地、基础设施和棚户区资产进行捆绑,这通过政府信用的金融化,进一步扩大了政府规模(毛捷和徐军伟,2019;刘畅等,2020)。另一方面,由债务引致的扩张并不仅限于商业银行,地方政府债务与影子银行的扩张相互促进(李程和贺凯然,2021),商业银行与证券公司、保险公司等金融机构之间的创新业务不断增加(吴永钢等,2019),这些都间接促进了金融行业的扩张。与此同时,政府债务扩张引致资源向公共部门以及与土地相关非制造业部门(如金融、房地产以及各类城投平台等)倾斜,给私有部门和制造业带来了不确定性,⑤这种不确定性会引致劳动力转而投向更为稳定的体制内,使得体制内部门可以在招聘中设置严格的学历“准入门槛”,形成对高技能劳动力的“虹吸”效应。
其次,公共部门和金融行业薪酬制度市场化程度较低,技能报酬扭曲,导致人力资本错配。公共部门“不管是个人绩效还是整体绩效都难以衡量”(韩雷等,2016),且“不以利润最大化作为目标”,这使得其薪酬制度不够市场化。金融行业薪酬制度准市场化主要体现在:一是其利润很大程度来自于其牌照价值和垄断势力,其实际产出较难通过市场化方式界定;二是在工资分配过程中难以真正按贡献分配,占据较大分配比重的是职级,而职级与入行年限强相关。张成(2015)认为,国有商业银行存在市场化程度不高、薪酬分配模式不合理现象。虽然政府对金融机构薪酬进行了监管,但由此产生的工资刚性也会提高国有企业员工工资水平,国有部门工资决定机制仍不够市场化 (薛欣欣和张艳,2014)。高于实际岗位产出的工资造成了公共部门的工资向上扭曲,使得一个本可以到实体企业创造更大价值的高技能劳动力只在公共部门承担了简单重复的工作,进而影响了经济增长(王启超等,2020)和实体企业创新(潘士远等,2021)。
最后,需要指出的是已有研究对人力资本错配的界定主要基于两个维度,即价格扭曲和数量错配(马颖等2018)。价格扭曲主要是对工资与边际产出之间的差异展开讨论(施炳展和冼国明,2012;张明志等,2017;蒲艳萍和顾冉,2019等);数量错配则针对人力资本数量在不同行业间的分配问题(袁志刚和解栋栋,2011;赖德胜和纪雯雯,2015;李静等,2017)。本文的人力资本错配主要指的是体制内部门的非市场化工资定价导致了部分本应进入生产行业的高技能劳动力滞留在公共部门,形成了人力资本浪费。
本文可能的边际贡献主要有:第一,从债务扩张视角解释了近年来中国公共部门和金融行业对人力资本“虹吸”效应产生的一个重要原因。第二,通过理论模型分析了政府债务扩张影响劳动力职业选择偏好的过程,以及由此导致人力资本错配的影响机制。第三,实证研究中从多维度进行对比分析,获得了丰富的结论,为破解制造业就业问题提供了微观层面的证据。第四,结论有新意,本文发现,加快市场化改革进程、规范政府举债行为和规制垄断一方面可以释放更多的高技能劳动力进入实体部门进行生产活动,另一方面会增加低技能劳动力的需求。即这一过程既减少了公共部门人力资本扭曲现象,同时也优化了人力资本配置,并扩大了就业。
二、理论模型
本节将利用模型阐述政府债务扩张和规模持续扩大对劳动力职业选择变化和人力资本错配的影响机制。在模型构建上借鉴了Murphy等(1991)的思想,不过在分析内容和方法上与之不同:Murphy等(1991)主要考察的是劳动力职业选择对经济增长的影响,本文则在考虑了中国公共部门和相关行业的具体特点的基础上,加入公共部门的“门槛效应”,讨论政府规模扩张和劳动力职业选择与人力资本错配之间的关系。
(一)基准模型。假定劳动力的技能
| $ r=AF\left(H\right)-wH $ | (1) |
其中,w表示工人工资率,即单位技能获得的工资。经理根据收入最大化的原则选择雇佣工人的规模:
一阶条件
| $ H=H\left(A\right)={{F}^{{'}}}^{-1}(w/A) $ | (2) |
从(1)式可以看出,经理收入技能弹性要大于1,即随技能的增加经理收入提高,并且收入提高的幅度要大于技能增加幅度。⑥全社会劳动力的分布是高技能劳动者选择当经理,低技能劳动者当工人,高低技能劳动者之间有临界技能值
| $ {\int }_{0}^{{A}^{*}}Af\left(A\right){\rm{d}}A={\int }_{{A}^{*}}^{1}H\left(A\right)f\left(A\right){\rm{d}}A $ | (3) |
拥有临界技能
| $ {A}^{*}F\left(H\left({A}^{*}\right)\right)-wH\left({A}^{*}\right)=w{A}^{*} $ | (4) |
通过(3)式和(4)式可确定工人工资w和经理与工人临界技能
| $ Y={\int }_{{A}^{*}}^{1}AF\left(H\right)f\left(A\right){\rm{d}}A $ | (5) |
总结以上的分析,在一个只有一种产品的社会中,利益最大化的驱动会使高技能劳动者雇佣低技能劳动者组成企业进行生产,高技能劳动者随着其技能的提高而获得更快的收入增加,低技能劳动者获得的工资收入与技能成线性关系,均衡状态如图1所示。

|
| 图 1 单个部门不同技能劳动力的职业选择和工资决定示意图 |
图1中横轴表示技能A,纵轴表示收入。均衡状态下,技能
| $ C=\left\{\begin{array}{c}wA,A\in [0,{A}^{*})\\ r\left(A\right),A\in [{A}^{*},1]\end{array}\right. $ | (6) |
在生产函数既定的前提下,均衡的临界技能
(二)加入政府的两部门模型。模型设定沿用传统经济学的基本假定,即政府只提供公共产品,并不提供实际产品。所以全社会仍然只有一种产品。因而政府部门的产出并不是具体的产品,而是维护市场和社会正常运行的治理水平。不同于基准模型中假定的理想的市场环境,现实中市场环境的正常运行需要政府进行治理。具体地,假定政府治理函数为
政府总收入T来自于对经理的利润征税,并全部用于公务员的工资支出,公务员的工资根据不同公务员的技术水平决定,如果令
| $ c\left(A\right)=\rho G\left(A\right) $ | (7) |
其中,
政府加入后主要有两种效率:一是税收效应,因为政府是非生产部门,政府的收入需要从生产部门征税;二是挤压效应,即政府部门加入后,对经理人收入可能产生负面影响,这种影响主要来自两个方面,政府调控政策产生的影响效应和政府在政策选择中有可能倾向于国有部门而导致对私有部门的“挤压”效应,可以假定不确定性与政府的规模正相关。
假定
对比基准模型,工人的需求函数并没有发生变化。如果不考虑政府部门的就业问题,税收和挤压效应相当于降低了一部分经理的利润,会导致工资降低,均衡的技能临界值
现在考虑政府部门是劳动力就业选择之一,此时劳动力存在三种选择:工人、经理和公务员。由于政府最低技能的限制要求,只有技能水平大于
| $ \begin{aligned} \varPsi \left(A\right)&= \left(AF\left(H\right)-wH\right)\left(1-t\right)\left(1-q\right)-\rho G\left(A\right)\\ &=\left(AF\left(H\right)-wH\right)\left(1-t\right)\left(1-q\right)-\frac{t\int \left(AF\left(H\right)-wH\right)\left(1-q\right)f\left(A\right){\rm{d}}A}{\int G\left(A\right)f\left(A\right){\rm{d}}A}G\left(A\right)\\ &=R\left(A\right)\left(1-t\right)\left(1-q\right)-t\left(1-q\right)\frac{\int R\left(A\right)f\left(A\right){\rm{d}}A}{\int G\left(A\right)f\left(A\right){\rm{d}}A}G\left(A\right)\\ &=R\left(A\right)\left(1-t\right)\left(1-q\right)-t\left(1-q\right)\frac{\stackrel-{R}}{\stackrel-{G}}G\left(A\right) \end{aligned}$ | (8) |
上式中的
政府规模虽然是外生决定的,但是其扩张必然会导致税收增加,因为规模扩大需要雇佣更多的劳动力,表现出的税率也高,因此t的变化事实上反映了政府扩张程度。
首先,如果需要保证有劳动力选择进入政府部门工作,(8)式必须满足以下条件:
| $ \varPsi \left({A}_{2}\right)=R\left({A}_{2}\right)\left(1-t\right)\left(1-q\right)-t\left(1-q\right)\frac{\stackrel-{R}}{\stackrel-{G}}G\left({A}_{2}\right) < 0 $ | (9) |
(9)式表示技能水平为
当政府确定规模
工人临界技能
| $ \left(1-t\right)\left(1-q\right)R\left({A}_{1}\right)=w{A}_{1} $ | (10) |
经理临界技能
| $ \left(1-t\right)\left(1-q\right)R\left({A}_{3}\right)=\rho G\left({A}_{3}\right) $ | (11) |
工人技能供求相等条件:
| $ {\int }_{0}^{{A}_{1}}Af\left(A\right){\rm{d}}A={\int }_{{A}_{1}}^{{A}_{2}}H\left(A\right)f\left(A\right){\rm{d}}A+{\int }_{{A}_{3}}^{1}H\left(A\right)f\left(A\right){\rm{d}}A $ | (12) |
总税收等于公务员的总工资:
| $ t\left(1-q\right)\left[{\int }_{{A}_{1}}^{{A}_{2}}R\left(A\right)f\left(A\right){\rm{d}}A+{\int }_{{A}_{3}}^{1}R\left(A\right)f\left(A\right){\rm{d}}A\right] = \rho \bar{G}$ | (13) |
上述条件决定了均衡条件下的
总结两部门模型的均衡结果,相对于单个部门的情况,个人的职业多了当公务员这一选择,三种职业工资与技能的关系是:工人的工资与技能是线性关系,
| $\begin{aligned} \; \\ C=\left\{\begin{array}{l}wA,A\in \left[0,{A}_{1}\right)\\ r\left(A\right)or 0,A\in \left[{A}_{1},{A}_{2}\right)\cup \left({A}_{3},1\right]\\ c\left(A\right),A\in \left[{A}_{2},{A}_{3}\right]\end{array}\right. \end{aligned} $ | (14) |
正常情况下经理的收入为
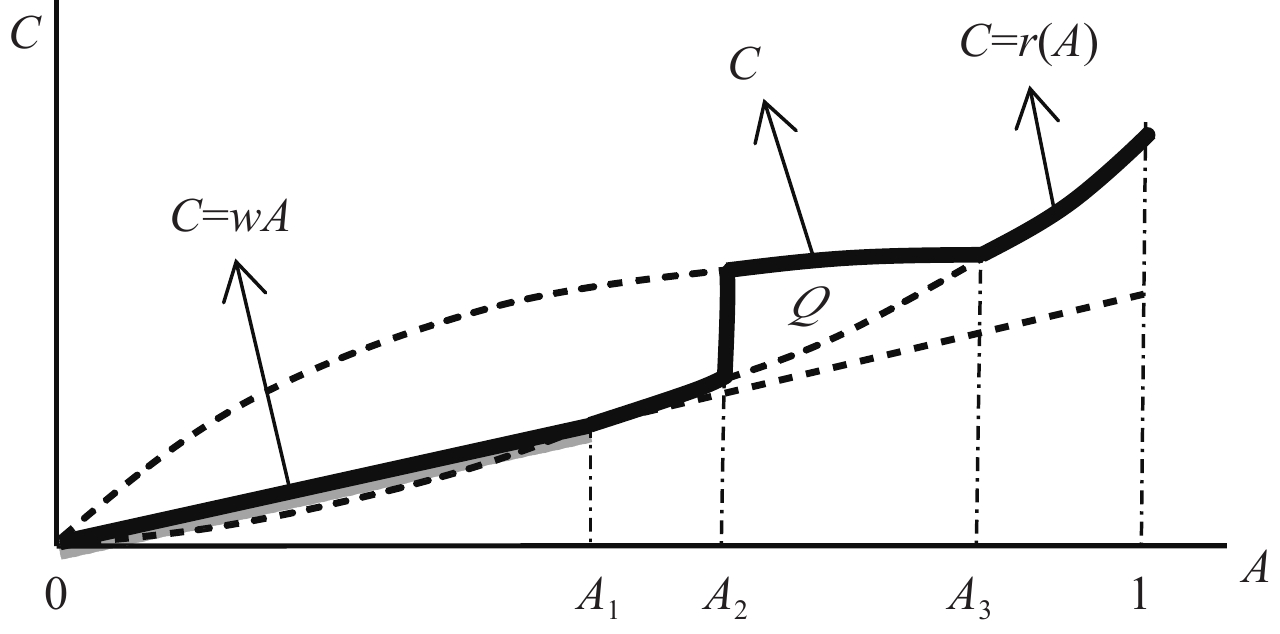
|
| 图 2 加入政府部门后不同技能劳动力的职业选择和工资决定示意图 |
加入政府部门之后,经理的最优雇佣决策并没有发生变化,如果不考虑劳动力流向政府部门,即劳动力的相对供给没有发生变化,那么经理和工人的临界技能水平也不变,但是工资水平w会下降。考虑一部分高技能劳动力进入政府部门后,生产中高技能劳动力相对供给减少会产生两种效应:一是生产中的高技能劳动力的数量减少会导致一部分低技能劳动力选择当经理,亦即工人与经理的临界技能水平降低,
接下来分析政府规模扩张导致的均衡变化,可以通过观察税率变化推断由此造成的影响。对(8)式两端求导可得:
| $ \frac{\partial \varPsi }{\partial t}=-\left[\left(1-q\right)+{q}^{{'}}\left(1-t\right)\right]R\left(A\right)-(1-q-t{q}^{{'}})\frac{\stackrel-{R}}{\stackrel-{G}}G\left(A\right) $ | (15) |
上式中,
因此,(15)式表示在政府规模扩张过程中,通过税收和挤压效应会影响经理的预期利润和公务员的工资。随着政府规模扩张,经理的预期利润下降,而作为公务员的收入会上升。如果初始是均衡的,随着政府规模扩张,会导致均衡的经理临界技能
政府规模扩张导致劳动力职业选择的变化会使得不同部门人力资本配置情况发生变化,接下来详细分析这种影响。
从人力资本数量来看,实体部门高技能劳动力为:
| $ E={\int }_{{A}_{1}}^{{A}_{2}}Af\left(A\right){\rm{d}}A+{\int }_{{A}_{3}}^{1}Af\left(A\right){\rm{d}}A $ | (16) |
政府部门高技能劳动力为:
| $ P={\int }_{{A}_{2}}^{{A}_{3}}Af\left(A\right){\rm{d}}A $ | (17) |
首先,由于政府规模扩张导致部分原来在实体部门的高技能劳动力选择进入政府部门,实体部门高技能劳动力数量降低,体现为
从政府部门来看,公务员的最低技能要求会造成技能水平
| $ N={\int }_{{A}_{2}}^{{A}_{3}}\left[\rho G\right(A)-(1-t\left)\right(1-q\left)R\right(A\left)\right]f\left(A\right){\rm{d}}A $ | (18) |
此即图2中所示的Q区域。政府部门与实体部门的这种工资扭曲导致了劳动力的错配,不仅降低了最终产出,而且会导致实体部门劳动力的收入损失。
很显然,这种人力资本错配的损失在产出上的体现比较直观,实体部门高技能劳动力减少,产出必然降低。从收入来看,不仅工人的工资减少,政府的征税和不确定性还会导致经理的收入相应减少,只有公务员的收入是相对稳定的。总结有命题2:地方政府债务扩张引发劳动力职业选择变化将导致更多高技能劳动力进入政府部门。在政府部门工资制定非市场化的前提下,相同技能水平的劳动力在政府部门的工资要高于私人部门,进而出现政府部门人力资本冗余和生产部门人力资本稀缺的错配状况。政府的干预程度越深,这种效应体现得也就越明显。
三、计量模型和数据说明
(一)模型设定。针对命题1,考虑到被解释变量为劳动力职业选择,使用Logit模型进行回归,借鉴Nunn(2007),使用地方政府债务与劳动力技能水平的交叉项作为解释变量,具体模型设定如下:
| $ \begin{aligned} \mathrm{Pr}\left({Choice}_{ict}=1\right)&=\mathrm{Pr}\left({\alpha }_{0}+{\alpha }_{1}{X}_{ict}+{\alpha }_{2}{X}_{ict}\times {H}_{ct}+{\alpha }_{i}{D}_{i}+{\alpha }_{c}{E}_{c}+{\mu }_{c}+{v}_{t}+{\varepsilon }_{ict} > 0\right)\\ &=F\left({\alpha }_{0}+{\alpha }_{1}{X}_{ict}+{\alpha }_{2}{X}_{ict}\times {H}_{ct}+{\alpha }_{i}{D}_{i}+{\alpha }_{c}{E}_{c}+{\mu }_{c}+{v}_{t}\right) \end{aligned} $ | (19) |
其中,i、c和t表示t时期c地区的第i个体;Choice为职业选择的虚拟变量;
本文主要关注交叉项系数
针对命题2,需要验证在政府债务扩张的过程中,因劳动力职业选择变化导致的人力资本错配问题。计量模型设定如下:
| $ {Mismatch}_{ict}={\beta }_{0}+{\beta }_{1}{Choice}_{ict}+{\beta }_{2}{Choice}_{ict}\times {H}_{ct}+{\beta }_{i}{D}_{i}+{\beta }_{c}{E}_{c}+{\mu }_{c}+{v}_{t}+{\varepsilon }_{ict} $ | (20) |
其中,Mismatch表示人力资本错配,其他指标与(19)式相同。本文关注的重点并不仅仅是劳动力职业选择导致的影响,而是在政府扩张作用下的影响后果。因此,主要关心的仍然是交叉项的系数
(二)变量构建。
1. 被解释变量。劳动力职业选择Choice:劳动力选择公共部门和金融行业为1,否则为0。
人力资本错配Mismatch用于反映由于政府债务扩张导致劳动力职业选择变化所致使的人力资本在行业间的错配效应。实证中使用行业间人力资本价格扭曲程度衡量人力资本错配。
本文借鉴Mincer(1974)的思路和马颖等(2018)在考察行业间人力资本价格扭曲时的估算方法,不同的是本文通过估算行业间人力资本价格相对扭曲值来计算出个体收入的相对扭曲值,以此作为人力资本错配的衡量指标。具体地:假设Wij表示j行业第i个个体的工资收入,Hij表示该个体人力资本的数量。以ω表示人力资本的价格,Tj表示j行业人力资本扭曲系数,如果不存在扭曲,该系数为0,那么有:
| $ {W}_{ij}=\omega \left(1+{T}_{j}\right){H}_{ij} $ | (21) |
两边取对数有:
| $ {{\rm{ln}}W}_{ij}={\rm{ln}}\omega +\ln \left(1+{T}_{j}\right)+{{\ln}}{H}_{ij} $ | (22) |
在(22)式的基础上做一些简单的变形就可以进行回归估算。令
| $ {\ln W}_{ij}={\gamma }_{0}+{\xi }_{j}+{X}_{i}^{{'}}{\gamma }^{{'}}+{\varepsilon }_{ij} $ | (23) |
根据(23)式得到
令
| $ {\widehat{\xi }}_{j}-{\sum }_{j}{a}_{j}{\widehat{\xi }}_{j}=\ln\left(1+{T}_{j}\right)-{\sum }_{j}{a}_{j}\ln\left(1+{T}_{j}\right) $ | (24) |
其中,
| $ \frac{1+{T}_{j}}{1+{T}_{m}}=1+\frac{{T}_{j}-{T}_{m}}{1+{T}_{m}}=\mathrm{e}\mathrm{x}\mathrm{p}({\widehat{\xi }}_{j}-{\sum }_{j}{a}_{j}{\widehat{\xi }}_{j}) $ | (25) |
接下来结合(21)式和(25)式,可以得到个体i相对于所有行业平均的人力资本扭曲值:
| $ {Distortion}_{i}=\omega\left({T}_{j}-{T}_{m}\right){H}_{ij}={W}_{ij}\frac{1+{T}_{j}}{{T}_{j}-{T}_{m}}={W}_{ij}\frac{\mathrm{exp}\left({\widehat{\xi }}_{j}-{\sum }_{j}{a}_{j}{\widehat{\xi }}_{j}\right)-1}{\mathrm{e}\mathrm{x}\mathrm{p}({\widehat{\xi }}_{j}-{\sum }_{j}{a}_{j}{\widehat{\xi }}_{j})} $ | (26) |
同时考虑稳健性,采用另一种方法构建扭曲指标如下:
| $ {Skillgap}_{i}={skill}_{i}/\left(\frac{1}{N}{\sum }_{k=1}^{N}{skill}_{k}\right) $ | (27) |
式(27)中
借鉴黄群慧(2017),对实体部门的界定考虑两个层次:狭义上只考虑制造业,广义上除了制造业以外,还包括农业、工业(不包括制造业)和建筑业。结合本文的研究对象,主要针对狭义实体部门的界定计算指标
2.解释变量。政府债务扩张H:中国的地方政府债务分为两部分,一部分是由省级地方政府发行的地方政府债券,包括一般债务和专项债务,这部分属于显性债务;还有一部分是由各级地方政府融资平台所发行的债务,以及最终由政府兜底的国有企业的债务,这部分属于隐性债务。因此,本文考虑使用以下两个指标进行衡量:一是显性债务指标Exdebt,采用城市层面地方政府年末债务余额(包括一般债务和专项债务)占GDP比例取对数衡量;二是隐性债务指标Imdebt,采用省级层面融资平台债务与其他国有企业负债的和占GDP的比例取对数衡量。技能水平X:采用劳动力受教育程度Education衡量。
3. 控制变量。参考马颖等(2018)、余海跃和康书隆(2020)等文献,本文控制以下控制变量:基于劳动力个体层面的特征变量主要包括性别(Gender)、年龄(Age)、婚姻状况(Marrige)、健康状况(Health)、民族(Nation);基于区域层面控制变量包括人口(Population)、经济发展(GDP)、金融发展(Finance)、基础设施(Infrastructure)和开放程度(Openness)等。人口因素采用该地区的常住人口,包括农村和城镇人口的总和衡量,用以控制地区的人口总体规模;经济发展采用GDP和增长率PGDP衡量;金融发展水平用金融机构从业人数衡量;基础设施采用该地区所有公交车数量除以人口数表示;开放程度则使用进出口贸易总额占GDP的百分比衡量(均为对数)。考虑到各区域最低工资政策的影响,本文还控制了区域最低工资(Minwage)因素。
(三)数据。主要数据来源为中国家庭追踪调查(CFPS)数据。采用包括2010年、2012年、2014年、2016年和2018年的五次调查数据中户籍为城市的部分样本。⑨地区数据来自《中国城市统计年鉴》《中国区域经济统计年鉴》和万得(WIND)数据库。隐性债务数据借鉴了沈坤荣和施宇(2022)的做法,结合研究对象,主要统计了地方融资平台发债和地方国有企业的债务。
四、实证结果与分析
(一)基准回归结果。劳动力职业选择的Logit回归结果如表1所示,回归中控制了地区和时间固定效应。
| (1) | (2) | (3) | (4) | |
|
|
0.196***(0.020) | 0.186***(0.022) | ||
|
|
0.037**(0.017) | 0.036**(0.018) | ||
| Education | 0.102**(0.046) | 0.256***(0.048) | 0.750***(0.051) | 0.891***(0.054) |
| Exdebt | 0.834***(0.133) | 0.692***(0.145) | ||
| Imdebt | −0.038(0.081) | −0.049(0.147) | ||
| 控制变量 | 不控制 | 控制 | 不控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本数 | 8 774 | 8 333 | 19 215 | 18 397 |
| Pseudo R2 | 0.116 | 0.138 | 0.123 | 0.159 |
| 注:***、** 、* 分别表示在1%、5%和10%的水平上显著,括号内表示标准误。下表统同。 | ||||
从回归结果来看,无论是单独回归,还是加入各种控制变量之后,本文关注的主要解释变量
根据式(16),以人力资本扭曲值为被解释变量,回归结果如表2所示。列(1)、列(2)未考虑交叉项,列(1)仅以劳动力职业选择Choice作为解释变量进行回归,列(2)加入了控制变量。可以发现Distortion对Choice的回归系数在1%的水平上显著为正,说明劳动力选择公共部门确实会导致人力资本扭曲。列(3)和列(4)分别加入了不同指标衡量的政府债务扩张的交叉项
| (1) | (2) | (3) | (4) | |
|
|
0.964*(0.527) | |||
|
|
0.670**(0.280) | |||
| Choice | 2.023***(0.234) | 1.786***(0.278) | 0.876(1.232) | 3.722***(0.856) |
| Exdebt | −0.031(0.870) | |||
| Imdebt | −0.035(0.725) | |||
| 控制变量 | 不控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本数 | 11 181 | 10 010 | 4 911 | 10 010 |
| R-squared | 0.010 | 0.013 | 0.017 | 0.014 |
接下来基于行业间人力资本差异的角度进行分析。重点考察地方政府债务扩张导致的调节效应,从人力资本数量角度的回归同样有意义,仍主要关注交叉项系数。表3报告了回归结果。可以发现
| (1) | (2) | (3) | (4) | |
| Skillgap | Skillgap | Skillgap | Skillgap | |
|
|
0.081***(0.009) | 0.075***(0.009) | ||
|
|
0.023***(0.007) | 0.017***(0.006) | ||
| Choice | 0.042*(0.022) | 0.063***(0.020) | 0.320***(0.020) | 0.316***(0.019) |
| Exdebt | 0.004(0.014) | 0.035**(0.014) | ||
| Imdebt | 0.051***(0.004) | -0.022(0.017) | ||
| 控制变量 | 不控制 | 控制 | 不控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本数 | 8 774 | 8 333 | 19 215 | 18 397 |
| R-squared | 0.099 | 0.285 | 0.124 | 0.257 |
(二)内生性处理。2011年财政部允许少数省份作为试点自行发债,因此以2011年为第一个时间节点,考察自行发债后显性债务上升对劳动力职业选择和人力资本错配的影响。以试点省份为实验组,
以2015年为第二个时间节点,考察《国务院关于加强地方政府性债务管理的规定》(即“43号文”)和新《预算法》正式实施后隐性债务下降对劳动力职业选择和人力资本错配的影响。地方融资平台规模下降的省份为实验组,
| $\begin{aligned} \;\\ {Choice}_{ict}=&{\gamma }_{0}+{\gamma }_{1}{X}_{ict}+{\gamma }_{2}{Treat}_{ex/im}\times {Post}_{ex/im}\times {X}_{ict}+{\gamma }_{3}{Treat}_{ex/im}\times {X}_{ict}\\ & +{\gamma }_{4}{Post}_{ex/im} \times {X}_{ict}+{\gamma }_{5}{D}_{i}+{\gamma }_{6}{E}_{c}+{\omega }_{i}+{v}_{t}+{\varepsilon }_{ict} \end{aligned} $ | (28) |
其中,
| $ \begin{aligned} {Mismatch}_{ict}=&{\delta }_{0}+{\delta }_{1}{Choice}_{ict}+{\delta }_{2}{Treat}_{ex/im}\times {Post}_{ex/im}\times {Choice}_{ict}+{\delta }_{3}{Treat}_{ex/im} \times {Choice}_{ict}\\&+{\delta }_{4}{Post}_{ex/im} \times {Choice}_{ict}+{\delta }_{5}{D}_{i}+{\delta }_{6}{E}_{c}+{\omega }_{i}+{v}_{t}+{\varepsilon }_{ict} \end{aligned} $ | (29) |
其中,
PSM-DID法的回归结果如表4所示。表4展示了政府颁布相关政策后,显性债务上升和隐性债务下降分别对劳动力职业选择的影响。⑩列(1)展示了政策实施后显性债务扩大对劳动力职业选择的影响,交叉项系数显著为正表明显性债务扩大的影响依然显著。列(2)展示了政策实施后隐性债务下降对劳动力职业选择的影响,交叉项系数为负表示隐性债务下降的确会抑制高技能劳动力选择公共部门。人力资本错配的结论也与基准回归的结论一致,不再赘述。
| (1) | (2) | |
|
|
0.008***(0.002) | |
|
|
–0.008**(0.000) | |
| 控制变量 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 |
| 样本数 | 1 226 | 4 416 |
| R-squared | 0.855 | 0.906 |
(三)进一步分析。
1.拓展公共部门的范围:增加具有与政府部门相似特点的垄断国有企业。对本文结论进行进一步延伸,人力资本错配在政府部门、国有企业以及私人部门之间可能存在递进关系,即随着债务扩张,劳动力的职业选择首选为公务员,然后是国有企业,最后才是私营企业。由此可能将产生与此对应的人力资本错配。具体采用Multinomial Logit模型进行检验:
| $ {\Pr}\left({MChoice}_{ict}=k\right)=\frac{\exp\left({\beta }_{k}x\right)}{1+{\sum }_{k=1}^{2}\exp\left({\beta }_{k}x\right)} $ | (31) |
回归结果如表5所示,本文关注的核心解释变量是交叉项,其回归系数很大程度上可以说明由于政府债务扩张导致的高技能劳动力在职业选择上的变化。在面临私营企业、国有企业和政府部门时,高技能劳动力的首选是政府部门,次选是国有企业。
| (1) | (2) | (3) | (4) | |
| k=1 | k=2 | k=1 | k=2 | |
|
|
0.115***(0.022) | 0.253***(0.024) | ||
|
|
0.023(0.019) | 0.058***(0.020) | ||
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本数 | 7 883 | 7 883 | 16 833 | 16 833 |
| Pseudo R-squared | 0.110 | 0.110 | 0.128 | 0.128 |
| LR检验 | 1 743.21(0.0000) | 4 393.43(0.0000) | ||
接下来本文继续考察劳动力在多元职业选择中对人力资本错配产生的影响。回归思路与基准回归相一致,具体如表6所示。
| (1) | (2) | (3) | (4) | |
| Distortion | Distortion | Skillgap | Skillgap | |
|
|
0.424*(0.247) | 0.052***(0.005) | ||
|
|
0.349***(0.130) | 0.012***(0.003) | ||
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本数 | 9 570 | 4 693 | 9 570 | 9 570 |
| R-squared | 0.013 | 0.016 | 0.013 | 0.014 |
采用Distortion和Skillgap作为被解释变量进行回归得到的交叉项回归系数均显著为正,说明政府债务扩张导致了劳动力职业选择发生了变化,在面对私营企业、国有企业和政府部门情况下,高技能劳动力的职业选择倾向仍然会导致人力资本错配。
2.考虑地区市场经济发展程度差异影响。理论上,如果地区的市场经济发展程度越高,那么由政府债务扩张导致的劳动力职业选择倾向效应会越弱。本文使用樊纲和王小鲁编制的市场化指数衡量地区的市场经济发展程度,实证中使用该指数的倒数Market进行回归,Market越大表示该地方政府的市场化程度越低,市场经济发展越滞后,具体回归结果如表7所示。
| (1) | (2) | (3) | |
| Choice | Distortion | Skillgap | |
|
|
0.030***(0.004) | ||
|
|
−0.139**(0.056) | 0.009***(0.001) | |
| 控制变量 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 |
| 样本数 | 18 397 | 10 010 | 18 397 |
| R-squared | 0.162 | 0.014 | 0.259 |
回归结果显示,Choice对
五、总结和政策性建议
近年来高技能劳动力大量进入公共部门和金融行业,导致这些部门高技能劳动力相对冗余,而实体部门高技能劳动力则出现短缺,本文基于政府债务扩张的视角,从理论和实证两个方面研究了这个问题产生的原因和后果。
理论分析表明,基于土地财政的地方政府债务扩张会导致政府部门和金融行业规模扩大,进而提高对劳动力的需求。同时,这些部门规模的扩张会给私有部门和实体部门带来不确定性。这两个方面的共同作用会导致更多的劳动力选择进入相对稳定的体制内工作。由于体制内普遍存在“学历门槛”,并且薪酬制度市场化程度较低,因而对其他部门的高技能劳动力形成了“虹吸”效应,同时也导致了人力资本的错配效应。
基于微观调查数据的实证研究发现,高技能劳动力更倾向于选择政府部门以及金融行业工作,政府债务扩张会显著强化这种效应,进一步导致人力资本错配。拓展分析发现,如果将企业根据雇主类型区分为私营企业、国有企业与政府部门,那么地方政府债务扩张会导致高技能劳动力在这三种类型职业选择中的倾向性更加明显,由此也形成了人力资本错配。同时还发现,地区债务扩张导致的劳动力职业选择变化和人力资本扭曲对年轻人影响更大,而地区的市场经济发展水平对这种效应能起到更好的抑制作用。
本文的研究发现为解决实体部门与其他部门人力资本错配问题提供了可能的参考思路。根据结论,提出以下几点政策建议:第一,从规范地方政府行为角度来看,可考虑逐步降低地方政府对于土地财政的依赖,规范其举债行为。特别要限制其通过土地加杠杆以及连同金融部门而进行的无序扩张行为。在经济下行压力较大和中央政府提出要稳定房地产市场,“房住不炒”的大背景下,地方政府一方面需要拓展新的财政收入来源,另一方面需要调整支出方式。尤其要提升政府的市场化程度,精简编制,节约支出,以此释放更多的高技能劳动力投入实体部门。第二,从完善市场竞争环境的角度来看,需要提高市场化程度,加强对垄断行业的规制,并逐步放开一些行业的准入,允许民营企业参与竞争,在增加经济活力的同时提高行业竞争程度,缩小国有部门和私有部门的差距,为私有部门吸引更多高技能劳动力创造条件。第三,从收入分配的角度来看,对于以非生产性垄断国企为主的行业工资进行规制,引导其将考核和激励机制与市场接轨,解决人员工资刚性和人员固化的问题,真正实现按岗位贡献分配报酬。第四,从劳动力就业导向方面,需要引导包括公共部门在内的所有用人单位破除唯学历论,根据具体岗位要求选择适应于本岗位的劳动力。第五,从产业结构的角度来看,政策上需要进一步向实体部门倾斜。可通过构建多部门协调的产业孵化基地,以此集中大量高技能劳动力参与实体经济,更好地为实体经济服务。
① 报录比例=审核通过人数/招录人数。数据来源于人力资源社会保障部发布的公开数据。
② 田俊荣,赵展慧,王政等.制造业引才须综合施策,人民网,2018,http://finance.people.com.cn/n1/2018/0917/c1004-30296477.html。
③ 智联招聘. 2020年冬季中国雇主需求与白领人才供给报告,2020。
④ 相对于市场化的企业或机构(比如制造业),公共部门与金融行业中劳动者的工作量比较难以量化,难以依据其创造的价值制订工资水平,工资确定更多是结合其“级别”和所处的岗位。
⑤ 梁平汉和高楠(
⑥ 把H看成A的函数,由
⑦ 治理函数的假定体现了政府与生产部门工资决定差异。政府部门的工资与技能和“资历”挂钩,不是以实际可测度的产出为依据,因此“ 技能边际产出”递减;生产部门充分市场化,以实际边际产出决定工资水平,高技能人才“边际技能产出递增”,说明高端的人才在生产部门能实现更大的价值。
⑧ 以上推导过程参考马颖等(2018)的方法,详细推导说明不再赘述。
⑨ 全样本的回归结果与仅选择户籍为城市部分的回归结果相一致,但后者更为符合现实情况。
⑩ 对于人力资本错配的影响与基准回归相一致,限于篇幅,不再展示。
| [1] | 范剑勇, 莫家伟. 地方债务、土地市场与地区工业增长[J]. 经济研究, 2014(1): 41–55. |
| [2] | 桂林, 陈宇峰, 尹振东. 官员规模、公共品供给与社会收入差距: 权力寻租的视角[J]. 经济研究, 2012(9): 140–151. DOI:10.3969/j.issn.1005-913X.2012.09.081 |
| [3] | 韩雷, 陈华帅, 刘长庚. “铁饭碗”可以代代相传吗?——中国体制内单位就业代际传递的实证研究[J]. 经济学动态, 2016(8): 61–70. |
| [4] | 黄群慧. 论新时期中国实体经济的发展[J]. 中国工业经济, 2017(9): 5–24. |
| [5] | 江曙霞, 罗杰, 黄君慈. 信贷集中与扩张、软预算约束竞争和银行系统性风险[J]. 金融研究, 2006(4): 40–48. |
| [6] | 赖德胜, 纪雯雯. 人力资本配置与创新[J]. 经济学动态, 2015(3): 22–30. |
| [7] | 李程, 贺凯然. 影子银行与地方政府债务杠杆率结构性风险的关系研究[J]. 数量经济研究, 2021(1): 73–91. |
| [8] | 李静, 楠玉, 刘霞辉. 中国经济稳增长难题: 人力资本错配及其解决途径[J]. 经济研究, 2017(3): 18–31. |
| [9] | 梁平汉, 高楠. 实际权力结构与地方政府行为: 理论模型与实证研究[J]. 经济研究, 2017(4): 135–150. |
| [10] | 刘畅, 曹光宇, 马光荣. 地方政府融资平台挤出了中小企业贷款吗?[J]. 经济研究, 2020, (3): 50-64. http://www.cnki.com.cn/Article/CJFDTotal-JJYJ202003007.htm |
| [11] | 马颖, 何清, 李静. 行业间人力资本错配及其对产出的影响[J]. 中国工业经济, 2018(11): 5–23. |
| [12] | 毛捷, 徐军伟. 中国地方政府债务问题研究的现实基础——制度变迁、统计方法与重要事实[J]. 财政研究, 2019(1): 3–23. |
| [13] | 毛毅. 金融业与实体经济行业间工资差距对中国经济增长的影响研究[J]. 财贸研究, 2020(12): 49–60. |
| [14] | 梅冬州, 温兴春. 外部冲击、土地财政与宏观政策困境[J]. 经济研究, 2020(5): 66–82. |
| [15] | 潘士远, 朱丹丹, 徐恺. 人才配置、科学研究与中国经济增长[J]. 经济学(季刊), 2021(2): 427–444. |
| [16] | 蒲艳萍, 顾冉. 劳动力工资扭曲如何影响企业创新[J]. 中国工业经济, 2019(7): 137–154. |
| [17] | 任重, 周云波. 垄断对我国行业收入差距的影响到底有多大?[J]. 经济理论与经济管理, 2009(4): 25–30. |
| [18] | 沈坤荣, 施宇. 地方政府隐性债务的表现形式、规模测度及风险评估[J]. 经济学动态, 2022(7): 16–30. |
| [19] | 施炳展, 冼国明. 要素价格扭曲与中国工业企业出口行为[J]. 中国工业经济, 2012(2): 47–56. |
| [20] | 王启超, 王兵, 彭睿. 人才配置与全要素生产率——兼论中国实体经济高质量增长[J]. 财经研究, 2020(1): 64–78. |
| [21] | 吴永钢, 赵航, 卜林. 中国金融体系内极端风险溢出关系研究[J]. 南开经济研究, 2019(5): 98–121. |
| [22] | 薛欣欣, 张艳. 国有部门与非国有部门工资差距趋于合理吗?——基于反事实估计的比较分析[J]. 山东大学学报(哲学社会科学版), 2014(6): 88–98. |
| [23] | 叶林祥, 李实, 罗楚亮. 行业垄断、所有制与企业工资收入差距——基于第一次全国经济普查企业数据的实证研究[J]. 管理世界, 2011(4): 26–36. |
| [24] | 余海跃, 康书隆. 地方政府债务扩张、企业融资成本与投资挤出效应[J]. 世界经济, 2020(7): 49–72. |
| [25] | 袁志刚, 解栋栋. 中国劳动力错配对TFP的影响分析[J]. 经济研究, 2011(7): 4–17. |
| [26] | 张成. 薪酬管理机制改革必要且可行——基于国有商业银行视角[J]. 银行家, 2015(7): 46–48. DOI:10.3969/j.issn.1671-1238.2015.07.011 |
| [27] | 张明志, 铁瑛, 傅川. 工资扭曲对中国企业出口的影响: 全球价值链视角[J]. 经济学动态, 2017(6): 58–72. |
| [28] | 张双长, 李稻葵. “二次房改”的财政基础分析——基于土地财政与房地产价格关系的视角[J]. 财政研究, 2010(7): 5–11. |
| [29] | 张晓晶, 刘学良, 王佳. 债务高企、风险集聚与体制变革——对发展型政府的反思与超越[J]. 经济研究, 2019(6): 4–21. |
| [30] | Antonovics K, Golan L. Experimentation and job choice[J]. Journal of Labor Economics, 2012, 30(2): 333–366. DOI:10.1086/663356 |
| [31] | King A G. Occupational choice, risk aversion, and wealth[J]. ILR Review, 1974, 27(4): 586–596. DOI:10.1177/001979397402700407 |
| [32] | Miller R A. Job matching and occupational choice[J]. Journal of Political Economy, 1984, 92(6): 1086–1120. DOI:10.1086/261276 |
| [33] | Mincer J A. Schooling, experience, and earnings[M]. New York: National Bureau of Economic Research, 1974. |
| [34] | Murphy K M, Shleifer A, Vishny R W. The allocation of talent: Implications for growth[J]. The Quarterly Journal of Economics, 1991, 106(2): 503–530. DOI:10.2307/2937945 |
| [35] | Nunn N. Relationship-specificity, incomplete contracts, and the pattern of trade[J]. The Quarterly Journal of Economics, 2007, 122(2): 569–600. DOI:10.1162/qjec.122.2.569 |
| [36] | Paglin M, Rufolo A M. Heterogeneous human capital, occupational choice, and male-female earnings differences[J]. Journal of Labor Economics, 1990, 8(1): 123–144. DOI:10.1086/298239 |
| [37] | Schuetze H, Wood J. Immigrant networks, occupational choice, and match quality[R]. Technical Report, Mimeo, 2013. |

