一、引　言

后危机时代全球性杠杆化浪潮成为主导宏观经济与政策演变的重要力量。就我国而言，国有企业的杠杆率显著高于民营企业，这是我国管理经济杠杆化进程的“牛鼻子”（钟宁桦等，2016；蒋灵多等，2019）。对此，我国于2015年启动供给侧结构性改革，不仅将改革尤其是国有企业改革视为经济去杠杆的重要策略，还提出要采用“兼并重组”“完善现代企业制度”“建立健全市场主体退出制度”等方式，“积极稳妥降低企业杠杆率”。从现实看，在供给侧结构性改革下，我国宏微观杠杆率渐趋稳定。相关研究或者集中于分析微观层面单一企业对“去杠杆”方式的选择（许晓芳等，2020；周茜等，2020；许晓芳和陆正飞，2022），或者侧重于探讨宏观政策下杠杆化模式与稳增长之间的抉择（潘敏和袁歌骋，2018；刘莉亚等，2019；庄子罐等，2022），涉及金融供给侧结构性改革去杠杆效应的研究文献大多立足于跨国视角（刘晓光等，2019；刘哲希等，2020；梅冬州和宋佳馨，2021），而缺少针对我国供给侧结构性改革去杠杆效应的分析。在此背景下，本文将探讨国有企业监管体制这一供给侧结构性改革的重要方面所具有的去杠杆效应。这不仅能为供给侧结构性改革效果提供更加明确的经验证据，而且对于我国宏观调控实现“稳增长”与“防风险”的平衡、促进高质量发展具有重要的指导意义。

本文选择从国有企业监管视角来审视供给侧结构性改革的去杠杆效应，主要有以下三个原因：第一，国有企业在我国宏观调控和经济增长中具有重要地位，不仅在产品市场上促成独特垂直生产结构，还在以信贷市场为代表的要素市场上引导定价机制（Liu 等，2021）。因此，国有企业承担逆周期调节的角色，发挥“串联”商品市场与要素市场的作用（郭婧和马光荣，2019）。第二，近年来我国在供给侧结构性改革时往往多措并举持续优化去杠杆政策，我们很难干净地甄别单一措施的影响。部分文献直接采用杠杆率变化率进行分析（许晓芳等，2020；周茜等，2020），而这种处理可能导致对去杠杆政策的评估陷入“鸡生蛋”与“蛋生鸡”的循环论证中。第三，国有企业监管体制改革既内生于国有企业改革这种局部结构性改革，又隐含政府内部不同部门以及不同层级之间的经济决策权限调整，从而契合我国供给侧结构性改革的主要特征。即国有企业监管体制改革既不是发达经济体系所倡导的以局部性为显著特征的结构性改革，也不是供给侧与结构性改革的简单组合，而是以供给侧为立足点、以结构调整为目标、以更深入市场化改革为手段的全局性方案（郭克莎，2022）。此外，在本文所关注的2003年国有企业监管体制集中性改革前后，我国已走出亚洲金融危机阴霾并处于平稳增长态势中，宏观调控框架也在人民银行大区行制度和分税制改革中得以稳定，从而能够很好凸显以国资委成立为标志的国有企业监管体制改革的影响。

本文选择始于20世纪90年代“抓大放小”改革的隶属关系变更来反映集中性国有企业监管体制下上级政府对下级政府的监管授权，考察其对国有企业杠杆率的影响。本质上，隶属关系是立足于所有者与监管者双重角色，政府对国有企业的分类界定（黄群慧，2022）。国有企业属于全民所有，不同层级政府作为国有企业的实际出资人，能够以所有者身份向国有企业委派高级管理人员，影响其经营决策。国有企业的委托代理链可能较长，行政层级较高的政府，尤其是中央政府必须选择特定形式的监管授权。

本文整理了各级政府网站上含有国有企业字眼的文件，发现自2003年集中性监管体制建立以来，除了国资委外，其他部委对国有企业事项也发布了大量文件。当以上述文件数量来反映监管集中性时，其与国有企业杠杆率之间存在格兰杰因果关系。而地方政府的发文主要来自非国资委部门，其占比在多数省份的大多数时间内超过90%，地方层面国资委独立发文较少。这说明我国国有企业监管体制具有一定分权，地方政府可能主要借助非国资委部门发文，维护中央监管的权威性并保留其监管独立性。换言之，国有企业监管既不是完全分散型，也不是完全集中型，而是具有授权的集中性监管。事实上，2017年全国金融工作会议就强调，系统性风险防控应坚守全国层面的规则统一与风险处置的属地原则。2020年接连发生国有企业债务违约事件，这也要求监管部门与地方政府落实监管与属地责任。2022年的《金融稳定法》草案更是明确，地方政府“应当按照职责分工或国家金融稳定发展统筹协调机制的要求”，履行“金融风险防范化解处置职责”。这些不仅体现了政府对国有企业所担负的监管者角色，更是表明存在中央对地方的监管授权。即隶属关系变更隐含了集中性监管体制下上级政府对下级政府的监管授权。

国有企业改革始于以微观决策自主权扩大为主要标志的放权让利阶段，随后经历以产权制度调整为手段、以现代企业制度为目标的微观制度创新阶段，还走过以“国家所有、分级管理、分工监督、授权经营”为基本原则、以国有资产管理体制改革为抓手的国有资本发展阶段，还在“做大做强做优”国有资本的改革思路下转入管理体制由以“管企业”为主转向以“管资本”为主的混合所有制改革阶段，目前进入以增强活力与效率并促进新发展格局为目标的国资国企高质量发展阶段（黄群慧，2022）。可见，除了放权让利阶段外，其他阶段均隐含国有企业监管体制改革成分，在微观制度创新阶段与国有资本发展阶段主要表现为政府与国有企业之间关系的调整，在混合所有制改革阶段强调以“内部监督”“外部监督”和“社会监督”为代表的“三位一体”监督框架的重要性，而国资国企高质量发展阶段通过优化国有资本布局与战略性调整，强化以“管资本”为主的管理体制，还立足于监管者视角推进分类改革。这些改革通过完善国有企业监管体制，不仅在宏观上协调了政府与市场的关系，还在微观上构建起“产权清晰、权责明确、政企分开、管理科学”的现代企业制度。

本文以隶属关系变更来反映国有企业监管体制授权，从国有企业监管体制视角探讨了供给侧结构性改革所具有的去杠杆效应。本文的研究贡献主要表现在：第一，拓展了以Garicano和Rossi-Hansberg（2015）为代表的企业组织理论模型，融入了抵押贷款约束和拥有信贷资源集中配置能力的内部资本市场，此时国有企业监管体制能够通过以内部决策分权为代表的组织结构与杠杆率产生关联。这有助于识别出国有企业监管体制对其杠杆率的整体影响，并清晰地揭示出这种影响的具体机制与制约因素。第二，将以2003年国资委成立为标志的国有企业监管体制集中性改革作为准自然实验，利用准自然实验的分组条件和工具变量，借助准自然实验对非随机性的处理和工具变量的外生性，控制了非随机性、反向因果和遗漏变量可能导致的内生性问题。

二、经验事实

隶属关系变更在20世纪90年代的“抓大放小”改革中被正式使用，采取了“抓大”与“放小”这种初步的分类改革思路，其中“放小”就包括隶属关系由较高层级政府变更为较低层级政府（Hsieh和Song，2016）。基于1998—2013年工业企业数据的分析表明，这种变更既不完全是隶属关系沿政府层级的逐级下放，也不完全是由较高层级政府向较低层级政府的一次性下放，而是包含多种类型，既有中央直接下放到省、中央或省直接下放到市以及中央、省或市直接下放到县这种一次性下放，又有这种一次性下放持续与间断推进的组合。

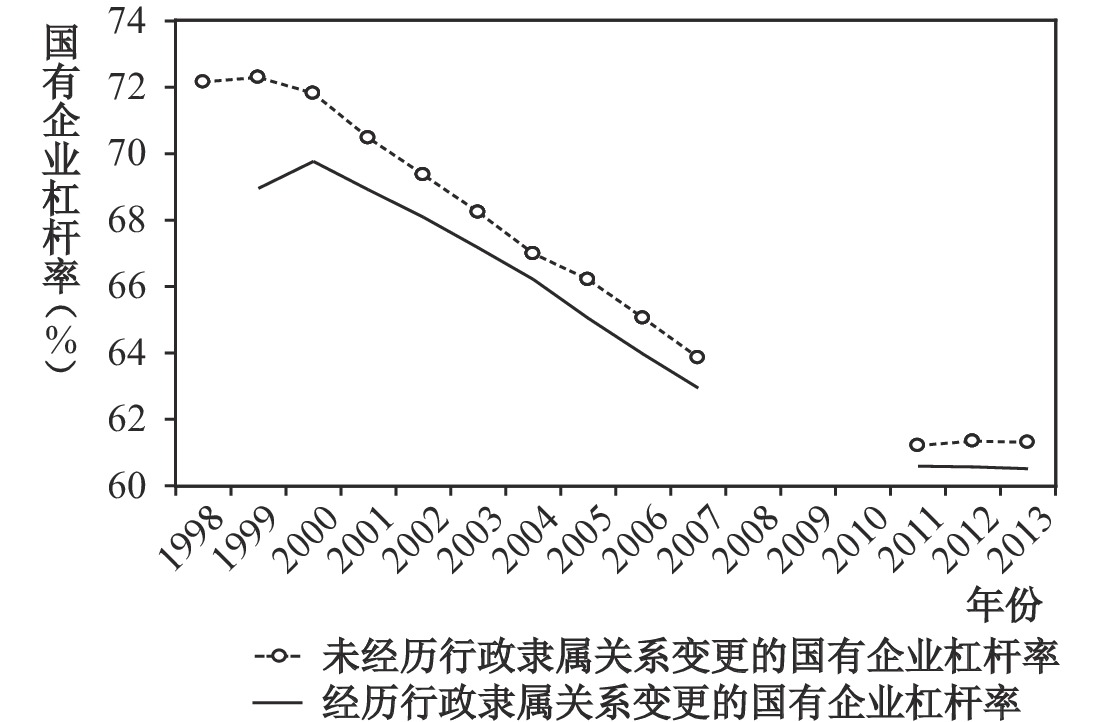
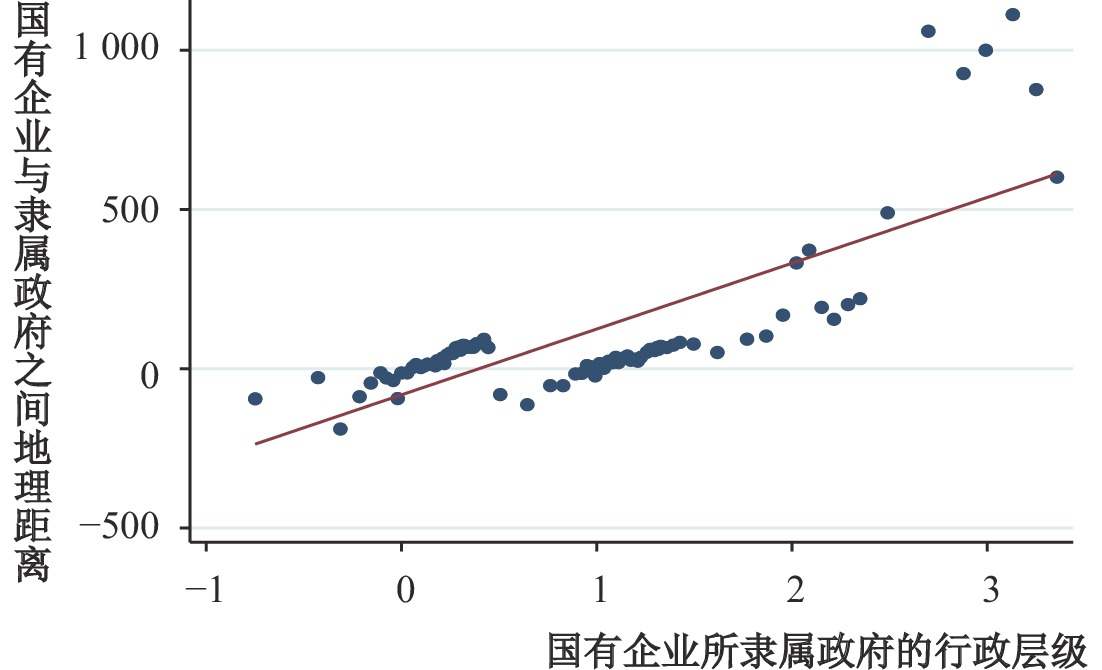
在集中性国有企业监管体制下，隶属关系变更意味着较高层级政府对较低层级政府的监管授权。图1得到以下经验事实：在所隶属政府层级影响同质的前提下，隶属关系发生变更之后，国有企业杠杆率降低。同时，国有企业通常未选址于隶属政府所在地，而是位于隶属政府下辖的较低层级行政区划内，使得隶属关系变更可能带来其与隶属政府的位置变化。本文根据企业地址与行政区划的经纬度来计算两者距离，并使用虚拟变量Degree来刻画政府层级，隶属中央时取值为3，隶属省、市和县及以下政府时分别取值为2、1和0。图2显示，两者距离与政府层级正相关。这预示隶属关系变更会促使两者距离缩短，沟通成本降低，监管效率提高，从而杠杆率降低，符合经验事实。

三、理论分析

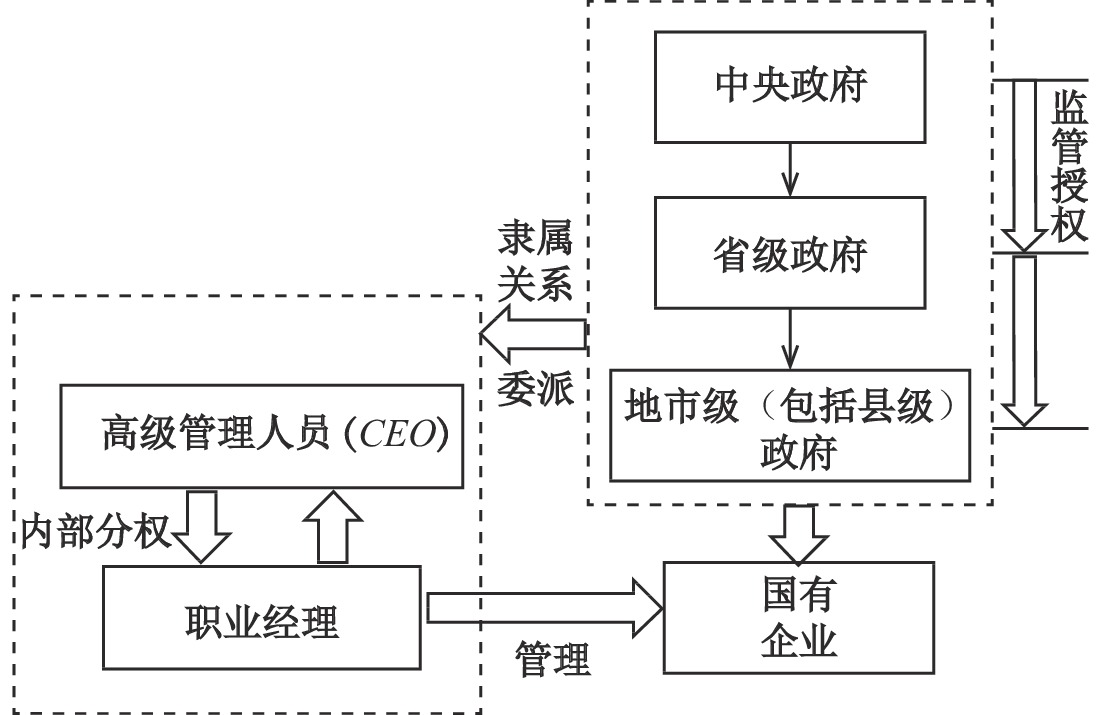
根据经验事实，图3将国有企业内部组织结构分为两个层级，并纳入政府层级，将隶属关系变更转为上下级政府的监管授权。基于此并借鉴Garicano和Rossi-Hansberg（2015）的研究，本文构建企业组织结构模型。

在国有企业中，高级管理人员由隶属政府委派，职业经理则负责经营，两者共同完成生产。将生产视为随机管理问题 $ \xi $ ，其概率密度 $ f(\xi ) $ 为 $ [0,1] $ 区间上的减函数。所有问题解决之后正常产出，否则产出为零。介于0和 $ \mathop \xi \nolimits_M $ 之间的问题由职业经理解决，大于 $ \mathop \xi \nolimits_M $ 的问题则交给高管人员解决。高管人员和职业经理需要支付信息成本（即纵向沟通成本 $ h $ 和信息获取成本 $ \alpha $ ）。理论上，层级越多，信息分享越多，信息获取成本 $ \alpha $ 越低；但同时，层级多可能会降低信息质量，增加纵向沟通成本 $ h $ 。

国有企业的有效产出为 $ Y = n[\lambda F(\mathop \xi \nolimits_M ) + 1 - F(\mathop \xi \nolimits_M )]\mathop K\nolimits^\beta $ ，其中 $ n $ 为生产单位数， $ F(\mathop \xi \nolimits_M ) $ 为由职业经理所解决的管理问题占比，K为资本， $ \beta $ 为资本的产出弹性（介于0和1之间）。 $ \lambda $ 不仅为职业经理专注生产的概率，还表示组织上下级目标一致性，其取值介于0和1之间。

（一）企业组织结构决策

在国有企业内部，高级管理人员进行组织结构决策，其目标函数为：

其中， $ \omega $ 为职业经理工资。同时，高管人员面临纵向沟通成本约束，即 $ [1 - F(\mathop \xi \nolimits_M )]nh = 1 $ 。高级管理人员的决策变量是分权 $ \mathop \xi \nolimits_M $ 和生产单位数 $ n $ ，由此构建如下拉格朗日函数：

其中， $ \varphi $ 为纵向沟通成本约束所对应的拉格朗日乘子。最优一阶条件为：

结合式（2）和式（3）可以得到：

式（4）为决策分权 $ \mathop \xi \nolimits_M $ 的最优条件。内部决策分权对物质资本K的影响为：

式（5）表明，内部决策分权需要与之匹配的资本扩张，这也是企业规模对内部决策分权的约束。即企业规模越大，管理下级的难度越大，而分权能够弥补这种不足。

（二）企业投资与融资决策

企业不仅有多个层级，还有多个生产单位。因此，企业不仅要考虑授权问题，更要在多个生产单位之间调配资源。为了凸显内部资本市场的集中融资优势，高管人员统一对外融资，再转贷给生产单位。由于信息不对称，不仅高层级无法控制低层级生产，外部投资者也无法确保资金有效利用。借鉴Rocheteau 等（2018）的思想，贷款以有效产出为抵押。

其中， $ \mu $ 介于0和1之间， $ \mu $ 越大，对外融资依赖程度越高。同时，国有企业因政府担保而在融资市场上受到优待，均衡时会用尽贷款限额，即 $ B = n\mu [\lambda F(\mathop \xi \nolimits_M ) + 1 - F(\mathop \xi \nolimits_M )]\mathop K\nolimits^\beta $ 。据此，杠杆率 $ b $ 为：

1. 企业融资决策。企业融资利率为R_L，以内部资金价格R_M转贷给生产单位形成资本K，由此得到内部资本市场的目标函数： ${\max} \; {{\Pi}_{IM}} = n{R_M}K - {R_L}B - {\chi}B^2/2$ ，其中 $\chi B^2/2$ 为内部资本市场的运作成本， $ \chi \gt 0 $ 为其效率，χ越小，内部资本市场效率越高。内部资本市场的决策变量为内部资金价格R_M，其直接影响生产单位对资本的需求K，由此得到关于内部资金价格R_M的最优条件：

均衡时内部资本市场的目标函数为零，由此得到企业融资的均衡条件：

$ n{R_M}K = {R_L}B + {\chi}B^2/2 $

(9)

需要强调的是，式（8）和式（9）均为内部资本市场所必须满足的均衡条件，式（8）决定融资价格，式（9）决定融资规模。而为了避免分析复杂化，随后的分析只考虑式（9）。

2. 企业投资决策。企业投资决策的目标函数为 $ V(K) = \Pi ( {\xi_M},n,K) - {R_M}nK - \phi B^2/2 $ ，其中 $ \phi B^2/2 $ 为监管对负债所施加的成本， $ \phi \geqslant 0 $ 为监管对债务的约束程度， $ \phi $ 越大，监管集中性越强。将式（1）和式（9）以及纵向沟通成本约束代入投资目标函数，决策变量资本需求K的最优化条件为：

$ \mathop K\nolimits^\beta = \frac{{[\lambda F(\mathop \xi \nolimits_M )(1 - \mu \mathop R\nolimits_L ) + 1 - F(\mathop \xi \nolimits_M )][1 - F(\mathop \xi \nolimits_M )]h}}{{(\chi + \phi )\mathop {[\mu \lambda F(\mathop \xi \nolimits_M )]}\nolimits^2 }} $

(10)

式（10）表明，内部决策分权程度越高，企业对资本的需求越小。从一般均衡视角看，式（4）和式（10）分别为资本供给与需求曲线。前者的含义是，从事前看，内部决策分权程度越高，较低层级的决策自由度越大，通过扩大资本而获得的收益越多；后者的含义是，从事后看，内部决策分权扩大通过资本需求扩张而产生的收益小于融资成本，导致资本需求减少。

式（10）和式（4）相结合可以得到企业内部决策分权的决定条件：

根据式（11）可以得到国有企业监管体制特征 $ \phi $ 对企业内部决策分权程度 $ \mathop \xi \nolimits_M $ 的影响：

式（12）表明，对国有企业监管的授权程度越高，其内部决策分权程度越高，这符合直觉。此外，根据式（7）可以得到监管体制授权对国有企业杠杆率的一阶导数：

式（13）考察了国有企业监管授权作为事后约束通过事前组织结构决策对杠杆率的影响。那么，事后监管能通过资本需求而影响杠杆率吗？从杠杆率表达式看，确实存在这种可能。而本文的决策次序是，先组织结构决策，再投融资决策。这意味着若仅考察事后监管通过资本需求对杠杆率的影响，则会忽视事后监管对事前决策的制约。基于此，本文以事前组织结构为中介变量，考察事后监管的影响。在式（13）中， $ \partial K/\partial \mathop \xi \nolimits_M $ 应大于零。由于 $ \lambda $ 和 $ \beta $ 均介于0和1之间，结合式（13）可知， $ \partial b/\partial \phi > 0 $ ，即监管体制授权程度越高，国有企业杠杆率越低，这与经验事实一致。基于此，本文提出理论假说1：国有企业监管体制授权会使国有企业去杠杆。

同时，由式（13）可得：

结合式（11）—式（14），本文提出理论假说2：以隶属关系变更为代表的国有企业监管授权所具有的去杠杆效应源于监管授权对企业内部决策分权的正向作用。

分析货币政策 $ \mathop R\nolimits_L $ 、融资约束 $ \mu $ 、纵向沟通成本 $ h $ 、内部资本市场效率 $ \chi $ 以及上下级目标一致性 $ \lambda $ 的影响，可以得到：

$ \frac{\partial }{{\partial \mu }}(\frac{{\partial b}}{{\partial \phi }}){\text{ = }}\underbrace{\frac{\partial }{{\partial \mu }}(\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }})\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }}}_{正}{\text{ + }}\underbrace{\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }}\frac{\partial }{{\partial \mu }}(\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }})}_{负} $

(16)

$ \frac{\partial }{{\partial h}}(\frac{{\partial b}}{{\partial \phi }}){\text{ = }}\underbrace{\frac{\partial }{{\partial h}}(\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }})\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }}}_{负}{\text{ + }}\underbrace{\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }}\frac{\partial }{{\partial h}}(\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }})} _{负} < 0 $

(17)

$ \frac{\partial }{{\partial \lambda }}(\frac{{\partial b}}{{\partial \phi }}){\text{ = }}\underbrace{\frac{\partial }{{\partial \lambda }}(\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }})\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }}}_{正}{\text{ + }}\underbrace{\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }}\frac{\partial }{{\partial \lambda }}(\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }})}_{正} > 0 $

(18)

$ \frac{\partial }{{\partial \chi }}(\frac{{\partial b}}{{\partial \phi }}){\text{ = }}\underbrace{\frac{\partial }{{\partial \chi }}(\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }})\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }}}_{正}{\text{ + }}\underbrace{\frac{{\partial b}}{{\partial \mathop \xi \nolimits_M }}\frac{\partial }{{\partial \chi }}(\frac{{\partial \mathop \xi \nolimits_M }}{{\partial \phi }})}_{负} $

(19)

根据式（15）—式（19），本文提出理论假说3：货币政策越紧缩（ $ \mathop R\nolimits_L $ 越高）或纵向沟通成本越高（ $ h $ 越高），监管体制授权的去杠杆效应越强；而上下级目标一致性越强（ $ \lambda $ 越大），监管体制授权的去杠杆效应越弱。

四、实证设计

本文数据来自1998—2013年工业企业数据库，涵盖特定规模以上所有国有企业及其隶属关系信息。本文借鉴Brandt 等（2012）的方法，处理行业代码和样本识别等问题；同时，参考聂辉华等（2012）的研究，对缺失数据和异常值进行清洗，最终得到409 008个国有企业样本。

（一）被解释变量：国有企业杠杆率

本文以国有资本与实收资本之比超过30%作为国有企业的识别标准，并结合控股类型，补充缺失值，以总负债与总资产之比来测度企业杠杆率。

（二）核心解释变量：监管授权

本文以隶属关系变更来反映监管授权，在隶属关系变更当年及以后，监管授权变量取值为1，否则为0。1998—2013年工业企业数据中缺少2008—2010年的隶属关系变更信息。

（三）机制变量：内部决策分权

本文借鉴梁平汉和高楠（2017）的研究，以非国有股份占比来衡量内部决策分权，这一占比越大，企业内部决策分权程度越高。

（四）控制变量

与钟宁桦等（2016）以及谭小芬和张文婧（2021）等文献一致，本文的控制变量包括：（1）企业规模，等于总资产的自然对数；（2）企业年龄，等于存续年份减去开工时间加1之后的自然对数；（3）经营性现金流，用经营性现金流与总资产之比来表示；（4）盈利能力，用销售利润率来表示；（5）有形资产比例，用固定资产净值与存货之和在总资产中的占比来表示；（6）成长机会，用销售收入增长率来表示；（7）非债务税盾，用固定资产累计折旧额在总资产中的占比来表示。

（五）其他变量

1. 监管授权的替代变量：（1）国有企业与其所隶属政府之间的距离。（2）与隶属关系变更相伴的政府层级虚拟变量，国有企业隶属于中央政府时取值为3，隶属于省级政府时取值为2，隶属于市级政府时取值为1，隶属于县级政府时取值为0。（3）国有企业监管体制指标，即反映中央向地方授权的纵向授权以及地方层面在国资委与非国资委部门之间分权的横向授权。本文整理了国资委等中央部委网站上含有国有企业字眼的文件，以中央发文代表监管集中性，以地方与中央发文之比代表集中性监管下的纵向授权，其中既包含地方对中央文件的直接转发，又包含地方政府的针对性发文。从纵向授权看，地方政府针对国有企业的发文紧跟中央，两者走势一致；在绝大部分时间内，中央发文远多于地方，体现了监管集中性。从横向授权看，地方多数发文集中于非国资委部门，这是因为国资委体现了中央监管集中性，而地方监管既要维护这种集中性，又要保留其监管的相机抉择性。上述指标展现出具有授权特征的集中性监管。

2. 监管授权的工具变量：（1）隶属关系变更到特定层级的企业数量占比。（2）借助中国经济社会大数据平台，筛选出“五年规划”所强调的行业，并将冠以“重点”“支柱”“优先发展”“做大做强”“大力发展”“着力培养”的行业视为支持行业，与两位行业代码匹配，由此确定重点扶持行业，定义产业政策虚拟变量；参照Huang 等（2017）的研究，将石油和天然气开采、石油加工、炼焦及核燃料加工业、航空航天及其他设备制造业、核力发电、电力热力、燃气和水供应业作为战略性行业；“三线建设地区”包括贵州、四川（含重庆）、云南、陕西、甘肃、宁夏、青海、山西、河北、河南、湖南、湖北和广西等省或自治区；基于销售收入得到HHI指数，以此反映行业竞争程度，其数值越大，表明竞争越弱。另一个工具变量根据产业政策虚拟变量、战略性行业虚拟变量、三线建设地区虚拟变量以及行业竞争程度来构造。

3. 稳健性检验所涉及变量：（1）财政分权与金融分权。财政分权以地区人均财政收入/（人均中央财政收入+人均地区财政收入）来测算，金融分权以各省银行贷款占全国贷款总额的比重来衡量。（2）“省直管县”与“扩权强县”。如果国有企业所在地区实施“省直管县”改革，则变量取值为1，否则为0。采用类似的方法定义“扩权强县”变量。（3）纵向沟通成本。与Huang 等（2017）一致，选择省级公共资本进行衡量。（4）上下级目标一致性。以地方文件所披露的经济增长目标为基础，使用实际增长与增长目标之差的绝对值再除以经济增长目标，衡量增长目标完成度，其数值越大，完成目标的压力越大，上下级目标一致性越弱。同时，选择李虹和邹庆（2018）所构造的环境规制指数来反映环境目标，其数值越大，政府对环境的规制越严。

4. 货币政策：货币政策通过调控流动性直接影响企业融资，从而影响杠杆率。同时，企业负债形成也是内生货币的创造。只有剥离货币政策的外生变化，才能反映其对杠杆率的真实影响。本文借鉴Chen 等（2018）的思想，采用马尔科夫转换模型来估计以广义货币M2为代表的数量型货币政策规则，反映货币政策的外生变化。

五、实证分析

（一）基准回归分析

本文借鉴Huang等（2017）以及谭小芬和张文婧（2021）的思路，构建了如下静态面板模型来分析国有企业监管授权与国有企业杠杆率之间的关系：

其中，lever为国有企业杠杆率，dec为国有企业隶属关系变更虚拟变量，X为控制变量， $ {\lambda _n} $ 、 $ {\lambda _t} $ 和 $ {\lambda _j} $ 分别为地区、时间与四位代码行业固定效应。

表1结果显示，监管授权对国有企业杠杆率的影响显著为负，这表明监管授权会使国有企业去杠杆，符合理论假说1。企业规模的系数显著为负，企业年龄的系数显著为正，这可能体现出企业在短期债务违约风险与未来增长之间的权衡（Kieschnick和Moussawi，2018）；经营性现金流和盈利能力的系数显著为负，与优序融资理论一致；有形资产比例的系数显著为负，这是因为有形资产越多往往代表企业规模越大，有形资产能起到与企业规模相似的作用；成长机会的系数显著为正，表明成长性越好，融资需求越强，在内源融资无法满足需要时，企业会增加外部融资；非债务税盾会减弱债务税盾避税的激励，抑制杠杆率。整体上，隶属关系变更对国有企业杠杆率的影响符合理论假说1，主要控制变量的影响符合预期。

（二）稳健性检验

1. 替换核心解释变量。本文将核心解释变量替换为企业与其所隶属政府的地理距离、隶属政府层级虚拟变量以及国有企业监管体制授权指标。在变量替换后，监管授权对国有企业杠杆率的影响系数依然为负，且在大多数情况下显著。

2. 更改固定效应。隶属关系变更不仅与地理距离有关，还与行业和政府层级有关。为此，本文在基准回归中控制了地区与行业固定效应。从我国经济体制演变看，相关因素随时间而变化，如产业政策下的战略性行业选择；由于各个地区存在资源禀赋差异，产业政策在地区间也有所不同。据此，本文调整了固定效应形式，监管授权对国有企业杠杆率的影响依然为负，控制变量结果也与基准回归结果一致。

3. 改变国有企业识别方法。与谭小芬和张文婧（2021）相同，本文将国有企业的识别标准由股份占比改为登记注册类型。监管授权变量及控制变量结果与基准回归结果一致。

4. 控制其他宏观政策因素的影响。与国有企业监管体制改革同步的不仅有分税制改革、“省直管县”以及“扩权强县”改革，还有金融分权。只有很好地控制这些改革措施，才能识别国有企业监管体制的影响。鉴于金融分权与财政分权高度关联，本文控制了这两个因素，并加入地方人均GDP、第二产业增加值与GDP之比、信贷增量与GDP之比以及地方财政支出与收入之比作为控制变量。此外，由于“扩权强县”和“省直管县”同属政府组织结构变动，本文还控制了这两项改革。在控制这些宏观政策因素后，监管授权对国有企业杠杆率的影响依然显著为负。

（三）内生性处理

1. 工具变量法。隶属关系变更根植于“抓大放小”改革，目的是“增效”。而债务过度膨胀是低效的一种表现，可能成为隶属关系变更的决定性因素。据此，本文参考谭语嫣等（2017）的思路，选择隶属关系变更到特定政府层级的企业数量占比作为工具变量。其合理性在于：一方面，隶属关系变更的企业越多，变更到特定层级的企业越多，从而满足相关性要求；另一方面，隶属关系变更所涉及的企业数量为总量指标，不受杠杆率这一微观指标的影响，从而满足外生性要求。

Huang 等（2017）以及Kong 等（2022）强调地理距离和行业竞争对隶属关系变更的影响。与地理距离相比，行业竞争的外生性更强。行业竞争会影响微观企业杠杆率，而不会受制于微观杠杆率。与隶属关系变更相关的地理位置是企业内生决策，其与投融资决策具有天然关联。从“抓大放小”改革看，隶属关系变更是由管辖政府基于职能和目标所做的自主决策，受到多重因素的影响，而最重要的因素是产业政策。因此，在运用行业竞争作为工具变量时，必须排除产业政策的影响。此外，关系到国计民生的战略性行业不会实施隶属关系变更，因而也必须排除。曾位于“三线建设地区”的国有企业与其所隶属政府之间的关系难以用市场机制解释，而是取决于政府基于国内外经济政治形势所做出的战略决策，属于广义产业政策，因而也必须排除。据此，本文构造了另一个工具变量：（1−产业政策虚拟变量−战略性行业虚拟变量）×行业竞争程度×（1−三线建设地区虚拟变量）。上述工具变量排除了与隶属关系变更无关的行业与区域特征，保留了市场机制发挥最大作用的信息。

表2结果显示，内生性检验在1%的水平上拒绝监管授权外生的零假设。第一步回归显示，工具变量对核心解释变量具有显著影响，在特定政府层级上“下放”的企业较多时，监管幅度增大，效率下降，从而会抑制隶属关系进一步变更。这符合直觉，也满足相关性要求。工具变量外生性检验的F统计量均超过1%显著性水平的临界值，从而满足外生性要求。在第二步回归中，弱识别检验的Kleibergen-Paap Wald rk F统计量均大于10，表明本文工具变量不存在弱识别问题。识别不足检验的Kleibergen-Paap rk LM统计量的伴随概率均远小于0.1，表明不存在识别不足问题。在过度识别检验方面，由于1998—2013年工业企业数据中缺少2008—2010年的隶属关系变更信息，回归残差的方差与协方差矩阵不满秩，当回归聚类到时间时无法计算过度识别检验的统计量，其他情形下Hansen J统计量的伴随概率均大于0.1，表明不存在过度识别问题。

整体上，本文工具变量选择合理，工具变量回归结果也与基准回归结果一致。即在控制隶属关系变更与国有企业杠杆率可能存在的反向因果关系后，两者依然呈现负向关系。

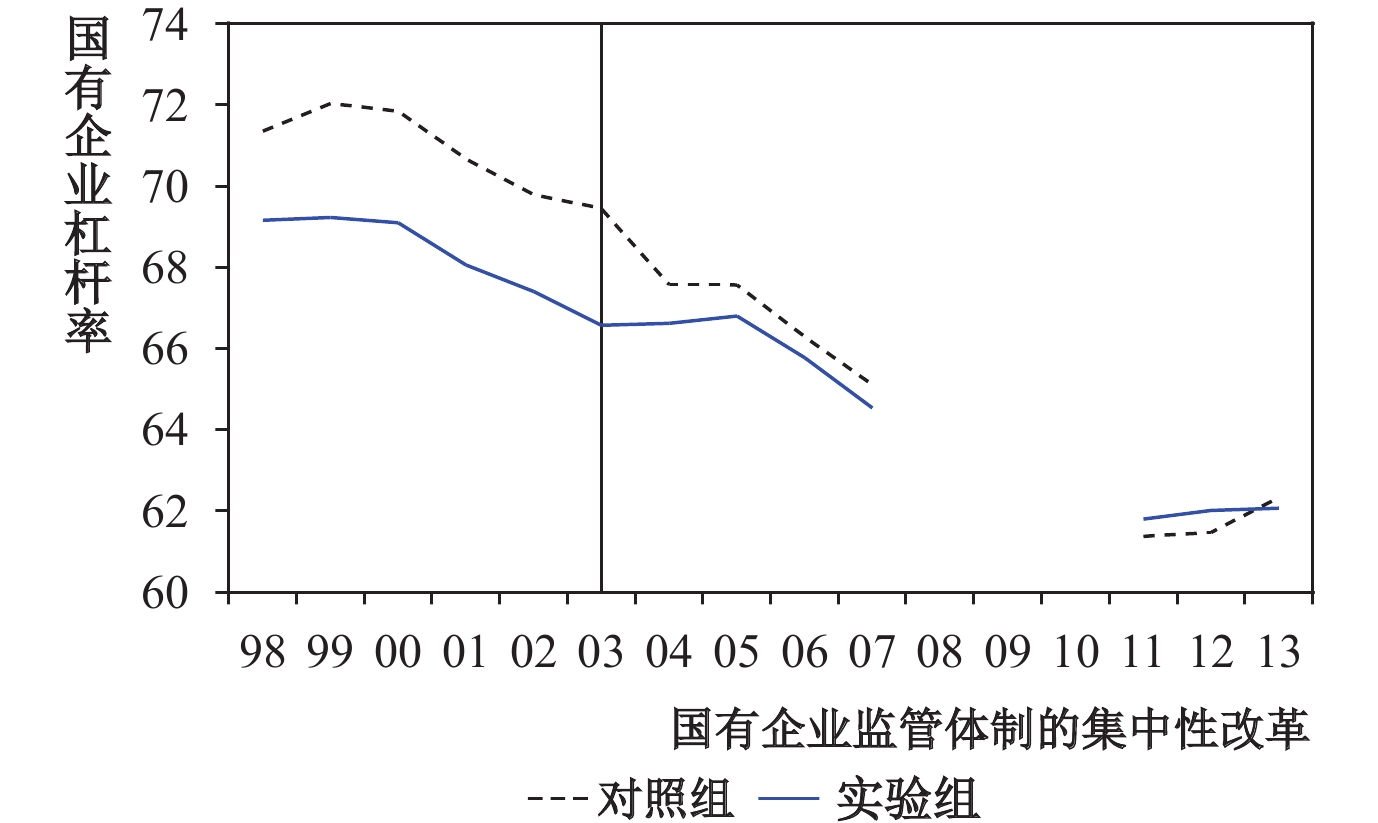
2. 双重差分法。基准回归与工具变量回归无法解决非随机性所导致的内生性问题。本文基于国有企业监管体制集中性改革（以2003年国资委成立为标志）来构造准自然实验。根据工具变量回归，本文以区域—政府行政层级维度上隶属关系变更的国有企业占比作为分组变量，将2003年这一占比高于均值的区域—政府行政层级组合作为对照组（即未来隶属关系发生变更概率较低组），反之为实验组。根据本文逻辑，如果隶属关系变更隐含国有企业的监管授权，那么在2003年国有企业监管体制集中性改革之后，监管集中性上升，与对照组相比，实验组杠杆率均值上升。据此，借鉴Li 等（2016）以及Kong 等（2022）的思路，本文构建了如下模型：

其中， $ DE{C_{ijnt}} $ 为反映国有企业所隶属政府特征的函数，在监管体制改革之前，管辖政府层级上隶属关系变更的国有企业占比低于均值时为1，即实验组，反之为对照组。 $ Tim{e_t} $ 在2003年之前取值为0，在此之后为1。交互项 $ DE{C_{ijnt}} \times Tim{e_t} $ 的系数 $ {\alpha _1} $ 反映监管体制改革前后以隶属关系变更为代表的监管授权对国有企业杠杆率的影响差异，其符号预期为正。同时，借鉴Li 等（2016）的思想，本文还引入了 $ DE{C_{ijnt}} \times t $ ，其中 $ t $ 等于国有企业所处年份与本文样本起始年份1998年之差。

表3列（3）和列（4）中的交互项系数 $ {\alpha _1} $ 显著为正，表明始于2003年的监管体制集中性改革弱化了监管授权，推高了国有企业杠杆率。这从反面证实了以隶属关系变更为代表的监管授权会使国有企业去杠杆。列（1）和列（2）是基于准自然实验之前样本的回归结果，显示实验组与对照组的差异显著。

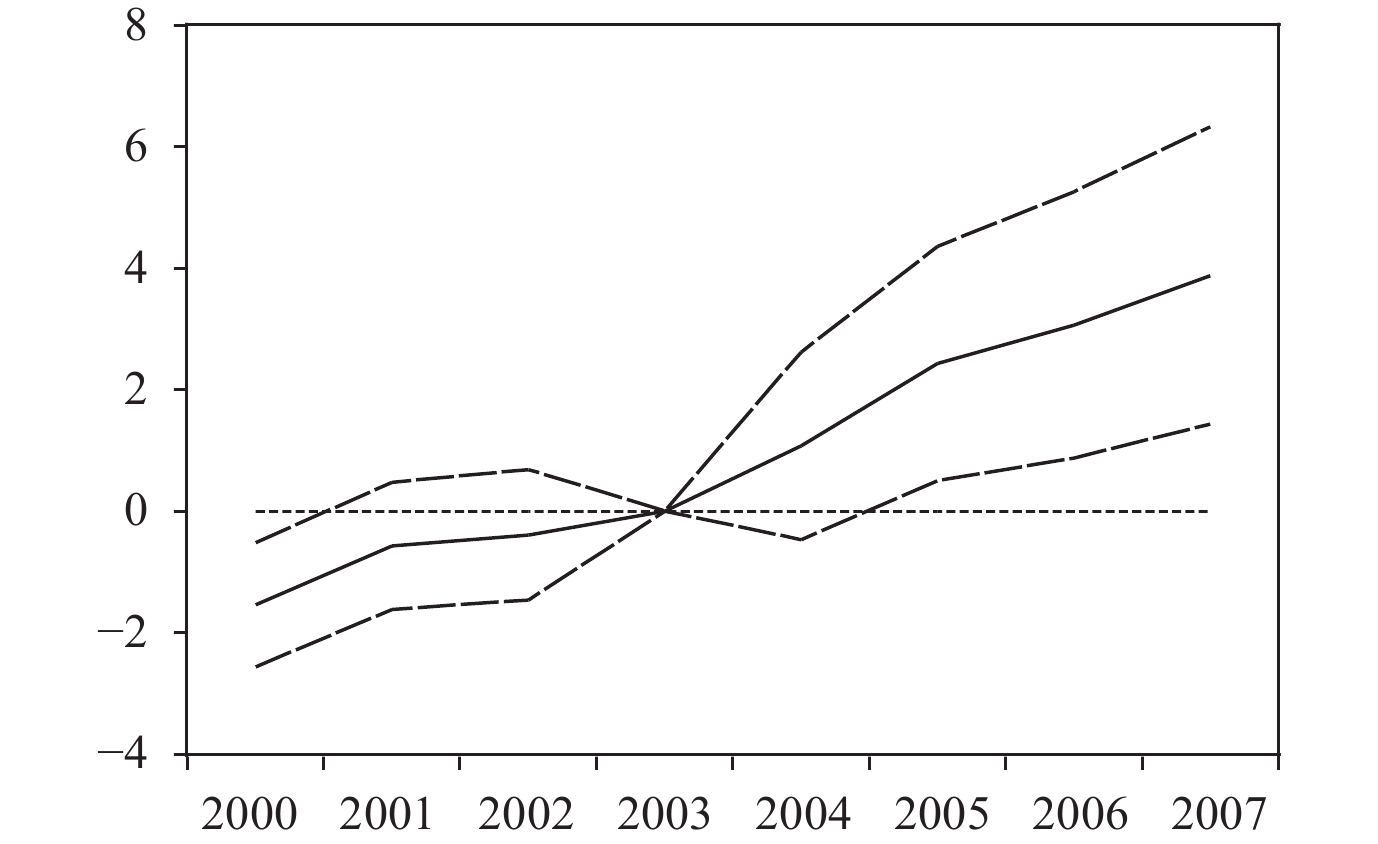
上述结论有效不仅要求在准自然实验之前实验组与对照组保持一致趋势，还要证实这次改革导致实验组杠杆率相对于对照组呈上升态势。准自然实验分组依赖于2003年区域—政府行政层级上发生隶属关系变更的国有企业分布状况。为了避免非随机性的影响，本文以各年度各政府行政层级上隶属关系变更的国有企业占比作为分组变量，采用倾向得分匹配法，逐年寻找最匹配的实验组与对照组。表3中列（5）至列（7）表明，这次改革促使实验组的杠杆率相对上升。

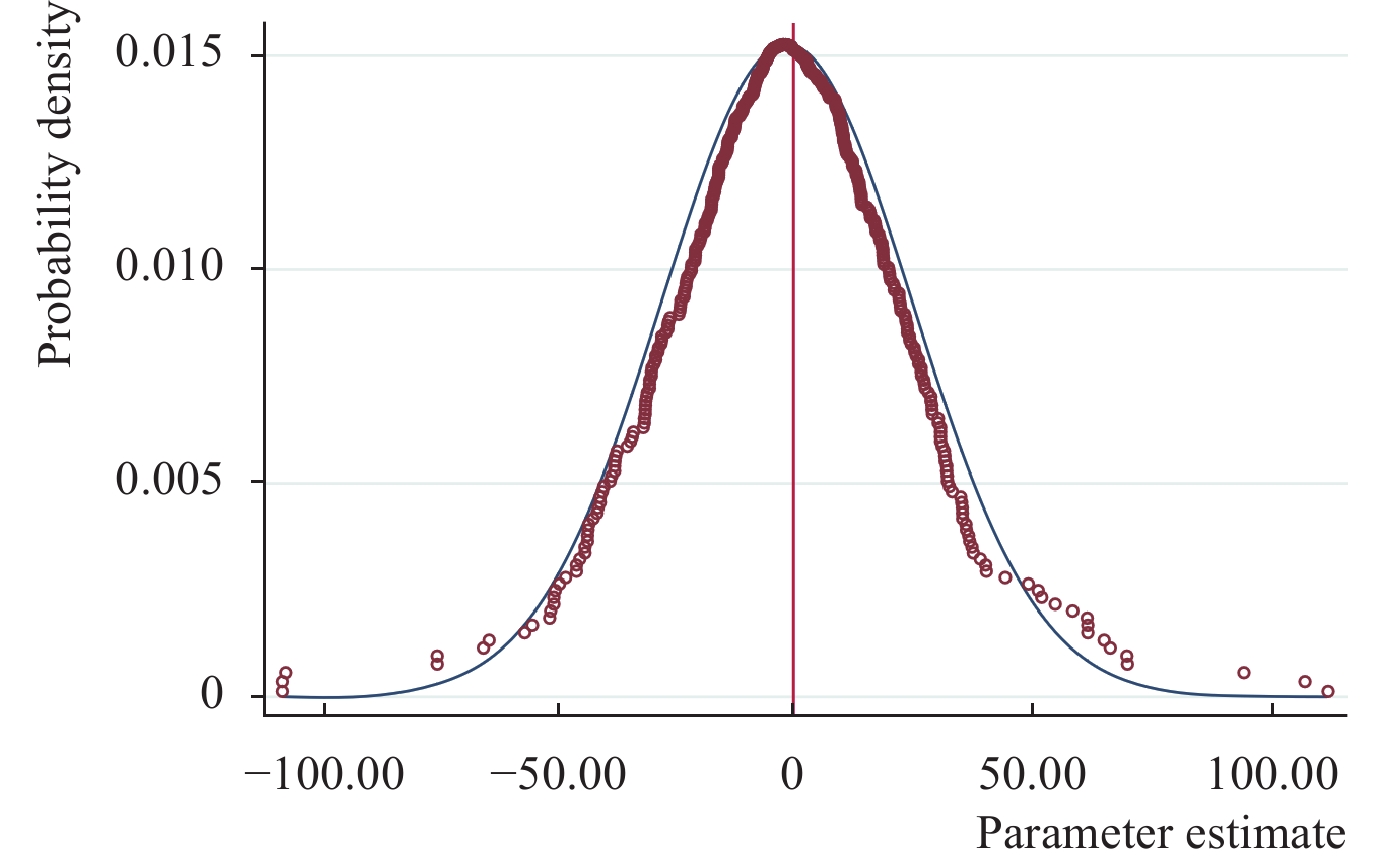
此外，借鉴Kong 等（2022）的思想，本文做了以下安慰剂检验：一是根据现有工业企业数据中每年发生隶属关系变更的企业数来形成虚拟样本；二是计算年份—地区—政府行政层级上发生隶属关系变更的企业数与年份—地区上国有企业总数之比，将这一占比与从区间[0，1]上的均匀分布函数中抽取的随机数进行比较，将这一占比大于随机数的年份—地区维度样本设为对照组，反之为实验组；三是重复500次，考察式（21）中系数 $ {\alpha _1} $ 的分布状况。安慰剂检验表明，本文结果不是由外生偶然因素所驱动。

整体上，本文通过构造以2003年国资委成立为标志的国有企业监管体制集中性改革这一准自然实验，从反面揭示了以隶属关系变更为代表的监管授权会使国有企业去杠杆。

六、影响机制分析

根据理论假说2，监管授权主要通过影响内部决策分权而影响杠杆率。本文采用两种方式对此进行检验。第一种方式是，借鉴毛捷等（2022）提出的三步法，第一步检验监管授权对国有企业杠杆率的影响（即基准回归），第二步利用式（22）检验监管授权对机制变量的影响，第三步利用式（23）检验机制变量对国有企业杠杆率的影响。

第二种方式是，借鉴钱雪松等（2015）的思想，采用中介效应模型。与第一种方式相比，中介效应模型使用的估计方法不同，而且能够检验机制显著性，并对其解释度进行分解。同时，考虑到针对中介效应显著性的Sobel-Goodman检验不能完全反映隐藏其中的中介作用，本文还采用自举法（Bootstrap）进行1 000次重复估计，测算其置信区间。

就第一种方式而言，表4中列（1）至列（5）显示，隶属关系变更虚拟变量以及监管纵向与横向授权对企业内部决策分权具有显著的正向影响，而国有企业与其所隶属政府之间的地理距离以及隶属政府层级虚拟变量则具有负向影响。其经济含义是，在隶属关系变更之后，国有企业更易扩大内部决策分权；监管体制纵向与横向授权程度越高，国有企业内部决策分权程度越高；而国有企业与其所隶属政府之间的地理距离越近、隶属政府层级越低，国有企业内部决策分权程度越高。列（6）至列（10）显示，内部决策分权对国有企业杠杆率的影响显著为负，表明扩大内部决策分权会使国有企业去杠杆，这与理论假说2一致。

就第二种方式而言，表5结果显示，若以隶属关系变更作为监管授权变量，其对杠杆率的解释度最大，其下限为31.4%，上限为38.33%；其次是监管纵向授权，其下限为16.38%，上限为21.01%；接下来是地理距离，其解释度达到10%；最小的是隶属政府层级，其解释度不足5%。这不仅体现了以隶属关系变更作为监管授权变量的合理性，还表明以内部决策分权为核心的中介效应能够对杠杆率产生足够效果。

整体上，以隶属关系变更为代表的国有企业监管体制授权能够通过扩大企业自主决策来降低国有企业杠杆率，这种以内部决策分权为核心的中介效应对杠杆率的解释度达到30%。

七、异质性分析

根据上文理论分析，本文构建了以下模型进行异质性分析：

其中， $ \mathop H\nolimits_{M,ijnt} $ 为异质性分析变量。本文关注的是系数 $ {\alpha _1} $ ，当 $ {\alpha _1} $ 大于零时，异质性分析变量会减弱监管授权对国有企业杠杆率的影响，反之会增强监管授权的影响。

表6结果显示，除了融资约束指标与监管授权的交互项系数不显著外，其他变量与监管授权的交互项系数均显著。具体而言，宽松的货币政策、较低的内部纵向沟通成本、较高的企业效率以及基于环境规制的上下级目标一致性会减弱监管授权对国有企业杠杆率的影响，而所隶属政府面临的稳增长压力则会增强这种影响。

本文还根据异质性分析变量是否大于均值，定义虚拟变量重新进行了分析。与表6相比，除了融资约束与监管授权的交互项系数不显著外，企业效率以及基于环境规制的上下级目标一致性与监管授权的交互项系数也不显著，其他变量与监管授权的交互项系数则均显著。

整体上，宽松的货币政策和企业内部较低的纵向沟通成本会弱化监管授权对国有企业杠杆率的影响，而所隶属政府面临的稳增长压力则会增强这种影响，这与理论假说3一致。

八、结论与政策建议

我国实施的供给侧结构性改革取得了积极的去杠杆效果。本文探讨了国有企业监管体制这一供给侧结构性改革的重要方面所具有的去杠杆效应。研究发现，以隶属关系变更为代表的监管授权与国有企业杠杆率之间呈现负向关系。经过一系列稳健性检验和内生性分析，这一结果依然成立。这缘于监管授权对以内部决策分权为代表的微观组织结构的正向影响，这一中介效应对国有企业杠杆率的解释程度超过30%。此外，宽松的货币政策和企业内部较低的纵向沟通成本会弱化监管授权对国有企业杠杆率的影响，而所隶属政府面临的稳增长压力则会增强这种影响。

基于上述研究结论，本文提出以下政策建议：首先，在供给侧结构性改革过程中，不仅要从宏观上多措并举持续优化改革措施，更要从微观上监测由此可能引起的组织结构变化，逐步形成宏微观统一且相互衔接的供给侧结构性改革总体框架。其次，持续推进具有授权特征的国有企业监管体制集中性改革。通过监管体制集中性，主导并塑造地方监管，以协调地方政府行为，形成地方政府的有效合作，守住不发生区域性系统性风险的底线；通过监管授权，发挥地方自主监管的信息优势与激励约束，提高监管效率，使得地方竞争与合作关系在中央与地方纵向关系引导下实现平衡。最后，在高质量发展阶段，以货币政策为代表的宏观政策实施精准调控，不仅以“稳增长”与“防风险”之间的有效权衡与长期均衡作为重要约束条件，还不能忽视政府组织结构的作用，以达到调控力度适度性与调控目标精确性的有机统一。