一、引　言

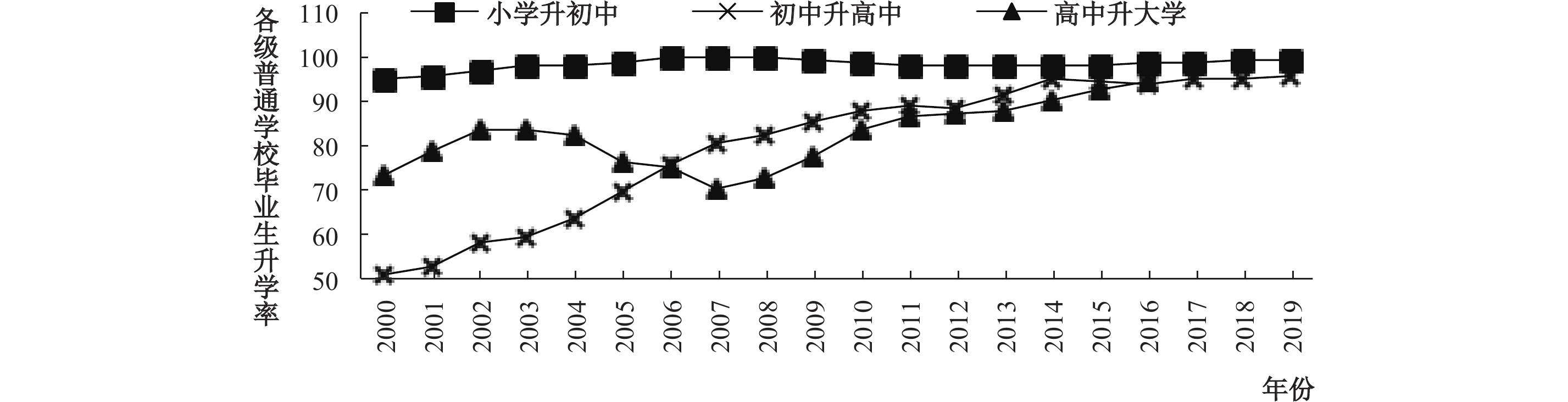
教育是提高人民综合素质、促进人的全面发展的重要途径。21世纪以来，中国在提高广大人民群众受教育水平上取得了显著成就。图1显示，近20年我国义务教育阶段小学升学率呈现平稳发展态势，在2019年达到99.5%；初中升学率大幅跃升，从2000年的51.2%提高到2019年的95.5%。得益于1999年高校扩招政策的实施，高中升学率在2016年超过90%。可见，现阶段我国已基本建成义务教育全面普及、高中教育趋向普及、高等教育从大众化到普及化的教育体系。

伴随着教育规模的逐步扩大，党中央、国务院大力推进教育公平，出台了一系列政策举措。2017年党的十九大报告承诺“努力让每个孩子都能享有公平而有质量的教育”。随后，2019年印发的《中国教育现代化2035》明确提出“发展中国特色世界先进水平的优质教育”“推动各级教育高水平高质量普及”“实现基本公共教育服务均等化”等面向教育现代化的战略任务。2022年党的二十大报告再次提出“加快建设高质量教育体系”“促进教育公平”等宏伟目标。由此可见，党和国家对于教育事业高度重视，在建成世界上规模最大的教育体系、实现教育普及水平历史性跨越的背景下，也在尽一切努力办好人民满意的更加公平和更高质量的教育。

教育公平关键在于提供了平等的机会。如果付出的努力不同而导致教育结果不同，并不一定是教育不公平；如果付出的努力相同，因户口、性别、家庭背景等环境变量存在差异而导致的教育结果不同，就可以视为教育不公平，或称之为教育的机会不平等。长久以来，不平等一直是学界和政策制定者感兴趣的重要话题。以往研究主要集中于收入机会不平等（史新杰等，2018；李莹和吕光明，2019），后来机会不平等逐步拓展到教育领域（Golley和Kong，2018；张楠等，2020；江求川和任洁，2020）。大量文献探讨了影响中国教育不平等的原因，其中主要的因素包括户籍分割造成的城乡不平等（Yang等，2014；Golley和Kong，2018）、地理因素造成的区域不平等（Hannum和Wang，2006；Yang等，2014）、教育和社会经济地位的代际持续性造成的不平等（邹薇和马占利，2019），以及性别（Wu和Zhang，2010；Yang等，2014；Golley和Kong，2018）等因素造成的不平等。然而，多数文献忽视了努力因素在其中发挥的作用。仅有的少数研究以耐心、学习时长或者自评努力来衡量努力因素，主要考查了基础教育阶段的机会不平等（张楠等，2020；江求川和任洁，2020）。此外，随着党的十九大报告提出追求“有质量的教育公平”，2021年政府工作报告进一步明确“建设高质量教育体系”，党的二十大报告则要求“加快建设高质量教育体系”，我国人民群众不再满足于享有教育机会，而是期望获得更高质量的教育（杨成荣等，2021）。因此，处于“发展更加公平更高质量教育”的时代环境中，教育质量的机会不平等也值得关注。

本文可能有以下几点贡献：首先，在研究主题上，大量文献更多地关注了收入的机会不平等，与之相比，探讨教育机会不平等变化趋势的研究还比较少。本文通过使用中国家庭收入调查（CHIP）2002—2018年四轮数据，描绘了近20年我国教育不平等的演变，并将教育不平等分解为教育机会不平等和教育努力不平等，从而探讨了努力因素在教育不平等中的解释力度。其次，在研究方法上，本文在事前参数法测度教育机会不平等的基础上，通过基于回归分析的Shapley值分解计算得出各个环境因素对于教育机会不平等的贡献及其变化趋势。值得注意的是，由于子女的受教育年限存在向上溢出效应，^①即父母可能会根据子女的人力资本水平来调整自身的知识水平，这就导致父母受教育年限和子女受教育年限之间存在反向因果关系；此外，一些不可观测的因素例如基因或者家庭经历的冲击事件有可能同时影响父代和子代的教育水平从而造成遗漏变量。本文运用工具变量法以及异方差构造的工具变量作为补充，力图克服由于遗漏变量和反向因果关系而造成的内生性问题，在此基础上汇报各环境变量影响教育机会不平等的贡献度及变动。最后，在研究内容上，现有研究主要关注教育机会在数量上的不平等，对教育质量的不平等研究尚存在不足。本文从教育获得数量和质量两个层面研究环境因素和努力程度的作用，不仅关注了以个体受教育年限衡量的数量层面的教育机会不平等，还关注了以个体上重点高中或大学衡量的质量层面的教育机会不平等，补充了该主题的研究文献。

本文研究发现：第一，近20年中国的教育不平等呈现下降趋势；教育机会不平等也在2018年出现较大降幅。第二，基于回归分析的Shapley值分解结果表明，户口和父亲受教育年限是贡献较大的两个环境变量。随着时间推移，户口对教育机会不平等的解释力度逐渐减小，而父亲受教育年限对教育机会不平等的解释力度逐渐增大。第三，从教育质量的角度出发，近年来家庭背景因素在解释重点大学教育机会不平等中占据主要地位。第四，采用工具变量法以及异方差工具变量法克服内生性问题之后，本文结果依旧显示户口在教育机会不平等中的解释力度逐渐减小，而父亲受教育年限的解释力度越来越大。第五，通过努力来消解教育机会不平等的可能性逐年增加；然而，努力仍未在高质量教育获得中发挥重要作用。

二、文献综述

（一）教育不平等和教育机会不平等的测度。衡量教育不平等主要包括绝对指标和相对指标两种方式。绝对指标通常使用方差和标准差来测度，代表个体受教育情况于整体受教育情况而言的偏离程度。相对不平等指标主要包括教育基尼系数和教育变异系数等，其中应用最广泛的就是教育基尼系数。与绝对指标相比，教育基尼系数具有良好的统计特性（Thomas等，2001），更能反映出不同地点和不同时间下教育不平等的变化程度。除此之外，广义熵指数也是较好的衡量教育不平等的指标（万广华，2008）。以这些方法为基础，一些学者关注了教育不平等的变化，并发现随着时间推移，全球教育不平等呈现下降趋势（Benaabdelaali等，2012）。同时，已有诸多研究发现我国教育不平等也呈现下降趋势（Thomas等，2001；Yang等，2014；Golley和Kong，2018）。

然而，目前多数文献讨论的是教育结果不平等，即总量上的教育不平等，而忽视了教育不平等中的结构性因素，即教育机会不平等和教育努力不平等。Roemer（1998）通过构建“环境—努力”二元框架分析影响个人成就的因素，并将经济社会中的不平等分为两类。其中，因环境不同导致的不平等定义为“机会不平等”，因努力不同导致的不平等定义为“努力不平等”。明确了机会不平等的定义后，学者们开始关注如何测度机会不平等。Ferreira和Gignoux（2011）依据是否需要识别努力程度，将机会不平等的测度方法划分为“事前法”和“事后法”。事前法将所有个体分为不同组别，每个组别中的个体拥有相同环境。事后法将个体分为不同部分，每个部分中的个体拥有相同努力。由于事后法中的努力程度难以观测和衡量，在研究中应用不多，本文主要关注的是事前法。依据是否需要预先确定回归方程的形式，事前法通常又分为参数法和非参数法。与非参数法相比，参数法并不受限于环境因素的数量，应用范围更广泛（Golley和Kong，2018）。因此，下文主要运用参数法测度教育机会不平等。

随着机会不平等的测度方法日趋成熟，越来越多的文献开始探讨机会不平等的程度及其在一系列经济结果不平等中（例如收入、消费、健康等）所占的比例。然而，有关教育机会不平等测度的研究还相对较少。基于国际学生评估项目（PISA），Ferreira和Gignoux（2010）发现，土耳其15岁学生的阅读、数学和科学分数的机会不平等占总体不平等的27%—33%。国内相关文献中，基于2008年中国综合社会调查数据，靳振忠等（2019）测算了中国高等教育获得的机会不平等程度。张楠等（2020）运用2013—2014年中国教育追踪调查数据关注了基础教育阶段的机会不平等，并发现我国基础教育机会不平等程度高于其他东亚及东南亚国家。江求川和任洁（2020）运用相同数据发现，初中低年级学生的教育结果差距中约有6%—11%由教育机会不平等所致，而高年级学生的教育机会不平等约有8%—22%。

（二）教育不平等的影响因素。在户口层面，一些研究发现无论是从国家范围（Yang等，2014）还是从出生年份层面（Golley和Kong，2018），户口都是造成教育不平等的最大因素。大量研究证实了父母教育和职业等家庭背景与教育不平等之间密切相关（邹薇和马占利，2019）。Golley和Kong（2018）发现，家庭背景指标（父母教育和政治身份）是影响子女教育不平等的重要变量，尤其是对于年轻出生组而言。主要原因在于较高文化资本的家庭中，父母能为子女提供更好的指导和更多的教育资源，使得子女通过继承父母的文化资本水平，从而获得更高的教育成就（李春玲，2010）。在性别方面，虽然有几项研究已经证实了20世纪90年代中期教育成就中存在性别不平等（Zhou等，1998），但是最近的研究发现，这种性别差距已经显著缩小（Wu和Zhang，2010；Yang等，2014；Golley和Kong，2018）。性别对于教育不平等的贡献度随着时间的推移逐渐下降（Golley和Kong，2018），甚至有学者发现，2005年大学入学率的性别差距已经发生逆转（Wu和Zhang，2010）。年龄是影响教育不平等的另一个重要因素。一些研究以5年为一个出生队列估计年龄对教育不平等的影响（Hannum和Wang，2006；巫锡炜，2014；Golley和Kong，2018），发现教育不平等程度随着队列的推移而上升，主要是因为初中升高中阶段的教育机会不平等不断上升；也有研究使用4年、6年和9年的混合出生队列，得出了相似的结论（Yang等，2014）。地区也是解释教育不平等的因素之一（Hannum和Wang，2006；Yang等，2014；Golley和Kong，2018）。基于2000年人口普查数据，Hannum和Wang（2006）探讨了出生省份和教育机会之间的相关性，并认为区域不平等导致了教育分层现象。

纵观以往研究，国内很少有学者讨论教育的机会不平等及其变化趋势。虽然有研究得出教育机会不平等的总体趋势是下降的结论，但忽视了努力在其中的作用，也没有讨论教育质量的不平等变化趋势。而且很少有学者对教育机会不平等进行分解，相应地，目前还没有研究探讨各因素解释教育机会不平等的力度随着时间推移发生何种变化。此外，既往大多数相关研究都没有处理内生性问题，因而在因果推断上存在不足。综上，基于CHIP2002—2018年四轮调查数据，本文测算了近20年教育机会不平等的变化趋势；通过Shapley值分解计算得出不同环境因素在教育机会不平等中发挥的作用；进一步运用工具变量法以及异方差构造的工具变量作为补充，力图克服由于遗漏变量和反向因果关系而造成的内生性问题；同时采用方差分解思路估计了努力因素在多大程度上能够缓解教育机会不平等；并从教育质量层面探讨了接受重点高中或高等教育的机会不平等现象，以期能为下一步实现“有质量的教育公平”目标提供相应的政策启示。

三、数据和方法

（一）数据和变量。本文数据来源于中国家庭收入调查（CHIP）2002年、2007年、2013年和2018年的微观样本。对原始数据进行如下处理：对于CHIP2002而言，1936年之前出生的群体较少，因此保留出生在1936年及之后的样本；本文关注的是已经完成学校教育的群体，因此还限定在1980年及之前出生的样本。相应地，由于这几轮样本的抽样过程和问卷内容非常相似，CHIP2007保留出生于1941—1985年的样本；CHIP2013保留出生于1946—1990年的样本；CHIP2018保留出生于1951—1995年的样本。所有样本最终受教育程度的学业完成情况均为毕业。对于同住样本，分别匹配已婚户主/配偶和同住子女、户主和同住父母、配偶和同住父母。对于不同住样本，分别匹配户主和不同住父母、配偶和不同住父母、已婚户主/配偶和不同住子女。由于四次调查所覆盖的省份不同，在模型中还将控制省份虚拟变量。

通过上文梳理近年来国内外文献可以发现，与不平等有关的研究中常见的环境变量包括个人特征和家庭背景两个方面。考虑到调查问卷中相关变量的可获得性，结合已有研究和文献，本文选取的环境变量包括性别（男=1）、户口（农村=1）、年龄、家庭规模、父亲受教育年限、父亲职业和地区。根据CHIP调查问卷中的题项，本文将教育程度划分为小学及以下、初中、高中（职高/技校/中专）、大专、大学本科、研究生及以上。相应地，受教育年限分别赋值为6、9、12、15、16、19。结合具体职业的性质和工作内容，本文将职业分为农民、机关和事业单位、个体户、专业技术人员、企业职工或工人，以及其他不便分类的工作。此外，地区包括东部、中部和西部。主要变量的描述性统计如表1所示。在考虑本文所用相关变量存在缺失值的情况下，最终回归方程可用样本量分别为2002年27 720个，2007年22 398个，2013年31 879个，2018年35 897个。^②

（二）模型和方法。

1. 教育机会不平等的测度。本文关注的主要问题之一是如何衡量教育机会不平等。基于文献综述，主要遵循Roemer（1998）以及Ferreira和Gignoux（2011）的研究思路，构建如下方程：

$ {y}_{i}=f\left({C}_{i},{E}_{i},{u}_{i}\right) $

(1)

其中， $ {y}_{i} $ 代表个体受教育年限； $ {C}_{i} $ 是环境变量，包括性别、年龄、家庭规模、户口、父亲受教育年限、^③父亲职业和地区等； $ {E}_{i} $ 是努力变量； $ {u}_{i} $ 为影响受教育年限的其他不可测因素，例如运气等。一般认定环境变量 $ {C}_{i} $ 是外生的，而个体努力程度 $ {E}_{i} $ 可能会受到包括环境在内的一系列因素的影响。这意味着上式可以更准确地表示为：

$ {y}_{i}=f\left[{C}_{i},{E}_{i}\left({C}_{i},{v}_{i}\right),{u}_{i}\right] $

(2)

本文主要运用的是参数法，基于Ferreira和Gignoux（2011）的研究，将（2）式进一步表示为：

$ {y}_{i}=\beta {C}_{i}+{\varepsilon }_{i} $

(3)

通过上述回归方程估计出参数后，参照Juárez和Soloaga（2014）测度机会不平等的直接法来衡量教育机会不平等。首先，需要构造一个反事实教育分布。具体而言，由回归方程估计出的系数和真实环境变量值，得出个体的预测教育年限，这意味着处于相同环境的个体可以获得相同结果，相当于消除了组内差异，只存在组间差异，也就是环境带来的作用（机会不平等）。运用直接法构造的反事实教育分布可以表示为：

$ \widehat{{y}_{i}}={\widehat{\beta }C}_{i} $

(4)

基于式（4），需要选择不平等指数进一步计算教育机会不平等程度。本文选用文献中常用的广义熵指数（GE）进行测度。广义熵指数的表达式如下：

其中， $ n $ 为样本数， $ {y}_{i} $ 为个体 $ i $ 的受教育年限， $ \stackrel{-}{y} $ 为样本平均受教育年限。 $ \alpha $ 代表给予不同教育分布样本的教育差距的权重， $ \alpha =1 $ 代表给予不同教育差距以相同权重， $ GE\left(1\right) $ 被称为泰尔指数； $ \alpha =0 $ 代表给予低水平教育差距以较大权重， $ GE\left(0\right) $ 被称为平均对数离差； $ \alpha =2 $ 代表给予高水平教育差距以较大权重， $ GE\left(2\right) $ 被称为变异系数平方的一半。

$ GE\left(0\right) $ 和 $ GE\left(1\right) $ 的计算方式都涉及对数值，Golley和Kong（2018）认为 $ GE\left(2\right) $ 是衡量教育机会不平等的最佳选择。下文主要以 $ GE\left(2\right) $ 作为不平等指数，预测教育年限 $ \widehat{{y}_{i}} $ 的 $ GE\left(2\right) $ 指数可以表示为：

$ {IOA}_{D}=I\left(\left\{\widehat{{y}_{i}}\right\}\right) $

(6)

上式可以理解为教育机会不平等的绝对程度。相应地，教育机会不平等的相对程度可以通过计算教育机会不平等占教育不平等的比例而得：

$ {IOR}_{D}=\frac{I\left(\left\{\widehat{{y}_{i}}\right\}\right)}{I\left(\left\{{y}_{i}\right\}\right)} $

(7)

其中， $ I\left(\left\{{y}_{i}\right\}\right) $ 为个体真实受教育年限的 $ GE\left(2\right) $ 指数。以上即为直接法的主要步骤。

2. 教育机会不平等的分解。本文关注的第二个主要问题是不同环境变量在影响教育机会不平等中的贡献程度如何。为了测算各个环境变量对于教育机会不平等的解释力度，本文将采用Shorrocks（2013）提出的基于回归方程的Shapley值分解方法。首先，假定回归方程中有 $ k $ 个环境变量，逐步剔除每个环境变量。由于每个变量都有“进入”或“退出”两种选择，因此共有 $ {2}^{k} $ 个排列组合。其次，分别计算包含与不包含某个环境变量的教育机会不平等程度的差值，由于其他环境变量出现的顺序不同会产生不同结果，因此，针对该环境变量而言能得到 $ {2}^{k-1} $ 个结果。最后，对所有结果取均值，就能得出该环境变量的贡献度。

具体而言，基于式（3）和式（4）可以得出预测受教育年限 $ \widehat{y} $ 与其所对应的由所有环境变量 $ C $ 决定的教育机会不平等程度，写作 $ {IO}_{\widehat{y}} $ 。为了考察某环境变量 $ {c}_{m} $ 对教育机会不平等的贡献度，先将 $ {c}_{m} $ 剔除，再次估计教育机会不平等程度，写作 $ {IO}_{\widehat{{y}_{m}}} $ 。两次测算出的教育机会不平等的差值 $ {IO}_{\widehat{y}}-{IO}_{\widehat{{y}_{m}}} $ 即为 $ {c}_{m} $ 对于教育机会不平等的第一轮边际贡献。如果在第一轮剔除另一个环境变量 $ {c}_{n} $ ，此时 $ \widehat{{y}_{n}} $ 对应教育机会不平等程度为 $ {IO}_{\widehat{{y}_{n}}} $ ，而在第二轮再次剔除 $ {c}_{m} $ ，这种情形下，同时剔除 $ {c}_{m} $ 和 $ {c}_{n} $ 之后 $ \widehat{{y}_{mn}} $ 对应的教育机会不平等程度为 $ {IO}_{\widehat{{y}_{mn}}} $ 。两次测算出的教育机会不平等的差值 $ {IO}_{\widehat{{y}_{n}}}-{IO}_{\widehat{{y}_{mn}}} $ 即为 $ {c}_{m} $ 对于教育机会不平等的第二轮边际贡献。依此类推，环境变量 $ {c}_{m} $ 被剔除的所有顺序带来的 $ k $ 轮边际贡献的均值即为其对教育机会不平等的贡献度。

四、实证分析

（一）教育不平等的变化趋势。本节首先关注的是2002—2018年教育结果不平等的现状和演变。为了全面考察这段时期教育不平等的变化趋势，参照已有研究设定（万广华，2008；Yang等，2014），本节选用多种不平等指标测度教育的不平等程度，包括基尼系数、变异系数、泰尔指数和平均对数离差等。其中，基尼系数被广泛用于研究收入不平等，也可以用来衡量教育不平等，因为教育基尼系数可以有效地表征教育分配的变化（Yang等，2014）。

如表1所示，教育不平等基本是逐年降低的，表现为各个不平等指标几乎都呈现下降趋势。其中，基尼系数从0.236下降到0.177，泰尔指数从0.081下降到0.046，平均对数离差从0.095下降到0.047，变异系数平方的一半从0.089下降到0.053。对比Benaabdelaali等（2012）的研究结果可知，中国的教育不平等程度较低，表现为我国教育基尼系数低于同时期全球其他国家、发展中国家和东亚国家的教育基尼系数。^④这意味着随着我国义务教育的普及和高等教育的扩招，个体的平均受教育年限不断延长，特别是对于弱势群体而言，增加了他们接受更多教育的概率，整体层面的国民素质得到提高，教育不平等呈现下降趋势。进一步观察广义熵指数的估计结果，2002年和2007年 $ GE\left(0\right) $ 的数值最大，而2013年和2018年 $ GE\left(2\right) $ 的数值最大；且 $ GE\left(0\right) $ 从2002年到2018年的降低速度更快。由于 $ GE\left(0\right) $ 赋予较低水平的教育差距以较大权重，相反， $ GE\left(2\right) $ 赋予较高水平的教育差距以较大权重。这意味着2002—2018年，教育不平等从主要集中于低教育层级群体转为高教育层级群体；在较低教育层级的群体中，不平等现象缓解的程度更大。

（二）教育机会不平等的变化趋势−数量角度。为了进一步分析教育不平等中的机会不平等，根据参数法的思路，本节将从教育数量的角度探讨我国教育机会不平等的现状及变化趋势。表2基于式（3）首先汇报了2002—2018年各环境因素影响受教育年限的基准回归结果，各年份变量系数的符号和显著性一致。相较于女性或农村群体，男性或城市群体的受教育年限更长；表现为各调查年份性别因素（以男性为基准）的系数值都正向显著，而户口因素（以农村为基准）的系数值都负向显著。年龄对个体受教育年限的影响效应显著为负，与其他因素相比，其系数绝对值最低。各调查年份中家庭规模对个体受教育年限的影响效应呈负向显著，而父亲受教育年限的系数值都正向显著。相较于东部，中、西部地区对各年份受教育年限的影响效应显著为负。

根据上文各环境因素影响受教育年限的基准回归结果以及第三部分介绍的估计方法，本节将以此为基础计算教育机会的不平等程度。表3展现了2002—2018年教育机会不平等变化趋势及Shapley值分解结果。首先，与教育不平等的变化趋势相似，机会不平等系数也基本呈现下降趋势。其中，教育机会不平等相对系数在2018年降低为0.352。其次，各年份户口和父亲受教育年限构成了教育机会不平等的主要来源。其中，户口对教育机会不平等的贡献最大，但是贡献度逐年降低，具体表现为从2002年的44.11%减少到2018年的30.40%。父亲受教育年限对于教育机会不平等的贡献也非常大，且贡献度从2002年的15.86%逐年升高，并于2018年超过户口的贡献度，达到32.09%，成为贡献度最大的因素。父亲职业作为家庭背景的另一个重要变量，其贡献度则从2002年的18.79%降低到2018年的8.79%。上述结论拓展了Golley和Kong（2018）运用2010年和2012年中国家庭追踪调查来测度教育机会不平等的研究。此项研究测算得出户口是教育机会不平等的最大贡献因素，而本文进一步发现，2018年父亲受教育年限对教育机会不平等的解释力度已经超过户口。原因一方面可能来自于户籍制度改革的推进，另一方面可能在于教育扩招等政府干预政策虽然降低了户籍制度和父亲职业等衡量家庭社会经济地位的因素对教育机会不平等产生的影响，但是难以阻断教育的代际传递，表现为高学历父母倾向于为子女争取更多更好的学习资源。事实上，诸多有关收入机会不平等的研究（史新杰等，2018；李莹和吕光明，2019）也得出了类似结论。这表明教育机会不平等有可能是上述因素作用于收入机会不平等的重要传导机制。

此外，性别对于教育机会不平等的贡献基本呈现逐年下降的趋势，表现为从2002年的5.46%下降到2018年的0.99%，成为贡献最小的因素。即，近年来性别并不是教育机会不平等的主要来源，这与靳振忠等（2019）的研究结果相似。然而，这与Golley等（2019）有关收入机会不平等的研究得出的结论相反，其发现性别是造成中国收入机会不平等的最大因素，占绝对收入机会不平等的28%。这一对比富有意义，虽然不同性别对教育机会不平等的解释力度很低，但其却是收入机会不平等的重要来源。与2002年相比，地区因素对于教育机会不平等的贡献度在2018年有所上升。这与靳振忠等（2019）和张楠等（2020）的研究结论一致，意味着区域间的发展差距使得各类教育资源存在数量和质量上的差异，最终将导致教育机会的差距。

（三）教育机会不平等的变化趋势−质量角度。上文主要是从教育数量的角度探讨了我国教育机会不平等的现状及变化趋势，本节将探讨我国教育质量机会不平等程度的演变。参照已有研究（唐俊超，2015），基于CHIP问卷设计，本文以题项“如果文化程度是高中或高中以上，那么高中毕业的学校类型为重点中学”衡量重点高中，以题项“如果有大学以上学历（包括大学专科或大学本科），那么大学毕业院校的类型为985/211院校”衡量重点大学。^⑤需要说明的是，2007年CHIP调查没有询问和重点学校有关的信息，因此下文不做讨论。另外，由于2002年和2013年CHIP调查中仅有城镇问卷询问了重点大学的信息，为了使得最终结果具有可比性，下文主要关注的是城镇样本中上重点大学的机会不平等的年份变化趋势。

表4是基于Probit模型计算得出的各年份教育质量不平等程度及环境变量的Shapley值分解结果。^⑥首先，与2002年相比，近年来上重点高中的整体不平等程度有所下降，表现为修正后的相异性指数^⑦从0.178下降到0.137；上重点大学的城镇不平等程度略有提升，相异性指数从0.060上升到0.073，变化幅度较小。其次，本文重点关注的两个变量中，户口因素在接受重点高中教育机会不平等中的贡献度呈现下降趋势。与之相反，2018年父亲受教育年限对于高质量教育机会不平等的贡献度与2002年相比都更大。以重点大学为例，2002—2018年父亲受教育年限的贡献度从5.1%升高到42.43%，成为贡献度最大的因素，而且这一数值高于上文从教育数量视角而得出的32.09%。此外，父亲职业对于城镇样本上重点大学机会不平等的解释力度也呈现逐年上升趋势，2018年的贡献度仅次于父亲受教育年限。上述结果表明，对于城镇群体而言，近年来家庭背景因素在解释重点大学教育机会不平等中占据主要地位。依据最大化维持不平等（MMI）和有效维持不平等（EMI）假设可知，只有在优势地位群体接受高等教育饱和的情况下才会惠及劣势群体，此时高等教育在数量上的机会不平等能够有所下降。随后，家庭背景因素（例如父亲受教育年限）将进一步影响子女是否能上重点大学，即优势地位群体依旧垄断高质量的教育机会（李春玲，2010）。

（四）内生性检验。值得注意的是，式（3）在设定的过程中可能会存在内生性问题：一方面，子女的受教育年限存在向上溢出效应（Frankenberg等，2002；De Neve和Kawachi，2017），^⑧由于父母可能会根据子女的人力资本水平来调整自身的知识水平，因此父母受教育年限和子女受教育年限之间存在反向因果关系；另一方面，还存在一些不可观测的因素同时影响父代和子代的教育水平，例如基因或者家庭经历的冲击事件，所以有可能构成遗漏变量。考虑到内生性问题的存在且会对回归系数造成影响，本节将采用工具变量法来解决上述难题。

参照Gayle等（2018）和Uddin（2019）等的研究设定，本节主要采用两个方面的工具变量，^⑨选取思路如下：第一，父亲受教育年限可能与其年龄相关。例如，已有学者研究发现，接受高等教育客观上会推迟初婚年龄，由于男性一般会为步入婚姻承担比较多的经济压力，因此大学毕业后需要具备一定的财富积累才能结婚（朱州和赵国昌，2022）。这种现象可能进一步导致生育子女时的年龄也会偏大，即父亲在子女出生时所处的年龄与其自身的受教育年限具有相关性。但是，父亲的年龄很难对子女受教育年限带来直接效应（Gayle等，2018），因此，本节将使用子女出生时的父亲年龄作为工具变量。第二，父亲的受教育水平与其所在省份的同龄人的教育水平是相关的，因为相同区域和年龄的个体面临着相似的教育政策或者分享着相似的教育资源，而这不会直接作用于本家庭子女的教育程度（Uddin，2019），所以本节还将按照年龄和省份划分的平均父亲受教育年限作为工具变量。

表5展现了环境因素影响受教育年限的2SLS回归结果。如表所示，首先，Hausman检验结果显示拒绝原假设，说明存在内生性，需要进行工具变量法回归。运用Cragg-Donald Wald F统计量和Kleibergen-Paap rk Wald F 统计量进行弱工具变量的识别检验，观察发现两项统计量都大于Stock和Yogo（2005）所列出的10%水平下的临界值，拒绝了存在弱工具变量的原假设。其次，各调查年份中同一省份的平均父亲受教育年限的系数值显著为正，而子女出生时的父亲年龄与父亲受教育年限之间的相关性由负向显著转为正向显著。本文猜测出现这种逆转现象的原因在于随着大学教育的扩招，初婚年龄会有所推迟。事实上，已有研究发现高等教育对男性的初婚推迟效应大于女性（朱州和赵国昌，2022）。相应地，他们的生育年龄可能也会顺延。因此，子女出生时的父亲年龄与父亲受教育年限之间呈现正相关。

基于上述回归结果，表6列（1）—列（4）展现了各环境因素影响教育机会不平等的 Shapley值分解。与此同时，本节还将使用Lewbel（2012）的异方差工具变量法作为上述结果的补充，即通过异方差来构造工具变量。^⑩表6列（5）—列（8）进一步展现了上文外生工具变量和异方差构造的工具变量同时加入回归方程后的Shapley值分解。总体而言，上述基于2SLS回归的Shapley值分解结果与表3基于OLS回归的结果基本一致。克服内生性问题之后，在其他条件不变的情况下，户口对教育机会不平等的解释力度逐渐减小，而父亲受教育年限的解释力度逐渐增大。此外，附录表A2^⑪还展现了上文外生工具变量和异方差构造的工具变量同时加入回归方程的情况下各环境因素影响个体上重点高中（大学）的Shapley值分解结果，限于篇幅未在正文中列出。结果同样表明，近年来代际间的教育传递效应在高质量教育机会不平等中有越来越大的解释力度。

五、稳健性检验

为确保上述结果的可靠性，将从三方面进行稳健性检验：首先，上文主要根据Golley和Kong（2018）的研究，基于变异系数平方的一半 $ GE\left(2\right) $ 测度教育机会不平等。本节将参照Yang等（2014）的研究，以个体受教育年限的对数作为被解释变量，基于平均对数离差 $ GE\left(0\right) $ 测度机会不平等。表7显示，近20年教育机会不平等系数呈现逐年下降趋势。Shapley值分解结果表明，户口对教育机会不平等的贡献度逐年降低，而父亲受教育年限的贡献度逐年上升，且在2018年成为解释力度最大的因素，高达31.80%。此外，由于CHIP的调查问卷中并没有直接给出家庭规模变量，上文通过匹配数据获得家庭总人口数来衡量家庭规模。然而，此变量可能并不是教育获得的前定变量。因此，本节删除家庭规模变量之后重新回归，观察表7发现，户口和父亲受教育年限依旧是贡献较大的两个环境变量。随着时间推移，户口对教育机会不平等的解释力度逐渐减小，而父亲受教育年限的解释力度逐渐增大。上述结果都验证了原文结论的稳定性。

其次，上文已经初步得出教育机会不平等呈现逐年下降趋势。由于CHIP调查的四轮数据覆盖的省份并不相同，基于罗楚亮和刘晓霞（2018）的研究设定，本节选取了四轮调查中出现过2次及以上的省级地区，最终包含16个省级地区。^⑫由于城镇住户中可能涵盖来自农村地区、通过接受教育而获得城镇户口的群体，如果不考虑从农村到城市居住状态的变化，就会产生严重的选择偏差。因此，本节还参照Knight等（2011）的研究，将城镇样本中有过“农转非”经历的群体统一划入农村样本。表8汇报了Shapley值分解结果。^⑬与2002年相比，2018年教育机会不平等有所下降。其中，户口因素对于教育机会不平等的贡献度减小；相反，父亲受教育程度的贡献度增大。

最后，上文表明随着时间推移，父亲受教育年限对于教育机会不平等的贡献度越来越大。本节将关注母亲受教育年限在教育机会不平等中的作用。表8展现了将父亲受教育年限替换为母亲受教育年限的Shapley值分解结果。^⑭随着时间推移，母亲受教育年限在教育机会不平等中的贡献度也呈现逐渐增大的趋势。上述结果与原文结论基本一致，验证了本文结果的稳定性。

六、拓展分析

Roemer（1998）的“环境—努力”二元分析框架认为，无法控制的环境变量和可以控制的努力变量共同决定了个体的受教育年限，而回归方程（3）省略了所有努力变量，将其简单地纳入残差项中。如果努力变量和环境变量相关，则可能存在因遗漏努力变量而造成的内生性问题。因此，本节将在式（3）中加入努力变量，进一步考察环境和努力对于教育不平等的解释力度及变化趋势。

参照Roemer（1998）、Checchi和Peragine（2010）、邹薇和马占利（2019）等学者的研究思路，本文设定努力程度E_i =（个体受教育年限−个体同龄人受教育年限均值）−（父亲受教育年限−父亲同龄人受教育年限均值）。其中，右边第一项括号内代表个体与同龄人相比获得的额外教育成就，第二项括号内代表家庭背景带来的额外教育资源，两项相减代表个体通过努力而获得的额外教育成就，由此计算得出个体的努力程度，将高于样本均值设定为高努力群体，低于样本均值设定为低努力群体。

基于附录表A4^⑮的回归结果，参照已有研究（史新杰等，2018；张楠等，2020）的设定，本文运用方差分解法得到努力和环境对教育不平等的贡献度。^⑯表9展现了2002—2018年努力与环境贡献度的变化趋势。由于努力因素只包含一个变量，因此环境因素的相对贡献度普遍更高。观察发现，努力因素的贡献度在2018年达到26.48%，高于2002年的13.45%。由环境变量造成的机会不平等是减小的，而通过努力来消解教育机会不平等的可能性越来越大。

进一步地，表10汇报了努力和环境变量在接受重点高中或重点大学（教育质量）不平等中的贡献度及变化趋势。为了便于比较，本节同时展现了高中教育和高等教育阶段（教育数量）不平等的相应结果。如表所示，与教育获得数量相比，努力在教育获得质量尤其是上重点大学不平等中的贡献度很小，2002年仅为0.11%，即使2018年提高至11.42%，仍旧远低于同年份在高等教育阶段不平等中的贡献度30.85%。也就是说，个体的努力程度很难在高质量教育获得中发挥重要作用，正如表4显示，以父亲受教育年限为代表的家庭背景变量仍然是子代接受高质量教育机会的关键因素（靳振忠等，2019）。这一结论再次表明，随着时间推移，教育扩张政策极大提高了个体努力在高等教育获得数量中的作用，即接受高等教育的机会不平等有所下降；然而，现阶段教育扩张并没有显著提升个体努力在高等教育获得质量中的作用。

七、结论与启示

基于中国家庭收入调查2002—2018年四轮调查数据，本文测算了中国教育机会不平等系数及其变化趋势；采用Shapley值分解得出各个环境变量对教育机会不平等的贡献度；同时将努力变量纳入分析框架，运用方差分解方法估计了努力在多大程度上可以缓解教育不平等。本文主要结论如下：第一，无论采取何种不平等的测度指标，近20年中国的教育不平等呈现下降趋势；而教育机会不平等也在2018年呈现较大降幅。第二，基于回归分析的Shapley值分解结果表明，户口和父亲受教育年限是贡献较大的两个环境变量。随着时间推移，户口对教育机会不平等的解释力度逐渐减小，而父亲受教育年限的解释力度逐渐增大。第三，从教育质量的角度出发，近年来家庭背景因素在解释重点大学教育机会不平等中占据主要地位。第四，采用工具变量法以及异方差工具变量法克服内生性问题之后，本文结果依旧显示户口对教育机会不平等的解释力度逐渐减小，而父亲受教育年限的解释力度逐渐增大。第五，纳入努力变量的结果表明，努力的贡献度都在2018年更高，即通过努力来消解教育机会不平等的可能性越来越大。然而，努力仍未在高质量教育获得中发挥重要作用。

本文有如下启示：首先，随着时间推移户口因素在教育获得中的影响效应逐渐减小，因此持续破除城乡二元结构有可能是减少中国教育机会不平等的重要途径。具体到相应的措施上，可以建立农户子女上大学的专项扶持计划并将其作为一项长期工作坚持下去，还可以通过免除借读费和赞助费，放宽随迁子女入学限制等方式，保障农民工等弱势群体子女在流入地享受平等的教育机会。其次，本文发现父亲受教育年限对教育机会不平等的解释力度逐渐增大，一定程度上说明代际持续性的影响效应越来越大。除了先天性的遗传因素之外，很有可能是受教育程度越高的父母掌握了更科学的教育理念，而近年来诸多研究表明父母的养育模式对子女早期的认知能力和非认知能力以及未来的教育获得能产生巨大的影响。因此，提高家庭教育有可能促进社会阶层的代际流动性，从而改善教育机会的不平等现象。最后，继续加大教育资源投入，为弱势群体提供更多的公共教育资源。通过完善教育政策制定和机制设计的方式，例如逐步延长义务教育年限来提高国民整体素质。事实上，目前我国的内蒙古自治区已经全面实施了十二年义务教育。此外，推动教育扩张政策的同时还需要提高教育质量，从供给层面扩大优质教育的数量，从而满足人民日益增长的对于优质教育的需求，避免因家庭社会经济地位造成的高质量教育获得的机会不平等。

　　* 感谢中国收入分配研究院提供的中国家庭收入调查（CHIP）数据，同时也感谢匿名审稿专家和编辑提出的宝贵意见。

① 此处感谢匿名审稿专家的提醒以及提供的相关参考文献。

② 限于篇幅，主要变量的描述性分析未列出，详见工作论文。

③ 参照多数研究的设定（李春玲，2010；史新杰等，2018；李莹和吕光明，2019），本文实证分析中主要以父亲受教育年限作为影响子女受教育年限的重要变量之一。下文稳健性检验还将考察母亲受教育年限在教育机会不平等中发挥的作用。

④ Benaabdelaali等（2012）计算得出2010年发达国家（24个）教育基尼系数为0.19；其他国家（146个）、发展中国家（122个）、东亚国家（19个）的教育基尼系数分别为0.34、0.36、0.27。

⑤ CHIP调查中，样本若有多个大学学历，以第一次获得的大学学历为准。

⑥ 附录表A1汇报了2002—2018年各环境变量对高质量教育获得的Probit回归结果，详见工作论文。

⑦ 由于上文的受教育年限是连续变量，而本节使用的教育质量是离散变量。因此，将参照Chávez-Juárez和Soloaga（2015）提出的修正相异性指数测算质量层面的教育机会不平等。

⑧ 此处感谢匿名审稿专家提出的宝贵建议以及相关参考文献。

⑨ 现有的多数研究通常将“学制改革”“基础教育扩张”等教育政策冲击作为父母教育的工具变量（李云森和齐豪，2011；林莞娟和张戈，2015；杨娟和高曼，2015）。本文在实证分析过程中曾经参照林莞娟和张戈（2015）的研究，尝试使用1978—1982年中小学学制改革作为父亲受教育年限的工具变量。由于政府事先确定学制改革的实施时间且改革所处时代的户籍制度非常严格，因此，可以假定学制改革制度对于父亲受教育年限的影响具有外生性。然而，由于CHIP2002年和2007年的调查年份较早，实证分析过程中运用此工具变量会使得样本量缺失严重，尤其是当本文想要探讨克服内生性问题之后的教育质量的机会不平等，即被解释变量为上重点大学（高中）时，可用的样本量无法充分体现结果的有效性和说服力。所以正文不再对此进行讨论。

⑩ 详见本文工作论文。

⑪ 详见本文的工作论文。

⑫ 包括北京、河北、山西、辽宁、江苏、浙江、安徽、山东、河南、湖北、湖南、广东、重庆、四川、云南、甘肃。

⑬ 附录表A3分别展现了不同限定条件下各调查年份的OLS回归结果，详见本文的工作论文。

⑭ 本文在实证分析过程中还进行了同时考虑父亲和母亲受教育年限的Shapley值分解，所得结果与原文结论基本一致，限于篇幅未列出。

⑮ 详见本文的工作论文。

⑯ 本节主要讨论的是Romer情境下努力与环境对教育不平等的贡献度，即环境对努力回归的残差项 $ {v}_{i} $ 可以理解为不考虑环境变量影响的“纯努力”，以此作为努力变量纳入教育估计函数中。除此之外，本文在实证分析过程中也讨论了Barry情境下努力与环境对教育不平等的贡献度，即使用努力的原值来衡量努力变量。两者的结果基本一致，限于篇幅，不再详细讨论。