一、引　言

长期稳定经济增长的核心是全要素生产率的提高，而全要素生产率提高的关键因素是技术进步和人力资本增长。技术进步的关键因素是技术投入，人力资本增长的关键因素是教育投入，而教育投入的核心内容则是公共教育投入，因此技术投入和公共教育投入决定了一个经济体的长期经济增长趋势。一个经济体的技术投入和公共教育投入取决于多种因素，但是对于少子化进程问题，学术界较少关注。

从生育率的客观趋势来看，我国的人口出生率与总和生育率呈不断下降的态势。自20世纪90年代以后，我国的总和生育率就开始进入下降通道，第七次人口普查显示，2020年总和生育率已降低至1.3。虽然自2014年以来，我国不断放开生育限制，但效果有限，2021的人口出生率更是下降至7.52‰，创1949年以来的历史新低。从居民的主观生育意愿来看，我国育龄妇女的生育意愿不断下降。从影响生育意愿的经济条件来看，我国居民的生育成本可能过高，短期内难以有效降低。根据《中国生育成本报告2022》的统计，中国居民把一个孩子抚养到年满18岁所花的成本为人均GDP的6.9倍，而美国是4.11倍，日本是4.26倍。从影响生育率的人口因素来看，我国初婚登记人口数不断下降，而初婚登记人口数与生育率密切相关。从客观趋势、主观意愿、抚育成本、人口条件来看，我国生育率的下降趋势可能难以逆转。因此，如何在给定的生育率水平下合理安排技术投资和公共教育投入以实现经济持续稳定增长才是政府更应当考虑的问题，而这个问题从因果逻辑的角度可表述为：生育率如何影响均衡的技术投资和公共教育投入？

从理论上，生育率对技术投资和公共教育投入存在重要的影响。从政府的中央计划者角色来看，当少子化进程加速、生育率降低时，下期的劳动力数量就会减少，如果不采取措施，下期产出将会下降，从而经济增长放缓。因此为维持经济的可持续增长，政府应该改革经济增长模式。从长期经济增长的角度，最有效的方式是提高全要素生产率，而全要素生产率的核心在于提高劳动者素质和加快技术进步。因此政府应当增加公共教育投入来提高子代的人力资本水平，并且增加技术投资来提高技术进步率。但在一定的预算约束下，究竟是增加技术投资还是公共教育投入抑或兼而有之，则值得商榷。这个问题从理论角度可表述为：在一个一般均衡经济系统中，生育率如何影响技术投资和教育投入？学术界直接研究生育率对技术投资影响的文献十分有限，但在一定程度上，生育率对技术投资影响问题可转化为劳动力与技术进步的相关性问题，Susskind（2017）、Acemoglu和Restrepo（2020）、Chiacchio等（2018）研究发现随着技术投资的增加和技术进步的加快，技术投资可以替代劳动力。学术界研究生育率对公共教育投入影响的文献亦十分有限，但在一定程度上，生育率对公共教育投入影响问题可表述为生育率与教育投入的相关性问题，部分文献对此进行了研究：Becker和Lewis（1973）认为生育率与教育投入的相关性取决于二者的收入弹性。Barro和Becker（1989）分析了生育率与教育投入的替代条件。陈昆亭（2008）认为生育率的增加对长期人力资本的累积具有正向影响，即生育率与教育投入正相关。刘小鸽和司海平（2017）认为家庭子代的规模减小会使子代获得的教育投入增加，即生育率与教育投入负相关。Fan和Zhang（2013）、贾俊雪等（2021）认为，生育率与子女教育投入的关系取决于父母的人力资本水平。Strulik等（2013），Galor和Weil（2000）在统一的框架内研究生育率与技术投资和教育投入的关系。总体上，现有文献在研究生育率与技术投资、公共教育投入的关系方面存在如下不足：第一，研究生育率对技术投资影响的文献十分有限；第二，在有限的研究生育率与教育投入关系的文献中，极少有文献区分私人抚育成本与公共教育投入；第三，极少有文献在统一的框架下，以生育率为自变量同时研究其对技术投资和公共教育投入的影响；第四，技术投资与公共教育投入来源于税收，但讨论少子化如何影响技术投资与公共教育投入税率调整的文献非常有限。可以预期，在不同的社会生产条件下，生育率对均衡技术投资和公共教育投入的影响并不相同，从而应当增加技术投资还是公共教育投入的均衡结果也不一样。在我国当前的社会生产条件与少子化背景下，生育率水平如何影响均衡技术投资和公共教育投入值得更深入地研究。

基于对技术投资和公共教育投入的影响，生育率对内生经济增长具有重要影响。在一个一般均衡的经济系统中，生育率对技术投资和公共教育投入具有重要影响，从而对技术进步和人力资本累积具有重要影响，这种影响会传导至工资水平、总资本收益率，并最终影响总产出、劳均产出和人均产出。生育率对内生经济增长也具有重要影响。不同的工资水平、总资本收益率、总产出、劳均产出、人均产出组合代表了不同的内生经济增长模式，如何基于给定的生育率水平，分析不同社会生产条件下内生经济增长的模式具有重要意义。此外，基于对技术投资和公共教育投入的影响，生育率对居民福利也具有重要影响。在代际交叠的视角下，代表性消费者的福利水平由年轻时期的消费、老年时期的消费和子代的人力资本构成，生育率直接影响着人力资本累积，年轻时期和老年时期的消费受到内生经济增长模式的影响，而内生经济增长模式受到生育率的影响，因此生育率对居民福利具有重要影响。学术界研究少子化或生育率对居民福利水平影响的文献较少，研究生育率对长期经济增长影响的文献比较丰富，但以研究生育率对经济增长的直接影响为主，并且分歧较大，就结论而言大致可分为三种：少子化促进经济增长，少子化阻碍经济增长和少子化对经济增长的影响取决于当期的时代条件。Li和Zhang（2007）、汪伟（2010）认为生育率下降能够促进经济增长。Liao（2013）认为少子化可以促进经济增长。而郭凯明等（2013）、汪伟（2017）认为少子化对经济增长的影响取决于时代条件。Becker 等（1999）、刘永平和陆铭（2008）以教育投入和技术进步为中介变量讨论了生育率对经济的影响。总体上，现有文献在研究生育率与社会生产及居民福利的关系方面存在如下不足：第一，在研究生育率对经济增长影响的诸多文献中，以技术投资和公共教育投入为中介变量的文献比较有限；第二，研究少子化对居民福利影响的文献十分有限。我国的少子化进程不断加速，这对我国的可持续发展提出了挑战。在这样的时代条件下，讨论少子化进程对技术投入和公共教育投入的影响，进而分析少子化对长期经济增长和居民福利的影响具有重要的现实意义。

本文的主要结论为：少子化进程的加速会推动技术投资的提高，其影响的大小取决于抚育成本占总财富的比例，如果该比例高于50%，技术投资对生育率变化表现为富有弹性，否则表现为缺乏弹性。少子化进程的加速也会推动公共教育投入的提高，而公共教育投入对生育率变化始终表现为富有弹性。少子化能否通过推动技术投资和公共教育投入的提高而推动经济持续增长取决于抚育成本占总财富的比例、经济状况和生产方式。在当前我国的生产模式下，若抚育成本占总财富的比例低于45%，则可以推动经济持续增长，反之会减缓经济增长；若该比例低于20.53%，则可以提高居民福利水平，反之可能降低居民福利水平。在当前的生育率水平下，可能不存在能够同时实现居民福利持续上升以及经济可持续增长的生育率区间，生育率的轻微上升可以促进经济的持续增长和人均产出的提高，但会降低代表性消费者的终生效用水平。因此，在当前的生产模式下，政府应采取可控的生育刺激政策以轻微地提高生育率，并持续优化养老保障体系以增加代际间的联系，同时优化产业结构、转变教育模式、优化R&D研发模式以逐渐转变社会生产模式。

本文的贡献可归纳如下：第一，通过建立统一的模型，分析了生育率对技术投资与公共教育投入的影响以及少子化促进技术投资与公共教育投入增长的条件；第二，研究了政府作为技术基础设施投资人角色下，针对少子化问题进行税率调整的条件；第三，以技术投资与公共教育投入为中介，分析了生育率对内生经济增长各因素的影响以及少子化促进工资、总资本收益率、产出持续增长的条件；第四，以技术投资与公共教育投入为中介，分析了生育率对居民福利的影响以及少子化促进居民福利上升的条件。本文为研究在新时代人口结构状态下，少子化进程对技术投资和公共教育投入的影响路径提供了理论依据，为调节技术投资和公共教育投入的中介效应及制定合理生育率目标提供了模型支撑。

本文余下的文章结构安排如下：第二节为模型构建，构建一个包含内生教育投入和技术投资的一般OLG模型；第三节为均衡决策分析，对模型进行求解与均衡解的分析；第四节为数值模拟，对相关结论进行检验与进一步分析；最后给出结论与对应政策建议。

二、模型构建

（一）基本假设

代表性消费者的一生分为三期，即少年期、中年期和老年期，在少年期接受抚育和教育，中年期工作，老年期退休。代表性消费者在少年期通过接受抚育和教育累积人力资本，人力资本累积在中年期可提高其劳动效率进而提高全社会的劳动生产率。代表性消费者在中年期无弹性地提供一单位劳动，劳动分为技术生产性劳动和物质生产性劳动两种。代表性消费者在少年期和中年期不会死亡，在老年期面临死亡风险，其没有留存遗产的动机，但会因死亡风险而被动留存遗产。代表性消费者是代际利他主义者，关心子代的质量即人力资本，人力资本由抚育成本和公共教育投入共同决定，其中抚育成本和子代的数量均外生决定。代表性消费者父代的数量记为 $ {n}_{t-1} $ ，子代的数量记为 $ {n}_{t+1} $ ，将代表性消费者的数量标准化为1。社会中存在技术生产部门和物质生产部门，技术生产部门利用技术投资和劳动人口中的研究与试验发展人员提供的劳动力推动技术进步，物质生产部门需利用技术进步、储蓄转化的资本和劳动人口中的非研究与试验发展人员提供的劳动力进行实际产品与服务的生产。政府向居民征税以用于技术投资和公共教育投入，税率由政府基于代表性消费者效用最大化原则确定，征得税收完全用于技术投资和公共教育投入。

（二）代表性消费者

1. 效用函数

代表性消费者终身效用由中年期的消费、老年期的消费、子代的人力资本三部分构成，代表性消费者的终身效用函数为：

$ {U}_{t}=\mathrm{ln}{c}_{y,t}+\beta {p}_{t+1}\mathrm{ln}{c}_{o,t+1}+\upsilon \mathrm{ln}{h}_{t+1} $

(1)

其中， ${c}_{y,t}$ 为代表性消费者中年期的消费， $ \beta $ 为时间偏好因子，衡量代表性消费者对未来消费的主观折旧， $ {p}_{t+1} $ 为老年期的预期生存概率， ${c}_{o,t+1}$ 为老年期的消费， $ \upsilon $ 为子代质量偏好参数， $ {h}_{t+1} $ 为子代的人力资本。

2. 少年期

在少年期，代表性消费者接受抚育与教育，从而实现人力资本的累积。代表性消费者在少年期的人力资本累积函数为：

$ {h}_{t}={h}_{t-1}{e}_{t-1}^{\lambda }{b}_{t-1}^{1-\lambda } $

(2)

其中， $ {h}_{t-1} $ 为代表性消费者父代的人力资本，衡量了人力资本累积中的遗传作用。 $ {e}_{t-1} $ 为t−1期对每个子代的公共教育投入， $ \lambda $ 为公共教育投入的人力资本累积弹性，衡量了人力资本中公共教育的作用。 $ {b}_{t-1} $ 为t−1期的抚育成本， $ 1-\lambda $ 衡量了人力资本累积中私人教育投入的作用。

3. 中年期

在中年期，代表性消费者开始工作，获得工资收入，同时会得到因父母死亡而遗留的遗产，工资与分得遗产之和构成代表性消费者的总财富。代表性消费者以工资收入缴纳技术投资与公共教育投入税，同时对每个子代投入固定的抚育成本，余下的用于储蓄和消费。代表性消费者在中年期的预算约束可表示为：

$ {c}_{y,t}={w}_{t}(1-{\sigma }_{t})+{l}_{t}-{s}_{t}-{b}_{t}{n}_{t+1} $

(3)

其中， $ {w}_{t} $ 为t时期的工资水平， $ {\sigma }_{t} $ 为政府征收的用于技术投资和公共教育投入的税率，^① $ {l}_{t} $ 为代表性消费者获得的遗产， $ {s}_{t} $ 为储蓄， $ {b}_{t} $ 为抚育成本， $ {n}_{t+1} $ 为代表性消费者的子代数量。其中，代表性消费者所获得的被动遗产可表示为：

$ {l}_{t}=(1-{p}_{t}){n}_{t-1}{s}_{t-1}{r}_{t} $

(4)

其中， $ {r}_{t} $ 为t时期的总资本收益率。类似式（2），代表性消费者子代的人力资本累积函数为：

$ {h}_{t+1}={h}_{t}{e}_{t}^{\lambda }{b}_{t}^{1-\lambda } $

(5)

4. 老年期

在老年期，代表性消费者不再工作，同时开始面临死亡风险。其消费由储蓄的总资本回报构成，代表性消费者老年期的预算约束为：

$ {c}_{o,t+1}={s}_{t}{r}_{t+1} $

(6)

其中， $ {r}_{t+1} $ 为t+1期的总资本收益率。

（三）技术生产部门

社会中存在技术生产部门，技术生产部门利用先期的技术积累、劳动人口中的研究和试验发展人员提供的劳动以及技术投资作为生产要素来推动技术进步，技术进步方程即技术生产方程，可表示为：

$ {A}_{t+1}={A}_{t}{(\varphi {n}_{t+1}{h}_{t+1})}^{1-\gamma }{d}_{t}^{\gamma } $

(7)

其中， $ {A}_{t} $ 为t时期的技术进步， $ \varphi $ 为劳动人口中研究和试验发展人员的比例， $ \mathrm{\gamma } $ 为技术投资的技术进步弹性， $ {d}_{t} $ 为技术投资。

（四）物质生产部门

社会中存在物质生产部门，物质生产部门利用技术进步、资本和劳动作为要素进行产品和服务的生产，其中技术进步由技术生产部门提供，资本由储蓄转化，劳动由人口中的非研究和试验发展人员提供，物质生产函数可表示为：

$ {Y}_{t+1}={A}_{t+1}{s}_{t}^{\alpha }{\left[(1-\varphi ){h}_{t+1}{n}_{t+1}\right]}^{1-\alpha } $

(8)

联立式（5）、（7）、（8）可得t+1期的社会总产出为：

基于式（10）可求得t+1期的工资水平为：

基于式（10）可求得t+1期的总资本收益为：

（五）政府

政府为中央计划者，其目标是最大化代表性消费者的终生效用，角色为税收管理人、基础技术投资人和公共教育投资人，职责是向处于中年期的代表性消费者征税并将之用于当期的技术投资和教育投入，因此政府的预算约束为：

$ {w}_{t}{\sigma }_{t}={d}_{t}+{n}_{t+1}{e}_{t} $

(12)

三、均衡决策分析

基于代表性消费者最大化原则，联立式（3）、（5）、（6）、（10）、（11）可求得政府的均衡技术投资和公共教育投入分别为：

$ {d}_{t}=\frac{({{w}}_{{t}}+{{l}}_{{t}}-{{b}}_{{t}}{{n}}_{{t}+1})\gamma \beta {p}_{t+1}}{1+\alpha \beta {p}_{t+1}+\gamma \beta {p}_{t+1}+\lambda \beta {p}_{t+1}(2-\alpha -\gamma )+v\lambda } $

(13)

$ {e}_{t}=\frac{({{w}}_{{t}}+{{l}}_{{t}}-{{b}}_{{t}}{{n}}_{{t}+1})\left[\lambda \beta {p}_{t+1}(2-\alpha -\gamma )+v\lambda \right]/{n}_{t+1}}{1+\alpha \beta {p}_{t+1}+\gamma \beta {p}_{t+1}+\lambda \beta {p}_{t+1}(2-\alpha -\gamma )+v\lambda } $

(14)

（一）少子化对技术投资与公共教育投入的影响

基于式（13）可求得均衡技术投资对生育率的弹性为：

$ \frac{\partial \mathrm{ln}{d}_{t}}{\partial \mathrm{ln}{n}_{t+1}}=\frac{-{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}-{b}_{t}{n}_{t+1}} <0 $

(15)

由式（15）可以看出，均衡技术投资与生育率呈负相关，但均衡技术投资的生育率弹性绝对值大于1还是小于1则并不确定，其取决于子代的抚育成本 $ {b}_{t}{n}_{t+1} $ 占总财富 $ {w}_{t}+{l}_{t} $ 的比例 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ ：若 $\dfrac{1}{2} < \dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} <1$ ，则均衡技术投资的生育率弹性绝对值大于1；若 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < \dfrac{1}{2}$ ，则均衡技术投资的生育率弹性绝对值小于1。式（15）包含了一种度量技术投资必要性的指标，即抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 。当抚育成本与总财富比小于50%时，面对少子化问题，政府没有进行高水平技术投资的必要性。但当抚育成本与总财富比大于50%而小于100%时，面对少子化问题，政府有必要通过高水平的技术投资以实现经济发展的“弯道超车”。

基于式（14）可求得均衡公共教育投入对生育率的弹性为：

$ \frac{\partial \mathrm{ln}{e}_{t}}{\partial \mathrm{ln}{n}_{t+1}}=-\frac{{w}_{t}+{l}_{t}}{{w}_{t}+{l}_{t}-{b}_{t}{n}_{t+1}} <-1 $

(16)

由式（16）可以看出，均衡公共教育投入与生育率呈负相关，且均衡公共教育投入对生育率的弹性绝对值大于1，是富有弹性的。这表明如果少子化进程难以扭转，为实现代表性消费者效用最大化，政府应当大幅度提高公共教育投入。

联立式（12）—（14）可求得政府在t期实行的基础技术投资和公共教育税率水平为：

$ {\sigma }_{t}=\frac{(1+{l}_{t}/{w}_{t}-{b}_{t}{n}_{t+1}/{w}_{t})\left[\gamma \beta {p}_{t+1}+\lambda \beta {p}_{t+1}(2-\alpha -\gamma )+v\lambda \right]}{1+\alpha \beta {p}_{t+1}+\gamma \beta {p}_{t+1}+\lambda \beta {p}_{t+1}(2-\alpha -\gamma )+v\lambda } $

(17)

基于式（17）可求得生育率对均衡税率的影响为：

$ \frac{\partial \mathrm{l}\mathrm{n}{\mathrm{\sigma }}_{t}}{\partial \mathrm{l}\mathrm{n}{n}_{t+1}}=-\frac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}-{b}_{t}{n}_{t+1}} <0 $

(18)

式（18）表明，当少子化加速时，为实现代表性消费者效用最大化，政府须提高基础技术投资和公共教育税率。注意到式（18）中税率的提高并不附带任何条件，只要政府的目标是实现代表性消费者效用最大化，当少子化进程加速时，政府就必须提高税率。当 $\dfrac{1}{2} < \dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} <1$ 时，税率对生育率的变化是富有弹性的，反之为缺乏弹性的。

（二）少子化对内生经济增长的影响

政府的目标是实现当期居民的效用最大化，在给定的生育率水平下，政府通过对技术投资和公共教育投入的合理安排以实现该目标。通过影响技术投资和公共教育投入的安排，少子化进程将影响内生经济增长的各个方面，包括未来的工资水平、总资本收益率、产出、劳均产出和人均产出。

基于代表性消费者效用最大化原则，可求得代表性消费者均衡储蓄为：

$ {s}_{t}=\frac{（{w}_{t}+{l}_{t}-{b}_{t}{n}_{t+1}）\alpha \beta {p}_{t+1}}{1+\alpha \beta {p}_{t+1}+\gamma \beta {p}_{t+1}+\lambda \beta {p}_{t+1}(2-\alpha -\gamma )+v\lambda } $

(19)

联立式（10）、（13）、（14）、（19），并令 $ {C}_{0}=\lambda \beta {p}_{t+1}(2-\alpha -\gamma )+v\lambda $ ， $ {C}_{1}=1+\alpha \beta {p}_{t+1}+\gamma \beta {p}_{t+1}+{C}_{0} $ ， $ {C}_{2}={A}_{t}{\varphi }^{1-\gamma }{(1-\varphi )}^{1-\alpha }{({h}_{t}{b}_{t}^{1-\lambda })}^{2-\alpha -\lambda } $ ，

，可求得t+1期对数工资水平为：

基于式（20）可求得生育率对下期工资的影响为：

因此，t+1期的工资随生育率上升而增长的抚育成本与总财富比条件是:

$ \frac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} <(2-\alpha -\gamma )(1-\lambda )-1 $

(22)

$ (2-\alpha -\gamma )(1-\lambda )-1 >0 $

(23)

式（22）表明，t+1期的工资水平能否随生育率上升而增长取决于抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 和当期社会的生产方式，即取决于劳动产出弹性 $ 1-\alpha $ 、人力资本对抚育成本的弹性 $ 1-\lambda $ 以及技术进步的人力资本弹性 $ 1-\gamma $ 。给定社会的生产方式，如果 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 低于社会生产方式参数方程 $ (2-\alpha -\gamma )(1-\lambda )-1 $ ，则生育率上升会带来t+1期工资的持续增长，否则会使t+1期工资下降。

联立式（11）、（13）、（14）、（19），令

，可得到对数总资本收益率的动态演化方程为：

由式（24）可求得t+1期总资本收益率对生育率的弹性为：

由式（25）可得到总资本收益率随生育率上升而增长的抚育成本与总财富比条件为：

$ \frac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} <(2-\alpha -\gamma )(1-\lambda )$

(26)

由式（26）可以看出，总资本收益率能否随生育率上升而增长取决于抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 及当期的社会生产方式，如果给定当期的社会生产方式，则取决于抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 是否小于某一特定水平 $ (2-\alpha -\gamma )(1-\lambda )$ 。如果 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < (2-\alpha -\gamma )(1-\lambda )$ ，则生育率上升会带来t+1期总资本收益率的上升，否则会使t+1期总资本收益率下降。式（26）相比式（22）是一个相对宽松的条件，并不要求社会生产的参数方程满足某些条件，这似乎表明少子化进程中实现总资本收益率增长比实现工资水平增长相对更容易。

联立式（9）、（13）、（14）、（19）可求得t+1期的对数总产出为：

基于式（27）可得到产出对生育率的弹性为：

故而总产出随生育率上升而增长的抚育成本与总财富比条件为：

$ \frac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} <\frac{(2-\alpha -\gamma )(1-\lambda )}{2} $

(29)

由式（29）可以看出，下期总产出能否随生育率上升而增长取决于抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 及当期的社会生产方式，如果给定当期的社会生产方式，则取决于抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 是否低于某一特定水平 $\dfrac{(2-\alpha -\gamma )(1-\lambda )}{2}$ 。如果 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < \dfrac{(2-\alpha -\gamma )(1-\lambda )}{2}$ ，则生育率上升促进下期产出的提高，否则会导致下期产出下降，从而导致经济增长停滞。

基于式（27）可求得t+1期的对数劳均产出为：

从而劳均产出对生育率的弹性为：

因此，t+1期的劳均产出随生育率上升而增长的抚育成本与总财富比条件为:

$ \frac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} <(2-\alpha -\gamma )(1-\lambda )-1 $

(32)

$ (2-\alpha -\gamma )(1-\lambda )-1 >0 $

(33)

注意到式（32）、式（33）与式（22）、式（23）的形式完全一致，因此可得到如下结论：t+1期的劳均产出能否随生育率上升而增长取决于抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 和当期社会的生产方式，在给定当期的社会生产方式的情况下，如果 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 低于决定社会生产方式的参数方程 $ (2-\alpha -\gamma )(1-\lambda )-1 $ ，则少子化进程会带来t+1期劳均产出的持续增长，否则会使t+1劳均产出下降。

基于式（27）可求得t+1期的对数人均产出为：

由式（34）可求得t+1期人均产出对生育率的弹性为：

由式（35）可以得到人均产出随生育率上升而增长的抚育成本与总财富比条件为：

由式（36）可以看出，t+1期人均产出对生育率弹性的符号不但取决于抚育成本与总财富比 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}$ 和当期社会的生产方式，还取决于代表性消费者在t+1期的预期生存概率 $ {p}_{t+1} $ ，而且会随着生育率的变化而变化。

（三）少子化对代表性消费者终生效用的影响

通过影响政府的技术投资和公共教育投入行为，生育率将最终影响代表性消费者的终生效用，这种影响从方向上看并不是确定性的，既可能使代表性消费者的终生效用上升，也可能使之下降。接下来，基于生育率对技术投资和公共教育投入的影响，进一步分析生育率对代表性消费者终生效用的影响，以分析少子化实现代表性消费者终生效用上升的条件。

令

，联立式（1）、（3）、（5）、（6）、（10）、（11）、（13）和（14），可得到代表性消费者的终生效用为：

基于式（37）可求得生育率对代表性消费者终生效用的影响为：

由式（38）可求得代表性消费者终生效用随生育率上升而增长的抚育成本与总财富比条件为：

$ \frac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} <\frac{\mathrm{\beta }{p}_{t+1}(2-\alpha -\gamma )(1-\lambda )-\mathrm{\nu }\mathrm{\lambda }}{1+2\mathrm{\beta }{p}_{t+1}} $

(39)

$ \nu <\frac{\beta {p}_{t+1}(2-\alpha -\gamma )(1-\lambda )}{\lambda } $

(40)

由式（39）可以看出，少子化进程能否增进代表性消费者终生效用依赖于代表性消费者的抚育成本与总财富比、生存概率、社会生产条件、对子代的质量偏好。可以看出，少子化进程实现代表性消费者终生效用上升的条件也依赖于抚育成本与总财富比低于特定水平。这意味着两种情况：第一种情况，存在某一特定而微妙的最优抚育成本与总财富比范围，使得在此范围内，随着少子化进程加速，政府的技术投资和公共教育投入安排既能实现经济的可持续增长，也能实现居民福利水平的上升。第二种情况，随着少子化进程的加速，经济的可持续增长和居民福利水平的上升是一对矛盾的综合体，政府的技术投资和公共教育投入安排要么只能实现经济的可持续增长，要么只能实现居民福利水平上升。

四、数值模拟

（一）参数设定

根据我国现行法律对职工退休年龄的规定，本文以60岁为平均退休年龄，这与郭凯明和颜色（2016）、汪伟和王文鹏（2021）等的设定一致。根据世界银行的统计数据，我国居民的平均工作年限为40.1年，因此以0—20岁为少年期，20—60岁为中年期，60—100岁为老年期，此设定与《中国人身保险业经验生命表（2010—2013）》规定的我国人口极限寿命为105岁基本一致。本文数值模拟从t−1时期开始，t+1时期结束，所涉及的统计数据多始于1978年，且需要保证t+1期终点超过2020年才有意义，因此选择1978年为t−1期的代表性时点，基于每期40年的设定，以2018年为t期的代表性时点，2058年为t+1期的代表性时点。

根据《中国统计年鉴2000》公布的数据，我国1978年城镇单位就业人员平均工资为615元，根据国家统计局公布的数据，我国2018年城镇单位就业人员平均工资为82413元，根据世界银行公布的以GDP平减指数为基准的通货膨胀率，可求得以1978年为基期的2018年累积GDP平减指数为674.84，从而以1978年价格为基准的2018年平均工资为12212.23元，因此将1978年和2018年的平均工资 ${w}_{t-1}、{w}_{t}$ 分别设为615.00元、12212.23元。根据世界银行公布的数据，我国1978年的储蓄率为39.28%，2018年的储蓄率为44.94%。另外根据《中国统计年鉴2000》《中国统计年鉴2021》，我国1978年的平均可支配收入为171元，2018年的可支配收入为28228元，从而以1978年价格为基准的2018年实际可支配收入为4182.92元，基于1978的实际可支配收入可计算得到当年的储蓄 $ {s}_{t-1} $ 为67.17元，基于2018年的实际可支配收入可计算得到当年的储蓄 $ {s}_{t} $ 为1879.79元。

根据国家卫生健康委员会发布的《2018年我国卫生健康事业发展统计公报》，我国的人口平均预期寿命可以达到77岁。另外，根据文章的模型设定，假设极限寿命为100岁，可以计算t期的预期生存概率为 $ {p}_{t}=77/100=0.77 $ 。根据《中国可持续发展总纲（国家卷）》的预期，到2050年中国人口的平均预期寿命可以达到85岁，而根据WHO《World Health Statistics 2018》报告，平均预期寿命最高的国家日本为84.2岁。因此，预期85岁的目标可以达到，可设定t+1期预期生存概率为 $ {p}_{t+1}=85/ 100=0.85 $ 。根据模型设定， $ {n}_{t-1} $ 衡量的是平均每个t期处于中年期的代表性消费者的父代数量，而 $ {n}_{t+1} $ 衡量的是其子代的数量，根据原国家卫计委1982的1‰人口生育率抽样调查估计，我国1980年的总和生育率为2.31，即1980年平均每个代表性消费者的子代数量为 $ 2.31/2=1.155 $ ，从而可设定平均每个t期处于中年期的代表性消费者的父代数量为 $ {n}_{t-1}=1/1.155= 0.8658 $ ，根据第七次全国人口普查结果，2020年我国育龄妇女总和生育率为1.3，故设定t时期的生育率基准值为 $ {n}_{t+1}=1.3/2=0.65 $ 。根据“中国义务教育阶段城市家庭子女教育成本研究课题组”的调查显示，我国家庭的平均教育支出占到家庭收入的30%，基于此可计算得到每个子女的抚育成本 $ {b}_{t}=3861.14 $ 元。尹向飞和欧阳峣（2019）估计出我国1996—2016年的全要素生产率年均增长率为1.64%，故令 $ {A}_{t}={1.0164}^{40}=1.9168 $ 。王开科和曾五一（2020）估计出我国1978—2017年的资本回报率在7.28%—13.05%之间，据此求几何平均值可计算得到1978—2017年间我国的平均资本回报率为11.20%，进而求得1978—2018年间的累积总资本收益率为 $ {r}_{t}=69.85 $ 。

赵志耘等（2006）计算出我国1978—2004年间的平均资本产出弹性为 $ \mathrm{\alpha }=0.56 $ ，与郭凯明和颜色（2016）、贾俊雪等（2021）、汪伟和王文鹏（2021）等采用的 $ \mathrm{\alpha }=0.5 $ 基本一致。吴延兵（2006）运用 2002 年中国制造产业横截面数据发现R&D投入的产出弹性约为 0.1，故可设定技术投资的技术进步弹性基准值为 $ \gamma =0.1 $ ，基于资本产出弹性和边际报酬不变的模型假设，可求得人力资本投入的产出弹性为0.44，根据基准的 $\alpha、\gamma$ 可校准得到公共教育投入的人力资本累积弹性为 $ \lambda =0.3283 $ ，基于 $ \mathrm{\lambda } $ 和当期的储蓄，可校准得到我国居民的子代质量偏好参数为 $ \nu =0.0047 $ 。根据统计局公布的数据，2018年我国研究和试验发展人员占劳动人口的比例为0.55%，因此设定 $ \varphi =0.0055 $ 。采用一年期存款利率1.5%为标准，以40年为一期，计算得到时间偏好因子 $ \;\beta =0.55 $ 。

根据联合国人口基金会公布的《2020年世界人口状况报告》，发达国家中总和生育率最低的国家为韩国，达到1.1，考虑到中国的总和生育率持续下行的事实，可设定 $ {n}_{t+1}=1.1/2=0.55 $ 为最坏情况下t+1期的标准化子代数量，基于此可计算当期可分得的遗产 $ {l}_{t} $ ，假设家庭以全部财富用于教育支出，可校准得到每个代表性消费者所能抚育的最大子代数量为3.46，因此本文取t+1期平均每个代表性消费者生育率（以下简称生育率）的范围为 ${n}_{t+1}\in \left[\mathrm{0.55,3.46}\right]$ 。

（二）模拟结果

1. 在当前生育率水平下经济增长和社会福利水平上升的条件分析

上述的参数设定确定了当前的社会生产条件，因此可基于这些参数设定，首先求出在当前社会生产条件和生育率水平下，内生经济增长各个方面和代表性消费者终生效用随总和生育率上升而增长的抚育成本与总财富比条件。

由式（22）可求得当前生育率水平下，抚育成本与总财富比为 $ \dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}}=28.83\mathrm{\%} $ 。满足工资和劳均产出随总和生育率上升而增长的抚育成本与总财富比临界值为 $ (2-\alpha -\gamma )(1-\lambda )-1=-9.99\% $ ，故而条件 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < (2-\alpha -\gamma )(1-\lambda )-1\mathrm{和}\mathrm{条}\mathrm{件}(2-\alpha -\gamma )(1-\lambda )-1 > 0$ 均不满足，即在当前生育率水平和生产条件下，生育率上升会带来工资和劳均产出的持续下降。满足总资本收益率随总和生育率上升而增长的抚育成本与总财富比临界值为 $ (2-\alpha -\gamma )(1-\lambda )=90.01\% $ ，故条件 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < (2-\alpha -\gamma )(1-\lambda )$ 成立，即在当前生育率水平和生产条件下，生育率上升会带来总资本收益率的持续上升。满足总产出随总和生育率上升而增长的抚育成本与总财富比临界值为 $\dfrac{(2-\alpha -\gamma )(1-\lambda )}{2}=45.00\%$ ，故条件 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < \dfrac{(2-\alpha -\gamma )(1-\lambda )}{2}$ 成立，即在当前生育率水平和生产条件下，生育率上升会带来总产出的持续上升。满足人均产出随总和生育率上升而增长的抚育成本与总财富比临界值为： $\dfrac{(2-\alpha -\gamma )(1-\lambda )-\dfrac{{n}_{t+1}}{{p}_{t+1}+{n}_{t+1}}}{2-\dfrac{{n}_{t+1}}{{p}_{t+1}+{n}_{t+1}}}=29.79\%$ ，故条件 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < \dfrac{(2-\alpha -\gamma )(1-\lambda )-\dfrac{{n}_{t+1}}{{p}_{t+1}+{n}_{t+1}}}{2-\dfrac{{n}_{t+1}}{{p}_{t+1}+{n}_{t+1}}}$ 成立，即在当前生育率水平和生产条件下，生育率上升会带来人均产出的上升。

代表性消费者终生效用随总和生育率上升而增长的抚育成本与总财富比临界值为 $\dfrac{\mathrm{\beta }{p}_{t+1}(2-\alpha -\gamma )(1-\lambda )-\mathrm{\nu }\mathrm{\lambda }}{1+2\mathrm{\beta }{p}_{t+1}}=20.53\%$ ，子代质量偏好临界值为 $\dfrac{\beta {p}_{t+1}(2-\alpha -\gamma )(1-\lambda )}{\lambda }=0.4208$ ，子代质量偏好条件 $\nu < \dfrac{\beta {p}_{t+1}(2-\alpha -\gamma )(1-\lambda )}{\lambda }$ 满足，但抚育成本与总财富比条件 $\dfrac{{b}_{t}{n}_{t+1}}{{w}_{t}+{l}_{t}} < \dfrac{\mathrm{\beta }{p}_{t+1}(2-\alpha -\gamma )(1-\lambda )-\mathrm{\nu }\mathrm{\lambda }}{1+2\mathrm{\beta }{p}_{t+1}}$ 不满足，即在当前生育率水平和生产条件下，生育率上升会带来代表性消费者终生效用的下降。

2. 可行参数与生育率范围下的均衡解分析

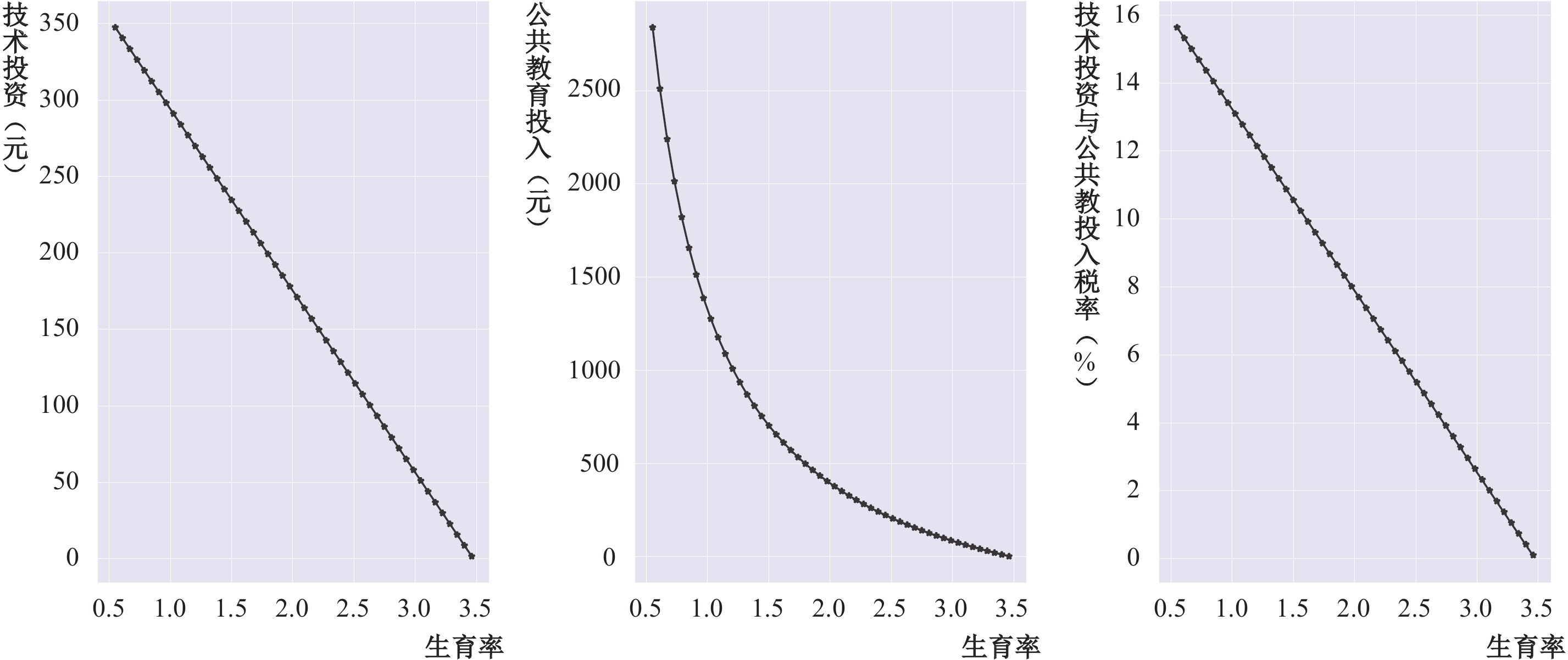
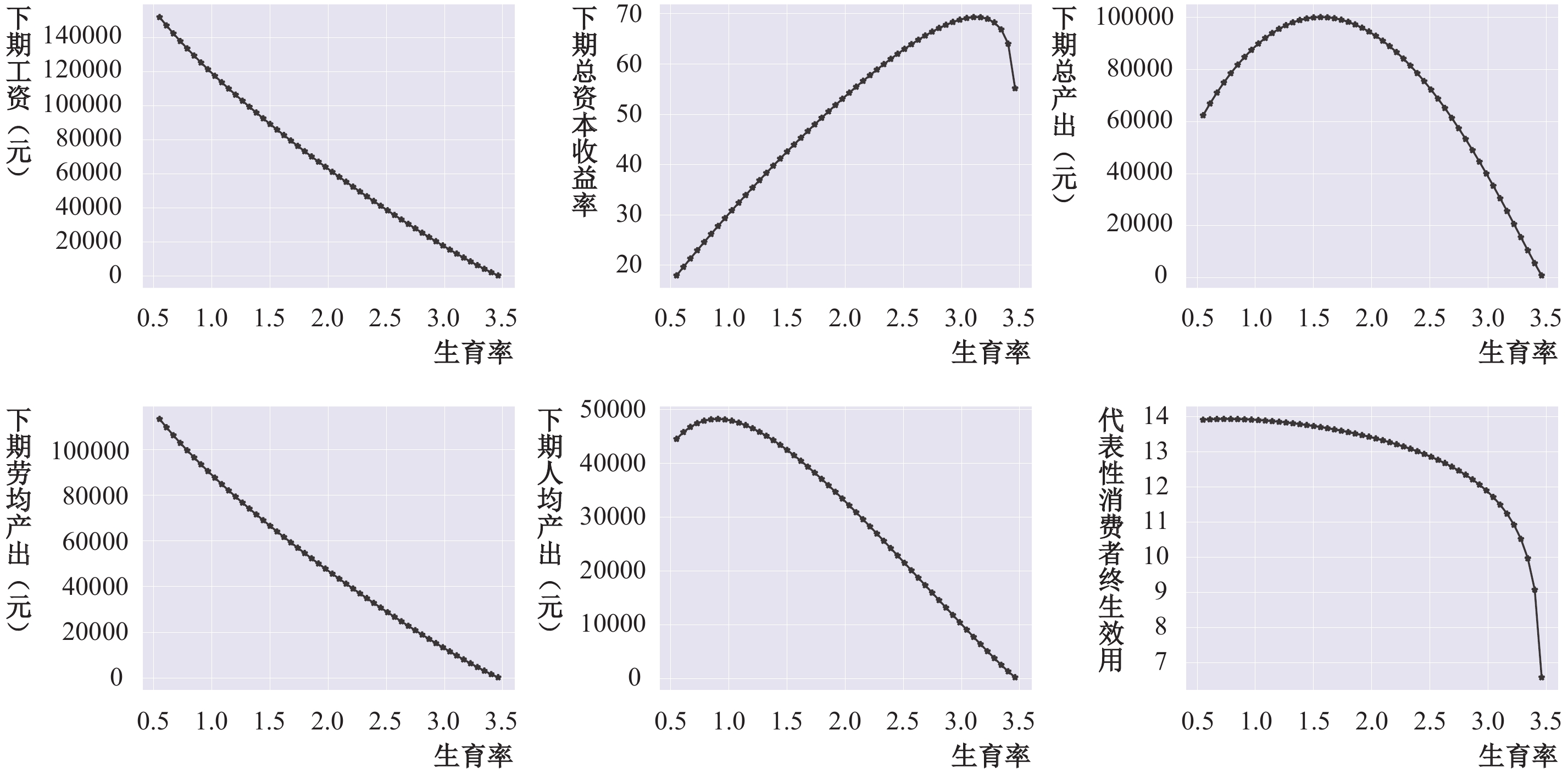
基于给定的参数和生育率范围，可模拟在不同生育率水平下均衡的技术投资、公共教育投入与相应的税率水平，模拟结果如图1所示。基于均衡的技术投资和公共教育投入，可进一步模拟不同生育率水平下的下期工资、总资本收益率、总产出、劳均产出、人均产出与代表性消费者终生效用，模拟结果如图2所示。

由图1可以看出，在给定的参数下，生育率与技术投资呈负向的线性关系，与公共教育投入呈负向的、边际递减的非线性关系，与技术投资和公共教育投入税率呈负向的线性关系。当生育率上升至3.46左右时，技术投资、公共教育投入、税率均趋近于0，这意味着我国当前的社会生产方式已经难以承受生育率的大幅上升，生育率的大幅上升将耗尽代表性家庭的预算约束，从而完全挤出技术投资、公共教育投入等内生经济增长投资因素。

由图2可以看出，在给定的参数下，生育率与下期工资、下期劳均产出呈边际递减的负相关关系，其原因在于：当生育率极低时，未来的劳动供给也变得相对稀缺，从而劳动的价值即工资开始上升。但当生育率开始上升后，未来的劳动供给也开始增加，劳动的价值逐渐下降。

在给定的参数下，生育率与下期总资本收益率呈先正后负的非对称关系，相关性转换的临界生育率水平约在3.1（即实际总和生育率为6.2左右），其原因在于：当生育率较低时，资本变得相对不稀缺，从而资本的价值即总资本收益率也较低。但当生育率开始上升后，未来的劳动力供给增加，资本开始变得相对稀缺，从而资本的价值即总资本收益率开始上升。但当生育率上升到一定水平后，经济增长开始停滞，从而总资本收益率上升的幅度开始下降。当生育率继续上升超过临界水平后，资本相对稀缺带来的上升效应将低于经济增长停滞带来的下降效应，总资本收益率开始下降。

在给定的参数下，生育率与下期总产出呈先正后负的非对称关系，相关性转换的临界生育率水平约为1.5（即实际总和生育率为3.0左右），其原因在于：我国当前的生育率水平可能偏离了均衡的经济增长模式所要求的生育率水平，因此当生育开始上升时，劳动和资本结构得到优化，公共教育支出和技术投资回归合理水平，从而经济得以持续增长。但当生育上升到一定水平后，劳动和资本结构将开始恶化，公共教育支出和技术投资也变得不足，从而经济增长开始停滞。这表明我国目前的生产模式可能不支持生育率的大幅上升。

在给定的参数下，生育率与下期人均产出呈先正后负的非对称关系，相关性转换的临界生育率水平约为0.8（即实际总和生育率为1.6左右），其原因在于：我国当前的生育率水平可能偏离了均衡的经济增长模式所要求的生育率水平，因此当生育开始上升时，劳动和资本结构得到优化，从而趋近于均衡经济增长要求的结构，经济得到持续增长。当生育率超过临界水平后，由于人口规模上升带来的边际总产出提高低于上文中超过生育率临界值前的水平，从而导致总产出持续增长，但是人均产出开始下降。

在给定的参数下，生育率与代表性消费者的终生效用呈边际递增的负相关关系，其原因在于：代表性消费者的终生效用虽然受到中年期消费、老年期消费和子代质量等多方面的影响，但总体而言受到中年期消费、老年期消费的影响最大，而老年期的消费主要受到中年期储蓄的影响，因此代表性消费者的终生效用主要受到中年期储蓄和消费的影响。由于抚育成本是固定的，子代数量上升会大幅挤压代表性消费者的储蓄和消费，从而其终生效用随生育率的上升而下降。

3. 社会生产参数的影响分析

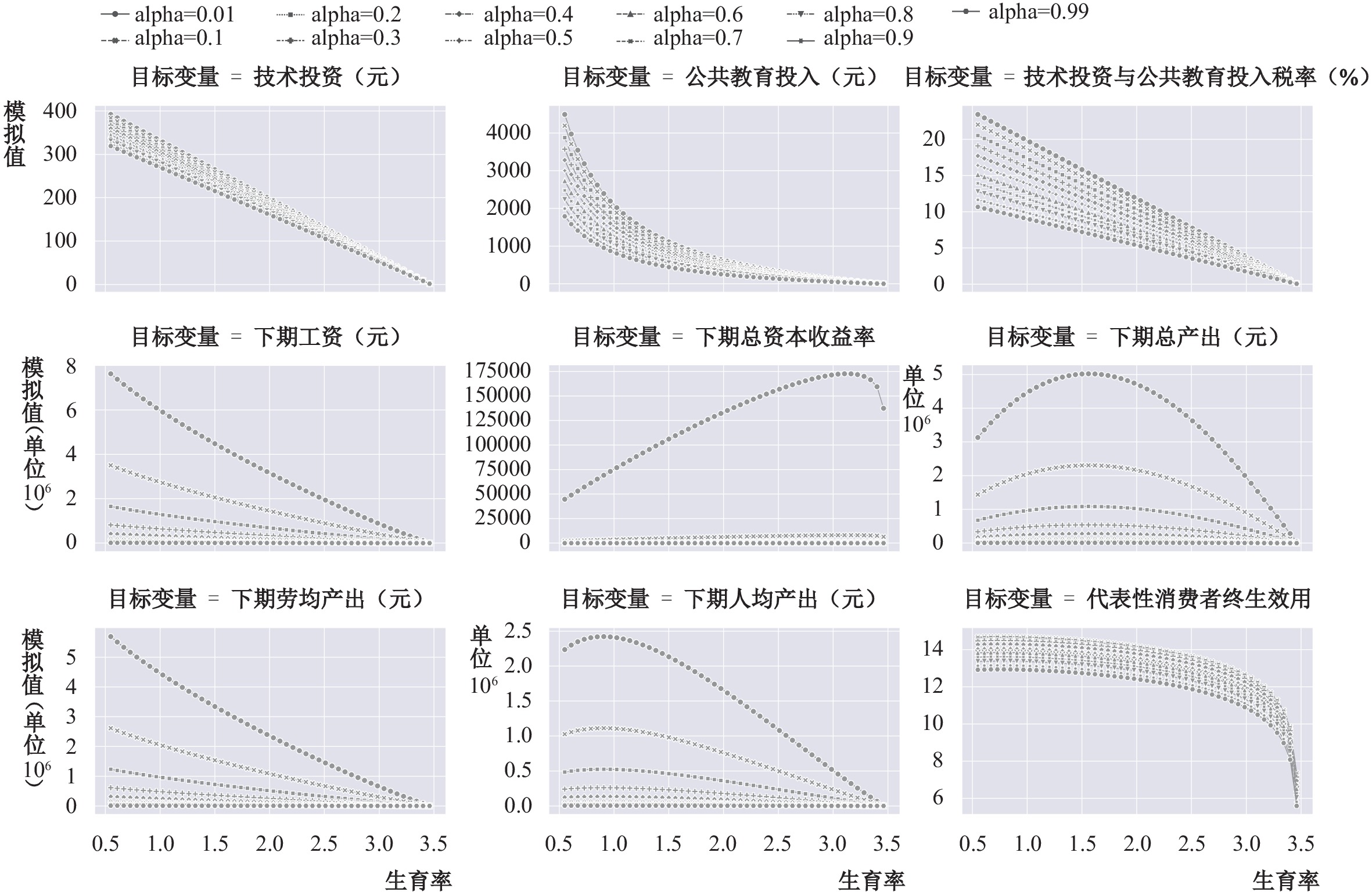
接下来分析社会生产关键参数（资本产出弹性 $ \mathrm{\alpha } $ 、公共教育投入的人力资本累积弹性 $ \mathrm{\lambda } $ 、技术投资的技术进步弹性 $ \mathrm{\gamma } $ ）在不同水平下（即 $\mathrm{\alpha }、\mathrm{\beta }、\mathrm{\gamma }\in \left[\mathrm{0.01,0.99}\right]$ ）对生育率与技术投资、公共教育投入、内生经济增长、居民福利水平的影响。其中，资本产出弹性 $ \mathrm{\alpha } $ 的影响如图3所示。

由图3可以看出，总体上，给定生育率水平， $ \mathrm{\alpha }\mathrm{­} $ 与技术投资、公共教育投入、税率、下期工资、下期总资本收益率、下期总产出、下期劳均产出、下期人均产出均负相关，与代表性消费者终生效用呈倒“U”形关系。当 $ \mathrm{\alpha } $ 处于极低水平时，下期总资本收益率等都变得极高，因此优化产业结构、降低资本的产出弹性对经济增长具有重要意义。

根据图表分析结果，^②总体上，如果给定生育率水平的情况下， $ \mathrm{\lambda } $ 与技术投资、下期工资、下期总资本收益率、下期总产出、下期劳均产出、下期人均产出、代表性消费者终生效用均呈负相关，与公共教育投入、税率呈正相关。当 $ \mathrm{\lambda } $ 极低时，公共教育投入变得极低，技术投资变得极高，受此影响，下期内生经济增长和代表性消费者终生效用都变得较高。因此，在技术投资和公共教育投入二者之中，政府更应当改善教育模式，并且降低公共教育投入的人力资本累积弹性。另外，总体上， $ \mathrm{\gamma } $ 与技术投资、公共教育投入、税率、下期工资、下期总资本收益率、下期总产出、下期劳均产出、下期人均产出、代表性消费者终生效用均呈负相关。而 $ \mathrm{\gamma } $ 对技术投资的影响极小，但对公共教育投入的影响较大，对内生经济增长的影响相对温和。因此，若教育模式无法立即改变，降低技术投资的技术进步弹性和增加研究人员在技术进步中的贡献可以有效促进经济增长。

五、结论与政策建议

如何在确定的生育率水平下安排技术投资和公共教育投入是少子化进程中保持经济持续增长的关键。因此，本文建立了一般均衡世代交叠模型，理论分析了生育率对技术投资和公共教育投入的影响，并基于此进一步分析了生育率对税率、内生经济增长、居民效用的影响。本文基于理论分析的结论进行了数值模拟，较全面地分析了如何在少子化背景下安排技术投资和公共教育投入及其影响。理论分析表明：均衡公共教育投入与生育率呈负相关，且均衡公共教育投入对生育率的弹性绝对值大于1，是富有弹性的。均衡技术投资与生育率呈负相关，但均衡技术投资的生育率弹性绝对值大于1还是小于1取决于子代的抚育成本占总财富的比例。无论当期的抚育成本与总财富比处于何种水平，均衡公共教育投入对生育率弹性的绝对值始终大于均衡技术投资对生育率弹性的绝对值。均衡技术投资和公共教育投入税率与生育率呈负相关，弹性绝对值大于1还是小于1也取决于子代的抚育成本占总财富的比例。数值模拟表明：在给定的参数下，生育率与技术投资呈负向的线性相关，与公共教育投入呈边际递减的负向非线性相关，与技术投资和公共教育投入税率呈负向的线性相关，与下期工资和劳均产出呈边际递减的负向非线性相关，与下期总资本收益率、下期总产出、下期人均产出呈先增后减的倒“U”形关系，与代表性消费者终生效用呈边际递增的负向非线性相关。我国当前的社会生产方式可以支持生育率的轻微提高，但是可能难以承受生育率的大幅上升。在决定社会生产方式的各参数中，资本产出弹性与下期总产出负相关，与代表性消费者终生效用呈到“U”形关系。

因此，面对少子化问题，给出以下政策建议：第一，采取可控的生育刺激政策以提高生育率。在当前的生产模式下，总和生育率的轻微上升至1.6左右时可以同时促进经济增长和人均产出的提高，并且不会大幅降低代表性消费者的终生效用。第二，优化现收现付制的养老保障体系，增加代际间的联系。生育率的轻微上升会降低代表性消费者终生效用的原因在于代际间的联系不够紧密，从而父代无法享受下期人均产出上升带来的益处，优化养老保障体系可缓解这个问题。第三，优化产业结构，降低资本产出弹性，增加劳动产出弹性。数值分析表明，资本产出弹性越低，下期产出和下期人均产出越高。

① 在现实中，政府并非直接征收基础技术投资和公共教育税，而是把征收的税收用于技术投资和教育支出，但对于代表性消费者，这相当于对个人征税。

② 限于篇幅，下文的图表分析省略，读者若是感兴趣可向作者索取。