一、引　言

近年来，5G、大数据、人工智能等智能革命代表性技术逐渐成熟，开始大规模应用。智能时代的到来意味着技术创新和技术应用两个阶段的研发效率上升，即受到正向的研发效率冲击。那么，研发效率上升将如何影响创新发展和经济增长？拥有知识产权和不拥有知识产权的企业受到的影响是否有所不同？两者能否协调发展？作为保护创新的重要手段，知识产权保护在研发效率冲击下具有什么作用？厘清这些问题将有助于加深我们对科技创新机制的理解，助力高质量发展，提升经济增长潜力。为了回答这些问题，本文区分了两类研发效率，即创新效率和应用效率，分别对应技术创新和技术应用两个研发阶段；同时，还区分了两类企业，即注重知识积累的创新型企业和注重知识利用的模仿型企业。

本文利用2011—2017年的省级面板数据，首先从实证的角度探讨了两类研发效率冲击对未来全要素生产率（TFP）的影响，以及知识产权保护在其中的作用。具体而言，本文基于中国规模以上工业企业的R&D经费支出和技术改造经费支出的省级数据，衡量两类企业在积累知识和利用知识过程中的研发费用，从而识别两类研发效率冲击。实证结果表明，创新效率的提高会促进未来TFP增长，知识产权保护与这一正向作用没有显著的联系；应用效率的提高则会抑制未来TFP增长，而加强知识产权保护能够减弱这一负向作用。

随后，本文建立了一个含有内生增长的两部门动态随机一般均衡（DSGE）模型。在模型中，创新型企业和模仿型企业分别雇用研发劳动来积累知识和利用知识，创新型企业的知识积累活动受到创新效率冲击的影响，模仿型企业的知识利用活动受到应用效率冲击的影响。模仿型企业不积累知识，其通过付费购买知识使用权和免费获取溢出知识这两种方式来获得创新型企业的知识。知识产权保护水平越高，模仿型企业付费获取的知识占比越高。

经过参数校准，本文模拟了两种知识产权保护水平下创新效率冲击和应用效率冲击的影响，得到了与实证分析一致的结果，为实证分析中发现的经验事实提供了理论依据。模拟结果表明，正向的创新效率冲击通过鼓励创新型企业的知识积累活动，促进TFP和总产出持续加速增长，尽管短期会对模仿型企业产生负面影响，但在中长期有利于模仿型企业发展。知识产权保护在创新效率冲击中的作用不大，主要是因为模仿型企业受到的负面影响通过知识租金反馈到创新型企业，抵消了知识产权保护对创新型企业知识积累活动的激励作用。正向的应用效率冲击通过提高模仿型企业的知识利用率，在短期内促进了TFP和总产出增长，但挤出了创新型企业的研发劳动，从而降低了知识积累速度，使得中长期TFP和总产出下降，阻碍了两类企业的中长期发展。知识产权保护在应用效率冲击中的作用比较明显，主要是因为模仿型企业受到的正面影响通过知识租金反馈到创新型企业，产生正向的反馈作用，促进创新型企业的知识积累，削弱了挤出效应所产生的负面影响。知识产权保护水平越高，正向的反馈作用越强，中长期经济发展受到的负面影响越小。

本文的核心结果在于，正向的应用效率冲击有利于短期经济发展而不利于中长期经济发展。这意味着由应用效率推动的经济繁荣可能会损害经济增长潜力。其现实逻辑主要在于，重大技术迅速大规模应用抢占了技术创新领域的人才，使得知识积累放缓，经济增长潜力下降，最终中长期经济发展水平低于最优发展路径。加强知识产权保护能够有效避免这一风险。

本文与知识产权保护的理论文献密切相关。目前，已有大量文献从理论上研究了知识产权保护的经济效应，主要是基于南北框架下的内生增长模型（Grossman和Helpman，1991；Helpman，1993；Lai，1998；朱东平，2004；郭春野和庄子银，2012；杨轶波，2018），还有部分聚焦发展中国家经济发展的研究（刘小鲁，2011；陈凤仙和王琛伟，2015）。本文与这些文献的区别主要有三点：第一，从研究内容看，上述文献主要关注知识产权保护对技术创新、经济增长和社会福利的影响，而本文则关注知识产权保护在研发效率冲击中的作用。第二，从理论机制看，上述文献主要关注溢出知识的免费获取，强调知识产权对国内企业模仿国外先进技术的抑制作用，通常假定知识产权保护降低模仿率或溢出率，或者提高模仿成本，而忽略了知识产权的交易。在本文模型中，模仿型企业可以通过付费购买知识使用权和免费获取溢出知识这两种方式获得创新型企业的知识。因此，本文既强调知识产权保护对国内企业模仿国内技术的抑制作用，也强调知识产权保护对国内企业技术创新的激励作用，以及模仿型企业对创新型企业的反馈作用。近年来，随着产业不断向中高端迈进，中国与发达国家的技术差距明显缩小，技术模仿变得愈加困难。中国企业之间的技术差距较大，国内企业对国内技术的模仿及其对技术创新的抑制不容忽视。^①因此，本文模型与近年来国内外现状更加相符。第三，从研究方法看，上述文献大多是基于内生增长模型的静态研究或比较静态研究，本文则是基于含有内生增长的DSGE模型的动态研究。

本文也与中国研发效率的研究相关。现有文献主要关注中国研发效率或创新效率的测量（朱有为和徐康宁，2006；官建成和陈凯华，2009；陈凯华等，2015；熊曦等，2019），并从实证角度探究了大量影响因素（肖文和林高榜，2014；韩先锋等，2015；戴魁早和刘友金，2016；钟昀珈等，2016；潘健平等，2019；赵甜和方慧，2019；姜军等，2020），而较少探讨研发效率变化对宏观经济的影响及其机制。陈凤仙和王琛伟（2015）是鲜见的将研发效率与知识产权保护结合起来研究的文献。他们通过构建一国经济内的双寡头模型，分析了不同研发效率水平下的最优知识产权保护。本文在某种程度上是在陈凤仙和王琛伟（2015）界定的创新型国家建设的高级阶段，进一步研究了两类研发效率冲击的宏观经济影响和知识产权保护的作用。当然，本文模型更加丰富且贴近现实。

本文还属于含有内生增长的DSGE模型研究。含有内生增长的DSGE模型是在普通DSGE模型中嵌入内生增长机制的模型，适合于研究经济增长与经济波动相互影响的中长期问题。近十年，国外相关文献迅速增长并逐渐成熟，如Comin和Gertler（2006）、Comin等（2014）、Kung和Schmid（2015）、Moran和Queralto（2018）、Anzoategui等（2019）、Bianchi等（2019）以及Queralto（2020）等。内生增长机制一般包括技术创新和技术采用两个过程，经济趋势的处理也更加清楚合理。与国外文献相比，国内文献相对较少，且内生增长机制比较简单。例如，徐舒等（2011）在DSGE模型中引入R&D投入和技术转化，研究了技术扩散对中国经济波动的影响。而徐舒等（2011）的内生增长机制实际上只内生化了技术应用过程，技术创新仍是外生的。本文的内生增长机制刻画了创新型企业与模仿型企业之间的知识互动，不仅包括知识积累和知识利用两个过程，还引入了知识服务商，既打开了知识产权交易市场，又避免了对具体知识产权的追踪，使得模型具有较好的微观基础。与国外文献相比，本文区分了创新型企业和模仿型企业，更便于研究中国的创新问题。

值得一提的是，允许模仿型企业通过付费购买知识使用权和免费获取溢出知识这两种方式获得创新型企业的知识，是本文模型的一个重要理论创新。一方面，关于知识产权的现有文献主要关注溢出知识的免费获取，忽略了知识产权的交易。另一方面，关于技术创新和采用的现有文献（Comin和Gertler，2006；Anzoategui等，2019）假设采用者只能通过购买获得创新者的新技术，忽略了溢出知识的免费获取，因而难以用于知识产权保护的研究。与这两类文献相比，本文模型既允许模仿型企业通过购买知识使用权获取知识，又考虑了模仿型企业免费获取溢出的知识。这一设定丰富了企业间的知识流动途径，不但能够对知识使用权进行定价，而且便于使用模仿型企业付费获取的知识占比来衡量知识产权保护水平。因此，本文模型既能用于知识产权保护的研究，又能用于知识产权交易的研究。

本文主要有三个贡献。第一，本文揭示了研发效率冲击的宏观影响以及知识产权保护的作用，而现有文献较少将研发效率与知识产权保护结合起来研究。第二，本文创新性地指出，由应用效率推动的短期繁荣可能会损害经济增长潜力。据我们所知，鲜有文献关注到这一重要现象。第三，本文还是含有内生增长的DSGE模型研究的一个拓展，模型中允许模仿型企业通过两种方式获取知识是一个重要的理论创新。

二、经验事实

本部分利用2011—2017年的省级面板数据，探讨创新效率冲击和应用效率冲击对未来TFP增长率的影响，以及知识产权保护的作用。由于研发效率冲击很难观测，本文通过衡量企业在积累知识和利用知识过程中的研发费用来识别两类冲击。其合理性主要在于，创新效率和应用效率的变化势必引起相关研发费用的同步同向变化。

（一）回归方程

为了考察两类研发效率冲击对未来TFP增长率的影响，本文构建了如下的回归方程：

其中，被解释变量 $ dln{TFP}_{i,t+s} $ 表示第 $ t+s $ 期省份 $ i $ 的TFP增长率。在解释变量中， $ {RDgdp}_{i,t} $ 表示第 $ t $ 期省份 $ i $ 中企业在积累知识过程中的经费支出与当地生产总值之比， $ {TechRgdp}_{i,t} $ 表示企业在利用知识过程中的经费支出与当地生产总值之比。 $ {IPP}_{i,t} $ 表示知识产权保护水平，它与 $ {RDgdp}_{i,t} $ 和 $ {TechRgdp}_{i,t} $ 的交叉项分别用于探讨知识产权保护在两类研发效率冲击中的作用。 $ {X}_{i,t} $ 为控制变量， $ {\theta }_{t} $ 为年份固定效应， $ {\epsilon }_{i,t+s} $ 为扰动项。

（二）变量与数据

被解释变量 $ dln{TFP}_{i,t+s} $ 根据索洛余值法得到。具体而言，基于2001—2017年不包括西藏的30个省、直辖市、自治区的面板数据，以就业人员人均GDP增长率为被解释变量，就业人员人均资本存量为解释变量，进行OLS回归分析，在回归过程中控制省份固定效应。回归得到的资本收入份额约为0.515，所以各省份TFP增长率为：

$ dln{TFP}_{i,t}=dln\left(\frac{{GDP}_{i,t}}{{L}_{i,t}}\right)-0.515\times dln\left(\frac{{K}_{i,t}}{{L}_{i,t}}\right) $

其中， $ dln\left(X\right) $ 表示变量X的对数差分。 $ {GDP}_{i,t} $ 为各省份地区生产总值， $ {L}_{i,t} $ 为各省份就业人数， $ {K}_{i,t} $ 为各省份资本存量。资本存量 $ {K}_{i,t} $ 通过永续盘存法计算得到，初始值采用张军等（2004）以当前价格计算的2000年资本存量，其中重庆和四川的初始资本存量按3∶7分配。地区生产总值、固定资本形成总额、固定资产投资价格指数以及固定资产折旧数据来源于CSMAR数据库，就业人数来源于各省份统计年鉴。

对于解释变量 $ {RDgdp}_{i,t} $ 和 $ {TechRgdp}_{i,t} $ ，本文使用各省份规模以上工业企业R&D经费支出和技术改造经费支出，分别衡量企业在积累知识和利用知识过程中发生的研发费用。这两类经费支出数据均来源于CSMAR数据库。各省份知识产权保护指数 $ IP{P}_{i.t} $ 的构造方法与魏浩和巫俊（2018）相同，等于全国知识产权保护指数与各省份执法力度的乘积。各省份执法力度包括律师人数、专利侵权案件结案率和专利未被侵权率三项指标。中国知识产权保护指数来源于世界经济论坛发布的《全球竞争力报告》，各省份律师人数来源于各省份统计年鉴，专利侵权案件结案率和专利未被侵权率的数据来源于CSMAR数据库。

考虑到企业研发费用可能受到当地经济情况的影响而产生内生性问题，本文构建了以下三个工具变量，捕捉两类企业研发费用变动中受到全国性冲击的影响：

$ {RDgdp}_{it}^{IV}=\frac{{\overline{{RD}}}_{i}}{{\sum }_{i}{\overline{RD}}_{i}}\times \frac{{RD}_{t}}{GD{P}_{t}} $

$ {TechRgdp}_{it}^{IV}=\frac{{\overline{TechR}}_{i}}{{\sum }_{i}{\overline{TechR}}_{i}}\times \frac{{TechR}_{t}}{GD{P}_{t}} $

$ {PhD}_{it}^{IV}=\frac{{\overline{University}}_{i}}{{\sum }_{i}{\overline{University}}_{i}}\times \frac{{PhD}_{t}}{Populatio{n}_{t}} $

其中，工具变量 $ {RDgdp}_{it}^{IV} $ 、 $ {TechRgdp}_{it}^{IV} $ 和 $ {PhD}_{it}^{IV} $ 分别表示样本区间内各省份R&D经费支出年均值 $ {\overline{RD}}_{i} $ 、技术改造经费支出年均值 $ {\overline{TechR}}_{i} $ 和高校个数年均值 $ {\overline{University}}_{i} $ 与全国年均值之比，同对应的当期全国R&D经费支出 $ {RD}_{t} $ 与国内生产总值 $ GD{P}_{t} $ 之比、全国技术改造经费支出 $ {TechR}_{t} $ 与国内生产总值 $ GD{P}_{t} $ 之比、全国博士生毕业人数 $ {PhD}_{t} $ 与全国总人口 $ Populatio{n}_{t} $ 之比的乘积。 $ {RD}_{t}/GD{P}_{t} $ 、 $ {TechR}_{t}/GD{P}_{t} $ 和 $ {PhD}_{t}/Populatio{n}_{t} $ 分别用于识别全国性的创新效率冲击、应用效率冲击和研发劳动供给变动。这三个工具变量的变动来源均为全国性冲击，而受省份内部的时变因素影响较小，因而可以较好地避免由当地的短期经济因素变动所引起的研发费用与TFP的短期联动效应的影响。

然而，上述工具变量无法避免由当地的长期经济结构特征所引起的研发费用与TFP的长期联动效应带来的内生性问题。对于这一内生性问题，本文通过安慰剂检验对估计结果进行验证。具体而言，在回归方程中，本文将基于上述工具变量分析两类研发效率冲击对未来TFP增长率的影响；而在安慰剂检验中，本文将基于上述工具变量检验两类研发效率冲击对过去TFP增长率的影响。若本文的估计结果是由各省份长期经济结构的差异所引起的，则工具变量中各省份的差异来源应该不仅能够解释各省份未来TFP增长率的差异，也能够解释各省份过去TFP增长率的差异，安慰剂检验结果应显著，反之则不显著。

控制变量包括当期的TFP水平 $ {TFP}_{i,t} $ 、知识产权保护指数 $ {IPP}_{i,t} $ 、出口占地区生产总值比重 $ EXPgd{p}_{i,t} $ 、城镇人口占比 $ Urban{R}_{i,t} $ 、劳动报酬占地区生产总值比重 $ LaborInc{S}_{i,t} $ 、每平方千米运营铁路里程数 $ RWare{a}_{i,t} $ 以及就业人口平均受教育年限 $ EducYea{r}_{i,t} $ 。对于变量 $ EXPgd{p}_{i,t} $ 、 $ Urban{R}_{i,t} $ 、 $ LaborInc{S}_{i,t} $ 、 $ RWare{a}_{i,t} $ 以及 $ EducYea{r}_{i,t} $ 的选取，本文借鉴了金相郁（2007）以及庞瑞芝和杨慧（2008）的研究。就业人口平均受教育年限 $ EducYea{r}_{i,t} $ 的数据来自《中国人口和就业统计年鉴》，其他变量的数据均来自CSMAR数据库。

（三）回归结果

回归结果如表1所示。列（2）为基准回归结果，估计方法为两阶段最小二乘（2SLS）工具变量回归。容易看到， $ RDgdp $ 的系数在5%的水平上显著为正，表明创新效率的提高可以促进未来第3期的TFP增长。 $ TechRgdp $ 的系数在1%的水平上显著为负，表明应用效率的提高会抑制未来第3期的TFP增长。交叉项 $ RDgdp\times IPP $ 的系数不显著，表明知识产权保护在创新效率冲击中对TFP增长没有明显作用。交叉项 $ TechRgdp\times IPP $ 的系数在1%的水平上显著为正，表明知识产权保护在应用效率冲击中对TFP增长有明显的促进作用。

基准回归结果具有稳健性。在使用广义矩估计（GMM）的列（3）中，解释变量的系数与列（2）几乎相同。在未使用工具变量的列（1）中，虽然 $ TechRgdp $ 和 $ TechRgdp\times IPP $ 的系数显著程度有所下降，但是仍与列（2）一致。 $ TechRgdp $ 和 $ TechRgdp\times IPP $ 的系数显著程度下降表明列（1）的确存在内生性问题。列（4）和列（5）使用与列（2）不同时期的TFP增长率作为被解释变量，也得到了相似的结果。在使用未来第2期TFP增长率的列（4）中， $ TechRgdp $ 的系数不显著， $ TechRgdp\times IPP $ 的系数变小且显著程度下降。而在使用未来第4期TFP增长率的列（5）中， $ TechRgdp $ 和 $ RDgdp\times IPP $ 的系数在1%的水平上显著，且系数的绝对值都大于列（4），表明应用效率的提高对TFP增长的抑制作用在一定时期内增强，知识产权保护在应用效率冲击下对TFP增长的促进作用也在一定时期内增强。

在安慰剂检验中，本文使用滞后3期的各省份TFP增长率作为被解释变量，回归结果如列（6）所示。可以看到， $ TechRgdp $ 、 $ RDgdp\times IPP $ 和 $ RDgdp\times IPP $ 的系数均不显著， $ RDgdp $ 的系数虽显著，但符号与列（2）相反，说明本文的结果不是由各地长期经济结构的差异所引起的。以其他滞后期TFP增长率作为被解释变量的回归结果也与列（6）类似。

三、理论模型

本部分将企业区分为注重知识积累的创新型企业和注重知识利用的模仿型企业，建立一个含有内生增长的两部门DSGE模型。在模型中，经济主体包括家庭、创新型企业、模仿型企业、知识服务商和最终产品企业。

创新型企业雇用研发劳动来积累知识，其研发活动受到创新效率冲击的影响。模仿型企业雇用研发劳动来利用知识，其研发活动受到应用效率冲击的影响。模仿型企业自身不积累知识，通过付费购买知识使用权和免费获取溢出知识这两种方式获得创新型企业积累的知识。本文以模仿型企业付费获取的知识占社会知识存量的比例来衡量知识产权保护水平。模仿型企业的付费知识占比越高，知识产权保护水平越高。因为知识积累过程通常较为缓慢，所以模型中一期代表一年。所有价格变量为最终产品的相对价格。

（一）代表性家庭

经济中存在一个无限期存活的代表性家庭，通过选择消费 $ {C}_{t} $ 、普通劳动 $ {L}_{t} $ 、研发劳动 $ {H}_{t} $ 以及下一期的债券持有量 $ {B}_{t+1} $ ，最大化预期加总折现效用：

$ {E}_{t}{\sum }_{s=0}^{\infty }{\beta }^{s}\left[\mathrm{l}\mathrm{n}\left({C}_{t+s}\right)-\frac{{\left({\xi }^{L} {L}_{t+s}\right)}^{1+\eta }+{\left({\xi }^{H} {H}_{t+s}\right)}^{1+\eta }}{1+\eta }\right] $

其中， $ \beta \in \left(\mathrm{0,1}\right) $ 为代表性家庭的主观折现因子， $ {\xi }^{L} > 0 $ 为普通劳动偏好参数， $ {\xi }^{H} > 0 $ 为研发劳动偏好参数， $ \eta $ 为Frisch劳动供给弹性的倒数。令 $ {r}_{t} $ 为实际利率， $ {W}_{t}^{L} $ 为普通劳动工资， $ {W}_{t}^{H} $ 为研发劳动工资， $ {D}_{t} $ 为企业的股息分红，则代表性家庭的预算约束为：

$ {C}_{t}+\frac{{B}_{t+1}}{{r}_{t}}={W}_{t}^{L}{L}_{t}+{W}_{t}^{H}{H}_{t}+{B}_{t}+{D}_{t} $

（二）中间产品企业和知识服务商

中间产品由两类企业生产：注重知识积累的创新型企业（部门 $ n $ ）和注重知识利用的模仿型企业（部门 $ m $ ）。部门 $ i\in \{n,m\} $ 的企业在 $ \left[\mathrm{0,1}\right] $ 上连续分布，部门内的产品完全替代，可加总得到部门总产出：

$ {Y}_{n,t}={\int }_{0}^{1}{Y}_{n,j,t}dj,\;\;{Y}_{m,t}={\int }_{0}^{1}{Y}_{m,j,t}dj $

部门 $ i\in \{n,m\} $ 的企业 $ j $ 使用资本 $ {K}_{i,j,t} $ 并雇用普通劳动 $ {L}_{i,j,t} $ 来生产中间产品，生产函数为Cobb-Douglas函数：

$ {Y}_{i,j,t}={\left({K}_{i,j,t}\right)}^{\alpha }{\left({A}_{i,j,t}{L}_{i,j,t}\right)}^{1-\alpha } $

其中， $ \alpha \in (0,    1) $ 为资本收入份额。 $ {A}_{i,j,t} $ 为企业全要素生产率，由企业实际利用的知识内生决定：

$ {A}_{i,j,t}={u}_{i,j,t}{N}_{i,j,t} $

其中， $ {N}_{i,j,t} $ 表示部门 $ i $ 的企业 $ j $ 可使用的知识存量， $ {u}_{i,j,t} $ 表示部门 $ i $ 的企业 $ j $ 对可使用的知识存量的利用率。企业 $ j $ 通过投资 $ {I}_{i,j,t} $ 积累资本 $ {K}_{i,j,t} $ ，积累方程为：

$ {K}_{i,j,t+1}=\left(1-{\delta }_{K}\right){K}_{i,j,t}+{I}_{i,j,t} $

其中， $ {\delta }_{K}\in (0,    1) $ 为资本折旧率。

1. 创新型企业。创新型企业 $ j\in [0,    1] $ 自行积累知识存量，假设其知识存量可以完全利用，知识利用率 $ {u}_{n,j,t}\equiv 1 $ ，且无需支付额外的知识利用成本。

每期期初，创新型企业 $ j $ 拥有知识存量 $ {N}_{n,j,t} $ 。在 $ t $ 期，创新型企业 $ j $ 雇用研发劳动 $ {H}_{n,j,t} $ 进行知识积累。借鉴Comin和Gertler（2006）以及Anzoategui等（2019），假设单位研发劳动的平均知识创造量为 $ {\chi }_{n,t}{N}_{n,t}{\left({H}_{n,j,t}\right)}^{\varrho -1} $ 。其中，变量 $ {\chi }_{n,t} $ 为创新效率，即创新型企业的研发效率，是平稳的外生冲击，假设 $ \mathrm{l}\mathrm{n}\left({\chi }_{n,t}\right) $ 服从参数为 $ {\rho }_{n} $ 和 $ {\sigma }_{n} $ 的 $ AR\left(1\right) $ 过程。系数 $ \varrho \in (0,    1) $ 表示拥塞效应的程度，造成研发劳动的边际报酬递减。企业个体平均知识创造量与社会知识总量 $ {N}_{n,t} $ 成正比，说明社会知识总量具有正向溢出效应。因此，创新型企业 $ j $ 的知识积累方程为：

$ {N}_{n,j,t+1}=\left(1-{\delta }_{N}\right){N}_{n,j,t}+{\chi }_{n,t}{N}_{n,t}{\left({H}_{n,j,t}\right)}^{\varrho } $

(1)

其中， $ {\delta }_{N}\in \left(\mathrm{0,1}\right) $ 为知识过时率。过时的知识可以理解为被社会发展所淘汰的一些技术知识，如胶卷、磁带和留声机的制作，这类知识对提高企业全要素生产率不再有作用。

创新型企业 $ j $ 在每期期初将其所拥有的知识存量 $ {N}_{n,j,t} $ 的使用权出租给知识服务商，获得租金回报。假设每单位知识的租金为 $ {P}_{N,j,t} $ ，则创新型企业 $ j $ 的预算约束为：

其中， $ {D}_{n,j,t} $ 表示创新型企业的股息分红。创新型企业 $ j $ 在预算约束下最大化股息贴现值 $ {\sum }_{s=0}^{\infty }{\Lambda }_{t+s}{D}_{n,j,t+s} $ ，其中 $ {\Lambda }_{t} $ 为随机贴现因子。根据创新型企业最优化问题，在对称性条件下，可以得到创新型企业的最优知识存量和最优研发劳动投入：

$ {Q}_{N,t}\left[{\chi }_{n,t}{N}_{n,t} \varrho {\left({H}_{n,t}\right)}^{\varrho -1}\right]={W}_{t}^{H} $

(3)

其中， $ {Q}_{N,t} $ 为知识的影子价格， $ {P}_{N,n,t} $ 为创新型企业单位知识的平均租金。方程（2）的含义为单位知识的当期价值等于单位知识下一期所带来的收益的贴现值。单位知识下一期所带来的收益包括下一期的价值、知识存量的边际收益和出租知识使用权的收益。方程（3）的含义为单位研发劳动所创造的知识的价值等于研发工资。值得注意的是，若无知识产权保护，方程（2）中将不会出现 $ {P}_{N,n,t} $ 。因此，根据方程（1）和方程（3），知识产权保护增加了创新型企业单位知识的收益，提高了知识的影子价格，激励了创新型企业投入更多的研发劳动，从而加快了知识积累。

2. 知识服务商。知识服务商每期向创新型企业 $ j $ 支付知识租金 $ {P}_{N,j,t}{N}_{n,j,t} $ 以获得知识使用权，并对知识和知识使用权进行打包，打包的知识为 $ {N}_{n,t}={\int }_{0}^{1}{N}_{n,j,t}dj $ 。假设在知识服务商打包的过程中， $ 1-\omega \in \left(\mathrm{0,1}\right) $ 比例的知识发生溢出，被模仿型企业免费获得。知识服务商将剩余未溢出知识 $ \omega {N}_{n,t} $ 的使用权按照每单位知识单期的价格 $ {P}_{N,t} $ 出售给模仿型企业。由利润最大化和零利润可得：

$ {P}_{N,n,t}=\omega {P}_{N,t} $

(4)

本文使用 $ \omega $ 来衡量知识产权保护水平。 $ \omega $ 越高，则模仿型企业付费获得的知识占比越大，知识产权保护水平越高。本文假定所有知识都能被模仿型企业获得，要么是付费获取，要么是免费获取。毫无疑问，现实中付费获取的知识必然受到知识产权保护。知识产权保护范围越广、执法越严，付费知识的占比就越高，因而本文的衡量方式是自然而合理的。需要注意的是，本文模型中的知识主要指的是企业开发的、用于生产的专利技术。现实中，由于专利的保护期限最长不超过二十年，并非所有知识都会申请专利，部分知识会以商业秘密的形式存在，很难被其他企业获得。但鉴于这部分知识占比较低，且模仿型企业不能完全利用所有知识，模型中将其当作溢出知识处理并无大碍。

3. 模仿型企业。模仿型企业 $ j\in [0,    1] $ 自身不积累知识，但可以通过两种方式获得创新型企业所积累的知识：一是免费获得溢出的知识 $ (1-\omega ){N}_{n,t} $ ；二是向知识服务商购买知识使用权 $ {\overline{N}}_{m,j,t} $ ，单位知识使用权的购买价格为 $ {P}_{N,t} $ 。因此，模仿型企业 $ j $ 可使用的知识存量为：

$ {N}_{m,j,t}={\overline{N}}_{m,j,t}+(1-\omega ){N}_{n,t} $

模仿型企业通过雇用研发劳动 $ {H}_{m,j,t} $ 来提高其对知识的利用率 $ {u}_{m,j,t} $ ，假设两者的关系如下：

$ {u}_{m,j,t}={\frac{1}{\gamma }{\chi }_{m,t}\left({H}_{m,j,t}\right)^{\gamma }} $

(5)

其中， $ \gamma \in (0,    1) $ 为知识利用率关于研发劳动的弹性。因此， $ {H}_{m,j,t} $ 越多，企业的知识利用率越高，但知识边际利用率越低。变量 $ {\chi }_{m,t} $ 为应用效率，即模仿型企业的研发效率，是平稳的外生冲击，假设 $ \mathrm{l}\mathrm{n}\left({\chi }_{m,t}\right) $ 服从参数为 $ {\rho }_{m} $ 和 $ {\sigma }_{m} $ 的 $ AR\left(1\right) $ 过程。

模仿型企业 $ j $ 的预算约束为：

其中， $ {D}_{m,j,t} $ 为模仿型企业的股息分红。模仿型企业 $ j $ 在预算约束下最大化股息贴现值 $ {\sum }_{s=0}^{\infty }{\Lambda }_{t+s}{D}_{m,j,t+s} $ 。根据模仿型企业的最优化问题，在对称性条件下，可以得到模仿型企业的最优知识使用权购买价格和最优研发劳动投入：

$ \left(1-\mathrm{\alpha }\right) \frac{{P}_{m,t}{Y}_{m,t}}{{N}_{n,t}}={P}_{N,t} $

(6)

$ \frac{\gamma \left(1-\alpha \right){P}_{m,t}{Y}_{m,t}}{{H}_{m,t}}={W}_{t}^{H} $

(7)

方程（6）的含义为单位知识的边际收益等于其使用权的购买价格。方程（7）的含义为单位研发劳动的边际收益等于研发工资，等式左边也可以看作单位研发劳动对知识利用率的改变量乘以知识利用率的边际收益。

（三）最终产品企业

最终产品企业将两类中间产品打包生产为最终产品，生产函数为CES（Constant Elasticity of Substitution）函数：

$ {Y}_{t}={\left(\varphi {Y}_{n,t}^{(\sigma -1)/\sigma }+\left(1-\varphi \right){Y}_{m,t}^{(\sigma -1)/\sigma }\right)}^{\sigma /(\sigma -1)} $

其中， $ {Y}_{n,t} $ 和 $ {Y}_{m,t} $ 分别为创新部门和模仿部门的总产出， $ \varphi \in \left(\mathrm{0,1}\right) $ 为创新部门的相对占比， $ \sigma > 0 $ 为两类中间产品的替代弹性。令两类中间产品的价格分别为 $ {P}_{n,t} $ 和 $ {P}_{m,t} $ ，则由成本最小化和零利润可得：

$ {Y}_{n,t}={\varphi }^{\sigma }{\left(\frac{{P}_{n,t}}{{P}_{t}}\right)}^{-\sigma } {Y}_{t},\;\;{Y}_{m,t}={\left(1-\varphi \right)}^{\sigma }{\left(\frac{{P}_{m,t}}{{P}_{t}}\right)}^{-\sigma } {Y}_{t} $

$ {P}_{t}={\left({\varphi }^{\sigma }{P}_{n,t}^{1-\sigma }+{\left(1-\varphi \right)}^{\sigma }{P}_{m,t}^{1-\sigma }\right)}^{1/(1-\sigma )} $

（四）市场出清及其他

出清条件包括产品市场出清、普通劳动市场出清和研发劳动市场出清。其中，产品市场出清条件为 $ {Y}_{t}={C}_{t}+{I}_{t} $ 。总投资 $ {I}_{t}={I}_{n,t}+{I}_{m,t} $ 。普通劳动市场和研发劳动市场出清的条件分别为 $ {L}_{t}={L}_{n,t}+{L}_{m,t} $ 和 $ {H}_{t}={H}_{n,t}+{H}_{m,t} $ 。定义社会整体的全要素生产率为：

$ {TFP}_{t}=\frac{{Y}_{t}}{{\left({K}_{n,t}+{K}_{m,t}\right)}^{\alpha } {L}_{t}^{1-\alpha }} $

（五）趋势变量与知识增长率

在模型中，创新型企业和模仿型企业的TFP增长趋势都由创新部门知识存量 $ {N}_{n,t} $ 决定。因此，创新部门所积累的社会知识总量 $ {N}_{n,t} $ 是长期生产率提高和经济增长的唯一来源。参考Bianchi等（2019）， $ {N}_{n,t} $ 可以被视作趋势变量。社会知识总量 $ {N}_{n,t} $ 也决定了总产出（ $ {Y}_{t} $ ）、总消费（ $ {C}_{t} $ ）、总投资（ $ {I}_{t} $ ）、资本存量（ $ {K}_{n,t} $ 和 $ {K}_{m,t} $ ）等非平稳变量的长期趋势。为了得到平稳变量，只需把相应的非平稳变量除以社会知识总量 $ {N}_{n,t} $ 或关于 $ {N}_{n,t} $ 的趋势表达式。

与外生增长DSGE模型不同的是，本文模型中趋势增长率不是常数或者外生的随机变量，而是一个内生决定的变量，即知识增长率 $ {\mu }_{n,t}\equiv {N}_{n,t+1}/{N}_{n,t} $ 。由知识积累方程（1）可得：

$ {\mu }_{n,t}=\left(1-{\delta }_{N}\right)+{\chi }_{n,t} {\left({H}_{n,t}\right)}^{\varrho } $

(8)

在长期，增加创新部门的研发劳动投入 $ {H}_{n,t}={\int }_{0}^{1}{H}_{n,j,t}dj $ ，可以提高社会知识总量的增长率，提升社会生产率，加速经济增长。

四、模拟分析

本部分在上文建立的两部门DSGE模型中模拟两类研发效率冲击的影响。首先进行参数校准，然后展示基本的模拟结果，最后进行稳健性讨论。值得注意的是，模型中一期代表一年。

（一）参数校准

待校准的参数可分为三类：一是文献中的常见参数，二是研发活动相关参数，三是外生冲击相关参数。首先对常见的参数进行校准。参考Chang等（2016），中国劳动收入份额 $ \alpha $ 设为0.5。由于模型中一期代表一年，贴现系数 $ \beta $ 为文献中常见值0.99的年化值 $ {0.99}^{4}\approx 0.96 $ 。关于资本年折旧率，张军等（2004）的估计结果为9.6%，且大部分研究中国经济波动的文献选取0.10，所以 $ {\delta }_{K} $ 设为0.10。Frisch劳动供给弹性的倒数 $ \eta $ 设为3，与徐舒等（2011）以及胡永刚和郭新强（2012）一致。普通劳动偏好 $ {\xi }^{L} $ 的校准值使总劳动时间L为0.4，与Chang 等（2015）一致。由于创新型企业和模仿型企业的产品具有较强的替代性，两类产品的替代弹性 $ \sigma $ 设为10，与国内文献对中间产品替代弹性的赋值一致。

研发活动相关参数主要基于中国规模以上工业企业2012—2019年数据进行校准，同时参考一些国外文献。在校准过程中，中国规模以上工业企业中有R&D活动的企业被视作创新型企业，而没有R&D活动的企业被视作模仿型企业，同时规模以上工业企业的技术改造经费支出被视作模仿型企业的研发费用。中国规模以上工业企业有R&D活动的企业平均占比约为22%，所以模型中创新部门的相对占比 $ \varphi $ 的取值为0.451，使得在稳态下创新部门产值占总产值的比例 $ {P}_{n}{Y}_{n}/Y $ 为22%。基于中国R&D人员折合全时当量、规模以上工业企业技术改造经费支出和R&D经费支出的数据，本文对模型中总研发劳动H的稳态值进行估计（H=0.00272 ），^②进而对研发劳动偏好 $ {\xi }^{H} $ 进行校准。

研发活动相关参数还包括知识积累相关参数和知识利用相关参数。在知识积累方面，关于知识过时率 $ {\delta }_{N} $ ，参考Anzoategui等（2019）的季度校准值0.02，本文设为0.08。关于拥塞效应系数 $ \mathrm{\varrho } $ ，Griliches（1990）利用1945—1987年美国专利年度数据得到的估计值约为0.9，Anzoategui等（2019）利用1984—2008年美国季度数据得到的贝叶斯后验均值为0.372。Anzoategui等（2019）认为季度数据得到的估计值小于年度数据得到的估计值，是因为更高频率的研发劳动投入调整会产生更高的调整成本，从而造成更严重的边际报酬递减。因此，考虑到模型中一期代表一年，且中国处于技术追赶阶段，创新部门研发劳动边际报酬递减规律较强， $ \mathrm{\varrho } $ 设为0.5。创新效率稳态 $ {\chi }_{n} $ 的校准值使稳态知识增长率 $ {\mu }_{n} $ 为1.071，与中国2012—2019年GDP年均增长率一致。

在知识利用方面，应用效率稳态 $ {\chi }_{m} $ 取值为0.046，知识利用率对研发劳动的弹性 $ \gamma $ 取值为0.040，模仿型企业付费知识占比即知识产权保护水平 $ \omega $ 取值为0.003。^③这三个参数的取值意味着：第一，稳态时模仿型企业能够完全利用上一期的知识存量，即知识利用率的稳态值 $ {u}_{m}=(1-{\delta }_{N})/{\mu }_{n}=0.859 $ ；第二，稳态时模仿型企业和创新型企业的研发劳动之比为0.36，与中国规模以上工业企业技术改造经费支出与R&D经费支出的比值一致；第三，稳态时模仿型企业购买知识使用权支出与创新型企业研发支出之比为2.6%，与中国规模以上工业企业购买国内技术经费支出与R&D经费支出比值的均值一致。

对于外生冲击相关参数，由于缺乏信息，同时为了方便对比两类研发效率冲击的影响，本文将研发效率持续性系数 $ {\rho }_{n} $ 和 $ {\rho }_{m} $ 都设为0.75，标准差 $ {\sigma }_{n} $ 和 $ {\sigma }_{m} $ 都设为0.01。

（二）结果分析

为了更加清楚地展示知识产权保护在两类研发效率冲击下的作用，本文考虑两种知识产权保护水平。一种是基准保护水平（ $ \omega =0.003 $ ），该取值基于中国规模以上工业企业购买国内技术经费支出和R&D经费支出数据，通过对模型进行校准得到，反映中国现阶段的知识产权保护水平。另一种是严格保护水平（ $ \omega =0.2 $ ），反映中国未来可能达到的知识产权保护水平。在该保护水平下，创新型企业的知识租金收入与研发费用的稳态比值约为1，即知识积累活动的成本恰好由模仿型企业承担。需要注意的是，两种知识产权保护水平下的模型稳态是不同的。因此，本文比较各变量偏离其初始稳态的百分比，使两种知识产权保护水平下的脉冲响应具有可比性。

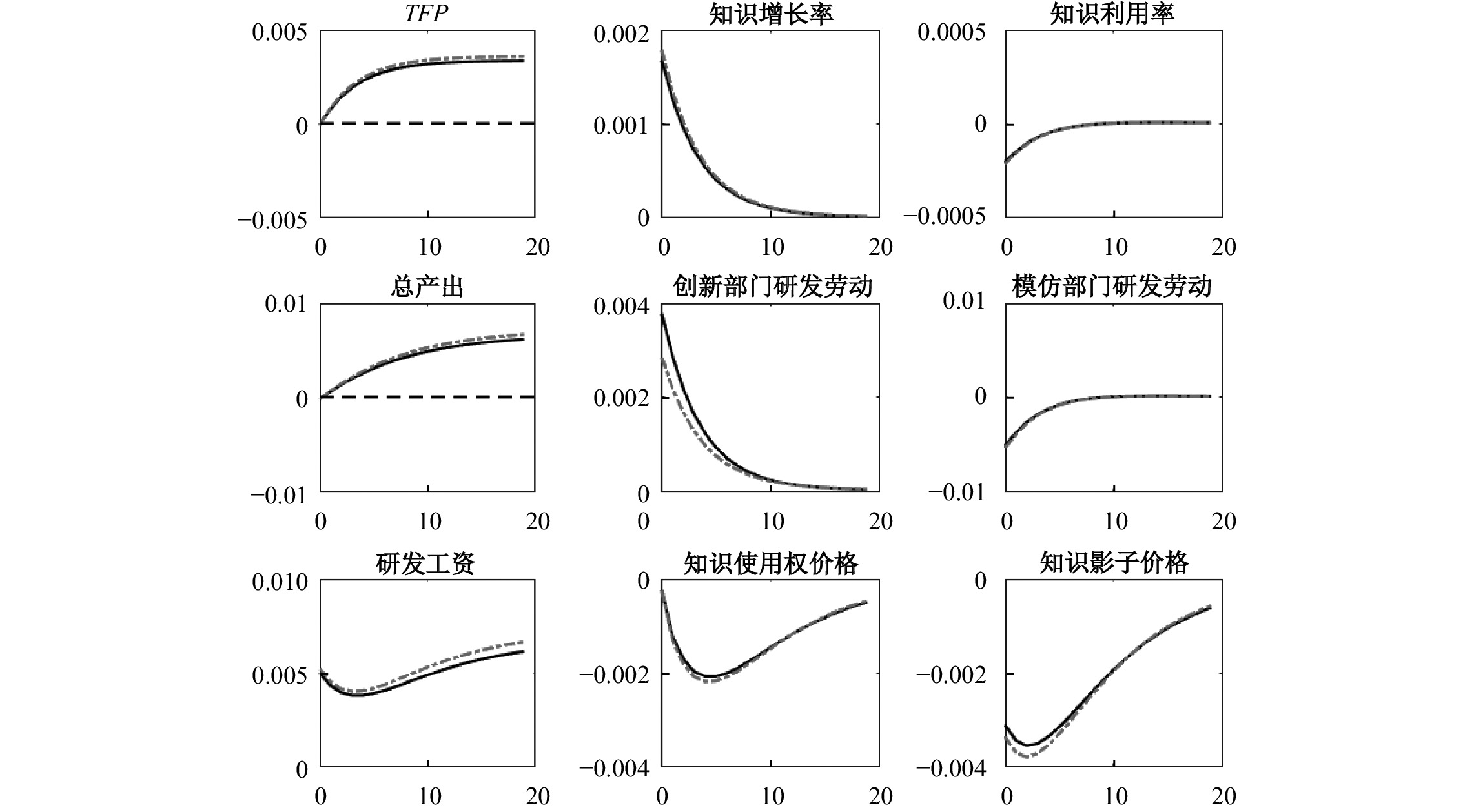
1. 创新效率冲击。创新效率冲击的脉冲响应曲线如图1所示，其中实线表示基准保护水平（ $ \omega =0.003 $ ），虚线表示严格保护水平（ $ \omega =0.2 $ ）。在基准保护水平下，正向的创新效率冲击导致创新型企业单位研发劳动投入所产生的新知识增加，鼓励创新型企业增加研发劳动投入 $ {H}_{n,t} $ ，促使知识增长率 $ {\mu }_{n,t} $ 上升。创新型企业研发劳动投入的增加和知识增长率的上升共同促使研发工资上升。知识存量的加速增长提高了中长期TFP和总产出水平，也使创新部门产出上升。知识存量的加速增长还使知识使用权的供给增加，知识的边际产出下降，从而降低了知识使用权价格和知识影子价格。此外，创新型企业研发劳动的增加挤出了模仿型企业的研发劳动投入 $ {H}_{m,t} $ ，降低了其知识利用率 $ {u}_{m,t} $ ，导致短期内其产出下降，TFP和总产出也下降，对经济造成负面影响。而从中长期看，模仿型企业可使用的知识存量因社会知识总量上升而增加，所以其产出仍会增长。

综上所述，正向的创新效率冲击通过促进知识积累，在中长期对TFP水平以及两类企业的产出均产生了正面影响。也就是说，正向的创新效率冲击不仅有利于创新型企业发展，也有利于模仿型企业的中长期发展。值得注意的是，正向的创新效率冲击导致中长期TFP明显上升，与表1列（2）中 $ RDgdp $ 的系数显著为正一致。

对于知识产权保护在创新效率冲击中的作用，模仿型企业知识利用率下降会对知识使用权的需求产生些许负面影响，并通过知识租金反馈到创新型企业，从而产生一定的负向反馈作用。这一反馈作用随知识产权保护水平的提高而增强。如图1虚线所示，在模仿型企业的负向反馈作用下，严格保护水平下的知识使用权价格和知识影子价格的下降幅度更大，从而创新型企业研发劳动和知识增长率的上升幅度减小。此外，更高的知识产权保护水平激励创新型企业投入更多的研发劳动，使得相同规模的创新效率上升带来的知识积累加速更加显著。在本文校准下，激励作用占据主导，更高的知识产权保护水平增强了正向创新效率冲击对知识存量、TFP和总产出的积极作用。不过，由于存在负向反馈作用，两种知识保护水平下知识增长率和TFP的脉冲响应曲线差别较小，这与表1列（2）中交叉项 $ RDgdp\times IPP $ 的系数不显著是一致的。

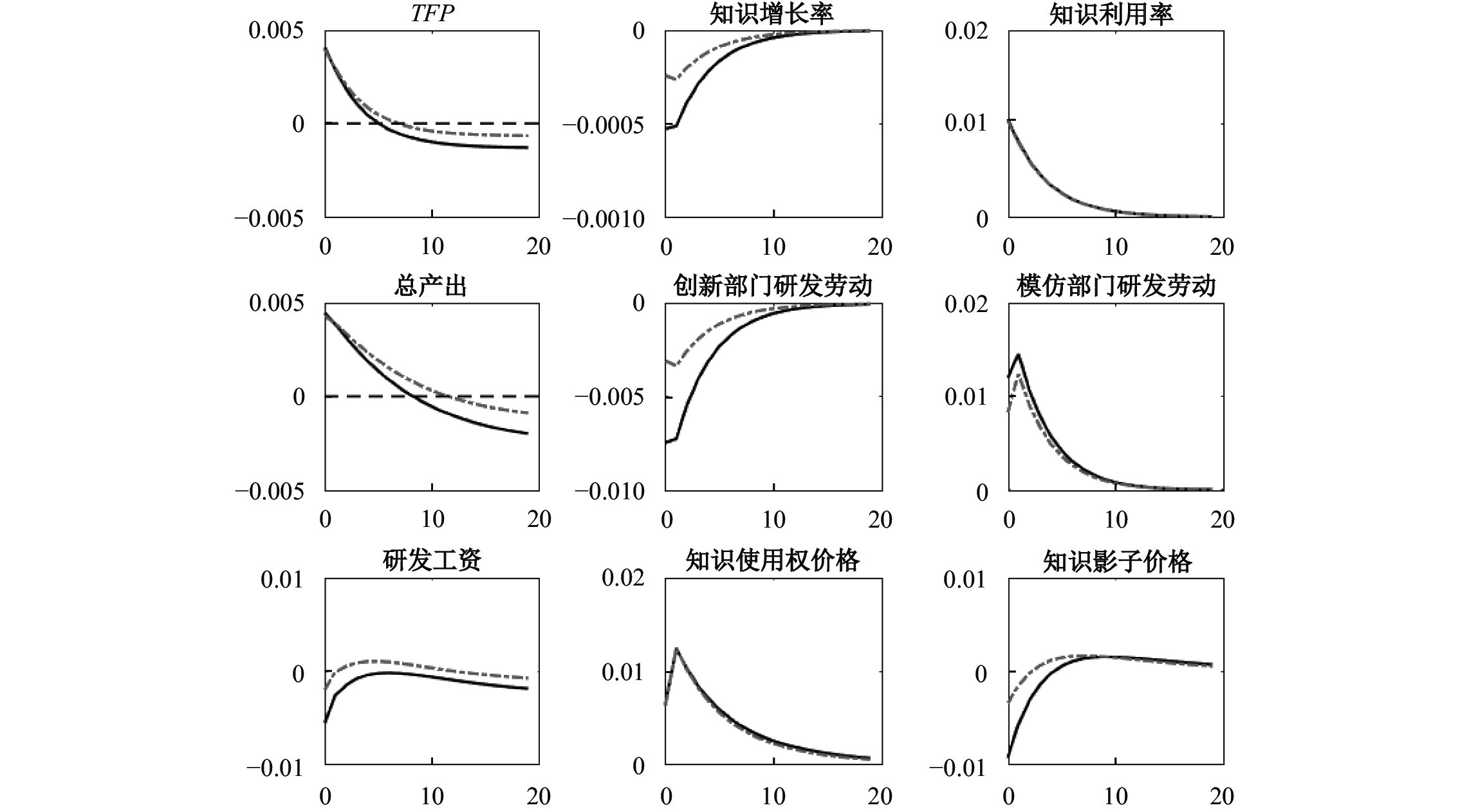
2. 应用效率冲击。应用效率冲击的脉冲响应曲线如图2所示。同样地，实线表示基准保护水平（ $ \omega =0.003 $ ），虚线表示严格保护水平（ $ \omega =0.2 $ ）。在基准保护水平下，正向的应用效率冲击提高了模仿型企业的知识利用率 $ {u}_{m,t} $ ，并鼓励模仿型企业投入更多的研发劳动 $ {H}_{m,t} $ ，从而对模仿部门产出、总产出和TFP具有短期的正面影响。然而，模仿型企业研发劳动投入的增加挤出了创新型企业的研发劳动投入 $ {H}_{n,t} $ ，降低了知识积累速度 $ {\mu }_{n,t} $ ，从而减少了创新部门的产出和知识使用权的供给。模仿型企业知识利用率的上升提高了知识使用权的边际产出，所以知识使用权的需求增加。供给减少和需求增加共同导致知识使用权价格上升，增加了创新型企业单位知识存量的知识租金，形成了正向反馈作用。

在中长期，由于知识增长率的持续下降，两个部门的产出和TFP都有所下降，低于初始稳态水平。这表明正向的应用效率冲击虽在短期内有利于模仿型企业发展和经济增长，但不利于创新型企业发展和知识积累，最终在中长期不利于模仿型企业发展和经济发展。正向的应用效率冲击导致中长期TFP明显下降，这与表1列（2）中 $ TechRgdp $ 的系数显著为负一致。

上述结果表明，正向的应用效率冲击带来的短期繁荣可能会损害经济增长潜力。联系现实，在知识产权保护水平较低的情况下，若某项重大技术（如人工智能）的应用成为可能，企业会热衷于实现技术的商业应用，高薪聘请研究人员，导致技术创新（知识积累）领域的人才流入技术应用（知识利用）领域，从而使整个社会的创新能力下降。经济发展在短期内会呈现繁荣的景象，但由于透支了经济发展的潜力，经济发展水平最终低于最优发展水平。

对于知识产权保护在应用效率冲击中的作用，知识产权保护使模仿型企业的知识利用率上升，反馈到创新型企业，从而产生正向反馈作用。这一正向反馈作用削弱了模仿型企业在研发劳动市场上对创新型企业的挤出效应。知识产权保护水平越高，反馈作用越强。如图2虚线所示，严格保护水平下知识影子价格的下降幅度更小，创新型企业研发劳动和知识增长率的下降幅度减小，模仿型企业研发劳动和知识利用率的上升幅度也减小，从而使知识使用权购买价格的上升幅度减小。在中长期，由于模仿型企业持续的正向反馈作用，知识增长率累计减小的幅度不断扩大，因此严格保护水平下的TFP和总产出都明显高于基准保护水平，与表1列（2）中交叉项 $ TechRgdp\times IPP $ 的系数显著为正一致。这表明加强知识产权保护能够有效减轻应用效率冲击带来的短期繁荣对经济增长潜力的损害，使模仿型企业的发展也能带动创新型企业的发展和知识积累，从而使经济发展处于更加合理的轨道上。

（三）稳健性讨论

首先讨论参数的影响。应用效率冲击持续性参数 $ {\rho }_{m} $ 、拥塞效应系数 $ \varrho $ 和Frisch劳动供给弹性的倒数 $ \eta $ 对核心结果都可能有较大影响。本文采用与上文不同的参数值对模型重新校准。^④

图3中（1）、（3）和（5）是不同参数值下TFP的变化，（2）、（4）和（6）是不同参数值下知识产权保护对TFP变化幅度的改变。可以看到，所有参数值下应用效率冲击都会降低中长期TFP，且知识产权保护都能改善中长期TFP，表明本文核心结果是稳健的。

图3中（1）和（2）展示了应用效率冲击持续性参数 $ {\rho }_{m} $ 的影响。子图（1）表明， $ {\rho }_{m} $ 越大，中长期TFP下降幅度越大。在现阶段，智能技术的应用将是一场持久的革命，这意味着应用效率冲击对经济增长潜力的损害可能会非常严重。子图（3）和（4）展示了拥塞效应系数 $ \varrho $ 的影响。子图（3）表明， $ \varrho $ 越大，中长期TFP下降幅度越大。一般而言，经济发展程度越高，科技水平越处于世界前列，研发劳动的边际知识产出下降得越慢，即 $ \varrho $ 越大。对于正处于技术赶超阶段的国家， $ \varrho $ 将逐渐变大，因而需要越来越重视知识产权保护。子图（5）和（6）展示了Frisch劳动供给弹性的倒数 $ \eta $ 的影响。根据子图（5）， $ \eta $ 越小，中长期TFP下降幅度越大。这主要是因为研发劳动供给在正向的应用效率冲击下减少， $ \eta $ 越小，研发劳动供给减少得越多。子图（2）、（4）和（6）均显示，应用效率冲击对TFP的影响越严重，知识产权保护对中长期TFP的改善程度越大，再次表明了知识产权保护的积极作用。

为了进一步验证结论的稳健性和模型的有效性，本文还对模型进行了贝叶斯估计。由于观测量较少，大部分参数的后验均值与先验均值差别不大。应用效率冲击持续性参数 $ {\rho }_{m} $ 的后验均值为0.608，拥塞效应系数 $ \varrho $ 的后验均值为0.216，均低于本文的校准值，相应地应用效率冲击对经济增长潜力的损害程度也较低。但后验均值拟合的是估计期内的整体情况，随着中国的技术进步和近年来智能技术的大规模应用， $ {\rho }_{m} $ 和 $ \varrho $ 都将更加接近校准值，贝叶斯估计在某种程度上体现的是经济增长潜力受损害程度的下限。

方差分解结果显示，创新效率冲击和应用效率冲击是最重要的波动来源。GDP增长率历史分解结果显示，2018—2019年，应用效率冲击对GDP增长率具有较大的正向贡献，而创新效率冲击对GDP增长率具有较大的负向贡献，与本文的主要结论一致。贝叶斯估计产生的模型数据与规模以上工业企业技术购买经费支出增长率、中国知识产权保护指数、发明专利申请数、科研机构R&D资金增长率、高校R&D资金增长率等外部数据具有较高的拟合度，在很大程度上表明本文模型是有效的，尤其是在知识产权保护方面。

五、结论与政策建议

本文从实证和理论两个角度探讨了研发效率冲击的宏观影响以及知识产权保护的作用。本文通过刻画创新型企业与模仿型企业之间的知识互动，构建了含有内生增长的两部门DSGE模型，并模拟了两种知识产权保护水平下两类研发效率冲击的影响。研究表明：第一，正向的创新效率冲击通过鼓励创新型企业的知识积累活动，促进了TFP和总产出持续加速增长，在中长期也有利于模仿型企业发展。第二，正向的应用效率冲击通过提高模仿型企业的知识利用率，促使短期内TFP和总产出提高，但抑制了创新型企业的知识积累活动，使得中长期TFP和总产出下降，从而不利于两类企业的中长期发展。第三，知识产权保护在创新效率冲击中没有明显作用，但在应用效率冲击中有明显的积极作用，加强知识产权保护能够有效避免由应用效率推动的短期繁荣对经济增长潜力的损害。

现阶段，5G、大数据、人工智能等技术正全面步入应用阶段，相关企业不惜以高薪大量招聘研究人才，恰如应用效率冲击下模仿型企业增加研发劳动投入。若被高薪聘请的研究人才来自科技前沿领域，则前沿领域将出现人才流失，正如创新型企业的研发劳动被模仿型企业挤出。在应用效率冲击下，重大技术迅速应用带来的经济繁荣固然令人欣喜，但科技前沿领域的人才流失将抑制技术创新，损害经济增长潜力，导致经济发展后劲不足。鉴于此，本文提出以下政策建议：第一，政府加强知识产权保护，完善立法和制度建设，并不断提高执法力度，维护科技贡献者的利益。第二，在关注技术应用的同时，政府还应关注科技前沿领域是否出现人才流失，适当提高前沿领域科研人员的待遇，激励青年人才进入前沿领域探索。第三，为专利技术转让提供更好的服务，加强专利技术的市场化建设，促进专利成果转化，让发明创造者能够获得更多收益，也让获得专利技术的企业更好地发展。

① 吴超鹏和唐菂（2016）的实证结果表明，减少研发溢出是知识产权保护促进企业创新的重要渠道。

② 基于中国2012—2019年工业企业数据，R&D人员折合全时当量约为总就业人数的0.5%，由此推算创新部门研发劳动 $ {H}_{n} $ 为0.002。基于模型假设和数据定义，可将规模以上工业企业的R&D经费支出与模型中创新型企业的研发劳动工资支出相对应，将技术改造经费支出与模型中模仿型企业的研发劳动工资支出相对应。由于数据中规模以上工业企业技术改造经费支出与R&D经费支出的比值约为36%，模仿部门研发劳动 $ {H}_{m} $ 设为 $ {0.36H}_{n} $ 。综上，社会总研发劳动等于两个部门研发劳动之和 $ H={H}_{n}+{H}_{m}=0.00272 $ 。

③ 张勋和乔坤元（2016）利用1985—2013年中国省级面板数据和空间计量方法，估计得到各经济圈的技术扩散参数，本文中模仿型企业的付费知识占比 $ \omega $ 的校准值在其估计结果区间[0.001，0.020]内。

④ 重新校准时，基准知识产权保护水平下创新型企业的知识租金收入与研发费用的稳态比值为2.6%，严格知识产权保护水平下创新型企业的知识租金收入与研发费用的稳态比值为1。对 $ {\rho }_{m} $ 的重新校准不会改变知识产权保护水平 $ \omega $ 的值，但对 $ \varrho $ 和 $ \eta $ 的重新校准会改变 $ \omega $ 的值。