
2022第48卷第7期
一、引 言
根据《金融业发展和改革“十二五”规划》,利率市场化改革的目标不仅在于放开政府对利率的行政控制,还要建立形成合理利率水平和结构体系的市场化机制,也要提高中央银行基于市场化方式的利率调控能力。因此,利率市场化应该是一个“放得开”“形得成”和“调得了”的改革过程。以往有关利率市场化改革效应的研究均基于“放得开”的视角展开(谭语嫣等,2017),这在利率市场化与企业融资约束关系的研究领域也不例外(战明华等,2013;赵平,2014;钱龙,2019)。
利率管制的“放得开”固然有利于消除管制型信贷配给现象,缓解中小民营企业融资约束(McKinnon,1973;Shaw,1973)。但在利率管制与中小民营企业融资约束的关系中,信贷市场利率能否基于风险定价而“形得成”,即银行的信贷风险定价能力如何,也会对中小民营企业融资约束产生重要影响。这是因为,在利率管制“放得开”之后,如果银行无法对中小民营企业的规模和所有制性质,以及与之密切联系的治理模式、经营理念和运作环境所传递的风险特质进行有效定价,那么这类借款人将会重新陷入Stiglitz和Weiss(1981)所称的均衡信贷配给状态,中小民营企业融资约束问题仍将无解。因此,银行信贷风险定价能力不足,导致与中小民营企业风险相匹配的贷款利率“形不成”,是利率管制放松缓解中小民营企业融资约束效果的重要影响因素。
本文在既往的“放得开”基础上加入“形得成”因素,在经典欧拉投资方程的框架内,利用中小民营制造业上市公司数据,基于多种实证策略,重新考察了利率市场化改革与中小民营企业融资约束的关系。研究发现,利率管制放松缓解中小民营上市企业融资约束的作用,除了已有研究关注较多的主效应外,还存在依赖银行信贷风险定价能力的调节效应−银行信贷风险定价能力越强,利率管制放松的融资约束缓解力度越大。如果不考虑银行信贷风险定价能力及其调节作用,利率管制放松缓解中小民营企业融资约束的作用较弱、稳健性不足;而在控制了此影响后,情况则显著不同。这意味着以往的相关研究显著低估了利率管制放松对中小民营上市企业的融资约束缓解效应。
本文将利率市场化的含义定位在“放得开、形得成”层面,突破了已有研究只聚焦利率管制“放得开”内容的局限,从而丰富和拓展了中国利率市场化改革与中小民营企业融资约束关系的认知,这是本文的主要贡献。具体而言,一是创新性地构建了银行信贷风险定价能力指数,区分利率“放得开”和“形得成”的维度,细致考察了利率市场化对中小民营企业融资约束的影响;二是首次考察了银行信贷风险定价能力对利率管制放松改革影响中小民营企业融资约束的调节作用;三是基于欧拉投资方程,运用了三种不同的实证策略,结果更具稳健性,揭示的信息量也更大。
二、文献述评与研究假设
通过金融自由化改革提高利率水平、消除管制型信贷配给,是改善中小民营企业融资约束的政策选择(McKinnon,1973;Shaw,1973)。20世纪80年代以来,一些金融抑制严重的发展中国家和新兴市场经济体经历了以放开利率管制为核心内容的金融自由化改革。在此背景下,学术界对这些国家金融自由化与企业融资约束的关系进行了大量实证研究,结论大多支持金融自由化具有缓解民营企业,特别是中小民营企业融资的作用(Harris等,1994;Laeven,2003)。顺着McKinnon(1973)和Shaw(1973)的思路,中国学界和业界普遍认为放松利率管制有助于改善中小民营企业的贷款可得性(赵平,2014)。通过收益覆盖风险的价格机制,将银行拓展中小民营企业贷款的积极性调动起来,是利率管制放松缓解中小民营企业融资约束的重要机制,早期相关研究的主要逻辑正在于此。
随着研究的深入,与利率管制放松相关联的市场竞争机制也提供了一种解释。即在利率管制放松后,存贷款市场竞争加剧,银行利差缩小,利润减少。银行息差“收窄”现象(李宏瑾,2015;彭建刚等,2016)在贷款利率下限管制放开后的优质企业信贷领域尤为明显(李瑞鹏等,2016)。盈利状况趋紧会使银行信贷投放逐渐向风险较高、议价能力较弱但需求强劲的借款人群体转移(刘婷婷,2016;李瑞鹏等,2016;陈胜蓝和马慧,2018),中小民营企业的信贷可获得性将得到改善。
这类文献在实证检验时往往将融资约束分解为信贷可得性和价格成本两个方面,或者只关注其中的一个维度(张伟华等,2018;钱龙,2019)。而利率市场化一般会推高中小民营企业的信贷成本,所以难以判断利率市场化对中小民营企业融资约束的影响。因此,需要联系信贷风险水平、货币政策立场、金融市场供求状况等方面的因素。将企业利率成本上升作为价格视角下融资约束加剧的证据,或者仅从资金可得性改善来判断利率市场化缓解了融资约束,这样做都是不妥的。采用Fazzari等(1988)创立的“投资—现金流”敏感性分析方法来间接测度企业融资约束,不失为一种更好的选择。这种方法检验企业投资是否在边际意义上显著依赖内部资金,若依赖则说明以内部资金为参照点,外部融资应更贵更难,即企业存在外部融资约束。这种方法显然能避免直接从数量与价格维度考察中小民营企业融资约束问题时面临的量价不一致困境。当然,一些反映企业融资约束的综合指标,如SA(Hadlock和Pierce,2010)指标,也具有同样的优势。
使用竞争机制将利率市场化改革与中小民营企业融资约束联系起来的文献,一方面在讨论利率市场化的异质性影响才关注这个议题,相关的专题研究并不多(胡援成和张朝洋,2016;祝佳等,2020);另一方面,大多立足于信贷竞争会使贷款资源从大型或国有企业向中小民营企业转移的假说(李瑞鹏等,2016;刘婷婷,2016;陈胜蓝和马慧,2018)。从这类文献的检验结果看,利率市场化对国有企业融资约束的影响显著不同于中小民营企业,甚至可能会加剧其融资约束(战明华等,2013;祝佳等,2020)。近年来,一些运用双重差分方法研究利率市场化影响企业融资约束的文献,构造控制组与处理组企业截面差异的依据也正在于此。
如上所述,利率管制放松改革诚然会通过价格和竞争机制,促使银行拓展中小民营企业贷款,中小民营企业受到的管制型信贷配给将趋弱甚至消失,但新的信贷配给形式−Stiglitz和Weiss(1981)理论中的均衡信贷配给现象会随之出现。因此,中小民营企业面临的融资约束并不必然随利率管制放松而得到缓解。造成这一后果的原因在于,在信息不对称市场条件下,银行无法根据中小民营企业的风险状况进行准确定价。归根到底,这是一个银行信贷风险定价能力不足的问题。通俗来说,利率管制放松仅解决了银行向中小民营企业的“愿贷”问题,至于在多大程度上“能贷”“敢贷”,还要视其信贷风险定价能力的情况而定。
在国内一些利率市场化效应的理论分析中,银行信贷风险定价能力的提升是利率市场化改革的必然要求与结果(李宏瑾,2015),甚至是内生于利率市场化改革的题中应有之意(曹远征,2013),但尚没有文献将其从利率市场化改革内涵中剥离出来进行考察。相关研究从理论假说提出到具体计量分析,均没有考虑银行信贷风险定价能力的作用,这相当于隐含了银行具有这种能力,或者其信贷风险定价能力必然随利率管制放松而同步提高的假设。国外文献虽然关注到信贷风险定价能力问题,但是主要从银行信用评分等风险定价技术层面,研究新技术运用对小额信贷的可得性、利率水平和风险的影响(Walke等,2018)。
综上所述,现有研究将利率市场化的含义锁定在去管制化改革的“放得开”层面,并没有考虑市场利率基于风险定价的“形得成”内容。此外,从融资约束的研究方法看,不少文献从融资成本、信贷可得性或者两者兼而有之进行研究,这不利于对中小民营企业的融资约束影响做出综合准确的判断。本文提出以下假设并运用“投资−现金流”敏感性方法进行检验:在利率市场化改革不断推进的背景下,利率管制放松缓解中小民营企业融资约束的作用,依赖于银行信贷风险定价能力的提升。
三、中国利率管制放松与信贷风险定价能力的测度
利率管制放松是指存贷款利率先围绕央行基准利率浮动,最终“换锚”至某种市场基准利率,并由市场供求决定其水平和期限结构。信贷风险定价能力则指银行根据借款人及项目风险而实施差别利率定价的能力。
本文通过编制指数的方式来测度利率管制放松和银行信贷风险定价能力。利率管制放松指数的构造相对简单。本文参照胡晖和张璐(2015)的做法,按年度梳理出中国利率管制放松的一系列政策事件,然后根据重要性(一般性、重大和特别重大)给这些政策事件赋值(0.5、1和2)后获得。银行信贷风险定价能力指数的编制则比较复杂。本文运用贷款利率浮动和不良贷款率的省级面板数据,编制了一个反映中国银行业省区贷款风险定价与信贷风险分布匹配状况的指数,测度中国银行业的信贷风险定价能力。具体而言,首先用贷款利率浮动数据编制各省区贷款利率浮动指数序列,然后按年度计算省区截面贷款利率浮动指数变异系数(标准差/均值),接着利用省区不良贷款率数据,计算年度省区截面不良贷款率变异系数,最后用后者减去前者取绝对值,得到中国银行业的信贷风险定价能力时间序列数据,具体的编制如(1)式所示。
| $ {Riskp}_{t}=│\dfrac{\sqrt{\dfrac{1}{k-1}\sum _{i=1}^{30}{\left({nplr}_{i,t}-\dfrac{1}{k}\sum _{i=1}^{30}{nplr}_{i,t}\right)}^{2}}}{\dfrac{1}{k}\sum _{i=1}^{30}{nplr}_{i,t}}-\dfrac{\sqrt{\dfrac{1}{k-1}\sum _{i=1}^{30}{\left({rflo}_{i,t}-\dfrac{1}{k}\sum _{i=1}^{30}{rflo}_{i,t}\right)}^{2}}}{\dfrac{1}{k}\sum _{i=1}^{30}{rflo}_{i,t}} $ |
其中,
利用(1)式计算的银行信贷风险定价能力指数是一种逆序度量,其数值越大,表示银行信贷风险定价能力越弱。下面对其背后的逻辑进行简要阐释。
第一,(1)式的逻辑建立在省区贷款利率浮动的信贷风险定价含义基础上。在金融市场全国一体化,特别是大银行信贷资金总行统筹管理体制下,长期显著存在的中国省际贷款利率浮动差异最有可能体现无法通过跨区资金流动消除的省际信贷风险差异。这意味着中国省区贷款利率浮动水平含有银行业机构对省区信贷风险的定价信息。如果将央行贷款基准利率视作全国信贷市场供求状况和平均违约风险的反映(蔡晓慧,2013),那么省区贷款利率浮动水平的区域信贷风险定价含义更加明确。在经济运行中,各省区的经济金融和社会信用环境差异显著,内生于当地社会经济系统的各省区信贷风险因此而大为不同。全国性大银行在银行体系中居主导地位,虽然在机构设置、内部考核和业务经营方面具有浓厚的省区特征,但是总行一级法人制的分支行制度使其在全国范围内按“风险—收益”平衡的原则优化信贷资源配置。在这种背景下,各省区的信贷风险不同,银行对其风险定价会有差异。综上所述,从理论上抽象出中国银行业机构对不同省区存在一个总体信贷风险定价的概念不失合理性,编制的省区贷款利率浮动指数是对这个定价的具体量化。
第二,(1)式在省区层面有效刻画了银行信贷风险定价对信贷风险分布的匹配状况。(1)式右边第一项是省区截面不良贷款率变异系数,刻画特定年份的省区信贷风险分布信息;而第二项是贷款利率浮动指数变异系数,捕捉特定年份的省区贷款风险定价分布信息。对银行而言,省区信贷风险的分布具有客观性,主要由各省区的宏观经济与微观主体状况决定,但省区信贷风险的定价分布却是银行主动实施省区信贷风险定价的结果。基于这样的理解,省区不良贷款变异系数与贷款利率浮动指数变异系数之差的绝对值,能够从总体上刻画中国银行业省区信贷风险定价行为对省区信贷风险分布的匹配与跟踪能力,而本文对中国银行业信贷风险定价能力的测度正是以这种匹配与跟踪能力为标准。这两个变异系数相差越大,说明银行业信贷风险定价行为对省区信贷风险分布的匹配与跟踪能力越弱,相应的银行信贷风险定价能力也越弱。显然,基于(1)式编制的指数是对中国银行业信贷风险定价能力的逆序测度。
由于利率管制放松指数与银行信贷风险定价能力指数的量级差异较大,本文使用Z-Score方法对其进行了标准化处理,处理后的变量均值为0、方差为1。两个指数的具体情况见图1。
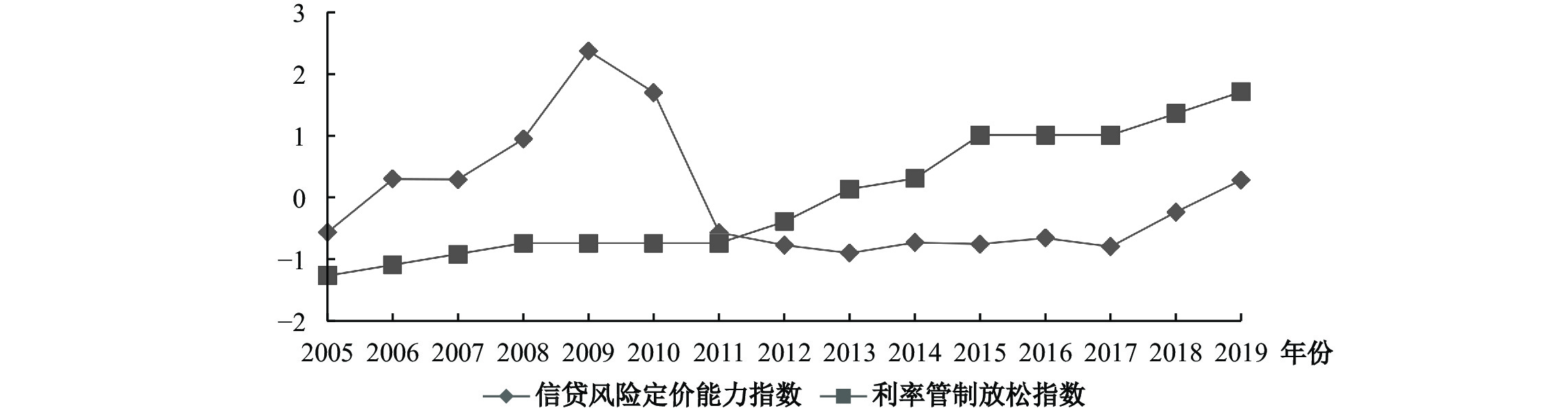
|
| 图 1 中国利率管制放松与银行信贷风险定价能力指数 |
四、研究设计
(一)模型
Fazzari等(1988)开创的“投资—现金流”敏感性分析是利用微观数据检验企业融资约束问题的主流方法。本文的计量工作基于欧拉投资方程的“投资—现金流”敏感性框架展开。
1. 模型思想
欧拉投资方程是公司价值最大化关于资本存量的一阶条件,融资约束变量存在于目标函数的限定条件中,经拉格朗日函数的构造而进入欧拉投资方程。借鉴Harrison和McMillan(2003)以及Laeven(2003),欧拉投资方程表示如下:
| $ (1 - \delta )\beta _{t + 1}^t{E^t}\left[{\gamma _{t}}{\left(\frac{{\partial \pi }}{{\partial I}}\right)_{t + 1}}\right] = {\left(\frac{{\partial \pi }}{{\partial K}}\right)_t} + {\left( {\frac{{\partial \pi }}{{\partial I}}} \right)_t}$ | (2) |
(2)式刻画的是企业投资如何在相邻两期优化配置的问题。
基于(2)式,根据γ的不同取值及其对企业投资的跨期优化配置效应,有两类企业融资约束检验思想。一类是当γ=1时,企业不存在融资约束,其投资决策与内外融资方式无关。因此,企业下一期投资对(2)式右边π所包含的当期经营现金流(内部资金)不存在正向敏感性,即没有依赖关系。如果实证检验发现了下一期投资对当期现金流的正向敏感性,则表明企业不存在融资约束的假设(γ=1)并不成立,应将其视为企业存在融资约束的证据。另一类是当0<γ<1时,企业存在融资约束,且γ的取值越小,融资约束越紧,(2)式左边的下一期边际投资成本现值也越小。当企业融资约束因各种冲击而变得更紧时,下一期边际投资成本现值降低,当期投资的机会成本变得更高。此时,企业用下一期投资来替代当期投资(即当期投资推迟到下一期)的优化调整行为将不可避免,下一期投资必然增加。如果实证检验发现融资约束代理变量对下一期投资具有显著的正向影响,无疑应是企业的真实融资约束使然,且系数估计值越大,表明企业面临的融资约束越紧。
2. 模型设定
Harrison和McMillan(2003)以及Laeven(2003)基于企业不存在融资约束的假设(即γ=1),将满足凸性和对称性的企业投资调整成本函数设定为
| $ {\left(\frac{I}{K}\right)}_{i,t}={{\beta }_{1}\left(\frac{I}{K}\right)}_{i,t-1}+{\beta }_{2}\left({\frac{I}{K}}\right)_{i,t-1}^{2}+{\beta }_{3}\left({\frac{Y}{K}}\right)_{i,t-1}+{\beta }_{4}{\left(\frac{CF}{K}\right)}_{i,t-1}+{d}_{t}+{f}_{i}+{v}_{i,t} $ | (3) |
其中,I、K、Y和CF分别表示投资、资本存量、净产出和经营性净现金流(产出扣除投资调整成本和劳动力成本后的余额)。i和t分别表示企业和时间。
从基于欧拉投资方程的企业融资约束现有研究来看,上述三种实证策略在不同的文献中都是单独使用的,未见有同时使用的先例,表1列示了部分相关文献的情况。
| 实证策略 | 代表文献 | 刊发杂志 |
| “投资—现金流”
敏感性分析 |
Laeve(2003)、战明华等(2013)、胡晖和张璐(2015)、Sakai(2020) | Financial Management、经济学季刊、经济评论、 Journal of Corporate Finance |
| “投资—现金持有量”
敏感性分析 |
Harrison等(2004)、胡援成和张朝洋(2016) | Journal of development Economics、商业经济与管理 |
| “投资—融资约束”
敏感性分析 |
Harrison和McMillan(2003)、Héricourt 和Poncet(2009)、Whited(1992)、罗长远和陈琳(2011) | Journal of International Economics、Economic Systems、Journal of Finance、世界经济 |
为了揭示更多的信息,本文从“放得开”和“形得成”视角检验利率市场化对中小民营企业融资约束的影响,同时基于“投资—现金流”“投资—现金持有量”和“投资—融资约束”敏感性分析展开,三种实证策略对应的模型如(4)式、(5)式和(6)式所示。
| $ {\left(\frac{I}{K}\right)}_{i,t}=X+{\beta }_{5}{Dere}_{t} \times {\left(\frac{CF}{K}\right)}_{i,t-1}+{\beta }_{6}{Riskp}_{t}\times{\left(\frac{CF}{K}\right)}_{i,t-1}+{\beta }_{7}{Dere}_{t}\times{Riskp}_{t}\times{\left(\frac{CF}{K}\right)}_{i,t-1} $ | (4) |
| $ {\left(\frac{I}{K}\right)}_{i,t}={X'}+{\rho }_{1}{Dere}_{t}\times{\left(\frac{CS}{K}\right)}_{i,t-1}+{\rho }_{2}{Riskp}_{t}\times{\left(\frac{CS}{K}\right)}_{i,t-1}+{\rho }_{3}{Dere}_{t}\times{Riskp}_{t}\times{\left(\frac{CS}{K}\right)}_{i,t-1} $ | (5) |
| ${\left(\frac{I}{K}\right)}_{i,t}=X+{\phi }_{1}{Fcon}_{i,t-1}+{{\phi }_{2}{Dere}_{t}\times{Fcon}_{i,t-1}+\phi }_{3}{Riskp}_{t}\times{Fcon}_{i,t-1} +{\phi }_{4}{Dere}_{t}\times{Riskp}_{t}\times{Fcon}_{i,t-1}$ | (6) |
(4)式是基于欧拉方程的“投资—现金流”敏感性实证模型,X表示(3)式等号右边部分,Dere和Riskp分别表示利率管制放松和信贷风险定价能力变量,
根据本文提出的研究假设,在(4)式、(5)式和(6)式中,利率管制放松、信贷风险定价能力和现金流(存量现金持有、融资约束变量)三者交互项的系数(
(二)变量与数据
本文在同花顺(iFinD)2005—2019年我国沪深两市全部制造业民营上市公司的基础上,根据最终实际控制人和企业规模大小,遴选出中小民营上市公司作为研究样本。为了消除异常值对计量结果的影响,本文剔除了以下样本数据:(1)同时具有A股、B股和H股的公司;(2)ST或PT的公司;(3)企业特征变量上下1%的数据。经过筛选,本文得到582家中小民营上市公司。本文主要变量定义与描述性统计见表2。
| 变量 | 计算方法 | 均值 | 标准差 | 最小值 | 最大值 | 观测数 |
|
|
购建固定资产等长期资产支付的现金/期初总资产 | 0.0793 | 0.0786 | 0.0011 | 0.4486 | 4 399 |
|
(营收比) |
营业收入/期初总资产 | 0.6732 | 0.3681 | 0.0870 | 2.4719 | 4 991 |
|
(现金流比) |
经营性现金流净额/期初总资产 | 0.0727 | 0.0916 | −0.1969 | 0.3649 | 4 991 |
|
(持现比率 ) |
货币资金/期初总资产 | 0.1979 | 0.1394 | 0.0106 | 0.6933 | 4 991 |
|
(融资约束) |
利息支付/
|
0.2296 | 0.1855 | 0.0000 | 0.7792 | 3 480 |
|
(利率管制放松) |
基于政策事件按赋值法编制 | 17.6 | 2.7521 | 14 | 22.5 | 8 730 |
|
(风险定价能力) |
省区贷款定价对其风险分布的匹配程度 | 0.3649 | 0.3932 | 0.0007 | 1.3354 | 8 730 |
五、实证结果分析
本文模型(4)、模型(5)和模型(6)的回归结果见表3中第Ⅱ列。由于原始的银行信贷风险定价能力指数(Riskp)是逆向指标,为了方便解读计量结果,本文在回归时通过取负数的方式对其做了正向化处理。考虑到现有相关文献都是从“放得开”层面研究利率市场化对(中小)民营企业融资约束的影响,为了考察控制“形得成”因素前后的实证结果变化,本文还只考虑利率管制放松的影响,回归结果见表3中第Ⅰ列。
| 模型(4) | 模型(5) | 模型(6) | ||||
| Ⅰ | Ⅱ | Ⅰ | Ⅱ | Ⅰ | Ⅱ | |
|
|
0.988*** | 0.990*** | 1.117*** | 1.148*** | 0.867*** | 0.824*** |
| (0.081) | (0.085) | (0.127) | (0.116) | (0.119) | (0.134) | |
|
|
−2.01*** | −1.996*** | −2.154*** | −2.245*** | −1.406*** | −1.241*** |
| (0.241) | (0.251) | 0.379) | (0.341) | (0.376) | (0.406) | |
|
|
0.015*** | 0.015*** | 0.031*** | 0.029*** | 0.004 | 0.007 |
| (0.005) | (0.005) | (0.006) | (0.006) | (0.007) | (0.007) | |
|
|
0.576*** | 0.789*** | 0.211*** | 0.187*** | ||
| (0.155) | (0.261) | (0.044) | (0.041) | |||
|
|
0.228* | 0.464** | ||||
| (0.143) | (0.194) | |||||
|
|
0.187*** | 0.207** | ||||
| (0.062) | (0.092) | |||||
|
|
−0.002*** | −0.004*** | ||||
| (0.007) | (0.013) | |||||
|
|
−0.010* | −0.023** | ||||
| (0.006) | (0.010) | |||||
|
|
−0.010*** | −0.012*** | ||||
| (0.003) | (0.004) | |||||
|
|
0.765* | |||||
| (0.445) | ||||||
|
|
0.638* | |||||
| (0.355) | ||||||
|
|
0.228 | |||||
| (0.211) | ||||||
|
|
−0.047* | |||||
| (0.025) | ||||||
|
|
−0.035* | |||||
| (0.020) | ||||||
|
|
−0.016 | |||||
| (0.012) | ||||||
| 常数项 | 0.001 | 0.002 | −0.013** | −0.018*** | 0.004 | 0.008 |
| (0.004) | (0.004) | (0.005) | (0.007) | (0.007) | (0.008) | |
| AR(1) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| AR(2) | 0.346 | 0.372 | 0.772 | 0.758 | 0.379 | 0.423 |
| Hansen | 0.526 | 0.388 | 0.193 | 0.184 | 0.247 | 0.847 |
| 工具变量数 | 298 | 283 | 221 | 226 | 245 | 316 |
| 观测数 | 3 648 | 3 648 | 3 637 | 3 637 | 2 660 | 2 660 |
| 公司数 | 577 | 577 | 577 | 577 | 536 | 536 |
| 注:*、**和***分别表示在10%、5%和1%的水平上显著,括号内为Windmeijer(2005)稳健标准误。 | ||||||
(一) 结果分析
1. 利率管制放松对中小民营企业融资约束的影响
利率管制放松对中小民营企业融资约束的影响,分为独立影响的主效应和依银行信贷风险定价能力而定的调节效应两部分,前者是线性的,后者则具有非线性特征。
(1)主效应部分
根据表3的回归结果,不论是否控制银行信贷风险定价能力(第Ⅰ列未控制,第Ⅱ列控制),反映融资约束的
(2)调节效应部分
如表3第Ⅱ列所示,利率管制放松、信贷风险定价能力分别与现金流净额、存量现金持有和融资约束变量的交互项系数分别为−0.047、−0.035和−0.016,前两者在10%的水平上显著,后者虽不显著,但p值为0.192,显然不算很大。这说明从利率管制放松来看,银行信贷风险定价能力越强,利率管制放松缓解中小民营上市企业融资约束的作用越突出。在边际意义上,当利率管制放松一个单位时,中小民营上市企业与银行信贷风险定价能力相关的融资约束平均能够缓解0.47×Riskp−以模型(4)的估计结果为例。现有相关研究没有考虑银行信贷风险定价能力的调节效应,本文的实证结果意味着这些文献的估计结果是有偏的。
2. 银行信贷风险定价能力提升对中小民营上市企业融资约束的影响
银行信贷风险定价能力对中小民营企业融资约束的主效应使用模型(4)、模型(5)和模型(6)中的系数
第一,信贷风险定价能力提升会强化融资约束的实证发现,是在模型中控制了利率管制放松及其与信贷风险定价能力交互影响的条件下出现的结果。其现实解读是:随着信贷风险定价能力的提升,银行获取并处理借款人信息的风险定价技术会迭代演进,经营欠透明且风险复杂的借款人及其项目能被银行做出准确的风险评估与定价。但由于利率管制放松因素的影响已经被固定,银行将无法通过执行较高的利率来覆盖风险。对于因风险定价能力提升而新纳入信贷视野的企业和项目,银行以前因“不敢贷”而持回避态度,现在面临的是“敢贷”但“不愿贷”的情况。
第二,随着银行信贷风险定价能力的提升,中小民营上市企业的融资约束趋紧,这种现象与银企间信息不对称问题得到缓解以及我国资本市场制度的一些内在缺陷有关。在银行信贷风险定价能力提升的背景下,更多类型的信息会纳入银行的信用评估程序,银企间的信息不对称问题将趋于缓解,企业上市身份所承载的信息“滤波器”功能被弱化(战明华等,2013),上市与否对企业融资约束的意义不再清晰,信贷决策更加依赖于借款申请企业本身的质量信息。过去注重“上市光环”、盲目“傍”上市公司的情况已经越来越少见。此外,我国资本市场制度存在一些内在缺陷,包装上市、财务造假、大股东侵占、不实信息披露、违规担保、“僵尸化”运行等问题一直以来都比较突出。随着信贷风险定价能力的提升,银行越来越有能力透过企业的“上市光环”对申请人做出更加准确的风险评估。对于超出风险偏好的企业和项目,银行会以“不能贷、不愿贷、不敢贷”的态度回避应对。
第三,随着银行信贷风险定价能力的提升,更多的非上市中小微企业成为银行信贷拓展的新方向。近些年,金融科技快速发展,银行开展中小微企业贷款的风控定价和成本高企痛点大为改善,这类业务的商业可持续性问题显著弱化,原本主要服务于大企业、大项目、大城市的大型银行也开始下沉服务,强力拓展小微企业信贷市场(金洪飞等,2020)。
综上所述,本文发现银行信贷风险定价能力提升会加剧中小民营上市企业融资约束,这既与本文控制了利率管制放松影响的模型结构有关,又与银行信贷风险定价能力提升背景下的企业上市身份“信息滤波器”功能弱化,以及信贷资源向更多的非上市中小微企业转移相联系。就后两者而言,这一结果恰好可能是银行信贷风险定价能力提升对上市和非上市中小民营企业融资约束具有异质性影响的体现。当然,考虑到银行信贷风险定价能力所发挥的调节作用,这一结果显然只是银行信贷风险定价能力影响中小民营上市企业融资约束问题的一个方面而已。
(二)稳健性检验
本文从两个方面进行稳健性检验。一方面,替换利率管制放松变量对模型(4)、模型(5)和模型(6)重新进行回归;另一方面,对模型(3)的“投资—现金流”敏感性源于融资约束还是代理冲突进行检验。
本文借鉴王舒军和彭建刚(2014)的研究,构造了利率管制放松的替代变量。回归结果表明,利率管制放松、信贷风险定价能力以及两者交互项分别与现金流、现金存量和融资约束变量交互项的系数符号与表3完全一致,显著性更高。不论是否控制信贷风险定价能力及其与利率管制放松的交互影响,回归结果也与表3完全一致。在未控制的回归中,无论融资约束强度还是利率管制放松的缓解效应,都明显地比控制时要弱。这说明上文的估计结果具有良好的稳健性。
根据Jensen(1986)的自由现金流假说,企业“投资—现金流”敏感性有可能反映了股东和管理层代理冲突所导致的过度投资问题,而并非融资约束。本文从两个方面对“投资—现金流”敏感性的来源进行了检验。一是将机构持股比率(Inssharei,t)和股权集中度(Sconcentri,t)这两个治理变量引入基准模型(3)进行回归。如果这两个治理变量对“投资—现金流”敏感性没有显著的负向影响,则可认为“投资—现金流”敏感性与企业代理问题无关。二是根据Hadlock和Pierce(2010)的融资约束SA指标对样本企业进行分组,然后基于基准模型(3)进行回归,考察融资约束不同的企业“投资—现金流”敏感性是否存在显著差异。
根据引入企业治理变量的检验结果,无论是机构持股比率、股权集中度①还是两者交互项的回归,均没有发现显著减弱“投资—现金流”敏感性的证据。这表明本文实证检验的“投资—现金流”敏感性可以排除代理冲突所导致的过度投资。根据融资约束SA指标的分组回归,强融资约束和弱融资约束企业组的“投资—现金流”敏感性系数分别为0.101和0.089,且两者至少在5%的水平上显著。显然,在强融资约束企业组,投资对现金流的敏感性更高。这证实了“投资—现金流”敏感性是对企业融资约束良好的间接测度。
六、个案研究:基于特定政策事件冲击的DID分析
上文基于中小民营上市企业的非平衡面板数据研究表明,银行信贷风险定价能力提升对利率管制放松缓解中小民营企业融资约束具有调节效应。这意味着以往文献关注的利率管制放松对中小民营企业融资约束的影响,还有赖于银行信贷风险定价能力。如果基于利率管制放松和银行信贷风险定价能力提升的特定政策事件,从“个案分析”的角度采用双重差分(DID)方法做进一步检验,这无疑将使本文的实证结果更加丰富,结论也更加稳健。
2013年,我国同时发生了两项重大金融政策事件:一是完全放开了贷款利率管制,二是银行业开始实行“巴塞尔协议Ⅲ”。前者推动了“去管制”意义上的利率市场化改革,有利于促进信贷市场竞争;而后者则提高了银行业风险管理水平,使信贷风险的事先识别计量、事中定价管理和事后化解处置开始向国际标准靠拢,这对银行信贷风险定价能力的提升是一个显著的外生推动。在时间维度上,两者对中小民营企业融资约束的影响“天然”重叠并交织在一起。如果以2013年为界设置0—1虚拟变量,则能捕捉利率管制放松和信贷风险定价能力提升的交互影响因素信息。接着,进一步选择与中小民营上市企业对标的大型民营上市企业作为对照组,这样就可以再构造一个反映截面企业规模差异的0—1虚拟变量。最后,将上述时间和截面虚拟变量通过交乘的方式形成虚拟变量
| $ {\left(\frac{I}{K}\right)}_{i,t}={{\beta }_{1}\left(\frac{I}{K}\right)}_{i,t-1}+{\beta }_{2}\left({\frac{I}{K}}\right)_{i,t-1}^{2}+{\beta }_{3}\left({\frac{Y}{K}}\right)_{i,t-1}+{\beta }_{4}{\left(\frac{CF}{K}\right)}_{i,t-1} +{\beta }_{5} {D}_{DID}+{\beta }_{6}{D}_{DID} \times {\left(\frac{CF}{K}\right)}_{i,t-1}+{d}_{t}+{f}_{i}+{v}_{i,t} $ | (7) |
现有相关文献做双重差分分析的逻辑是想通过发现利率市场化政策事件对处理组和对照组的差异性影响的“果”来识别利率市场化这个“因”(陈胜蓝和马慧,2018)。这种逻辑一个不可回避的问题是,由于利率市场化对处理组和对照组同时产生影响,并不存在类似自然实验中对照组完全不受外生事件影响的情形,因此将差异性这个“果”归因于利率市场化的逻辑,完全建立在利率市场化具有这种差异性影响的先验假设基础上。但无论根据理论分析还是实证研究提出这种假设,其严谨性和客观性都存疑。本文做双重差分分析的目的不是为了识别民营上市企业融资约束缓解的利率市场化原因,而是要用贷款利率管制放开和“巴塞尔协议Ⅲ”同年实施的政策事件,通过“个案分析”的方式,在与大型民营上市企业对比的意义上,进一步检验银行信贷风险定价能力提升是否存在调节效应。
本文的DID分析以制造业大型民营上市企业为对照组。大型民营企业的认定标准、数据来源、采集范围和必要的预处理均与中小民营上市企业(处理组)完全相同。与上文讨论的三种融资约束检验策略一致,本文还将模型(7)中的现金流量(
| Ⅰ 现金流 | Ⅱ 现金持有量 | Ⅲ 融资约束变量 | |||||||
| 前后1年 | 前后2年 | 前后3年 | 前后1年 | 前后2年 | 前后3年 | 前后1年 | 前后2年 | 前后3年 | |
|
|
0.065* | 0.088*** | 0.086*** | 0.058 | 0.060** | 0.069 | |||
| (0.040) | (0.031) | (0.024) | (0.041) | (0.030) | (0.086) | ||||
|
|
0.042** | 0.011 | 0.008 | ||||||
| (0.021) | (0.018) | (0.012) | |||||||
|
|
0.002 | −0.047 | 0.032 | ||||||
| (0.042) | (0.035) | (0.057) | |||||||
|
|
−0.010 | −0.014 | −0.009 | −0.002 | 0.010 | −0.002 | −0.001 | −0.016 | −0.019 |
| (0.012) | (0.010) | (0.008) | (0.017) | (0.019) | (0.013) | (0.015) | (0.014) | (0.013) | |
|
|
−0.017 | −0.118* | −0.094* | ||||||
| (0.082) | (0.062) | (0.054) | |||||||
|
|
−0.016 | −0.075 | −0.021 | ||||||
| (0.062) | (0.071) | (0.048) | |||||||
|
|
−0.282** | −0.157* | −0.239*** | ||||||
| (0.135) | (0.087) | (0.088) | |||||||
| 注:*、**和***分别表示在10%、5%、1%的水平上显著,括号内为稳健标准误。 | |||||||||
从表4中可以看到,
七、结论性评述
本文引入银行信贷风险定价能力的作用,重新考察了中国利率市场化改革对中小民营企业融资约束的影响效应。研究发现:第一,银行信贷风险定价能力的提升对利率管制放松缓解中小民营上市企业融资约束的效应存在显著的放大作用。无论是基于“大样本”面板数据的回归,还是基于特定重大政策事件的DID“个案分析”,均支持这一点。这意味着以往文献关注的利率管制放松对中小民营上市企业融资约束的影响,除了直接的线性效应外,还存在被忽视的依赖于银行信贷风险定价能力状况的非线性影响。第二,如果不控制银行信贷风险定价能力及其调节作用,则会系统性地显著低估利率管制放松对中小民营上市企业融资约束的缓解效应。这意味着以往只聚焦“放得开”层面的利率市场化对中小民营上市企业融资约束影响的实证研究低估了利率管制放松的影响。第三,银行信贷风险定价能力对中小民营上市企业融资约束的影响具有两面性,存在负面冲击的证据。负面冲击源于银行信贷资源向更多的非上市中小民营企业和小微企业转移。
利率管制放松甚至完全取消虽然不能从根本上解决中小民营企业的融资约束问题(Stiglitz和Weiss,1981),但是根据本文的研究结论,这一改革政策带来的边际改善效应可期。我国正式的存贷款利率管制已经完全取消,但自律定价组织对存款利率较窄的区间限价管理、地方政府对银行贷款定价的各种间接干预以及利率“双轨制”仍存在的事实,意味着通过利率市场化改革来缓解中小民营企业融资约束仍有空间。由于利率管制放松缓解中小民营企业融资约束的作用依赖于银行信贷风险定价能力的提升,利率管制放松改革不能单独推进,而应辅之以有助于银行信贷风险定价能力提升的政策措施。随着银行信贷风险定价能力的提升,相对处于中小微企业群体“头部”位置的中小民营上市企业,面临的融资约束将会趋紧,这是银行信贷资源向更多的非上市中小微企业转移的结果。因此,提升银行的信贷风险定价能力以缓解中小民营企业融资约束,将更具长尾效应的性质和普惠金融发展意义,而这正是中国融资领域长期以来最期望发生的事情。通过监管手段引导银行等信贷机构开发适用于此类贷款的风险定价模型,提升银行尤其是大型银行在这一细分信贷市场领域的风险定价能力,应是政策的一个重要着力点。
近年来,在政府大力缓解中小企业尤其是小微企业“融资难、融资贵”问题的政策氛围中,大型银行机构快速下沉服务,使小微企业贷款可得性大为改善,融资成本也大幅下降。但这是否符合风险定价原则,以及银行自主定价能力是否受到行政干预,都是值得讨论的问题。如果答案是否定的,那么偏离风险定价原则的低价放贷行为将不具商业可持续性,对银行的风险防控也会产生负面冲击,政府部门应当对此问题予以关注。
① 借鉴夏纪军(2017),股权集中度使用前十大股东持股比率的平方和表示。
| [1] | 蔡晓慧. 融资约束的度量及其检验——基于债务融资溢价视角[J]. 浙江社会科学, 2013(6): 20–30. |
| [2] | 曹远征. 利率市场化核心是风险定价[J]. 经济研究信息, 2013(11): 5–8. |
| [3] | 陈胜蓝, 马慧. 贷款可获得性与公司商业信用——中国利率市场化改革的准自然实验证据[J]. 管理世界, 2018(11): 108–120. DOI:10.3969/j.issn.1002-5502.2018.11.010 |
| [4] | 丁剑平, 王婧婧. 中国制造业企业对利率和融资约束敏感度的检验[J]. 当代财经, 2013(7): 47–54. |
| [5] | 胡晖, 张璐. 利率市场化对成长型企业融资约束的影响——基于对中小板企业的研究[J]. 经济评论, 2015(5): 141–153. |
| [6] | 胡援成, 张朝洋. 公司融资约束缓解: 利率市场化与中小银行发展——来自中国上市公司的经验证据[J]. 商业经济与管理, 2016(10): 57–68. DOI:10.3969/j.issn.1000-2154.2016.10.006 |
| [7] | 金洪飞, 李弘基, 刘音露. 金融科技、银行风险与市场挤出效应[J]. 财经研究, 2020(5): 52–65. |
| [8] | 李宏瑾. 利率市场化对商业银行的挑战及应对[J]. 国际金融研究, 2015(2): 65–76. |
| [9] | 李瑞鹏, 何平, 朱婕. 放松贷款利率管制与商业银行贷款效率[J]. 经济学报, 2016(1): 52–82. |
| [10] | 刘婷婷. 利率市场化、特许经营权与信贷定价[J]. 宏观经济研究, 2016(3): 62–72. |
| [11] | 罗长远, 陈琳. FDI是否能够缓解中国企业的融资约束[J]. 世界经济, 2011(4): 42–61. |
| [12] | 彭建刚, 王舒军, 关天宇. 利率市场化导致商业银行利差缩窄吗? ——来自中国银行业的经验证据[J]. 金融研究, 2016(7): 48–63. |
| [13] | 钱龙. 利率市场化增加企业信贷成本了吗? ——基于中国某省信贷数据的研究[J]. 金融论坛, 2019(5): 32–45. |
| [14] | 谭语嫣, 纪洋, 黄益平. 利率市场化改革对经济效率的影响[J]. 世界经济, 2017(4): 3–28. |
| [15] | 王舒军, 彭建刚. 中国利率市场化进程测度及效果研究——基于银行信贷渠道的实证分析[J]. 金融经济学研究, 2014(6): 75–85. |
| [16] | 夏纪军. 股权集中度与公司治理绩效[J]. 世界经济文汇, 2017(3): 46–63. |
| [17] | 战明华, 王晓君, 应诚炜. 利率控制、银行信贷配给行为变异与上市公司的融资约束[J]. 经济学(季刊), 2013(4): 1255–1276. |
| [18] | 张伟华, 毛新述, 刘凯璇. 利率市场化改革降低了上市公司债务融资成本吗?[J]. 金融研究, 2018(10): 106–122. |
| [19] | 赵平. 中国贷款利率自由化与中小企业贷款供给约束——基于S−W贷款供给曲线的理论分析[J]. 经济理论与经济管理, 2014(8): 78–88. DOI:10.3969/j.issn.1000-596X.2014.08.007 |
| [20] | 祝佳, 郑文华, 吴非. 利率市场化、生命周期与企业融资约束[J]. 商业经济与管理, 2020(3): 50–62. |
| [21] | Fazzari S M, Hubbard R G, Petersen B C, et al. Financing constraints and corporate investment[J]. Brookings Papers on Economic Activity, 1988(1): 141–206. DOI:10.2307/2534426 |
| [22] | Hadlock C J, Pierce J R. New evidence on measuring financial constraints: Moving beyond the KZ index[J]. The Review of Financial Studies, 2010, 23(5): 1909–1940. DOI:10.1093/rfs/hhq009 |
| [23] | Harris J R, Schiantarelli F, Siregar M G. The effect of financial liberalization on the capital structure and investment decisions of indonesian manufacturing establishments[J]. The World Bank Economic Review, 1994, 8(1): 17–47. DOI:10.1093/wber/8.1.17 |
| [24] | Harrison A E, Love I, McMillan M S. Global capital flows and financing constraints[J]. Journal of Development Economics, 2004, 75(1): 269–301. DOI:10.1016/j.jdeveco.2003.10.002 |
| [25] | Harrison A E, McMillan M S. Does direct foreign investment affect domestic credit constraints?[J]. Journal of International Economics, 2003, 61(1): 73–100. DOI:10.1016/S0022-1996(02)00078-8 |
| [26] | Héricourt J, Poncet S. FDI and credit constraints: Firm-level evidence from China[J]. Economic Systems, 2009, 33(1): 1–21. DOI:10.1016/j.ecosys.2008.07.001 |
| [27] | Jensen M C. Agency costs of free cash flow, corporate finance, and takeovers[J]. The American Economic Review, 1986, 76(2): 323–329. |
| [28] | Laeven L. Does financial liberalization reduce financing constraints?[J]. Financial Management, 2003, 32(1): 5–34. DOI:10.2307/3666202 |
| [29] | McKinnon R I. Money and capital in economic development[M]. Washington: Brookings Institution, 1973. |
| [30] | Myers S C, Majluf N S. Corporate financing and investment decisions when firms have information that investors do not have[J]. Journal of Financial Economics, 1964, 13(2): 187–221. |
| [31] | Sakai H. Did financing constraints cause investment stagnation in Japan after the 1990s?[J]. Journal of Corporate Finance, 2020, 64: 101673. DOI:10.1016/j.jcorpfin.2020.101673 |
| [32] | Shaw E S. Financial deepening in economic development[M]. New York: Oxford University Press, 1973. |
| [33] | Stiglitz J E, Weiss A. Credit rationing in markets with imperfect information[J]. The American Economic Review, 1981, 71(3): 393–410. |
| [34] | Walke A G, Fullerton Jr T M, Tokle R J. Risk-based loan pricing consequences for credit unions[J]. Journal of Empirical Finance, 2018, 47: 105–119. DOI:10.1016/j.jempfin.2018.02.006 |
| [35] | Windmeijer F. A finite sample correction for the variance of linear efficient two-step GMM estimators[J]. Journal of Econometrics, 2005, 126(1): 25–51. DOI:10.1016/j.jeconom.2004.02.005 |


