
2022第48卷第5期
2. 俄克拉荷马大学 经济系, 美国 诺曼 73019;
3. 上海理工大学 管理学院, 上海 200093
2. Department of Economics, University of Oklahoma, Norman 73019, the United States;
3. School of Business, University of Shanghai for Science and Technology, Shanghai 200093, China
一、引 言
平台经济发展至今已取得相当的成就,成为我国经济发展的重要动力。以电商和顺风车行业为例,根据《中国电子商务报告2020》的数据:“2020年全国电子商务交易额达37.21万亿元,其中网上零售额11.76万亿元”;根据《2014—2020中国顺风车行业发展蓝皮书》发布的统计数据:“从2014年9月到2019年底,顺风车主和乘客共同互助行驶了260亿公里,减少近700万吨碳排放,全国各地累计注册车辆3000万台,注册乘客3亿人,全年合乘出行36.4亿人次”。然而,平台经济在便利生活的同时,也存在一定的弊端。与线下实体交易相比,消费者在互联网平台购买产品(服务)前无法获得全部信息。因此低质量的商家在加入平台后,有机会利用这种信息不对称损害消费者权益。以顺风车行业为例,多次安全事件发生后,滴滴顺风车下线整改,高德顺风车也悄悄下线。在滴滴下线后,继续运营的平台依然安全事故不断。
顺风车行业爆出的一系列问题引起了平台及监管部门对行业安全规制的思考,其中争议最大的滴滴出行在重新上线后发布了一系列整改方案:在司机注册时调查综合背景、验真三证以及调查是否为失信被执行人;在行程前设定车主常用地点、人脸识别、号码保护等;行程中app上线各类安全功能,例如110报警、行程分享、异常提醒、车主全程开启app等;行程后还通过安全专线、黑名单、评分等策略形成评价体系。总的来看,滴滴的整改策略可以分为两部分。第一,对顺风车主提出了极高的注册要求,在预防事故发生的同时,也导致更多本身不会发生事故的司机因为繁琐的注册手续望而却步。严格的司机准入要求大大限制了顺风车的便利性。第二,加强平台自身安全能力,从行程跟踪到服务反应及各类安全教育措施,这类行为投入的只是平台的人力和相应算法的开发,并未对非事故司机造成额外负担,在保持高效匹配的同时提高了安全出行的可能。
随着平台经济的发展,匹配质量日渐成为社会关注的重要问题,其他平台也通过与滴滴类似的方式提高最终产品(服务)质量:淘宝、京东、拼多多等平台出台了一系列政策,严厉打击贩假和侵权等违法店铺;各大外卖平台通过严格的商家认证程序和更全面的评分体系来提高平台商户质量。相关部门也十分关注平台经济的正常运行和监管,从2019年陆续出台和实施了一系列法律法规,②要求现有平台在享受平台经济红利的同时,进一步规范自身行为,承担更高的市场责任。因此为更好地服务国家发展、监管平台经济的战略需求,文章结合各平台现有政策及监管部门提出的相关意见,以滴滴目前完成的整改方案为例,构建模型分析司机准入门槛和平台安全建设两类整改措施的有效性。本文考虑更为宽泛的安全监管目的为保证经由平台提供的产品(服务)质量,因此既适用于顺风车行业,也可适用于其他以提供商品为核心的平台。从滴滴整改方案来看,对司机准入的控制可以对应为淘宝和饿了么等对商家准入的控制;对滴滴平台功能的完善可以对应为淘宝和饿了么等建立的评价和人工服务等体系。最终本文提出三类政府规制政策:政府设定司机准入标准、政府设定平台安全建设标准以及政府和平台共同制定安全建设标准。文章模拟了各类规制政策效果,希望能为监管部门提供一定的理论参考。
与本文研究相关的文献可以分为三个方面,第一个方面的文献是关于双边平台匹配机制的研究。根据不同市场的特点,学者们分别从匹配效率(Caillaud和Jullien,2003)、交易数量(Rochet和Tirole,2003)以及用户数量外部性(Armstrong,2006;Armstrong和Wright,2007)的角度建立了相应的理论模型。从市场特征出发,现实平台更多发挥的是匹配商家产品(服务)和消费者需求的作用。因此本文将借鉴Caillaud和Jullien(2003)通过匹配效率刻画外部性的方法,假定最终匹配成功率取决于平台两边注册的人数。第二个方面的文献涉及对平台自我治理责任的探讨。管制低质量商家加入平台,保证平台产品质量和保障消费者权益是现阶段平台需要承担的社会责任。国外学者在早期指出平台企业不但扮演商业角色,其在平台系统中的独特地位和拥有的相关准入权利使得平台企业具有了监管和维护“公共利益”的能力(Farrell和Katz,2000;Gawer和Cusumano,2002;Rochet和Tirole,2006)。国内学者对平台内部监管提出了更为具体的意见。吴德胜(2007)从解决在线交易信任问题的角度,提出平台型企业应通过建立信用评价系统、寻求第三方支付或者托管、完善争议解决机制等手段减轻在线交易中的囚徒困境问题。汪旭晖和张其林(2016)系统剖析了阿里巴巴使用的“温室管理”模式,认为这一模式更好地适应了平台经济下商业模式快速跃迁的特点,较传统的科层雇佣或契约产权的管理模式具有更强的有效性以及更广的适用性。针对近年出台的网约车市场规制政策,王小芳和赵宇浩(2016)以及薛志远(2016)都进行了相关述评,二者均建议放开针对网约车司机的规制,认为应通过平台建设保证最终网约车服务质量。甄艺凯(2017)则通过理论模型分析规制政策的效果,得出现有针对司机数量的规制政策会损害社会福利,价格监管是相较数量监管更优的策略。肖红军和李平(2019)从“底线要求”“合理期望”以及“贡献优势”三个层级,界定了平台型企业作为独立运营主体、商业运作平台和社会资源配置平台应承担的相应社会责任,提出了社会责任生态化治理的新范式。上述研究着重分析了平台自我治理的效果,但私人监管往往存在动机不足、权力有限并且容易滋生内部腐败的问题(王勇和冯骅,2017),特别是依靠平台自身很难解决平台上的机会主义问题,因此平台的治理也离不开外部的政府监管。第三个方面的文献着重探讨了平台与政府之间的监管关系,主要分为三个角度:一是从单一政府监管主体角度,刘奕和夏杰长(2016)认为政府对平台型企业的监管既要依据其经济特点创新相应制度,也要坚持底线思维,努力解决安全隐患等底线问题;熊鸿儒(2019)认为政府对于平台的治理要包容灵活和开放透明,顺应数字经济与平台经济的发展规律,最大限度地激励创新,并有效保护消费者。二是从“政府+企业”双重监管主体角度,Scott(2002)认为政府和企业应共同合作、发挥各自相应优势,从而实现维护市场竞争秩序和保障消费者权益的目的。汪旭晖和张其林(2015)从资源配置、平台定价、税务征管、外部监管及内部管理五个角度,分别比较了平台和政府各自治理下的优劣及其发展规律,最终得出应建立“平台—政府”双元管理范式,通过平台自治规则以及政府法律规定共同管理平台交易。王勇和冯骅(2017)、于洋和马婷婷(2018)均认为应建立政府为辅、平台为主的双重监管体系,其中王勇和冯骅(2017)分析了平台自我监管手段的优点及其局限,认为应通过政府辅助监管以弥补相应局限;于洋和马婷婷(2018)则结合平台治理现象,分析了以“传统行政发包制为辅、以企业自我管理为主”这一治理模式的运行逻辑,最终得出这一政府与平台企业的合作治理模式是在资源技术和产权安排双重约束下的理性选择。王勇等(2020)进一步通过构建动态博弈模型,对比了平台和政府各自不同监管方式的实际影响,他们认为在监管中二者扮演的角色并非简单的互补或替代关系,二者合作监管下的市场产品质量高于任何一种单一监管模式。三是从更多主体角度,应建立政府、平台和社会群体共同参与的治理体系。其中王俐和周向红(2019)认为政府、平台以及社会群体在治理过程中存在各自的弱点,政府传统的治理框架难以与平台经济新特征相匹配,平台企业追求利润的本质会损害治理效率,公民“有限理性”和社会组织主体缺失的特点会使其治理参与不足。方兴东和严峰(2019)进一步提出应从“法治、公治、自治”三个层面多管齐下,构建全新的治理机制。其中法治是由政府主导和基于公权力建立的治理体系;共治是平台经济下,包括平台在内的各利益相关方建立的治理机制;自治则要求自主性较强的网民群体参与平台的治理和建设。最终通过构建三层联动的治理机制来解决平台经济发展过程中的相应难题。
与现有研究相比,本文的创新性和贡献主要体现在以下三个方面:(1)已有文献多从平台建设的角度考虑对商家产品质量的控制,且多基于后续评价体系。而本文着眼于滴滴平台整改策略的同时,探讨准入门槛和平台自身建设两种监管手段对平台产品平均质量的影响,研究结果具有更强的现实意义。(2)从平台最优和社会最优两个角度,详尽讨论了运用两种治理手段的激励,并剖析了平台和政府运用两种治理手段时激励的异同。(3)结合不同市场环境讨论了三种可行监管手段的有效性,为监管部门提出了切实可行的建议。本文研究结果表明,与社会最优相比,平台自身安全建设努力存在一定不足,对准入门槛的设置存在过严或过松的问题。本文讨论了政府设定准入门槛、政府设定平台建设标准以及政府和平台联合设定安全建设标准三种监管手段,研究发现提高准入门槛仅在成本效率极高的情况下有效;政府和平台联合设定安全建设标准在绝大多数情况下都是最有效的监管手段;在多数情况下,政府设定平台安全建设标准效率高于政府设定准入门槛标准,且从现实操作来看其可行性也更强。
二、基础模型
基于顺风车市场现状,本文研究建立在存在一家垄断平台和两类司机的市场上,司机接入平台为消费者提供高质量或低质量服务,两类司机总数标准化为1:“好司机”(
当低质量出行服务损害消费者权益时,平台也会受到相应惩罚,惩罚力度为
为简化分析,依据现实情况,本文对模型参数提出以下假设:(1)两类司机对准入门槛的敏感系数不同,
在上述设定下,可以得到乘客的效用函数为:
| $ u=\left(v-p\right)({\mathrm{n}}_{g}+e{ \times n}_{b})-(H+p)(1-e){n}_{b} $ | (1) |
其中,
| $ {\pi }_{g}=\left(1-\alpha \right)p-\beta \times s-c $ | (2) |
| $ {\pi }_{b}=\left(1-\alpha \right)p-\gamma \times s-c $ | (3) |
最终销售收入的
平台的利润函数为:
| $ \begin{aligned} \;\\ \mathrm{\pi }=\alpha \left({{n}}_{g}+{{n}}_{b}\right)p-L\left(1-e\right){{n}}_{b}-{k}_{e}{e}^{2}-{k}_{s}{s}^{2} \end{aligned}$ | (4) |
由(4)式可知,平台利润函数由四部分组成:
| 变量名称 | 变量定义 |
|
|
消费者获得高质量服务时的效用 |
|
|
消费者获得低质量服务时的损害 |
|
|
消费者购买服务付出的价格 |
|
|
平台设置的司机准入门槛 |
|
|
平台自身安全建设成果 |
|
|
司机准入门槛设立、平台安全建设的成本系数 |
|
|
|
|
|
|
|
|
加入平台的
|
|
|
事故发生后对平台的惩罚力度 |
|
|
平台的收入抽成系数 |
在上述基础模型设定下,本文将基于平台服务质量提升的角度分析平台使用两类质量监管手段的激励效果。并进一步从社会最优角度分析如何设置两类监管控制手段。最后结合现实环境,分析政府可能采取的三类规制手段,即政府设定准入标准、政府设定平台安全建设标准以及政府和平台共同制定安全建设标准的实际效果。
三、平台最优与社会最优的对比分析
作为本文研究基准,本节将从平台利润最大化和社会总福利最大化两个角度,分别探讨完全由平台或政府选择
(一)平台决策和政府决策的激励分析。根据司机利润和服务成本,求解最终加入平台的司机人数。设
| $ {n}_{g}=\frac{\lambda \left(\right(1-\alpha )p-{s}\times \beta )}{\bar{c}} $ | (5) |
| $ {n}_{b}=\frac{(1-\lambda )\left(\right(1-\alpha )p-{s}\times \gamma )}{\bar{c}} $ | (6) |
首先考虑影响平台和政府决策的效应,平台决策以自身利润最大化为目标,政府决策以社会福利最大化为目标。平台利润由(4)式给出,社会福利由下面三部分组成:
| $ A=v\left({n}_{g}+e{\times n}_{b}\right)-H(1-e){n}_{b} $ | (7) |
| $ B={n}_{g}\beta s+{n}_{b}\gamma s+{c}_{g}+{c}_{b} $ | (8) |
| $ C=L\left(1-e\right){{n}}_{b}+{k}_{s}{s}^{2}+{k}_{e}{e}^{2} $ | (9) |
A式用以衡量消费者加入平台获得服务的收益;B式衡量司机群体的总成本,其中
| $ {c}_{g}=\lambda {\int }_{0}^{\widehat{g}\left(c\right)}\frac{c}{\bar{c}}dc=\bar{c}\frac{{{n}_{g}}^{2}}{2\lambda } ,{c}_{b}=(1-\lambda ){\int }_{0}^{\widehat{b}\left(c\right)}\frac{c}{\bar{c}}dc=\bar{c}\frac{{{n}_{b}}^{2}}{2(1-\lambda )} $ | (10) |
最终社会福利表达式可整理为:
| $ \begin{aligned} SS=&A-B-C= v\left({{n}}_{g}+e{{n}}_{b}\right)-H\left(1-e\right){{n}}_{b}-L\left(1-e\right){{n}}_{b} -[\left({n}_{g}\beta s+{n}_{b}\gamma s\right)+\\ &\left(\bar{c}\frac{{{n}_{g}}^{2}}{2\lambda }+\bar{c}\frac{{{n}_{b}}^{2}}{2\left(1-\lambda \right)}\right)]-{k}_{s}{s}^{2}-{k}_{e}{e}^{2} \end{aligned} $ | (11) |
首先比较平台和政府在制定安全建设努力
| $ \frac{\partial \pi }{\partial e}=L{n}_{b}-2{k}_{e}e , \frac{\partial SS}{\partial e}=(v+H+L){n}_{b}-2{k}_{e}e $ | (12) |
从(12)式可得在安全建设方面,平台选择
命题1:在任意给定的
命题1反映了当平台根据自身利润进行选择时,其制定的安全标准总是低于政府的需要。尽管现实中很多顺风车平台都声称要把消费者的安全放在第一位。但在实际操作时,平台总是从自身利益最优出发,很难完全做到像宣传中所说的“以消费者安全作为首要目标”。因此其制定的安全标准
下面比较平台和政府在制定司机筛选要求
| $ \frac{\partial \pi }{\partial s}=\left[\alpha p\left(\frac{\partial {n}_{g}}{\partial s}+\frac{\partial {n}_{b}}{\partial s}\right)\right]-\left[L\left(1-e\right)\frac{\partial {n}_{b}}{\partial s}\right]-2{k}_{s}s=0 $ | (13) |
| $ \frac{\partial SS}{\partial s}=\left[v\left(\frac{\partial {n}_{g}}{\partial s}+e\frac{\partial {n}_{b}}{\partial s}\right)\right]-\left[\left(H+L\right)\left(1-e\right)\frac{\partial {n}_{b}}{\partial s}\right]-[\frac{\partial \left({n}_{g}\beta s+{n}_{b}\gamma s\right)}{\partial s}+\frac{\bar{c}{n}_{g}}{\lambda }\frac{\partial {n}_{g}}{\partial s}+\frac{\bar{c}{n}_{b}}{1-\lambda }\frac{\partial {n}_{b}}{\partial s}]-2{k}_{s}s=0 $ | (14) |
(13)式和(14)式中提供
三种效应综合决定了平台设定的
命题2:在任意给定的
命题2反映了在准入要求方面,三种效应对平台和政府选择的影响。由于平台在交易中只获得了部分剩余,因此其维护交易的激励更小,更期望通过设定高的司机准入要求降低事故对其带来的损害。在单纯考虑事故带来总损失方面,平台只考虑自身的损失,政府则需要考虑事故带来的全部损失。因此从事故损失方面平台设定的司机准入要求低于政府的要求。最后从司机成本方面,平台完全不考虑司机的成本,而政府希望最小化司机成本。因此从成本方面,平台设定的司机准入要求高于政府要求。最终,剩余提取、事故损失和司机成本三种效应综合决定了平台和政府选择的司机准入要求。
(二)均衡求解。通过求解一阶条件,最终可以得到平台最优下的均衡为:
| $ {s}^{\mathrm{*}}=\frac{2\bar{c}{k}_{e}(L\gamma \left(1-\lambda \right)-p\alpha (\gamma +\beta \lambda -\gamma \lambda \left)\right){-L}^{2}p\left(1-\alpha \right)\gamma {\left(1-\lambda \right)}^{2}}{4{\bar{c}}^{2}{k}_{e}{k}_{s}-{L}^{2}{\gamma }^{2}{(1-\lambda )}^{2}} $ | (15) |
| $ {e}^{\mathrm{*}}=\frac{L(1-\lambda )(2\stackrel-{c}{k}_{s}p\left(1-\alpha \right)-\gamma (L\gamma \left(1-\lambda \right)-p\alpha (\gamma +\beta \lambda -\gamma \lambda )\left)\right)}{4{\stackrel-{c}}^{2}{k}_{e}{k}_{s}-{L}^{2}{\gamma }^{2}{(1-\lambda )}^{2}} $ | (16) |
社会最优下的均衡为:
| $ {e}^{FB}=(H+L+v)(1-\lambda )\frac{(2\bar{c}{k}_{S}p\left(1-\alpha \right)-\left(L+H+p-p\alpha \right){\gamma }^{2}-p(1-\alpha \left)\right(\beta -\gamma \left)\right(\beta +\gamma )\lambda +\gamma (v\beta +(L+H)\gamma \left)\lambda \right)}{4{\bar{c}}^{2}{k}_{e}{k}_{s}-{\left(H+L+v\right)}^{2}{\gamma }^{2}{\left(1-\lambda \right)}^{2}-4\bar{c}{k}_{e}\left({\gamma }^{2}\right(1-\lambda )+{\beta }^{2}\lambda )} $ | (17) |
| $ {s}^{FB}=\frac{2\stackrel-{c}{k}_{e}(\left(L+H\right)\gamma \left(1-\lambda \right)-v\beta \lambda )-p{\left(L+H+v\right)}^{2}\left(1-\alpha \right)\gamma {\left(1-\lambda \right)}^{2}}{4{\stackrel-{c}}^{2}{k}_{e}{k}_{s}-{\left(H+L+v\right)}^{2}{\gamma }^{2}{\left(1-\lambda \right)}^{2}+2\stackrel-{c}{k}_{e}\left({\gamma }^{2}\right(1-\lambda )+{\beta }^{2}\lambda )} $ | (18) |
运用包络定理,分析在均衡解下参数变化对平台利润以及社会福利的影响,见表2:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(三)
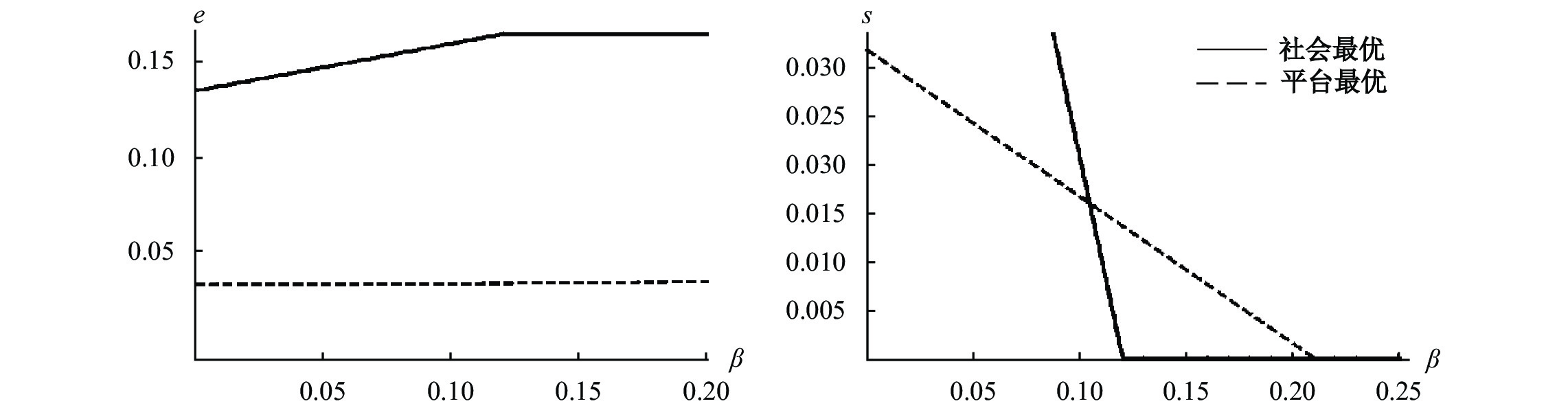
| $ {s}^{\mathrm{*}}={[\frac{2}{63}-\frac{20\beta }{133}]}^+ \text{,} {e}^{\mathrm{*}}=Min[\frac{2}{63}+\frac{\beta }{133},\frac{1}{30}] $ | (19) |
社会福利最大化下的均衡为:
| $ {s}^{FB}={\left[\frac{26-216\beta }{213-108{\beta }^{2}}\right]}^+\text{,}{e}^{FB}=Min[\frac{29+54\beta -18{\beta }^{2}}{213-108{\beta }^{2}},\frac{1}{6}] $ | (20) |
|
|
图 1
|
图1的结果说明
(四)
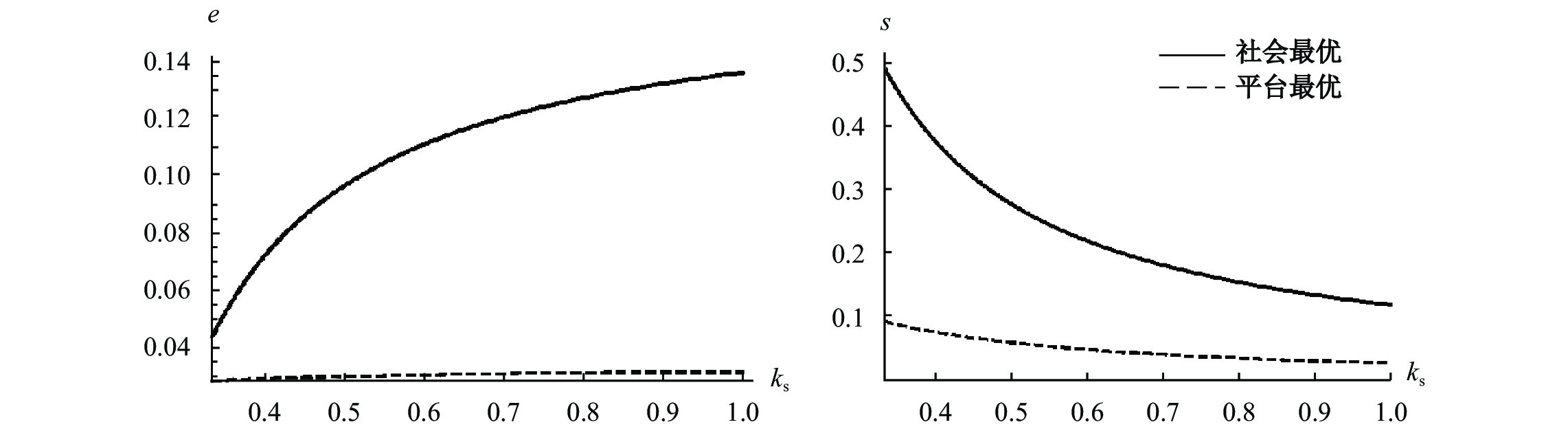
| $ {s}^{\mathrm{*}}=\frac{38}{1200{k}_{s}-3}\text{,}{e}^{\mathrm{*}}=\frac{40{k}_{s}-2}{1200{k}_{s}-3} $ | (21) |
社会最优下的均衡为:
| $ {s}^{FB}=\frac{26}{3(80{k}_{s}-9)}\text{,}{e}^{FB}=\frac{40{k}_{s}-11}{240{k}_{s}-27} $ | (22) |
图2的结果说明
|
|
图 2
|
(五)
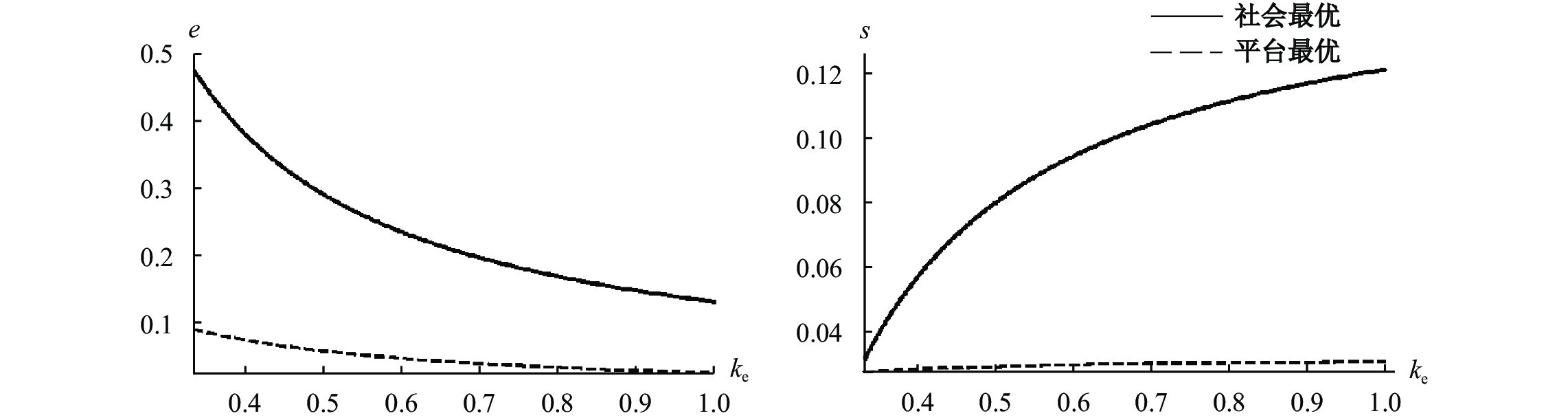
| $ {s}^{\mathrm{*}}=\frac{2-40{k}_{e}}{3-1200{k}_{e}}\text{,}{e}^{\mathrm{*}}=\frac{38}{1200{k}_{e}-3} $ | (23) |
社会最优下的均衡为:
| $ {s}^{FB}=\frac{10-36{k}_{e}}{15-228{k}_{e}}\text{,}{e}^{FB}=\frac{29}{3(76{k}_{e}-5)} $ | (24) |
|
|
图 3
|
图3的结果与图2类似,在
命题3:从安全建设角度来看,平台选择的
命题1和命题2分别从平台利润最大化和社会福利最大化的角度分析了平台和政府在制定安全建设标准和司机准入要求上激励的异同。命题3的结论进一步反映了不同效应带来的具体结果:(1)在安全建设方面,平台制定的安全标准永远低于政府的要求;(2)在“好司机”对准入门槛敏感度较小时,平台设定的司机准入要求过于宽松;在“好司机”对准入门槛敏感度较大时,平台设定的司机准入要求过于严格;(3)准入门槛的成本系数越大,平台设定的司机准入门槛与政府的最优选择之间差异越小。
四、三种监管政策效果的对比分析
本文第三节研究了平台自我规制与政府管制下选择
在上述三种政策下,博弈顺序有所不同。在安全投入标准下:第一阶段,由政府根据社会福利最大化,要求平台设定令
(一)
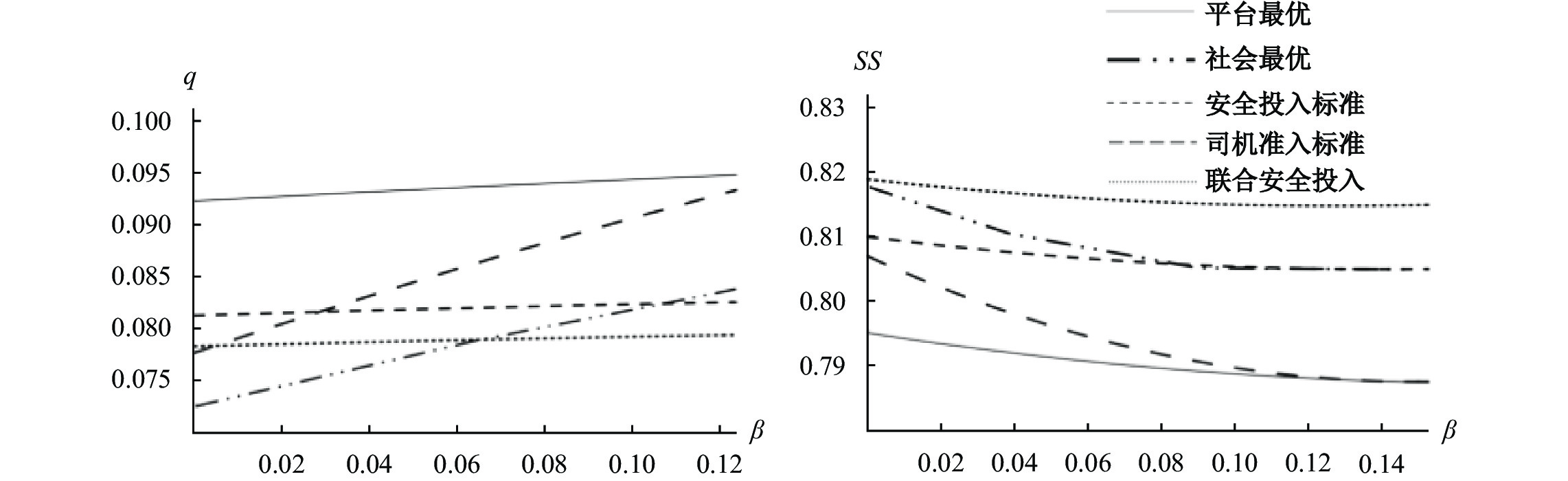
|
| 图 4 β对监管政策的影响 |
在以社会福利最大化为目标时,联合安全投入下的社会总福利最大,甚至能够实现高于政府单独管制下的社会总福利。原因在于当政府和平台分别设定
除联合安全投入外,安全投入标准明显优于司机准入标准,且两者的社会福利差距随
在仅考虑出行安全的情况下,联合安全投入下的事故率最低。但与上文提到的一样,政府提供的
命题4:当司机准入门槛会阻止
命题4说明在准入筛选会对
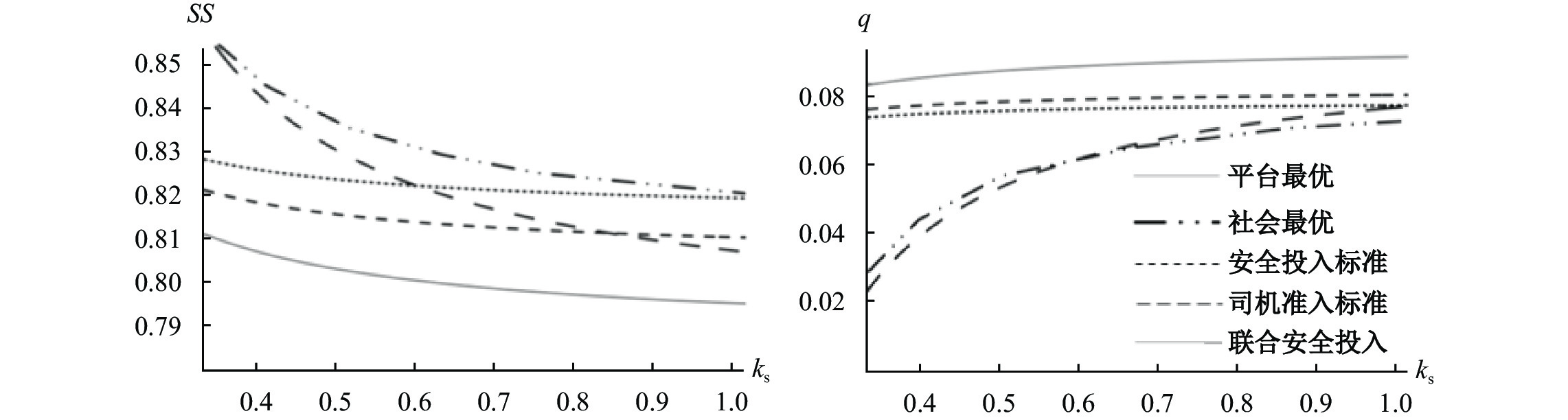
(二)
从安全出行的角度,
|
|
图 5
|
命题5:当司机准入筛选不对
命题4考虑了司机准入敏感度对监管政策效果的影响,命题5的结论则反映了成本效率对三类监管政策效果的影响。当司机准入标准对
五、结论与启示
本文以顺风车市场为例,分析了平台常用的两种质量监管手段,即“司机准入门槛”和“安全建设”发挥作用的具体机制,以及平台如何运用这两种手段提升司机服务质量,保障消费者权益。并比较了平台最优和社会最优下使用两种质量监管手段激励的异同,进而分析了主要市场参数对竞争均衡的影响。最终从政府和平台联合监管的角度,结合不同参数区间讨论了三种监管政策的实际效果,为相关部门提出了切实可行的监管意见。本文主要的研究结论以及政策启示如下:给定司机准入门槛时,平台为安全建设作出的努力远小于政府的要求。给定安全建设努力时,不完全收入抽成效应、内生负外部性效应和内部化司机成本效应三者共同决定了司机准入的要求。不完全的收入抽成效应和内部化司机成本效应使得社会最优更偏好宽松的司机准入要求,内生负外部性效应提高了社会最优下的司机准入要求。在“好司机”对准入要求敏感度较小时,平台设定的司机准入要求过于宽松;在“好司机”对准入要求敏感度较大时,平台设定的司机准入要求过于严格。
基于均衡结果,本文进一步结合平台自我治理激励的变化趋势分析了三类政府和平台联合监管政策的效果,为相关部门监管提供了一定参考。监管政策的选择应结合相关市场环境,当市场中“好司机”对准入筛选相对敏感时,监管部门应认识到平台自我设定的准入门槛能够较好地阻止“坏司机”进入,此时监管重点应在安全建设方面,通过政府自我建设或对平台提出强制要求等手段,从安全教育、加强安全响应、事中记录和事后评价等角度提升平台的安全建设程度。当市场中“好司机”对准入筛选并不敏感时,监管方式的选择应结合两种手段的相对成本效率:在司机准入筛选具有一定成本效率时,平台自身的安全建设激励相对较强,此时监管重点应在准入筛选方面,通过强制要求平台更全面掌握司机信息和更严格设定准入门槛等手段,从源头上阻止“坏司机”进入市场;当司机准入筛选不具备成本优势时,监管重点仍为安全建设方面,此时政府可通过与平台合作完成安全建设或强制要求平台提高安全建设程度等方式保障出行安全及其效率。
现实中各类平台也在准入门槛及平台建设方面做了大量的工作,因此从产品(服务)安全保障方面,本文结果可以进一步推广至对电商和外卖等其他互联网平台的监管。未来对平台产品(服务)安全保障方面的研究可以从价格市场化、需求扩张以及应用大数据等判定司机或商家质量的角度做进一步的拓展。
① 资料来源:https://baijiahao.baidu.com/s?id=1650691678434007770&wfr=spider&for=pc,访问时间:2021.12.12。
② 2019年1月1日,《中华人民共和国电子商务法》正式实施;2019年8月,国务院专门出台了《关于促进平台经济规范健康发展的指导意见》。
③ 在
④ 通过改变
| [1] | 方兴东, 严峰. 网络平台“超级权力”的形成与治理[J]. 人民论坛·学术前沿, 2019(14): 90–101. |
| [2] | 刘奕, 夏杰长. 共享经济理论与政策研究动态[J]. 经济学动态, 2016(4): 116–125. |
| [3] | 王俐, 周向红. 结构主义视阈下的互联网平台经济治理困境研究——以网约车为例[J]. 江苏社会科学, 2019(4): 76–85. |
| [4] | 王小芳, 赵宇浩. 中国网约车规制政策述评[J]. 长安大学学报(社会科学版), 2016(3): 109–115. DOI:10.3969/j.issn.1671-6248.2016.03.019 |
| [5] | 汪旭晖, 张其林. 平台型网络市场“平台—政府”双元管理范式研究——基于阿里巴巴集团的案例分析[J]. 中国工业经济, 2015(3): 135–147. |
| [6] | 汪旭晖, 张其林. 平台型电商企业的温室管理模式研究——基于阿里巴巴集团旗下平台型网络市场的案例[J]. 中国工业经济, 2016(11): 108–125. |
| [7] | 王勇, 冯骅. 平台经济的双重监管: 私人监管与公共监管[J]. 经济学家, 2017(11): 73–80. |
| [8] | 王勇, 刘航, 冯骅. 平台市场的公共监管、私人监管与协同监管: 一个对比研究[J]. 经济研究, 2020(3): 148–162. |
| [9] | 吴德胜. 网上交易中的私人秩序——社区、声誉与第三方中介[J]. 经济学(季刊), 2007(3): 859–884. |
| [10] | 肖红军, 李平. 平台型企业社会责任的生态化治理[J]. 管理世界, 2019(4): 120–144. DOI:10.3969/j.issn.1002-5502.2019.04.012 |
| [11] | 熊鸿儒. 我国数字经济发展中的平台垄断及其治理策略[J]. 改革, 2019(7): 52–61. |
| [12] | 薛志远. 网约车数量管制问题研究[J]. 理论与改革, 2016(6): 108–113. |
| [13] | 于洋, 马婷婷. 政企发包: 双重约束下的互联网治理模式——基于互联网信息内容治理的研究[J]. 公共管理学报, 2018(3): 117–128. |
| [14] | 甄艺凯. 网约车管制新政研究[J]. 中国工业经济, 2017(8): 81–99. |
| [15] | Armstrong M. Competition in two-sided markets[J]. The RAND Journal of Economics, 2006, 37(3): 668–691. DOI:10.1111/j.1756-2171.2006.tb00037.x |
| [16] | Armstrong M, Wright J. Two-sided markets, competitive bottlenecks and exclusive contracts[J]. Economic Theory, 2007, 32(2): 353–380. DOI:10.1007/s00199-006-0114-6 |
| [17] | Caillaud B, Jullien B. Chicken & egg: Competition among intermediation service providers[J]. The RAND Journal of Economics, 2003, 34(2): 309–328. DOI:10.2307/1593720 |
| [18] | Farrell J, Katz M L. Innovation, rent Extraction, and integration in systems markets[J]. The Journal of Industrial Economics, 2000, 48(4): 413–432. |
| [19] | Gawer A, Cusumano M A. Platform leadership: How intel, microsoft, and cisco drive industry innovation[M]. Boston, MA: Harvard Business School Press, 2002. |
| [20] | Rochet J C, Tirole J. Platform competition in two-sided markets[J]. Journal of the European Economic Association, 2003, 1(4): 990–1029. DOI:10.1162/154247603322493212 |
| [21] | Rochet J C, Tirole J. Two-sided markets: A progress report[J]. The RAND Journal of Economics, 2006, 37(3): 645–667. DOI:10.1111/j.1756-2171.2006.tb00036.x |
| [22] | Scott C. Private regulation of the public sector: A neglected facet of contemporary governance[J]. Journal of Law and Society, 2002, 29(1): 56–76. DOI:10.1111/1467-6478.00211 |

