
2022第48卷第3期
一、引 言
宏观经济运行通常伴随着明显的“繁荣和衰退”循环往复的周期性波动现象。对该现象成因的解释主要有三种,第一种认为经济系统存在着极强的内生周期性驱动力量,第二种认为是由各种持续性或间歇式的异质性外生冲击(例如技术冲击、消息冲击和不确定性冲击等)导致,而第三种则关注经济周期波动的形成是否部分源于政府不恰当的经济政策。这些研究互为补充,进一步完善了经济周期理论。然而,从政策制定者的视角,第三种解释更为重要,因为它对政府宏观调控模式的正确选择具有理论参考价值和现实指导意义。在后危机时代货币政策遭受超低利率限制和边际效应递减的现实背景下,财政政策被寄予助推经济复苏的厚望。对我国而言,财政不仅是国家治理的基础和重要支柱,也是稳增长和调结构的重要手段,不可忽略其周期性特征对经济周期和财政效率的重要影响。因此,本文的主要着眼点在于,将财政政策的周期性特征纳入经济周期分析范畴,识别出中国经济周期和财政政策周期的波动演化态势和时变交互区间,从全国层面和省级层面揭示财政政策周期与经济周期的协调和错配问题,并进一步测度在经济周期和财政政策周期视角下的财政支出乘数,这既可为解释中国过去高增长高波动现象提供一个财政政策的视角,也有助于实现未来财政政策的逆周期精准调控和跨周期优化设计。
国际宏观经济学研究中一个公认的典型化事实是新兴市场经济体和发展中国家普遍存在着财政政策顺周期现象。导致财政政策出现顺周期的原因有很多,国外主流的观点主要从金融约束和政治扭曲两方面进行解释。金融约束是指,由于新兴市场经济体的国家信誉和金融深度等方面与发达国家存在较大差距,它在经济衰退时期难以向国际资本市场融到足额资金,国际信贷市场准入的失败和财政收入的恶化使得政府别无选择,只能紧缩财政支出(Gavin和Perotti, 1997;Caballero和Krishnamurthy, 2004)。那么,为何这些国家没有在经济繁荣时期实施逆周期财政政策以优化财政资源的跨周期配置呢?许多研究从政治摩擦的视角解释。一类解释是,政府内部不同政治派别之间的利益冲突和策略互动引发对经济扩张时期丰富财政资源的争夺(即所谓的“贪婪效应”或“公共池效应”),最终导致财政支出过度扩张,跨期支出平滑目标失败(Tornell和Velasco, 1992; Talvi和Vegh, 2005)。另一类解释诉诸政治委托代理过程的信息不对称难题(Alesina等, 2008)。Frankel等(2013)研究发现,在过去十年中,大约有三分之一的发展中国家能够成功逃离“顺周期性陷阱”,其中制度质量的提升是关键。
国内也涌现了大量有关于财政政策周期性的研究,主要探讨我国财政政策周期性特征和相关原因,但由于研究方法、数据样本区间以及问题切入角度不同,现有文献的结论存在一定的差异。方红生和张军(2009)认为我国地方政府实施的财政政策具有“扩张偏向”,具体体现为经济繁荣时期的顺周期性和经济衰退时期的逆周期性,并将其解释为财政分权体制下地方政府竞争和预算软约束相互作用的结果。闫坤和刘陈杰(2015)、孙天琦等(2010)也得到了类似的结论。丛树海和张源欣(2018)研究发现我国财政政策实施效果具有顺周期性,其中财政预算收入的顺周期性是造成财政支出与经济周期趋同的重要原因。基于不同口径预算结构赤字的测算,曾晓安等(2015)验证我国财政政策主要体现逆周期性,但该研究存在个别数据过短的缺点。贾俊雪等(2012)通过制度溯源,认为地方政府为了兼顾自身利益和贯彻中央政策意图,其财政支出行为最终呈现出省级顺周期和全国逆周期的悖论性特征。石绍宾等(2019)则发现地方政府和中央政府的税收政策周期性出现背离,前者顺周期,后者逆周期,这导致宏观层面的税收政策是非周期的。此外,还有一些学者发现政府教育支出和地方政府债务也具有顺周期特征(司海平等, 2018; 梅冬州和韦彩宁, 2019)。与国际流行的“金融约束论”和“政治扭曲论”不同,在财政政策周期性成因和趋势转变上,我国学者主要着眼于我国财政分权体制下特有的政治周期、晋升激励、地方政府投资竞争、金融分权、贸易开放等因素的影响(郭庆旺和赵旭杰, 2012; 肖洁等, 2015; 毛捷等, 2019; 王立勇和祝灵秀, 2019)。
尽管国内外如此之多的研究揭示了财政政策周期性的存在,但很少有文献就财政政策的周期性如何影响经济周期这一问题进行更为细致和详实的探讨,更多文献还是停留在简短的文字描述上。这个问题本质上也涉及财政支出乘数研究。实际上,后危机时代盛行的财政乘数研究只探讨了财政政策影响产出的数量特征,未充分关注财政政策熨平经济周期波动的能力,这是当前财政乘数研究的一个重大缺陷。从这个意义上,如果财政政策是顺周期的,那么财政乘数越大,越是妨害经济,因为它加剧了经济周期性波动。在经济周期视角下将财政政策周期性特征考虑进来可弥补该缺陷。回顾我国改革开放以来的经济发展历程,可以发现两个重要的典型化事实,一是经济新常态以前的经济增长呈现出高增长高波动的态势,那么,这之间是否存在不恰当的顺周期财政政策引致的可能性?二是在面临诸如亚洲金融风暴、全球金融危机和新冠肺炎疫情等巨大负向外部冲击时,我国逆周期的财政政策总能产生明显的效果,这个效果究竟有多大,其短、中、长期经济效应如何变化?本文将在经济周期和财政周期互动的视角下,通过对经济周期视角下的顺周期和逆周期财政乘数的测算回答这两个问题。此外,为了进一步厘清财政政策影响产出的具体路径,本文一并计算出消费乘数和投资乘数,这对于实现财政政策的精准调控具有重要的现实意义。
原则上,要准确识别经济周期的演化态势,就要准确测度产出缺口的时变趋势。然而,产出缺口不可观测,只能采用计量模型进行测度。现有研究主要使用各种滤波方法、生产函数法、状态空间模型或DSGE模型估计产出缺口,其中HP滤波由于简单易用而备受欢迎。然而,HP滤波方法由于存在平滑参数的选取没有理论依据、尾部样本偏倚等弊端一直饱受争议。Hamilton (2018)开发了一种新的滤波方法,能够保留HP滤波若干优势,同时解决HP滤波的潜在缺陷。因此,本文采用汉密尔顿滤波方法估计产出缺口,包括宏观层面和省级层面。同理,该方法也能用于估计财政支出的周期性成分,以此测度财政支出周期状况。根据“瓦格纳法则”,财政政策服务于经济社会的方方面面,随着国民收入增长和经济规模扩张,财政支出会以更大比例增长,最终呈现的结果将会是财政支出占GDP比重逐渐增加。所以理论上财政支出应该有一个与潜在经济增长相匹配的潜在趋势,偏离这个潜在趋势的成分就被定义为财政支出的周期性成分。由于经济存在周期性波动,政府会依据经济周期态势进行财政相机抉择,因此财政支出也会呈现出围绕其潜在趋势发生周期性的扩张或收缩的迹象。
本文首先运用汉密尔顿滤波方法估计我国的产出缺口和财政周期,然后运用时变参数向量自回归模型从宏观层面测度我国经济周期和财政政策周期之间的时变交互影响,最后运用非线性的面板工具变量局部投影模型从省级维度测度经济周期和财政周期视角下的财政支出乘数。研究结果表明:第一,从宏观层面看,亚洲金融风暴、全球金融危机和新冠肺炎疫情爆发等事件对我国经济周期的负面冲击促使财政政策逆周期扩张,而财政周期扩张对经济周期复苏具有显著的推动作用;第二,从省级层面看,地方财政支出乘数在经济紧缩时期更高,这个规律对东、中、西部三大经济区域同样适用;第三,无论是从宏观层面还是省级层面,顺周期财政政策都有较高的时间占比,而顺周期的财政政策是引致中国经济周期波动的重要政策因素,尤其是东部和中部地区,顺周期财政政策的乘数效应十分显著;第四,我国地方政府实施的财政政策并没有对居民消费产生显著的促进作用(体现在消费乘数几乎为零),而投资乘数保持较高水平,经济紧缩时期高达1.15,这表明我国财政政策对经济增长的乘数效应主要通过投资渠道实现。
本文的研究贡献如下:首先,当前学术界发现财政支出乘数非常依赖于外部经济环境,经济周期、金融摩擦、汇率制度等经济特征都会对财政乘数产生显著的影响(许祥云,2013),而本文研究发现财政政策的乘数效应不仅仅取决于外部经济环境,还可能取决于自身的行为特征(例如财政支出的周期性等)。与此同时,在研究经济周期不同阶段财政支出乘数是否存在差异时,Auerbach和Gorodnichenko (2012)、陈诗一和陈登科(2019)均是从国家层面探讨这个问题,本文从省级视角重新审视地方财政支出乘数是否存在经济周期异质性。研究发现,“财政支出乘数在经济紧缩时期更高”的观点在省级层面同样成立。其次,本文认为测算财政乘数时考虑财政政策周期性是至关重要的,并从财政乘数的视角进一步验证了我国顺周期的财政政策主要通过对投资的乘数效应来引致经济波动。最后,本文还提出“消费乘数”和“投资乘数”的概念,探讨我国财政支出稳定经济增长是通过何种渠道实现的。
本文的结构安排如下:第二部分介绍经济周期和财政周期的分析和测度;第三部分介绍本文所使用的计量方法;第四部分进行实证结果分析;第五部分是结论和政策建议。
二、经济周期和财政周期的分析和测度
经济周期和财政政策存在双向因果关系,两者存在极强的内生性。那么,财政政策在我国经济增长历程和经济周期形成中究竟发挥了怎样的作用?图1展示了我国1994—2020年财政预算收支状况和经济增长率的时变趋势图,从中可以得出如下几个事实:第一,我国财政预算收入增长率和财政预算支出增长率的趋势呈现出高度一致性,说明我国财政政策有“量入为出”的特征。第二,我国财政预算赤字率具有显著的逆周期趋势,①在经济增长率上升时期,财政预算赤字率下降,而在经济增长率下降时期,财政赤字率却不断上升。第三,我国财政预算支出占GDP的比重不断上升,这与“瓦格纳法则”的理论预测相一致,财政政策在经济增长中的重要性不容忽视。
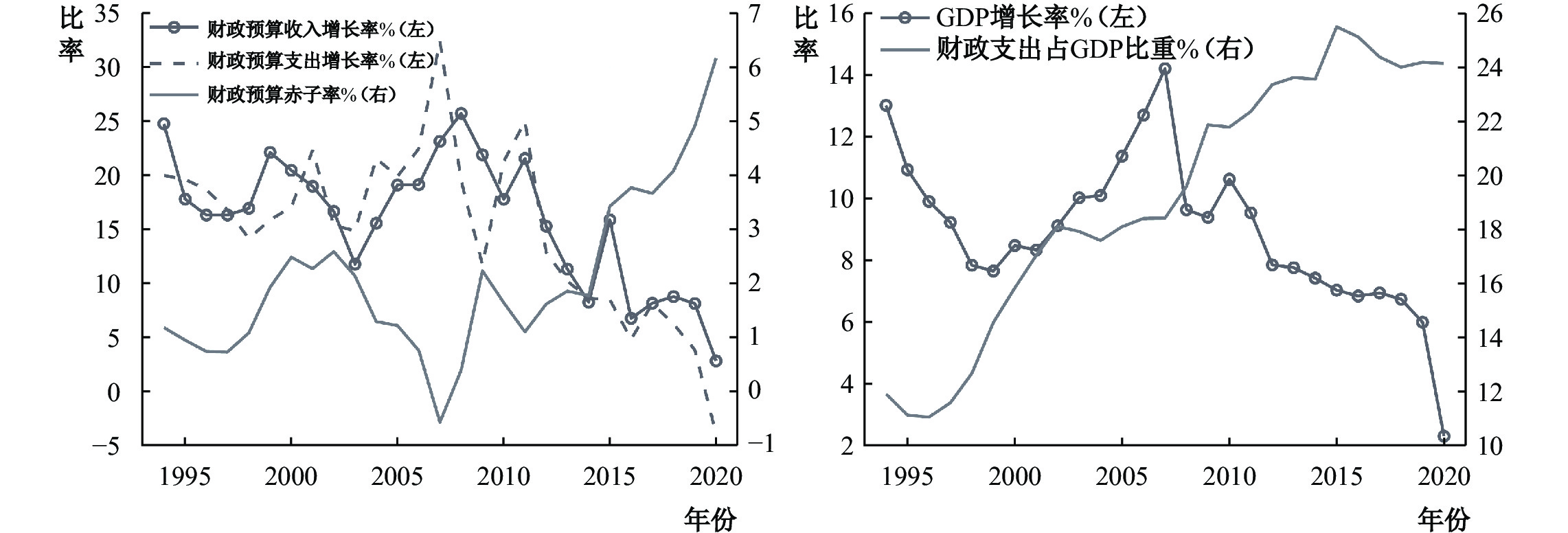
|
| 图 1 财政预算收支状况、财政预算赤字率和经济增长率 |
如何更加准确测度经济周期和财政周期是本论文的基础。Hamilton (2018)已经从计量理论上证明了汉密尔顿滤波占优于HP滤波。本文首先借鉴郑挺国和王霞(2010)的做法,对实际GDP进行季节调整,然后取对数,最后再利用汉密尔顿滤波提取实际GDP的周期性成分(即循环项)作为产出缺口的代理变量。同理,本文对财政支出进行季节调整后取对数,采用汉密尔顿滤波提取该序列的周期性成分,以此作为财政支出周期的代理变量。为了度量每一个时点财政支出究竟是顺周期的还是逆周期的,本文根据产出缺口和财政支出周期的符号是否一致来定义财政周期。从经济意义上,当产出缺口大于零时,意味着实际产出高于潜在产出,即经济处于扩张状态,反之则为经济紧缩状态。当财政支出周期性成分大于零,意味着财政支出处于扩张状态,反之,则意味着财政支出处于紧缩状态。当财政支出的周期性成分的符号与产出缺口的符号相同时,本文认为这些时点政府实施的是顺周期的财政政策,否则便是逆周期的财政政策。本文将此策略分别用于宏观层面和省级层面的财政政策周期分析,并识别出顺周期财政政策和逆周期财政政策的各自时间占比。
表1是对宏观层面和省级层面运用“符号一致性”策略识别出的不同经济状态所占比例。②对宏观层面而言,我国实施顺周期财政政策的时间占比为47.6%(即21.9%+26.7%),从省级层面看,顺周期财政政策的时间占比为65.2%(即35.4%+29.8%)。无论是宏观层面还是省级层面,财政政策的顺周期特征都是显著存在的。然而省级层面顺周期财政政策的时间占比远高于宏观层面,这极可能是中央财政支出具有逆周期调控取向,从而在宏观层面上减少了顺周期财政政策的时间占比。从省级层面看,经济扩张时期的扩张性财政政策占比最高(35.4%),说明地方政府在经济周期的繁荣阶段有财政支出扩张偏向,其内在原因可能在于地方官员具有推动经济增长以谋求政治晋升的动机,而经济繁荣时期恰好为该动机的实现提供了充足的税源。从宏观层面看,经济紧缩时期的扩张性财政政策时间占比最高(34.3%),这主要得益于中央对全国经济周期稳定的把握,中央可以通过多种手段(包括财政手段和行政手段)规范地方财政支出行为以实现经济平稳运行(贾俊雪等,2012),在全国经济面临重大负向冲击时甚至会动员各层级政府的力量实行力度更大的逆周期财政政策。
| 四种经济状态的比例 | 宏观层面 | 省级层面 | 性质 |
| 经济扩张时期的扩张性财政政策 | 21.9% | 35.4% | 顺周期财政政策 |
| 经济扩张时期的紧缩性财政政策 | 17.1% | 18.8% | 逆周期财政政策 |
| 经济紧缩时期的扩张性财政政策 | 34.3% | 16.0% | 逆周期财政政策 |
| 经济紧缩时期的紧缩性财政政策 | 26.7% | 29.8% | 顺周期财政政策 |
| 合计 | 100% | 100% |
本文的研究涉及财政政策周期和经济周期之间的内在关联,也考虑到经济周期和财政政策周期的互动对财政政策有效性的影响。首先,从理论上看,财政政策周期的扩张或收缩会推动经济周期同向变动,因此实施逆周期的财政政策对于熨平经济波动至关重要。从财政政策周期和经济周期的协调或错配的角度,顺周期的财政政策至少有两大危害,一是加剧经济周期波动,二是损害了财政资源的跨周期配置,经济扩张时期采取顺周期的财政政策可能导致无法积累足够的财政资源用于衰退时期的财政赤字扩张。其次,凯恩斯理论认为,在经济收缩时期,由于存在大量的闲置产能,扩张性财政政策对私人投资的挤出效应很小,因此逆周期的财政政策能够发挥更大的乘数效应。然而,凯恩斯理论并没有告诉我们,当财政政策是顺周期时,它产生的乘数效应到底有多大,而财政政策的顺周期现象却是世界范围内绝大多数发展中国家曾经发生过(或正在发生)的现实。在后危机时代,学术界进行了大量的实证研究,主要探索各种外部经济特征(例如经济周期、金融摩擦等)是否对财政支出乘数产生重大影响,但却很少考虑财政政策自身特征的影响。与此同时,不难发现,凯恩斯的财政政策有效性理论主要从国家层面进行思考,“经济收缩时期的财政政策有效性更高”的观点在区域层面是否也成立有待探讨。因此,本文将从我国省级层面,基于经济周期和财政政策周期视角,对我国省级财政支出乘数进行实证分析。
最后,本文的研究也对实现财政政策的跨周期优化设计具有一定启示意义。要对财政政策进行跨周期优化设计,首先要对中国经济周期的形成和发展有一个准确的判断,其次是要明确财政政策的目标和职能。所谓“跨周期”(即跨经济周期),有两层含义,第一层是跨同一个经济周期的不同阶段。第二层是跨不同的经济周期,财政政策不能只盯住短周期,还要兼顾中长期的发展,这就要求财政政策具有可持续性。因此,保持逆周期的政策立场是实现跨周期政策设计的重要基础,而跨周期政策设计则是逆周期政策调控的升华。要实现财政政策的跨周期优化设计,还要强化财政政策有效性,这样才能确保以更小的财政负担撬动更大的增长潜力,同时也有利于实现财政政策可持续性。
三、计量模型构建和实证测算思路
(一) TVP-VAR模型
参考Nakajima (2011)的思路,构建TVP-VAR模型如下:
| $ {y_t} = {c_t} + {B_{1t}}{y_{t - 1}} + \cdots + {B_{st}}{y_{t - s}} + {e_t},\;\,{e_t} \sim N\left( {0,\,{\Omega _t}} \right) $ | (1) |
其中,
| $ \begin{array}{*{20}{c}} {{\beta _{t + 1}} = {\beta _t} + {u_{\beta t}},} \\ {{a_{t + 1}} = {a_t} + {u_{at}},} \\ {{h_{t + 1}} = {h_t} + {u_{ht}},} \end{array}\quad \;\left( {\begin{array}{*{20}{c}} {{\varepsilon _t}} \\ {{u_{\beta t}}} \\ {{u_{at}}} \\ {{u_{ht}}} \end{array}} \right) \sim N\left( {0,\;\left( {\begin{array}{*{20}{c}} I&O&O&O \\ O&{{\Sigma _\beta }}&O&O \\ O&O&{{\Sigma _a}}&O \\ O&O&O&{{\Sigma _h}} \end{array}} \right)} \right) $ | (2) |
其中,对于
本文构建包含经济周期、财政周期和通货膨胀的三变量TVP-VAR模型,其中经济周期用产出缺口来衡量,财政周期用财政支出周期性成分代表,两者都是前文运用汉密尔顿滤波估计得到,通货膨胀使用CPI同比价格指数代理。所有的变量均通过ADF检验,满足平稳性。模型滞后阶数采用2阶的常规设定。样本区间为1995年第一季度至2021年第一季度,数据来源于中经网统计数据库。本文使用Nakajima (2011)开发的TVP-VAR模型算法进行计算,蒙特卡洛模拟11000次。
(二) 工具变量局部投影模型
如果已知省级财政支出冲击
| $ \sum\nolimits_{h = 0}^k {{y_{i,t + h}}} = {\alpha _{i,k}} + {\delta _{t,k}} + {m_k}\sum\nolimits_{h = 0}^k {{g_{i,t + h}}} + {\gamma _k}ct{r_{i,t - 1}} + {\varepsilon _{i,t + k}},\;\;k = 0,1,2,\cdots,H\; $ | (3) |
其中,
上述方法是线性的,只能测算出线性的省级财政支出乘数,如果要测算不同经济状态下的省级财政支出乘数,需要将模型(3)拓展至如下非线性的形式:
| $ \begin{gathered} \sum\limits_{h = 0}^k {{y_{i,t + h}}} = {I_{i,t - 1}}\left[ {{\alpha _{i,k}} + {\delta _{t,k}} + {\gamma _k}ct{r_{i,t - 1}} + {m_{r,k}}\sum\limits_{h = 0}^k {{g_{i,t + h}}} + {\varepsilon _{i,t + k}}} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} + (1 - {I_{i,t - 1}})\left[ {{\alpha _{i,k}} + {\delta _{t,k}} + {\gamma _k}ct{r_{i,t - 1}} + {m_{e,k}}\sum\limits_{h = 0}^k {{g_{i,t + h}}} + {\varepsilon _{i,t + k}}} \right],\;\;k = 0,1,2,\cdots,H\; \hfill \\ \end{gathered} $ | (4) |
在模型(4)中,
本质上,模型(4)相当于分样本回归,将数据集划分为不同的经济状态的样本分别进行回归。如果我们关注顺周期和逆周期的财政政策是否会产生不同的乘数效应,根据前文的“符号一致性”识别策略,划分顺周期财政政策和逆周期财政政策的两样本,也能分别测算得到顺周期财政乘数和逆周期财政乘数。此外,由于财政支出扩张稳定经济增长主要是通过拉动消费和投资实现,为了厘清我国省级财政支出对经济增长的影响路径,本文提出“消费乘数”和“投资乘数”的概念,前者衡量一个单位的财政支出能促进消费增加多少个单位,后者衡量一个单位的财政支出能促进投资增加多少个单位。在计算上,只需将模型(3)和模型(4)的被解释变量替换成消费(用省级社会消费品零售额代表)或投资(用省级固定资产投资代表),便可以测算出消费乘数和投资乘数。
需要注意的是,以上有关于省级财政支出乘数测算的前提是事先识别出外生的省级财政支出冲击
| $ {g_{i,t}} = {\alpha _i} + {\delta _t} + \gamma \times ct{r_{i,t - 1}} + shoc{k_{i,t}} $ | (5) |
其中,
四、实证结果分析
(一) TVP-VAR模型实证结果分析
图2呈现了三个特定时点(点线代表亚洲金融危机时期、虚线代表全球金融危机时期、实线代表全球新冠肺炎爆发时期)的脉冲响应函数。图2的第一行第二列是经济周期
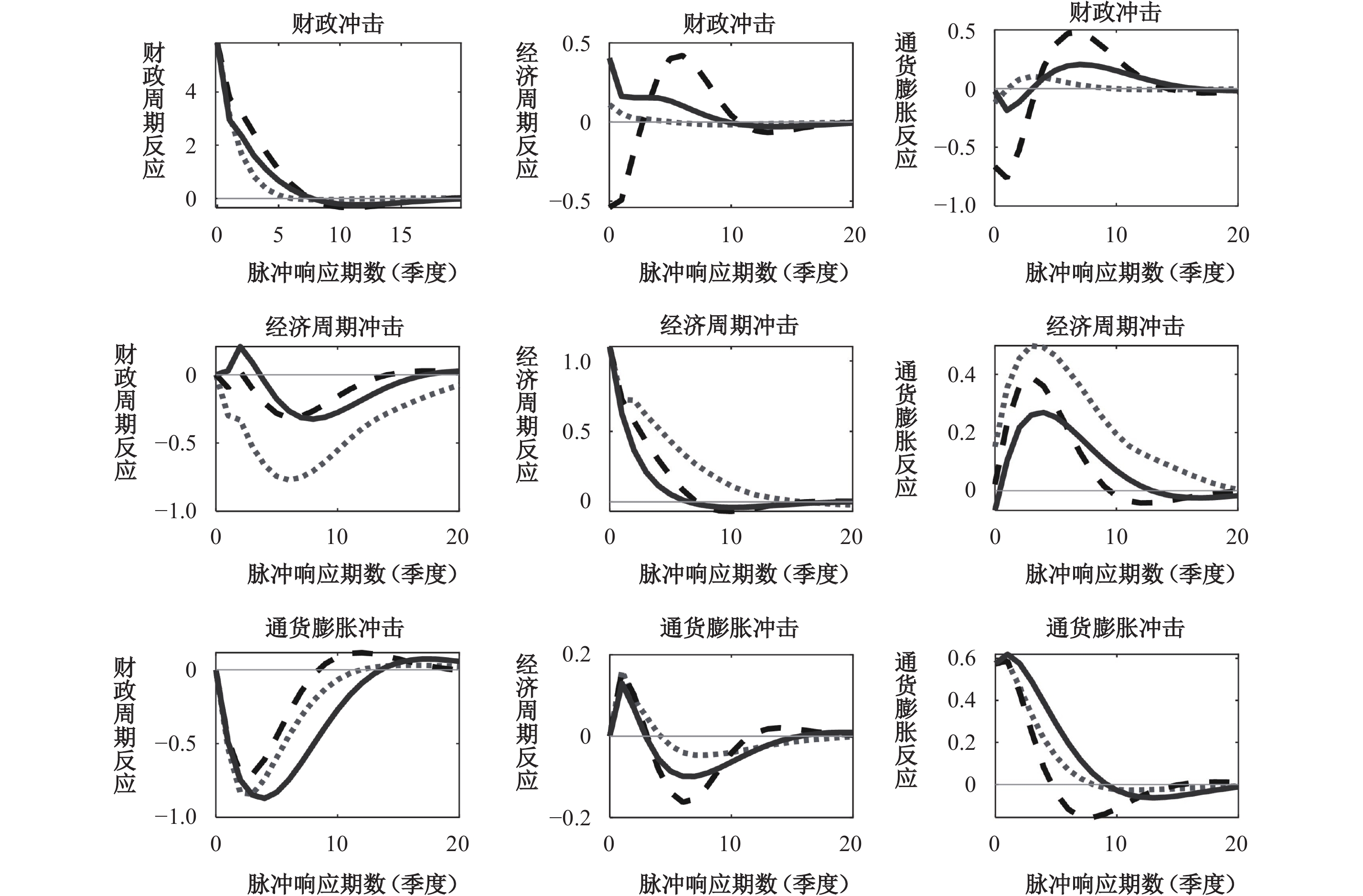
|
| 图 2 特定时点的脉冲响应函数 注:图中点线、虚线和实线分别表示1998年第3季度、2009年第1季度和2020年第1季度的脉冲响应函数,各自代表亚洲金融危机、全球金融危机和新冠肺炎疫情三个典型的经济衰退时期。横轴代表脉冲响应期数,纵轴代表相对应变量的脉冲响应的数值。 |
(二)工具变量局部投影模型实证结果分析
本文所使用的31个省(市、区)的省级GDP、财政支出、财政收入、社会消费品零售额和固定资产投资主要来自中经网统计数据库,数据区间为2005年第1季度—2021年第1季度。所有季度数据均经过价格处理和Census-X12季节调整。
1. 线性模型的省级财政支出乘数估计
图3呈现了线性的工具变量局部投影模型测度的省级财政支出乘数(左图)和有效F统计量(右图),后者用来判断省级财政支出冲击

|
| 图 3 省级财政支出乘数(左)和有效F统计量(右) |
那么,省级财政支出乘数较低是否意味着我国地方政府的财政支出效率普遍较低呢?要回答这个问题,至少还要考虑两个因素。第一个因素是省级财政支出乘数可能存在着区域异质性。线性模型本质上衡量的是平均效应,不同区域间的经济发展状况和财政效率可能存在较大的差异。为此,本文将省级面板样本划分为东部、中部和西部,重新测算三个区域的省级财政支出乘数。表2呈现了计算结果,东部的省级财政支出乘数约为0.6且非常显著,中部的乘数约为0.3同样显著,而西部的乘数几乎为零,同时也不显著。我国省级财政支出效率呈现出东部、中部和西部逐级递减的空间分布格局。此外,还必须考虑的第二个因素是省级财政支出的溢出效应。例如,如果广东省一单位的财政支出促使广东省GDP增加0.6个单位,但同时促使其他地区的GDP增长0.5个单位(即财政支出的溢出乘数为0.5),此时广东省的财政支出对全国经济增长的乘数效应为1.1。财政溢出效应的存在是由于不同省份之间存在着贸易往来等经济联系,地方财政支出扩张促使当地居民收入提高,当地居民会购买其他地区的商品或服务,这种需求溢出效应带动了其他地区的经济增长。尤其是在当前互联网购物平台迅猛发展和物流配送系统十分发达的现实背景下,财政溢出效应极有可能是正向且越来越大的。这种正向的财政溢出效应客观上削弱了省级财政支出乘数,但强化了财政溢出乘数和区域间的经济循环,有助于提高宏观层面的财政支出乘数。财政溢出效应也是导致宏观层面的财政支出乘数和地区层面的财政支出乘数产生差异的重要因素(付一婷等, 2021)。因此,基于省级财政支出乘数存在区域异质性和财政溢出效应两个因素,我们必须客观看待测算的平均省级财政支出乘数较小的事实,而不是直接对省级财政政策效率做出否定的判断。
| 脉冲响应期数 | 全国 | 东部 | 中部 | 西部 |
| 第4期 | 0.049** | 0.288*** | 0.194 | 0.008 |
| 第8期 | 0.086*** | 0.439*** | 0.342** | 0.013 |
| 第12期 | 0.090*** | 0.552*** | 0.277* | 0.002 |
| 注:*、**和***分别代表在10%、5%和1%的显著性水平下显著,下表同。 | ||||
2. 经济周期视角下的省级财政支出乘数
根据汉密尔顿滤波测算出各省份的产出缺口,将产出缺口小于零的时期定义为经济紧缩时期,将产出缺口大于零的时期定义为经济扩张时期,运用非线性的面板工具变量局部投影模型分别测算不同经济周期阶段的省级财政支出乘数。图4展示了经济扩张时期(左)和经济紧缩时期(右)的省级财政支出乘数,从中可以发现在经济周期不同阶段的省级财政支出乘数的显著差异。经济扩张时期的省级财政支出乘数小于0.05,从统计意义上也不显著异于零。而经济紧缩时期的省级财政支出乘数随着脉冲响应期数的增加不断上升,最终稳定在0.3左右,从置信区间看也显著异于零。前文使用线性模型测算得到的省级财政支出乘数约为0.09,介于经济扩张时期的0.05和经济紧缩时期的0.3之间,这进一步表明了线性模型测算得到的乘数是经济扩张时期乘数和经济紧缩时期乘数的某种加权平均值。这个结果进一步论证了凯恩斯理论中“财政政策在经济衰退时期更有效”的观点在我国中观层面也是成立的。
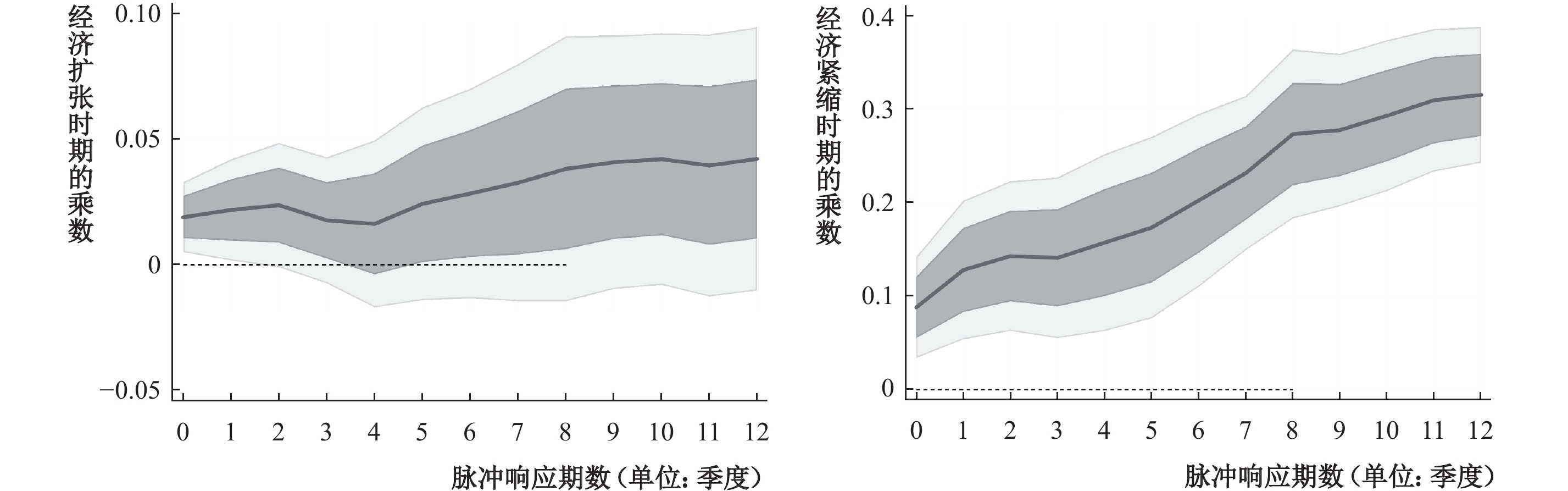
|
| 图 4 经济扩张时期(左)和经济紧缩时期(右)的省级财政支出乘数 |
当然,以上是基于全样本的分析,我们也许感兴趣不同地区的省级财政支出乘数是否也遵循逆周期规律。因此,本文进一步对东部、中部和西部的情况进行分析,表3呈现了不同经济周期阶段各区域的乘数大小。对东部而言,经济扩张时期的省级财政支出乘数最终稳定在0.15左右,但并不显著,而经济紧缩时期的省级财政支出不仅十分显著(在1%的显著性水平下都是显著异于零),还随着脉冲响应期数的增加而增加。第12期的省级财政支出乘数约为0.8,远高于经济扩张时期的乘数。对中部而言,经济扩张时期的省级财政支出乘数最高达到0.38,而经济紧缩时期的省级财政支出乘数最高达到0.63,两者都是显著异于零的,但经济紧缩时期的乘数更高。对西部而言,经济扩张时期的乘数与零没有显著差异,但经济紧缩时期的乘数非常显著,数值达到0.2。因此,“经济紧缩时期的省级财政支出乘数更高”的观点对于不同经济区域也是成立的,地方政府应当坚持逆周期的财政政策调控取向,这不仅可以平抑区域经济周期波动,也有助于提升整体财政支出效率。
| 脉冲响应期数 | 东部 | 中部 | 西部 | |||
| 经济扩张时期 | 经济紧缩时期 | 经济扩张时期 | 经济紧缩时期 | 经济扩张时期 | 经济紧缩时期 | |
| 第4期 | 0.079 | 0.370*** | 0.037 | 0.478** | 0.003 | 0.129** |
| 第8期 | 0.141 | 0.588*** | 0.231 | 0.626*** | −0.006 | 0.203*** |
| 第12期 | 0.145 | 0.776*** | 0.386** | 0.304 | −0.009 | 0.214*** |
3. 考虑财政政策周期性的省级财政支出乘数
当前财政乘数研究的一个缺陷是没有考虑到财政政策的周期性特征,即便得出“经济衰退时期财政乘数更高”的观点,也并不意味着这是一个好事,因为在经济衰退时期一些政府采取的是紧缩性财政政策,尤其是一些新兴市场经济体。本文根据前文的“符号一致性”策略识别出省级维度的顺周期财政政策和逆周期财政政策区间,运用非线性的工具变量局部投影模型测算出顺周期和逆周期省级财政支出乘数。由图5可知,顺周期的省级财政支出乘数约为0.05,其数值较小,且置信区间较宽,大多数时期并不显著。逆周期的省级财政支出乘数随着脉冲响应期数的增加呈现上升的趋势,最终稳定在0.15左右,对于所有的脉冲响应函数期数而言都是显著异于零的。与前文的思路类似,为了更加全面地评估顺周期和逆周期财政政策的乘数效应,本文进一步对东部、中部和西部三大区域的情况进行分析。表4呈现了三大区域的顺周期和逆周期财政支出乘数,可以发现,东部和中部的顺周期财政政策的乘数效应最终分别达到0.61和0.38,且十分显著,而西部的顺周期财政政策的乘数效应并不显著。从经济总量占比看,东部和中部的经济总量占全国经济总量的绝大多数,东部和中部的顺周期财政政策有相当大的乘数效应,它们会造成国家层面经济周期波动加剧。我国经济新常态以前的经济增长呈现出高增长高波动的特征,这之间很可能存在着财政政策顺周期引致的因素。从地方政府的政策动机看,地方官员有政治晋升的激励,而以往的政绩考核主要依据经济增长数量,在经济扩张时期,地方政府能获得更多的税源,因此该时期有更大的财力实行扩张性的财政政策促进经济增长,而非采用紧缩性的财政政策平抑经济波动。实际上,地方政府运用财政政策推动经济数量增长的方式是通过基建投资来实现,后文在进行投资乘数测算时也能进一步论证这个事实。反观逆周期财政政策的乘数效应,东部高达0.78,中部高达0.63,西部达到0.21,统计上均显著异于零,且比顺周期财政政策的乘数效应更高一些。这更加论证了逆周期财政政策调控的必要性,不仅避免了顺周期财政政策加剧经济周期波动的情况,而且在财政支出效率上,逆周期调控也有着更高的效率。
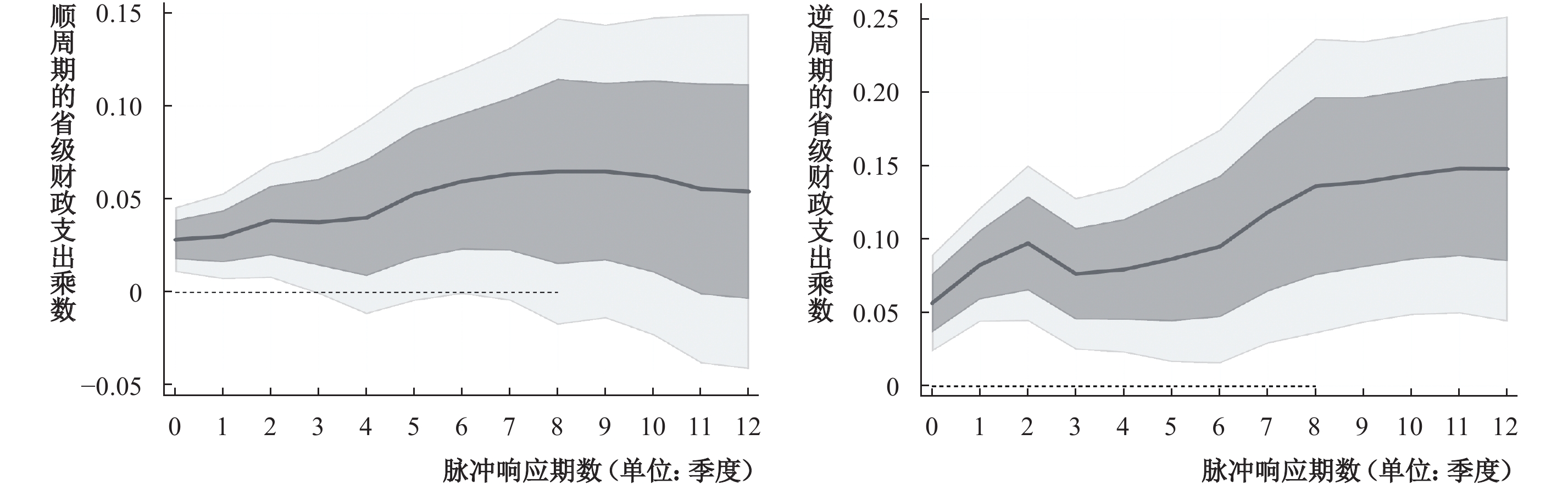
|
| 图 5 顺周期(左)和逆周期(右)的省级财政支出乘数 |
| 脉冲响应期数 | 东部 | 中部 | 西部 | |||
| 顺周期财政政策 | 逆周期财政政策 | 顺周期财政政策 | 逆周期财政政策 | 顺周期财政政策 | 逆周期财政政策 | |
| 第4期 | 0.28** | 0.37*** | 0.08 | 0.48** | −0.02 | 0.13** |
| 第8期 | 0.46*** | 0.59*** | 0.39*** | 0.63*** | −0.04 | 0.20*** |
| 第12期 | 0.61*** | 0.78*** | 0.38** | 0.30 | −0.07 | 0.21*** |
4. 财政政策稳定经济增长的路径探索:基于消费乘数和投资乘数的视角
财政政策有效性的大小主要取决于它是否能有效促进居民消费和私人投资,因此有必要从消费乘数和投资乘数的视角对财政政策稳定经济增长的路径进行探索,这也有助于我们理解历年来地方政府在进行财政政策决策时究竟有怎样的目标偏好和行为动机。本文首先测算线性模型下的消费乘数和投资乘数,然后测算不同经济周期阶段以及顺周期和逆周期视角下的消费乘数和投资乘数。
表5呈现了消费乘数的测算结果。从线性模型看,消费乘数为负数,这说明地方财政政策对居民消费产生了挤出效应,但并不显著。在经济周期视角下,能够观察到经济扩张时期的消费乘数为负数,而经济紧缩时期的消费乘数为正数,但两者数值与零十分接近且都不显著。即便考虑财政政策周期性,无论是实施顺周期的财政政策还是逆周期的财政政策,消费乘数都不显著。这说明我国历年来的财政政策对居民消费几乎没有促进作用。表6呈现了投资乘数的测算结果。可以看到,线性模型测算得到的投资乘数数值高达0.61,统计意义上十分显著。从经济意义上讲,地方政府多增加一个单位的财政支出,能够促使当地投资增加0.61个单位。即便是考虑经济周期异质性,投资乘数仍然显著,在经济扩张时期,投资乘数达到0.5左右,而在经济紧缩时期,投资乘数高达1.15,这进一步说明了我国省级财政支出乘数在经济紧缩时期更高的原因在于经济紧缩时期的财政支出对投资有更高的促进作用。在考虑财政政策周期性时,顺周期的财政政策对投资的乘数效应比逆周期的财政政策更大,也更显著。因此地方政府采取的顺周期财政政策主要通过投资渠道引致经济波动,这个结果在一定程度上能够解释为什么经济新常态以前我国经济的大起大落常常伴随着投资的过冷和过热,顺周期财政政策确实是过去导致我国经济周期波动加剧的一个政策因素。黄赜琳和朱保华(2015)运用实际经济周期模型研究发现,引入财政支出冲击更能够解释中国经济波动。本文从财政乘数的视角进一步论证了这个事实。由此可见,财政支出乘数高是一把“双刃剑”,只有合理规范政府的财政行为,在政策方向具备合理性的前提下,政策工具的有效性才能真正服务于中国经济的发展。
| 脉冲响应期数 | 线性模型 | 经济周期视角 | 财政政策周期性视角 | ||
| 经济扩张时期 | 经济紧缩时期 | 顺周期财政政策 | 逆周期财政政策 | ||
| 第4期 | −0.017 | −0.020 | 0.015 | −0.013 | −0.008 |
| 第8期 | −0.016 | −0.020 | 0.011 | −0.021 | 0.011 |
| 第12期 | −0.016 | −0.014 | 0.003 | −0.024 | 0.015 |
| 脉冲响应期数 | 线性模型 | 经济周期视角 | 财政政策周期性视角 | ||
| 经济扩张时期 | 经济紧缩时期 | 顺周期财政政策 | 逆周期财政政策 | ||
| 第4期 | 0.20** | 0.04 | 0.66* | 0.23 | 0.04 |
| 第8期 | 0.52*** | 0.34** | 1.09*** | 0.45** | 0.25 |
| 第12期 | 0.61*** | 0.49*** | 1.15*** | 0.56*** | 0.25 |
另外,为何消费乘数和投资乘数存在如此大的差异?本文认为这是我国财政支出结构不合理导致。我国过去经济快速增长的重要驱动力量是投资,地方政府向来重视财政支出的生产性支出,导致财政政策对投资具有较高的乘数效应。财政支出结构的不合理也是导致收入分配不合理的重要原因。政府部门需要优化财政支出结构,向民生领域给予更多的支持,发挥对居民消费的引领作用,才能更有效地增强财政政策的实施效果。
五、研究结论和政策建议
本文综合运用汉密尔顿滤波、TVP-VAR模型、工具变量局部投影法从宏观层面和省级层面研究中国经济周期和财政政策周期之间的内在联系以及不同经济状态下的省级财政支出乘数,主要得到以下研究结论:首先,无论是从宏观层面还是省级层面,顺周期财政政策的时间占比都比较高,这成为引致中国经济波动的重要政策因素,尤其是东部和中部地区,顺周期的省级财政支出乘数较高;其次,TVP-VAR模型的研究结果显示,我国在面临重大负向经济冲击时,财政周期趋于扩张,为经济周期复苏提供了重要的政策支持,且政策调控效果在不断改善;再次,省级财政支出乘数不仅具有区域异质性,还具有经济周期异质性;最后,机制分析表明,我国财政政策可能几乎不对居民消费产生显著的促进作用,反而对投资具有更强的乘数效应,尤其是在经济紧缩时期,投资乘数高达1.15,这进一步论证了我国历年来的财政政策主要是通过投资渠道来促进经济增长。
基于以上研究结论,本文提出如下政策建议:第一,加强和完善对区域经济周期的实时监测,在进行财政预算安排时纳入区域经济周期的信息。这样能够确保经济收缩的地区能够得到更大的财政资源支持以实现财政政策的逆周期扩张,同时又能对经济扩张的地区施加必要的财政预算约束。此外,由于经济紧缩时期的省级财政支出乘数更高,将财政资源适度向经济收缩的地区倾斜,也有利于提升国家整体的财政支出效率。第二,我国地方层面的财政政策对投资具有很强的乘数效应,短期内地方政府仍然应当发挥“稳投资”的作用。财政政策也要适当关注“新基建”领域的新型投资,既要积极拓展投资空间,也要稳定财政政策对私人投资的乘数效应。第三,财政政策应优化支出结构,对教育、医疗等民生领域给予更多的关注,强化对居民消费的乘数效应,才能更加有效地实现财政政策的提质增效,从而引导供给和需求在更高水平实现均衡。第四,本文的研究还为实现财政政策逆周期精准调控和跨周期优化设计提供重要的启示。坚持财政政策逆周期调控的意义至少有三个:一是避免顺周期的财政政策加剧经济波动,二是有利于优化财政资源的跨周期配置,三是可以提升财政政策有效性。与此同时,要实现财政政策的跨周期优化设计,应当做到三点:首先是坚持逆周期立场,为我国经济增长的稳定性和可持续性保驾护航;其次是促使财政政策提质增效,这既需要保持财政政策对投资的较高的乘数效应,同时也要通过优化财政支出结构,进一步增强财政政策对居民消费的引领作用,从而保证财政政策具有更高的整体效率,以更少的财政负担成本撬动更大的经济增长潜力;最后是务必确保财政政策的可持续性,虽然提升财政政策有效性也有利于节省财政资源,但政府仍然应当主动进行“开源”和“节流”,建立稳健的中长期财政框架,保证充足的财政空间,为中国进一步延续长周期经济增长提供财政政策支持。
① 本文对每年财政预算赤字率的计算方式为:100×(名义财政预算支出-名义财政预算收入)/名义GDP。
② 宏观层面使用时间序列样本的时间跨度为1995年第1季度—2021年第1季度,省级层面使用面板数据的时间跨度为2005年第1季度—2021年第1季度。
③ 参考Bernardini等 (2020)的做法,对每个省的实际GDP使用平滑参数为10000的HP滤波方法得到潜在产出。在稳健性检验中,潜在产出使用汉密尔顿方法来估计,并不影响最终财政乘数测算结果。
④ 如不特别说明,后文呈现的所有乘数估计值的置信区间也分别为68%和90%。
| [1] | 陈诗一, 陈登科. 经济周期视角下的中国财政支出乘数研究[J]. 中国社会科学, 2019(8): 111–129. |
| [2] | 丛树海, 张源欣. 财政政策的顺周期实施效应特征与基本成因[J]. 财贸经济, 2018(6): 30–42. DOI:10.3969/j.issn.1002-8102.2018.06.004 |
| [3] | 方红生, 张军. 中国地方政府竞争、预算软约束与扩张偏向的财政行为[J]. 经济研究, 2009(12): 4–16. |
| [4] | 付一婷, 陈润东, 刘金全. 经济周期和空间分异视角下的财政资源再配置——基于全国和省级财政乘数的分析[J]. 财贸经济, 2021(9): 97–111. DOI:10.3969/j.issn.1002-8102.2021.09.007 |
| [5] | 郭庆旺, 赵旭杰. 地方政府投资竞争与经济周期波动[J]. 世界经济, 2012(5): 3–21. |
| [6] | 黄赜琳, 朱保华. 中国的实际经济周期与税收政策效应[J]. 经济研究, 2015(3): 4–17. |
| [7] | 吕冰洋, 毛捷. 高投资、低消费的财政基础[J]. 经济研究, 2014(5): 4–18. |
| [8] | 贾俊雪, 郭庆旺, 赵旭杰. 地方政府支出行为的周期性特征及其制度根源[J]. 管理世界, 2012(2): 7–18. |
| [9] | 毛捷, 刘潘, 吕冰洋. 地方公共债务增长的制度基础——兼顾财政和金融的视角[J]. 中国社会科学, 2019(9): 45–67. |
| [10] | 梅冬州, 韦彩宁. 公共债务与政府教育支出的顺周期性[J]. 财政研究, 2019(6): 32–45. |
| [11] | 石绍宾, 尹振东, 汤玉刚. 财政分权、融资约束与税收政策周期性[J]. 经济研究, 2019(9): 90–105. DOI:10.3969/j.issn.1672-5719.2019.09.080 |
| [12] | 司海平, 刘小鸽, 魏建. 地方政府债务融资的顺周期性及其理论解释[J]. 财贸经济, 2018(8): 21–34. DOI:10.3969/j.issn.1002-8102.2018.08.002 |
| [13] | 孙天琦, 杨岚, 苗文龙. 中国财政政策是否具有顺周期性[J]. 当代经济科学, 2010(3): 1–10. DOI:10.3969/j.issn.1002-2848.2010.03.001 |
| [14] | 王立勇, 祝灵秀. 贸易开放与财政支出周期性——来自PSM-DID自然实验的证据[J]. 经济学动态, 2019(8): 40–55. |
| [15] | 肖洁, 龚六堂, 张庆华. 分权框架下地方政府财政支出与政治周期——基于地级市面板数据的研究[J]. 经济学动态, 2015(10): 17–30. |
| [16] | 闫坤, 刘陈杰. 中国财政政策顺周期行为: 财政分权与预算软约束[J]. 经济学动态, 2015(8): 64–70. |
| [17] | 曾晓安, 王志刚, 胡祖铨. 中国财政政策: 顺周期还是反周期?[J]. 财政研究, 2015(11): 2–9. |
| [18] | 郑挺国, 王霞. 中国产出缺口的实时估计及其可靠性研究[J]. 经济研究, 2010(10): 129–142. |
| [19] | Alesina A, Campante F R, Tabellini G. Why is fiscal policy often procyclical?[J]. Journal of the European Economic Association, 2008, 6(5): 1006–1036. DOI:10.1162/JEEA.2008.6.5.1006 |
| [20] | Auerbach A J, Gorodnichenko Y. Measuring the output responses to fiscal policy[J]. American Economic Journal: Economic Policy, 2012, 4(2): 1–27. |
| [21] | Avellan L, Vuletin G. Fiscal procyclicality and output forecast errors[J]. Journal of International Money and Finance, 2015, 55: 193–204. DOI:10.1016/j.jimonfin.2015.02.008 |
| [22] | Bernardini M, De Schryder S, Peersman G. Heterogeneous government spending multipliers in the era surrounding the Great Recession[J]. The Review of Economics and Statistics, 2020, 102(2): 304–322. DOI:10.1162/rest_a_00830 |
| [23] | Blanchard O, Perotti R. An empirical characterization of the dynamic effects of changes in government spending and taxes on output[J]. the Quarterly Journal of economics, 2002, 117(4): 1329–1368. DOI:10.1162/003355302320935043 |
| [24] | Caballero R J, Krishnamurthy A. Fiscal Policy and Financial Depth[R]. NBER Working Paper No.10532, 2004. |
| [25] | Driscoll J C, Kraay A C. Consistent covariance matrix estimation with spatially dependent panel data[J]. The Review of economics and statistics, 1998, 80(4): 549–560. DOI:10.1162/003465398557825 |
| [26] | Frankel J A, Vegh C A, Vuletin G. On graduation from fiscal procyclicality[J]. Journal of Development Economics, 2013, 100(1): 32–47. DOI:10.1016/j.jdeveco.2012.07.001 |
| [27] | Gavin M, Perotti R. Fiscal policy in latin america[J]. NBER Macroeconomics Annual, 1997, 12: 11–61. DOI:10.1086/654320 |
| [28] | Hamilton J D. Why you should never use the Hodrick-Prescott filter[J]. The Review of Economics and Statistics, 2018, 100(5): 831–843. DOI:10.1162/rest_a_00706 |
| [29] | Nakajima J. Time-varying parameter VAR model with stochastic volatility: An overview of methodology and empirical applications[J]. Monetary and Economic Studies, 2011, 29: 107–142. |
| [30] | Olea J L M, Pflueger C. A robust test for weak instruments[J]. Journal of Business & Economic Statistics, 2013, 31(3): 358–369. |
| [31] | Ramey G, Ramey V A. Cross-country evidence on the link between volatility and growth[J]. The American Economic Review, 1995, 85(5): 1138–1151. |
| [32] | Ramey V A, Zubairy S. Government spending multipliers in good times and in bad: Evidence from US historical data[J]. Journal of Political Economy, 2018, 126(2): 850–901. DOI:10.1086/696277 |
| [33] | Talvi E, Végh C A. Tax base variability and procyclical fiscal policy in developing countries[J]. Journal of Development economics, 2005, 78(1): 156–190. DOI:10.1016/j.jdeveco.2004.07.002 |
| [34] | Tornell A, Velasco A. The tragedy of the commons and economic growth: why does capital flow from poor to rich countries?[J]. Journal of Political Economy, 1992, 100(6): 1208–1231. DOI:10.1086/261858 |

