
2022第48卷第1期
一、引 言
数字经济时代,消费者数据作为最具价值的资产已融入经济价值创造过程中(李三希等,2021)。越来越多的网络零售平台(京东、携程等)收集消费者购买和评价等数据(许恒等,2020),并与上游供应商共享,以精准迎合消费升级趋势,为消费者提供高质量和个性化商品。美的、海尔等品牌加入苏宁易购“C2M反向定制”战略计划,希冀借助苏宁庞大的消费者数据库实现产品精准供给;淘宝越来越注重将消费者数据赋能商家,一方面推动商家更好地经营产品并提升服务质量,提高用户体验;另一方面,提升商家的平台依赖度。依托消费者数据,并以此为消费者提供高质量产品已经是企业竞争优势的重要来源,对我国高质量经济增长具有重要意义。
然而,企业利用消费者数据在推动产品质量提升的同时,针对消费者的“大数据杀熟”越来越普遍(Borgesius和Poort,2017)。亚马逊基于消费者购买历史对Diamond Rio MP3执行动态定价,差异幅度高达40%;携程、去哪儿等针对不同手机品牌消费者推荐不同价位酒店,形成价格歧视。“大数据杀熟”实质是一级价格歧视,不仅容易损害消费者利益,更可能干扰市场秩序。《关于平台经济领域的反垄断指南》明确指出“大数据杀熟”构成了滥用市场支配地位差别待遇的行为。一方面是基于消费者数据的产品质量创新,另一方面是基于消费者数据的一级价格歧视,这形成了消费者数据的双重价值。从消费者数据双重价值视角探讨下游网络零售平台与上游供应商数据共享策略及其影响社会福利的作用机理,明确数据利用的合法性和有效性,对我国加快数据共享、完善数据要素市场化配置具有重要参考价值。
数据共享引致的消费者数据双重价值无论是对消费者,还是上游供应商及下游网络零售平台都产生了重要影响。对消费者而言,数据共享引致的质量创新正效应和价格歧视负效应改变了消费者购买选择,影响消费者向谁购买产品。对下游网络零售平台而言,首先,价格歧视有助于攫取超额利润,但消费者对歧视定价的关切将降低网络零售平台价格歧视的动机;其次,数据共享在提升供应商产品质量的同时引致了生产成本增加,批发价格上升,降低网络零售平台数据共享的动机;第三,产品质量提升有利于增加消费者购买,需求效应对网络零售平台有利。对上游供应商而言,首先,质量创新效应不仅意味着高竞争优势,也意味着高生产成本,形成成本增加效应;其次,价格歧视对质量创新的影响具有不确定性,一方面,基于价格歧视的批发价格上升为供应商的质量创新提供了资金支持,另一方面,批发价格上升已经为供应商带来超额利润,反而可能会降低其质量创新动机。更重要的是,纵向结构主体对质量创新效应、成本增加效应和需求再分配效应的不同需求导致的纵向结构不协调会影响社会福利。
本文基于上游供应商、下游网络零售平台和消费者相互作用的利益关系构建三方博弈模型,结果表明:网络零售平台是否数据共享与上游供应商特征有关,当产品质量差异及消费者偏好成本均较低时,网络零售平台倾向于和高质量供应商共享数据,且数据共享提高了高质量供应商的利润;网络零售平台总是愿意与低质量供应商共享数据,上游低质量供应商和下游网络零售平台的利润会同时增加。数据共享引致了最大幅度的质量创新,但高质量供应商的产品质量创新程度低于低质量供应商的产品质量创新程度。数据双重价值使得无论是单一渠道数据共享,还是双渠道同时数据共享,总可以改善社会福利,高质量供应商和低质量供应商的同时数据共享最大程度地提升了社会福利。收益共享契约一定程度上可以削弱双重加价,实现纵向结构协调。
消费者数据作为价格歧视的价值特征是学术界重要的研究热点(Goldfarb和Tucker,2011;Acquisti等,2016)。企业获取消费者数据后,执行价格歧视成为利润获取的必然选择(Conitzer等,2012)。Rhee和Thomadsen(2017)考虑质量异质企业的价格歧视策略,发现无论是高质量还是低质量企业,将对重复购买的消费者提供低价。蒋传海等(2018)关注消费者多样性偏好和拥塞效应下的歧视定价,发现歧视定价可能形成“囚徒困境”。Chung(2020)剖析了远视型和短视型消费者对价格歧视的影响,指出企业针对远视型消费者更可能实施价格歧视。鉴于此,价格歧视的福利效应也成为讨论的重点。Esteves和Cerqueira(2017)认为价格歧视增加了企业利润,但降低了消费者剩余,社会福利下降。Li(2018)指出企业通过价格歧视改变竞争对手的定价行为,从而改变社会福利。Amaldoss和He(2019)发现价格歧视是否能改善社会福利与消费者对价格歧视关切程度有关。但上述研究考虑的是基于行为的价格歧视,本质上是三级价格歧视,即针对不同类型消费者歧视定价。
数字经济的发展推动网络零售平台执行基于数据的一级价格歧视。Choe等(2018)指出一级价格歧视会对不同偏好消费者产生不同影响,企业是否利用数据值得商榷。Choudhary等(2005)得到完全歧视定价将加剧市场竞争,可能损害企业利润,但可以改善社会福利。李三希等(2021)发现一级价格歧视提升了消费者剩余和社会福利。但上述研究忽略了数据质量创新的作用。王世强等(2020)考虑存在质量差异企业的歧视定价与质量创新行为,得到歧视定价引发的过度竞争会导致产品质量下降。但就检索结果看,基于消费者数据关注质量创新和歧视定价双重价值的研究仍显不足。而且,上述研究均是在水平市场结构中考虑消费者数据的应用。而网络零售平台为实现基于数据的产品质量提升需要与上游供应商数据共享。下游网络零售平台需要内生决定是否及如何进行数据共享,质量创新与歧视定价的内在互动机理有待挖掘。
一些学者在水平市场结构中引入第三方数据供应商。Chen等(2001)指出数据供应商的数据共享使得企业可以区分忠诚消费者和非忠诚消费者,进而实现数据供应商和企业的双赢。Montes等(2019)在存在水平差异的双寡头结构中考虑第三方数据供应商的数据共享,得到独家共享还是同时共享取决于消费者对价格歧视的关切程度。然而,上述研究所涉及的第三方数据供应商不参与市场竞争。但现实中的网络零售平台不仅是数据供应商,更直接参与市场竞争。例如,京东与海尔共享消费者数据以提升海尔产品质量;同时,京东基于PLUS会员政策对消费者实施价格歧视。Abhishek等(2015)、Tan和Carrillo(2017)将诸如京东自营、苏宁易购等类似的市场结构定义为经营型结构,即下游网络零售平台直接面向消费者销售产品,而上游供应商收取批发价格。但上述研究忽略了基于数据的质量创新和价格歧视。在考虑消费者数据的前提下,上游供应商和下游网络零售平台基于双重加价的纵向关系仍不明确,是否可以通过某种方式实现上游供应商和下游网络零售平台间的协调也需要关注。
与既有文献相比,本文进行了四个方面的改进:第一,考虑基于消费者数据的一级价格歧视。既有文献多考虑基于行为的价格歧视,实际上是三级价格歧视。然而,网络零售平台基于大数据技术可以精准感知消费者偏好,推动一级价格歧视成为现实。第二,基于消费者数据的双重价值,挖掘质量创新和一级价格歧视的内在联系。当消费者数据可以同时被用于质量创新和价格歧视时,企业的定价行为和质量创新行为将发生改变,形成与既有研究不同的逻辑。第三,在由上游供应商和下游网络零售平台构成的纵向结构中分析数据共享策略,解析收益共享契约是否及如何实现纵向结构协调。第四,纳入上游供应商的垂直质量差异,解析供应商如何基于消费者数据内生决定质量创新水平,形成纵向结构下的内生决定数据共享策略及其社会福利效应。
二、模型设计与基本假设
考虑单位长度线性市场中是有两个上游供应商(
其中,
关于上游供应商的生产成本,本文采用Jinji和Toshimitsu(2004)的设定,假设无论是高质量供应商还是低质量供应商,固定成本均为0;但边际成本存在差异,高质量产品和低质量产品的单位生产成本分别为
其中,
进一步,社会福利函数为:
非数据共享的博弈时序为:第一,上游两家供应商同时决定批发价格
三、不同数据共享情形下的市场均衡
(一)非数据共享情形下的市场均衡(UU)
在非数据共享情形下形成的纵向市场竞争结构中,购买高质量产品和低质量产品的无差异消费者偏好为
| ¯xUU=t−pUUH+pUUL+qH−qL2t | (5) |
此时,高质量产品市场份额为
对应的社会福利为:
命题1:(a)高质量产品批发价格高于低质量产品批发价格,即
由于高质量供应商的边际生产成本较高(
(二)高质量渠道网络零售平台数据共享情形下的市场均衡(DU)
当高质量渠道的网络零售平台
对低质量渠道的网络零售平台而言,基于利润最大化的一阶和二阶条件,统一定价为:
高质量渠道的网络零售平台的价格歧视决策为:
考虑第二阶段供应商的批发价格决策,基于利润最大化的一阶条件和二阶条件,得到:
考虑第一阶段高质量供应商基于消费者数据进行的产品质量创新,得到:④
| βDUH=1qH③ | (13) |
此时,对应的社会福利为:
引理1:高质量渠道数据共享时,基于消费者数据的产品质量提升水平为
为实现高质量渠道的数据共享,需满足
为更加清楚地观察式(15)中高质量渠道数据共享的实施条件,本文通过数值模拟进行分析,令
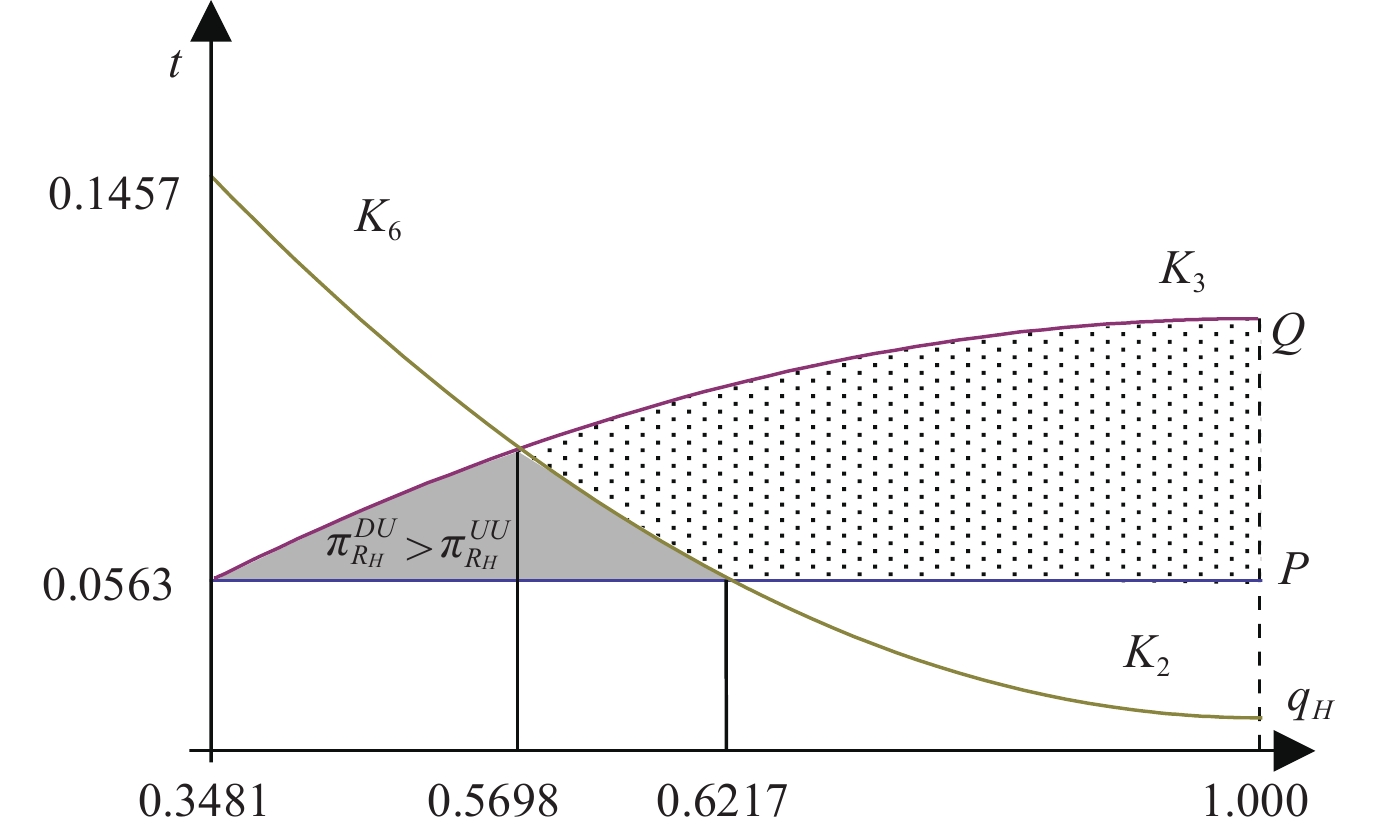
|
|
图 1
不同参数范围内的数据共享(
|
进一步比较数据共享前后低质量渠道上游供应商和下游网络零售平台的利润,得到:⑧
| πDUML−πUUML<0,πDURL−πUURL<0④ | (16) |
命题2:(a)当质量参数
对上游供应商而言,数据共享提升了高质量渠道的产品质量,尽管生产成本上升,但质量提升正效应明显,上游供应商倾向于数据共享。对下游网络零售平台而言,是否数据共享取决于价格歧视的影响。数据共享从三个方面影响下游网络零售平台的利润。第一,数据共享提升了高质量渠道下游网络零售平台的产品质量,市场份额增加,需求效应对利润提升产生正向影响;⑨第二,数据共享提升了高质量渠道上游供应商的生产成本,批发价格可能上升,批发价格效应对利润提升具有不确定性;⑩第三,数据共享有利于下游网络零售平台歧视定价,但可能导致高质量渠道的平均销售价格下降,歧视价格效应对利润提升具有不确定性。⑪如式(17)所示,数据共享是否提升下游网络零售平台利润取决于批发价格
当参数
命题2(b)表明,高质量渠道内部的数据共享对与其竞争的低质量渠道产生负向影响。当高质量渠道可以从数据共享中获利时,必然对低质量渠道产生负向影响。有意思的是,即使数据共享恶化了高质量渠道整体利润,低质量渠道也没有从数据共享中得到正向溢出效应。对于低质量渠道的上游供应商,数据共享导致其批发价格和市场份额同时下降,最终对上游供应商的利润获取产生负向影响。⑫对于低质量渠道的下游网络零售平台,尽管批发价格下降,但其需要降低零售价格以应对价格歧视的负向影响,利润随之下降。⑬
进一步考虑数据共享对社会福利的影响,比较式(8)和式(14),得到:
命题3:高质量渠道的数据共享总是可以提升社会福利。
上游供应商通过数据共享获得消费者偏好信息有利于推动产品质量提升,进而改善社会福利。然而,数据共享引致下游网络零售平台的歧视定价可能会恶化社会福利。当同时考虑质量提升和价格歧视时,命题3表明数据共享改善了社会福利。但数据共享对社会福利的改善并不如此简单,取决于高质量渠道和低质量渠道的福利水平。对于高质量渠道,取决于数据共享引致的质量创新效应(
显而易见,质量创新效应为正,成本增加效应为负,且质量创新效应的正向作用大于成本增加效应的负向作用,有利于社会福利提升。然而,需求再分配效应对社会福利的影响变得复杂。当
(三)低质量渠道网络零售平台数据共享情形下的市场均衡(UD)
本部分考虑仅有低质量渠道的网络零售平台
低质量渠道的网络零售平台的价格歧视决策为:
基于式(20)和式(21)的均衡价格,得到上游供应商的批发价格决策:
进一步可以得到低质量供应商的产品质量创新水平及社会福利水平,分别为:⑭
比较低质量渠道数据共享对各参与主体利润的影响,得到:
考虑数据共享对社会福利的影响,比较式(8)和式(23),得到:
| SWUD−SWUU>0 | (25) |
引理2:低质量渠道数据共享的最优产品质量提升水平为
命题4:(a)低质量渠道数据共享实现了上游供应商和下游网络零售平台利润的同时增加;(b)低质量渠道数据共享降低了高质量渠道利润;(c)低质量渠道数据共享可以提升社会福利。
比较引理1与引理2,低质量渠道的数据共享总是可以实现更高水平的产品质量提升,即
对低质量渠道的供应商而言,由于产品质量实现了极大程度的提高,导致其可以制定较高的批发价格,同时,在低质量渠道处购买的消费者份额增加,数据共享总是可以提升供应商的利润。⑮对低质量渠道的网络零售平台而言,与命题2(a)类似,数据共享对网络零售平台的影响取决于需求效应、价格歧视效应和批发价格效应。但与高质量渠道的数据共享不同,当低质量渠道执行数据共享时,需求效应对网络零售平台利润提升产生正向影响;价格歧视效应对网络零售平台利润提升产生正向影响;批发价格效应对网络零售平台利润提升产生负向影响。⑯需求效应和价格歧视效应的正向影响大于批发价格效应的负向影响,数据共享对网络零售平台有利。命题4(b)和命题2(b)一致,低质量渠道数据共享引致的利润增加是以竞争渠道的利润下降为代价。命题4(c)和命题3一致,数据共享总可以提升社会福利。
对比高质量渠道数据共享和低质量渠道数据共享对社会福利的影响,得到:
当且仅当质量参数
命题5:高质量渠道数据共享对社会福利的影响水平可能高于低质量渠道。
正如命题3所讨论,数据共享通过质量创新效应、成本增加效应和需求再分配效应实现社会福利的提升。条件1和条件2表明消费者偏好成本参数
(四)不同产品质量渠道网络零售平台同时数据共享情形下的市场均衡(DD)
当高质量渠道和低质量渠道同时数据共享时,竞争渠道的产品质量同时提升,且同时实施价格歧视。假设高质量渠道质量提升水平为
考虑第二阶段上游供应商的批发价格决策,基于利润最大化的一阶条件及二阶条件得到:
考虑高质量供应商和低质量供应商基于消费者数据的产品质量创新
| βDDH=1qH,βDDL=1qL① | (30) |
此时,对应的社会福利为:⑱
| SWDD=2−t4 | (31) |
比较竞争渠道同时数据共享(DD)与竞争渠道非数据共享(UU)下的社会福利,得到:
| SWDD−SWUU>0 | (32) |
引理3:竞争渠道同时数据共享时,最优的质量提升水平为
命题6:高质量渠道与低质量渠道的同时数据共享将实现社会福利的改善。
命题3、命题4和命题6表明无论是单一渠道还是双渠道数据共享都会实现社会福利改善。当双渠道数据共享时,一方面,数据共享实现产品质量的极大程度提升,质量创新效应最高;另一方面,数据共享引致市场上只存在一种质量的产品,高质量和低质量渠道均分市场,市场失衡情况得到最大程度改善,需求再分配效应对社会福利改善的正效应最高。质量创新效应和需求再分配效应的正向影响将抵消成本增加效应的负向影响,社会福利提升。
Encaoua和Hollander(2007)同样纳入了质量创新和完全价格歧视,但本文与其有所不同。第一,Encaoua和Hollander(2007)仅考虑质量差异,本文在质量差异的基础上进一步纳入水平差异。此时,在由质量差异和水平差异构成的框架中,本文一级价格歧视是针对消费者水平偏好形成的定价决策,而非针对消费者质量偏好形成的定价决策。第二,Encaoua和Hollander(2007)构建的是由两个零售商形成的水平竞争结构,本文则在由上游两个供应商和下游两个网络零售平台形成的纵向结构中考虑质量创新和一级价格歧视。纵向结构形成的双重加价使得数据共享策略更为复杂。第三,尽管Encaoua和Hollander(2007)同时纳入了质量创新和一级价格歧视,但其质量创新与消费者数据无关。相反地,本文考虑的是数据双重价值,即当且仅当基于数据的质量创新可以被实施时,基于数据的价格歧视可以被实施。
四、网络零售平台数据共享策略选择、协调及社会福利分析
(一)网络零售平台的数据共享策略选择
当考虑数据共享策略选择时,不仅需要考虑数据共享对网络零售平台的影响,更需要关注数据共享对供应商的影响。因此,本文考虑数据共享对渠道总利润的影响,当渠道总利润提升时,数据共享可以被实施。⑲构建基于不同数据共享组合的支付矩阵,如图2所示。

|
| 图 2 四种数据共享组合的支付矩阵 |
对低质量渠道而言,存在
命题7:当质量参数
令
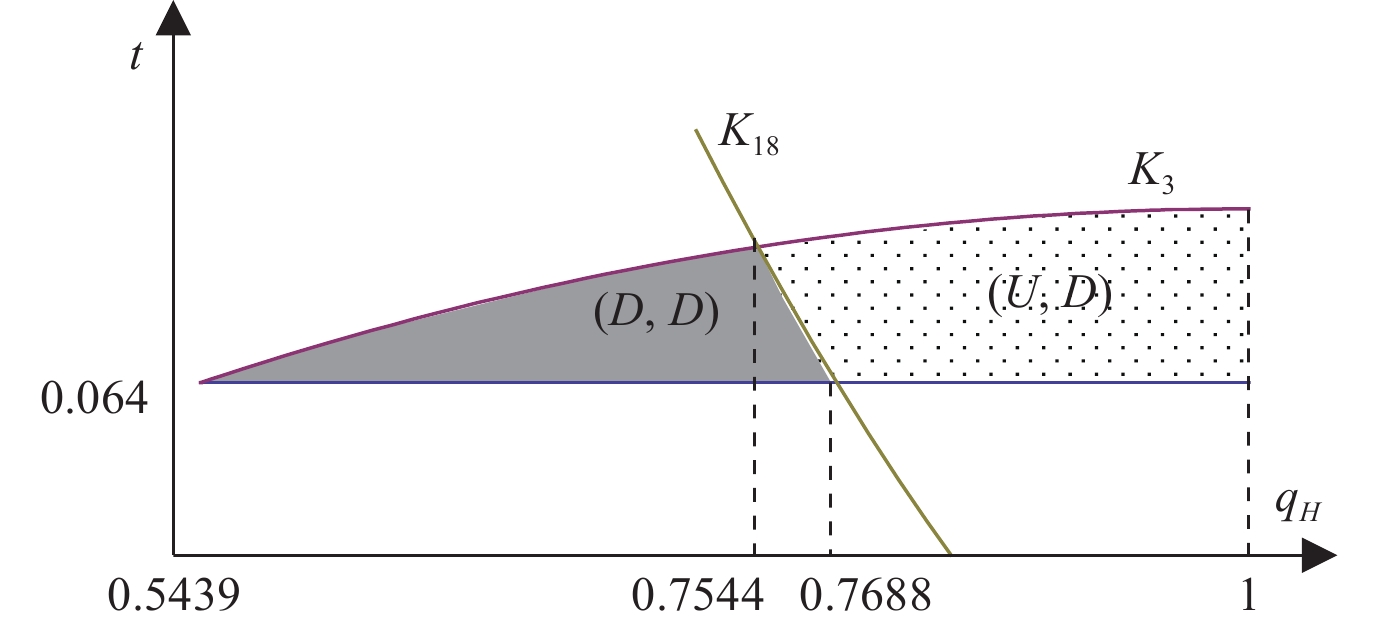
|
| 图 3 网络零售平台数据共享策略选择均衡 |
(二)基于收益共享契约的纵向结构协调
在由上游供应商和下游网络零售平台形成的纵向分离结构中,双重加价使纵向供应链整体利润无法达到最优,造成资源错配和效率损失。Cachon和Lariviere(2005)、应珊珊和蒋传海(2018)认为收益共享契约可以克服双重加价问题。
命题7表明,低质量渠道总是数据共享,高质量渠道是否数据共享是有条件的,即UD结构和DD结构。基于此,首先考虑UD结构下收益共享契约如何解决双重加价问题,进一步考虑DD结构下收益共享契约如何解决双重加价问题。㉑参照Cachon和Lariviere(2005),以UD结构高质量和低质量供应商同时实施收益共享契约为例,双渠道收益共享契约的目标是纵向一体化利润最大化,以上标“
纵向结构一体化情形下,高质量渠道和低质量渠道的企业利润表达式分别为:
低质量渠道中网络零售平台的价格歧视决策为:
进一步考虑低质量渠道的产品质量创新,基于利润最大化的一阶及二阶条件,得到:
将式(37)代入式(35)和式(36)中,得到双渠道同时一体化下的价格分别为:
考虑上游供应商的收益共享契约策略,以上标“’”表示。收益共享契约策略下,低质量供应商的决策变量是
收益共享契约下的博弈时序为:第一,上游供应商决定收益共享率
对于高质量网络零售平台,基于利润最大化的一阶和二阶条件,得到统一定价决策为:
低质量渠道的网络零售平台的价格歧视决策为:
若收益共享契约能够解决双重加价问题,则收益共享契约决策下的最优零售价格
同时,收益共享契约策略下,供应商和网络零售平台的利润不低于UD结构分离决策情形下的均衡(第三部分情形三的UD均衡)。即需要存在收益共享率
命题8:UD结构下,当双渠道供应商同时执行收益共享契约时,可以实现纵向结构协调。
命题8给出了一个有趣的结论。UD结构下,当只有低质量供应商执行收益共享契约时,由于低质量渠道的目标是实现一体化利润最大化,其较高的竞争优势使得高质量网络零售平台的零售价格下降;进一步地,导致基于此零售价格的低质量渠道的歧视性定价下降。㉒此时,当仅有低质量供应商执行收益共享契约时,反而不能实现供应商和网络零售平台利润的同时增加。相反地,当高质量供应商和低质量供应商同时实施收益共享契约时,同时实现一体化利润的追求者将首先推动高质量网络零售平台制定较高的零售价格,进而推动低质量网络零售平台制定较高的歧视性价格,此时,收益共享契约将实现供应链的协调。
(三)网络零售平台数据共享的社会福利分析
命题7给出了高质量渠道及低质量渠道数据共享的均衡,对比对应的社会福利,存在:
命题9:高质量渠道和低质量渠道同时执行数据共享实现了社会福利最高。
既有文献大多认为价格歧视可能损害社会福利,Chung(2020)指出与统一定价相比,价格歧视降低了社会福利;Ikeda和Toshimitsu(2010)考察企业同时进行价格歧视和质量创新,得到社会福利是否改善与消费者类型有关。基于此,对价格歧视进行外部规制是有必要的(王世强等,2020;李三希等,2021)。而命题3、命题4、命题6表明,基于质量提升的价格歧视有利于社会福利改善,即消费者数据需要实现双重价值。命题9进一步验证了基于一级价格歧视的市场竞争加剧与社会福利的关系。当高质量渠道和低质量渠道同时基于消费者数据进行一级价格歧视时,会加剧市场竞争,进而对社会福利的改善程度更大。更重要的是,本文考虑高质量渠道和低质量渠道的数据共享不仅仅是执行价格歧视,更能实现产品质量的提升,将进一步推动社会福利改善。
五、结论与政策建议
数字经济时代下,越来越多的网络零售平台与其上游供应商共享消费者数据,不仅推动了基于消费者数据的质量创新,也形成了基于消费者数据的一级价格歧视,产生了消费者数据的双重价值。然而,数据双重价值改变了上游供应商和下游网络零售平台的纵向竞争关系,对如何执行数据共享提出了新要求。本文研究结果表明:第一,当且仅当产品质量异质性较低且消费者偏好成本较低时,高质量渠道的数据共享可以被实施;低质量渠道的数据共享对上游供应商和下游网络零售平台都有利;低质量渠道的占优均衡是数据共享,高质量渠道是否数据共享取决于质量参数及消费者偏好成本参数。第二,数据共享提升了产品质量,高质量渠道的质量创新水平低于低质量渠道的质量创新水平。第三,收益共享契约在一定程度上可以解决上游供应商与下游网络零售平台的双重加价问题,实现纵向结构协调。第四,当数据共享在导致价格歧视的同时能引致产品质量创新,数据共享则有利于社会福利改善,且双渠道同时数据共享对社会福利改善最有利。
本文基于消费者数据的双重价值属性考察了企业最优数据共享策略选择、纵向结构协调和社会福利影响,得到了与既有研究完全不同的结论。现有文献普遍认为数据共享对提升企业利润有利,但基于数据的价格歧视可能对社会福利不利(Chen等,2001;Montes等,2019)。本文结果则表明,消费者数据的双重价值属性不仅改变了价格竞争的逻辑(统一定价—三级价格歧视—一级价格歧视),也形成了基于消费者数据的质量创新,引致了质量创新效应、成本增加效应和需求再分配效应,进而实现了社会福利改善。与此同时,通过收益共享契约可以增加上游供应商和下游网络零售平台的利润,实现纵向结构协调,进而解决双重加价问题。
本文结论对数字经济时代下消费者数据的利用给出了理论支持。消费者数据的特殊性引致当前的数据利用存在极大争议,尤其是基于消费者数据的价格歧视。2021年4月13日,市场监管总局、中央网信办、税务总局联合召开互联网平台企业行政指导会,对“大数据杀熟”和“信息泄露”等问题进行严肃整治。实际上,“大数据杀熟”和“信息泄露”通过侵犯消费者利益、损害市场竞争秩序实现互联网平台的扩张,此种数据滥用行为必须扼制。然而,当消费者数据利用是以提升产品质量、创造经济价值为目标时,数据共享则需要提倡,这也是加快数据要素市场化配置改革的核心。基于此,政府在消费者数据利用监管过程中,需要细分互联网平台的数据利用目的,一方面,当互联网平台基于大数据挖掘、信息共享等技术提升服务水平或优化产品质量时,政府部门需要放松监管条件,加快推动释放数字经济红利;另一方面,当数据利用仅仅是“大数据杀熟”,而不创造任何正向利益时,政府部门需要给予严厉打击,并坚决根治。只有提高互联网领域消费者数据利用的规范性,才能为实现我国高质量经济增长,推动数字经济建设提供保障。
①
②
③
④ 求解高质量供应商利润最大化一阶条件,存在额外两组解
⑤
⑥
⑦
⑧
⑨
⑩
⑪
⑫
⑬
⑭
⑮
⑯
⑰
⑱
⑲ 当数据共享引致渠道整体利润增加时,上游供应商和下游网络零售平台可以通过制定数据共享协议实现各自利润的同时增加。
⑳
㉑ 正文中以UD结构下双渠道供应商的收益共享契约为例。限于篇幅,关于UD结构下低质量供应商以及DD结构下双渠道供应商收益共享契约的均衡求解可向作者索取。
㉒ 本文也考虑了仅有低质量渠道的收益共享契约,得到此种收益共享契约不能实现纵向结构协调。
| [1] | 蒋传海, 杨万中, 朱蓓. 消费者寻求多样化、拥塞效应和厂商歧视定价竞争[J]. 财经研究, 2018(1): 100–112. |
| [2] | 李三希, 武玙璠, 鲍仁杰. 大数据、个人信息保护和价格歧视——基于垂直差异化双寡头模型的分析[J]. 经济研究, 2021(1): 43–57. |
| [3] | 王世强, 陈逸豪, 叶光亮. 数字经济中企业歧视性定价与质量竞争[J]. 经济研究, 2020(12): 115–131. |
| [4] | 许恒, 张一林, 曹雨佳. 数字经济、技术溢出与动态竞合政策[J]. 管理世界, 2020(11): 63–79. DOI:10.3969/j.issn.1002-5502.2020.11.006 |
| [5] | 应珊珊, 蒋传海. 收入共享契约下价格歧视及配置效率分析[J]. 管理科学学报, 2018(10): 74–83. DOI:10.3969/j.issn.1007-9807.2018.10.006 |
| [6] | Abhishek V, Jerath K, Zhang Z J. Agency selling or reselling? Channel structures in electronic retailing[J]. Management Science, 2015, 62(8): 2259–2280. |
| [7] | Acquisti A, Taylor C, Wagman L. The economics of privacy[J]. Journal of Economic Literature, 2016, 54(2): 442–492. DOI:10.1257/jel.54.2.442 |
| [8] | Amaldoss W, He C. The charm of behavior-based pricing: When consumers’ taste is diverse and the consideration set is limited[J]. Journal of Marketing Research, 2019, 56(5): 767–790. DOI:10.1177/0022243719834945 |
| [9] | Borgesius F Z, Poort J. Online price discrimination and EU data privacy law[J]. Journal of Consumer Policy, 2017, 40(3): 347–366. DOI:10.1007/s10603-017-9354-z |
| [10] | Cachon G P, Lariviere M A. Supply chain coordination with revenue-sharing contracts: Strengths and limitations[J]. Management Science, 2005, 51(1): 30–44. DOI:10.1287/mnsc.1040.0215 |
| [11] | Choe C, King S, Matsushima N. Pricing with cookies: Behavior-based price discrimination and spatial competition[J]. Management Science, 2018, 64(12): 5669–5687. DOI:10.1287/mnsc.2017.2873 |
| [12] | Chung H S. Quality choice and behavior-based price discrimination[J]. Journal of Economics, 2020, 131(3): 223–236. DOI:10.1007/s00712-020-00711-x |
| [13] | Conitzer V, Taylor C R, Wagman L. Hide and seek: Costly consumer privacy in a market with repeat purchases[J]. Marketing Science, 2012, 31(2): 277–292. DOI:10.1287/mksc.1110.0691 |
| [14] | Choudhary V, Ghose A, Mukhopadhyay T, et al. Personalized pricing and quality differentiation[J]. Management Science, 2005, 51(7): 1120–1130. DOI:10.1287/mnsc.1050.0383 |
| [15] | Chen Y X, Narasimhan C, Zhang Z J. Individual marketing with imperfect targetability[J]. Marketing Science, 2001, 20(1): 23–41. DOI:10.1287/mksc.20.1.23.10201 |
| [16] | Encaoua D, Hollander A. First-degree discrimination by a duopoly: Pricing and quality choice[J]. The B. E. Journal of Theoretical Economics, 2007, 7(1): 1–19. |
| [17] | Esteves R B, Cerqueira S. Behavior-based pricing under imperfectly informed consumers[J]. Information Economics and Policy, 2017, 40: 60–70. DOI:10.1016/j.infoecopol.2017.06.007 |
| [18] | Goldfarb A, Tucker C E. Privacy regulation and online advertising[J]. Management Science, 2011, 57(1): 57–71. DOI:10.1287/mnsc.1100.1246 |
| [19] | Ikeda T, Toshimitsu T. Third-degree price discrimination, quality choice, and welfare[J]. Economics Letters, 2010, 106(1): 54–56. DOI:10.1016/j.econlet.2009.09.024 |
| [20] | Jinji N, Toshimitsu T. Minimum quality standards under asymmetric duopoly with endogenous quality ordering: A note[J]. Journal of Regulatory Economics, 2004, 26(2): 189–199. DOI:10.1023/B:REGE.0000038931.63101.0d |
| [21] | Li K J. Behavior-based pricing in marketing channels[J]. Marketing Science, 2018, 37(2): 310–326. DOI:10.1287/mksc.2017.1070 |
| [22] | Montes R, Sand-Zantman W, Valletti T. The value of personal information in online markets with endogenous privacy[J]. Management Science, 2019, 65(3): 1342–1362. DOI:10.1287/mnsc.2017.2989 |
| [23] | Rhee K E, Thomadsen R. Behavior-based pricing in vertically differentiated industries[J]. Management Science, 2017, 63(8): 2729–2740. DOI:10.1287/mnsc.2016.2467 |
| [24] | Tan Y L, Carrillo J E. Strategic analysis of the agency model for digital goods[J]. Production and Operations Management, 2017, 26(4): 724–741. DOI:10.1111/poms.12595 |

