
2021第47卷第10期
一、引 言
中国经济“新常态”下,过去依靠“三驾马车”拉动的经济增长模式已较难持续,提升经济效率才是未来维持中高速经济增长的关键所在。然而一些研究表明,20世纪90年代末以来中国城市层面的生产效率呈现持续性下降趋势(邵军和徐康宁,2010;邓晓兰等,2019)。有学者分别从财政分权的视角和技术进步速度减缓的视角予以解释(颜鹏飞和王兵,2004;邓晓兰等,2019)。另一类有力的解释与房地产行业密切相关。自2008年金融危机以来,中国经济发展可能存在“脱实向虚”的趋势,成为抑制实体经济和高质量发展的原因之一。房地产投机者“炒房”行为的盛行使得房地产业或许成为虚拟经济的代表性行业之一,可能挤占了实体经济生产所用的投资资金,也进一步推高了资产价格和生产成本(Krippner,2005)。由于房地产行业的生产率水平远低于其他行业(陈斌开和张川川,2016;蔡跃洲和付一夫,2017),城市生产效率也因高房价导致的“资源错配”受到抑制(陈斌开等,2015)。资源错配主要是由市场中生产资料和销售产品的相对价格扭曲所致(Brandt等,2013),而较高的住房价格可能造成了资产相对价格的扭曲,进一步形成了资本等生产资料由高生产率流向低生产率企业的“倒挂机制”(陈斌开等,2015),行业间的这种资源错配最终导致生产率的下降。余泳泽和李启航(2019)也曾指出,房价快速上涨对服务业的“锁定效应”和生产率的“侵蚀效应”可能导致了城市整体生产率的降低。
为引领房地产市场回归理性,政府陆续出台信贷、财税、土地、投资等多方面措施予以调控。2016年,中央经济工作会议(下称会议)首次提出“房住不炒”作为中国房地产市场调控的主要原则。此后两年,会议均提出要完善促进房地产市场平稳健康发展的长效机制。在新冠肺炎疫情影响国民经济的2020年,中央政府仍强调坚持“房住不炒、租购并举、因城施策”的调控方针,进一步将房地产与实体经济的协同发展作为国民经济未来发展的方向。①可见,打击房地产市场投机需求、完善房地产市场长效调控机制将是未来一段时间政府的工作重点之一。而房产税作为一种资本税,其功能定位之一是抑制房地产市场的投机炒作,其与限购、限售等行政干预手段相比,无论是在政策稳定性、调控温和性还是效果持续性上都更能体现对房地产市场的长效调控功能,对于促进房地产市场平稳发展以及经济“脱虚向实”具有不可替代的作用。2011年,上海和重庆率先开展了房产税改革,许多学者以此为依据对房产税的效果进行了定性和定量研究,焦点多集中在房产税政策对于充实地方财政、抑制房价非理性上涨、改变居民消费储蓄、促进城市间产业转移以及银行信贷决策等方面的效果(Bai等,2014;Cebula,2019;范子英和刘甲炎,2015;刘友金和曾小明,2018;刘建丰等,2020),但少有关注到房产税作为房地产市场长效调控的主要机制,对于中国城市长期发展动力的影响。
在中国的经济背景下,作为国民经济的支柱性产业,房地产关联宏观经济的方方面面,其长期稳定发展是经济持续平稳增长的重要前提。②房产税作为调控房地产市场供需关系的长效机制,不仅作用于房地产业本身,理论上还可通过抑制投机需求稳定房价,从而影响到城市行业间资源配置,对扭转经济“脱实向虚”趋势、改善城市经济增长效率产生积极的影响。为验证该假设,本文把上海市2011年房产税改革作为一项准自然实验,利用合成控制法分析房产税政策的出台对于城市经济效率的实际影响。结果显示,上海的房产税提升了城市生产率。对比重庆市的房产税政策实施效果后发现,上海市的房产税税基相对较宽,且“增量起征、溯及既往”的独特方式能够进一步扩大房产税税基,较好地处理了政策过渡期对房地产业发展和城市经济发展的协调问题,一定程度上缓解了住房价格非理性增长,优化了本市的行业资本配置和劳动力配置,进而显著提升了生产率。
2020年5月,中共中央和国务院印发《关于新时代加快完善社会主义市场经济体制的意见》,强调要稳妥推进房地产税立法;十四五规划也指出房产税作为直接税和地方税收的主要来源,将是今后税收制度改革的重点。③但直到现在,学术界和政府部门对于中国房产税政策如何设计仍有争议。本文研究贡献为:首先通过合成控制法证明了房产税政策对城市经济效率具有正向溢出效应。在丰富房产税政策效果研究的同时,也对城市生产率的提升路径提供了新的视角。其次,我们也验证了上海市房产税政策提振经济效率的具体机制,证明了房产税主要通过抑制投机需求,尤其是缓解住房价格的非理性上涨,进一步改善行业间资本配置结构和劳动力就业结构,提升了城市生产率。最后,我们对比了重庆的房产税设计方案和细则发现,“宽税基”的设计方案有利于减少房地产市场投机行为,“增量起征,溯及既往”的征税方式能够平衡房地产业发展和城市经济效率提升,可作为改革过渡期的一个政策选择。结合研究结论,我们从城市生产率提升的角度对房产税政策实施提出了一些针对性的建议。
文章安排如下:第二部分是制度背景与理论假说,第三部分是实证分析设计,第四部分是基准回归及稳健性检验,第五部分是对本文逻辑机制的验证,最后是文章的结论和建议。
二、制度背景与理论假说
本文的逻辑机制参见图1。具体来说,城市生产效率的提高与城市资源配置密切相关,但实施房产税政策的直接目的是打击非理性投机需求,进而稳定住房价格。因此,研究房产税政策对城市生产率的影响,首先需要厘清房价对行业间资源配置的影响。

|
| 图 1 房产税影响城市经济效率的逻辑机制 |
(一)房价、资源配置与城市生产率
房价快速上涨主要通过信贷市场以及劳动力市场的资源配置来影响城市生产率。具体表现如下:
1. 房价过快上涨会造成信贷市场扭曲,对实体经济的信贷资金形成挤出。泡沫理论指出,房地产市场过度繁荣会产生两种效应,一是资产的流动性效应,即通过资产抵押品的升值缓解实体企业的融资约束,二是杠杆效应,即通过房地产投资的超额回报挤出实体经济信贷资金。在中国房价快速上涨的过程中,相对于流动性效应而言,杠杆效应作用更大(Chen和Wen,2017;Miao和Wang,2018;余静文等,2017)。一方面,出于信贷风险的考虑,房价持续增长会使得银行等金融机构更倾向于将有限资金投入房地产及相关行业(Campello等,2010),这无疑增加了其他行业的融资约束,也进一步使得信贷资金错配到高利润低效率的企业(Miao和Wang,2018)。另一方面,资本的逐利性往往迫使企业选择收益高、风险低且回报周期短的投资项目,使企业陷入一种长期的“低技术锁定”状态(王文春和荣昭,2014;余静文等,2017)。Miao和Wang(2014)将投机性资产泡沫纳入内生增长模型中,发现有限的资金会流入含有投机性泡沫的经济部门,抑制了生产性部门对其主业的创新投入。
2. 高房价会造成劳动力要素市场扭曲,导致劳动力资源错配。自17世纪末就有不同学者指出行业间收入差距会导致劳动力行业间转移(Petty,1690;Kuznetsova等,2019),而劳动力行业就业结构的变化则会直接影响到经济增长(范剑勇等,2001;王会强等,2009)。房价高涨使得房地产相关行业利润激增,并以高薪吸引更多劳动者进入,使得创新能力和生产率较低的房地产相关行业挤占了实体企业的劳动力资源(Charles等,2013),同时高房价还会间接拉高其他生产性行业的用工成本,推动工资福利的提高,使得这些行业引入高技能劳动力进行创新活动的激励下降,进而抑制了城市生产效率的提高(董直庆等,2014;陆铭等,2015)。
综上,房价过高会扭曲资本要素市场以及劳动力要素市场的资源配置状况,使得信贷资源和劳动力资源大量流入房地产行业,从而影响城市生产率的提升。
(二)房产税政策与城市生产率
投机理论认为,房价波动和房地产市场泡沫的主要原因是对住房投机性需求的增加,因此各国政府通常着重调控住房市场的投机需求(Gholizadeh,2014;Huang和Shen,2017)。目前来看,各国政府更加重视房产税政策在抑制投机需求中的长效作用(徐虹,2013)。理论上,房产税的征收可以直接增加住房持有人的持有成本和空置成本,进而降低投机者预期收益,有助于从根本上抑制投资者的投机性住房需求,从而有效缓解房价非理性增长(Bai等,2014;Cebula,2019)。这种效应直接关系到资源在行业间的配置。2011年1月,上海市与重庆市政府相继发布了对部分个人住房征收房产税的暂行办法。不过,两市政策细则存在较大差异,其抑制投机效果也会存在不同。具体如表1所示。
| 上海市 | 重庆市 | |
| 范围 | 全市 | 渝中区、江北区等主城九区 |
| 征税对象 | (1)本市居民家庭市内新购第二套及以上住房
(2)非本市无业者本市新购住房 |
(1)个人拥有独栋商品住宅或新购高档住房
(2)非本市无业者新购第二套及以上普通住房 |
| 税率 | 0.6%(×70%)或0.4%(×70%) | 0.5%、1%、1.2% |
| 免税面积 | 合并计算全部住房面积人均60平方米及以下免征房产税 | 存量独栋房免税面积180平方米
新购的独栋或高档住房免税面积100平方米 |
| 减免优惠 | (1)本市居民改善性换购需求
(2)本市居民子女婚姻购房需求 (3)人才唯一住房需求 (4)本市工作生活的外地居民唯一住房需求 上述四种情况给予暂免征收或退还 |
(1)特殊困难可申请延期缴纳
(2)对非本市无业者具备有户籍、有企业、有工作任一条件的予以免征和退还 (3)对因不可抗力因素造成应税房产毁损的,可申请酌情减征或免征 |
| 过渡政策 | 应税住房发生权属转移的,原产权人应缴清房产税税款。即在政策实施之初,原则上不对原有存量房征税。一旦发生房产交易行为,则会根据已登记房屋信息对相关主体的全部存量住房按规定征税。 | 无 |
| 注:2017年1月,重庆市修改房产税暂行办法,将针对非本市无业者的征税房屋类型由新购第二套及以上普通住房扩展为新购首套及以上普通住房。但本文主要研究2011年房产税试点的政策效果,且文章所用数据截至2016年,因此此次修改对本文结果影响不大。 | ||
根据表1,政策设计的差异主要包括三点:(1)征税对象上,重庆只对独栋和高档住宅征税,税基更窄;而上海面向本市所有住宅房屋类型征税,税基相对更宽。针对外来人员,重庆只对其购买的第二套及以上住宅征收房产税,而上海则对非本市无业者新购住宅一律征收房产税。可见,上海对炒房行为的打击更严。(2)免税政策上,上海按照全部住房面积计算的人均免税面积不超过 60 平米暂免征收房产税。这从一定程度上保证了自住型消费者的基本生活需求。此外,一系列减免优惠也保障了居民的合理住房需求,并抑制了非本地居民的房产投机行为,目的性和引导性更强。(3)过渡期设计,相较于重庆,上海市房产税的一个亮点在于“增量起征,溯及既往”,即先对增量房征收,而新的房屋交易行为成为对相关纳税主体全部存量房征税的触发机制。相对于只对增量房征税,这种模式征税力度更大,相对于同时对存量与增量房征税,这种模式实施阻力较小。随着新增交易行为的增多,越多的存量住房被纳入征税范围,税基也会越宽,对投机行为的抑制效果在后期可能更大。
政策对比表明,上海市房产税税基相对更宽,针对性和目的性更强,主要打击对象是“炒房行为”,主要纳税主体是投机型消费者,其整体政策设计可能在抑制投机需求方面更具优势,能在保障合理住房需求的同时逐渐减少房地产投机,实现需求结构的平稳调整,更能够抑制房地产市场价格过度上涨,进而引起资本和劳动力资源在城市行业间的优化配置,有利于提升经济效率。本文以上海房产税作为主要分析对象,并对比重庆市房产税,分析政策细则不同引起的效果差异。据此提出假说1和2。
假说1:上海市房产税改革推动了城市生产率的提升。
假说2:上海市房产税改革对城市生产率的提升主要通过抑制投机行为,稳定住房价格实现。
进一步,房地产市场投机行为的抑制将对信贷市场和劳动力市场的行业间资源配置形成优化,这也直接反映到城市生产率的提高上。在信贷市场上,房产税会降低房地产市场的预期房价,弱化杠杆效应,缓解房地产业对其他实体企业信贷资源的挤出,改善信贷市场扭曲从而为非房地产企业创造良好的融资环境,优化了信贷资金的行业配置。在劳动力市场上,开征房产税通过缓解房价过快增长来缓解部分购房者的负担,减轻劳动者的生存成本和企业的用工成本,缓解劳动力资源从城市及实体行业中的流出,使得劳动力尤其是高技能劳动者较为理性地选择就业方向,从而优化劳动力资源在行业上的配置。据此提出假说3a和3b。
假说3a:上海市房产税改革有利于行业间资本要素的优化配置。
假说3b:上海市房产税改革有利于行业间劳动力要素的优化配置。
三、实证分析设计
(一)识别策略
为了衡量房产税政策对于城市生产效率的实际影响,本文以2011年上海市实施的房产税政策作为一项准自然实验,采用合成控制法(Synthetic control method,SCM)进行政策效应的估计。合成控制法的原理与双重差分法及倾向得分匹配法相似,均是基于一定的政策冲击,通过比较实验组与控制组在政策冲击后变量的差值来评估政策效应(Abadie和Gardeazabal,2003)。不过,合成控制法是根据变量数据特征为多个控制组个体赋予差异化权重,从而构造出一个与实验组各方面特征极其相似的虚拟组,通过分析政策发生后实验组与合成的虚拟组之间的差距得到政策效果估计。
在本文中,假设可以得到M+1个城市在T期的生产率面板数据。其中第1个城市为试点城市,其余M个城市是控制组,
| $ {\Delta _{1t}} = TFP_{1t}^1 - TFP_{1t}^0\;\;\;\;{T_0} \leqslant t \leqslant T $ | (1) |
上式中,上海在
| $ TFP_{it}^0 = {\delta _t} + {\theta _t}{Z_i} + {\lambda _t}{\mu _i} + {\varepsilon _{it}} $ | (2) |
上式是潜在生产率决定方程。其中
| $ \sum\nolimits_{i=2}^{M+1}{w}_{i}{TFP}_{it}={\delta }_{t}+{\theta }_{t}\sum\nolimits_{i=2}^{M+1}{w}_{i}{Z}_{i}+{\lambda }_{t}\sum\nolimits_{i=2}^{M+1}{w}_{i}{\mu }_{i}+\sum\nolimits_{i=2}^{M+1}{w}_{i}{\varepsilon }_{it} $ | (3) |
假设存在一组权重向量
| $ \begin{aligned} \mathop \sum \nolimits_{i = 2}^{M + 1} w_i^*TF{P_{i1}} =& TF{P_{11}},\mathop \sum \nolimits_{i = 2}^{M + 1} w_i^*TF{P_{i2}} = TF{P_{12}}, \cdots \cdots ,\mathop \sum \nolimits_{i = 2}^{M + 1} w_i^*TF{P_{i{T_0}}} = TF{P_{1{T_0}}}\\ & {\text{且}}\mathop \sum \nolimits_{i = 2}^{M + 1} w_i^*{Z_i} = {Z_1} \end{aligned} $ | (4) |
那么,根据Abadie等(2010)的证明,如果
| $ \widehat {{\Delta _{1t}}} = TFP_{1t}^1 - \widehat {TFP_{1t}^0} = = TFP_{1t}^1 - \sum\nolimits_{i = 2}^{M + 1} {w_i^*} TF{P_{it}}\;\;\;\;\;{T_0} \leqslant t \leqslant T $ | (5) |
(二)变量选择和数据来源
1. 变量设计
基准回归的被解释变量利用了上海市全要素生产率作为衡量城市生产效率的指标,本文将2001—2016年作为城市生产率的计算周期。此外,考虑到各城市的经济发展状况和社会特征,本文选择全国其余33个大中城市(剔除同样实施房产税的重庆市)作为控制组,通过对控制组城市生产率加权平均来模拟计算2011年后,上海市假如未实施房产税政策时的城市生产率,并与实际征收房产税政策后的情况进行对比,评估房产税政策对城市生产率的影响。
本文测算城市全要素生产率的方法为Solow剩余法。根据严成樑等(2016)的做法,假设规模报酬不变(即
本文选取了以下四类变量:(1)地区经济发展水平。地区经济发展状况直接影响到该地生产率,故引入人均GDP、地区对外开放程度、各城市产业结构以及各城市人均资本存量等变量。(2)地区人力资本水平。引入人均工资、城市人力资本水平和城市科教事业建设水平等变量。(3)地区基础设施建设水平。引入客运总量、人均货运量、人均医院床位数和人均城市道路面积等变量。(4)地区制度因素。我们引入政府财政自给率。直属于省级或中央领导的城市可能获得发展的便利条件,因此我们还根据“是否属于副省部级及以上城市”,⑤构造了虚拟变量以控制行政等级制度的影响。
2. 数据来源与描述性统计
基准回归所用数据主要来源于2001—2016年中国《城市统计年鉴》,部分城市早期的财政收支数据来源于中国《区域经济统计年鉴》。需要说明的是,本文利用历年省级层面的CPI指数和固定资产投资价格指数对各城市的人均GDP和人均工资等进行价格平减。具体如表2和表3所示。
| 变量类型 | 符号 | 基本定义 | 度量方式 |
| 被解释变量 | lnTFP | 城市全要素生产率 | Solow剩余法 |
| 地区经济
发展水平 |
lnpcGDP | 人均GDP | 以2001年不变价计算的人均GDP的对数 |
| FDI | 对外开放程度 | 各城市实际利用外商投资额/GDP | |
| lnpcK | 人均资本存量 | 根据张军等(2004)计算人均资本存量 | |
| industry | 产业结构 | 各城市第二产业产值/GDP | |
| 地区人力
资本水平 |
lnsalary | 人均工资 | 各城市人均工资的对数 |
| college | 城市人力资本水平 | 各城市每万人普通高等学校在校生人数 | |
| eduspend | 城市科教事业建设水平 | 各城市科学教育事业费用支出/财政支出 | |
| 地区基础设
施建设水平 |
lnpassenger | 客运总量 | 各城市客运总量的对数 |
| freight | 人均货运量 | 各城市人均货运量 | |
| hospital | 医院床位数 | 各城市人均医院床位数 | |
| lnroad | 城设道路建设 | 各城市人均城市道路面积的对数 | |
| 地区制度
因素 |
fiscal | 财政自给率 | 各城市财政收入/财政支出 |
| level | 是否属于副省部级及以上城市 | level=1,属于副省部级及以上的城市
level=0,不属于副省部级及以上的城市 |
| 变量 | 观测值数量 | 平均值 | 标准差 | 中位数 | 最小值 | 最大值 |
| lnTFP | 544 | 1.6120 | 3.2640 | 1.4880 | −6.1410 | 8.6970 |
| lnpcGDP | 544 | 9.7640 | 0.4120 | 9.7140 | 8.5670 | 11.9300 |
| FDI | 542 | 0.0389 | 0.0308 | 0.0325 | 0.0000 | 0.1540 |
| lnpcK | 544 | 11.4200 | 0.8100 | 11.4700 | 9.4600 | 13.0500 |
| lnsalary | 544 | 9.5130 | 0.3790 | 9.4850 | 2.5200 | 10.2900 |
| college | 544 | 0.0554 | 0.0286 | 0.0485 | 0.0020 | 0.1310 |
| eduspend | 543 | 0.1650 | 0.0449 | 0.1680 | 0.0530 | 0.4970 |
| lnpassenger | 476 | 9.4450 | 0.9280 | 9.4370 | 7.6690 | 12.2100 |
| freight | 476 | 0.0035 | 0.0020 | 0.0029 | 0.0007 | 0.0116 |
| hospital | 544 | 0.0056 | 0.0020 | 0.0051 | 0.0024 | 0.0127 |
| lnroad | 544 | 2.3780 | 0.4630 | 2.3620 | 0.8550 | 4.1590 |
| industry | 544 | 0.4500 | 0.0784 | 0.4620 | 0.1860 | 0.6160 |
| fiscal | 544 | 0.7610 | 0.1730 | 0.7760 | 0.0400 | 1.5410 |
| level | 544 | 0.5290 | 0.5000 | 1.0000 | 0.0000 | 1.0000 |
| 注:城市客运总量和城市货运总量在2015年后统计口径发生变化,故所用数据为非平衡面板数据;个别缺失值已根据前后两年数据的平均值予以补充。FDI的最小值是0,原因是兰州市的“实际使用外资金额”在2001年和2003年的《城市统计年鉴》中均为0。为排除因数据误差造成的合成偏误,我们在后续回归中依次尝试进行截尾处理,或剔除掉个别数据具有异常值的城市重新合成进行检验,结果不会发生改变。 | ||||||
四、政策效应的估计结果
(一)房产税政策效应评估
合成控制法选取了广州、深圳、西宁和乌鲁木齐4市来合成上海市生产率。其中广州和深圳的经济政治特征与上海市较为类似,权重分别为0.476和0.312;西宁和乌鲁木齐的权重分别为0.186和0.025。使用合成控制法拟合得到的RMSPE值为0.035,⑥说明该方法能够较好地拟合出上海市生产率。表4进一步展示了在房产税政策实施前,上海市生产率以及相关预测变量的合成值和真实值对比情况。可以看到,在政策实施前,生产率合成值与真实值更为接近,说明合成控制法构造的反事实能够较好地拟合出房产税政策实施前的真实情况。
| 主要变量 | 上海
真实值 |
上海
合成值 |
34市
均值 |
差异度 |
| lnTFP | 0.4465 | 0.4412 | 1.9210 | 0.0119<3.3024 |
| lnpcGDP | 10.4275 | 10.2084 | 9.7340 | 0.0210<0.0665 |
| FDI | 0.0609 | 0.0459 | 0.0440 | 0.2460<0.2773 |
| lnpcK | 11.7819 | 11.6025 | 10.9770 | 0.0152<0.0683 |
| lnsalary | 10.0411 | 9.7867 | 9.4800 | 0.0253<0.0559 |
| college | 0.0316 | 0.0467 | 0.0470 | 0.4766<0.4875 |
| eduspend | 0.1515 | 0.1419 | 0.1500 | 0.0636>0.0100 |
| lnpassenger | 9.1999 | 9.8622 | 9.3010 | 0.0720>0.0110 |
| 0freight | 0.0051 | 0.0047 | 0.0030 | 0.0824<0.4171 |
| hospital | 0.0066 | 0.0064 | 0.0050 | 0.0240<0.2386 |
| lnroad | 2.3362 | 2.7075 | 2.2310 | 0.1589>0.0450 |
| industry | 0.4672 | 0.4559 | 0.4600 | 0.0241>0.0154 |
| fisical | 0.8610 | 0.7676 | 0.7690 | 0.1085>0.1069 |
| level | 1.0000 | 0.7880 | 0.5290 | 0.2120<0.4710 |
| 注:差异度比较,即(合成值−真实值)/(真实值)取绝对值与(均值−真实值)/(真实值)取绝对值后比较。 | ||||
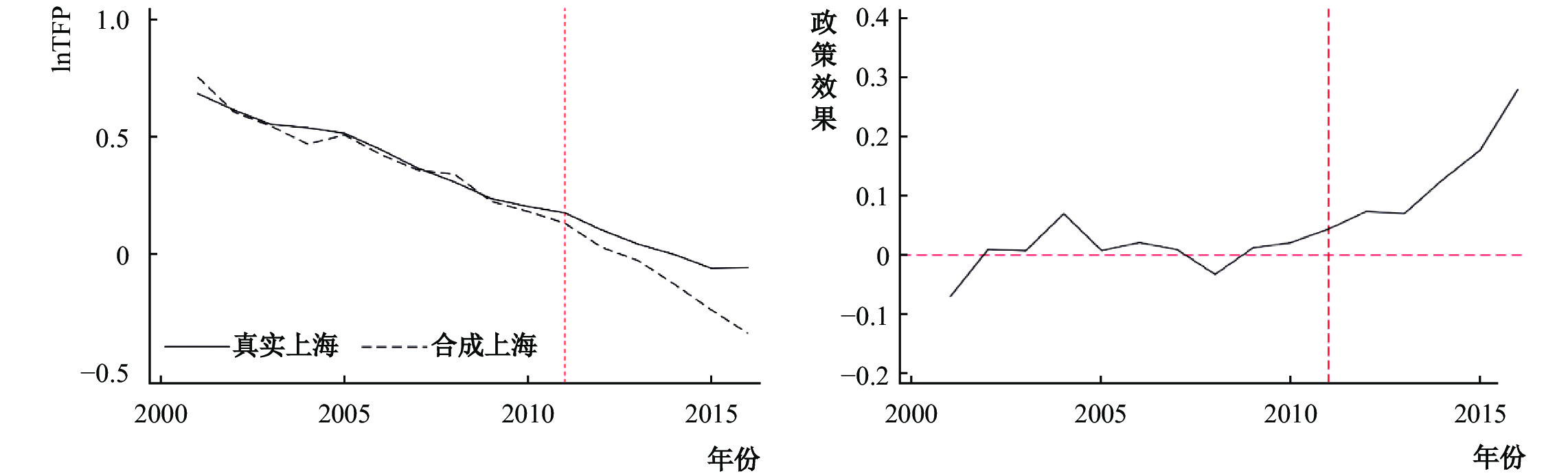
图2是房产税政策对城市生产率的效果评估,左图展示了2001—2016年上海市生产率的真实值和合成值的对比情况。自2000年以来,上海市生产率的真实值一直呈现下降趋势,年均下降幅度达4.7%,在2011年房产税政策实施后,下降幅度逐渐放缓,2016年略有增加。如前文所述,中国城市层面生产率下降的一大重要原因是房地产行业的过度繁荣,利润率高但生产效率低的房地产行业吸纳了过多的信贷资本和劳动力,造成了资源在行业间配置的不合理,成为阻碍城市经济高质量发展的重要因素(陆铭等,2015;陈斌开和张川川,2016)。
|
| 图 2 上海房产税政策对城市全要素生产率的效果评估 |
对比左图两条线,可以看到政策实施前实线与虚线基本重合,这也说明上海和合成上海的生产率十分接近,拟合效果较为理想。但在2011年后,上海市生产率真实值均高于其合成值。右图直观展示了房产税政策效果,如图所示,政策效果随着时间的变化在不断扩大,说明与不开征房产税相比,政策在很大程度上缓解了生产率的下降幅度,且后期作用更大,原因正如前文所述,上海市房产税的政策设计对抑制投机具有较强针对性和目的性,其过渡期设计的特殊性也使税基越来越宽,故政策效果会不断扩大。另一方面,城市生产率的改善需要通过资源配置的逐步优化来实现,因此房产税政策对生产率的改善效果呈现逐步释放的态势是符合常理的。该结果证明了假说1成立。
(二)稳健性检验
1. 排序检验
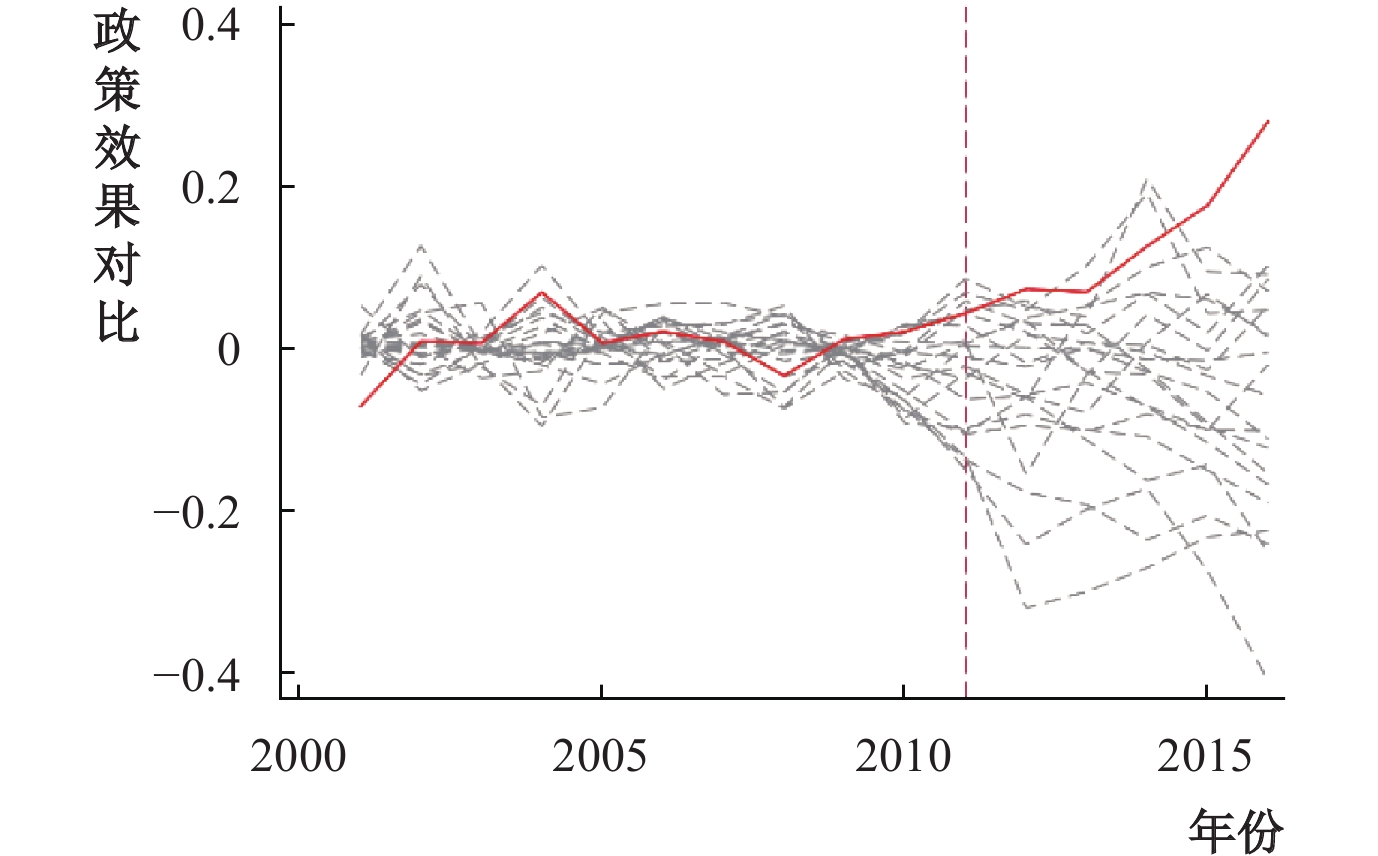
本文进行了安慰剂检验(Placebo test)。根据合成控制法基本思想,利用排序检验来判断其他城市在2011年后是否出现了类似于上海市的状况。其思想是假设所有样本城市在2011年后均经历了房产税改革,利用合成控制法一一构造出每个城市的反事实生产率,评估各城市在假设状况下的政策效果,并与上海市实际实施房产税后的政策效果相比较。若差距较大,则说明房产税政策对上海市生产率的影响是显著的。合成控制法要求在政策实施前,用于合成的城市能够较好地拟合出样本城市,即RMSPE较小,故排除2011年前RMSPE值超过上海市1.5倍的城市(共12个),⑦利用剩余样本城市进行排序检验(参见图3)。从图3可以看出,2011年前各城市生产率的变动程度相差并不大,但2011年之后,上海市生产率与其他城市差距持续拉大。类似于统计惯用的判断标准显著性水平,这表明仅有1/20的概率,即5%的可能性会出现上海和合成上海生产率之间的变动差距,房产税的政策效果较为明显。
|
| 图 3 各城市全要素生产率的变动程度分布 |
2. 变换合成城市
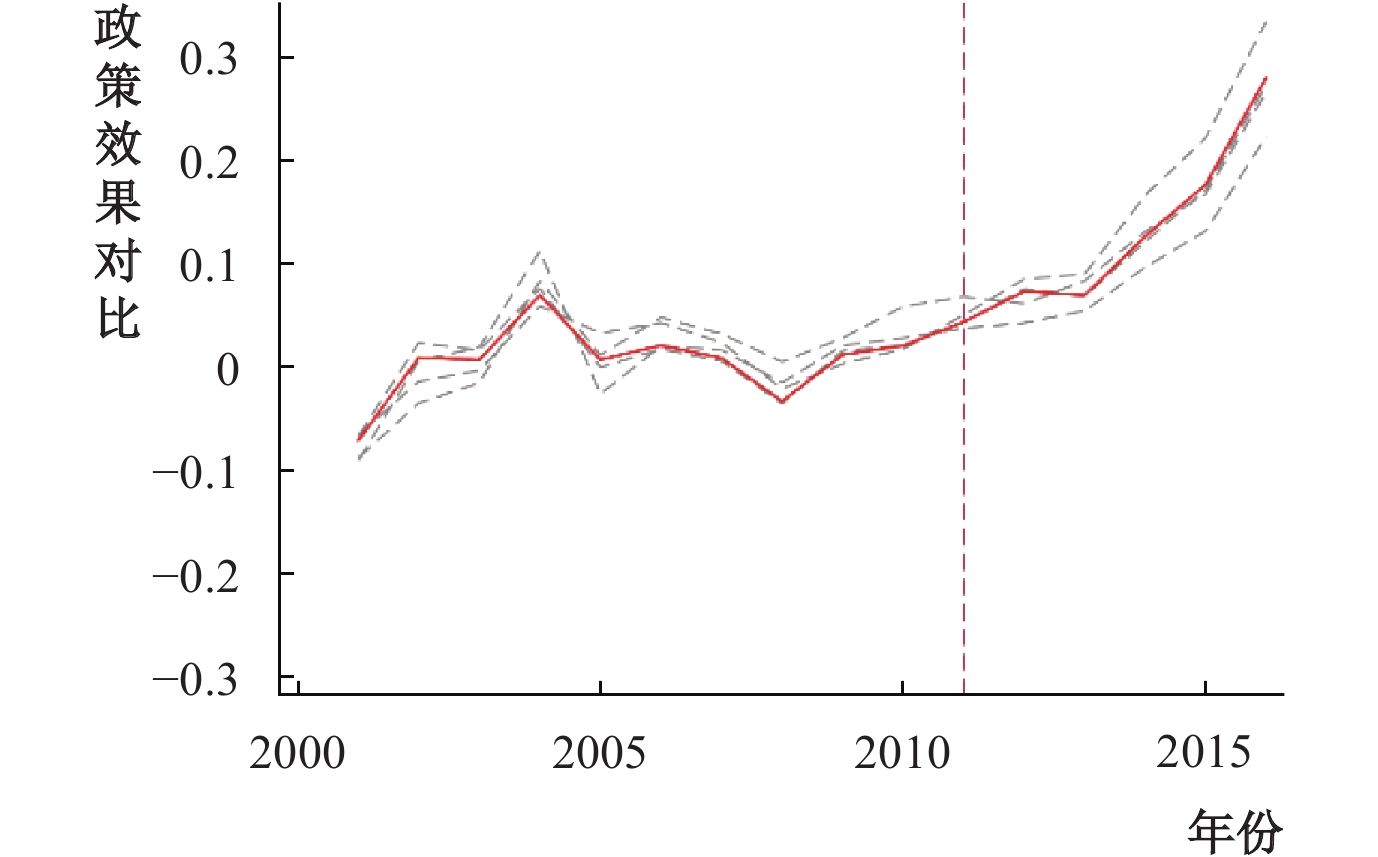
本文通过依次变换用于合成的控制组城市来进行稳健性检验。具体而言,基准回归选择了广州、深圳、西宁和乌鲁木齐,在进行检验时,则依次剔除掉1个城市,并使用其余32个城市重新合成。重复4次后,依次与基准回归的政策效果进行比较。图4中,实线是包含全部4个城市的合成结果,其余虚线是依次剔除掉4个城市后重新合成的结果。从图4可以总结得出两点结论,一是在2011年前,重新合成的结果虽仍围绕0上下波动,但相较于原合成结果而言,波动幅度较大,说明重新合成损失了部分拟合优度,原合成结果拟合效果更好;二是在2011年后,重新合成得到的政策效果均为正值,虽然与原合成结果相比政策效果有所差异,但差异并不明显,总体上都呈现出生产率相对回升的趋势。以上两点结论均说明本文的合成结果较为稳健。
|
| 图 4 变换合成城市的检验 |
3. 替换实验组
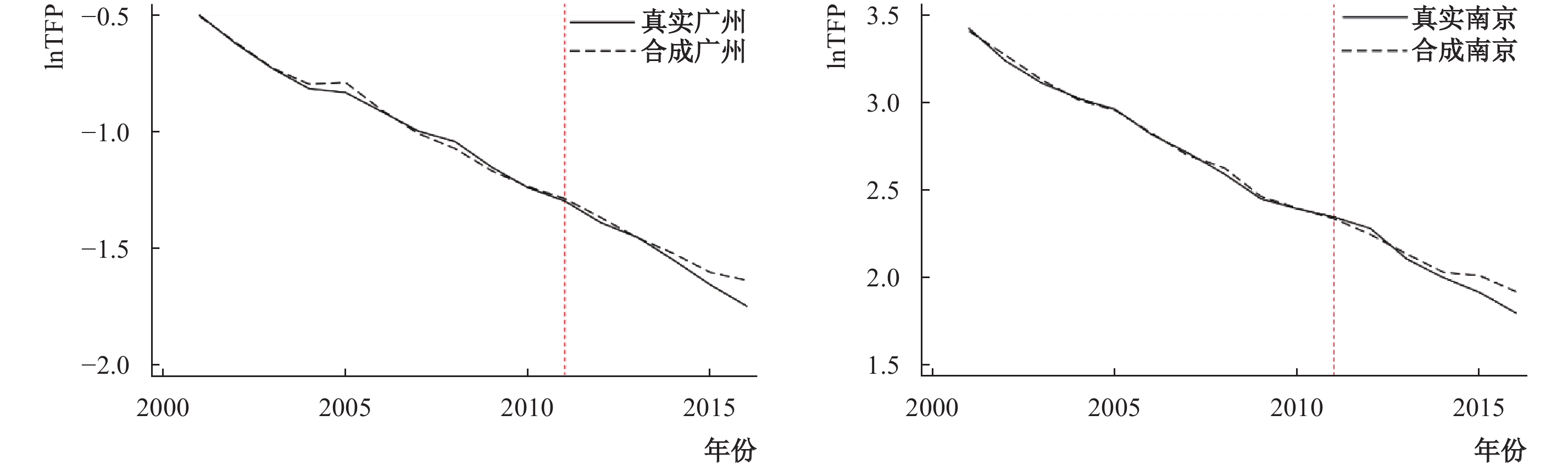
本文选择广州(权重最大)和南京(无权重)作为实验组进行检验。图5为广州和南京的拟合情况。在2011年政策实施前后,两市生产率的合成值与实际值差别均不大,两条线基本重合,这证明了不同于上海市,在2011年后广州和南京的生产率均未发生突变,也能在一定程度上证明是房产税的实施导致了上海市生产率的突变。
|
| 图 5 分别替换广州和南京为实验组的稳健性检验 |
五、政策效应的机制验证
(一)房产税政策抑制房地产市场投机需求
为验证假说2,即房产税政策对城市生产率的提升主要通过抑制房地产市场投机行为,尤其是缓解住房价格的过快上涨来实现,文章进一步评估了上海市房产税政策对城市住宅房屋成交情况的影响。在机制验证部分,由于合成控制法严格要求合成组权重非负且和为1,并高度依赖控制变量的选择,而机制部分所用数据难以满足要求,因此将改用Hsiao等(2012)在合成控制法的基础上提出的回归控制法(Regression control method,HCW)。⑧
指标选择上,由于投机需求与消费者个体行为特征有关,一般较难对其直接进行量化,故本文选择以“住宅商品房成交面积”和“住宅商品房平均售价”作为房地产市场投机行为的代理变量。原因在于,成交面积在一定程度上反映了市场供需。如前文所述,上海市房产税政策对新增交易行为征税实际上是对全部存量房征税的“触发机制”,并规定了每户人均60平米的免税面积,因此从理论上来说,自住型消费者一般不会感知到房产税政策的存在。根据相关政策推测,政策出台后全市住宅房屋成交面积的相对下降大部分将来自于投机需求的减少,因此以住宅商品房成交面积作为投机需求的代理变量相对合理。其次,投机需求是造成房价波动的首要原因(Gholizadeh,2014;Huang和Shen,2017),投机性交易的相对减少更会进一步表现在住房价格上,故本文选择“住宅商品房平均售价”作为度量投机行为的代理变量进行进一步检验。相关变量数据均来自于《中国房地产统计年鉴》。
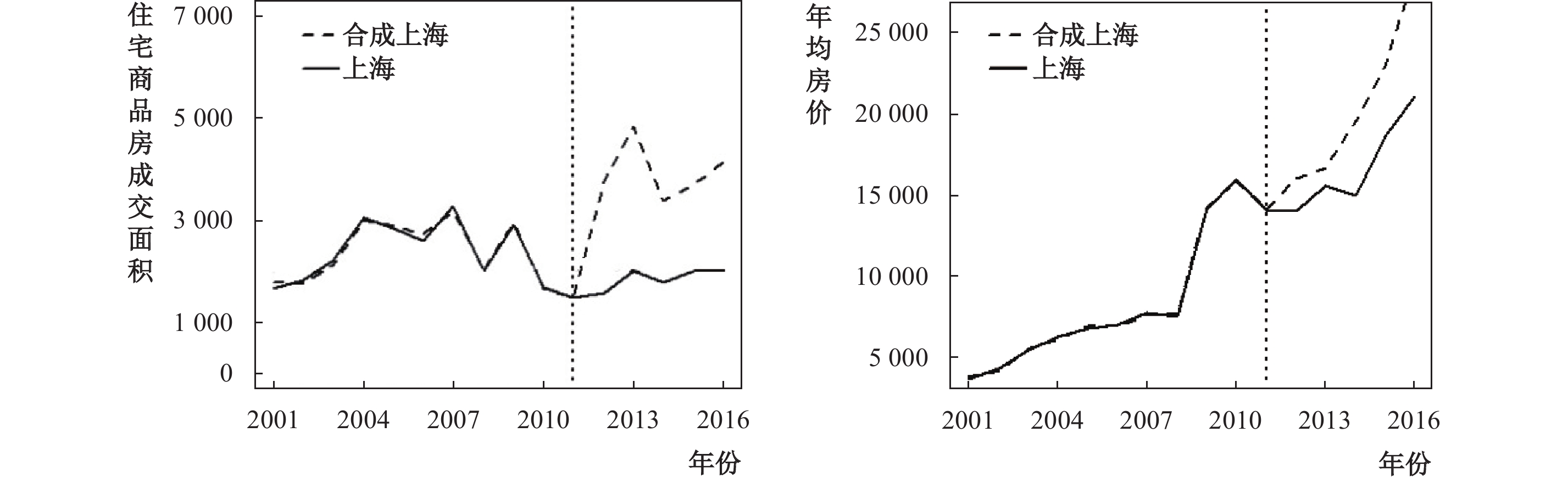
参考Hsiao等(2012)等文,我们根据政治经济、地理位置和产业发展等因素,构造了用于合成的控制组。⑨通过AICC、AIC和BIC准则,以及拟合优度R2选择最优合成城市。图6分别评估了房产税改革对住宅房屋成交面积和房价的影响,最终选取杭州(4.056***)、厦门(4.227***)、成都(−2.732***)和哈尔滨(4.244***)合成房屋成交面积,选取北京(0.834***)、天津(−1.308***)、合肥(3.864***)和海口(−1.764***)合成房价,⑩调整后R2分别为0.984和0.999。不管是成交面积还是房价,2011年政策实施后的真实值均低于其合成值,且这一差距在政策实施后的几年间呈现扩大的趋势。⑪这说明上海市房产税政策设计的特殊性有效抑制了在政策过渡期的住房投机需求,同时也是使得上海市生产率的下降幅度减慢并开始回升的重要原因之一。该结果验证了本文的理论假说2。
|
| 图 6 房产税对上海市房屋成交面积和房价的影响 |
(二)房产税政策优化行业间资本配置
为验证假说3a,本文评估了房产税对行业间资本配置的影响。资本配置的优化通常指的是信贷资金从非实体经济流到实体经济。简单起见,本文将制造业与房地产业分别作为实体经济与非实体经济的代表,通过房产税政策实施前后,两个行业吸纳资金情况的变化对比来验证房产税政策是否可以优化行业间资本配置。变量选择上,由于缺乏市级层面的分行业信贷资金,分别选择省级层面的规模以上工业企业流动资产,以及房地产开发企业的本年实际到位资金作为制造业和房地产业所获信贷资金的替代变量,利用市级固定资产投资占省级的比重,将省级数据匹配到市级层面研究。数据来自于中经网统计数据库以及《城市统计年鉴》。
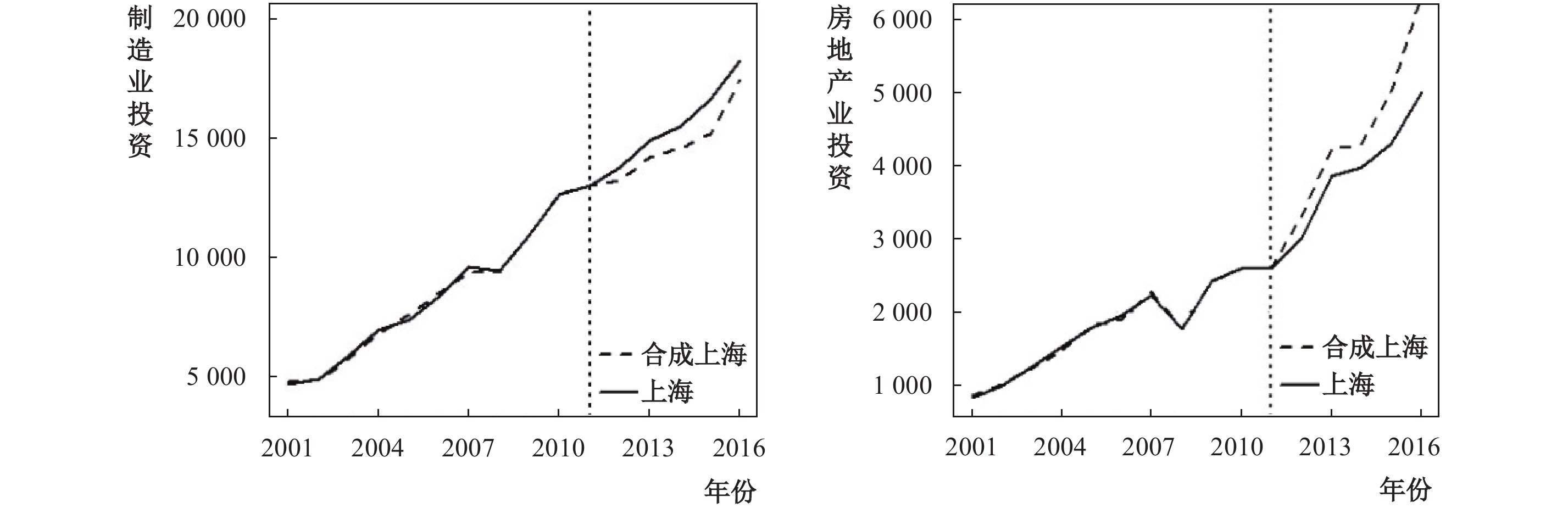
图7是房产税政策对制造业与房地产业资本配置的影响。选取了宁波(1.399***)、济南(−1.106*)和广州(1.301***)合成制造业投资,调整后R2为0.998;选取了北京(0.179***)、合肥(−2.488***)、南昌(11.472***)和海口(2.086**)合成房地产业投资,调整后R2为0.997。左图中,在2011年房产税政策实施前,真实上海和合成上海的规模以上工业企业流动资产走势高度重合,但在政策实施后,实际制造业投资明显高于合成值,且此后几年差距略有扩大。右图中,政策实施后虽然房地产开发企业的实际到位资金与其合成值均呈增长趋势,但前者的增长幅度明显低于后者,且两者差距不断扩大。可见,尽管两个行业的实际吸纳资金数额都在上升,但房产税政策的实施的确有效增加了制造业吸纳的资金量,也确实抑制了上海市房地产行业吸纳资金量的增长,使得整个市场的资金产生“脱虚向实”的趋势,有助于缓解实体经济信贷资金投资不足的现状。该结果验证了本文的假说3a。
|
| 图 7 2001—2016年房产税对上海市行业间信贷资源配置的影响 |
(三)房产税政策优化行业间劳动力配置
为验证假说3b,本文评估了房产税政策对行业间劳动力要素配置的影响。劳动力在实体经济与非实体经济之间的流动在一定程度上代表了人力资源的配置情况,因此本文选择以劳动力行业就业结构作为城市劳动力要素配置的替代变量。劳动力就业结构的相关数据来源于《城市统计年鉴》,⑫计算方法是行业城镇单位从业人员数与全市城镇单位从业人员数之比,同样将制造业和房地产业分别作为实体经济和非实体经济的代表。回归控制法选取了福州(2.771***)、厦门(−1.260***)和济南(1.524***)合成制造业劳动力就业规模,调整后R2为0.934;选取了北京(−0.912***)、太原(1.493***)、南京(−4.034***)和南昌(1.701***)合成房地产业劳动力就业规模,调整后R2为0.945。
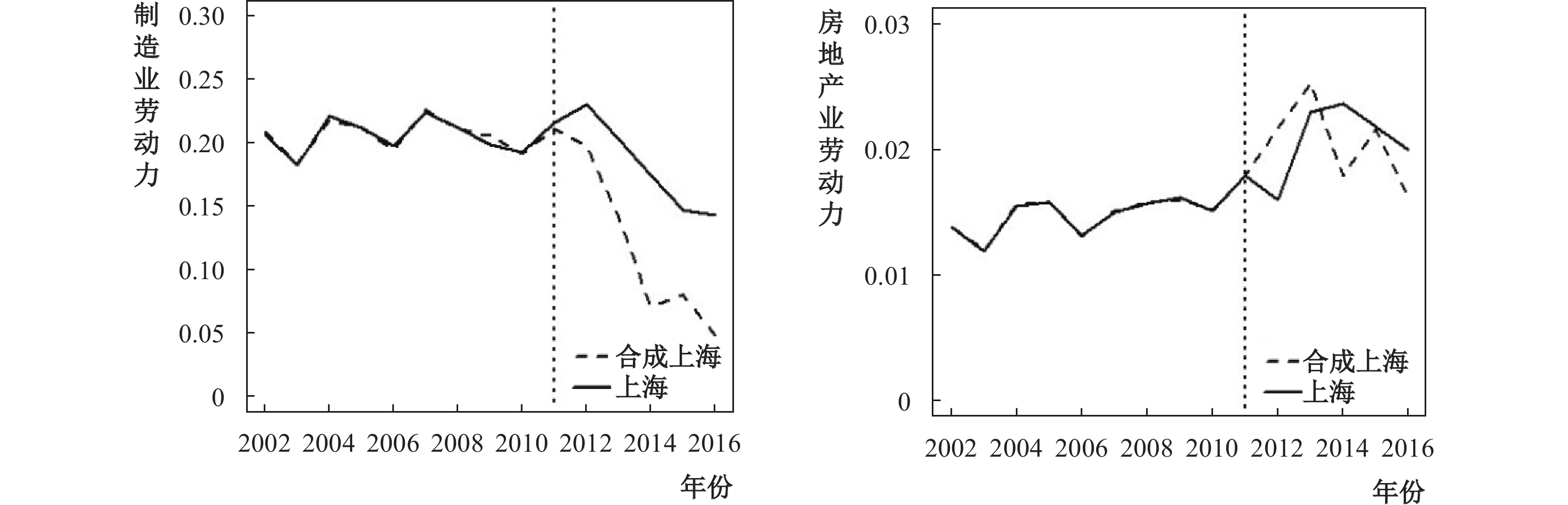
图8左图,在政策实施后的第一年,实际制造业劳动力就业份额有所上升,此后虽与合成值同样呈现下降趋势,但真实值远高于合成值且差距快速扩大,这说明房产税的落实一定程度上稳定了实体经济的劳动力规模,对抑制制造业劳动力人口过度流出起到了较大作用。右图中,2012和2013年,合成上海的房地产业劳动力份额较快增长,大于真实值涨幅。长期来看,虽然上海市房产税对维持制造业内部劳动力规模的效果日益明显,但对房地产业劳动力规模的影响并不确定。结合上海市经济背景对上述原因进行分析,一是可能与上海市劳动力的就业大趋势和产业结构调整有关;⑬二是可能与上海市房地产市场的独特性以及劳动力工资粘性有关,长期以来住房需求量不断增加,在房地产市场利润虚高的背景下,工资粘性特征使得就业人数不会轻易流出房地产市场。但房价的相对下降确实同时降低了制造业和房地产业劳动人口的生活成本,保证了制造业劳动力人数的一定规模。总体而言,上海市房产税政策对房地产业劳动力份额的抑制效果并不明确,但有效保持了实体经济的劳动力规模,一定程度上改善了劳动力流出制造业的大趋势,满足了实体经济的基本用工需求。该结果一定程度上证明了假说3b成立。
|
| 图 8 2002—2016年房产税对上海市劳动力行业就业结构的影响 |
(四)对照检验−重庆市房产税政策效应估计及机制验证
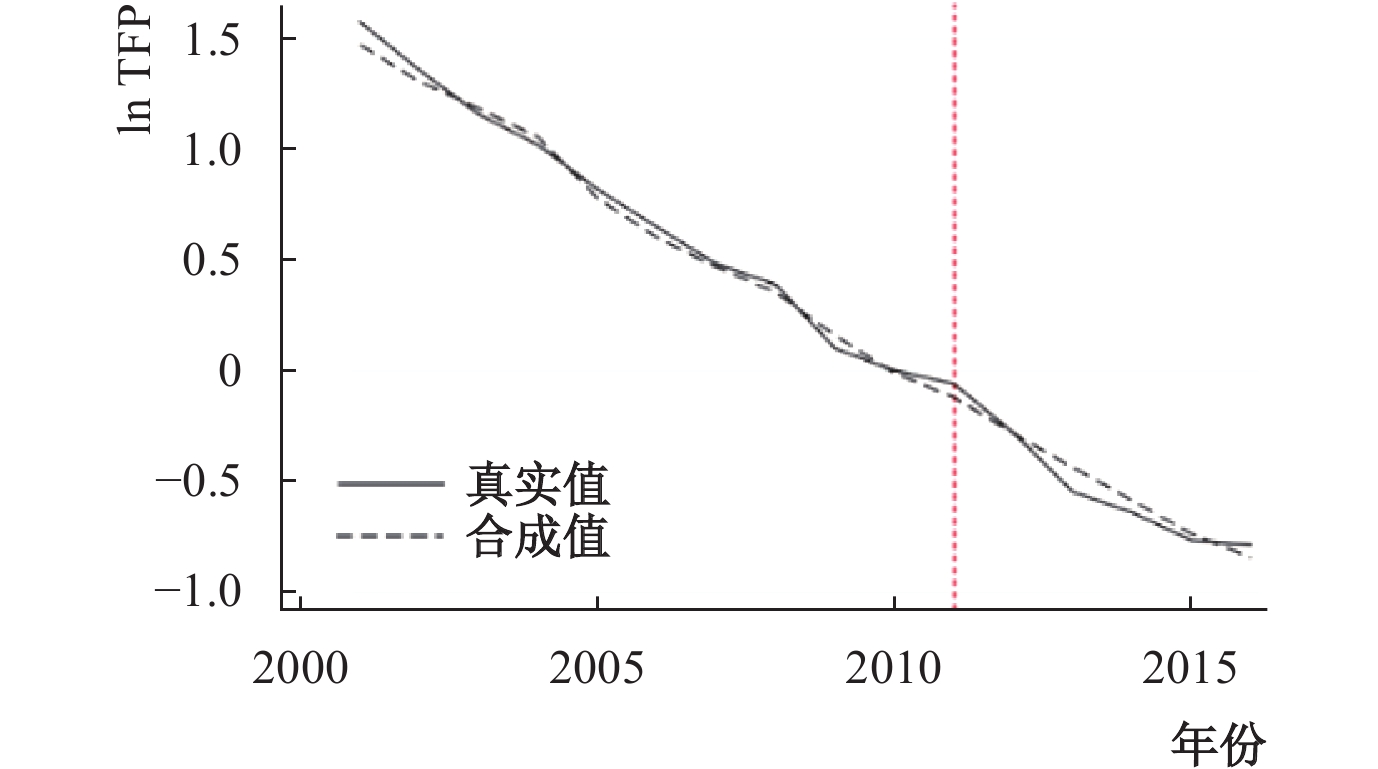
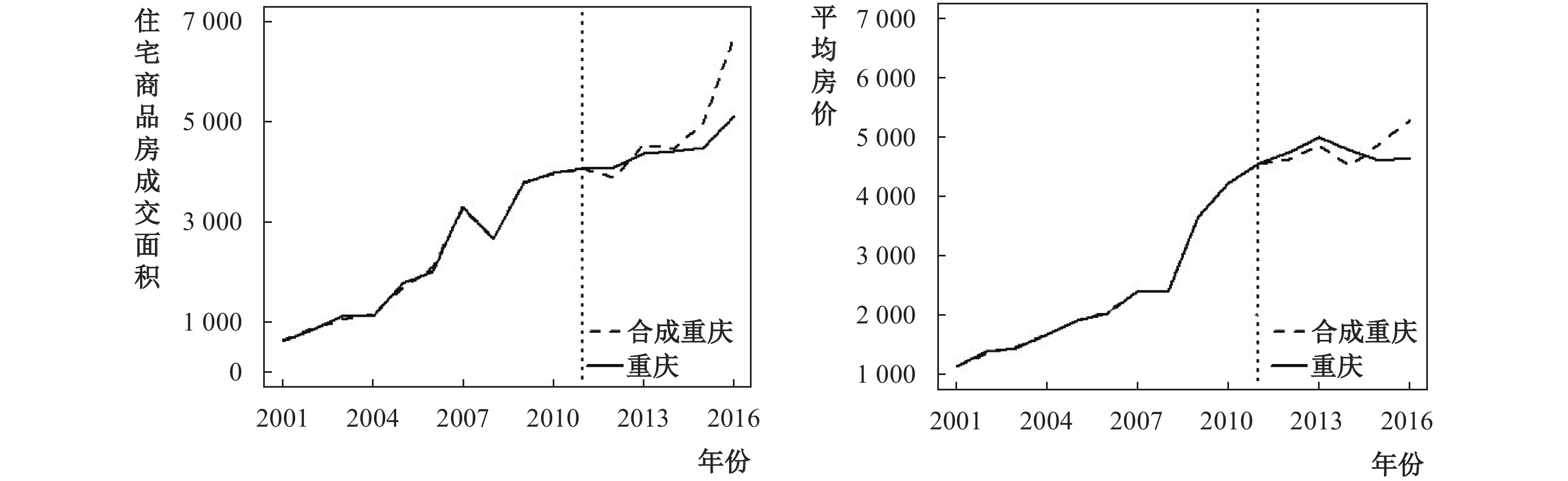
图9验证了房产税政策对重庆市生产率的影响。合成重庆市生产率的城市及权重分别为石家庄(0.355)和福州(0.645),RMSPE值为0.0496。结果表明,重庆市生产率在政策实施后并没有特别显著的变化。在对投机需求的评估上,合成重庆房屋成交面积的城市及权重分别为天津(−0.893***)、合肥(1.985***)和郑州(1.886***),合成房价的城市为杭州(0.164***)、武汉(0.423***)、长沙(0.328***)、成都(−0.386***)和西安(0.265***),调整后的R2分别为0.998和1。图10显示,房产税政策实施后,重庆市的房屋成交面积没有明显降低,可能较难有效抑制房屋价格,这与Bai等(2014)的结论较为一致。
|
| 图 9 房产税对重庆市生产率的影响 |
|
| 图 10 房产税对重庆市房屋成交面积和房价的影响 |
六、结论与建议
本文以2011年中国上海市房产税改革试点作为一项准自然实验,采用合成控制法对房产税政策对于城市生产效率的影响进行了估计。文章结果显示,房产税政策能够通过抑制投机需求和缓解房价的非理性上涨来优化资源配置,尤其是改善行业间信贷资金流向以及劳动力行业就业结构,从而提升城市生产率。
上海和重庆房产税政策效果的不同源自两市政策细节的差异。对比发现,重庆的房产税针对独栋和高档住房征税,易使购房者倾向选择购买中低档住房避税。而上海的房产税则面向所有住宅房屋类型征税,相较重庆来说更接近国外“宽税基、低税率”的设计方案(傅樵,2010),有利于减少市场投机行为,维稳房屋价格,实现对城市生产率的提升。该结果为“宽税基、低税率”方案具有的政策优势(任强,2015;邵磊等,2020)提供了更多佐证。此外,上海市“增量起征、溯及既往”的房产税设计,在精准打击房地产投机行为的同时兼顾了房地产市场的合理需求,税基也会随着时间变化不断变宽,更有利于维持房地产业的稳定发展。本文的政策建议为:(1)宽税基,低税率。征税对象上,要面向所有住房类型征税,避免因结构性扭曲导致的投机行为。税率设计上,参考各国房产税率设计与我国经济状况,也不宜制定过高税率。(2)精准打击,抑制投机。房产税减免退税及其他优惠政策应在保障合理住房需求的同时,抑制炒房投机行为。(3)循序渐进,做好过渡。房产税政策的推进难以一蹴而就,各种阻力可通过一些过渡机制来有效缓解。比如上海市试点的“增量起征、溯及既往”过渡机制就有利于缓和纳税人抵触情绪,实现政策的平稳过渡与长效调控。
① 政策资料来源:《中共中央关于制定国民经济和社会发展第十四个五年规划和二〇三五年远景目标的建议》。
② 《中国住房金融发展报告(2019)》。
③ 《中共中央关于制定国民经济和社会发展第十四个五年规划和二〇三五年远景目标的建议》。
④ 本文利用该方法计算35个大中城市的基期资本存量,主要由于中国早期市级层面的固定资本形成额数据较为缺乏。1995年的省级资本存量则直接利用张军(2004)的数据。
⑤ 在我国35个大中城市中,第1等级为包含4个直辖市的正省部级城市,第2等级为包含10个省会城市和5个计划单列市的副省部级城市,第3等级为包含剩余16个省会城市的正厅级城市。
⑥ Root Mean Square Prediction Error,均方预测误差的平方根,该值越接近于0说明拟合效果越好。
⑦ Abadie等(2010)指出,一般保留RMSPE是政策实施前实验组样本1.5—2倍以内的样本城市进行排序检验。若RMSPE值相差过大,说明利用合成控制法进行拟合存在较大误差,因此政策实施后产生的差异很可能是由于拟合效果不好所致。
⑧ 方法转换原因在于合成控制法存在一定局限:(1)要求合成组城市权重非负且和为1;(2)高度依赖控制变量的选择,控制组的经济特征与干预前的结果变量均要与实验组足够接近。限于篇幅,不再详细说明,有需要可向作者索取。
⑨ 为确保合成结果的稳健性,我们同样通过替换合成城市进行检验,限于篇幅原因不再报告,有需要可向作者索取。
⑩ 括号内分别为用于合成的城市权重以及显著性,下同。
⑪ 对房价的影响与Bai等(2014)的结论一致。
⑫ 由于数据统计口径不一致,本文仅使用2002—2016年的行业劳动力数据。
⑬ 《上海市来沪人员就业状况报告(2018)》显示,近年来从事第二产业的劳动力数量持续小幅下降,而第三产业的劳动力增长速度较快。
| [1] | 蔡跃洲, 付一夫. 全要素生产率增长中的技术效应与结构效应——基于中国宏观和产业数据的测算及分解[J]. 经济研究, 2017(1): 72–88. |
| [2] | 陈斌开, 金箫, 欧阳涤非. 住房价格、资源错配与中国工业企业生产率[J]. 世界经济, 2015(4): 77–98. |
| [3] | 陈斌开, 张川川. 人力资本和中国城市住房价格[J]. 中国社会科学, 2016(5): 43–64. |
| [4] | 邓晓兰, 刘若鸿, 许晏君. 经济分权、地方政府竞争与城市全要素生产率[J]. 财政研究, 2019(4): 23–41. |
| [5] | 董直庆, 刘迪钥, 宋伟. 劳动力错配诱发全要素生产率损失了吗? ——来自中国产业层面的经验证据[J]. 上海财经大学学报, 2014(5): 94–103. |
| [6] | 范剑勇, 颜燕, 王加胜. 改革以来就业结构变动及其对经济增长的贡献[J]. 宏观经济研究, 2001(9): 43–47. |
| [7] | 范子英, 刘甲炎. 为买房而储蓄——兼论房产税改革的收入分配效应[J]. 管理世界, 2015(5): 18–27. |
| [8] | 傅樵. 房产税的国际经验借鉴与税基取向[J]. 改革, 2010(12): 57–61. |
| [9] | 侯一麟, 任强, 马海涛. 中国房地产税税制要素设计研究[M]. 北京: 经济科学出版社, 2016. |
| [10] | 刘甲炎, 范子英. 中国房产税试点的效果评估: 基于合成控制法的研究[J]. 世界经济, 2013(11): 117–135. |
| [11] | 刘建丰, 于雪, 彭俞超, 等. 房产税对宏观经济的影响效应研究[J]. 金融研究, 2020(8): 34–53. DOI:10.3969/j.issn.1674-5477.2020.08.005 |
| [12] | 刘友金, 曾小明. 房产税对产业转移的影响: 来自重庆和上海的经验证据[J]. 中国工业经济, 2018(11): 98–116. |
| [13] | 陆铭, 张航, 梁文泉. 偏向中西部的土地供应如何推升了东部的工资[J]. 中国社会科学, 2015(5): 59–83. |
| [14] | 任强. 房产税: 美国实践及借鉴[J]. 财政研究, 2015(1): 53–57. |
| [15] | 邵军, 徐康宁. 我国城市的生产率增长、效率改进与技术进步[J]. 数量经济技术经济研究, 2010(1): 58–66. |
| [16] | 邵磊, 任强, 侯一麟. 基础教育均等化措施的房地产资本化效应[J]. 世界经济, 2020(11): 78–101. |
| [17] | 王会强, 姚爱科, 郝琳琳. 河北省经济增长与就业结构的变动分析[J]. 河北大学学报(哲学社会科学版), 2009(2): 53–56. DOI:10.3969/j.issn.1000-6378.2009.02.013 |
| [18] | 王文春, 荣昭. 房价上涨对工业企业创新的抑制影响研究[J]. 经济学(季刊), 2014(1): 465–490. |
| [19] | 徐虹. 我国房地产市场的分层调控政策研究[J]. 中央财经大学学报, 2013(5): 71–77. |
| [20] | 严成樑, 吴应军, 杨龙见. 财政支出与产业结构变迁[J]. 经济科学, 2016(1): 5–16. |
| [21] | 颜鹏飞, 王兵. 技术效率、技术进步与生产率增长: 基于DEA的实证分析[J]. 经济研究, 2004(12): 55–65. |
| [22] | 余静文, 谭静, 蔡晓慧. 高房价对行业全要素生产率的影响——来自中国工业企业数据库的微观证据[J]. 经济评论, 2017(6): 22–37. |
| [23] | 余泳泽, 李启航. 城市房价与全要素生产率: “挤出效应”与“筛选效应”[J]. 财贸经济, 2019(1): 128–143. DOI:10.3969/j.issn.1002-8102.2019.01.010 |
| [24] | 张军, 吴桂英, 张吉鹏. 中国省际物质资本存量估算: 1952-2000[J]. 经济研究, 2004(10): 35–44. |
| [25] | Abadie A, Diamond A, Hainmueller J. Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program[J]. Journal of the American Statistical Association, 2010, 105(490): 493–505. DOI:10.1198/jasa.2009.ap08746 |
| [26] | Abadie A, Diamond A, Hainmueller J. Comparative politics and the synthetic control method[J]. American Journal of Political Science, 2015, 59(2): 495–510. DOI:10.1111/ajps.12116 |
| [27] | Abadie A, Gardeazabal J. The economic costs of conflict: A case study of the Basque Country[J]. American Economic Review, 2003, 93(1): 113–132. DOI:10.1257/000282803321455188 |
| [28] | Bai C E, Li Q, Ouyang M. Property taxes and home prices: A tale of two cities[J]. Journal of Econometrics, 2014, 180(1): 1–15. DOI:10.1016/j.jeconom.2013.08.039 |
| [29] | Brandt L, Tombe T, Zhu X D. Factor market distortions across time, space and sectors in China[J]. Review of Economic Dynamics, 2013, 16(1): 39–58. DOI:10.1016/j.red.2012.10.002 |
| [30] | Campello M, Graham J R, Harvey C R. The real effects of financial constraints: Evidence from a financial crisis[J]. Journal of Financial Economics, 2010, 97(3): 470–487. DOI:10.1016/j.jfineco.2010.02.009 |
| [31] | Cebula R. Are property taxes capitalized into housing prices in Savannah, Georgia? An investigation of the market mechanism[J]. Journal of Housing Research, 2019, 18(1): 63–75. |
| [32] | Chen K J, Wen Y. The great housing boom of China[J]. American Economic Journal: Macroeconomics, 2017, 9(2): 73–114. DOI:10.1257/mac.20140234 |
| [33] | Gholizadeh A A. Capital gains tax and housing price bubble: A cross-country study[J]. Iranian Economic Review, 2014, 18(2): 47–71. |
| [34] | Hsiao C, Ching H S, Wan S K. A panel data approach for program evaluation: Measuring the benefits of political and economic integration of Hong kong with mainland China[J]. Journal of Applied Econometrics, 2012, 27(5): 705–740. DOI:10.1002/jae.1230 |
| [35] | Huang J, Shen G Q. Residential housing bubbles in Hong Kong: Identification and explanation based on GSADF test and dynamic probit model[J]. Journal of Property Research, 2017, 34(2): 108–128. DOI:10.1080/09599916.2017.1321574 |
| [36] | Krippner G R. The financialization of the American economy[J]. Socio-Economic Review, 2005, 3(2): 173–208. DOI:10.1093/SER/mwi008 |
| [37] | Kuznetsova A, Askarov A, Gusmanov R, et al. Differentiation of labor productivity level and wages as a basis for changes in labor market[J]. Polish Journal of Management Studies, 2019, 20(2): 345–357. DOI:10.17512/pjms.2019.20.2.29 |
| [38] | Miao J J, Wang P F. Sectoral bubbles, misallocation, and endogenous growth[J]. Journal of Mathematical Economics, 2014, 53: 153–163. DOI:10.1016/j.jmateco.2013.12.003 |
| [39] | Miao J J, Wang P F. Asset bubbles and credit constraints[J]. American Economic Review, 2018, 108(9): 2590–2628. DOI:10.1257/aer.20160782 |
| [40] | Petty W. Political Arithmetick[M]. London: Robert Clavel and Hen. Mortlock, 1690. |


