
2021第47卷第4期
一、引 言
自2008年中央政府实施“四万亿”财政刺激计划之后,地方政府的隐性债务①问题日益成为影响宏观经济运行和经济发展的重要因素(Bai等,2016;Chen等,2020)。尽管受到中央政府严格的限制,但地方政府依然可以通过融资平台(LGFVs)以各种方式进行举债,造成隐性债务规模的不断膨胀。根据财政部的统计,截至2017年,中国地方政府债务余额高达16.47万亿元,而根据一些学者的估计,实际负债可能达到30.27万亿元。②地方隐性债务的无序扩张不仅可能在短期中诱发“灰犀牛”式的系统性金融风险(毛锐等,2018),也会恶化资源配置效率,“挤出”制造业企业的融资(Liang,等 2017)和投资(Huang,等 2020),从而削弱中国经济的长期发展动能。
与已有文献相比,本文聚焦于隐性债务扩张的另外一个重要的、但却被忽视的经济影响,即其对企业研发(R&D)活动和产出的抑制作用。总体而言,中国企业的研发活动在过去20年间实现了“爆发性”的增长:2000年至2016年,企业内部研发费用从895.66亿元增加至15 676.75亿元;与此同时,全国专利申请数从26 184件上升至715 397件,③企业研发创新行为对全社会科技进步的贡献率不断上升(Boeing等,2016)。然而,这一长期趋势在2010年之后出现了某种程度的“逆转”:企业内部研发经费增速从 2000 年至 2010 年的年均 22%下降至 2010 年之后的年均 14%。无独有偶,中国全要素生产率(TFP)增速在同一时期也出现了明显的放缓:根据国家信息中心的测算,中国全要素生产率增速从2001—2009年间年均2.07%的水平下降至2010年之后的年均1.89%。。面对隐性债务规模的不断膨胀和企业研发活动增速的下降,很多中国经济的观察者产生了这样的疑问,过高的地方债务水平是否会抑制微观企业的创新?这一影响的潜在作用机制是什么?这些都是本文希望回答的问题。
本文基于2008年至2017年非金融业上市公司数据和手工搜集的地方政府隐性债务数据,研究了地方政府隐性债务水平对微观企业研发投入和专利申请的影响。实证结果显示,城市隐性债务水平对当地企业的专利申请具有显著的“抑制作用”,并且导致了企业内部研发费用的缩减,这表明隐性债务同时在研发投入和产出两个维度上“挤出了”企业研发活动。接下来,我们对上述影响所依赖的内在传导机制进行了分析,发现政府研发补贴和长期外部借款的减少是隐性债务挤出企业研发活动的潜在机制。最后,本文还对主要实证结果进行了异质性分析和稳健性检验,结果表明,隐性债务的“挤出效应”主要体现在高预算约束企业、国有企业和非一线城市上市企业样本上。
本文对相关领域研究的边际贡献主要体现在如下几个方面:(1)较早地在地级市层面上研究了地方债务对企业研发投入和产出的影响,并识别出两条可能的传导机制,加深了对地方政府债务经济影响的认识;(2)实证分析充分利用地方隐性债务水平在地区层面的差异(variation),一方面使得我们无需依赖较长的政府债务时间序列数据,另一方面避免了跨国研究中可能存在的由不同国家制度差异所带来的内生性问题;(3)在数据方面,我们手工搜集了1140家融资平台层面的债务数据,并在此基础上测度了地级市政府隐性债务水平。与现有主流研究相比,本文对隐性债务的测度更加准确。最后,在当前面临新冠疫情冲击,地方政府财政再次面临困难的背景下,如何在实施积极有为的财政政策的同时,避免对企业研发创新活动的过度“挤出”,保持未来中国经济“高质量”发展的动力,值得各级政府决策者思考。本文的研究为解决上述现实问题提供了较为重要的启示。
二、文献综述与研究假设
政府债务对经济增长具有重要影响。凯恩斯主义的观点认为,在经济处于衰退期时,为了应对有效需求不足,政府需要采用积极的财政政策刺激经济,这一过程必然会带来政府债务水平的飙升。然而,2007年全球金融危机和随之而来的大衰退(Great Recession)凸显了债务对于经济增长和金融体系的负面影响。2009年末爆发的欧洲债务危机更促使经济学家思索政府债务对于经济发展复杂的长期作用。Elmendorf和Mankiw(1999)在研究中首先提出政府债务可能对私人融资具有某些“挤出效应”。进一步地,研究者发现政府债务与经济增长之间存在着“非线性”的关系:当政府债务超过某一“门槛水平”(threshold)时,对增长的影响方向会从正转变为负。Reinhart和Rogoff(2010)是较早注意到这种 “非线性”关系的文献。迄今为止,上述研究关注的主要是一国政府债务总水平的影响,针对地方政府债务的研究相对匮乏。毛捷和黄春元(2018)利用“城投债”发行数据检验了地方政府债务与地区经济增长的关系。他们的实证结果证实跨国研究中的“倒U形”关系在地区层面依然存在,并且这一关系呈现出显著的区域差异。
宏观上理解政府债务与经济增长的关系固然重要,但是经济学家更希望了解这些影响背后的微观机制,尤其是债务对企业融资、投资和创新等行为的影响。Fan等(2012)检验了一系列与公司资本结构相关的制度性因素,发现在发展中国家,政府债务会显著地“挤出”私人公司的融资。Graham等(2014)发现了政府债务对私人企业融资具有“挤出效应”,而这一效应来源于投资者的资产优化与调整行为。Graham等(2015)进一步发现,政府借款行为可以解释美国企业在过去一个世纪中不断上升的杠杆率。与西方国家不同,中国政府债务的主体是地方政府债务。Liang等(2017)发现地方政府债务“挤出了”民营企业的融资。Huang等(2020)基于工业企业数据库考察了地方政府债务对工业企业投资的“挤出”效应。论文实证结果显示,地方政府的债务率显著地降低了民营制造业企业的投资率,而对国有企业没有显著影响。
与此同时,针对隐性债务与企业研发行为的研究依然十分缺乏。Croce等(2019)是较早讨论政府债务与企业创新关系的研究,他们发现:过高的政府债务会提高那些更依赖于研发的公司(high-R&D firms)的风险溢价,这增加了经济中不确定因素,进而导致公司创新速度的放缓。④熊虎和沈坤荣(2019)基于省级层面的地方政府债务余额数据的研究发现:地方政府过度负债显著地挤出了地区整体和企业个体的技术创新产出,一个可能的作用机制是地方政府债务降低了企业的信贷可得性。综合已有研究和理论分析,我们可以得到假设一:地方政府债务会对企业研发行为和研发产出产生“挤出”效应。
除了试图识别出地方隐性债务水平与企业研发活动之间的因果关系,本文还希望在已有文献的基础上,分析这一关系产生的内在机制。经济学家对中国企业研发活动的影响因素进行了较为深入的研究。一些研究主要关注公司自身特征对研发行为的影响,如国际投资(毛其淋和许家云,2014)、融资约束(鞠晓生,2013)、民营化(Fang等,2017)等。然而与一般的投资活动相比,企业的创新活动具有风险大、产出不可预测等特点。因此,企业的研发决策和产出往往受制于外部宏观环境,包括经济不确定性(顾夏铭等,2018)、商业周期(Aghion等,2012)和金融体系(钟腾和汪昌云,2017)等。
在外部因素中,政府的财税制度和财税政策,无论是否针对创新活动,都可能对微观企业的研发行为和产出产生影响。已有研究发现:过高的公司税会显著抑制企业的创新行为(Mukherjee等,2017;李林木和汪冲,2017),或导致创新行为的“跨区域”转移(Akcigit等,2018)。除了一般性的税收政策,各级政府越来越多地采取主动措施“激励”企业从事研发活动,其中既包括针对创新行为的研发补助、税收优惠,也包括更广泛意义上的“产业政策”。大量文献已经证实了与研发相关的政府补贴和产业政策可以有效地刺激企业的研发活动,增加研发产出(毛其淋和许家云,2015;黎文靖和郑曼妮,2016),并且针对研发创新的补贴具有更加显著的“激励效果”(郭玥,2018)。而这些补贴中的相当比例来自于地方政府,因为研发所引起的“技术溢出”最直接的受益者就是当地经济。
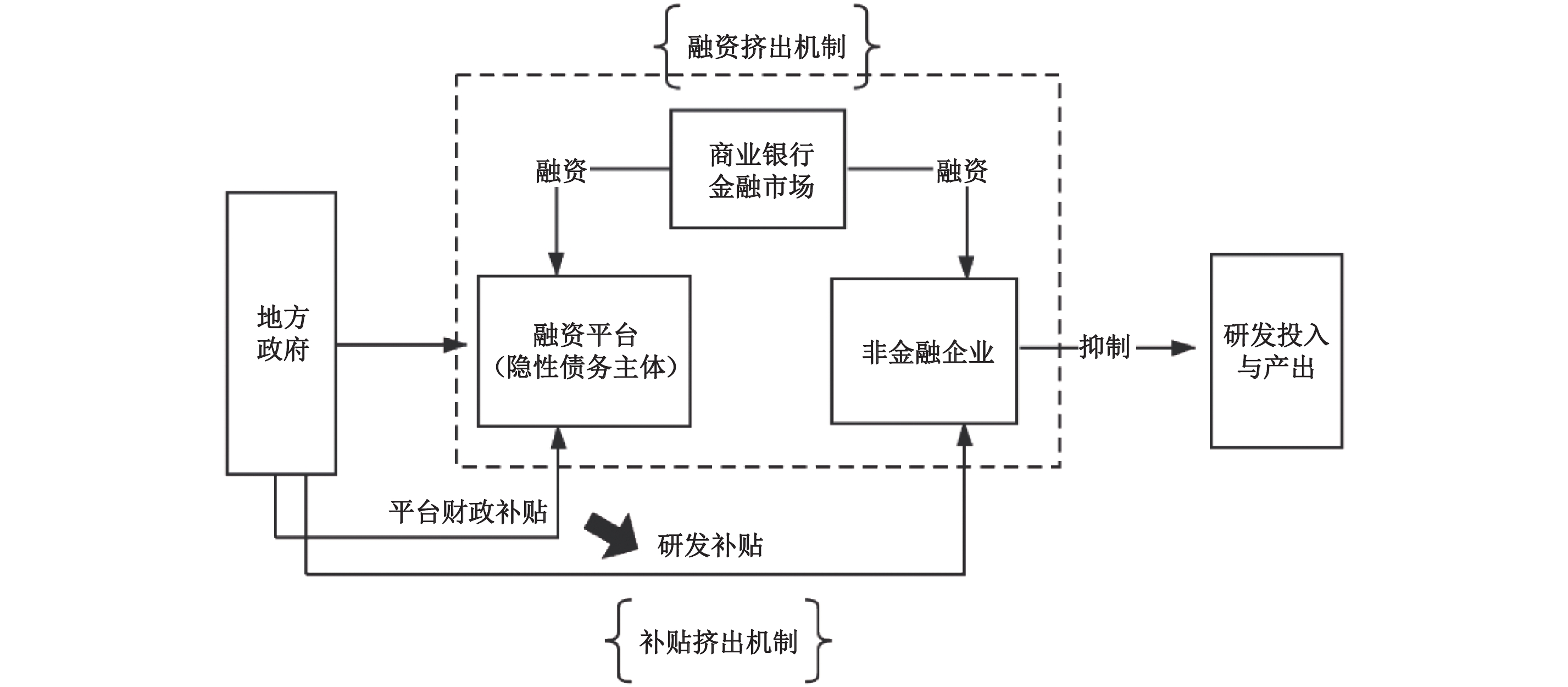
同时,为了支持融资平台发行“城投债”和其他债权融资工具,地方政府往往会给予其大量的财政补贴和增资,以帮助融资平台满足“发改委”规定的债券发行准入门槛。⑤张路(2020)发现,在“城投债”发行前后,地方政府给予融资平台的财政补贴数量比一般年份高21%。此外,在隐性债务存续的过程中,地方政府仍然需要保持足够的财政资源以应对可能的偿债需求。在地方财政本来已经处于“紧平衡”的状态下,过高的地方负债水平会显著压缩本来可用于发放研发补贴的财政资源,进而导致当地企业研发活动和研发产出的下降(见图1)。综合以上分析,我们可以得到本文的研究假设二(“补贴挤出机制”):地方政府隐性债务通过降低政府补贴数量抑制企业研发产出。
|
| 图 1 隐性债务影响企业创新的潜在机制 |
由于企业研发活动在很大程度上依赖外部获得的金融资源,企业的外部融资可得性对其研发行为和产出具有重要的影响,这在宏观上又可以体现为金融发展对企业研发的作用。遵循这一思路,Hsu等(2014)基于上市公司的跨国数据,研究了金融发展对制造业企业创新行为的影响。他们发现,金融发展尤其是股权市场的发展,可以有效地促进那些具有较高外部融资依赖度的行业中企业的专利申请数量。贾俊生等(2017)针对中国制造业上市公司的实证研究发现:不同于美国,信贷市场发展对中国企业创新具有显著的促进作用,而资本市场融资功能的不完善限制了其作用发挥。他们认为主要是中国资本市场发展不够完善,企业的创新行为仍然主要依靠银行信贷的支持。
当具有政府隐性担保的融资平台占用当地大量的信贷资源时,商业银行会减少对当地制造业企业的信贷供给(Liang等,2017)。更重要的是,中国的银行信贷市场具有明显的“区域分割”特征(Huang等 2020),这会造成即使企业愿意支付更高的利息,也很难从其他地区的金融机构获得所需资金。在这种情况下,那些预算约束较为严重的企业可能被迫缩减与研发有关的投入,而将资金用于日常经营上。这就解释了地方政府隐性债务是如何通过企业融资影响创新活动的。⑥此外,由于隐性债务以长期债务为主,这一抑制效应更有可能体现在对企业“长期负债”的影响上(见图1)。由此,我们可以得到假设三(“融资挤出机制”):地方政府隐性债务通过挤出企业融资,尤其是长期负债,对企业研发产生抑制作用。
三、计量模型
为了研究地方隐性债务水平对企业研发创新活动的影响,本文构建了如下的固定效应模型作为基准回归模型:
| $INNO{V_{i,c,t}}\; = \;\alpha \;{\rm{ + }}\;{\beta _1} \times LG{D_{c,t(t - 1)}}\; + \;\sum\nolimits_j^{} {{\vartheta _j} \times XF_{i,t(t - 1)}^j} {\rm{ + }}\sum\nolimits_k^{} {{\delta _k} \times XC_{c,t(t{\rm{ - }}1)}^k} \; + \;{\gamma _c}\; + \;{\eta _t}\; + \;{\varepsilon _{i,c,t}}$ | (1) |
其中,被解释变量
除了识别隐性债务与企业研发之间的因果关系,本文还试图分析这一关系背后潜在的作用渠道,为此我们构建如下的计量方程。在方程(2)和方程(3)中,我们分别考察地方隐性债务水平对企业接受政府补贴和外部融资的影响,进而对假设一和假设二进行实证检验。
| $Subsid{y_{i,c,t}}\; = \;\alpha \;{\rm{ + }}\;{\beta _2} \times LG{D_{c,t}}\; + \;\sum\nolimits_j^{} {{\vartheta _j} \times XF_i^j} {\rm{ + }}\sum\nolimits_k^{} {{\delta _k} \times XC_{c,t}^k} \; + \; FE \; + \;{\varepsilon _{i,c,t}}$ | (2) |
| $Loa{n_{i,c,t}}\; = \;\alpha \;{\rm{ + }}\;{\beta _3} \times LG{D_{c,t}}\; + \;\sum\nolimits_j^{} {{\vartheta _j} \times XF_i^j} {\rm{ + }}\sum\nolimits_k^{} {{\delta _k} \times XC_{c,t}^k} \; + \; FE \; + \;{\varepsilon _{i,c,t}}$ | (3) |
其中,subsidy代表企业接受的政府财政补贴,Loan代表企业的外部融资;地方隐性债务水平(
四、样本与变量
(一)数据来源和样本处理。本文的企业数据来自于国泰安(CSMAR)数据库。作者选取2008—2017年中国沪深A股、中小板、创业板上市公司作为企业样本,并剔除了其中的金融类公司、ST公司,最终样本由3138家上市公司的9643个观测值构成。
本文采用的地方政府隐性债务数据来自融资平台财务信息。目前,学者在研究地方隐性债务问题时面临的一个问题是缺乏全面而准确的数据。迄今为止,我们唯一能够获得的官方统计数据是国家审计署在2011年和2013年发布的两次统计公报,⑦其中统计了各省的隐性债务数量。研究者在实践中往往采用“城投债”发行额作为隐性债务的近似(Liang等,2017)。然而,债券只占融资平台债务很小的比例,这一处理方法可能导致严重的测量误差问题(Huang等,2020)。为此,我们手工搜集了1140家发行过“城投债”的地方政府融资平台的财务信息,其中包括各种类型的负债信息,以此为基础我们测算出全国276个地级行政单位的隐性债务水平。地级市层面的宏观经济数据和地方政府财政数据主要来自历年的《中国城市统计年鉴》。
(二)变量选择。
1. 研发产出。本文采用公司当年的专利申请数(Patent)衡量公司的研发产出,并进一步区分了发明专利(Invention)和实用新型专利(Utility)申请数量,以反映不同专利申请种类在创新性方面的差异。所有专利申请数都经过对数化处理。
2. 研发投入。参考已有文献,本文分别采用研发规模和研发密度两个指标度量企业的研发投入,前者定义为企业内部研发费用的对数值,后者定义为企业内部研发费用与营业收入之比,两个指标的数值越大,意味着企业的研发投入水平越高。
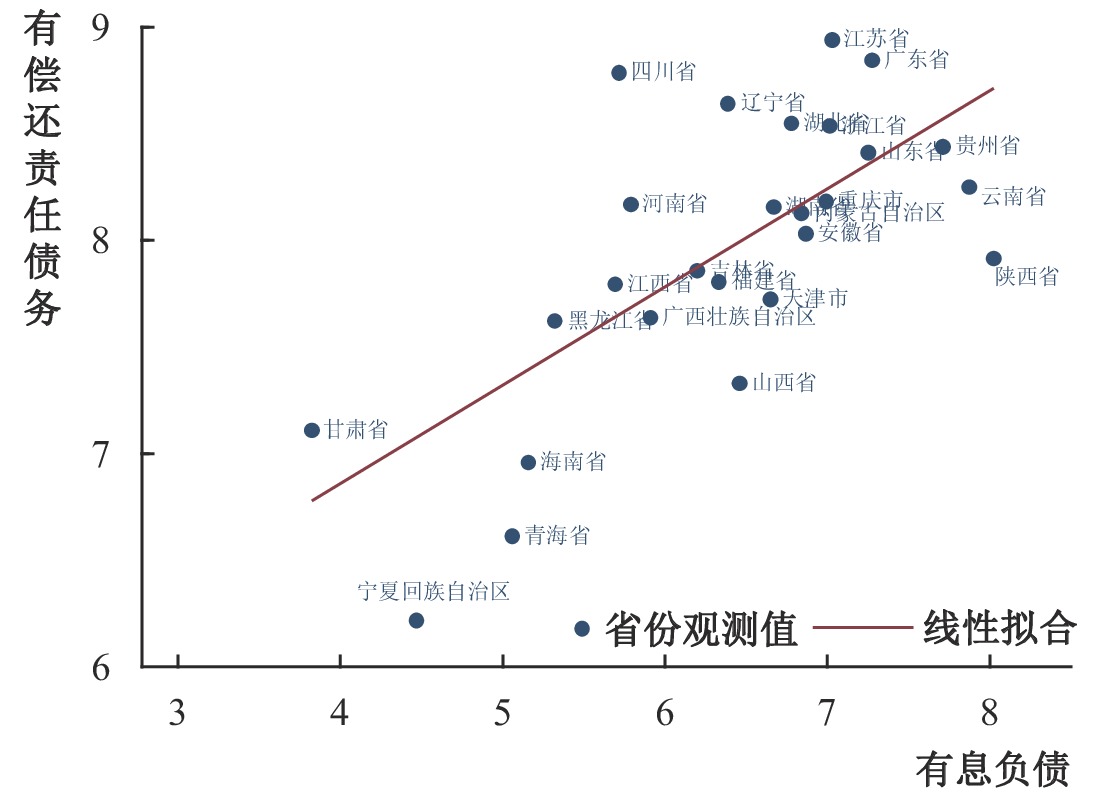
3. 隐性债务水平。参考Liang等(2017)、Huang等(2020)等研究,本文用融资平台存量债务与地方GDP之比来衡量地方隐性债务水平(LGD)。具体而言,我们通过手工搜集的方式,获得曾经发行过“城投债”⑧的1140家融资平台的财务信息,⑨其中包括长期借款、短期借款、一年内到期的非流动性负债、应付债券等有息负债项目。我们加总这些有息负债项目后得到融资平台的存量(刚性)债务。最后,对同一地级市的不同融资平台的存量债务进行加总,获得地方融资平台债务总量,作为地方隐性债务分布的一个近似。为了检验这一方法的合理性,图2展示了采用上述过程构造的省级隐性债务总额和2013年国家审计署公布的地方政府负有偿还义务的债务总额的相关情况。二者的相关性接近0.6,整体而言,我们构造的隐性债务指标是(审计署口径下)地方政府债务分布情况的一个良好近似。此外,我们还在工作论文附录中的图A1中报告了2014年地方隐性债务水平在全国地级市层面的分布情况,可以发现江苏省、浙江省、贵州省以及部分东北地区城市的政府隐性债务水平较高。
|
| 图 2 省级隐性债务与地方政府有偿还责任债务比较 注:省级隐性债务数据是基于该省地方政府融资平台资产负债表中的有息负债信息计算的;(省级)地方政府有偿还责任债务数据来自国家审计署2013年公布的审计公报。以上债务数据均经过自然对数处理。 |
4. 政府补贴与外部融资。本文第二部分中提出了地方隐性债务影响企业研发活动的两个潜在渠道:财政补贴和外部融资。CSMAR数据库提供了公司财务报告附注披露的补贴金额和补贴项目明细,由此我们能够计算出上市公司所接受的政府财政补助总额(subsidy)。然而,一些文献(郭玥,2018)指出,只有针对研发活动的政府补助才能激励企业的研发创新投入。因此,我们进一步通过“关键词搜索”的方式,筛选出那些可能属于研发补助的项目,并通过加总得到企业每一年获得的研发补助总额(RDsubsidy)。其次,采用企业资产负债表中的长期借款和短期借款衡量企业的外部融资。
5. 控制变量。在估计模型(1)—模型(3)时,我们详细控制了企业特征变量和城市宏观变量,包括企业资产规模(size)、托宾Q(TobinQ)、无形资产比率、现金流比率、杠杆率、资产收益率(ROA)、城市国内生产总值对数(GDP)、金融发展水平(FinDev)、固定资产投资和政府预算内财政缺口。其中,企业规模(Size)采用公司年末总资产的自然对数;托宾Q(TobinQ)采用股权市值和净债务市值之和与总资产的比率,代表企业投资和成长机会;无形资产比率定义为无形资产与总资产之比;现金流比率(Cash)定义为企业经营和投资活动现金流与总资产之比,衡量企业的流动性状况;杠杆率(Leverage)定义为企业总负债比总资产,衡量企业财务风险;资产收益率(ROA)定义为净利润与总资产之比,衡量企业的盈利能力。城市宏观变量方面,城市人均GDP取自然对数;金融发展水平定义为城市贷款余额与城市GDP之比;固定资产投资水平(FixInv)定义为城市固定资产投资总额与城市GDP之比;政府预算内财政缺口定义为:(预算内财政收入−预算内财政支出)/城市GDP,用来测度城市预算内财政压力;最后,采用“每万人拥有的在校大学生数量”作为该城市人力资本存量的代理变量(HC)。所有变量均经过1%的winsorize缩尾处理。
(三)特征事实和描述性统计。表1分别报告了企业变量和城市变量的主要描述性统计结果,我们对所有连续性水平变量均经过了对数化处理和1%的缩尾处理,以防止离群值对估计结果的影响。
| 观测值 | 均值 | 标准差 | 最小值 | 中位数 | 最大值 | |
| 企业变量 | ||||||
| patents | 11 449 | 1.810 | 1.630 | 0 | 1.790 | 6.050 |
| invents | 11 449 | 1.250 | 1.350 | 0 | 1.100 | 5.200 |
| utility | 11 449 | 1.160 | 1.400 | 0 | 0.690 | 5.240 |
| RDexp | 8 020 | 8.460 | 1.400 | 4.410 | 8.440 | 12.32 |
| size | 11 438 | 12.83 | 1.310 | 10.47 | 12.61 | 17.93 |
| TobinQ | 11 433 | 2.210 | 1.940 | 0.150 | 1.650 | 11.24 |
| Intangible | 11 438 | 0.0500 | 0.0600 | 0 | 0.0400 | 0.380 |
| cash | 11 438 | −0.0200 | 0.100 | −0.350 | −0.0100 | 0.250 |
| leverage | 11 438 | 0.440 | 0.210 | 0.0500 | 0.440 | 0.940 |
| ROA | 11 438 | 0.0400 | 0.0500 | −0.160 | 0.0300 | 0.200 |
| 城市变量 | ||||||
| LGD | 2 024 | 0.087 | 0.070 | 0 | 0.0500 | 0.340 |
| GDP | 2 024 | 11.76 | 0.610 | 9.900 | 11.79 | 13.10 |
| FinDev | 2 013 | 0.840 | 0.450 | 0.280 | 0.690 | 2.450 |
| fixInv | 2 003 | 0.750 | 0.240 | 0.210 | 0.730 | 1.400 |
| budget gap | 1 767 | −0.030 | 0.030 | −0.130 | −0.0200 | 0.0100 |
| HC | 1 970 | 5.080 | 4.190 | 0.180 | 3.860 | 18.41 |
| 数据来源:CSMAR数据库、作者手工搜集以及《城市统计年鉴》。 | ||||||
五、实证结果分析
(一)基准回归。表2报告了基准回归模型(1)的估计结果。我们首先关注隐性债务水平⑩对企业专利申请数量(研发产出)的影响:列(1)中变量LGDt−1的系数
接下来我们进一步考察隐性债务与企业研发投入的关系。表2列(4)中报告了隐性债务对企业研发投入的影响。在控制企业总规模的条件下,变量LGDt的估计系数在5%的水平上显著为负,这表明地方隐性债务会抑制当地企业的研发投入规模。在控制变量方面,企业上一期的资产规模(Size)和盈利状况(ROA)对大多数研发变量具有正向影响,其他控制变量的符号大多与已有文献保持一致。最后,表2中所有回归结果的R2均在0.8以上,这说明基准计量模型对企业的研发活动具有相当的解释力。
| (1)专利申请(patents) | (2)发明申请(invents) | (3)实用新型申请(utility) | (4)研发投入规模(RDexp) | |
|
$LG{D_{t{\rm{ - }}1}}$
|
−0.768**(0.389) | −0.371(0.378) | −0.366(0.307) | |
|
$LG{D_t}$
|
−0.802**(0.401) | |||
| Size | 0.128***(0.0478) | 0.162***(0.0459) | 0.0999**(0.0418) | 0.486***(0.0722) |
| TobinQ | −0.0337***(0.00973) | −0.0182**(0.00703) | −0.0278***(0.00802) | 0.0514***(0.0147) |
| 无形资产 | −0.103(0.424) | −0.00937(0.342) | −0.443(0.394) | −0.309(0.451) |
| 现金比 | −0.118(0.101) | −0.0761(0.0904) | 0.0167(0.0878) | −0.212**(0.0828) |
| 杠杆率 | 0.0734(0.133) | 0.138(0.118) | 0.0749(0.109) | 0.193(0.175) |
| ROA | 1.500***(0.280) | 1.086***(0.229) | 1.125***(0.245) | 1.413***(0.326) |
| GDP | 0.0360(0.119) | 0.143(0.127) | 0.0224(0.108) | 0.210**(0.0958) |
| FinDev | −0.0801(0.0523) | −0.0568(0.0494) | −0.0886*(0.0450) | 0.157*(0.0881) |
| fixInv | 0.296*(0.164) | 0.263(0.167) | 0.278*(0.146) | −0.0143(0.133) |
| budget_gap | 0.377(1.149) | 0.114(1.181) | −0.248(1.084) | −0.139(0.871) |
| HC | 0.00346(0.00928) | −0.00343(0.00955) | −0.00192(0.00959) | −0.0140(0.00962) |
| 常数项 | −0.268(1.579) | −2.606(1.681) | −0.363(1.393) | −0.495(1.464) |
| 观测值 | 11 449 | 11 449 | 11 449 | 6 249 |
| R2 | 0.820 | 0.808 | 0.814 | 0.916 |
| 企业固定效应 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 |
| 注:所有回归采用的是城市层面上的聚类稳健型标准差(city-cluster robust standard error);***、**、*分别代表1%、5%和10%的显著性水平。 | ||||
在表2提供的基准回归的基础上,我们还需要进一步讨论解释变量可能存在的“内生性”问题。首先,由于我们在基准回归(1)中采用的是固定效应面板模型,所以那些不随时间变化的不可观察变量的影响已经被很好地控制了。此外,方程(1)中的解释变量滞后一期有效地排除了“逆向因果”问题存在的可能。迄今为止,最可能的内生性来源是某些不可观测的政策冲击或短期经济因素,会同时影响企业的研发活动和地方隐性债务水平。为了解决这一问题,我们参考Liang等(2017),选取解释变量的二阶滞后项(LGDt−2)作为解释变量的工具变量,并用两阶段最小二乘(2SLS)方法估计方程(1),以检验基准回归结果的可信性。⑪表3报告了相应的估计结果。我们发现,对于企业专利申请总数(patents)和研发投入规模(RDexp),解释变量隐性负债水平(LGD)的估计系数维持了原有的符号和显著性水平,并且估计系数略有增加(列(1)和列(4))。此外,在两阶段最小二乘(2SLS)方法估计下,隐性水平负债对实用新型专利申请数(utility)在10%的水平上具有显著的负向影响(列(3))。最后,表3列(5)还报告了第一阶段的估计结果,可以发现内生解释变量LGDt−1与作为其工具变量的二阶滞后项LGDt−2相关性明显,模型(5)的F统计量(185.8)显著大于10,从而基本排除了“弱工具变量”的可能。这一结果大体保证了工具变量选取的合理性。⑫
| (1)专利申请(patents) | (2)发明申请(invents) | (3)实用新型申请(utility) | (4)研发投入规模(RDexp) | (5)LGD | |
| 第二阶段 | 第一阶段 | ||||
|
$LG{D_{t{\rm{ - }}1}}$
|
−1.106**(0.545) | −0.677(0.613) | −1.272*(0.667) | ||
|
$LG{D_t}$
|
−1.130**(0.570) | ||||
|
$LG{D_{ - 1}}$
|
0.653***(0.0167) | ||||
| 观测值 | 9 443 | 9 443 | 9 443 | 6 059 | 9 443 |
| R2 | 0.010 | 0.011 | 0.009 | 0.015 | 0.945 |
| F统计量 | 185.8 | ||||
| 公司特征 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 城市特征 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 企业固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 注:所有回归采用的是城市层面上的聚类稳健型标准差(city-cluster robust standard error);***、**、*分别代表1%、5%和10%的显著性水平。 | |||||
我们进一步将地方隐性债务分解为长期隐性债务(
| (1)专利申请(patents) | (2)发明申请(invents) | (3)实用新型申请(utility) | (4)研发投入规模(RDexp) | |
|
$LGD_{t{\rm{ - }}1}^{Long}$
|
−0.833**(0.412) | −0.593*(0.313) | −0.652*(0.352) | |
|
$LGD_{{t - 1}}^{Short}$
|
−0.693(0.985) | 0.363(0.849) | 0.752(0.991) | |
|
$LGD_t^{Long}$
|
−0.367(0.406) | |||
|
$LGD_{t}^{Short}$
|
−1.435(1.182) | |||
| 观测值 | 11 449 | 11 449 | 11 449 | 7 093 |
| R2 | 0.821 | 0.808 | 0.829 | 0.914 |
| 公司特征 | 控制 | 控制 | 控制 | 控制 |
| 城市特征 | 控制 | 控制 | 控制 | 控制 |
| 企业固定效应 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 |
| 注:所有回归采用的是城市层面上的聚类稳健型标准差(city-clusterrobust standard error);***、**、*分别代表1%、5%和10%的显著性水平。 | ||||
(二)影响机制分析。表2—表4的估计结果基本证实了理论分析部分的假设一,即地方政府债务会在不同程度上抑制企业研发行为和研发产出。在此基础上,我们还希望进一步对发生这一“挤出效应”的机制进行探索。第二部分理论分析分别从政府补贴和企业外部融资两个角度讨论了地方隐性债务影响企业研发的内生机制,在这一节中,我们对这两个假设进行实证检验。
首先我们对方程(2)进行估计,被解释变量是上市公司接受的财政补贴总额和针对研发活动的补贴数额,解释变量是当期地方政府隐性债务水平。从表5的估计结果可以发现,隐性债务水平对财政补贴总额的影响(列(1))和对研发补贴的影响(列(2))均显著为负:地方隐性债务水平上升10%将导致当期企业获得的研发补助下降20.1%,这说明隐性债务确实挤出了制造业企业获得的财政补贴。考虑到现有文献已经提供了关于“政府研发补贴激励企业创新”的证据(郭玥,2018),这一实证结果证实了本文第二部分中提出的假设二,即地方政府隐性债务通过降低政府补贴数量抑制企业研发产出。
接下来,我们对方程(3)进行估计,并分别考虑存量债务、长期隐性债务和短期隐性债务对企业长期借款和短期借款的影响,回归结果报告在表5中。可以观察到,存量债务水平对企业的长期借款和短期借款都具有负向影响,但在统计上均不显著(列(3)、列(5));而长期隐性债务对企业的长期借款具有显著的“挤出”效应:长期隐性债务水平上升10%将导致同期企业长期借款降低33%(列(4))。这一实证结果支持了理论部分提出的假设三,同时,也为表4中发现的长期隐性债务与企业研发产出的紧密联系提供了机制上的解释。
| (1) | (2) | (3) | (4) | (5) | (6) | |
| 财政补贴 | 研发补贴 | 长期借款 | 短期借款 | |||
|
$LG{D_{}}$
|
−0.720*(0.382) | −2.010**(0.925) | −1.899(1.317) | −1.005(1.008) | ||
|
$LGD_{}^{Long}$
|
−3.298**(1.626) | −0.991(1.191) | ||||
|
$LGD_{}^{Short}$
|
2.711(4.259) | 0.123(2.980) | ||||
| 观测值 | 10 436 | 10 449 | 11 053 | 11 053 | 11 053 | 11 053 |
| R2 | 0.771 | 0.611 | 0.763 | 0.763 | 0.771 | 0.771 |
| 公司特征 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 城市特征 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 企业固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 注:所有回归采用的是城市层面上的聚类稳健型标准差(city-cluster robust standard error);***、**、*分别代表1%、5%和10%的显著性水平。 | ||||||
六、异质性分析与稳健性分析
在本节中,我们对第五部分中的主要实证结果进行一系列稳健性分析。⑮
首先,如果假设三(“融资挤出机制”)确实成立,那些融资约束程度较高企业的研发行为应当会被明显地“挤出”,而融资约束较低的企业所受影响并不明显。为此,我们参考Almeida等(2004),采用企业成立时间作为衡量融资约束的代理变量。⑯具体而言,我们在每一个观察年中,按照企业年龄的中位数,将样本中非金融上市公司划分为:低预算约束(成立时间长)和高预算约束(成立时间短)两个子样本,并在每一个样本上估计方程(3),并将结果报告在表6中。可以发现,对于低预算约束企业样本,尽管隐性债务水平的估计系数符号均为负,但都不显著(列(1)—列(4));而在高预算约束样本内,债务水平对专利申请总数、发明申请数和研发费用均有显著负向影响,这与假设三的理论预期相一致,即地方政府隐性债务通过挤出企业融资而对企业研发产生抑制作用。对于那些面临融资约束更严重的企业,挤出效应更明显。
| (1)patents | (2)invents | (3)utility | (4) | (5)patents | (6)invents | (7)utility | (8)RDexp | |
| 低预算约束 | 高预算约束 | |||||||
|
$LG{D_{t - 1}}$
|
−0.831 | −0.263 | −0.373 | −1.263** | −1.077** | −0.846 | ||
| (0.529) | (0.591) | (0.482) | (0.610) | (0.527) | (0.544) | |||
|
$LG{D_t}$
|
0.00628 | −1.076*** | ||||||
| (0.578) | (0.415) | |||||||
| 观测值 | 6 421 | 6 421 | 6 421 | 3 146 | 4 985 | 4 985 | 4 985 | 3 547 |
| R2 | 0.852 | 0.842 | 0.849 | 0.910 | 0.813 | 0.800 | 0.824 | 0.930 |
| 企业特征 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 企业固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 注:所有回归采用的是城市层面上的聚类稳健型标准差(city-cluster robust standard error);***、**、*分别代表1%、5%和10%的显著性水平。 | ||||||||
接下来,我们试图检验所有制对本文所研究的债务“挤出”机制的影响。将样本企业按照所有制划分为国有企业和非国有企业,并分别对基准模型进行估计,结果报告在表7中。可以发现,地方政府债务对国有上市企业主要体现为对研发产出的“挤出”上(列(1)—列(3)),而对非国有企业体现为对研发投入(费用)的“挤出”(列(8))。作者认为,第一种结果反映了国有企业在专利申请方面可能存在某些“策略性行为”,即当政府的财政(研发)补贴减少时,企业相应减少专利的申请(黎文靖和郑曼妮,2016)。另一种解释是,地方政府债务水平会降低国有企业的研发效率。与其相对应的是,非国有企业更加明显地在信贷市场上受到地方隐性债务的“挤出”。
| (1)patents | (2)invents | (3)utility | (4)RDexp | (5)patents | (6)invents | (7)utility | (8)RDexp | |
| 国有企业 | 非国有企业 | |||||||
| LGDt−1 | −1.519** (0.583) |
−1.061* (0.615) |
−0.932* (0.503) |
−0.196
(0.499) |
0.255
(0.419) |
0.125
(0.394) |
||
| LGDt | −0.615
(0.612) |
−0.708** (0.344) |
||||||
| 观测值 | 5 129 | 5 129 | 5 129 | 2 417 | 6 309 | 6 309 | 6 309 | 4 891 |
| R2 | 0.862 | 0.851 | 0.846 | 0.916 | 0.780 | 0.768 | 0.787 | 0.910 |
| 企业特征 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 企业固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 年份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 注:所有回归采用的是城市层面上的聚类稳健型标准差(city-cluster robust standard error);***、**、*分别代表1%、5%和10%的显著性水平。 | ||||||||
基准回归结果涵盖了来自276个城市的上市公司。然而,不同城市资本市场发展水平存在很大差异,北京、上海和深圳三大一线城市的上市公司占全部上市公司总数的24%,流通市值总额的47%,⑰而三城平均隐性债务水平为7.4%,低于全国平均水平。在这种情况下,样本中包括以上三个一线城市,可能导致我们低估地方隐性债务对企业研发行为的抑制作用。有鉴于此,将样本划分为“一线城市(北京、上海、深圳)”和“其他城市”两个子样本,并分别对基准模型进行估计,结果报告在表8中。可以发现,地方隐性债务对位于一线城市的上市公司的研发产出和研发投入的影响均不显著(列(1)–列(4)),并且对于企业实用新型专利申请数量的效应为正。与此形成对照的是,对于其他城市,地方隐性债务的抑制作用在统计上表现得十分显著(列(5)–列(8)),尤其是企业专利申请方面。表8的结果显示,如果我们将关注的重点聚焦于地方政府隐性债务风险集中的三四线城市,隐性债务对企业研发产出和投入的“挤出”效应就会变得愈加明显。
| (1)patents | (2)invents | (3)utility | (4)RDexp | (5)patents | (6)invents | (7)utility | (8)RDexp | |
| 一线城市 | 其他城市 | |||||||
|
$LG{D_{t - 1}}$
|
−1.226 | −1.835 | 0.176 | −1.268** | −0.846*** | −0.793** | ||
| (2.768) | (2.624) | (1.151) | (0.539) | (0.322) | (0.336) | |||
|
$LG{D_t}$
|
−1.532 | −0.530* | ||||||
| (0.637) | (0.316) | |||||||
| 观测值 | 2 918 | 2 918 | 2 918 | 1 808 | 8 524 | 8 524 | 8 524 | 5 277 |
| R2 | 0.851 | 0.849 | 0.840 | 0.920 | 0.825 | 0.805 | 0.826 | 0.915 |
| 企业特征 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 企业固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 注:所有回归采用的是城市层面上的聚类稳健型标准差(city-cluster robuststandard error);***、**、*分别代表1%、5%和10%的显著性水平。 | ||||||||
七、结 论
在中国经济步入“新常态”之后,中国政府充分认识到企业研发创新活动对经济发展的重要意义。党的十九大报告明确了“创新是引领发展的第一动力,是建设现代化经济体系的战略支撑”的判断。然而,中国企业的研发增速在2010年之后出现了明显放缓趋势,同期中国全要素生产率(TFP)增速也出现了明显的降低。那么,是否存在某些外生的经济因素导致了企业研发活动的“被动换挡”呢?我们的研究发现,2008年后不断膨胀的地方政府隐性债务可在相当程度上解释企业研发活动的变化趋势和地区差异。基于2008年至2017年非金融业上市公司数据和地方政府隐性债务数据,本文考察了地方政府隐性债务水平对微观企业的研发投入和专利申请的影响。实证结果显示,城市隐性债务水平对当地企业的专利申请具有显著的“抑制作用”,这表明隐性债务水平同时降低了企业的创新效率和研发投入。接下来,我们对上述影响所依赖的内在传导机制进行了分析,发现政府研发补贴和长期外部借款的减少是隐性债务挤出企业研发活动的潜在机制。最后,本文还进行了异质性分析和稳健性检验。
本文的发现具有较为重要的理论和现实意义。首先,无序扩张的地方政府隐性债务可能会严重扭曲地方的金融资源配置效率,“挤出”高生产率企业的融资需求和研发活动,“拖累”全要素生产率(TFP)的增长,并最终削弱中国经济的长期增长动能。其次,隐性债务挤出研发补贴反映出中国地方政府的决策偏好具有“短期化”倾向:更偏好用隐性债务支持能够短期见效的基础设施建设,而对长期见效的企业研发重视不足。为此,本文提出以下政策建议:(1)尽快建立起具有中国特色的市政债券市场,并使其风险与收益水平相适应,避免地方政府隐性债务在企业债和银行信贷市场对企业研发资金的“挤出”;(2)逐步剥离融资平台的债务融资属性,尝试将其改造为专注长期战略性投资的机构(借鉴新加坡淡马锡公司),助力地方经济的长期发展;⑱(3)积极建立地方性的企业研发基金(产业引导基金),支持企业的长期基础性研发活动。
① 下文中简称为隐性债务。
② 陈柳:各省地方政府隐性债务规模知多少?http://www.yangtze-idei.cn/index.php?m=content&c=index&a=show&catid=14&id=491。
③ 数据来源:《中国科技统计年鉴(2016)》。
④ 本文与Croce等(2018)的不同之处在于,我们关注的是地方(隐性)债务而非政府总债务,这使得我们能够充分利用地区间债务水平的横截面差异(cross-sectional variation),而不必依赖于较长的政府债务时间序列数据,并且避免了跨国研究中可能存在的、由不同国家制度差异所带来的内生性问题。
⑤ 发改委财金[2008]7号文规定,企业债发债企业必须满足:最近三年平均可分配利润(净利润)足以支付企业债券一年的利息。然而在现实中,融资平台承担大量低利润甚至无偿的公共事业服务职能,自身盈利能力较差,但其债务发行规模却很大。在本文的融资平台样本中,融资平台第一次发债前三年的营业利润 中位数为5 672万元,而债券利息的中位数为6 983万元,约有44.43%的融资平台的营业利润无法支付一年的债券利息,从而无法满足发改委提出的债券发行门槛条件。在这种情况下,来自地方政府各种名义的财政补贴对融资平台能够顺利在资本市场融资起到至关重要的作用。
⑥ Amore等(2013) 发现美国放松对商业银行异地经营的限制可以有效增加企业专利申请的数量和质量。
⑦ 分别是国家审计署2011年第35号审计公告和2013年第32号审计公告。
⑧ 这里所指的“城投债”包括地方政府融资平台在银行间市场和交易所市场上发行的公司债、企业债、中期票据、短期融资券、定向债务工具等。
⑨ 为了保证融资平台财务信息的观测期与上市公司样本观测期基本重合,我们在构造债务变量的过程中,排除了首次债券发行时间在2016年之后的融资平台公司。以避免过多新融资平台进入样本导致的地方债务水平的异常波动。
⑩ 在
⑪ 同理,LGDt−1作为LGDt的工具变量(第4列)。这一工具变量选取方式的逻辑在于:一方面不同时期的地方隐性债务水平具有很强的相关性。另一方面,如果内生性问题确实源于某些我们无法观测的短期政策冲击,那么这一冲击不太可能与更早时间(如t−2期)上的隐性债务水平相关,从而使得工具变量和残差项不相关,保证了工具变量的合理性。
⑫ 我们还采用了Arellano-Bond方法进行了估计,系数符号和显著性水平与
⑬ 长期隐性债务=长期借款+应付债券。
⑭ 短期隐性债务=短期借款+应付票据+一年内到期的借款。
⑮ 完整的异质性分析结果请查阅本文的工作论文版本。
⑯ 其经济逻辑在于,那些成立时间较长的公司具有更加完整的信贷历史记录,拥有更多的可抵押资产,从而更有可能与金融机构建立起更加长期的信贷关系。这使得成立时间较长公司面临相对而言更低的融资约束。
⑰ 2017年数据。
⑱ 这方面,合肥国资对京东方的支持是一个很好的尝试。
| [1] | 顾夏铭, 陈勇民, 潘士远. 经济政策不确定性与创新——基于我国上市公司的实证分析[J]. 经济研究, 2018(2): 109–123. |
| [2] | 郭玥. 政府创新补助的信号传递机制与企业创新[J]. 中国工业经济, 2018(9): 98–116. |
| [3] | 贾俊生, 伦晓波, 林树. 金融发展、微观企业创新产出与经济增长——基于上市公司专利视角的实证分析[J]. 金融研究, 2017(1): 99–113. |
| [4] | 鞠晓生. 中国上市企业创新投资的融资来源与平滑机制[J]. 世界经济, 2013(4): 138–159. |
| [5] | 李林木, 汪冲. 税费负担、创新能力与企业升级——来自“新三板”挂牌公司的经验证据[J]. 经济研究, 2017(11): 119–134. |
| [6] | 黎文靖, 郑曼妮. 实质性创新还是策略性创新? ——宏观产业政策对微观企业创新的影响[J]. 经济研究, 2016(4): 60–73. |
| [7] | 毛捷, 黄春元. 地方债务、区域差异与经济增长——基于中国地级市数据的验证[J]. 金融研究, 2018(5): 1–19. |
| [8] | 毛其淋, 许家云. 中国企业对外直接投资是否促进了企业创新[J]. 世界经济, 2014(8): 98–125. |
| [9] | 毛其淋, 许家云. 政府补贴对企业新产品创新的影响——基于补贴强度“适度区间”的视角[J]. 中国工业经济, 2015(6): 94–107. |
| [10] | 毛锐, 刘楠楠, 刘蓉. 地方政府债务扩张与系统性金融风险的触发机制[J]. 中国工业经济, 2018(4): 19–38. |
| [11] | 熊虎, 沈坤荣. 地方政府债务对创新的挤出效应研究[J]. 经济科学, 2019(4): 5–17. |
| [12] | 张路. 地方债务扩张的政府策略——来自融资平台“城投债”发行的证据[J]. 中国工业经济, 2020(2): 44–62. |
| [13] | 钟腾, 汪昌云. 金融发展与企业创新产出——基于不同融资模式对比视角[J]. 金融研究, 2017(12): 127–142. |
| [14] | Aghion P, Askenazy P, Berman N, et al. Credit constraints and the cyclicality of R&D investment: Evidence from France[J]. Journal of the European Economic Association, 2012, 10(5): 1001–1024. DOI:10.1111/j.1542-4774.2012.01093.x |
| [15] | Akcigit U, Grigsby J, Nicholas T, et al. Taxation and Innovation in the 20th Century[R]. NBER Working Paper No.24982, 2018. |
| [16] | Almeida H, Campello M, Weisbach M S. The cash flow sensitivity of cash[J]. The Journal of Finance, 2004, 59(4): 1777–1804. DOI:10.1111/j.1540-6261.2004.00679.x |
| [17] | Bai C E, Hsieh C T, Song Z M. The long shadow of a fiscal expansion[R]. NBER Working Paper No.22801, 2016. |
| [18] | Boeing P, Mueller E, Sandner P. China’s R&D explosion: Analyzing productivity effects across ownership types and over time[J]. Research Policy, 2016, 45(1): 159–176. DOI:10.1016/j.respol.2015.07.008 |
| [19] | Chen Z, He Z G, Liu C. The financing of local government in China: Stimulus loan wanes and shadow banking waxes[J]. Journal of Financial Economics, 2020, 137(1): 42–71. DOI:10.1016/j.jfineco.2019.07.009 |
| [20] | Croce M M, Nguyen T T, Raymond S, et al. Government debt and the returns to innovation[J]. Journal of Financial Economics, 2019, 132(3): 205–225. DOI:10.1016/j.jfineco.2018.11.010 |
| [21] | Elmendorf D W, Mankiw N G. Government debt[J]. Handbook of Macroeconomics, 1999, 1: 1615–1669. |
| [22] | Fan J P H, Titman S, Twite G. An international comparison of capital structure and debt maturity choices[J]. Journal of Financial and Quantitative Analysis, 2012, 47(1): 23–56. DOI:10.1017/S0022109011000597 |
| [23] | Fang L H, Lerner J, Wu C P. Intellectual property rights protection ownership and innovation: Evidence from China[J]. The Review of Financial Studies, 2017, 30(7): 2446–2477. DOI:10.1093/rfs/hhx023 |
| [24] | Graham J R, Leary M T, Roberts M R. A century of capital structure: The leveraging of corporate America[J]. Journal of Financial Economics, 2015, 118(3): 658–683. DOI:10.1016/j.jfineco.2014.08.005 |
| [25] | Graham J R, Leary M T, Roberts M R. How does government borrowing affect corporate financing and investment? [R]. NBER Working Paper No.20581, 2014. |
| [26] | Greenwood R, Hanson S, Stein J C. A gap-filling theory of corporate debt maturity choice[J]. The Journal of Finance, 2010, 65(3): 993–1028. DOI:10.1111/j.1540-6261.2010.01559.x |
| [27] | Hsu P H, Tian X, Xu Y. Financial development and innovation: Cross-country evidence[J]. Journal of Financial Economics, 2014, 112(1): 116–135. DOI:10.1016/j.jfineco.2013.12.002 |
| [28] | Huang Y, Pagano M, Panizza U. Local crowding-out in China[J]. The Journal of Finance, 2020, 75(6): 2855–2898. DOI:10.1111/jofi.12966 |
| [29] | Liang Y S, Shi K Wang L S, et al. Local government debt and firm leverage: Evidence from China[J]. Asian Economic Policy Review, 2017, 12(2): 210–232. DOI:10.1111/aepr.12176 |
| [30] | Mukherjee A, Singh M, Žaldokas A. Do corporate taxes hinder innovation?[J]. Journal of Financial Economics, 2017, 124(1): 195–221. DOI:10.1016/j.jfineco.2017.01.004 |
| [31] | Reinhart C M, Rogoff K S. Growth in a time of debt[J]. American Economic Review, 2010, 100(2): 573–578. DOI:10.1257/aer.100.2.573 |


