一、引　言

中国经济的发展既包含了世界各国发展的共性，因而在较大程度上可以由现有理论加以说明，也呈现出许多与其他国家不同的发展特征，需要从新的视角进行探讨。分析改革开放以来40多年的产出、消费和投资数据^①可以发现：第一，与发达国家相比，中国的经济波动更为剧烈，其中产出和消费波动分别约为发达国家的1.6倍和2.5倍，且消费波动大于产出波动。这与现有文献普遍采用持久性收入假说而得到的理性消费行为相去甚远。第二，中国经济波动呈现出不断缩小的趋势，且消费波动比产出波动下降更快。1978—1999年产出波动的标准差为3.44%，2000—2018年降至2.39%，降幅达30.5%；相应时期的消费标准差则从4.0%降至2.53%，降幅高达36.8%。第三，2008年以来中国经济增长率持续下滑，尽管其间政府实施了以 “四万亿”支出政策为代表的刺激措施，经济增长出现了短暂恢复，但是未能从根本上阻止经济下滑趋势。

学术界将中国经济发展奇迹归结为改革开放以来的一系列制度变革，既然体制改革是过去40多年中国经济高速增长的主要动因，那么作为逻辑上的一个必然推论，它们一定也是引起中国经济增长时快时慢、形成若干发展周期的重要因素。与政府购买、货币和信息等各种随机冲击，以及金融与非金融摩擦所造成的偏离趋势不同，从计划经济向市场经济的转变、民营企业如雨后春笋般的发展以及中国加入世界贸易组织等构成了对趋势本身的冲击，改变并支撑着中国较高的经济增长率，使中国经济的周期波动与趋势波动相交织。

为了说明上述特征，本文构建了包含具有持久效应的趋势冲击和流动性约束的小国开放经济动态随机一般均衡模型。研究结果表明：第一，改革开放以来，一系列制度变革是造成中国经济波动大于发达国家的重要原因。在推动中国经济生产效率上一个新台阶的同时，渐进式改革也改变了经济增长趋势，形成了对趋势本身的冲击。第二，中国经济存在明显的随机趋势，产出尤其是消费的较大波动由趋势冲击和周期冲击共同所致。第三，趋势冲击和周期冲击不足以解释消费的较大波动，尤其难以解释消费波动大于产出波动的事实，但两者与流动性约束相结合较好地解释了这一特征。趋势冲击的引入通过持久性收入假说扩大了消费波动，流动性约束的引入则通过降低消费的跨期替代增加了消费波动。第四，随着市场经济体制的逐渐完善，对经济波动影响短暂的周期冲击和影响持久的趋势冲击都显示出逐渐衰减的趋势，从而中国经济波幅逐渐缩小。由于趋势冲击的影响下降更快，周期冲击逐渐成为中国经济波动的主要来源。

二、文献概述

Kydland和Prescott（1982）在新古典经济增长模型的基础上，假定外生的随机技术进步是经济波动的主要驱动因素，构建了标准的实际经济周期（RBC）模型。此后，动态随机一般均衡（DSGE）方法逐渐成为分析宏观经济波动的主要方法之一，学者纷纷在此基础上进行拓展，从不同视角来分析经济波动。拓展途径大致可分为两种：一是引入新的冲击，如货币冲击（Ireland，2004）、信息冲击 （Khan和Tsoukalas，2012）等；二是拓展模型本身，如引入名义价格和工资粘性（Cho和Cooley，1995）、工作搜寻（Andolfatto，1996）等内容。

国内学者也开始利用DSGE方法来研究我国的经济波动问题。有学者直接在标准RBC模型的基础上引入专有冲击，如陈师和赵磊（2009）将投资专有技术冲击引入RBC模型中，同时引入内生可变的设备资本利用率假设，放大投资专有技术冲击对经济波动的影响，结果显示引入投资专有技术冲击的RBC模型能够解释90%的产出波动。也有学者基于国情来完善模型，如李浩等（2007）考虑到1978年以来我国对外开放程度日益提高且政府对经济具有较强干预的事实，构建了包含政府购买冲击的小国开放经济模型，结果显示模型对产出、消费和投资波动的解释力都在80%以上。胡永刚和刘方（2007）则认为，我国的劳动存在较高的调整成本，使得就业与产出表现为不相关甚至负相关，通过劳动的跨期替代放大经济波动的机制受到限制，而且信贷制度不完善增大了居民的消费波动，将劳动调整成本和居民借贷约束纳入模型中可以较好地刻画中国产出、就业、消费和投资等的实际变化。概括来看，这些文献具有两个共同特征：第一，拓展模型均从全要素生产率之外引入外生冲击，而鲜有文章进一步分析全要素生产率变化对经济波动的影响。由此产生的疑问是，仅用AR（1）随机过程所反映的技术冲击能否全面刻画全要素生产率的变化？第二，各类外生冲击的引入均采用AR（1）随机过程，这意味着冲击不会改变模型经济的长期增长趋势。然而，这与大部分转轨经济国家的波动事实并不相符。

将制度变迁与经济波动相联系的文献不多。制度经济学派更关注制度变迁对经济增长的贡献。合适的制度会降低生产成本和交易费用，提高产量（科斯等，1994）。适合本国发展现状的制度可以推动经济发展（Guseh，1997）。近年来，有部分学者开始研究制度变迁对经济波动的影响。Aguiar和Gopinath （2007）率先将代表制度变迁的趋势冲击引入RBC模型，在代表性居民具有完全信息的情况下，利用持久性收入假说分析指出趋势冲击是造成发展中国家消费波动大于产出波动的关键因素。而Boz等（2011）则认为，发展中国家具有更多的信息摩擦，制度变革的不确定性而非制度变革本身才是造成其经济周期特征不同于发达国家的关键因素。García-Cicco等（2010）利用包含趋势冲击和周期冲击的RBC模型，分析了阿根廷和墨西哥1900—2005年的长期宏观经济数据，指出趋势冲击和周期冲击对经济波动的解释力都非常弱，而同时包含金融摩擦、偏好冲击等因素的RBC模型则对这一时期的经济波动有较好的解释力。Chang和Fernández （2013）利用包含趋势冲击、周期冲击、利率冲击和金融摩擦的模型，分析了新兴市场国家的经济波动特征，指出金融摩擦扩大了周期冲击对经济波动的影响，而趋势冲击对经济波动的解释力较弱。关于制度变迁对经济波动的影响在学术界仍存在争论。

国内仅有少数文献采用实证分析方法来解释制度变迁对经济波动的影响。由于制度变革不能量化统计，学者通常选取代理变量进行刻画。杜婷和庞东（2006）以及张建辉和靳涛（2011）分析了市场化程度、非国有化水平和开放程度等制度代理变量对经济波动的影响，指出制度冲击具有持久性，对我国经济周期的变动方向和波动程度起到了较大的决定性作用。孙宁华和曾磊（2013）则基于灰色动态关联理论，将选取的几组代理变量合成具有代表性的制度变量，并将其嵌入RBC模型度量了制度变迁对经济波动的影响。由于简单假定制度冲击为AR（1）过程，而没有检验其合理性，因此这样的设定并不能刻画制度冲击可以影响经济增长趋势的特征。

制度变迁通过影响全要素生产率而对经济产生影响已成为学术界的共识（孙宁华和曾磊，2013），但其进入模型的形式尚不确定。本文选取学术界通用的几组代理变量进行单位根检验，结果显示制度变迁更适合用单位根过程进行刻画。这种设定具有两大优点：第一，传统RBC模型通常设定经济增长趋势是关于时间的线性或非线性函数，是可以预测的。本文采用单位根过程描述经济增长趋势，使其变得不可预测，更符合我国的实际情况。第二，从冲击的性质出发，依据冲击对经济的影响是否具有持久性，将全要素生产率的变化进一步区分为趋势冲击和周期冲击，从而为分析经济波动的驱动因素提供了新的视角。

三、中国经济波动的特征事实

本文利用中经网统计数据库中1978−2018年的产出、消费、投资、净出口等年度数据，通过CPI、固定资产投资价格指数和GDP平减指数等价格指标，将各宏观经济变量的名义值折算为以1978年为基期的实际值并取对数，^②然后用HP滤波^③剔除趋势，得到各变量的波动部分。本文分析得到以下特征事实：

（一）产出尤其是消费的波动较大

从表1中可以看出，中国的产出尤其是消费波动远大于发达国家。发达国家的消费波动普遍小于产出波动，而我国的消费波动大于产出波动。中国经济之所以表现出异于发达国家的特征，可能是因为：第一，发达国家的经济发展比较平稳，总体波幅相对较小；而中国由计划经济向市场经济转变过程中经历了一系列变革，势必造成较大波动。第二，发达国家的经济增长相对平稳，经济波动主要表现为对长期增长趋势的短暂偏离，理性居民通常通过调整储蓄来平滑各期消费，从而消费波动小于产出波动。而中国的体制变革对经济的影响相对持久，产出的变化在一定程度上反映了持久性收入的变化，从而引起消费的大幅波动。第三，中国的金融体系尚不完善，理性居民不能实现有效的消费跨期替代，同样会造成消费的大幅波动。

（二）总体波幅趋于缩小

林建浩和王美今（2013）根据经济波动情况将改革开放后划分为两个阶段：1978—1999年为“大波动”时期，经济波幅相对较大；而后一阶段为“大稳健”时期，经济波幅明显趋小。本文同样以2000年为界，考察改革开放后两个阶段产出和消费波动率的变化。数据显示，1978—1999年产出波动的标准差为3.44%，2000—2018年则降至2.39%，降幅达30.5%；消费波动的标准差则从4.0%降至2.53%，降幅达36.8%。这表明产出和消费的波动幅度都呈现下降趋势，且消费的波动幅度下降更快。这是否反映出我国的市场经济体制已建立发展，无论是制度变革所引起的趋势波动还是经济不确定性因素所引起的周期波动都有所减弱？这是否也预示着我国的金融体制日益完善，居民对消费的调整能力逐渐增强？

（三）体制改革与中国经济波动

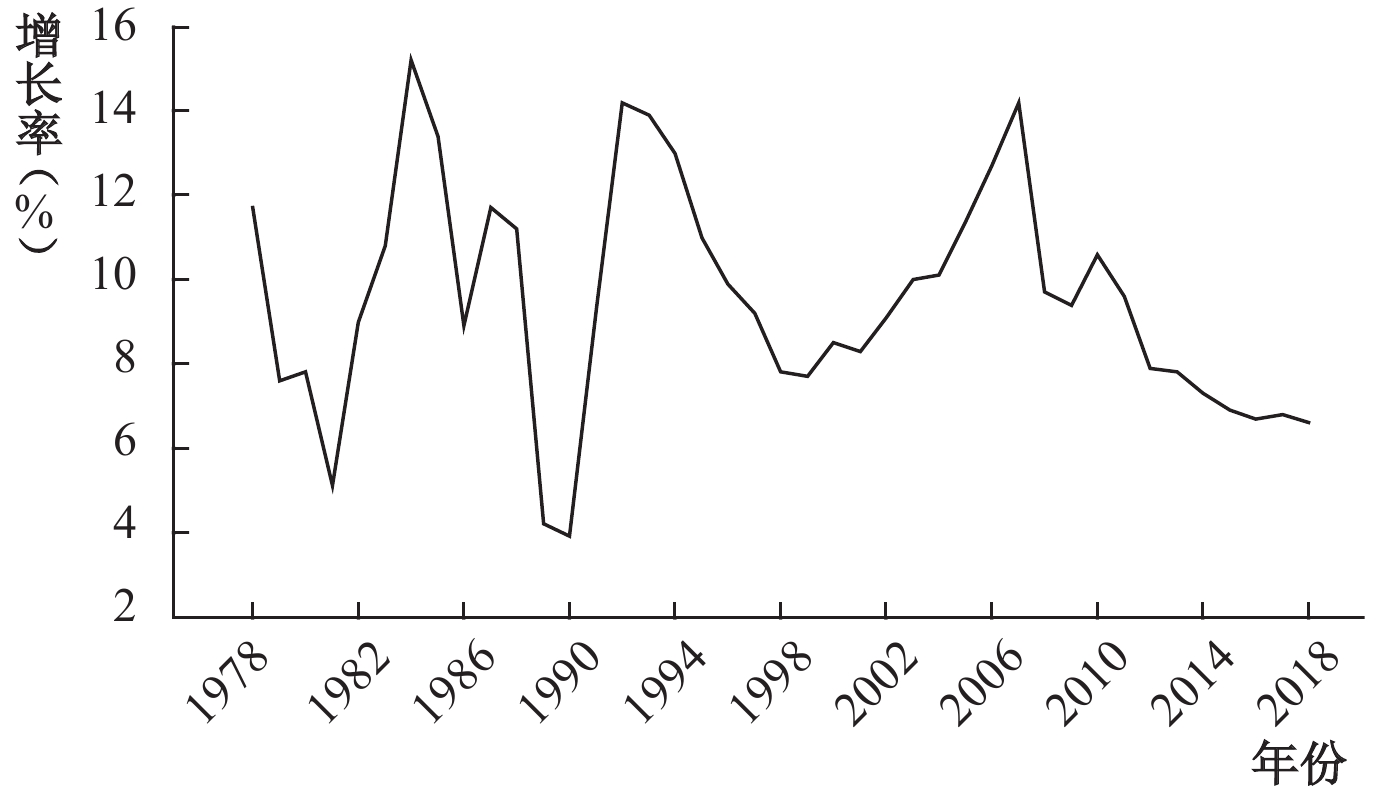
改革开放从1978年的农村家庭联产承包责任制开始，这一举措实现了土地集体所有权与经营权的分离，改变了农业生产的组织方式，被称为中国农村改革与发展的“第一次飞跃”。1992年初邓小平发表的“南巡讲话”是中国改革进入全新阶段的标志，建立和完善社会主义市场经济体制成为核心内容。国企改革全面铺开，私营企业迅速进入生产的各个领域，生产积极性和潜力得到了空前的释放。2001年中国加入WTO，极大地促进了国外先进产品和技术向我国的传播，使我国开始站在全球化角度进行资源配置，为经济增长提供了新的前所未有的机遇。从图1中可以看出，1978年至今，中国经济大体经历了3个周期，上述三次大的体制变革在时间上恰好对应经济的3个上升期。

（四）随机趋势的存在性检验与产出波动中持久性因素分析

王少平和胡进（2009）对我国1992—2008年产出的季度数据进行了单位根检验，结果显示我国经济具有随机增长趋势。本文将区间扩大为1978—2018年，采用年度数据进行了检验，得到相同的结论。与之不同的是，本文更关注这一随机趋势是如何产生的及其与经济波动之间的传导机制。如果随机趋势源自制度变革，在柯布—道格拉斯生产函数下，索罗残差也应具有随机趋势。为了验证这一猜测，本文对1978—2018年的索罗残差进行了ADF检验，其中资本数据参照陈昌兵（2014）的研究采用永续盘存法进行计算。

从表2中可以看出，无论产出还是索罗残差都是单位根过程。这表明：第一，中国经济确实存在随机趋势；第二，产出和索罗残差都具有随机趋势，说明趋势冲击主要通过影响全要素生产率而形成产出的随机趋势；第三，在利用RBC模型研究中国经济波动问题时，更贴近现实的模型应该使全要素生产率中同时包含周期冲击和趋势冲击。

上述检验得出中国经济增长的确具有随机趋势，有必要进一步测量趋势变化对经济波动的影响。由于趋势冲击对经济波动的影响具有持久性，本文通过测量经济波动中持久性因素的大小来衡量这一影响。借鉴Cochrane（1988）的方法，本文采用方差比进行测量。考虑到本文产出的数据量较小，采用如下的小样本修正统计量：

其中，

表示样本k阶差分方差的估计值，T为总样本量。我们对我国1978—2018年的实际产出数据进行分析，结果见表3。从中可以看出，随着 的增大，方差比呈现先增大后减小再增大的趋势。由于这一方差比仅在k充分大时才有效，我们选取较大的k值，发现k在30附近的方差比在1.6左右，表明经济波动中具有较强的持久性因素。但由于方差比对k的变化比较敏感，这种测量方法的参考价值较小。我们将在第四部分通过理论建模的方法来精确考察趋势波动对我国经济的影响。

（五）制度变迁形成随机趋势

全要素生产率中包含随机趋势，那么造成随机趋势的因素是什么？由于制度变迁能够对经济产生持久性影响，是不是制度变迁形成了随机趋势？如果是，那么制度变迁指标也应是单位根过程。基于此，本文对制度变迁指标进行单位根检验。由于制度变迁是一个抽象的概念，没有量化指标，因此本文参照张建辉和靳涛（2011）以及孙宁华和曾磊（2013）的研究，采用国内衡量制度变迁时通用的几个代理变量：（1）市场化程度（Marketization Degree），主要反映资源配置过程中市场化的广度和深度，具体用投资的市场化指数表示，即全社会固定资产投资中“外资、自筹资金和其他投资”占总投资的比重。（2） 非国有化率（Non-nationalization Rate），反映经济的多元化程度和非国有经济的活跃度。由于数据所限，本文采用1978—1999年国有及国有控股企业工业总产值与全部工业总产值的比率，以及2000—2018年规模以上国有企业工业总资产与规模以上工业企业总资产的比率，再用1与之作差表示非国有化率。（3） 政府干预度（Government Intervention Degree），反映市场受行政力量影响的大小，用一般公共预算支出与国内生产总值的比率表示。（4） 开放程度（Open Degree），反映经济的外向化水平，用进出口总额与国内生产总值的比率表示。ADF检验结果显示，^⑤上述4个变量均为单位根过程，说明制度变迁是造成随机趋势的重要因素。因此，在刻画制度变迁对经济形成的冲击时应以单位根过程表示，这有别于传统RBC模型中通常以AR（1）过程引入外生冲击的做法，也有助于研究持久性因素对经济波动的影响。

四、包含趋势冲击和流动性约束的小国开放经济模型

（一）厂商。假设厂商处于完全竞争经济中且只生产一种产品，产品用来投资或消费。体制改革通过改变经济增长趋势而影响产出。暂时性冲击影响生产率的周期部分。生产函数如下：

其中，

（ ）表示劳动的产出份额。表示全要素生产率中对经济影响短暂的周期性因素，周期冲击 服从AR（1）过程：

其中，

，服从期望为0、标准差为 的独立正态分布。体现劳动生产效率的变化，表示全要素生产率中对经济产生持久性影响的因素。

其中，

，表示稳态时的产出增长率。服从期望为0、标准差为 的独立正态分布。易证明 的对数服从随机游走过程。这一设定使产出的增长趋势不再是关于时间的线性或非线性函数，而是具有了随机性，从而刻画了经济增长趋势不可预测的特征，同时说明趋势的变化同样能够引起经济波动且更持久。若 ，则有：

虽然（4）式是（3）式的一个特例，但是两者表示的趋势冲击在模型中的传导机制却不相同。根据（4）式，各期的趋势冲击是相互独立的。而根据（3）式，在

的情况下，各期的趋势冲击是相关的，本期的趋势冲击会对以后各期的趋势冲击产生逐渐衰减的影响。研究发现（4）式更符合中国经济的实际情况。

（二）居民。假定社会中存在可以无限期存活的代表性居民，通过提供劳动和租让资本获得收入，并将收入在消费和储蓄之间进行分配以最大化终生期望效用。为了刻画居民在流动性约束条件下的行为，参照Campbell和Mankiw （1989）以及胡永刚和刘方（2007）的做法，本文将居民分为两类：第一类居民完全受流动性约束的限制，不拥有资本，只能通过提供劳动获得收入，并在当期全部消费。第二类居民拥有全部社会资本，不受借贷约束的限制，他们的各期收入包括劳动收入和资本收入，并将其进行消费和储蓄。储蓄又分为国内储蓄和国外储蓄，国内储蓄全部转化为国内投资，国外储蓄主要通过居民在国际债券市场上交易国际债券实现。假定两类居民的劳动是无差异的，且具有如下相同的效用函数：

其中，

表示居民类型，表示代表性居民基于第0期的全部信息对终生效用的期望算子，为贴现因子，为第 类居民在第 期的消费，为衡量一单位劳动对居民负效用大小的参数，表示第 类居民在第 期提供的个人劳动时间，^⑥为弗里斯劳动供给弹性。约束条件如下：

（6）式为第一类居民的约束条件，其中

是以单位最终产品表示的工资水平。为第一类居民占社会总人口的比例，若 ，则所有居民都不受流动性约束限制。对于劳动，区分个人劳动和社会劳动，假设每类居民每期拥有1单位个人时间，为第一类居民在第 期提供的个人劳动时间。同时，将各期的社会总时间也标准化为1，由于第一类居民占社会总人口的比例为 ，为第一类居民提供的社会劳动时间。（7）式为第二类居民的约束条件，为第 期的投资。为第 期的资本收益率，以单位最终产品表示。为第 期的资本存量。假设所有债券都为一期无风险国际债券，为第 期到期的债券。是以单位最终产品表示的债券价格。资本的运动方程为：

其中，

为折旧率。为资本调整成本参数，资本调整成本主要取决于本期资本存量的增长率相对于稳态经济增长率的变化。债券价格 的运动方程为：

其中，

表示世界利率水平，B表示稳态时的债务水平，（ ）表示债券价格对于债务水平变化的弹性参数。

（三）市场出清条件

市场出清条件为给定价格水平{

，厂商选择资本和劳动以实现利润最大化，居民选择劳动供给量、消费、投资和债券交易量以实现效用最大化；同时，资本市场、产品市场和劳动市场达到均衡，满足以下等式：

其中，

为第 期的净出口，为第 期第一类居民提供的社会劳动占社会总劳动的比例。

（四）模型均衡解

求解厂商的利润最大化问题，可得一阶条件如下：

（10）式和（11）式分别决定了厂商对资本和劳动的需求，共同决定了生产要素的投入比例。

关于第一类居民的效用最大化问题，求解可得：

由于受流动性约束的限制，第一类居民不能通过消费的跨期替代来提高终生效用，因此其终生效用最大化问题等价于各期效用最大化问题，仅需考虑对劳动和消费的当期分配，属于静态分析。（12）式决定了第一类居民对劳动和消费的选择。第二类居民的效用最大化问题需同时考虑消费和劳动的当期分配以及消费的跨期替代，属于动态分析。

资本的一阶条件为：

劳动的一阶条件为：

国际债券的一阶条件为：

（13）式和（14） 式与第一类居民的一阶条件（12）式共同决定模型经济中的劳动和资本供给，结合厂商对劳动和资本的需求方程（10）式和（11）式，可得各期劳动市场和资本市场的动态变化。

模型中共有2个外生变量

，3个价格变量 ，其中 为非平稳变量，12个内生变量，其中4个是平稳变量 ，8个是具有随机增长趋势的非平稳变量 。因此，求解模型共需15个方程，包括（1）式、（6）式至（15）式以及市场出清条件中的4个方程。首先，对非平稳变量要剔除趋势，方法是 ，其中 表示具有随机增长趋势的非平稳变量，表示第 期之前的随机趋势，表示剔除趋势之后的平稳变量。然后，求解模型的稳态解，对上述15个方程进行对数线性化，进而求出模型的政策方程，对模型经济进行分析。

（五）参数校准与估计

本文采用三种方法来校准模型中的参数：一些参数利用统计数据进行校准；一些参数参考大多数文献中的常用值；对于趋势冲击和周期冲击中包含的参数

，采用GMM方法进行估计。利用数据校准及从以往文献中获得的参数见表4。

利用数据校准得到的参数包括：

根据1978—2018年我国GDP增长率的均值校准为9.23%。根据1978—2018年净出口产出比的均值校准为0.02。从以往文献中获得的参数包括：采用陈昌兵（2014）中的数值0.0564，因为本文在核算资本存量时以该文献为基础，为保持一致仍采用该文献中的折旧率。对于 的取值，国内大多数文献认为在0.5左右，如Chow和Li（2002）取0.45，张军（2002）取0.501，本文将其设定为0.5。取值为0.95，栗亮和刘元春（2014）在分析季度数据时将贴现率校准为0.98，折算为年度数据为0.95。参照Huang等（2008）的研究取值为2，经验证，模型对该参数值并不敏感。参数 校准为22，对应于0.34的稳态社会劳动时间。对于参数 ，在0到5之间等距取21个值，分别进行二阶矩匹配，发现 时匹配效果最佳，故将其校准为1.5。参数 参照Aguiar和Gopinath （2007）的研究设定为0.001。胡永刚和刘方（2007）将参数 设为0.8，考虑到近些年来金融体制日益完善，该参数值应有所下降，将其校准为0.5，下文将改变其数值对模型进行稳健性分析。

采用GMM方法估计参数

至少需要4个矩条件，本文选取产出、消费、投资、净出口的方差、产出与其他变量的协方差以及产出的一阶自协方差8个矩条件进行参数估计。本文分别估计了不存在流动性约束的基准模型和存在流动性约束的扩展模型，以对比分析流动性约束对中国经济波动的影响。

假定

和 服从正态分布，表5显示，无论是否存在流动性约束，在10%的显著性水平上，的估计值都不显著。因此，我们令 ，此时各参数估计值的显著性明显提高。这意味着（4）式表示的趋势冲击更符合我国的实际状况，同时说明中国经济的增长趋势是一个确定性增长趋势和一个随机游走过程之和。基于此，下文将在趋势冲击为（4）式的情况下进行分析。

（六）动态模拟

矩匹配是检验模型经济对实际经济模拟情况的一个重要指标。下文分别比较存在和不存在流动性约束两种情况下，模型经济与实际经济的二阶矩。表6显示：第一，不存在流动性约束的模型没有刻画消费波动大于产出波动的事实，而加入流动性约束的模型很好地刻画了这一特征。这说明我国居民在消费过程中确实受到了信贷限制。由于不存在流动性约束的情况下消费波动小于产出波动，趋势冲击能否扩大消费波动尚不可知，下文将在冲击响应部分验证这一论断。第二，模型经济中消费与产出表现出较强的相关性，可能是因为趋势冲击的引入使产出的变化在一定程度上反映了收入的持久性变化，从而引起消费与产出同方向的大幅变化，增大了两者的相关性。第三，K-P值刻画的是存在流动性约束的情况下，模型经济二阶矩与实际数据相应二阶矩的比值，数值越接近100%，说明由模型得到的理论矩对实际矩的拟合越好。可以看出，对产出、消费和投资标准差的模拟准确度很高，除了对净出口与产出的相关系数估计过高外，其他理论矩都较好地拟合了实际矩。因此，含有流动性约束的模型很好地刻画了中国经济波动的特征。

本文与传统RBC模型的一个重要区别是将经济增长趋势随机化。这是否有助于更好地刻画我国的经济波动特征？下面将本文的结果与国内几篇具有代表性的相关文献进行比较。由于建模方法、使用数据的时间跨度以及统计口径不同，实际数据特征并不完全一致，本文主要比较相对比值及变化情况，结果见表7。

上述文献都反映了改革开放之后消费波动大于产出波动的事实。在模拟经济中，除了孙宁华和曾磊（2013）外，其他四篇文献都刻画了这一事实，且在模型中都引入了居民的借贷约束，说明借贷约束对刻画我国经济波动具有重要意义。而仅存在借贷约束并不够，根据研究内容的不同，学者引入了各种条件加以说明。例如，黄赜琳和朱保华（2015）引入了税收冲击和财政收支冲击，胡永刚和刘方（2007）引入了劳动调整成本，陈晓光和张宇麟（2010）引入了异质性消费者和异质性厂商并区分了政府消费和居民消费，本文则引入了制度变革所形成的趋势冲击。从K-P值看，孙宁华和曾磊（2013）对产出波动标准差的模拟值与实际值较为接近，但对消费和投资波动标准差的模拟值远小于实际值。黄赜琳和朱保华（2015）对消费波动标准差的模拟较为准确，对产出和投资波动标准差的模拟值则偏低。胡永刚和刘方（2007）对各经济变量标准差的模拟值都仅为实际值的一半。陈晓光和张宇麟（2010）准确模拟了产出和消费波动的标准差，但对投资波动标准差的模拟欠佳。本文则很好地模拟了消费、投资和产出波动标准差的变化，说明流动性约束和趋势冲击相结合对解释我国现阶段经济波动至关重要。

图2给出了产出、消费、投资和劳动对趋势冲击和周期冲击1个百分点正向变动的响应情况。需要注意的是，冲击响应反映的是冲击发生后变量各期偏离稳态的程度。周期冲击不改变经济增长趋势，所以去趋势步骤不会影响响应结果。趋势冲击改变了趋势本身，但为解模型剔除趋势后，仅保留了当期影响，不能反映其通过影响趋势本身而引起的各变量对稳态的偏离。从趋势冲击发生的第2期开始，各变量对稳态的偏离度应该是趋势冲击的即期响应与趋势本身变化所引起的对稳态的偏离度之和。为弥补这一缺失，图中的冲击响应从趋势冲击发生的第2期开始加入了与冲击大小相同的趋势本身变化。

图2显示，面对趋势冲击1个百分点的正向变动，产出、消费和投资最终将永久偏离初始稳态值1个百分点，说明趋势冲击对经济发展具有持久性影响，也使经济发展不可预测。而面对周期冲击，各经济变量最终将回归至初始稳态值。两类冲击的引入较好地说明了中国经济波动不仅是对趋势的偏离，也包含趋势本身的波动。这与中国较高的经济增长率及波动事实一致。

分析图2（a）和（e）可知，面对1%的趋势冲击，产出先上升约0.5个百分点，然后缓慢上升，最终偏离稳态值1个百分点。但面对1%的周期冲击，产出迅速上升1个百分点，而后呈驼峰状发展，逐渐回归稳态值。趋势冲击和周期冲击对产出的不同影响反映了理性居民和厂商对两类冲击的不同反应。从劳动供给角度看，面对趋势冲击，居民预期自己的工资收入持久上升，工资上涨的收入效应将大于替代效应，当期劳动提供量减少。面对周期冲击，由于影响短暂，工资上涨的替代效应大于收入效应，当期劳动提供量增加。图2（d）和（h）印证了上述变化。从厂商角度看，面对持久性的趋势冲击，厂商会制定合理的长期投资计划，而不是在趋势冲击当期大量增加投资；但面对周期冲击，厂商会利用短暂的有利时机大量增加投资，而后迅速减少投资。图2（c）和（g）印证了这一特征。

比较图2（b）和（f）可知，面对周期冲击，消费的当期反应更大。结合图2（a）和（e），面对趋势冲击，产出在当期有所上升，但消费的上升幅度更大。面对周期冲击，消费虽有较大上升，但小于产出的上升幅度。这一模拟结果与消费的持久性收入假说一致：面对正向的趋势冲击，理性居民预期自己的收入将持久性增加，从而更多地增加当期消费，导致消费的增幅超过产出的增幅。但面对正向的周期冲击，收入的上升是短暂的，居民的当期收入更多地用来储蓄以平滑消费，因而消费的增幅小于收入的增幅。影响短暂的周期冲击虽有助于解释较大的消费波动，但无法解释消费波动大于产出波动的特征，趋势冲击的引入则较好地说明了这一事实。本文还考察了不存在流动性约束时消费、产出等变量的冲击响应，结论与上述分析类似。

（七）趋势冲击和周期冲击影响的变化

趋势冲击和周期冲击共同影响中国经济波动。中国经济波动在多大程度上由趋势波动引起，从而与渐进式改革的阶段性特征相关联？又在多大程度上是对趋势的偏离所致，从而需要通过财政与货币政策进行调节？随着社会主义市场经济体制的逐步完善，趋势冲击和周期冲击对中国经济波动的影响程度是否发生了变化？本文尝试以2000年为界对改革开放后两个阶段分别进行参数估计，判断波动源标准差的变化，从而探究我国经济波动特征的变化。

表8显示，周期冲击的标准差下降了26.9%，趋势冲击的标准差下降了34.7%。这反映了我国经济波动源变化的两个特征：第一，趋势冲击和周期冲击的方差都在减小，因而相应阶段的产出与消费波动率都表现出下降的特征。第二，2000年之后趋势冲击对经济波动的影响下降更快，周期冲击对经济波动的影响相对增大。这种变化背后的原因是：前一阶段是计划经济体制向社会主义市场经济体制的过渡期，主要完成了价格体制、财税体制、金融体制和分配制度等的框架性布局，对企业的组织形式和生产资料的配置方式产生了根本性影响，对经济的冲击较为剧烈。后一阶段则主要是进一步完善上述体制，对经济波动的影响相对较小。而由于开放程度的不断提高，世界经济中不确定性因素对中国经济的影响逐渐增大。

方差分解可以测度两类冲击对中国经济波动的影响力。表9显示，趋势冲击解释了38.5%的产出波动，更多波动来自周期冲击。言外之意是，中国经济波动虽包含持久性因素，但主要受暂时性因素的影响。比较而言，趋势冲击对消费的解释力达到69.5%，主要是通过持久性收入假说而增大了消费波动。趋势冲击对投资和净出口的解释力也分别达到57.7%和88.1%。总体而言，趋势冲击对中国经济波动具有较强的解释力。

2008年国际金融危机之后，中国经济经历了史上最长的一轮调整期，此轮经济下行已经超出了学界通常定义的3—8年的周期波动范畴。那么，此轮经济下行是否由趋势下行和对趋势的向下偏离共同所致？如果回答是肯定的，那么在多大程度上由趋势冲击所致，从而属于新常态？又在多大程度上反映了周期冲击的影响，需要通过财政与货币政策进行调节？

Beveridge和Nelson （1981）将产出增长变化区分为确定性趋势、随机趋势和周期波动三部分。本文则通过理论建模的方法对随机冲击中的持久性成分和周期性成分分别进行了刻画。根据本文对生产函数的刻画，产出对数的随机增长趋势可以表示为：

其中，

表示产出的确定性趋势，表示随机趋势。对索罗残差的对数取一阶差分可得：

其中，

表示第 期的索罗残差。

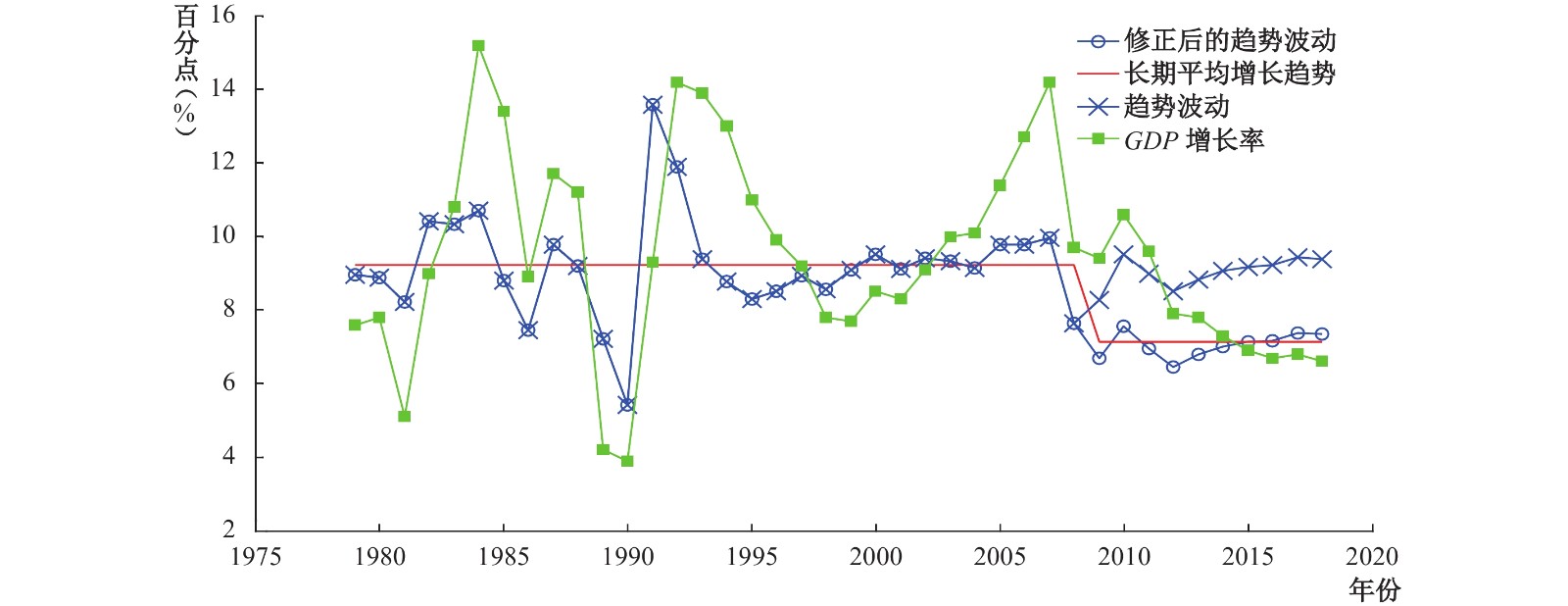
利用（2）式、（4）式、（17）式以及从实际数据得到的索罗残差，通过Kalman滤波来分离趋势波动和周期波动，可以得到各期随机趋势的变化图。从图3可以看出随机趋势变化的四个特点：第一，随机趋势的上升对应于改革开放之后三次大的体制变革，说明每一次重大改革都会对随机趋势产生提振效应。第二，模型中随机趋势的变化基本反映了改革开放后前30年经济发展的趋势特征，但并没有刻画出2008年以来经济的下行趋势。可能的原因是，前30年经济增速比较稳定，但2008年之后受美国次贷危机的影响，中国粗放式增长所形成的不合理经济结构开始暴露出问题，导致经济开始下行，经济增速正在进行状态切换。但模型中关于长期平均增长趋势的设定是一个固定值9.23%，没能反映增长趋势的状态切换。因此，我们对其进行简单修正，2008年之后采用剔除“四万亿”刺激措施影响的经济增长率均值7.14%，^⑦结果显示修正后的趋势波动恰当地刻画了2008年以来的趋势下行现象。第三，针对2008年以来的经济下行，国家实施了“四万亿”刺激计划，对经济仅有短暂的提振效应，并没有改变经济下行的趋势。2012年以来，国家开始进行经济结构调整，修正后的趋势波动显示2012年之后随机趋势表现出逐渐上升的态势，说明经济结构调整开始显现成效。第四，改革开放之后的前30年，经济增长趋势相对稳定，保持在9.97%的均值水平，但2008年之后修正的经济增长率均值仅为7.14%，可以简单估算在经济增长趋势的状态切换过程中，增长趋势下降了2.83个百分点。因此，2008年以来的经济下行约有37.2%是由趋势下行所致，更多地表现为经济的周期性波动。

（八）稳健性检验

合理的参数选择有助于模型对实际经济的刻画，好的模型不会因参数的小幅变化而改变其基本特征，即模型应具有对参数的稳健性。本文通过数据校准的参数具有客观性；从以往文献中获得的参数虽具有主观性，但也基本确定了参数的取值范围。为考察模型的稳健性，本文小幅改变这些参数的数值，观察模型对实际经济基本特征的刻画是否改变。表10给出了几种情况下的参数估计值。

在

的情况下，参数的估计值仍不显著，这里直接给出了 时的参数估计值，在此基础上进行二阶矩匹配以判断模型对实际经济的刻画能力。对比表6和表11可知：第一，在流动性约束较小的情况下，模拟的二阶矩与没有流动性约束的情况下相似，都没有刻画消费波动大于产出波动的事实。而随着流动性约束的增大，这一特征得到了刻画，说明了流动性约束对于刻画我国经济波动的重要性。这同时说明随着流动性约束的减弱，中国经济将会像发达国家一样表现出消费波动小于产出波动的特征。第二，根据矩匹配情况，各种情况下模型对实际经济都进行了很好的刻画。此外，各种情况下的冲击响应也都与上文分析比较接近，不再赘述。^⑧这说明模型具有较强的稳健性。

五、结　论

本文构建了包含制度变迁和居民流动性约束的小国开放经济DSGE模型，较好地解释了我国经济的波动特征。研究发现：第一，中国经济存在明显的随机趋势，从方差分解可以看出趋势冲击对各经济变量的波动具有较强的解释力，说明制度变迁是我国经济波动的主要驱动因素之一。第二，趋势冲击的引入使持久性收入假说成为解释消费波动大于产出波动的重要机制之一，流动性约束的引入通过降低消费的跨期替代而增大了消费波动，成为解释消费波动大于产出波动的又一机制，两者结合较好地解释了这一现象。第三，随着改革从框架性、方向性向深层次、精细化发展，我国经济总体波幅趋于缩小，周期扰动正逐渐成为经济波动的主要来源。第四，近10年来的经济下行是趋势下行和周期性下行共同所致。

基于上述研究结果，本文提出以下政策建议：第一，制度变迁是我国经济波动的主要驱动因素之一，制度变革意味着从一种规则转变为另一种规则，处理好两种规则之间的过渡，加大对变革方向和变革步骤的宣传，使居民能够提前形成预期，有助于减小制度变迁对经济波动的影响。第二，中国经济波动的驱动因素正在发生变化，周期性冲击正逐渐成为经济波动的主要驱动因素。这意味着随着经济改革逐渐走向深入，应对经济波动的侧重点应发生变化，政府应准备更加丰富的“政策工具箱”，以应对国际化背景下日益增加的不确定性因素所造成的短期波动。

① 本文中的中国经济数据主要来源于中经网统计数据库。

② 净出口含有负值，不能取对数，因而采用净出口产出比代替。

③ 用HP滤波剔除趋势时采用的参数值为100。

④ 本文采用GMM方法对产出、消费等变量波动的标准差进行估计，括号内为估计值的标准差，下同。

⑤ 受篇幅限制，检验结果没有列出，如有需要可向作者索取。

⑥ （5）式中也可将劳动表示为社会劳动

，不影响模型结论。

⑦ 仅测算2012—2018年的平均经济增长率作为代替。

⑧ 限于篇幅所限，没有一一列出，如有需要可联系作者。