
2020第46卷第10期
一、引 言
中国社会保险费率高企是一个不争的事实,其中养老保险费率偏高最受诟病。针对税费负担较重是困扰企业可持续发展的难题,国务院办公厅印发了《降低社会保险费率综合方案》,规定自2019年5月1日起城镇职工基本养老保险单位缴费率降至16%,并要求养老保险待遇水平不降和维持基金财务平衡。这是继2016年养老保险单位缴费率从20%阶段性降至19%后的再次下降,特别强调本次降低缴费率是适应经济发展新形势的长期性制度安排。降低缴费率的政策意图是减轻企业负担和促进经济增长,但在养老保险制度缺乏有效筹资渠道的情况下,欲维持已有的养老金替代率必然加剧基金收支失衡风险,而欲维持基金财务平衡又必然导致养老金替代率下降。因此,降低养老保险缴费率很难同时实现养老金替代率不降、基金财务平衡和经济增长三个目标,这意味着降费率存在政策目标上的“不可能三角”。
为了顺应人口预期寿命延长规律、缓解劳动力供给短缺和遏制人口抚养比快速上升趋势,借鉴发达国家经验,我国拟实施延迟退休政策。一方面,延迟退休通过增收减支方式能够改善养老保险基金财务状况,可以为缴费率下降创造空间(Galasso,2008;Kitao,2014;景鹏和胡秋明,2017;曾益等,2018);另一方面,延迟退休会引发个人生命周期资源作出适应性调整,通过作用于资本积累和劳动力供给对经济增长产生影响(Miyazaki,2014;严成樑,2016;耿志祥和孙祁祥,2017)。那么,延迟退休能破解养老保险降费率“不可能三角”吗?若能,伴随养老保险缴费率的下降,退休年龄应延迟多少岁?对于这些问题的回答,不仅有助于我们从经济增长与民生保障协调发展的视角评估降低养老保险缴费率和延迟退休的综合效应,而且也能为我国合理制定延迟退休政策提供决策参考,具有重要的现实意义。
目前,已有大量文献基于世代交叠模型来分析养老保险缴费率调整的经济效应。Ehrlich和Kim(2007)研究表明,提高缴费率会降低个人储蓄率和生育率,导致物质资本存量和劳动力供给下降,从而不利于经济增长;Yew和Zhang(2009)研究发现,如果父母对子女的数量偏好远低于对其福利偏好,那么养老保险将通过降低生育率和增加人力资本投资来改善社会福利,且最优缴费率介于16%—22%之间;Fanti和Gori(2010)认为,降低缴费率会通过增加物质资本积累来促进经济增长,从而证明了降低缴费率的同时可以提高养老保险待遇;彭浩然和陈斌开(2012)研究发现,缴费率与养老保险待遇之间呈倒U形关系,待遇最大化下的缴费率约为15.6%;景鹏和胡秋明(2016)认为,降低缴费率不仅能促进经济增长和增进社会福利,而且有助于推进多层次养老保险体系建设;彭浩然等(2018)研究发现,养老保险缴费率与公共教育税率之间存在一个最优组合,降低缴费率的同时加大公共教育投入可以促进经济增长和维持养老金替代率不变。
与退休年龄内生化相比,在外生退休年龄框架下考察延迟退休经济效应的文献还相对较少。Miyazaki(2014)研究发现,延迟退休一方面通过增加劳动力供给促进总产出增加,另一方面通过降低物质资本存量导致总产出减少,其对总产出的净效应取决于物质资本产出弹性;Fanti(2014)评估了延迟退休对总产出的短期和长期影响,认为延迟退休在短期内能提高总产出,但长期内会降低总产出;严成樑(2016)研究表明,无论养老保险制度是现收现付制还是基金积累制,延迟退休都将使得生育率上升,而延迟退休对经济增长的影响则因经济增长模式的不同而有所不同,延迟退休在新古典增长模式下能促进经济增长,在内生增长模式下则会抑制经济增长;耿志祥和孙祁祥(2017)考察了延迟退休对储蓄率、物质资本积累和经济产出的影响,发现延迟退休将降低储蓄率、物质资本积累和人均产出,但其对总产出的影响由两种效应的强弱对比决定,即因物质资本积累减少而引致的总产出下降和因劳动力供给增加而引致的总产出上升。
上述文献虽然对降低养老保险缴费率和延迟退休的经济效应进行了深入分析,但大多数文献没有将两者一并分析以考察其综合效应,也未从经济增长与民生保障协调发展的视角来探讨缴费率和退休年龄之间的关系。受严成樑(2016)的启发,我们考察中国经济增长驱动因素时发现:改革开放头30年,资本短缺带来的收敛效应、技术落后产生的后发优势以及劳动力的无限供给推动了中国经济高速增长,延缓了资本边际报酬递减趋势;大致在2008年前后,伴随劳动力无限供给特征消失和资本积累规模扩大,资本边际报酬递减趋势显现,依靠要素和投资驱动的增长方式逐渐失效,中国经济开始步入自主创新驱动的新阶段(胡永刚和石崇,2016)。根据资本边际报酬是否递减和技术进步是否外生来判断,当前及未来一段时期内,中国经济呈现出新古典增长特征;①但从长期看,通过研发、人力资本积累和干中学等手段使技术进步内生化,以及经济体制机制改革进一步提升资源配置效率,中国经济最终将转变为内生增长模式。②鉴于此,有必要在新古典增长框架和内生增长框架下对比分析降低养老保险缴费率和延迟退休的经济效应。
本文通过构建世代交叠模型研究发现:(1)在维持基金财务平衡的前提下,无论是新古典增长框架还是内生增长框架,降低养老保险缴费率都将使得总产出增长率上升和养老金替代率下降,从而证实了降费率存在政策目标上的“不可能三角”。(2)两种框架下,延迟退休都将使得养老金替代率上升,但其对总产出增长率的影响则截然相反,总产出增长率在新古典增长框架下能提高,而内生增长框架下却会下降。(3)延迟退休在两种框架下的不同经济效应使其破解降费率“不可能三角”的作用效果存在显著差异,即“不可能三角”在新古典增长框架下能得到有效破解,而在内生增长框架下则无法破解。相对于现有文献,本文的边际贡献体现为:(1)本文从经济增长与民生保障协调发展的视角考察了降低养老保险缴费率和延迟退休对总产出增长率和养老金替代率的影响,为公共经济领域的理论研究拓宽了视野。(2)本文证实了养老保险降费率存在政策目标上的“不可能三角”,并发现延迟退休能否破解降费率“不可能三角”取决于经济增长模式,为辩证地看待延迟退休的经济效应和合理制定延迟退休政策提供了依据。
二、理论模型
(一)个人
假设个人是同质的,代表性个人一生分为成年和老年两个时期,每个时期有一单位时间禀赋,成年期全部时间用于工作,老年期部分时间用于工作,剩余时间退休。t期进入成年期的个人通过供给劳动获得工资收入
| ${c_t} = (1 - \theta ){w_t} - {s_t} - v{w_t}{n_t}$ | (1) |
| ${d_{t + 1}} = {R_{t + 1}}{s_t} + x(1 - \theta ){w_{t + 1}} + (1 - x){P_{t + 1}}$ | (2) |
其中,
| ${U_t} = \ln {c_t} + \beta {\rm{ln}}{d_{t + 1}} + \varphi {\rm{ln}}{n_t}$ | (3) |
其中,
| ${d_{t + 1}} = \beta {R_{t + 1}}{c_t}$ | (4) |
| $\varphi {c_t} = v{w_t}{n_t}$ | (5) |
将式(4)和式(5)代入式(1)和式(2),得到个人最优储蓄
| ${s_t} = \frac{\beta }{{1 + \varphi + \beta }}(1 - \theta ){w_t} - \frac{{1 + \varphi }}{{1 + \varphi + \beta }}\frac{{x(1 - \theta ){w_{t + 1}} + (1 - x){P_{t + 1}}}}{{{R_{t + 1}}}}$ | (6) |
| ${n_t} = \frac{\varphi }{{v(1 + \varphi + \beta )}}\left[ {(1 - \theta ) + \frac{{x(1 - \theta ){w_{t + 1}} + (1 - x){P_{t + 1}}}}{{{w_t}{R_{t + 1}}}}} \right]$ | (7) |
(二)企业
假设完全竞争市场中存在无数个同质的生产性企业,它们以利润最大化为目标,使用资本和劳动,采用Cobb-Douglas技术进行生产,生产函数为:
| ${w_t} = A(1 - \alpha )k_t^\alpha $ | (8) |
| ${R_t} = A\alpha k_t^{\alpha - 1}$ | (9) |
(三)政府
从形式上看,当前我国基本养老保险制度实行“统账结合”模式,但由于庞大的制度转轨成本没有得到化解,迫使政府挤占个人账户资金来确保养老金按时足额发放,因此个人账户“空账”规模快速攀升,使得当初设计的“统账结合”制度变成了事实上的现收现付制度(彭浩然等,2018)。现收现付制下,政府向工作人口征收养老保险费全部用于支付当期退休人口的养老金,t期养老保险基金预算平衡式为:
| $\theta {w_t}{N_t} + x\theta {w_t}{N_{t - 1}} = (1 - x){P_t}{N_{t - 1}}$ | (10) |
其中,等号左边表示t期养老保险基金收入,包括成年劳动力缴费
| ${P_t} = {{\theta {w_t}({n_{t - 1}} + x)}/{(1 - x)}}$ | (11) |
养老金替代率反映了单位时间内养老金相对于工资收入的比重,是衡量个人退休后福利水平高低的重要指标。t期进入成年期的个人一生工资收入为
| ${\delta _t} = \frac{{{P_{t + 1}}}}{{({w_t} + x{w_{t + 1}})/(1 + x)}} = \frac{{\theta ({n_t} + x)(1 + x)}}{{1 - x}}\frac{{{w_{t + 1}}}}{{{w_t} + x{w_{t + 1}}}}$ | (12) |
(四)宏观均衡
我们将上述个人、企业和政府决策相结合,定义宏观均衡。给定初始资本总量
三、模型求解与均衡分析
本文在新古典增长框架和内生增长框架下考察降低养老保险缴费率和延迟退休对总产出增长率和养老金替代率的影响,探讨延迟退休能否破解降费率“不可能三角”,主要基于以下三点考虑:其一,一国经济增长模式将随着要素禀赋规模及结构变化和技术进步而发生改变,往往经历从新古典增长向内生增长的转变过程(Funke和Strulik,2000;严成樑,2016),中国经济同样如此。其二,与新古典增长框架相比,内生增长框架下的经济机制更加丰富,降低缴费率和延迟退休会通过生育率和资本积累两条渠道影响经济增长和养老金替代率。其三,通过对比,我们可以判别延迟退休破解降费率“不可能三角”的作用效果是否因研究框架(经济增长模式)不同而存在显著差异。
(一)基于新古典增长框架的分析
结合式(6)—式(9)、式(11)和
| $\frac{{\beta (1 - \theta )}}{{1 + \varphi + \beta }}A(1 - \alpha )k_t^\alpha = {k_{t + 1}}\left[ {({n_t} + x) + \frac{{1 + \varphi }}{{1 + \varphi + \beta }}\frac{{1 - \alpha }}{\alpha }(x + \theta {n_t})} \right]$ | (13) |
| $\left[ {\frac{{1 + \varphi + \beta }}{\varphi }v{n_t} - (1 - \theta )} \right]A(1 - \alpha )k_t^\alpha = {k_{t + 1}}\frac{{1 - \alpha }}{\alpha }(x + \theta {n_t})$ | (14) |
在新古典增长框架下,经济处于均衡状态时满足
| ${\left( {{k^*}} \right)^{1 - \alpha }} = \frac{{\beta A\alpha (1 - \theta )(1 - \alpha )}}{{\alpha (1 + \varphi + \beta )({n^*} + x) + (1 - \alpha )(1 + \varphi )(x + \theta {n^*})}}$ | (15) |
| ${\left( {{k^*}} \right)^{1 - \alpha }} = \frac{{A\alpha \left[ {(1 + \varphi + \beta )v{n^*} - \varphi (1 - \theta )} \right]}}{{\varphi (x + \theta {n^*})}}$ | (16) |
联立式(15)和式(16),可以求出均衡状态时的劳均资本
我们将式(15)和式(16)等号右边分别定义为
| $\frac{{d{n^*}}}{{d\theta }} = - \frac{{{\Omega _\theta }(\theta ,x,{n^*})}}{{{\Omega _{{n^*}}}(\theta ,x,{n^*})}} = - \frac{{{\Phi _\theta }(\theta ,x,{n^*}) - {\Xi _\theta }(\theta ,x,{n^*})}}{{{\Phi _{{n^*}}}(\theta ,x,{n^*}) - {\Xi _{{n^*}}}(\theta ,x,{n^*})}}$ | (17) |
| $\frac{{d{n^*}}}{{dx}} = - \frac{{{\Omega _x}(\theta ,x,{n^*})}}{{{\Omega _{{n^*}}}(\theta ,x,{n^*})}} = - \frac{{{\Phi _x}(\theta ,x,{n^*}) - {\Xi _x}(\theta ,x,{n^*})}}{{{\Phi _{{n^*}}}(\theta ,x,{n^*}) - {\Xi _{{n^*}}}(\theta ,x,{n^*})}}$ | (18) |
由式(15)可知,
| ${{d{n^*}}/{d\theta }} < 0$ | (19) |
由于
| $sign\left\{ {{{d{n^*}}/{dx}}} \right\} = sign\left\{ {{{{n^*}(1 - \theta )}/{(\theta {n^*} + x)}}} \right\} > 0$ | (20) |
于是得到结论1:在新古典增长框架下,若给定延迟退休岁数,降低养老保险缴费率将使得均衡状态的生育率和总产出增长率上升;若给定养老保险缴费率,延迟退休也将使得均衡状态的生育率和总产出增长率上升。
降低养老保险缴费率对生育率的影响包括三个方面:其一,降低缴费率使个人成年期的可支配收入增加,个人养育子女和进行储蓄的能力增强,前者直接提高生育率,后者通过提高资本总量引致工资率上升而间接提高生育率。其二,由于降低缴费率使养老保险基金收入减少,导致现收现付制下个人领取的养老金减少,因此理性行为人会增加成年期储蓄,以保障老年期消费。这既会通过提高资本总量而使生育率上升,又会通过挤占子女养育费用而使生育率下降。其三,降低缴费率使个人老年期的可支配工资收入增加,因此理性行为人会减少成年期储蓄,分别通过降低资本总量和增加子女养育费用而使生育率下降和上升。如果不考虑延迟退休,则没有该影响机制。在本文中,降低养老保险缴费率对生育率的促进作用更大,从而提高生育率。
延迟退休意味着个人需要在老年期继续工作一段时间,以获得可支配工资收入
由于新古典增长框架下均衡状态的总产出增长率等于生育率,因此降低养老保险缴费率和延迟退休使得生育率上升意味着它们能够促进经济增长。接下来,我们考察降低缴费率和延迟退休对养老金替代率的影响。将式(12)分别对
| $\frac{{d{\delta ^*}}}{{d\theta }} = \frac{{({n^*} + x) + \theta {{d{n^*}}/{d\theta }}}}{{1 - x}}$ | (21) |
| $\frac{{d{\delta ^*}}}{{dx}} = \frac{{\theta ({{d{n^*}}/{dx}} + 1)(1 - x) + \theta ({n^*} + x)}}{{{{(1 - x)}^2}}} > 0$ | (22) |
于是得到结论2:新古典增长框架下,若给定延迟退休岁数,降低养老保险缴费率对养老金替代率的影响不确定;若给定养老保险缴费率,延迟退休将使得均衡状态的养老金替代率上升。
养老金替代率是单位时间内的养老金与工资的比值,因此降低缴费率和延迟退休对养老金替代率的影响取决于其对单位时间内的养老金和工资的影响。观察式(21)可知,由于我们只得到
延迟退休对养老金替代率的作用机制为:一方面,延迟退休通过减少个人成年期的储蓄降低了均衡状态的劳均资本,使得单位时间内的工资和养老金都减少;另一方面,延迟退休通过增加缴费人数提高了养老保险基金收入,通过缩短养老金领取年限降低了养老保险基金支出,现收现付制下可以增加单位时间内的养老金。比较静态分析表明,延迟退休对单位时间内养老金的负向影响较小,甚至可能有正向影响,从而提高养老金替代率。
(二)基于内生增长框架的分析
根据Barro和Sala-i-Martin(2004)的做法,劳均产出函数为:
| ${w_t} = A(1 - \alpha )k_t^\alpha {({\bar k_t})^{1 - \alpha }}{\rm{ = }}A(1 - \alpha ){k_t}$ | (23) |
| ${R_t} = A\alpha k_t^{\alpha - 1}{({\bar k_t})^{1 - \alpha }}{\rm{ = }}A\alpha $ | (24) |
内生增长框架下,均衡状态的劳均资本和劳均产出不再收敛于常数,而是以一个恒定不变的速度
| $\frac{{{k_{t + 1}}}}{{{k_t}}}{\rm{ = }}\frac{{\beta A(1 - \theta )(1 - \alpha )}}{{(1 + \varphi + \beta )({n_t} + x) + (1 + \varphi )(x + \theta {n_t}){{(1 - \alpha )}/\alpha }}}$ | (25) |
| $\frac{{{k_{t + 1}}}}{{{k_t}}}{\rm{ = }}\frac{{A\alpha \left[ {v{n_t}{{(1 + \varphi + \beta )}/\varphi } - (1 - \theta )} \right]}}{{x + \theta {n_t}}}$ | (26) |
均衡状态时,
| $sign\left\{ {{{d{n^*}}/{d\theta }}} \right\} = sign\left\{ {{\Phi _\theta }(\theta ,x,{n^*}) - {\Xi _\theta }(\theta ,x,{n^*})} \right\} < 0$ | (27) |
| $sign\left\{ {{{d{n^*}}/{dx}}} \right\} = sign\left\{ {{\Phi _x}(\theta ,x,{n^*}) - {\Xi _x}(\theta ,x,{n^*})} \right\} = sign\left\{ {{{{n^*}(1 - \theta )}/{(\theta {n^*} + x)}}} \right\} > 0$ | (28) |
于是得到结论3:内生增长框架下,若给定延迟退休岁数,降低养老保险缴费率将使得均衡状态的生育率上升;若给定养老保险缴费率,延迟退休也将使得均衡状态的生育率上升。
内生增长框架下降低缴费率和延迟退休对生育率的影响机理与新古典增长框架相同,此处不再赘述。
内生增长框架下均衡状态的养老金替代率
综上所述,本文分别在新古典增长框架和内生增长框架下考察了降低养老保险缴费率和延迟退休对生育率、总产出增长率和养老金替代率的影响。均衡分析发现:新古典增长框架下,降低缴费率和延迟退休均能提高生育率和总产出增长率,前者对养老金替代率的影响方向不确定,而后者能提高养老金替代率;内生增长框架下,降低缴费率和延迟退休均能提高生育率,但两者对总产出增长率和养老金替代率的影响都不确定。
四、数值模拟
(一)参数取值
根据模型求解结果,待设定的参数有
1. 消费的时间偏好贴现因子
2. 父母对每个子女的养育费用占其工资收入的比重
3. 资本产出弹性
4. 全要素生产率
5. 个人对子女数量的偏好程度
(二)模拟结果分析
将参数基准值代入模型求解结果,数值模拟两种框架下降低养老保险缴费率和延迟退休对重要经济变量的影响。表2给出了新古典增长框架下的模拟结果。当退休年龄为55岁(不考虑延迟退休)时,生育率(总产出增长率)随缴费率的下降而上升,而养老金替代率随缴费率的下降而下降,表明现收现付制下,降低缴费率在提高生育率和促进经济增长的同时会降低退休人员福利水平,无法同时实现养老金替代率不降、基金财务平衡和经济增长三个目标。这一方面证实了降费率存在政策目标上的“不可能三角”;另一方面提示我们在降低缴费率时需要处理好经济增长与民生保障之间的关系,决不能只注重经济增长而忽视民生福祉受损。当养老保险缴费率为20%时,随着延迟退休岁数的增加,生育率(总产出增长率)和养老金替代率都不断上升,表明延迟退休在提高生育率和促进经济增长的同时改善了退休人员福利水平,可以起到破解降费率“不可能三角”的作用。
| 养老保险缴费率 | 0.2 | 0.19 | 0.18 | 0.17 | 0.16 | 0.15 | 0.14 | 0.13 | 0.12 | 0.11 | 0.1 |
| n*(g*) | 0.800 | 0.807 | 0.814 | 0.821 | 0.827 | 0.834 | 0.840 | 0.846 | 0.852 | 0.858 | 0.864 |
| δ* | 0.160 | 0.153 | 0.147 | 0.140 | 0.132 | 0.125 | 0.118 | 0.110 | 0.102 | 0.094 | 0.086 |
| 延迟退休岁数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| n*(g*) | 0.800 | 0.808 | 0.815 | 0.821 | 0.827 | 0.832 | 0.837 | 0.841 | 0.845 | 0.848 | 0.852 |
| δ* | 0.160 | 0.172 | 0.185 | 0.198 | 0.213 | 0.228 | 0.243 | 0.260 | 0.278 | 0.298 | 0.319 |
| 注:表2在考察降低养老保险缴费率对经济变量影响时,假设退休年龄为55岁(不考虑延迟退休);在考察延迟退休对经济变量影响时,假设养老保险缴费率为20%。 | |||||||||||
表3给出了内生增长框架下降低养老保险缴费率和延迟退休的模拟结果。可以看出,当退休年龄为55岁时,降低缴费率将使得生育率、劳均资本增长率和总产出增长率上升,但也将使得养老金替代率下降,相当于是用退休人员的福利受损换取了经济可持续增长,同样证实了降费率存在政策目标上的“不可能三角”。当养老保险缴费率为20%时,延迟退休将使得生育率和养老金替代率上升、劳均资本增长率和总产出增长率下降,相当于是用经济增速放缓换取了退休人员福利水平的提高。这一方面说明延迟退休有助于提高生育率和改善民生福祉,另一方面说明延迟退休通过抑制资本积累渠道对经济增长带来的负向影响大于其通过提高生育率渠道对经济增长带来的正向影响,导致延迟退休会抑制经济增长。从总产出增长率和养老金替代率的变化趋势来看,内生增长框架下降低缴费率和延迟退休的作用效果恰好相反,因此延迟退休在理论上存在破解降费率“不可能三角”的可能。
| 养老保险缴费率 | 0.2 | 0.19 | 0.18 | 0.17 | 0.16 | 0.15 | 0.14 | 0.13 | 0.12 | 0.11 | 0.1 |
| n* | 0.800 | 0.807 | 0.814 | 0.821 | 0.827 | 0.834 | 0.840 | 0.846 | 0.852 | 0.858 | 0.864 |
| γ* | 0.193 | 0.195 | 0.198 | 0.200 | 0.203 | 0.205 | 0.208 | 0.210 | 0.213 | 0.216 | 0.218 |
| g* | 0.155 | 0.158 | 0.161 | 0.164 | 0.168 | 0.171 | 0.174 | 0.178 | 0.181 | 0.185 | 0.189 |
| δ* | 0.031 | 0.030 | 0.029 | 0.028 | 0.027 | 0.026 | 0.024 | 0.023 | 0.022 | 0.020 | 0.019 |
| 延迟退休岁数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| n* | 0.800 | 0.808 | 0.815 | 0.821 | 0.827 | 0.832 | 0.837 | 0.841 | 0.845 | 0.848 | 0.852 |
| γ* | 0.193 | 0.181 | 0.170 | 0.161 | 0.153 | 0.145 | 0.139 | 0.133 | 0.127 | 0.122 | 0.117 |
| g* | 0.155 | 0.146 | 0.139 | 0.132 | 0.126 | 0.121 | 0.116 | 0.112 | 0.107 | 0.104 | 0.100 |
| δ* | 0.031 | 0.032 | 0.033 | 0.034 | 0.036 | 0.037 | 0.039 | 0.040 | 0.042 | 0.044 | 0.047 |
| 注:表3在考察降低养老保险缴费率对经济变量影响时,假设退休年龄为55岁(不考虑延迟退休);在考察延迟退休对经济变量影响时,假设养老保险缴费率为20%。 | |||||||||||
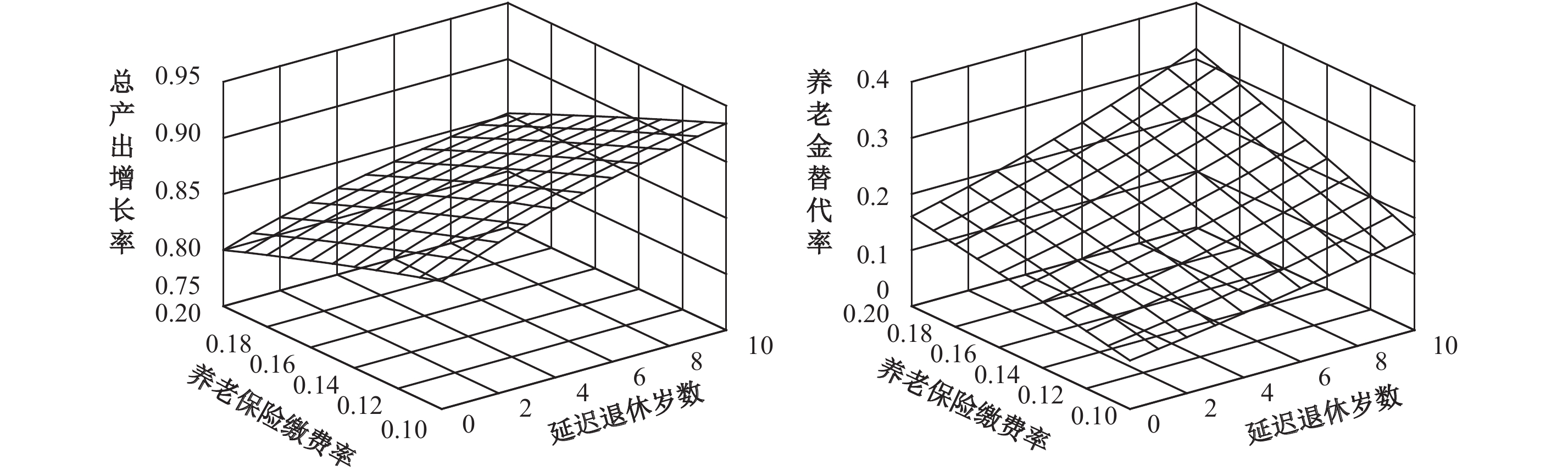
以上分析是在给定延迟退休岁数或养老保险缴费率的情况下,考察降低缴费率或延迟退休对重要经济变量的影响,而没有考虑两项政策配合实施产生的效应。事实上,降低养老保险缴费率政策已经在实施,而延迟退休方案虽未公布但政府释放的各种信号显示该项政策势在必行,这意味着未来中国极有可能是降低缴费率和延迟退休同时进行。为此,有必要分析两者的组合变化对总产出增长率和养老金替代率的综合影响,以全面揭示其经济效应。模拟结果如图1和图2所示,在给定延迟退休岁数的截面上,两种框架下降低养老保险缴费率都将使得总产出增长率上升和养老金替代率下降,进一步证实了降费率存在政策目标上的“不可能三角”。在给定养老保险缴费率的截面上,两种框架下延迟退休都将使得养老金替代率上升,但其对总产出增长率的影响存在显著差异,即延迟退休在新古典增长框架下能提高总产出增长率,而在内生增长框架下却会降低总产出增长率,这与严成樑(2016)的研究结论相符。在新古典增长框架下,降低缴费率和延迟退休都能促进经济增长,但降低缴费率将导致养老金替代率下降,延迟退休则有助于提高养老金替代率。因此,实施延迟退休政策可以在促进经济增长的同时抵消缴费率下降对养老金替代率的负面影响,达到破解降费率“不可能三角”的目的。在内生增长框架下,降低缴费率能够促进经济增长,但导致养老金替代率下降;延迟退休有助于提高养老金替代率,但会抑制经济增长。降低缴费率和延迟退休的政策效果具有抵消效应,延迟退休能否破解降费率“不可能三角”取决于两者之间的抵消效应。
|
| 图 1 新古典增长框架下养老保险缴费率和延迟退休不同组合的模拟结果 |

|
| 图 2 内生增长框架下养老保险缴费率和延迟退休不同组合的模拟结果 |
(三)敏感性分析
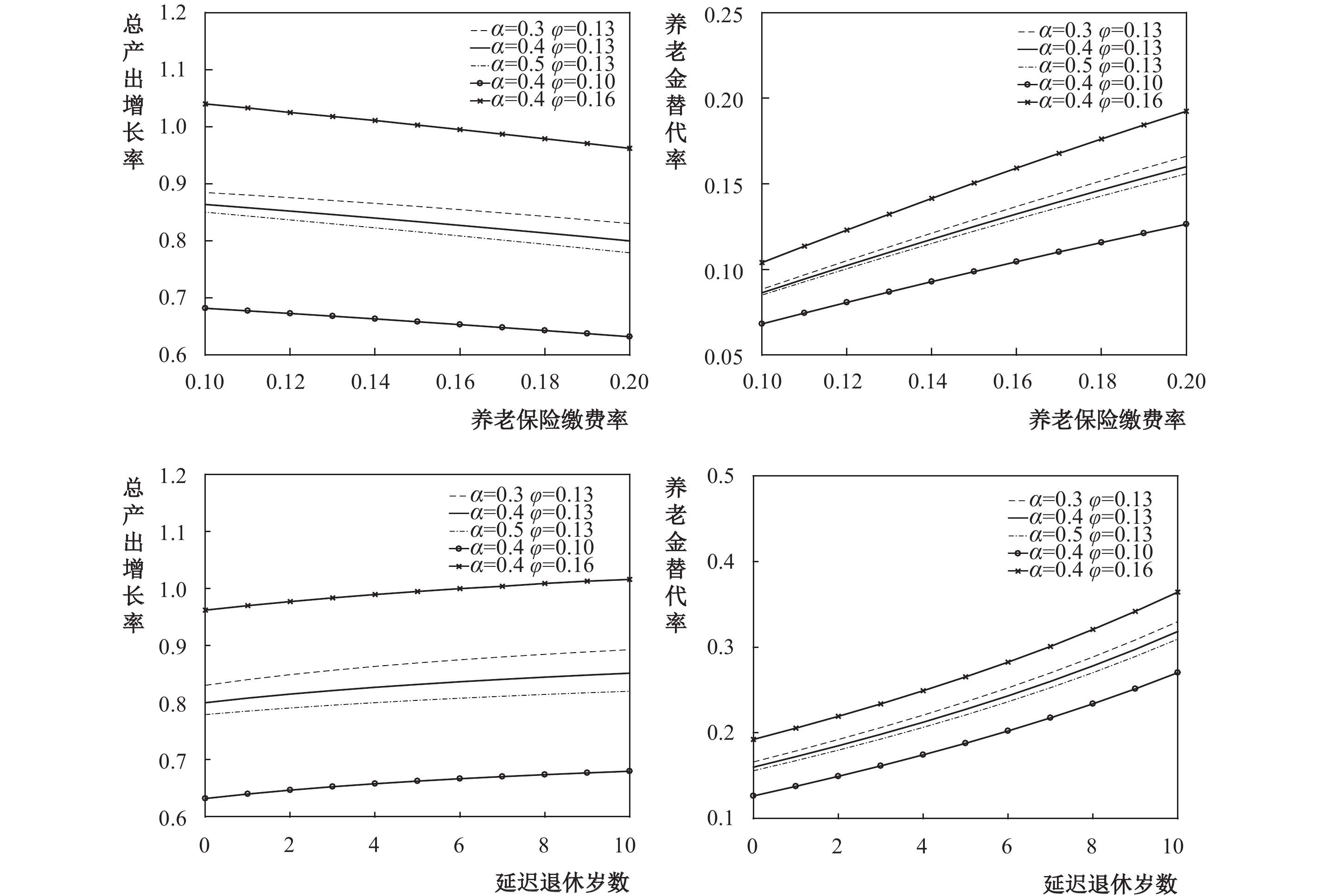
考虑到资本产出弹性
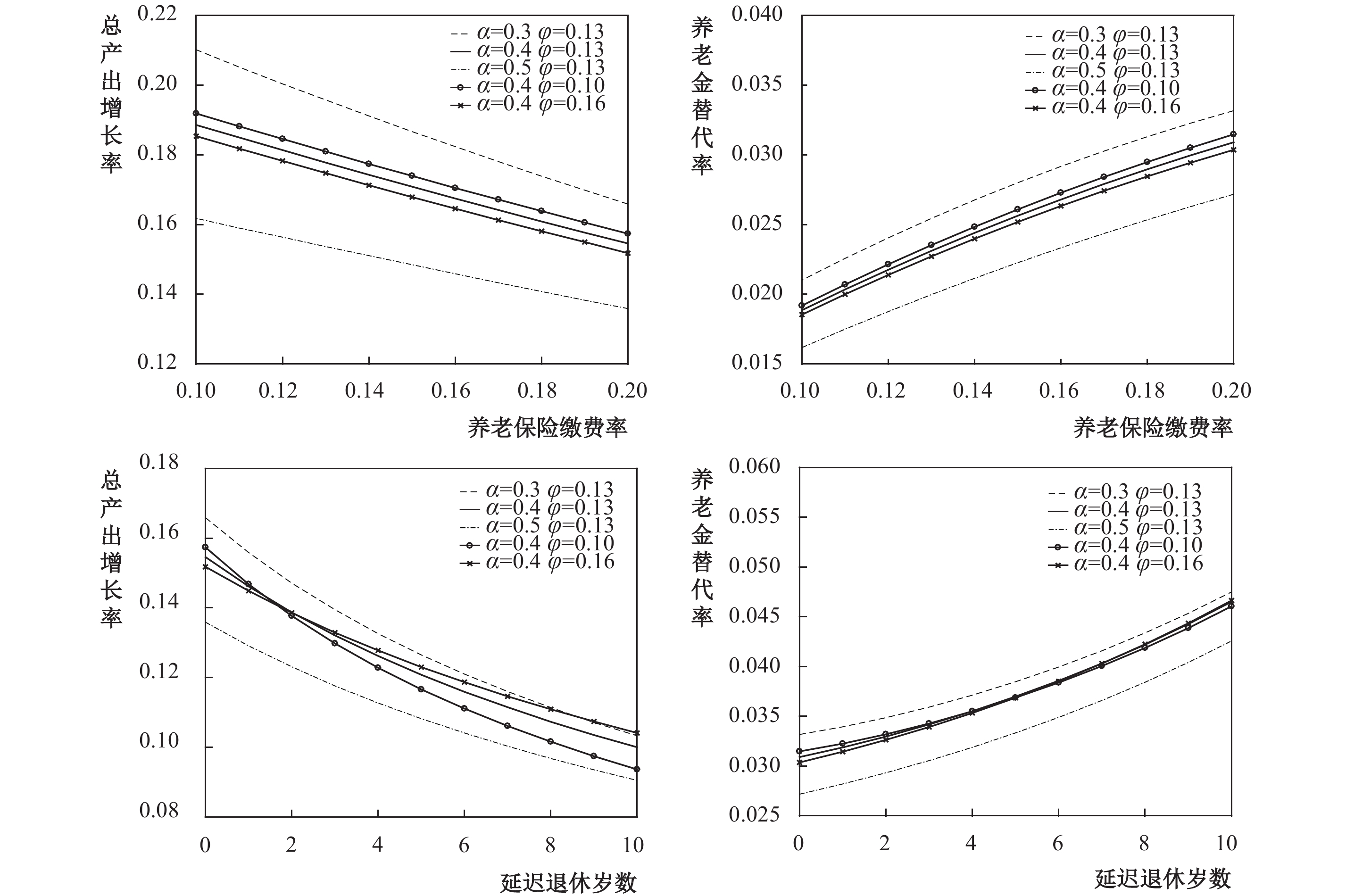
如图4所示,内生增长框架下改变
|
| 图 3 新古典增长框架下的敏感性分析结果 |
|
| 图 4 内生增长框架下的敏感性分析结果 |
随着资本产出弹性的提高,总产出增长率和养老金替代率都将下降,说明提高资本产出弹性会抑制经济增长和削减退休人员的福利水平,这与新古典增长框架下的结果保持一致。与基准情形相比,个人对子女数量的偏好程度越高,则降低缴费率后总产出增长率和养老金替代率越低,而延迟退休后两者都呈先下降后上升的变化趋势。这意味着在延迟退休过程中相应调整父母利他主义强度能够减弱延迟退休对经济增长的负向影响和增强其对养老金替代率的正向影响。
敏感性分析表明,资本产出弹性和个人对子女数量的偏好程度均不会改变降低缴费率和延迟退休对总产出增长率和养老金替代率的影响方向。资本产出弹性变化在内生增长框架下的影响更大,而个人对子女数量的偏好程度变化则在新古典增长框架下的影响更大。
(四)降费率过程中的延迟退休设定
对于总产出增长率,若降低缴费率有促进作用而延迟退休有抑制作用,则只有当延迟退休岁数T不高于临界值T1时,才能确保总产出增长率不降;对于养老金替代率,若降低缴费率有抑制作用而延迟退休有促进作用,则只有当延迟退休岁数T不低于临界值T2时,才能确保养老金替代率不降。结合前文的模拟结果,在新古典增长框架下,如果延迟退休岁数T≥T2,则可以在促进经济增长的同时确保养老金替代率不降;在内生增长框架下,如果延迟退休岁数T2≤T≤T1,则可以确保经济增长率和养老金替代率都不降。换言之,给定养老保险缴费率,欲使延迟退休破解降费率“不可能三角”,则延迟退休岁数在新古典增长框架下需满足T≥T2,而在内生增长框架下需满足T2≤T≤T1。据此,我们保持其他参数不变,数值模拟不同缴费率下分别实现总产出增长率不降目标和养老金替代率不降目标所需的延迟退休岁数临界值,结果如表4所示。
| θ | 0.2 | 0.19 | 0.18 | 0.17 | 0.16 | 0.15 | 0.14 | 0.13 | 0.12 | 0.11 | 0.1 |
| 新古典增长框架 | |||||||||||
| T1 | — | — | — | — | — | — | — | — | — | — | — |
| T2 | 0 | 0.57 | 1.19 | 1.90 | 2.64 | 3.47 | 4.38 | 5.39 | 6.47 | 7.68 | 9.02 |
| 破解
“不可能三角” |
√ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| 内生增长框架 | |||||||||||
| T1 | 0 | 0.35 | 0.71 | 1.08 | 1.46 | 1.85 | 2.25 | 2.66 | 3.08 | 3.51 | 3.95 |
| T2 | 0 | 1.01 | 2.04 | 3.10 | 4.19 | 5.35 | 6.56 | 7.82 | 9.17 | 10.59 | 12.11 |
| 破解
“不可能三角” |
× | × | × | × | × | × | × | × | × | × | × |
| 注:T1表示实现总产出增长率不降时的延迟退休岁数最大值,T2表示实现养老金替代率不降目标时的延迟退休岁数最小值。 | |||||||||||
在新古典增长框架下,欲维持原有养老金替代率,伴随缴费率的下降,则延迟退休岁数临界值T2需不断提高。例如,θ=16%时,T2=2.64,意味着缴费率降至16%时,退休年龄至少需要延迟2.64岁,才能确保养老金替代率不降。因此,在新古典增长框架下,延迟退休是一个合理且有效的政策选项,只要延迟退休岁数不低于临界值就能有效破解降费率“不可能三角”。在内生增长框架下,实现两种目标所需的延迟退休岁数临界值T1和T2均随着缴费率的下降而提高。例如,θ=16%时,T1=1.46,T2=4.19;θ=12%时,T1=3.08,T2=9.17。但是,任何缴费率水平下T1都小于T2,不满足条件T2≤T≤T1,说明内生增长框架下延迟退休无法破解降费率“不可能三角”,此时延迟退休的作用是失效的。
综上所述,延迟退休破解养老保险降费率“不可能三角”的作用效果在两种框架下存在显著差异,“不可能三角”在新古典增长框架下能得到有效破解,而在内生增长框架下则不能被破解,表明延迟退休能否破解降费率“不可能三角”取决于经济增长模式。目前,中国经济增长模式属于新古典增长模式,而从新古典增长模式转向内生增长模式是一个长期过程。因此,为了破解当下面临的养老保险降费率“不可能三角”,应高度重视延迟退休政策所带来的时间窗口,抢抓战略机遇期,尽快实施延迟退休以抵消缴费率下降带来的负面影响。④需要说明的是,尽管延迟退休在内生增长模式下破解降费率“不可能三角”是失效的,但可以借助人力资本积累和技术进步来化解延迟退休对经济增长的抑制作用。郭凯明和颜色(2016)研究表明,延迟退休在考虑人力资本因素的情况下能促进经济增长,那么延迟退休将能继续破解降费率“不可能三角”。此外,我们还可以通过国有资本划转、财政支出结构调整等方式来进一步破解降费率“不可能三角”。
五、结论与启示
本文基于新古典增长框架和内生增长框架,在基金财务平衡约束下,考察了降低养老保险缴费率和延迟退休对总产出增长率和养老金替代率的影响,探讨延迟退休能否破解养老保险降费率“不可能三角”。研究发现:第一,两种框架下降低缴费率都将使得均衡状态的总产出增长率上升和养老金替代率下降,无法同时实现养老金替代率不降、基金财务平衡和经济增长三个目标,证实了养老保险降费率存在政策目标上的“不可能三角”。第二,两种框架下延迟退休都将使得均衡状态的养老金替代率上升,但其对总产出增长率的影响却截然相反。在新古典增长框架下,延迟退休通过提高生育率而促进总产出增长率上升;在内生增长框架下,延迟退休通过提高生育率对总产出增长率的正向影响不足以弥补其通过抑制资本积累对总产出增长率的负向影响,从而降低总产出增长率。第三,延迟退休破解养老保险降费率“不可能三角”的作用效果在两种框架(经济增长模式)下存在显著差异。在新古典增长框架下,延迟退休可以在确保养老金替代率不降的同时提高总产出增长率,能够有效破解降费率“不可能三角”;而在内生增长框架下,延迟退休不能同时确保总产出增长率和养老金替代率都不降,无法破解降费率“不可能三角”。当前中国经济增长模式属于新古典增长模式,从破解养老保险降费率“不可能三角”的角度来看,延迟退休是一个有效政策选项,但随着经济增长模式逐渐转变为内生增长模式,我们需要警惕延迟退休带来的潜在不利影响。
基于上述结论,本文得到如下三点政策启示:第一,在理念层面,正确处理好经济增长与民生保障之间的关系,推进养老保险制度与经济社会良性互动发展。降低养老保险缴费率不应仅着眼于减轻企业负担和促进经济增长,还应坚守养老保险制度的核心目标,为退休人员提供适度稳定的老年经济保障并维持制度长期平稳运行,以更好体现“坚持在发展中保障和改善民生”的宗旨。第二,在政策层面,辩证地看待延迟退休的政策效应。我们既要看到短期内新古典增长模式下延迟退休能够破解降费率“不可能三角”的积极效应,也要看到长期内内生增长模式下其无法破解降费率“不可能三角”的消极效应,提前研究制定相关措施来消除或减轻延迟退休对经济增长的潜在不利影响。此外,在制定延迟退休政策时,宜采取小步渐进方式,并建立与缴费率关联的动态调整机制,这样不仅可以降低延迟退休的实施阻力,而且可以给企业和公众留有时间做好充分准备。第三,在配套措施层面,积极拓宽养老保险筹资渠道,多措并举化解基金潜在缺口。除延迟退休外,一方面通过完善基金征缴管理、提升累积基金运营管理水平、建立养老金待遇合理调整机制等实现基金的“开源节流”;另一方面通过划转国有资本和适当提高财政补贴规模等“外部筹资”来充实基金。
当然,本文的研究也存在一些不足,未来可改进的工作至少包括两个方面:一是在模型设定上,引入更多的经济机制和现实条件,如考虑人力资本、国有资本划转、财政支出结构调整等,从而更全面地探讨如何破解养老保险降费率“不可能三角”。二是在研究内容上,降低养老保险缴费率和延迟退休还会对社会公平产生深刻的影响,因而探讨两项政策可能产生的代内和代际不平等问题,也是未来一个重要的研究方向。
① 蔡昉和刘世锦在2016年北大赛瑟论坛主旨演讲中表示,当前中国经济增长越来越像新古典增长模式。资料来源:
② 中国人民大学研究员张杰认为,中国经济发展正处于逐步过渡到以内生驱动为主的进程中,将步入一个全新的内生型增长周期。资料来源:
③ 目前我国的总和生育率介于1.5−1.6之间,本文取值为1.6。另外,理论模型没有区分性别,每个人代表一个家庭,且都可以生育子女,模型中的生育率可理解为总和生育率的50%,则n=0.8。
④ 从现实需要看,延迟退休是顺应人口寿命延长规律、充分有效利用人力资源、缓解劳动力供给短缺和应对人口老龄化挑战的合理政策措施,理应尽快推出延迟退休政策。此外,弥补养老保险基金缺口和化解养老金赤字是延迟退休的自然延伸结果,并非其核心目标之所在。
| [1] | 耿志祥, 孙祁祥. 人口老龄化、延迟退休与二次人口红利[J]. 金融研究, 2017(1): 52–68. |
| [2] | 郭晗, 任保平. 结构变动、要素产出弹性与中国潜在经济增长率[J]. 数量经济技术经济研究, 2014(12): 72–84. |
| [3] | 郭凯明, 龚六堂. 社会保障、家庭养老与经济增长[J]. 金融研究, 2012(1): 78–90. |
| [4] | 郭凯明, 颜色. 延迟退休年龄、代际收入转移与劳动力供给增长[J]. 经济研究, 2016(6): 128–142. |
| [5] | 胡永刚, 石崇. 中国经济增长: 内生还是外生型[J]. 学术月刊, 2016(1): 87–100. |
| [6] | 景鹏, 胡秋明. 生育政策调整、退休年龄延迟与城镇职工基本养老保险最优缴费率[J]. 财经研究, 2016(4): 26–37. |
| [7] | 景鹏, 胡秋明. 企业职工基本养老保险统筹账户缴费率潜在下调空间研究[J]. 中国人口科学, 2017(1): 21–33. |
| [8] | 刘仁和, 陈英楠, 吉晓萌, 等. 中国的资本回报率: 基于q理论的估算[J]. 经济研究, 2018(6): 67–81. |
| [9] | 彭浩然, 陈斌开. 鱼和熊掌能否兼得: 养老金危机的代际冲突研究[J]. 世界经济, 2012(2): 84–97. |
| [10] | 彭浩然, 邱桓沛, 朱传奇, 等. 养老保险缴费率、公共教育投资与养老金替代率[J]. 世界经济, 2018(7): 148–168. |
| [11] | 严成樑. 延迟退休、内生出生率与经济增长[J]. 经济研究, 2016(11): 28–43. |
| [12] | 曾益, 刘凌晨, 高健. 我国城镇职工基本养老保险缴费率的下调空间及其财政效应研究[J]. 财经研究, 2018(12): 70–84. |
| [13] | Banerjee A, Meng X, Porzio T, et al. Aggregate fertility and household savings: A general equilibrium analysis using micro data[R]. NBER Working Paper No. W20050, 2014. |
| [14] | Barro R J, Sala-i-Martin X. Economic growth[M]. 2nd ed. Cambridge, MA: MIT Press, 2004. |
| [15] | Ehrlich I, Kim J. Social security and demographic trends: Theory and evidence from the international experience[J]. Review of Economic Dynamics, 2007, 10(1): 55–77. DOI:10.1016/j.red.2006.09.002 |
| [16] | Fanti L, Gori L. Increasing PAYG pension benefits and reducing contribution rates[J]. Economics Letters, 2010, 107(2): 81–84. DOI:10.1016/j.econlet.2009.01.001 |
| [17] | Fanti L. Raising the mandatory retirement age and its effect on long-run income and Pay-as-you-go (PAYG) pensions[J]. Metroeconomica, 2014, 65(4): 619–645. DOI:10.1111/meca.12055 |
| [18] | Funke M, Strulik H. On endogenous growth with physical capital, human capital and product variety[J]. European Economic Review, 2000, 44(3): 491–515. DOI:10.1016/S0014-2921(98)00072-5 |
| [19] | Galasso V. Postponing retirement: The political effect of aging[J]. Journal of Public Economics, 2008, 92(10-11): 2157–2169. DOI:10.1016/j.jpubeco.2008.04.012 |
| [20] | Kitao S. Sustainable social security: Four options[J]. Review of Economic Dynamics, 2014, 17(4): 756–779. DOI:10.1016/j.red.2013.11.004 |
| [21] | Miyazaki K. The effects of the raising-the-official-pension-age policy in an overlapping generations economy[J]. Economics Letters, 2014, 123(3): 329–332. DOI:10.1016/j.econlet.2014.03.011 |
| [22] | Yew S L, Zhang J. Optimal social security in a dynastic model with human capital externalities, fertility and endogenous growth[J]. Journal of Public Economics, 2009, 93(3-4): 605–619. DOI:10.1016/j.jpubeco.2008.10.005 |


