
2020第46卷第9期
2. 澳门城市大学 商学院,澳门 999078
2. Faculty of Business,City University of Macau,Macau 999078,China
一、引 言
在搜寻工作机会的过程中,劳动力会面临诸多因素的限制,如空间和信息的限制。劳动力在进行工作搜寻时,通常都会设定一个大致的空间范围:有的人因为安土重迁或语言不通,不愿意为了更好的就业机会而离开自己的国家或家乡;有的人即使和岗位处在同一城市,交通路线的缺乏与不便也会使工作岗位对其失去吸引力。在信息方面,工人获取招聘信息的能力限制了工作搜寻活动的范围:有些人通过熟人介绍,仅能接触到少量的工作机会;而有些人通过查阅报刊中的招聘信息,可以了解到更多的就业岗位。因此,空间和信息的限制使得劳动力必须在有限的范围内进行工作搜寻。
然而,随着信息技术和交通工具的发展,人们获取信息的能力、通勤的空间范围都得到了一定的提升,因此求职者的工作搜寻行为也发生了较大改变。互联网技术使得求职者可以在极短时间内筛选出大量符合条件的招聘信息,其获取信息的数量和效率明显优于熟人介绍或者查阅报刊。而日渐发达的城市交通,如地铁、城轨和高铁的开通等,使得劳动力有可能选择较远的工作岗位就业,甚至会接受跨市就业。因此,技术的进步逐步减少了工作搜寻中空间和信息的限制,劳动力的工作搜寻范围凭借着信息技术的进步在逐渐扩大。
由技术进步所带来的工作搜寻范围的扩大会造成什么影响?本文利用主体基建模( Agent-Based Model )方法进行仿真实验,研究工人的搜寻范围集体扩大对失业率、工资水平和市场的匹配效率等方面所产生的影响。
在瓦尔拉斯式的劳动力市场模型中,劳动力的供给和需求都可以瞬间调节从而达到均衡。因此在理想状态下,劳动力市场不应该存在失业现象。我们所观察到的失业被理解为工人和岗位之间的匹配摩擦,是一种暂时的错觉(罗默,2014)。因此,瓦尔拉斯式的劳动力市场模型并没有深入地考虑工人和岗位之间的匹配活动。
然而,现实世界中失业现象的长期存在证明了真实的劳动力市场并不是瓦尔拉斯式的市场,匹配摩擦并不是无关紧要的。因此,戴蒙德、莫滕森和皮萨里德斯建立了搜寻匹配模型(DMP模型),深入地研究了工人与岗位之间的匹配活动对劳动力市场的影响(皮萨里德斯,2012)。搜寻匹配模型认为匹配摩擦是必然存在的,并且是有成本的。为了将匹配摩擦考虑进来,模型建立了一个匹配函数以描述工人和岗位之间的匹配活动(皮萨里德斯,2012)。另外通过匹配函数,模型可以推导出许多关于劳动力市场的重要结论。
在70年代,搜寻匹配模型的一些基础性研究得到了完善和发展(McCall,1970;Mortensen,1970;Reuben,1971),学术界也有不少学者在此基础上进行了后续的扩展研究。在众多的扩展研究中,有一些学者关注了技术进步对搜寻匹配活动的影响。Aghion和Howitt(1992和1994)认为,生产技术的进步将通过“资本化效应”和“创造性破坏效应”对均衡失业率产生两种相反的影响。King 和 Welling(1995)认为,技术创新将使得工人进行更多的搜索,并且降低了总失业率。
但是上述的研究几乎都只关注生产技术的进步所带来的影响,而较少提到工作搜寻的技术进步。仅有Aghion在讨论“创造性破坏效应”时认为,技术进步在提高生产率的同时,也会促进工人和岗位的匹配,从而减少工人失业的等待时间,增加岗位和在职工人的分离率(Aghion,1992)。另外,皮萨里德斯在《均衡失业理论》中分析失业与搜寻强度时也提到,反映搜寻技术的搜寻成本函数“在整个经济周期中不太可能发生明显的变化,因此不是我们关心的变量”(皮萨里德斯,2012)。由此可见,在搜寻匹配模型的技术进步相关研究中,搜寻技术进步的影响是被忽略的,很少被学者提及。
尽管如此,在搜寻匹配模型的框架之外,仍然有一些学者注意到了工作搜寻的技术进步,并对其产生的影响进行探讨。Autor(2001)认为,数字技术和互联网使得工人和企业的搜寻行为发生了改变,这将影响工人和企业的匹配方式,而搜寻成本的降低将使得社会总福利增加,同时劳动力市场的匹配效率也得到提升。Kuhn和Skuterud(2004)利用访问数据发现,使用互联网搜寻工作虽然能够减少失业的时间,使得工人和企业更快地匹配,但是互联网的使用对于工资的提高没有帮助。Beard(2012)利用了美国人口普查局的数据,证明了互联网的使用减少了劳动力市场的匹配障碍。但是上述的研究都只是经验数据的实证研究,并没有从理论模型上探讨更为具体和详细的影响机制。
相较于现有文献,本文创新之处有二:一是与以往讨论生产技术进步不同,本文关注搜寻技术进步带来的工作搜寻范围扩大,并研究其对劳动力市场的影响;二是通过主体基模型和多主体模拟实验方法,更细致和微观地对劳动力失业进行分析,并且对不同类型失业进行了区分。
本文的余下部分安排如下:第二部分介绍了主体基建模方法与模拟实验以及在劳动力市场的研究领域的应用;第三部分是本文劳动力市场的基准模型的构建;第四部分是对基准模型的校准,并且本文利用校准好的基准模型还拟合出了与劳动力市场相关的典型事实特征(如菲利普斯曲线、贝弗里奇曲线和奥肯曲线);第五部分是实验组的设置与实验结果的分析;第六部分是本文主要的研究结论。
二、主体基建模方法
在国内外的学术界中,工人搜寻行为的相关研究大多采用数理模型或实证检验的方法。本文尝试采用一种新兴的经济学方法来进行研究,即主体基模型(Agent-Based Model)。ABM是一种用于模拟自动主体之间行为和互动的计算机模型。此类模型包含众多的微观主体,建模的要点在于赋予它们行为规则。当模型开始运行时,众多微观主体将依照已经设定好的规则进行互动,并产生宏观现象。由于模型的运行包含了诸多随机、非线性等因素,因此模型所表现出来的图景并不是简单的个体加总,而是具有一定的复杂性。
目前,ABM已被广泛地运用于生态学、物理学和社会科学等非计算机领域。有部分经济学领域的学者正在介绍和推广这种新兴的建模方法,并将该方法运用于金融、劳动力市场、国际贸易和税收等领域的研究。Tesfatsion是较早采用ABM方法研究劳动力市场的经济学学者,她在1998年的论文中利用ABM方法研究了劳动力市场不同的市场结构所带来的动态结果和社会福利影响(Tesfatsion,1998)。
在国内经济学界中,也有部分学者开始利用ABM方法在不同的经济学领域中开展各种研究。如董志强等(董志强,2011;董志强等,2015;董志强和李伟成,2019)采用演化博弈模型和随机演化仿真模型,证明了人类的公平偏好心理和禀赋效应均源于人类早期的进化过程,是具有适应性优势的行为模式。叶航(2012)也利用多主体计算机仿真方法,证明了只要公共品的回报足够大,公共品博弈中对于二阶搭便车行为的惩罚就能够保持演化稳定,从而化解了二阶社会困境。黄凯南和乔元波(2018)通过包含技术创新的复制者动态模型和仿真实验,考察产业技术与制度的共同演化问题,并分析共同演化过程的创新效应、模仿效应和规模效应及其对产业总体绩效的影响。韦立坚(2016和2017)利用ABM方法建立股市交易模型,通过计算机实验研究了股市流动性踩踏危机以及T+0交易制度等证券市场交易的相关话题。
还有一些学者曾经提倡采用ABM方法来研究劳动力市场。如Bergmann(1990)曾经呼吁采用微观仿真的方法来模拟劳动力市场的运行,他认为这种基于多主体微观行为的建模方法可以做到真正地连接宏观和微观两个层面。Tesfatsion认为,①学者采用ABM方法来研究劳动力市场时,可以利用其独特的建模思路和优势,重点可以关注社会网络、市场结构、地理限制和文化习俗等因素对劳动力市场的影响以及异质性工人在劳动力市场中的表现,这为我们对劳动力市场的理解提供新的视角。
不少学者已经在劳动力市场的研究中采用了ABM建模方法。如Tesfatsion(1998)采用ABM方法建立了劳动力市场雇佣合同网络,并重点关注在不同的市场结构下合作网络的演变。Neugart(2008)则采用ABM方法来评估政府资助的培训政策对市场的影响。Lewkovicz(2008)则试图利用多主体模型重现法国劳动力市场,并研究新型合同对劳动力市场稳定性的影响。Martin和Neugart(2009)则关注工人、政党和政府的劳动市场政策等政治经济因素之间的互动关系。国内也有一些学者利用ABM方法研究劳动力市场。比如,欧恺和秦向东(2008)利用基于主体的模拟实验,研究了不同的市场结构和不同期限的非就业补偿对工人和雇主的影响。刘怀宇等(2015)利用多主体模型,探讨了城乡二元结构对北京的农户家庭劳动力配置的决策机制。除了上述ABM劳动力市场研究以外,还有不少未提及的研究,在此就不一一赘述。
本文将利用ABM方法建立一个劳动力市场模型,为后续的模拟实验研究提供一个基准模型。与以往的搜寻匹配模型不同,本文的主体基模型不再是由单个主体来代表全体的工人或企业,而是一个由众多异质性的工人和企业所组成的多主体计算机模型。在模型当中,每个工人和企业将按照建模者指定的规则进行互动和交易,其中就包括了搜寻匹配活动、工资制定、生产和消费活动等经济行为。
ABM劳动力市场模型与传统的数理模型相比,有其自身的独特性。以往的数理模型大多以单一工人的行为来代表全体工人的行为,对企业的做法也是如此。然而,这种做法忽略了工人之间行为的相互影响:当一个失业工人获得了一个就业机会,这有可能意味着另一个失业工人失去了就业机会。ABM模型是由数量众多的主体构成的,如本文的劳动力市场模型中包含了大量的工人主体和企业主体,工人之间、企业之间、工人和企业之间的相互影响都可以在模型中体现出来。与传统的代表性单主体模型不同,ABM模型中众多主体之间同时进行的互动和交易构成了一个具有复杂性的动态系统,这可以为劳动力市场的研究提供一些新的理解。
ABM劳动力市场模型中的主体也有着非常独特的行为模式。在传统的数理模型中,工人主体对自身的收益和成本进行精确、复杂的计算,并且根据计算结果直接作出最优反应。但是行为经济学已经向人们揭示,经济行为主体往往是在信息不完全、理性计算不充分的情况下,作出偏离最优反应的决策。而ABM模型的优势之一在于,它可以很方便地对有限理性主体的行为进行刻画。如本文的ABM劳动力市场模型,工人所能够获取的信息仅仅局限于其搜寻范围,其关于成本和收益的计算也只依赖于非常有限的信息。模型中的工人还可以依据以往的历史经历来调整自己的行为,但是也只是理性程度非常低的适应性调整,并非经过周密计算的最优反应。因此,相较于假设行为主体的完全理性的模型,ABM劳动力市场模型对行为主体有限理性的刻画更加具有现实性。
本文的建模在三方面借鉴了Fagiolo等(2004)的思路:首先是工资的制定方式,Fagiolo为每个工人和企业都设置一个“期望工资”变量,并将两者的加权平均作为工资谈判的结果,而其中两者的权重反应了双方在工资制定中的谈判力;其次是工人和企业每期的变量调整,其中工人的期望工资将依据本期的就业情况进行调整,而企业的空缺岗位和期望工资也分别依据本期的盈利情况和招工情况进行调整;最后是劳动力市场和商品市场的关系。Fagiolo通过假设商品市场出清,令工人的所有收入都用于当期总产出的消费,从而通过全社会的工资总和除以总产量计算出单位商品的价格水平。本文的模型设置将在以上三个方面借鉴Fagiolo的做法,详见基准模型介绍部分。
由于Fagiolo研究的主要话题并不是工作搜寻,其模型对工人搜寻过程的刻画过于理想:每个工人会随机选择一个岗位进行配对,并有一定概率配对成功。其并没有更具体地考虑搜寻过程中各种成本、摩擦和权衡等限制因素。
与Fagiolo模型不同的是,本文将搜寻范围作为工作搜寻的限制因素考虑进来,成为本文重点关注的变量。本文模型中的工人无法进行全局搜索,而是被赋予一个搜寻范围,其搜寻的信息和活动空间将被限制在该范围之内,并在该范围内进行一系列有成本的搜寻活动。为了克服Fagiolo模型的不足,本文模型中的工人搜寻不仅存在搜寻范围的限制,而且会面临搜寻资源的约束和对失业保险的权衡:当工人的搜寻资源不足时,他将被迫停止搜寻;当就业的期望收入低于失业保险金额时,工人会选择自愿失业。通过对工人搜寻行为更细致的刻画,该模型将为后续的搜寻范围仿真实验和结果分析提供一个可靠的基础。
三、劳动力市场基准模型
考虑一个劳动力市场,其中包含工人和企业两类主体,数量分别为
(一)企业
企业的生产只考虑一种生产要素的投入,即劳动力。并且1个就业工人每期生产1单位产品。某企业
| yit=nit | (1) |
其中,
| πit=ptyit−nitwit | (2) |
其中,
每个企业都拥有一定的资产数量。企业
| Ci,t+1=Cit+πit | (3) |
当企业盈利(即
(二)工人
工人的每次就业只持续一个时期,因此每期都需要重新寻找工作。在搜寻工作时,工人们都有一套共同的搜寻规则:工人
| Vji=wsitaj−cji | (4) |
| cij=ϖtdij | (5) |
| ϖt=κˉwt−1 | (6) |
其中,
为了实现收益最大化,工人
然而,本模型假设应聘是有成本的,并且工人在应聘之前拥有一定数量的搜寻资源。初期的搜寻资源是外生给定的,往后每期的搜寻资源来源于上一期的消费剩余或者失业保险。当搜寻资源不足以支付应聘成本时,工人将被迫停止搜寻而失业;但是如果工人直到应聘成功时仍有搜寻资源,则剩余资源会被用于当期消费。
模型考虑了失业保险。每一个失业的工人将在本期获得与本期人均工资水平相关的失业保险
除了搜寻资源不足、就业净收益低于失业保险的原因导致工人失业之外,还有另外两种原因会导致工人在搜寻工作阶段失业:一种是工人的搜寻范围内没有任何企业或者没有任何空缺岗位;另一种是工人在本期的所有应聘都被拒绝,没有一次应聘成功。
(三)工资制定
每个企业在招聘时会公布一个期望工资水平
| wit=wsitσit+1nitnit∑j=1wsjt(1−σit) | (7) |
| σit=nitNit | (8) |
其中,
式(8)表达的是企业的谈判力
(四)消费市场
模型假设,所有企业生产的产量之和等于社会总产量,可表达为:
| Yt=I∑i=1yit | (9) |
根据所有就业工人的总收入和就业人数,可以计算出本期的人均工资水平,可表达为:
| ˉwt=J∑j=1wjtI∑i=1nit | (10) |
本期的每个就业工人可以根据工资制定的结果获得一定的工资收入,每个处于失业工人则会获得一定金额的失业保险
| bt=μˉwt | (11) |
而对于没有领取失业保险的就业工人,则将本期的消费剩余作为下一期的搜寻资源。为了简化,假设就业工人的消费剩余等于
另外,所有工人在本期所支付的应聘成本被视为本期消费的一部分。当工人应聘成功时搜寻资源仍有剩余,也被用于本期的消费。这意味着,上一期从收入中扣除用以作为搜寻资源部分,全部被用于本期消费。因此,本期全社会用于消费的最终金额为
| pt=J∑j=1wjt−btJ+bt−1JYt | (12) |
(五)动态调整
模型假设,企业和工人具有历史记忆,记忆的长度为两期。企业和工人在完成生产消费之后,将根据自己近两期的招工和就业情况,调整他们各自下一期的期望工资。期望工资的调整具体可表达为以下公式:
| 企业:wsi,t+1={wsit(1+ξ1),ξ1∈(0,3%)ifnitNit<ηorni,t−1Ni,t−1<ηwsit(1−ξ1),ξ1∈(0,3%)ifnitNit⩾ηandni,t−1Ni,t−1⩾η | (13) |
| 工人:wsj,t+1={wsjt(1+ξ2),ξ2∈(0,3%)ifsjt=1andsj,t−1=1wsjt(1−ξ2),ξ2∈(0,3%)ifsjt=0orsj,t−1=0 | (14) |
式(13)表达的是企业对于期望工资的调整。当企业
另一方面,企业也会对其岗位数量进行调整,如式(15)所示。当企业本期的利润相比于上期有所增长时,该企业在下一期则会扩大生产规模,增加1个单位的工作岗位。如果企业本期的利润是下降的,则在下一期则会选择缩小生产规模,减少1个单位的工作岗位。
| Ni,t+1={Nit+1ifπit>πi,t−1Nit−1ifπit<πi,t−1 | (15) |
(六)总结
以上是整个劳动力市场ABM模型的设定。该模型可以在计算机上利用Netlogo软件,以5个子程序的形式实现。5个子程序构成了一个循环,每个循环时长为1期,模型的运行就是不断地按顺序重复该循环。图1展示劳动力市场模型的流程图。模型在运行过程中,将生成每期的劳动力市场的宏观数据,如工人的失业率、收入、商品价格的增速和社会总产量等。

|
| 图 1 劳动力市场模型子程序流程图 |
四、校准和拟合
本节借鉴Fagiolo等(2004)的做法,模型的校准采用拟合典型事实方法,以重现劳动力市场的几个重要特征,校准后的基准模型的初始变量取值如表1所示。模型将运行5轮,每轮运行100期,再拟合出与劳动力市场相关的曲线,如菲利普斯曲线、贝弗里奇曲线和奥肯曲线。
| 变量 | 含义 | 初始取值 |
|
I
|
企业数量 | 50 |
|
J
|
工人数量 | 500 |
|
θ
|
工人对实际工资的接受底线 | 50% |
|
η
|
企业对招工比例的满意程度 | 1 |
|
aj
|
工人应聘的成功概率 |
P(aj=70%)=P(aj=80%)=P(aj=90%)=13
|
|
κ
|
人均工资对单位移动成本的影响系数 | 2.25% |
|
μ
|
人均工资对失业保险的影响系数 | 45% |
|
Ni1
|
初期企业岗位数量 | 服从
N(IJ,10)
分布
|
|
wsi1
|
初期企业期望工资 | 服从
N(100,10)
分布
|
|
wsj1
|
初期工人期望工资 | 服从
N(100,10)
分布
|
|
Ci1
|
初期资产存量 | 100 |
|
rj
|
搜寻范围半径 | 6 |
图2(a)—(c)三图是拟合典型事实特征的结果。②可以看出,基准模型所得到的宏观数据可以再现劳动力市场相关曲线的反向变动关系。因此,我们所建立的模型可以反映劳动力市场的运行机制,具有一定的现实性。

|
| 图 2 拟合的菲利普斯曲线、贝弗里奇曲线和奥肯曲线 |
五、实验组设置与结果分析
(一)实验组设置
我们将基准模型设置为“甲组”,并依照递增的工人搜寻范围设置另外三组,分别为“乙组”、“丙组”和“丁组”。各组搜寻范围设定如表2所示。在每个实验组中,模型将运行5轮,每轮总共运行500期。我们剔除掉前200期的不稳定数据,仅将后300期数据作为该轮的实验结果。以下所报告的每个实验组的结果,均为该组内5轮实验的平均结果。
(二)失业与收入分析
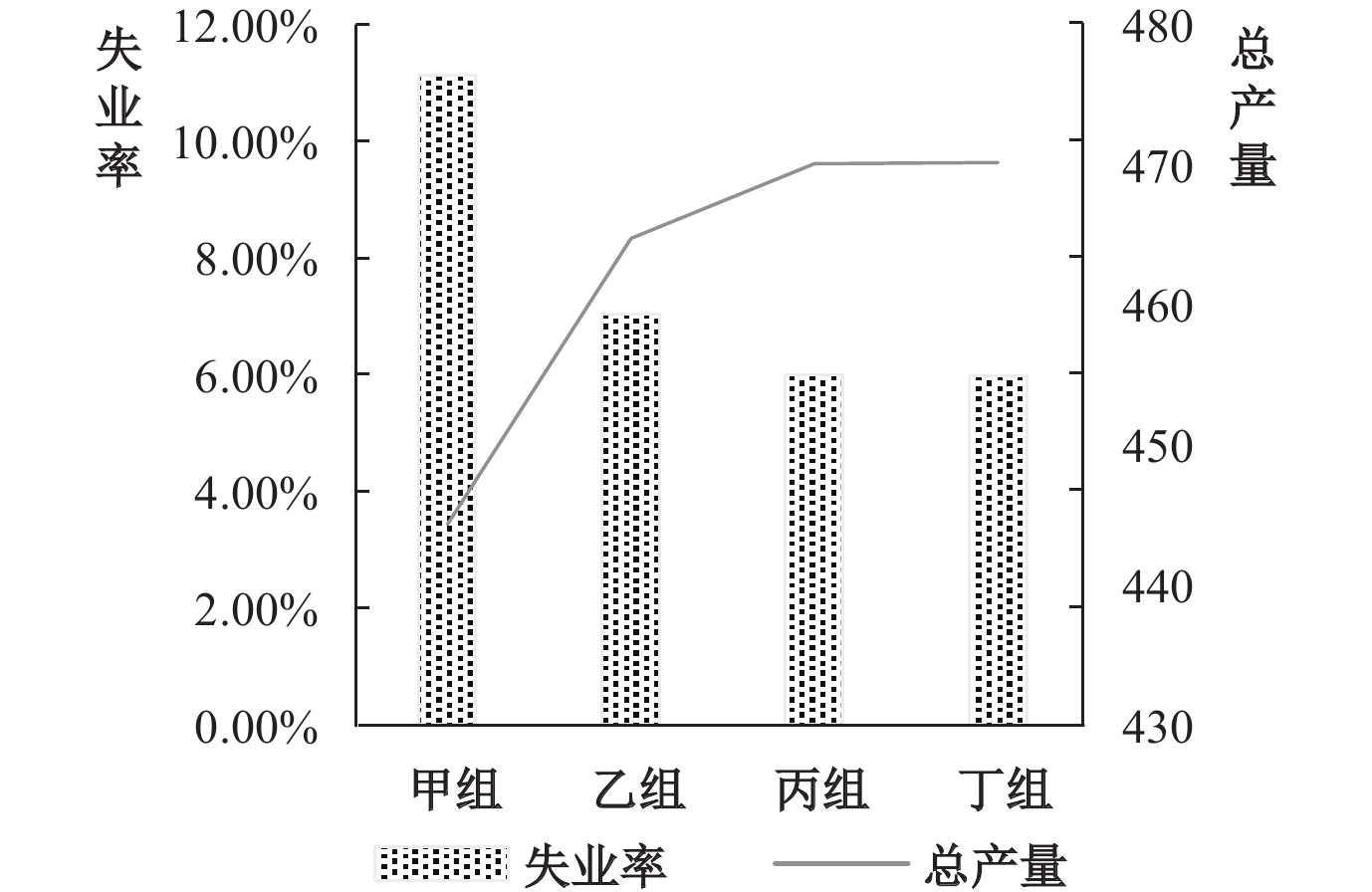
实验结果如图3所示,前三个实验组平均每期的失业率有显著的差异。③其中,工人搜寻范围越大的实验组,其失业率越低,总产量越高,但是存在边际效应递减的现象。这是因为模型设置了1个就业工人生产1单位的产量,因此搜寻范围的扩大在降低了失业率和增加就业的同时,也增加了社会的总产量。
|
| 图 3 各实验组的失业率和总产量 |
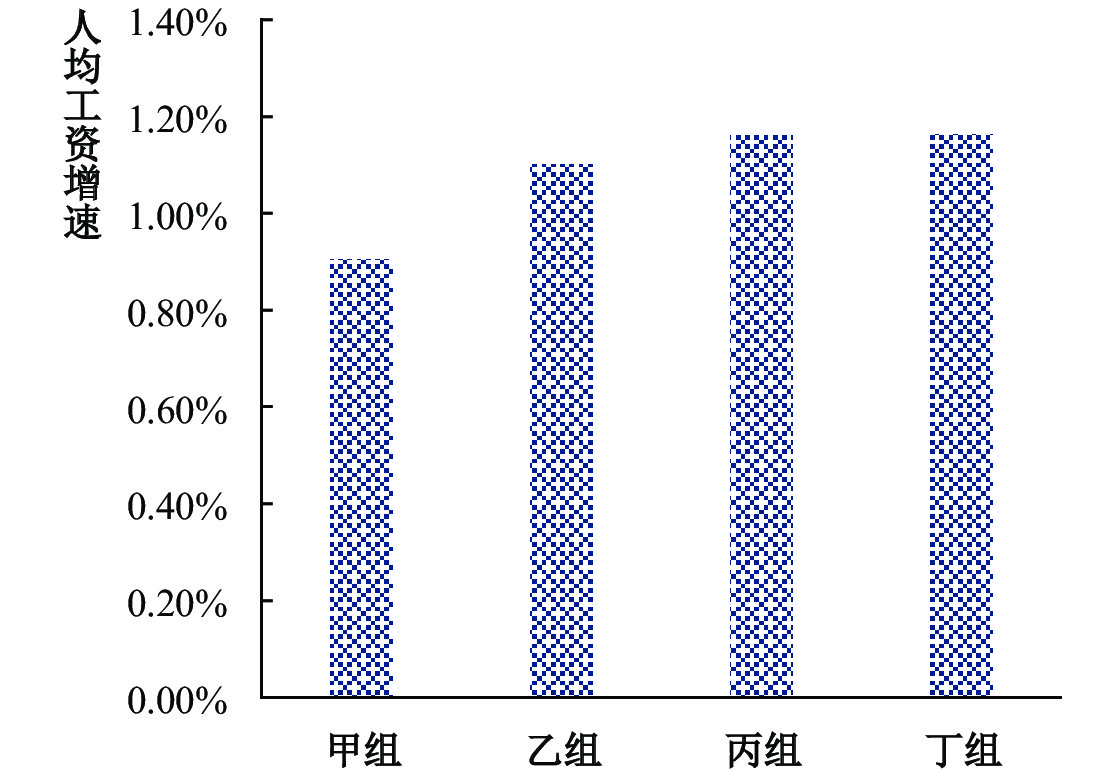
图4显示了各实验组在后300期的平均每期工资水平增速。可以看出,搜寻范围越大的实验组,其工资增速越高,但是同样会出现边际效应递减的现象。这是因为搜寻范围的扩大促进了工人们的就业,使得工人们的预期工资水平上升,此时企业必须提高工资才能获得足够的劳动力,这导致了整个劳动力市场的工资增速。
|
| 图 4 不同实验组平均每期的人均工资增速 |
对于失业率和工资增速,搜寻范围的影响都存在边际效应递减的现象。其原因在于,当搜寻范围逐渐扩大时,新增的工作机会都距离比较远,应聘成本较大。尤其是当搜寻范围过大的时候,很难对工人的就业改善起到正面作用,因此出现了边际效应递减的现象。
(三)不同类型的失业分析
本文还区分了不同类型的失业,如表3所示。基准模型的设置中,我们提到了导致工人失业的五种情况。通过对比不同的实验组中各类型失业率的差别,我们分析搜寻范围扩大对各类失业的影响,结果如表4所示。
| 失业类型 | 失业原因 |
| A | 搜寻范围内无企业或空缺岗位 |
| B | 就业的期望收益低于失业 |
| C | 因搜寻资源不足而中止搜寻 |
| D | 每次前往应聘,却都失败 |
| E | 应聘成功,但对工资谈判结果不满意 |
| 失业类型 | 甲组 | 乙组 | 丙组 | 丁组 |
| A | 6.79% | 3.11% | 1.58% | 0.89% |
| B | 0.00% | 0.07% | 0.44% | 0.80% |
| C | 0.32% | 0.69% | 0.99% | 1.16% |
| D | 3.15% | 1.62% | 0.71% | 0.33% |
| E | 0.87% | 1.57% | 2.26% | 2.79% |
A类失业指的是工人在其搜寻范围内无法搜寻到企业或者空缺的岗位,从而被迫失业。这类失业本质上是由于工人搜寻范围的局限所导致的,因此从实验结果可以看出,随着工人搜寻范围的扩大,工人获得更多的就业机会。而此类失业率将逐步减少,并且效果非常明显。因此,此类失业率对总失业的下降有着重要的贡献。
B类失业指的是工人在前往应聘之前,其预估的就业收益低于失业保险而选择失业,从而主动失业。实验结果表明,随着搜寻范围的扩大,此类失业率会略微地上升。原因在于,新增加的就业机会与工人距离都比较远,这将增加其应聘的成本,使得预估的就业收益可能低于社会提供的失业保险,从而增加工人主动选择失业的概率。
C类失业指的是工人在搜寻过程中因搜寻资源不足而导致的失业。实验表明,此类失业将随着搜寻范围的扩大而增加,其原因与B类失业相似,也是由于搜寻范围的扩大而带来的应聘成本的提高,导致搜寻资源在工作搜寻过程中成为更明显的约束。
D类失业指的是工人虽然每次都有机会和资源前往应聘,但是在搜寻所处范围内全部空缺岗位之后,仍然遭到众多企业的拒绝而最终失业。此类失业在搜寻范围扩大的过程中将逐渐减少。虽然工人单次应聘的成功率并不直接与搜寻范围相关,而这是外生给定且固定不变的,但是搜寻范围的扩大将增加工人的就业机会,使其可以应聘更多的岗位,从而减少最终失业的概率。也有部分原因在于,工人搜寻范围的扩大增加其应聘成本,使得此类失业转为B、C类失业。
E类失业是企业和工人进行工资谈判之后,工人认为谈判所形成的工资低于自己的预期水平,从而选择主动失业。实验表明,此类失业将随着搜寻范围的扩大而增加。原因在于,当工人连续多期地处于就业状态时,其期望工资水平将得到提升,从而也更加容易发生此类失业。搜寻范围的扩大在改善了工人就业环境的同时,也提升了其预期的工资水平,使得更多的工人对谈判所形成的工资不满意。
总结上述对各类失业的分析,可以看出,搜寻范围的扩大对不同类型的失业会造成不同的影响,通过此分析也可以识别出搜寻范围对总失业率的影响机制:从积极方面来看,工人搜寻范围的扩大,将使得工人获得更多的就业机会,减少最终应聘失败的概率;但是从消极方面来看,这将导致工人面临应聘成本过高、搜寻资源不足和期望工资过高等问题,从而影响其就业状况的改善。
(四)企业盈利环境和匹配效率分析
本文还分析了搜寻范围扩大对市场的盈利环境和匹配效率的影响。根据基准模型中的设定,企业的岗位数量将随其盈利状况进行动态调整。因此,我们考察劳动力市场上企业提供的岗位数量变化,也可以了解企业盈利状况的变化。
图5显示了各实验组后300期平均每期的岗位数量。可以看出,当工人的搜寻范围扩大时,市场上企业的劳动力需求将会增加,提供的岗位数量也会增加,但是会有较强的边际效应递减的现象。虽然丙组的岗位数量略微多于乙组,但差异在统计上并不显著。在丁组中,甚至出现岗位数量略微下降的情况,此差异在统计上也并不显著。这从侧面反映了工人搜寻范围的扩大,有助于改善企业的盈利状况和市场的盈利环境。对未来乐观的预期使得企业愿意扩大生产,提供更多的就业岗位,从而增加了劳动力需求,但是会有较强的效应边际递减现象。

|
| 图 5 各实验组平均每期的岗位数量 |
出现上述现象的原因在于,模型考虑了长期亏损企业的淘汰机制。能够在市场上留存下来的企业,大多都是能够生产盈利商品的企业。而市场中有更多的就业工人,就意味着更高的产量,市场中的企业也就获得更多的利润。因此,当工人的搜寻范围扩大时,工人的就业人数上升,更多的盈利商品被生产出来,从而提高了市场的盈利环境。由于企业也获得更多的利润,从而愿意提供更多的就业岗位。
另外,通过各组的失业人数和空缺岗位数量的对比,我们可以了解劳动力市场上匹配效率的变化。从图6我们可以看出,随着工人搜寻范围的扩大,市场上的失业人数呈下降趋势,而空缺的岗位数量则呈上升趋势,两者变动方向相反。然而,空缺岗位数量的增加并不能说明市场的匹配效率下降。

|
| 图 6 各实验组的平均失业人数和空缺岗位数量 |
表5展示了其他组相对于甲组空缺岗位的数量差异。其中,市场匹配效率的提升所带来的空缺岗位变化,可以通过观察失业人数的减少而得知。但与此同时,搜寻范围的扩大也会带来更多的劳动力需求,从而增加了空缺岗位的数量。由于对空缺岗位来说,劳动力需求增加的效应大于匹配效率提升的效应,因此我们最终看到的是失业人数和空缺岗位随着搜寻范围的扩大而反向变动。
| 组别 | 因匹配效率提升 | 因劳动力需求提升 | 空缺岗位的总变化 |
| 乙组 | −20.39 | +54.55 | +34.16 |
| 丙组 | −25.72 | +68.06 | +42.34 |
| 丁组 | −25.77 | +64.12 | +38.35 |
六、主要结论与未来研究
本文通过ABM方法建立了一个劳动力市场模型,研究工人搜寻范围扩大对劳动力市场的影响。通过模拟实验研究发现:(1)搜寻范围的扩大有助于减少工人们的失业和增加社会总产量,并且能够提高人均工资增速,但是存在边际效应递减的现象;(2)从更加微观的角度来分析,搜寻范围扩大能够增加工人的就业机会,减少最终失业的概率,但是也会带来搜寻资源不足、应聘成本过高和工人期望工资过高等负面效应;(3)整个市场的盈利环境会随着工人搜寻范围的扩大而得到改善,盈利的预期使得企业增加更多的工作岗位。虽然搜寻范围的扩大也会提升市场的匹配效率,但是空缺岗位的数量总体上仍然是有所增加的。
本文所得到的结论与Autor(2001)和Beard(2012)类似,都认为搜寻技术进步能够降低失业率和提升劳动力市场的匹配效率。但是与Kuhn和Skuterud(2004)所得的结论有所不同,本文认为搜寻技术进步有助于提升求职者的工资。在此基础上,本文还更深入地区分了五种失业情况和求职者的异质性,并且分析了搜寻技术进步对各种失业、各类求职者的影响。另外,本文还从企业的角度进行了考察,认为搜寻技术进步对企业的盈利也存在正面的影响。本文为理解搜寻技术进步对劳动力市场产生的影响提供了新的视角和见解。
在2019年的政府工作报告中,我国已将就业优先政策置于宏观政策层面。搜寻技术的运用与发展对于劳动力市场的积极作用应该更加受到重视。结合本文的研究结论和当前中国劳动力市场现状,以下将给出一些相关的政策启示:在大力发展互联网求职招聘、城市轨道交通、扩大求职者搜寻的空间范围和信息渠道的同时,也应该关注其应聘成本的降低。政府可以通过发展各种低成本的招聘形式和补贴应聘的交通路费等方法,切实降低求职者的应聘成本,让求职者愿意尝试更多的应聘机会,以避免由于搜寻技术进步导致的边际效应递减现象。另外,在面临经济下行压力时,更应该采取措施扩大劳动力的搜寻范围。这不仅能够缓解就业问题,还能够改善企业的盈利和增加劳动力需求,有助于企业渡过经济下行的困难期。
本文虽然在劳动力市场ABM模型基础上进行了初步的工人搜寻研究,但是对该话题的研究并不是本文唯一目的。我们希望借此研究,让更多的劳动经济学学者关注ABM方法,甚至在本文模型基础上进一步扩展,如考虑工人之间的搜寻范围和技术水平等差异,或者将教育系统纳入进来,建立一个关于“教育−就业”联动的ABM模型,用以研究更广泛的劳动经济学问题。
① 引自
② 图2(c)中,由于模型假设每个就业工人每期生产1个单位商品,所以失业率和社会总产量是完全线性关系,样本点均落在拟合直线上。
③ 由于篇幅所限,单因素方差分析没有给出。如果读者需要,可向作者索取。
| [1] | 戴维•罗默. 高级宏观经济学[M]. 吴化斌, 龚关译. 第4版. 上海: 上海财经大学出版社, 2014. |
| [2] | 董志强. 我们为何偏好公平: 一个演化视角的解释[J]. 经济研究, 2011(8): 65–77. DOI:10.3969/j.issn.1005-913X.2011.08.037 |
| [3] | 董志强, 魏下海, 李伟成. 再论公平偏好的演化起源: 改进的仿真模型[J]. 经济评论, 2015(1): 17–25. |
| [4] | 董志强, 李伟成. 禀赋效应和自然产权的演化: 一个主体基模型[J]. 经济研究, 2019(1): 182–198. |
| [5] | 黄凯南, 乔元波. 产业技术与制度的共同演化分析——基于多主体的学习过程[J]. 经济研究, 2018(12): 161–176. |
| [6] | 克里斯托弗·皮萨里德斯. 均衡失业理论[M]. 欧阳葵, 王国成译. 北京: 商务印书馆, 2012. |
| [7] | 刘怀宇, 曹诗男, 邓晶, 薛桂霞. 农户家庭劳动力配置决策机制探讨——一个多主体模型的视角[J]. 农业技术经济, 2015(2): 14–22. |
| [8] | 欧恺, 秦向东. 不同期限非就业补偿收益对工人和雇主的影响——基于主体的劳动力市场实验模拟研究[J]. 生产力研究, 2008(23): 139–141. |
| [9] | 韦立坚. T+0交易制度的计算实验研究[J]. 管理科学学报, 2016, 19(11): 90–102. DOI:10.3969/j.issn.1007-9807.2016.11.009 |
| [10] | 韦立坚, 张维, 熊熊. 股市流动性踩踏危机的形成机理与应对机制[J]. 管理科学学报, 2017, 20(03): 1–23. DOI:10.3969/j.issn.1007-9807.2017.03.001 |
| [11] | 叶航. 公共合作中的社会困境与社会正义——基于计算机仿真的经济学跨学科研究[J]. 经济研究, 2012(8): 132–145. DOI:10.3969/j.issn.1005-913X.2012.08.079 |
| [12] | Aghion P, Howitt P. A model of growth through creative destruction[J]. Econometrica, 1992, 60(2): 323–351. DOI:10.2307/2951599 |
| [13] | Aghion P, Howitt P. Growth and unemployment[J]. The Review of Economic Studies, 1994, 61(3): 477–494. DOI:10.2307/2297900 |
| [14] | Autor D H. Wiring the labor market[J]. Journal of Economic Perspectives, 2001, 15(1): 25–40. DOI:10.1257/jep.15.1.25 |
| [15] | Bergmann B R. Micro-to-macro simulation: A primer with a labor market example[J]. Journal of Economic Perspectives, 1990, 4(1): 99–116. DOI:10.1257/jep.4.1.99 |
| [16] | Fagiolo G, Dosi G, Gabriele R. Matching, bargaining and wage setting in an evolutionary model of labor market and output dynamics[J]. Advances in Complex Systems, 2004, 7(2): 157–186. DOI:10.1142/S0219525904000135 |
| [17] | Beard T R, Ford G S, Saba R P, et al. Internet Use and Job Search[J]. Telecommunications Policy, 2012, 36(4): 260–273. DOI:10.1016/j.telpol.2011.12.001 |
| [18] | King I, Welling L. Search, unemployment and growth[J]. Journal of Monetary Economics, 1995, 35(3): 499–507. DOI:10.1016/0304-3932(95)01198-W |
| [19] | Kuhn P, Skuterud M. Internet job search and unemployment durations[J]. American Economic Review, 2004, 94(1): 218–232. DOI:10.1257/000282804322970779 |
| [20] | Lewkovicz Z, Kant J D. A multi-agent simulation of a stylized French labor market: Emergences at the micro-level[J]. Advances in Complex Systems, 2008, 11(02): 217–230. DOI:10.1142/S0219525908001581 |
| [21] | Martin C W, Neugart M. Shocks and endogenous institutions: An agent-based model of labor market performance in turbulent times[J]. Computational Economics, 2009, 33(1): 31–46. DOI:10.1007/s10614-008-9149-z |
| [22] | McCall J J. Economics of information and job search[J]. The Quarterly Journal of Economics, 1970, 84(1): 113–126. DOI:10.2307/1879403 |
| [23] | Mortensen D. A theory of wage and employment dynamics[A]. Phelps E S. Microeconomic foundations of employment and inflation theory[M]. New York: Norton, 1970. |
| [24] | Neugart M. Labor market policy evaluation with ACE[J]. Journal of Economic Behavior and Organization, 2008, 67(2): 418–430. DOI:10.1016/j.jebo.2006.12.006 |
| [25] | Reuben G. Information and frictional unemployment[J]. American Economic Review, 1971, 61(3): 290–301. |
| [26] | Tesfatsion L. Preferential partner selection in evolutionary labor markets: A study in agent-based computational economics[A]. International Conference on Evolutionary Programming VII[C], Springer-Verlag, 1998, 13-24. |


