
2020第46卷第9期
一、引 言
公募基金为投资者提供了分散风险、获取长期投资收益的渠道,但国内基金投资者却表现出较明显的短期投资行为。①基金投资者过分重视基金的短期业绩,盲目追逐短期业绩亮眼的“爆款基金”,这些基金使投资者形成了“过去业绩将得到复制”的强烈预期,但投资者购买这类基金的收益并不高。②基金投资者的非理性交易行为也带来了“基金赚钱基民不赚钱”这一困扰公募基金行业的难题。
投资者追逐短期内具有极高收益的基金产品与“博彩偏好”有关。投资者对以小概率出现高收益的金融资产存在特殊偏好,由于这类资产类似彩票,这种偏好被称为博彩偏好。博彩偏好是个人投资者最明显的投资行为特征之一,个人投资者做投资决策时会赋予出现极高收益率这种小概率事件过高的权重,高估这种小概率极端事件在未来出现的可能性(Brunnermeier等,2007;Barberis和Huang,2008)。投资者的博彩偏好已经在股票市场(Kumar,2009;Eraker和Ready,2015;郑振龙和孙清泉,2013;陈文博等,2019;朱红兵和张兵,2020)、期权市场(Doran等,2012;Boyer和Vorkink,2014)和IPO市场(Green和Hwang,2012)得到验证。个人投资者在基金交易中的占比很高,但很少有研究关注基金投资者的博彩偏好。本文研究中国开放式基金投资者的博彩偏好对其基金交易行为的影响。基金的定期报告会披露报告期内资金的流入流出状况,我们可以直接观测到投资者的交易行为。
本文使用基金单月收益的历史最大值MAX来度量投资者的博彩偏好,这有着坚实的理论基础和实务上的便利性。Brunnermeier等(2007)以及Barberis和Huang(2008)的理论模型指出,小概率的极端正收益满足投资者效用最大化,MAX的含义与此相符。现实中MAX易于被投资者观测和理解,在股票市场得到了广泛应用(Bali等,2011,2017;朱红兵和张兵,2020)。本文要论证的是基金单月收益大涨导致投资者高估极端正收益出现的概率,从而买入基金以期在再次出现极高收益时获利,即MAX可以正向预测基金未来的资金流入。
|
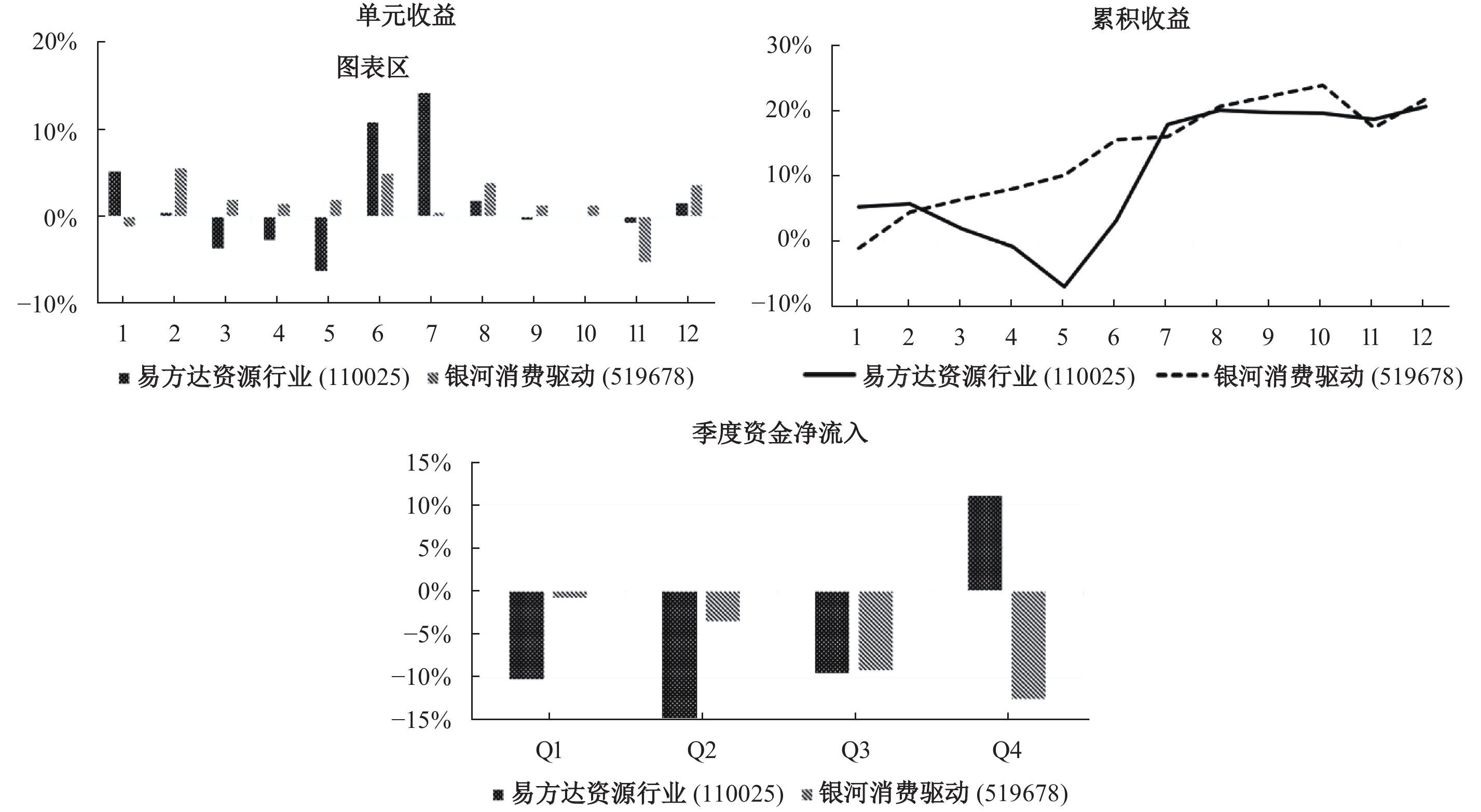
| 图 1 易方达资源行业(110025)和银河消费驱动(519678)收益和资金净流入 |
本文选取2005—2019年中国852只开放式股票型基金和偏股混合型基金作为样本,利用基金月度收益和半年度资金流量数据,检验了基金月度收益率最大值MAX与资金流入的关系。首先,检验了MAX是否可以正向预测基金未来的资金流入。研究结果显示,在控制了历史收益率等因素后,MAX与基金资金流入显著正相关。过去半年内最大月度收益MAX每增加1%,未来半年资金净流入增加约1.43%。在剔除了同期收益及其波动率的影响后,MAX仍然可以显著正向预测基金未来的资金流入。这说明基金投资者具有博彩偏好,会根据历史收益最大值MAX来选择基金。其次,研究了投资者基于MAX购买基金是否理性。研究发现,MAX并不能正向预测未来基金业绩,MAX越大,基金未来的收益越低。MAX每增加1%,基金未来半年经CAPM调整后的超额收益率降低0.15%。因此,基于MAX购买基金是不理性的。再次,检验了MAX—资金流入关系在理性程度不同的投资者群体中的差异性。由于个人投资者更容易出现行为偏误,本文推测MAX对个人投资者资金流入的影响更明显。研究发现,MAX可以显著正向预测个人投资者的资金净流入,对机构投资者资金净流入的影响则不明显。最后,证明了MAX—资金流入关系并不完全是由投资者的有限关注所引起的。尽管MAX可能使基金受到投资者更多的关注从而获得更多的资金流入,但是在控制了明星基金效应后,MAX与资金流入的正向关系仍然显著存在。此外,MAX指标比特质波动率和特质偏度更好地衡量了投资者的博彩偏好。在改变MAX的计算周期以及加入与资金净流入同期的基金收益后,结论仍然成立。同时,MAX能够正向预测未来一个季度的资金净流入,负向预测未来一个月的收益。
近年来,我国公募基金规模增长迅速,③已成为居民的重要投资渠道之一。我国基金投资者结构中个人投资者占比一直很高,其持有的基金资产比例2013年高达73%,近年来逐渐降低至50%左右,④基金个人投资者的交易行为对资金流入流出具有重要影响。本文发现,过去出现过极端正收益的基金会受到投资者尤其是个人投资者的追捧,但未来收益会更低。投资者如何克服非理性来选择基金,监管层如何稳定基金市场和保护投资者利益,本文的研究具有借鉴意义。此外,FOF基金在我国已经起步发展,⑤作为基金市场的创新亮点被投资者寄予厚望。本文的结论对于FOF构建投资组合和提升资产管理绩效也具有借鉴意义。
本文的边际贡献可能体现在:第一,直接证实了博彩偏好存在于基金市场,这加深了对中国基金投资者行为的认识,拓展了MAX异象的研究。以往的研究往往基于股票市场研究博彩偏好,因为股票价格波动比较剧烈,容易出现极端收益率MAX;而基金作为投资较分散化的产品,价格波动较小,但也存在MAX效应。基于股票市场的研究往往通过事后股价变化来倒推投资者偏好及其交易行为,本文使用基金的资金流动数据可以直接观测到基金投资者的交易行为,构建了“极端收益—投资者交易行为—基金业绩”的完整研究路径。研究发现,博彩偏好只存在于基金个人投资者中,对于机构投资者则不明显;过去出现过极端正收益的基金,未来收益会更低。这丰富了基金业绩影响因素的研究。第二,本文发现基金极端收益会影响投资者的基金选择行为,丰富了基金业绩—资金流动关系(Performance-Flow Relationship)的研究。以往关于基金业绩—资金流动关系的研究关注历史收益的均值或累计值对资金流动的影响,而较少关注其分布特征的影响。本文发现过去出现过极端正收益的基金在未来会获得更多的资金流入,这对于监管层监管基金的投资行为具有一定的启示。
二、文献回顾
(一)基金业绩—资金流动关系
基金业绩—资金流动关系(Performance-Flow Relationship)在学术界已有大量研究。国外研究普遍发现基金的前期业绩对资金流动具有正向影响,基金前期业绩越高,资金流入越多,即投资者表现为“追逐业绩”。此外,基金前期业绩与资金流动之间表现为凸关系(Chevalier和Ellison,1997;Sirri和Tufano,1998;Huang等,2007):投资者对绩优基金表现出强烈的申购偏好,即存在“明星效应”,但对绩劣基金却没有表现出较强的抛售意愿。国内学者也对基金业绩与资金流动的关系进行了大量检验,但并未得到一致的结论。陆蓉等(2007)以及李科和陆蓉(2011)发现国内基金市场存在“赎回异象”,业绩好的基金比业绩差的基金面临更大的赎回压力,资金流动与历史业绩负相关且为凹形关系。彭惠等(2012)发现“赎回异象”存在于基金当期业绩和老基金中,历史业绩并不存在“赎回异象”;基金的历史业绩越好,资金流入越多。肖峻和石劲(2011)发现基金历史回报率对资金净流量产生了显著的正向影响,认为“赎回异象”是一种假象,而且并不存在“明星效应”,这与姚颐和高兴(2013)的研究结果一致。林树等(2009)以及杨坤等(2013)则发现存在“明星效应”。也有文献研究了基金市场中机构投资者和个人投资者的行为差异,主要发现共同基金的聪明钱效应主要来自个人投资者(林煜恩等,2014),机构投资者的投资行为则没有表现出聪明钱效应(莫泰山和朱启兵,2013)。左大勇和陆蓉(2013)认为机构投资者和个人投资者的理性程度不同,发现个人投资者往往只看重历史业绩,不能分辨风险,而机构投资者则看重基金剔除风险因素后的超额收益。
由于样本区间、频率(季度、半年度或年度)和模型方法的不同,国内对基金业绩—资金流动关系的研究尚未得到一致的结论,且主要关注基金的历史平均业绩或累计业绩对资金流动的影响。实际上,收益率的分布特征如极端正收益也会影响投资者的选择。在其他条件相同时,投资者更喜欢购买曾经出现过极高收益的基金。
(二)博彩偏好、历史最大收益与资产价格
有些股票的收益分布特征与彩票相似,能以极低的概率出现极高的收益,这种股票被称为“彩票型股票”,投资者对这类股票的偏好被称为“博彩偏好”。之所以偏好这类股票,是因为投资者会高估资产收益率分布中极端正收益出现的概率(Tversky和Kahneman,1992;Barberis和Huang,2008),这种高估可以最大化投资者当前的效用(Brunnermeier等,2007)。投资者的博彩偏好会导致资产价格被高估,从而未来收益较低。Bali等(2011)构建衡量股票彩票特性的指标MAX,即过去一个月的最大日收益,研究了美国股票市场上投资者的博彩偏好对股价的影响。他们发现MAX与股票未来一个月的收益显著负相关,MAX最低组股票的月收益比其最高组股票高出1%以上。这种现象也存在于A股市场(朱红兵和张兵,2020)、期权市场(Doran等,2012;Boyer和Vorkink,2014)和IPO市场(Green和Hwang,2012)。这与投资者的博彩偏好相符,投资者愿意为彩票型资产支付更高的价格,从而导致未来收益较低。不同类型投资者的博彩偏好强度存在差异。Kumar(2009)发现个人投资者的博彩偏好更明显。Han和Kumar(2013)发现个人投资者持股比例高的股票更容易表现出彩票特征,容易被高估。Bali等(2017)也发现彩票型股票需求主要来自个人投资者而非机构投资者。
投资者的博彩偏好已经在股票市场上得到广泛验证,但在基金市场上的研究较少。这可能是因为基金收益率波动没有股票剧烈,不容易出现极端收益率,而且具有博彩偏好的投资者更喜欢投资于股票市场而非基金市场。但研究投资者博彩偏好对基金投资行为的影响非常重要,基金已经成为居民重要的投资渠道,且基金投资者具有与股票投资者相似的行为偏差(Barber等,2005;Bailey等,2011;伍燕然等,2016)。基金定期披露资金流入流出状况,便于更直观地研究博彩偏好对基金投资者交易行为的影响。本文基于基金市场数据拓展了投资者博彩偏好的研究。
三、研究设计
(一)样本选择与数据来源
本文的样本区间为2005—2019年,研究对象为中国基金市场上的股票型和偏股型主动管理的开放式基金。因为基金只在半年报和年报中披露基金持有人结构信息,所以本文数据的观测频率为半年。基金分红数据来自Wind金融终端,其他基金相关数据、Fama-French三因子和五因子数据、无风险利率数据以及股票指数数据均来自CSMAR数据库。本文按照Wind基金分类,首先挑选出普通股票型基金和偏股混合型基金,然后做了以下处理:(1)剔除分级基金;(2)剔除定期开放式基金和具有持有期限制的基金,这些基金不能自由地申购赎回;(3)剔除发生过转型的基金;⑥(4)剔除B、D、E、H和I类基金份额,这类基金占比很低,只能在指定的平台上或中国香港地区发售;(5)保留每只基金赎回起始日之后的相关数据。本文最终得到852只基金(A/C份额分开统计)的9464条“基金—半年度”观测数据。各年度基金数量见表1。
| 年度 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| 基金数量 | 43 | 69 | 108 | 152 | 189 | 227 | 268 | 324 |
| 年度 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
| 基金数量 | 373 | 399 | 446 | 558 | 624 | 739 | 850 |
(二)主要变量定义
1. 基金资金净流入(Flow):衡量一段时期内投资者的净申购情况。与以往的研究一致(Sirri和Tufano,1998;肖峻和石劲,2011),本文将基金资金净流入(Flow)定义为:
| $Flo{w_{i,t}} = \frac{{TN{A_{i,t}} - TN{A_{i,t - 1}}(1 + Retur{n_{i,t}})}}{{TN{A_{i,t - 1}}}}$ | (1) |
其中,TNAi,t和TNAi,t−1分别表示t期末和t−1期末的基金资产净值,Returni,t表示基金t期收益率,定义如下:
| $Retur{n_{i,t}} = \frac{{adjNA{V_{i,t}} - adjNA{V_{i,t - 1}}}}{{adjNA{V_{i,t - 1}}}}$ | (2) |
其中,adjNAVi,t和adjNAVi,t− 1分别表示t期和t−1期的基金份额复权单位净值(考虑分红拆分再投资)。本文主要研究半年度的资金净流入,稳健性检验中分析季度的资金净流入。
2. 机构投资者资金净流入(Flow_Ins)和个人投资者资金净流入(Flow_Ind):按照左大勇和陆蓉(2013)的方法,区分基金投资者中机构投资者和个人投资者的资金流入。
| $Flow\_In{s_{i,t}} = \frac{{Institutiona{l_{i,t}} \times TN{A_{i,t}} - Institutiona{l_{i,t - 1}} \times TN{A_{i,t - 1}} \times \left( {1 + Retur{n_{i,t}}} \right)}}{{TN{A_{i,t - 1}}}}$ | (3) |
| $Flow\_In{d_{i,t}} = \frac{{Individua{l_{i,t}} \times TN{A_{i,t}} - Individua{l_{i,t - 1}} \times TN{A_{i,t - 1}} \times \left( {1 + Retur{n_{i,t}}} \right)}}{{TN{A_{i,t - 1}}}}$ | (4) |
其中,Institutionali,t和Individuali,t分别表示t期机构投资者和个人投资者持有基金i份额所占比例,数据频率为半年度。
3. 基金极端正收益MAX。这是本文主要的解释变量,衡量投资者的博彩偏好,是基金过去半年的最大月收益,单月收益率的定义同式(2)。衡量博彩偏好的常用指标有收益率最大值MAX、(特质)偏度和(特质)波动率,但使用MAX衡量投资者博彩偏好在理论和实务上具有明显优势(Bali等,2011)。在Brunnermeier等(2007)以及Barberis和Huang(2008)的模型中,投资者基于“小概率”的“极端正收益”来最大化效用函数,进而导致资产价格被高估,MAX更能捕捉“极端正收益”的特性。在投资实践中,MAX指标也更容易被大众投资者获得和理解,从而容易在投资者挑选基金时发挥作用。
4. 基金收益率。基金原始收益率Returni,t的定义同(2)。关于基金业绩—资金流动关系的现有研究也常使用序数收益率来刻画基金历史业绩(Sirri和Tufano,1998;Ferreira等,2012;肖峻和石劲,2011;冯旭南和李心愉,2013),因此除了原始收益率外,本文还计算了原始收益率对应的序数收益率。基金i在t期的序数收益率Ranki,t定义如下:将原始收益率Returni,t分别按照股票型基金和偏股混合型基金⑦由小到大排序,Returni,t最低的基金序数回报率设为0,Returni,t最高的基金设为1,其他相应地转换为(0,1)区间上的对应值。序数收益率可以更直观地反映基金业绩的排名情况。本文进一步将序数收益率Ranki,t细分为三个指标,Low_Ranki,t、Middle_Ranki,t和High_Ranki,t,分别包含排名最低20%的绩劣基金、20%—80%的中等业绩基金以及最高20%的绩优基金。这三个变量均为有界的连续型变量。
在论证MAX对基金未来收益率的影响时,本文还使用了超额收益率。本文采用四种方式来衡量基金i在t期的超额收益Alphai,t,分别是未经风险调整的原始超额收益(基金原始收益率减去无风险利率)、经过CAPM、Fama-French三因子和五因子风险调整后的超额收益,无风险利率为CSMAR提供的一年期整存整取存款利率。⑧
5. 其他变量。基于现有研究文献(陆蓉等,2007;肖峻和石劲,2011;俞红海等,2014;李志冰和刘晓宇,2019),本文控制了其他可能影响基金资金流动的以下变量:基金收益波动率、基金规模、基金家族规模、基金成立时长、基金分红、市场收益率和年度虚拟变量。各变量定义见表2。
| 变量名称 | 变量符号 | 变量定义 |
| 基金资金净流入 | Flow | 衡量一段时期内投资者的净申购情况,见式(1) |
| 机构投资者资金净流入 | Flow_Ins | 衡量一段时期内机构投资者的净申购情况,见式(3) |
| 个人投资者资金净流入 | Flow_Ind | 衡量一段时期内个人投资者的净申购情况,见式(4) |
| 基金历史收益率的极大值 | MAX | 过去六个月的最大月收益率,稳健性检验中使用过去3个月和
12个月的最大月收益率 |
| 基金原始收益率 | Return | 一段时期内考虑分红拆分再投资的基金份额净值增长率,见式(2) |
| 基金序数收益率 | Rank | 将原始收益率由小到大转换为[0,1]区间上的对应值 |
| Low_Rank | 排名最低20%的绩劣基金的序数收益率 | |
| Mid_Rank | 排名20%—80%的中等业绩基金的序数收益率 | |
| High_Rank | 排名最高20%的绩优基金的序数收益率 | |
| 基金超额收益率 | Alpha | 采用四种方式衡量,分别是未经风险调整的原始超额收益(基金原始收益率减去无风险利率)、经过CAPM、Fama-French三因子和五因子风险调整后的超额收益 |
| 基金收益波动率 | Volatility | 基金当期日收益率的标准差 |
| 基金规模 | FundSize | 期末基金资产净值的自然对数 |
| 基金家族规模 | FamilySize | 期末基金公司旗下所有基金资产净值之和的自然对数 |
| 基金成立时长 | Age | 自基金成立次月至今所经历月份数的自然对数 |
| 基金分红 | Dividend | 基金在指定区间内的单位分红之和 |
| 市场收益率 | Rm | 上证综合指数在指定区间内的增长率 |
| 年度效应 | Year | 年度虚拟变量 |
| 明星基金 | Star | 虚拟变量,如果基金经理管理的产品在当年同类产品中排名靠前(前10%),则该基金经理被定义为明星基金经理,其管理的基金在下一年被定义为明星基金,Star取1 |
| 特质波动率 | Ivol | 回归方程
$ {R}_{i,t}-{r}_{f,t}={\alpha }_{i}+{\beta }_{i}\left({R}_{m,t}-{r}_{f,t}\right)+{\varepsilon }_{i,t} $
的残差项
$ {\varepsilon }_{i,t} $
的标准差
|
| 特质偏度 | Iskew | 回归方程
$ {R}_{i,t}-{r}_{f,t}={\alpha }_{i}+{\beta }_{i}\left({R}_{m,t}-{r}_{f,t}\right)+{\gamma }_{i}{\left({R}_{m,t}-{r}_{f,t}\right)}^{2}+{\varepsilon }_{i,t} $
的残差项
$ {\varepsilon }_{i,t} $
的偏度,参考Harvey和Siddique(2000) |
(三)模型设定
本文关心的问题是,投资者是否会高估基金极端正收益在未来出现的概率而买入过去出现过极端正收益的基金。为了研究基金过去极端正收益与未来资金流入的关系,借鉴现有文献(李科和陆蓉,2011;肖峻和石劲,2011;俞红海等,2014)的研究方法,本文使用如下的固定效应面板数据模型进行分析:
| $Flo{w_{i,t}} = {\beta _0} + {\beta _1}MA{X_{i,t - 1}} + {\gamma _{}}Control{s_{i,t{\rm{ - }}1}} + {\mu _i} + {\varepsilon _{i,t}}$ | (5) |
其中,Flowi,t表示基金i在t期的资金净流入,MAXi,t-1表示基金i在t−1期的最大月收益,Controlsi,t−1表示基金i在t−1期的控制变量,包括基金收益率、基金收益波动率、基金规模、基金家族规模、基金分红、市场收益和年度虚拟变量。若投资者会高估基金过去的极端正收益在未来出现的概率而买入基金,则MAXi,t−1对Flowi,t具有正向预测作用,即
本文还使用如下的面板数据固定效应模型来研究MAX对基金未来业绩的影响:⑨
| ${R_{i,t}} = {\beta _0} + {\beta _1}MA{X_{i,t - 1}} + {\gamma _{}}Control{s_{i,t{\rm{ - }}1}} + {\mu _i} + {\varepsilon _{i,t}}$ | (6) |
其中,Ri,t为基金在t期的收益,分别采用原始超额收益和经过CAPM、Fama-French三因子和五因子风险调整后的超额收益。
(四)描述性统计
表3报告了主要变量的描述性统计结果,表4报告了主要变量的相关系数。本文样本包括2005—2019年852只开放式股票型和偏股型基金的9464条“基金—半年度”观测数据。可以看到,样本区间内基金总体上呈现资金净流入状态,均值为15.03%,但波动明显,标准差高达228.02%,中位数为−6.62%。这说明资金流动在基金之间的差异较大,较多基金呈现资金净流出状态,较少基金获得资金净流入。将资金净流入区分为来自机构投资者(Flow_Ins)和个人投资者(Flow_Ind)后发现,样本区间内个人投资者的资金净流入更多,均值为8.4%,约为机构投资者3.51%的2.4倍;而个人投资者资金净流入的波动性更大,标准差为167.27%,约为机构投资者41.43%的4倍。这说明个人投资者和机构投资者在基金投资行为上存在较明显的差异。半年内基金最大单月收益(MAX)的均值为8.63%,最大值为45.54%。基金半年度原始收益率(Return)的均值为4.06%,中位数为0.22%,标准差为22.63%,说明基金收益在不同年份和不同产品间的差异较明显。基金分红(Dividend)较低,每份基金每半年分红0.03元。
| 变量 | 样本数 | 均值 | 标准差 | 最小值 | 中位数 | 最大值 |
| Flow(%) | 9 464 | 15.03 | 228.02 | −141.82 | −6.62 | 5 852.67 |
| Flow_Ins(%) | 9 464 | 3.51 | 41.43 | −118.13 | −0.01 | 666.24 |
| Flow_Ind(%) | 9 464 | 8.40 | 167.27 | −125.01 | −5.09 | 4 173.72 |
| MAX(%) | 9 464 | 8.63 | 6.32 | −2.47 | 6.83 | 45.54 |
| Return(%) | 9 464 | 4.06 | 22.63 | −50.56 | 0.22 | 160.31 |
| Volatility | 9 464 | 1.48 | 0.64 | 0.07 | 1.31 | 6.23 |
| FundSize | 9 464 | 20.59 | 1.68 | 7.76 | 20.86 | 24.45 |
| FamilySize | 9 464 | 24.79 | 1.39 | 17.81 | 24.83 | 28.21 |
| Age | 9 464 | 3.89 | 0.77 | 1.95 | 3.99 | 5.34 |
| Dividend | 9 464 | 0.03 | 0.14 | 0.00 | 0.00 | 3.10 |
| Rm(%) | 9 464 | 1.63 | 23.03 | −48.00 | 1.18 | 62.53 |
| 注:变量Flow、Flow_Ins和Flow_Ind在上下1%处做了截尾(winsorize)处理。 | ||||||
| Flow | Flow_Ins | Flow_Ind | MAX | Return | Volatility | Age | FundSize | FamilySize | |
| Flow_Ins | 0.71*** | ||||||||
| Flow_Ind | 0.72*** | 0.21*** | |||||||
| MAX | 0.11*** | 0.06*** | 0.12*** | ||||||
| Return | 0.16*** | 0.14*** | 0.14*** | 0.42*** | |||||
| Volatility | 0.06*** | 0.02 | 0.09*** | 0.47*** | 0.00 | ||||
| Age | −0.06* | −0.09*** | −0.01 | −0.12*** | −0.06*** | −0.17*** | |||
| FundSize | −0.18*** | −0.09*** | −0.16*** | −0.01 | 0.05* | −0.08*** | 0.32*** | ||
| FamilySize | −0.03 | −0.03* | 0.00 | −0.01 | 0.08*** | −0.08*** | 0.12*** | 0.43*** | |
| Dividend | 0.07* | 0.02 | 0.10*** | 0.01 | 0.06* | −0.03 | 0.03 | 0.01 | 0.00 |
| 注:*、**和***分别表示1%、5%和10%的显著性水平,下表同。 | |||||||||
四、基金极端收益与资金流动关系检验
本文认为投资者会高估极端正收益在未来出现的概率从而买入基金,导致MAX可以正向预测基金未来的资金流入。⑪表5报告了式(5)的估计结果。在控制上一期收益率对本期资金流动的影响时,本文分别使用了原始收益率(列(1))、原始收益率的序数收益率(列(2))和不同业绩基金的序数收益率(列(3))。可以看到,MAX的系数均在5%的水平上显著为正。以列(2)为例,过去半年内最大月收益MAX每增加1%,未来半年资金净流入增加约1.43%,约为样本区间内资金净流入均值(15.03%)的十分之一。对于一只资产净值为11.48亿元(样本中位数)的基金,这意味着1636万元的额外资金流入。此外,基金历史业绩正向影响未来资金流入。以列(2)为例,基金的序数收益率每增加10%,未来资金流入增加约6%;但列(1)中直接使用原始收益率的系数不显著,说明在控制了历史业绩中的极端正收益后,历史绝对业绩对未来资金净流入的影响变得不明显。⑩因此,投资者更看重历史绝对收益中的极端正收益。序数收益率Rank更能体现基金的排名情况,其回归系数显著为正说明基金的相对业绩对投资者的影响可能更大。而在列(3)中,序数收益率对未来资金流入的正向影响在中等业绩基金中最明显,在绩优基金中不明显,这与肖峻和石劲(2011)的结论一致。
| Flow | |||
| (1) | (2) | (3) | |
| MAX | 2.126*** | 1.429** | 1.462** |
| (2.857) | (2.405) | (2.449) | |
| Return | 0.358 | ||
| (1.513) | |||
| Rank | 0.586*** | ||
| (4.665) | |||
| Low_Rank | 0.592 | ||
| (1.049) | |||
| Mid_Rank | 0.502*** | ||
| (3.019) | |||
| High_Rank | 1.931 | ||
| (1.457) | |||
| Volatility | −4.972 | 8.094 | 7.704 |
| (−0.732) | (1.229) | (1.188) | |
| FundSize | −1.081*** | −1.084*** | −1.085*** |
| (−5.915) | (−5.927) | (−5.932) | |
| FamilySize | 0.102 | 0.113 | 0.113 |
| (1.407) | (1.570) | (1.576) | |
| Age | 0.064 | 0.077 | 0.075 |
| (0.667) | (0.797) | (0.769) | |
| Dividend | 0.385 | 0.416* | 0.418* |
| (1.587) | (1.721) | (1.729) | |
| Rm | 0.068 | 0.379*** | 0.384*** |
| (0.405) | (4.010) | (4.032) | |
| Intercept | YES | YES | YES |
| Fund Fixed Effect | YES | YES | YES |
| Year Fixed Effect | YES | YES | YES |
| Within R-squared | 0.148 | 0.150 | 0.150 |
| Observations | 9 464 | 9 464 | 9 464 |
上述结果与基金投资者具有博彩偏好一致:基金投资者在做投资决策时赋予小概率出现的极端正收益过高的权重,高估了其在未来出现的概率,从而倾向于买入过去出现过极端正收益的基金,期望高收益可以在未来重现。这导致过去出现过极端正收益的基金在未来获得了更多的资金流入。⑰
五、进一步分析
本文认为投资者买入过去出现极端正收益的基金是一种非理性行为。本节考察MAX对基金未来业绩的预测能力以及MAX与资金流动关系在理性程度不同的投资者样本中的差异性。
(一)基金MAX对基金未来业绩的影响
如果MAX可以正向预测未来基金业绩,即过去出现过极端正收益的基金未来业绩会更好,那么投资者基于MAX选择基金就是一种理性的行为。Bali等(2019)发现MAX指标可以正向预测对冲基金的未来业绩。本文通过研究MAX和基金未来业绩的关系来确认投资者基于MAX购买基金是不是一种理性行为。表6报告了式(6)的估计结果,⑫其中列(1)—列(5)分别表示MAX对未来原始收益、原始超额收益和经过CAPM模型、Fama-French三因子及五因子模型调整后的超额收益的影响。可以看到,MAX负向影响基金未来收益,基金过去月收益极端值越大,未来收益越低。以列(3)为例,MAX每增加1%,基金未来半年经过CAPM调整后的超额收益率降低0.15%。这说明投资者基于基金近期极端正收益MAX购买基金是一种非理性的投资行为。变量Return的系数显著为负,即基金过去收益率越高,未来业绩越差,说明我国基金的业绩持续性较差。本文的样本是主动型偏股基金,由于我国股票市场的热点切换频繁,系统性风险较高,基金经理若延续同一投资思路则无法连续获胜(姚颐和高兴,2013)。⑬
| Raw Return | Excess Return | CAPM Alpha | FF3 Alpha | FF5 Alpha | |
| (1) | (2) | (3) | (4) | (5) | |
| MAX | −0.493*** | −0.483*** | −0.151*** | −0.072* | −0.083* |
| (−9.172) | (−9.086) | (−3.369) | (−1.804) | (−1.803) | |
| Return | −0.236*** | −0.232*** | −0.156*** | −0.155*** | −0.184*** |
| (−14.748) | (−14.703) | (−10.686) | (−12.717) | (−13.967) | |
| Controls | YES | YES | YES | YES | YES |
| Within R-squared | 0.723 | 0.724 | 0.470 | 0.313 | 0.286 |
| Observations | 9 464 | 9 464 | 7 205 | 7 205 | 7 205 |
(二)基金MAX与资金流动关系在不同投资者中的表现
既然投资者基于MAX挑选基金是非理性的投资行为,那么MAX对基金流动的正向预测能力在非理性程度高的投资者中表现得应更明显。机构投资者与个人投资者的理性程度不同,与个人投资者相比,机构投资者往往投资经验更丰富,信息优势明显,更能客观对待基金历史极端正收益从而较少受其影响;个人基金投资者受心理偏差影响严重,更容易受历史极端正收益的影响,从而高估其在未来出现的概率。本文推测,MAX可以正向预测基金未来资金流入,这种现象在个人投资者中表现得更明显。本文研究了MAX分别对机构投资者资金流入Flow_Ins和个人投资者资金流入Flow_Ind的影响,表7报告了估计结果。可以看到,列(1)—列(3)中MAX的系数在统计上不显著,列(4)—列(6)中其系数至少在5%的水平上显著。这说明MAX可以显著正向预测个人投资者的资金净流入,对机构投资者资金流入的影响并不明显。这与本文的推测一致,即MAX对基金流动的正向预测能力在非理性程度高的投资者中表现得更明显。
| Flow_Ins | Flow_Ind | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | |
| MAX | −0.071 | 0.108 | 0.120 | 1.997*** | 1.139** | 1.162** |
| (−0.502) | (0.793) | (0.885) | (3.246) | (2.501) | (2.545) | |
| Controls | YES | YES | YES | YES | YES | YES |
| Within R-squared | 0.083 | 0.084 | 0.085 | 0.157 | 0.158 | 0.159 |
| Observations | 9 464 | 9 464 | 9 464 | 9 464 | 9 464 | 9 464 |
(三)控制投资者有限关注
投资者买入出现过极端正收益的基金也可能是因为有限关注。越吸引投资者注意力的资产越容易被投资者选择(Barber和Odean,2008)。如果基金过去出现过极端正收益,则容易引起投资者注意,投资者的买入行为可能仅仅是因为注意到了这类基金。为了说明投资者选择出现过极端正收益的基金不仅仅是因为有限关注的影响,本文在控制变量中加入了明星基金虚拟变量(Star)及其与MAX的交互项。如果MAX的系数在两组样本中差异明显,MAX是有限关注的代理变量,那么MAX×Star的系数应显著为负,即在高关注度(明星基金)样本中MAX的作用会显著减弱。考虑到基金极端收益与资金流动的关系只在全样本和个人投资者样本中显著存在,表8仅报告了这两个样本的估计结果,其中列(1)和列(3)控制了基数收益率,列(2)和列(4)控制了序数收益率。可以看到,MAX×Star的系数不显著且为正,即在高关注度样本中MAX对基金资金流入的影响并没有明显减弱。这说明本文观察到的MAX—资金流动关系并不完全由投资者有限关注所造成。⑮
| Flow | Flow_Ind | |||
| (1) | (2) | (3) | (4) | |
| MAX | 2.084*** | 1.456** | 1.951*** | 1.172** |
| (2.887) | (2.405) | (3.293) | (2.552) | |
| MAX×Star | 0.177 | 0.012 | 0.189 | 0.096 |
| (0.135) | (0.009) | (0.182) | (0.092) | |
| Star | 0.333* | 0.314* | 0.229* | 0.214 |
| (1.826) | (1.705) | (1.775) | (1.646) | |
| Controls | YES | YES | YES | YES |
| Within R-squared | 0.153 | 0.154 | 0.162 | 0.163 |
| Observations | 9 237 | 9 237 | 9 237 | 9 237 |
(四)控制特质波动率和特质偏度
除了MAX指标外,现有文献还使用特质波动率(Ivol)和特质偏度(Iskewness)来衡量投资者的博彩偏好(Kumar,2009)。因此,根据 Bali 等(2011)的做法,本文还控制了特质波动率和特质偏度。⑯估计结果见表9,其中奇数列控制了基金原始收益率,偶数列控制了原始收益率对应的序数收益率。从列(1)—列(4)中可以看到,特质波动率和特质偏度的系数为正,说明两者与基金未来资金净流入正相关,但绝大多数不显著。这说明特质波动率和特质偏度在衡量投资者博彩偏好方面不如MAX好,MAX更适合衡量投资者博彩偏好。从列(5)—列(8)中可以看到,在控制了特质波动率和特质偏度后,MAX对未来资金流入仍然具有显著的正向影响。
| Ivol | Iskewness | Ivol | Iskewness | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| MAX | 1.548** | 1.169* | 1.759** | 1.370** | ||||
| (2.087) | (1.954) | (2.206) | (2.163) | |||||
| Ivol | 4.605 | 4.749* | 3.864 | 4.191 | ||||
| (1.642) | (1.695) | (1.431) | (1.507) | |||||
| Iskewness | 0.035 | 0.037 | 0.029 | 0.031 | ||||
| (1.031) | (1.112) | (0.864) | (0.943) | |||||
| Controls | YES | YES | YES | YES | YES | YES | YES | YES |
| Observations | 7 205 | 7 205 | 7 205 | 7 205 | 7 205 | 7 205 | 7 205 | 7 205 |
| R-squared | 0.138 | 0.139 | 0.138 | 0.139 | 0.139 | 0.140 | 0.138 | 0.139 |
| 注:特质波动率(Ivol)和特质偏度(Iskewness)基于过去24个月的月度收益率数据计算,详见表2。 | ||||||||
六、稳健性检验
(一)改变MAX指标的计算周期
本文还使用过去3个月和12个月的最大月收益作为MAX指标。估计结果见表10中列(1)—列(4),MAX对未来资金流入的影响依然显著为正。
| 过去3个月 | 过去12个月 | 加入同期收益率 | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | |
| MAX | 1.699*** | 1.171*** | 1.641** | 1.566*** | 2.699*** | 1.381** |
| (4.855) | (2.942) | (2.298) | (2.620) | (3.495) | (2.300) | |
| Controls | YES | YES | YES | YES | YES | YES |
| Within R-squared | 0.148 | 0.147 | 0.143 | 0.146 | 0.153 | 0.150 |
| Observations | 9 458 | 9 458 | 8 614 | 8 614 | 9 464 | 9 464 |
(二)加入与资金净流入同期的基金收益
由于基金份额持有人数据半年度的公布频率,本文主要分析的数据频率均为半年,时间周期较长。投资者的基金选择行为不仅受到基金历史收益率的影响,还可能与同期的基金收益相关。虽然使用同期的基金收益率作为解释变量,研究对同期资金流入的影响,可能存在内生性问题(Kempf和Ruenzi,2008),但是作为稳健性检验的一种选择,并不影响我们对比研究结论。加入同期基金收益后的估计结果见表10中列(5)和列(6)。可以看到,在控制了同期基金收益的影响后,MAX对未来资金流入仍然具有显著的正向预测作用。
(三)MAX对未来季度资金净流入的影响
国内基金按季度披露资产净值状况,现有研究文献往往关注基金历史业绩对未来季度资金流入的影响。因此,本文考察了MAX对基金季度资金净流入的影响,估计结果见表11,其中列(1)—列(3)分别使用过去一个季度、半年和一年的最大月收益来定义MAX。可以看到,MAX对未来季度资金净流入产生了正向影响,而基于过去6个月计算的MAX影响最为明显。
| 过去3个月 | 过去6个月 | 过去12个月 | |
| (1) | (2) | (3) | |
| MAX | 0.272** | 0.462** | 0.349** |
| (2.097) | (2.306) | (2.008) | |
| Controls | YES | YES | YES |
| Within R-squared | 0.092 | 0.098 | 0.103 |
| Observations | 22 419 | 21 344 | 19 425 |
(四)MAX对未来一个月基金收益的影响
由于国内基金资金流动数据的最高频率为季度,为了进一步确保研究结果的稳健性,本文参考股票市场的相关研究文献(Bali等,2011;朱红兵和张兵,2020),使用式(6)分析了基金过去一个月的最大日收益率MAX对未来一个月收益率的影响,以间接考察MAX对投资者交易行为的影响。如果投资者对基金极端收益率的观测存在偏差(博彩偏好),出现极端收益率会吸引投资者过多买入基金从而推高基金当期收益,使得其未来收益降低,因此推测系数
| (1) | (2) | |
| MAX1 | −0.440*** | |
| (−14.242) | ||
| MAX2 | −1.335*** | |
| (−28.581) | ||
| Mret | −0.011** | 0.012** |
| (−2.310) | (2.470) | |
| Accmret | −0.071*** | −0.066*** |
| (−20.712) | (−19.809) | |
| Controls | YES | YES |
| Within R-squared | 0.206 | 0.212 |
| Observations | 52 743 | 52 743 |
七、结论与启示
现有理论研究指出,投资者的投资决策会受到资产收益率分布中极大值的影响,即存在博彩偏好。本文选取2005—2019年852只开放式股票型基金和偏股混合型基金,检验了基金月度收益率极大值MAX与未来资金流入Flow之间的关系。研究发现:(1)在控制了历史收益率等因素后,MAX与基金资金流入显著正相关,过去半年最大月收益MAX每增加1%,未来半年资金净流入增加约1.43%。(2)MAX并不能正向预测未来基金业绩,基金过去6个月的最大月收益越大,未来的收益反而越低。MAX每增加1%,基金未来半年经过CAPM调整后的超额收益率降低0.15%。这说明基于MAX购买基金是一种非理性的行为。(3)MAX可以显著正向预测个人投资者的资金净流入,对机构投资者资金流入的影响则不明显。(4)投资者的有限关注理论并不能完全解释基金MAX与资金流动的关系,而且MAX指标比特质波动率和特质偏度能够更好地衡量投资者的博彩偏好。在改变MAX的计算周期以及加入与资金净流入同期的基金收益后,结论仍然成立。此外,MAX能够正向预测未来一个季度的资金净流入,负向预测基金未来一个月的收益。
本文结论为理解基金业绩与资金流动关系提供了新视角,有助于加深对基金投资者行为的认识,对于基金个人投资者利益保护和基金监管有所启发。尽管我国公募基金市场规模增长迅速,但是发展历史较短,个人投资者仍占50%左右的份额。监管层应引导投资者注重公募基金的长期表现,而不要过分看重基金历史收益极值,引导投资者形成更加科学的投资理念。同时,本文也为基金监管提供了新视角和理论基础。基金经理的业绩报酬主要来自基金管理费,而管理费与基金规模正相关。因此,基金经理可能迎合投资者的博彩偏好,策略性地制造最大月收益来吸引资金流入从而扩大基金规模。Agarwal等(2019)发现,在美国基金市场上,规模小、成立时间短或业绩差的基金会通过持有更多的彩票型股票来迎合投资者的博彩偏好,而且在年末表现得更明显。这种行为增加了基金风险,降低了基金业绩,损害了投资者利益。监管部门应强化对这类高风险基金投资行为的监管。
① 据《上海证券报》报道,以中欧基金为例,半数以上客户会在买入基金后的3个月内赎回,七成客户会在6个月内赎回(参见2020年3月9日的报道《四类机构齐聚基金投顾 破解“基金赚钱基民不赚钱”痛点路漫漫》)。而美国的平均持有期限达到4年(彭惠等,2012)。
② 参见上海证券报2020年2月28日的报道《追涨爆款基金被套 专业人士支招拆解》。
③ 2010—2019年我国公募基金规模的年均增速高达22%,2019年末达到14.66万亿元。数据来源于Wind金融终端。
④ 数据来源于《中国证券投资基金业年报(2019)》。
⑤ 中国证监会在2014年发布的《公开募集证券投资基金运行管理办法》中正式提出公募基金FOF的概念;2016年发布《公开募集证券投资基金运作指引2号−基金中基金指引》,开启了国内公募FOF的时代;2018年,养老目标基金异军突起,并按规定采取FOF模式。截至2019年末,已有约90只FOF基金正式成立。
⑥ 比如,2017年中国证监会出台《关于避险策略基金的指导意见》,将保本基金调整为“避险策略基金”,并取消连带责任担保机制。2018年资管新规正式出台,明确规定金融机构开展资产管理业务时不得承诺保本保收益。很多原有的保本基金转型为混合型基金,转型前后的基金运作方式往往差异较大。因此,本文删掉了样本区间内发生过转型的基金。
⑦ 2014年8月8日施行的《公开募集证券投资基金运作管理办法》(以下简称《运作办法》)将股票型基金仓位下限从60%提高到80%。《运作办法》实施后注册的基金需按照其相关规定执行,实施前已经核准或注册的基金,在其实施之日起一年后开始执行。为满足监管要求,2015年8月部分原来的股票型基金转型为混合型基金。本文基于CSMAR数据库中的上海证券基金评级数据对基金类型做了相应调整。
⑧ 受篇幅限制,超额收益率的具体计算方法可向作者索取或参见《财经研究》工作论文版本。
⑨ 稳健性检验中使用了Fama-Macbeth回归(Fama和MacBeth,1973)。
⑩ 结合下文表7中区分机构投资者和个人投资者的实证结果,即使控制了历史极端收益MAX,机构投资者的资金净流入仍然与历史绝对业绩显著正相关,与MAX不显著相关;个人投资者的资金净流入在控制了历史极端收益MAX后与历史绝对业绩不显著相关,而与MAX正相关。这说明表5全样本回归结果中历史绝对业绩的回归系数不显著主要由个人投资者导致。结果详见《财经研究》工作论文版本。
⑪ 本文使用的回归模型均控制了基金个体固定效应和年份固定效应。
⑫ 出于稳健性考虑,本文还使用Fama-Macbeth回归模型(Fama和Macbeth,1973)分析了Flow与MAX之间的关系,其中个别MAX的系数虽然为正但在10%的水平上都不显著。
⑬ 即使业绩存在持续性,样本基金的业绩持续期位于牛市中后期且持续时间不长(韩守富,2011)。从下文表12中可以看到,基金过去一年的收益率负向预测未来一个月的收益率,过去一个月的收益率尚可以正向预测未来一个月的收益率,也说明我国基金业绩的持续性较差。
⑭ 感谢匿名审稿专家的建议。
⑮ 当然,本文并不反对MAX本身也会吸引投资者关注,但明星基金更容易引起关注,在相关文献中往往作为有限关注的代理变量。本文只是尽可能控制有限关注的影响,并不能完全剔除。
⑯ Bali等(2011)研究MAX对股票未来收益的影响时指出,作为投资者博彩偏好的代理变量,MAX可以负向预测股票未来收益;特质波动率/特质偏度也可以负向预测股票未来收益(被称为“特质波动率之谜”),因为特质波动率/特质偏度与MAX指标存在一定的正相关性。因此,三者往往都被用作博彩偏好的指标(Kumar,2009)。但是三者并不等同,MAX作为投资者博彩偏好的衡量指标有着坚实的理论基础(Brunnermeier等,2007;Barberis和Huang,2008),而特质波动率与股票未来收益之间的负相关关系被学者从多个角度解释,如短期反转、彩票型股票偏好、流动性、特质偏度、套利非对称性、有限套利等,但至今没有统一的解释(陆蓉和杨康,2019)。因此,既然MAX和特质波动率均与股票未来收益负相关,那么MAX也有可能是特质波动率的一个代理变量。这样的话,MAX可能就不是博彩偏好的一个代理指标,Bali等(2011)在控制了特质波动率后发现,MAX与未来股价仍然存在显著的负相关关系,从而说明MAX不是特质波动率的代理变量,两者影响股价的机制仍有区别。
⑰ 本文还使用历史超额收益率来控制历史收益,结论不变。另外,考虑到MAX与同期收益Return及其波动率Volatility高度正相关,本文还使用MAX对Return和Volatility回归的残差来控制多重共线性,结论不变。上述结果可以向作者索取或参见《财经研究》工作论文版本。
| [1] | 陈文博, 陈浪南, 王升泉. 投资者的博彩行为研究——基于盈亏状态和投资者情绪的视角[J]. 中国管理科学, 2019(2): 19–30. |
| [2] | 冯旭南, 李心愉. 参与成本、基金业绩与投资者选择[J]. 管理世界, 2013(4): 48–58. |
| [3] | 韩守富. 我国开放式基金的业绩持续性及其影响因素[J]. 经济管理, 2011(8): 128–133. |
| [4] | 李科, 陆蓉. 投资者有限理性与基金营销策略——基金大比例分红的证据[J]. 管理世界, 2011(11): 39–48. |
| [5] | 李志冰, 刘晓宇. 基金业绩归因与投资者行为[J]. 金融研究, 2019(2): 188–206. |
| [6] | 林树, 李翔, 杨雄胜, 等. 他们真的是明星吗? ——来自中国证券基金市场的经验证据[J]. 金融研究, 2009(5): 107–120. |
| [7] | 林煜恩, 陈秀玲, 池祥萱. 共同基金流量具有信息内涵吗?[J]. 经济研究, 2014(S1): 176–188. |
| [8] | 陆蓉, 陈百助, 徐龙炳, 等. 基金业绩与投资者的选择——中国开放式基金赎回异常现象的研究[J]. 经济研究, 2007(6): 39–50. |
| [9] | 陆蓉, 杨康. 有限关注与特质波动率之谜: 来自行为金融学新证据[J]. 统计研究, 2019(6): 54–67. |
| [10] | 莫泰山, 朱启兵. 为什么基金投资人的投资回报低于基金行业的平均回报——基于“聪明的钱”效应实证检验的解释[J]. 金融研究, 2013(11): 193–206. |
| [11] | 彭惠, 江小林, 吴洪. 偏股型开放式基金“赎回悖论”的动态特征及申购异象[J]. 管理世界, 2012(6): 60–73. |
| [12] | 伍燕然, 黄文婷, 苏凇, 等. 基金投资者处置效应的个体差异[J]. 国际金融研究, 2016(3): 84–96. |
| [13] | 肖峻, 石劲. 基金业绩与资金流量: 我国基金市场存在“赎回异象”吗?[J]. 经济研究, 2011(1): 112–125. |
| [14] | 杨坤, 曹晖, 宋双杰. 基金业绩与资金流量: 明星效应与垫底效应[J]. 管理科学学报, 2013(5): 29–38. DOI:10.3969/j.issn.1007-9807.2013.05.003 |
| [15] | 姚颐, 高兴. 明星基金具备明星效应吗?[J]. 财经研究, 2013(6): 93–105. |
| [16] | 俞红海, 陆蓉, 徐龙炳. 投资者名义价格幻觉与管理者迎合——基于基金拆分现象的研究[J]. 经济研究, 2014(5): 133–146. |
| [17] | 郑振龙, 孙清泉. 彩票类股票交易行为分析: 来自中国A股市场的证据[J]. 经济研究, 2013(5): 128–140. |
| [18] | 朱红兵, 张兵. 价值性投资还是博彩性投机? ——中国A股市场的MAX异象研究[J]. 金融研究, 2020(2): 167–187. |
| [19] | 左大勇, 陆蓉. 理性程度与投资行为——基于机构和个人基金投资者行为差异研究[J]. 财贸经济, 2013(10): 59–69. |
| [20] | Agarwal V, Jiang L, Wen Q. Why do mutual funds hold lottery stocks?[R]. Georgetown McDonough School of Business Research Paper No.3164692, 2019. |
| [21] | Bailey W, Kumar A, Ng D. Behavioral biases of mutual fund investors[J]. Journal of Financial Economics, 2011, 102(1): 1–27. DOI:10.1016/j.jfineco.2011.05.002 |
| [22] | Bali T G, Brown S J, Caglayan M O. Upside potential of hedge funds as a predictor of future performance[J]. Journal of Banking & Finance, 2019, 98: 212–229. |
| [23] | Bali T G, Brown S J, Murray S, et al. A lottery-demand-based explanation of the beta anomaly[J]. Journal of Financial and Quantitative Analysis, 2017, 52(6): 2369–2397. DOI:10.1017/S0022109017000928 |
| [24] | Bali T G, Cakici N, Whitelaw R F. Maxing out: Stocks as lotteries and the cross-section of expected returns[J]. Journal of Financial Economics, 2011, 99(2): 427–446. DOI:10.1016/j.jfineco.2010.08.014 |
| [25] | Barber B M, Odean T. All that glitters: The effect of attention and news on the buying behavior of individual and institutional investors[J]. The Review of Financial Studies, 2008, 21(2): 785–818. DOI:10.1093/rfs/hhm079 |
| [26] | Barber B M, Odean T, Zheng L. Out of sight, out of mind: The effects of expenses on mutual fund flows[J]. Journal of Business, 2005, 78(6): 2095–2119. DOI:10.1086/497042 |
| [27] | Barberis N, Huang M. Stocks as lotteries: The implications of probability weighting for security prices[J]. American Economic Review, 2008, 98(5): 2066–2100. DOI:10.1257/aer.98.5.2066 |
| [28] | Boyer B H, Vorkink K. Stock options as lotteries[J]. The Journal of Finance, 2014, 69(4): 1485–1527. DOI:10.1111/jofi.12152 |
| [29] | Brunnermeier M K, Gollier C, Parker J A. Optimal beliefs, asset prices, and the preference for skewed returns[J]. The American Economic Review, 2007, 97(2): 159–165. DOI:10.1257/aer.97.2.159 |
| [30] | Chevalier J, Ellison G. Risk taking by mutual funds as a response to incentives[J]. Journal of Political Economy, 1997, 105(6): 1167–1200. DOI:10.1086/516389 |
| [31] | Doran J S, Jiang D L, Peterson D R. Gambling preference and the new year effect of assets with lottery features[J]. Review of Finance, 2012, 16(3): 685–731. DOI:10.1093/rof/rfr006 |
| [32] | Eraker B O R, Ready M. Do investors overpay for stocks with lottery-like payoffs? An examination of the returns of OTC stocks[J]. Journal of Financial Economics, 2015, 115(3): 486–504. DOI:10.1016/j.jfineco.2014.11.002 |
| [33] | Fama E F, MacBeth J D. Risk, return, and equilibrium: Empirical tests[J]. Journal of Political Economy, 1973, 81(3): 607–636. DOI:10.1086/260061 |
| [34] | Ferreira M A, Keswani A, Miguel A F, et al. The flow-performance relationship around the world[J]. Journal of Banking & Finance, 2012, 36(6): 1759–1780. |
| [35] | Green T C, Hwang B H. Initial public offerings as lotteries: Skewness preference and first-day returns[J]. Management Science, 2012, 58(2): 432–444. DOI:10.1287/mnsc.1110.1431 |
| [36] | Han B, Kumar A. Speculative retail trading and asset prices[J]. Journal of Financial and Quantitative Analysis, 2013, 48(2): 377–404. DOI:10.1017/S0022109013000100 |
| [37] | Harvey C R, Siddique A. Conditional skewness in asset pricing tests[J]. The Journal of Finance, 2000, 55(3): 1263–1295. DOI:10.1111/0022-1082.00247 |
| [38] | Huang J, Wei K D, Yan H. Participation costs and the sensitivity of fund flows to past performance[J]. The Journal of Finance, 2007, 62(3): 1273–1311. DOI:10.1111/j.1540-6261.2007.01236.x |
| [39] | Kempf A, Ruenzi S. Family matters: Rankings within fund families and fund inflows[J]. Journal of Business Finance & Accounting, 2008, 35(1−2): 177–199. |
| [40] | Kumar A. Who gambles in the stock market?[J]. The Journal of Finance, 2009, 64(4): 1889–1933. DOI:10.1111/j.1540-6261.2009.01483.x |
| [41] | Sirri E R, Tufano P. Costly search and mutual fund flows[J]. The Journal of Finance, 1998, 53(5): 1589–1622. DOI:10.1111/0022-1082.00066 |
| [42] | Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5(4): 297–323. DOI:10.1007/BF00122574 |


