
2020第46卷第4期
2. 上海大学 金融信息研究中心,上海 200444
2. Research Center of Financial Information,Shanghai University,Shanghai 200444,China
一、引 言
金融衍生品对底层资产价格的影响一直是学术研究的重点,而作为最重要的衍生品之一,期权对底层资产未来走势的预测作用已经在诸多学术研究中被证实。期权隐含波动率σimp是底层资产风险的重要度量指标。σimp是期权内在价值状态和剩余到期期限τ的函数,记为σimp(moneyness, τ),在诸多文献中也常被称为隐含波动率曲面(implied volatility surface)。在Black和Scholes(1973)的有效市场假设下,σimp估计的是同一标的资产收益的波动状态,在不同的价值状态和剩余到期期限下应为常数。但学者相继发现在给定剩余到期期限时,函数σimp(moneyness, τ)在价值状态上出现“微笑”(implied volatility smile)的现象,即中间低两边高的下凸形态。Rubinstein(1985)最早记录到美国股指期权隐含波动率的微笑形态。之后,Dumas等(1998)分析标普500时发现,不同价值状态下的期权隐含波动率不仅出现“微笑”的现象,还表现出倾斜状态,即隐含波动率从OTM认沽到OTM认购逐渐降低。Foresi和Wu(2005)研究了世界主要金融市场的12只股指期权,发现股指期权隐含波动率从OTM认沽到OTM认购的微笑倾斜现象普遍存在。
在发现隐含波动率微笑现象之后,学者开始研究这一现象产生的原因和机制,主流观点主要有两种。第一种观点认为,隐含波动率微笑倾斜现象与底层资产收益分布的负尾部风险是高度相关的;而第二种则认为,这种倾斜现象是由市场参与者对市场的预期所导致的,或者说隐含波动率在不同价值状态下的差异反映了投资者对市场未来形势的看法。关于第一种观点,大多数研究指出,股票市场上尾部风险的增加与市场上OTM认沽期权的隐含波动率及相对价格变高是相互影响的。Bates(1991)认为,OTM认沽期权的交易数据包含底层资产收益分布的左尾部信息,底层资产收益分布的非对称性现象会反映在OTM认沽和OTM认购期权的相对价格中。Pan(2002)提出期权隐含波动率在不同价值状态下的倾斜现象主要来源于市场投资者对大幅下跌风险的恐慌情绪,研究表明尾部风险溢价(度量投资者对大幅下跌风险的恐慌情绪)在统计意义上对横截面上期权的波动率微笑倾斜现象有显著的解释能力。Bollen和Whaley(2004)也研究了隐含波动率倾斜与底层资产收益分布的关系。他们通过比较股指和个股发现,股指收益的左尾风险更高,即左边尾巴更厚,而股指期权的隐含波动率往往比个股期权更加倾斜。Yan(2011)则从理论上探讨了尾部风险与隐含波动率倾斜的相关关系,指出当期权临近到期且处于ATM的状态时,波动率微笑的局部斜率与股票的跳跃幅度和强度是高度相关的。
关于第二种观点,Bates(1991)提到,股指期权的价格数据反映了市场参与者对未来底层资产走势的预期。Bates(1991)指出,随着股票市场大幅下跌风险的增加,投资者根据自己的判断进行交易,导致OTM认沽期权的价格会明显高于OTM认购期权。由于期权这类衍生品的高杠杆特性,大量期权交易会对底层资产的未来走势产生影响;此外,相对于其他金融产品,期权产品的交易者有着更高的投研能力和更理性的判断能力,所以期权交易数据中的隐含信息对于判断市场未来走势是有价值的。Gârleanu等(2009)使用个股期权的隐含波动率水平来衡量同标的不同价值合约的昂贵性(expensiveness),指出隐含波动率水平反映了交易者对不同合约的偏好和需求量。Bollen和Whaley(2004)指出,标普500期权的隐含波动率形态在与尾部风险相关的同时,其倾斜现象也反映了市场上参与者对某些期权合约的供需平衡的状态。Xing等(2010)证明了个股期权的隐含波动率斜率对股市走向有显著的预测能力,且微笑形态越倾斜的个股在未来的表现越差。Yan(2011)指出,使用深度OTM期权数据会带来很大的测量误差,而使用接近ATM的期权数据构造局部隐含波动率微笑斜率来刻画股市的尾部风险更加合理。于是,Yan(2011)的尾部风险测度指标为ATM、临近到期认沽和认购期权的隐含波动率之差,使用个股期权数据证实了局部期权隐含波动率微笑斜率的增加会导致未来股票收益的显著下降。基于Gârleanu等(2009)的结论,Xing等(2010)解释隐含波动率微笑倾斜的预测能力是因为它捕捉到了期权市场上的知情交易信息。他们指出,交易者对个股有看法时会更多地在期权市场上进行操作,而股票市场对期权市场上的隐含信息反应较慢,使得期权数据中提取出的风险因子对未来股票市场的预测是非常有前瞻性的。
本文认为,底层资产收益的尾部风险与市场投资者的预期是相互影响的。具体而言,期权交易者在当期对未来市场持某种看法和预期时,会根据其看法和预期进行交易,进而影响市场的未来走势;而当期市场的状态以及市场上其他交易者的情绪将会反映在大量的期权交易数据中,这反过来也会对交易者所持看法和预期产生影响。本文认为,投资者的预期、知情信息与市场收益的尾部风险之间有较强的相关关系。期权数据中的隐含风险信息包含了当期期权交易者对未来底层资产的预期和看法,同时也涵盖了未来整个市场尾部风险的信息。因此,本文预期股票期权隐含风险能够显著预测未来股票市场的走势。本文致力于研究股指隐含波动率微笑形态中包含的风险信息,探究这些风险信息对股票收益的预测能力。本文选取中国上证50ETF期权,为了深度挖掘隐含波动率形态的风险含义,首先构造了隐含波动率水平风险因子,然后使用OTM认沽期权和ATM认购期权之间隐含波动率的倾斜程度,作为股票市场上的一个风险因子,实证分析这一因子对未来股票收益的影响。
上证50ETF期权于2015年2月9日正式上市交易,至今已有近五年的时间,其月度成交额不断攀升。由于数据的限制,早期的学术研究有一定的局限性。而2017年以来,一些研究有了合适容量的数据支持,但大多只是关于50ETF期权的定价问题及期权上市后对股票市场波动率的影响等。例如,宋焕雨(2015)、陈紫薇(2016)以及杨兴林和王鹏(2018)研究了中国50ETF的定价问题,张静和宋福铁(2016)、刘庞庞(2017)以及韦晓静(2018)主要研究了50ETF上市后股票市场特别是标的股指上证50的波动性变化。宋焕雨(2015)和陈紫薇(2016)分别使用加入GARCH项的Black-Sholes模型和Heston随机波动率模型,都得出比Black-Sholes模型定价精度更高的结果。杨兴林和王鹏(2018)则基于时变波动率的Black-Sholes模型,在正态分布、广义t分布和Edgeworth Expansion渐进分布这三种假设下,对50ETF期权进行了定价分析,发现非正态分布假设下的模型定价能力高于正态分布假设下的模型。对于50ETF上市后对股市波动率的影响,大多数研究都证实了首只期权的推出对市场有一定的稳定作用,波动率至少在上市后短期内有所降低。在使用更长时间段的数据后,刘庞庞(2017)和韦晓静(2018)发现这种影响是短期的,50ETF的推出对市场波动率的长期影响并不很显著。在2016年之前,由于数据的限制,关于中国股票期权的学术研究较少。基于相关研究的缺失,本文探究了股指期权的隐含波动率形态对未来股票走势的预测能力。研究发现,隐含波动率的倾斜程度对未来上证50指数收益的解释能力是显著且稳健的,在横截面上也能显著预测个股的未来收益;而隐含波动率水平这一因子对上证50指数的未来收益有很强的解释能力,但对个股的预测能力在各种实证模型设计下都不显著。
二、隐含波动率微笑斜率的度量
(一)数据特征
关于隐含波动率的计算,我们可以使用Black-Scholes模型倒推得到。在Black-Scholes模型的假设下,某股票认购期权在时刻t的理论价格为:
| Ct=StΦ(d1)−Ke−rTΦ(d2) |
其中,St为股票价格,K为执行价格,
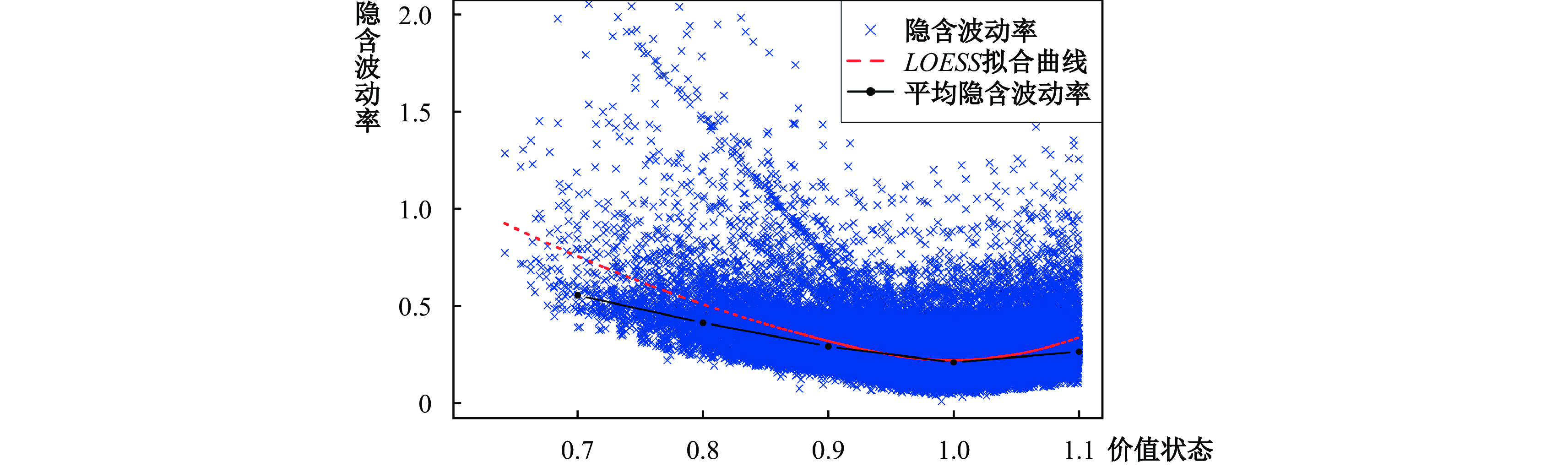
为了准确刻画隐含波动率的倾斜程度,本文首先研究了中国上证50ETF期权的数据特征。期权数据来自Wind数据终端,包含2015年2月9日到2019年5月30日1 874份期权合约的日均价、执行价格和期权类型(认沽或认购),其中认沽期权937份,认购合约937份。为了考察期权隐含波动率的形态,本文使用K/S来度量价值状态(Pan,2002;Foresi和Wu,2005;Christoffersen等,2009;Xing等,2010),将期权合约按照类型、价值状态和剩余期限(记为DTM,单位为日历天)进行分类,计算每个类别中样本期权的隐含波动率均值。图1描绘了所有剩余到期期限在60日以内的期权隐含波动率在价值状态上的形态(小于1的期权样本为认沽,大于1的期权样本为认购)。我们使用局部多项式回归(LOESS)方法,得到了隐含波动率关于价值状态的拟合曲线。图1中的虚线为拟合后的曲线,点线为每个区间内样本均值的连线。从中可以看出,上证50ETF期权隐含波动率“微笑”且“倾斜”的现象非常明显。
|
| 图 1 波动率微笑形态 |
(二)度量结果
本文使用两种方法来度量隐含波动率微笑斜率(slope of implied volatility)。对于第一种方法,借鉴Xing等(2010)的研究,考虑到接近到期日或深度虚值(执行价格远低于现价)期权的价格波动率过大,信息也可能被扭曲,从而影响估计精度,我们选择使用期限为10−60日的期权,作为刻画隐含波动率微笑斜率的样本。OTM认沽期权定义为价值状态K/S在区间[0.75,0.95]内的认沽期权,ATM认购期权定义为价值状态在区间[0.95,1.1]内的认购期权。隐含波动率微笑斜率的第一种测度指标定义如下:
| IVSOMA=σimpOTM认沽−σimpATM认购 |
对于第二种方法,考虑到量纲问题,使用log(K/S)来度量价值状态,通过最小二乘方法来拟合如下的线性函数:
| σimp=α+βlog(K/S) |
本文将回归系数β作为隐含波动率倾斜程度的第二种测度指标,记为IVSOLS;α表示剔除微笑倾斜形态后的隐含波动率水平,记为IVLevel,将其作为隐含波动率风险的度量指标。下文中,在不引起歧义的情况下,将上述两种测度统称为IVS。从IVSOMA和IVSOLS的定义来看,两个测度是负相关的。IVSOMA的数值越大,“微笑”形态越倾斜;而IVSOLS的数值越大,则越不倾斜。本文预期,如果隐含波动率的微笑倾斜程度对股票收益有预测作用,则IVSOMA和IVSOLS的预测能力都应是显著的,且对未来收益的预测方向是相反的。
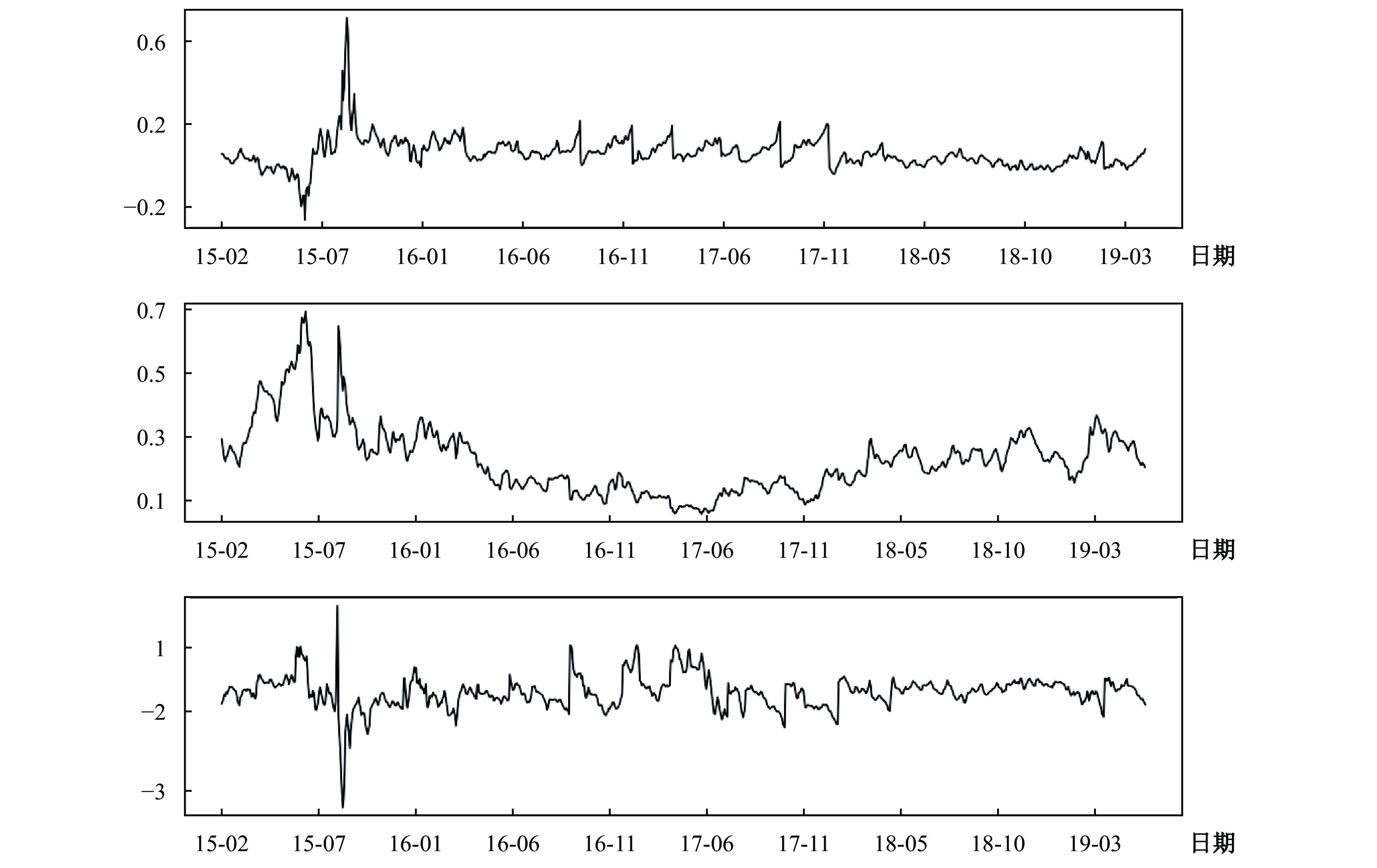
由于期权数量的限制,本文首先按上述标准来选择期权,然后对于每个交易日t,使用t−2、t−1和t这三个工作日的期权样本,计算IVSOMA、IVSOLS和IVLevel这三个因子。使用当天及之前两天的期权数据也能对因子的估计起到平滑作用,在一定程度上消除当天异常交易情况带来的噪声。图2给出了日频的IVSOMA、IVSOLS和IVLevel这三个风险因子的估计序列。从上证50ETF期权上市开始到2015年底,中国金融市场经历了罕见的大涨和大跌。从图2中的IVLevel序列也可以看出,这段时间的隐含波动率水平很高,而IVSOMA和IVSOLS也有较大的波动。2016年初到2019年,IVLevel经历了明显的下降和回升,但这段时间IVSOMA和IVSOLS并没有类似的趋势。这在一定程度上说明隐含波动率的水平和微笑倾斜程度分别度量了不同的风险信息。
|
| 图 2 期权隐含风险因子估计序列图 注:从上至下依次为IVSOMA、IVLevel和IVOLS的日频序列图。 |
三、隐含波动率微笑斜率的预测能力分析
本文将分两部分考察50ETF期权的IVS因子的预测能力。第一部分主要分析从期权数据中提取的IVS对股票指数未来收益的预测能力,在加入控制变量后检验当期的IVS对下期的股指超额收益是否有显著的解释能力。第二部分考察IVS对个股的定价能力,即在横截面上考察IVS在个股中是否被定价。首先对上证50成分股基于beta划分投资组合(beta-based portfolio sorting),为了检验IVS是否在整个股票市场上有稳健的定价能力,使用上证所有A股的数据进行Fama-MacBeth回归,最终得到IVS定价的显著性和IVS风险价格。
(一)IVS对上证50指数收益的预测能力分析
基于相关研究文献,除了IVS因子外,我们还控制了可能影响未来股指收益的一些变量,包括换手率(Turnover)、股息率(取对数,log(P/D))、成交量(Volume)、历史波动率(His.Vol.)、近一个月回报(1Month L.R.)和近三个月回报(3Months L.R.)。加入当期的隐含波动率微笑斜率IVSt,对未来一段时间τ内的上证50累计超额收益 IndRet, τ进行如下回归:
| IndRet,τ=αt,τ+βIVS,τIVSt+βContrs,τContrst+ϵt,τ | (1) |
其中,βIVS, τ 为IVS对未来股指超额收益的回归系数,向量βContrs, τ为所有控制变量的回归系数,IndRet, τ使用t到t+τ的累积超额收益。由于50ETF期权的数据有限,回归使用的是周频而不是月频数据。描述性统计显示,IVSOMA和IVSOLS的相关系数为−0.83,IVLevel和His. Vol.的相关性也非常高,达到0.77。
回归结果见表1。其中,Panel A、Panel B和Panel C分别对应未来8周、12周和24周的收益。列(1)、列(2)和列(3)分别是隐含风险因子IVSOMA、IVSOLS和IVLevel的单变量回归,列(4)、列(5)和列(6)是加入控制变量后的多变量回归。由于与IVLevel高度相关,His. Vol.没有放入列(6)回归中。在列(7)和列(8)中,我们使用IVLevel作为波动水平的代理变量重新进行了回归。
| Panel A:未来8周 | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| 截距 | 0.01 (1.81) | 0.01(0.75) | −0.09(−6.04) | −0.85(−1.77) | −0.64(−1.41) | −0.37(−0.87) | −0.74(−1.76) | −0.69(−1.63) |
| IVSOMA | −0.36(−4.12) | −0.35(−3.73) | −0.30(−3.58) | |||||
| IVSOLS | 0.04 (2.99) | 0.04 (2.42) | 0.05 (3.43) | |||||
| IVLevel | 0.35 (6.21) | 0.49 (6.18) | 0.48 (6.21) | 0.54 (6.82) | ||||
| Turnover | −0.10(−2.17) | −0.07(−1.67) | −0.14(−3.37) | −0.18(−4.26) | −0.18(−4.27) | |||
| Log(P/D) | −0.25(−3.46) | −0.24(−3.26) | −0.31(−4.91) | −0.31(−4.92) | −0.30(−4.84) | |||
| Volume | 0.05 (2.39) | 0.04 (1.98) | 0.03(1.51) | 0.05 (2.45) | 0.04 (2.29) | |||
| His.Vol. | 0.00(1.39) | 0.00(1.35) | ||||||
| 1Month L.R. | −0.23(−2.09) | −0.24(−2.04) | −0.07(−0.64) | −0.02(−0.17) | 0.03(0.28) | |||
| 3Months L.R. | 0.04(0.53) | 0.09(1.14) | 0.13 (2.02) | 0.05(0.86) | 0.09(1.44) | |||
| 拟合优度 | 7.77 | 4.25 | 16.14 | 23.49 | 20.40 | 31.10 | 35.40 | 35.00 |
| Panel B:未来12周 | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| 截距 | 0.01(1.08) | −0.00(−0.03) | −0.11(−6.85) | −0.67(−1.19) | −0.52(−0.91) | −0.48(−0.99) | −0.70(−1.41) | −0.66(−1.33) |
| IVSOMA | −0.31(−2.88) | −0.23(−2.08) | −0.17(−1.79) | |||||
| IVSOLS | 0.03(1.43) | 0.01(0.78) | 0.03(1.62) | |||||
| IVLevel | 0.47 (7.14) | 0.62 (6.69) | 0.61 (6.66) | 0.64 (6.90) | ||||
| Turnover | −0.04(−0.72) | −0.01(−0.26) | −0.13(−2.71) | −0.15(−3.09) | −0.15(−3.07) | |||
| Log(P/D) | −0.31(−3.73) | −0.30(−3.61) | −0.38(−5.25) | −0.37(−5.21) | −0.37(−5.17) | |||
| Volume | 0.05 (1.77) | 0.04(1.46) | 0.04(1.64) | 0.05 (2.06) | 0.04 (1.97) | |||
| His.Vol. | 0.00(1.51) | 0.00(1.30) | ||||||
| 1Month L.R. | −0.01(−0.06) | −0.03(−0.22) | 0.23 (1.84) | 0.26 (2.08) | 0.29 (2.21) | |||
| 3Months L.R. | 0.02(0.23) | 0.05(0.57) | 0.10(1.37) | 0.06(0.78) | 0.09(1.09) | |||
| 拟合优度 | 4.03 | 1.02 | 20.50 | 27.90 | 26.50 | 39.70 | 40.70 | 40.50 |
| Panel C:未来24周 | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| 截距 | 0.01(1.18) | −0.00(−0.35) | −0.15(−8.09) | −2.13(−3.82) | −1.90(−3.44) | −2.48(−5.40) | −2.55(−4.89) | −2.31(−4.49) |
| IVSOMA | −0.23(−1.83) | −0.14(−1.33) | −0.05(−0.52) | |||||
| IVSOLS | −0.02(−0.71) | −0.02(−1.32) | −0.02(−1.48) | |||||
| IVLevel | 0.65 (9.06) | 0.47 (4.95) | 0.46 (4.92) | 0.44 (4.63) | ||||
| Turnover | −0.06(1.23) | −0.02(−0.43) | −0.11(−2.14) | −0.11(−2.20) | −0.09(−1.66) | |||
| Log(P/D) | −0.19(−2.29) | −0.19(−2.32) | −0.17(−2.19) | −0.16(−2.13) | −0.18(−2.32) | |||
| Volume | 0.10 (4.14) | 0.09 (3.74) | 0.12 (5.16) | 0.12 (5.11) | 0.11 (4.73) | |||
| His.Vol. | 0.00 (3.64) | 0.00 (2.92) | ||||||
| 1Month L.R. | 0.03(0.28) | −0.03(−0.26) | 0.21(1.66) | 0.23 (1.71) | 0.16(1.21) | |||
| 3Months L.R. | 0.13(1.38) | 0.15(1.62) | 0.06(0.79) | 0.05(0.61) | 0.07(1.01) | |||
| 拟合优度 | 1.77 | 0.27 | 30.80 | 51.60 | 51.60 | 54.20 | 54.30 | 54.7 |
| 注:括号内为t值,加粗表示在5%的水平上显著,下表同。 | ||||||||
首先观察未来8周收益的回归结果,IVS的影响均显著,说明三个风险因子对未来收益的解释能力在未来8周非常稳定。IVSOMA对未来8周收益的回归系数为−0.36,根据描述性统计,如果IVSOMA从最大值0.62减小到最小值−0.22,未来8周的累积超额收益会增加30%。IVSOLS的系数为0.04,如果从最小值−3.07变化到最大值1.19,未来8周的累积超额收益会增加17%,而IVLevel则相应地能带来约 21.35%的增加。观察未来12周和24周收益的结果可以发现,IVS因子的系数相对于未来8周收益时有衰减的迹象,说明这一因子的预测能力在未来8周到12周之间开始减弱。比较而言,IVLevel的预测能力更加持久,且根据拟合优度,IVLevel比IVS对未来收益有更强的解释能力。
在研究了IVS和IVLevel各自的预测能力之后,我们同时使用这两个风险因子对上证50指数未来收益进行了回归。从列(7)和列(8)中可以看出,IVSOMA、IVSOLS 和IVLevel的系数显著性和数值与其他几列的估计结果比较一致。比如,Panel A和Panel B列(4)中IVSOMA的回归系数分别为−0.35和−0.23,在加入IVLevel一起回归时,列(7)中的系数分别为−0.30和−0.17,数值差异并不大。这说明IVS和IVLevel对上证50指数未来收益的预测机制完全不同,也揭示了期权隐含波动率形态中的这两个度量指标代表了两种完全不同的市场风险。
Yan(2011)从理论上给出了隐含波动率平均水平和倾斜程度的风险含义。他假设个股价格服从一个扩散(diffusive)−跳跃(jump)过程,证明隐含波动率在价值状态上的均值代表了底层资产的跳跃部分带来的风险,这部分风险属于比较“常规”的波动风险,会给资产走势带来“上上下下”的波动,但并不意味着任何下跌风险,而隐含波动率的倾斜水平则隐含了底层资产的尾部风险。具体而言,由于期权价格由参与交易的投资者的报价决定,IVLevel代表了市场对底层资产波动风险的看法。IVLevel增大说明市场认为上证50指数的波动风险上升,未来会给这一风险以补偿,从而收益增加;IVS则反映了市场参与者对未来市场走势预期信息的挖掘,隐含波动率微笑倾斜程度增加(即IVSOMA增加和IVSOLS减小)意味着OTM认沽期权与ATM认购期权在市场上的价差变大,说明期权交易者预期市场的下跌风险上升,而实证结果确实表明这预示着底层股票的下跌走势。
(二)IVS在横截面上对个股的定价能力分析
我们在这部分将研究期权隐含波动率的水平风险和倾斜风险对上证50指数成分股的定价能力。事实上,对指数未来走势有预测能力的风险因子并不一定在个股横截面上有定价能力。在上文中,作为从50ETF期权中提取的隐含风险,IVS和IVLevel对上证50指数的预测能力是非常直观的。但这两类因子是否在横截面上对上证50成分股有定价能力呢?要回答这个问题,需考虑投资者的风险厌恶(risk aversion)函数。如果某类风险在市场上能持续带来显著的风险溢价,则说明投资者对这类风险是厌恶的,当期在横截面上对这类风险有不同敞口的资产未来就会获得不同的风险溢价。因此,横截面上的预测能力是真正检验一个风险因子是否有定价能力更加严谨的依据。
为了研究IVS和IVLevel对个股的定价能力,本文使用上证50指数的所有成分股,首先计算个股收益在风险因子上的敞口(exposure)。这里以隐含波动率倾斜风险因子IVS为例,本文做以下回归:
| Ri,t=βi0+βim(Rm,f−rf,t)+βiIVSIVSt+ϵi,t |
其中,Ri, t为股票i的超额收益(减去当期的无风险收益rf, t),Rm, f为市场组合收益,βiIVS即为股票i在风险上的暴露。如果IVS对个股有定价能力,则差额收益中的一部分应是由股票在IVS上的敞口带来的。使用个股在IVS上的敞口可以计算风险因子的溢价贡献(premium或称为price of risk)λIVS。
| E[Ri]=λ0+λmβim+λIVSβiIVS | (2) |
在上述假设下,一只股票在IVS上的风险敞口越大(即βiIVS越大),未来的超额收益中IVS的溢价就越高(即λIVSβiIVS越大)。在风险因子对个股定价的研究中,λIVS也被称为风险因子的价格,而因子的定价能力就体现在λIVS的显著性和数值上。本文利用式(5)和式(6),分别使用基于IVS beta划分的投资组合收益和Fama-MacBeth回归这两种方法来研究IVS对个股的定价能力。
1. 基于IVS beta划分的投资组合收益分析
为了验证以上理论假设,我们首先使用基于beta划分投资组合的方法。估计个股在IVS上的敞口,然后根据IVS风险敞口来划分个股形成投资组合。第一步,使用t−k到t−1期的数据,拟合式(5),得到所有股票在IVS上的敞口
在个股未来收益预测部分,因子IVLevel的结果在不同的预测区间内和不同的投资组合构造方法下都不显著,这里不再展示。表2和表3分别是因子IVSOMA和IVSOLS的结果,我们分别使用了等权重和市值加权两种方法形成投资组合。其中,Panel A、Panel B和Panel C分别是投资组合在未来8周、12周和24周的超额收益和各模型alpha。列1到列5分别列示的是以
| Panel A:未来8周 | ||||||
| 1 | 2 | 3 | 4 | 5 | 5−1 | |
| 超额收益 | 0.160 | 0.138 | 0.160 | 0.081 | 0.054 | −0.107(−1.917) |
| C. alpha | 0.169 | 0.145 | 0.159 | 0.078 | 0.048 | −0.122(−2.002) |
| 3F. alpha | 0.174 | 0.146 | 0.144 | 0.054 | 0.031 | −0.143(−2.233) |
| 4F. alpha | 0.155 | 0.134 | 0.125 | 0.026 | 0.003 | −0.152(−2.443) |
| 5F. alpha | 0.187 | 0.157 | 0.155 | 0.068 | 0.052 | −0.135(−2.148) |
| Panel B:未来12周 | ||||||
| 1 | 2 | 3 | 4 | 5 | 5−1 | |
| 超额收益 | 0.161 | 0.146 | 0.143 | 0.084 | 0.052 | −0.108(−2.575) |
| C. alpha | 0.162 | 0.144 | 0.138 | 0.076 | 0.036 | −0.126(−2.806) |
| Panel B:未来12周 | ||||||
| 3F. alpha | 0.161 | 0.143 | 0.125 | 0.057 | 0.022 | −0.140(−2.985) |
| 4F. alpha | 0.154 | 0.139 | 0.123 | 0.041 | −0.001 | −0.156(−3.364) |
| 5F. alpha | 0.177 | 0.154 | 0.141 | 0.075 | 0.049 | −0.128(−2.836) |
| Panel C:未来24周 | ||||||
| 1 | 2 | 3 | 4 | 5 | 5−1 | |
| 超额收益 | 0.130 | 0.114 | 0.098 | 0.078 | 0.085 | −0.044(−1.331) |
| C. alpha | 0.127 | 0.110 | 0.092 | 0.071 | 0.071 | −0.057(−1.577) |
| 3F. alpha | 0.113 | 0.101 | 0.074 | 0.050 | 0.048 | −0.065(−1.879) |
| 4F. alpha | 0.107 | 0.096 | 0.074 | 0.040 | 0.034 | −0.073(−2.120) |
| 5F. alpha | 0.128 | 0.113 | 0.084 | 0.070 | 0.062 | −0.066(−2.104) |
| Panel A:未来8周 | ||||||
| 1 | 2 | 3 | 4 | 5 | 5−1 | |
| 超额收益 | 0.114 | 0.026 | 0.083 | 0.151 | 0.215 | 0.101(1.698) |
| C. alpha | 0.109 | 0.026 | 0.089 | 0.149 | 0.222 | 0.113(1.782) |
| 3F. alpha | 0.102 | 0.007 | 0.083 | 0.148 | 0.211 | 0.110(1.660) |
| 4F. alpha | 0.079 | −0.003 | 0.068 | 0.134 | 0.180 | 0.101(1.574) |
| 5F. alpha | 0.131 | 0.032 | 0.093 | 0.157 | 0.226 | 0.094(1.510) |
| Panel B:未来12周 | ||||||
| 1 | 2 | 3 | 4 | 5 | 5−1 | |
| 超额收益 | 0.100 | 0.019 | 0.093 | 0.165 | 0.206 | 0.106(2.253) |
| C. alpha | 0.088 | 0.013 | 0.089 | 0.157 | 0.208 | 0.120(2.459) |
| 3F. alpha | 0.085 | 0.000 | 0.083 | 0.145 | 0.199 | 0.114(2.258) |
| 4F. alpha | 0.064 | −0.006 | 0.082 | 0.139 | 0.186 | 0.122(2.424) |
| 5F. alpha | 0.114 | 0.026 | 0.101 | 0.158 | 0.210 | 0.096(1.983) |
| Panel C:未来24周 | ||||||
| 1 | 2 | 3 | 4 | 5 | 5−1 | |
| 超额收益 | 0.098 | 0.050 | 0.064 | 0.139 | 0.163 | 0.065(1.807) |
| C. alpha | 0.089 | 0.040 | 0.059 | 0.130 | 0.162 | 0.073(1.939) |
| 3F. alpha | 0.070 | 0.024 | 0.044 | 0.122 | 0.137 | 0.067(1.834) |
| 4F. alpha | 0.059 | 0.017 | 0.041 | 0.117 | 0.128 | 0.069(1.865) |
| 5F. alpha | 0.084 | 0.042 | 0.063 | 0.134 | 0.154 | 0.070(2.015) |
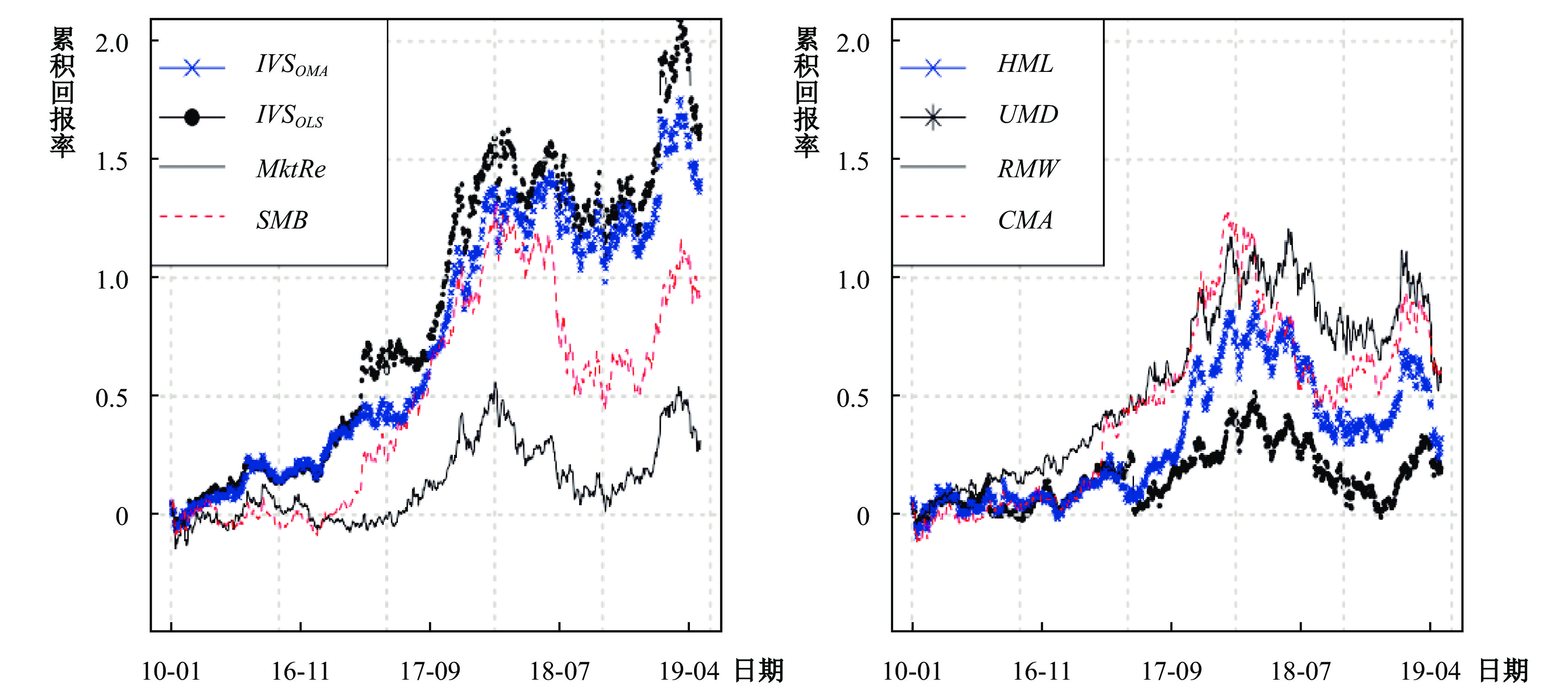
除了揭示投资者的风险偏好外,一个有显著定价能力的风险因子更加重要的作用是,我们可以根据这个因子来构造投资策略。接下来,我们使用以上所有的风险因子,构造基于单一因子beta的投资策略,以考察各因子对个股风险溢价的贡献率。具体方法与基于beta划分并分析投资组合的方法类似,首先估计个股在IVS上的敞口,然后根据IVS风险敞口来划分个股形成投资组合。首先使用t−k到t−1期的数据,拟合式(5),得到所有股票在IVS上的敞口
|
| 图 3 基于各风险因子 beta 投资组合的累积回报率 |
2. 基于IVS beta的Fama-MacBeth回归
在这一部分,我们使用检验因子定价能力的经典方法Fama-MacBeth回归来分析IVS对个股的定价能力分。Fama-MacBeth回归是由Fama和MacBeth(1973)年提出的两步(two-pass)回归法,主要用来测量风险因子对个股的定价能力。第一步,在第t期,计算个股在各风险因子上的beta。我们使用历史48周的日数据进行如下回归:
| Ri,t=βi0+βiIVSIVSt+βif1F1,t+⋯ |
为了保证结论的严谨性,我们在模型中加入了相关文献中比较得到认可的以下风险因子:MktRe、SMB、HML、UMD、RMW和CMA。因此,在这一步,我们分别考虑了以下模型:CAPM+IVS(Model I)、Fama-French三因子+IVS(Model II)、Carhart四因子+IVS(Model III)以及Fama-French五因子+IVS(Model IV)。
第二步,估计每个因子的风险价格λf。
| E[Ri]=λ0+λIVSβiIVS+λf1βif1+⋯ |
由于数据的限制,这一部分的移动窗口依然是周频的。在完成以上两步之后,每个模型都会得到每个因子的溢价贡献λft。表4报告了Fama-MacBeth回归结果,其中Panel A、Panel B和Panel C分别对应在Fama-MacBeth回归的第二步使用未来8周、12周和24周收益估计每个因子的风险价格。Panel C中IVS的风险价格相对较小,说明其对个股风险溢价的贡献在未来12周到24周之间逐渐减弱。而在Panel A和Panel B中,IVS风险价格的显著性是非常稳健的,且对未来12周超额收益的贡献在数值上与对未来8周的贡献基本一致,说明风险价格在未来12周内非常稳定。IVSOLS的结果在四个模型下并不是很稳健。但值得注意的是,在估计结果显著的情况下(Panel B和Panel C中的Model III),IVSOLS的风险定价能力在数值上基本高于包括IVSOMA在内的其他所有风险因子,这一结果与图3一致。
| Panel A:未来8周 | ||||||||
| IVSOMA | IVSOLS | |||||||
| Model I | Model II | Model III | Model IV | Model I | Model II | Model III | Model IV | |
| MktRe | −0.08(−1.85) | −0.09(−2.19) | −0.09(−2.09) | −0.09(−0.11) | −0.04(−0.95) | −0.04(−1.07) | −0.04(−1.02) | −2.56(−0.63) |
| IVS | −0.74(−4.59) | −0.96(−5.28) | −1.05(−5.68) | 0.09(0.10) | 6.29(3.81) | 8.37 (5.01) | 9.08 (4.92) | 2.54(0.63) |
| SMB | −0.05(−2.04) | −0.05(−2.10) | −0.09(−2.05) | −0.04(−1.36) | −0.03(−1.10) | −0.03(−0.63) | ||
| HML | 0.02(0.55) | 0.02(0.57) | −0.10(−4.59) | 0.01(0.32) | 0.01(0.19) | −0.06(−2.23) | ||
| UMD | −0.03(−1.07) | −0.02(−0.59) | ||||||
| RMW | 0.02(0.68) | 0.00(0.15) | ||||||
| CMA | 0.02(0.86) | −0.01(−0.25) | ||||||
| Panel B:未来12周 | ||||||||
| IVSOMA | IVSOLS | |||||||
| Model I | Model II | Model III | Model IV | Model I | Model II | Model III | Model IV | |
| MktRe | −0.09(−2.49) | −0.09(−2.70) | −0.09(−2.38) | 0.55(−1.73) | −0.04(−1.32) | −0.04(−1.21) | −0.03(−0.79) | 1.50(1.37) |
| IVS | −0.75(−6.06) | −0.94(−7.29) | −1.02(−7.58) | −0.56(−1.74) | 6.40 (4.69) | 8.44 (6.10) | 8.82 (5.73) | −1.52(−1.39) |
| SMB | −0.05(−2.60) | −0.05(−2.54) | −0.09(−2.71) | −0.04(−1.84) | −0.03(−1.31) | −0.02(−0.48) | ||
| HML | 0.01(0.40) | 0.01(0.34) | −0.11(−6.12) | 0.01(0.24) | 0.00(0.02) | −0.07(−3.09) | ||
| UMD | −0.04(−1.82) | −0.03(−1.33) | ||||||
| RMW | 0.02(0.62) | 0.00(0.11) | ||||||
| CMA | 0.03(1.35) | −0.01(−0.29) | ||||||
| Panel C:未来24周 | ||||||||
| IVSOMA | IVSOLS | |||||||
| Model I | Model II | Model III | Model IV | Model I | Model II | Model III | Model IV | |
| MktRe | −0.09(−3.38) | −0.10(−3.93) | −0.10(−3.94) | 0.01(0.10) | −0.05(−1.98) | −0.05(−1.95) | −0.04(−1.76) | 0.39(0.66) |
| IVS | −0.42(−4.32) | −0.44(−4.71) | −0.54(−5.51) | 0.00(0.02) | 4.68 (5.72) | 5.92 (7.92) | 6.34 (7.86) | −0.40(−0.67) |
| SMB | −0.06(−4.50) | −0.05(−3.79) | −0.10(−3.71) | −0.06(−4.04) | −0.04(−2.75) | −0. 02(−0.83) | ||
| HML | 0.00(0.11) | 0.00(−0.29) | −0.09(−6.97) | 0.01(0.32) | −0.01(−0.39) | −0.07(−4.85) | ||
| UMD | −0.05(−4.53) | −0.03(−1.92) | ||||||
| RMW | 0.01(0.74) | 0.00(0.17) | ||||||
| CMA | 0.03(1.52) | 0.01(0.42) | ||||||
四、内生性检验
考虑到期权隐含波动率微笑的倾斜程度与底层资产的尾部风险及其他隐含信息相关,我们在这里对IVS做内生性检验。本文根据Hausman(1978)的理论研究,使用两阶段最小二乘法,对隐含波动率微笑斜率IVSt与上证50指数收益回归中的内生性进行检验。本文使用两个变量作为IVSt的工具变量。第一个工具变量,使用Bollerslev和Todorov(2011)的方法,从上证50ETF期权中提取隐含尾部风险(implied tail risk),作为IVS中的尾部风险信息和期权隐含尾部风险溢价的度量(Andersen等,2019),记为TRtimp。TRtimp的计算方法参照Bollerslev和Todorov(2011),首先假设上证50价格Xt在P测度下服从一个扩散−跳跃过程。
| dXtXt=atdt+σtdWt+∫R(ex−1)~μP(dt,dx) |
然后,假设在Q测度下,Xt的跳跃强度过程
| νQ(dx)=(ϕ+t×e−α+tx1{x>0}+ϕ−t×e−α−t|x|1{x<0}) |
此时,价格Xt的隐含尾部下跌风险(implied tail risk)为:
| TRimpt=τϕ−te−α−t|kt|(α−tkt(α−tkt+2)+2)/(α−t)3 |
使用期权价格数据可以估计出ϕt-和αt-,代入式(11)即可得到TRtimp。第二个工具变量,使用上证50的周换手率(Turnover),作为50指数的情绪指标(Ding等,2014;张强和杨淑娥,2009;陆静等,2017)。第一步,我们进行如下回归:
| IVSt=π0+π1Z1,t+π2Z2,t+ϵIVSt |
其中,
| IndRet,τ=αt,τ+β2SLSIVS^IVSt+βZ1Z1,t+ϵt,τ |
首先考察上述两个工具变量对IVS的解释能力,使用TRimp和Turnover对IVS进行回归,结果见表5。从中可以看出,两个工具变量对IVS的影响都显著,对IVSOMA和IVSOLS的解释能力(拟合优度)分别达到了34.40%和21.10%。然后通过Hausman检验来分析
| 截距 | TRimp | Turnover | F检验 | 拟合优度 | |
| IVSOMA | 0.70 (11.15) | 0.33 (8.98) | −0.16(−8.31) | P<0.0001 | 34.40 |
| IVSOLS | −0.31(−7.25) | −1.66(−6.77) | 0.74(5.76) | P<0.0001 | 21.10 |
| 2SLS | OLS | Diff | S.E. | Hausman检验 | ||
| 未来8周 | IVSOMA | −0.39 | −0.26 | 0.13 | 0.17 | 0.69(0.41) |
| IVSOLS | 0.015 | 0.025 | −0.010 | 0.038 | 0.08(0.78) | |
| 未来12周 | IVSOMA | −0.30 | −0.10 | −0.20 | 0.19 | 1.17(0.28) |
| IVSOLS | 0.006 | 0.008 | −0.002 | 0.042 | 0.00(0.96) | |
| 注:2SLS一列表示使用两阶段最小二乘法得到的IVS估计系数,OLS一列表示使用普通最小二乘法得到的IVS估计系数,Diff一列表示2SLS与OLS的系数估计结果之差,S.E.表示这一差值的标准误,Hausman检验一列给出了卡方统计值,括号内为P值。 | ||||||
五、结 论
本文首先探讨了中国上证50ETF期权隐含波动率的形态,数据分析发现其在价值状态上呈现出微笑倾斜,而且随着期权到期日的临近,这种微笑倾斜的形态更加明显。本文进一步采用两种不同的测度指标来刻画上证50ETF期权隐含波动率的形态特征:一是隐含波动率水平,二是隐含波动率微笑倾斜程度。研究表明,期权隐含波动率水平与微笑倾斜程度包含了不同的风险信息。
本文在分析隐含波动率微笑倾斜程度对未来股票收益的影响时,使用虚值认沽期权和实值认购期权波动率之间的差异和斜率来度量隐含波动率微笑倾斜程度,并以剔除“倾斜”的隐含波动率水平作为另一个形态特征。研究发现,在预测上证50指数未来收益时,期权隐含波动率微笑倾斜程度和隐含波动率水平的系数都是显著的。隐含波动率微笑倾斜程度越大,未来上证50指数收益越低,这种影响在未来12周内是非常稳定的,在未来12周到24周之间开始衰减。隐含波动率水平对上证50指数的预测能力比较持久,在24周内都比较稳定。当将两个风险变量放在同一模型中对上证50指数未来收益进行回归时,我们发现两个变量的数值和显著性并没有太大的变化。进一步研究发现,隐含波动率微笑倾斜程度对个股有显著的定价能力,而隐含波动率水平则没有。上述结果说明期权隐含波动率中提取出来的这两个度量指标代表着两种不同的市场风险,对未来市场的预测机制不尽相同。期权隐含波动率水平代表了市场对底层资产波动风险的看法,其数值增加说明市场认为上证50指数的波动风险上升,未来上证50指数会给予补偿,但对横截面上的个股没有显著影响;而期权隐含波动率微笑倾斜程度则反映了市场参与者对未来市场走势预期信息的挖掘,隐含波动率微笑倾斜程度增加意味着虚值认沽期权与实值认购期权在市场上的价差变大,说明期权交易者预期市场的下跌风险上升,预示着底层股票的下跌走势,并能传导到个股中。因此,在期权隐含波动率整体形态中,与隐含波动率水平相比,隐含波动率微笑倾斜是更好的股票风险溢价因子。
| [1] | 陈国进, 许秀, 赵向琴. 罕见灾难风险和股市收益——基于我国个股横截面尾部风险的实证分析[J]. 系统工程理论与实践, 2015(9): 2186–2199. DOI:10.12011/1000-6788(2015)9-2186 |
| [2] | 陈紫薇. 基于Heston随机波动模型的上证50ETF期权定价与对冲研究[D]. 大连: 大连理工大学硕士学位论文, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10141-1016216224.htm |
| [3] | 刘庞庞. 期权市场对现货市场波动率影响的实证分析——基于上证50ETF期权上市前后的比较[J]. 统计与信息论坛, 2017(10): 50–58. DOI:10.3969/j.issn.1007-3116.2017.10.007 |
| [4] | 陆静, 裴饴军, 吴琴琴. 投资者情绪影响香港股票市场吗?[J]. 系统工程理论与实践, 2017(1): 80–90. DOI:10.12011/1000-6788(2017)01-0080-11 |
| [5] | 王鹏, 杨兴林. 基于时变波动率与混合对数正态分布的50ETF期权定价[J]. 管理科学, 2016(4): 149–160. DOI:10.3969/j.issn.1672-0334.2016.04.013 |
| [6] | 韦晓静. 基于双重差分模型期权对股市波动性的实证检验[J]. 统计与决策, 2018(9): 164–168. |
| [7] | 谢尔登·纳坦恩伯格. 期权波动率与定价[M]. 韩冰洁译. 北京: 机械工业出版社, 2014. |
| [8] | 杨兴林, 王鹏. 基于时变波动率的50ETF参数欧式期权定价[J]. 数理统计与管理, 2018(1): 162–178. |
| [9] | 张静, 宋福铁. 上证ETF50期权上市对标的股票的影响——基于流动性和波动性的视角[J]. 金融发展研究, 2016(3): 59–65. DOI:10.3969/j.issn.1674-2265.2016.03.010 |
| [10] | 张强, 杨淑娥. 噪音交易、投资者情绪波动与股票收益[J]. 系统工程理论与实践, 2009(3): 40–47. DOI:10.3321/j.issn:1000-6788.2009.03.007 |
| [11] | Andersen T G, Fusari N, Todorov V. The pricing of tail risk and the equity premium: Evidence from international option markets[J]. Journal of Business & Economic Statistics, 2019. DOI:10.1080/07350015.2018.1564318 |
| [12] | Bakshi G, Kapadia N, Madan D. Stock return characteristics, skew laws, and the differential pricing of individual equity options[J]. Review of Financial Studies, 2003, 16(1): 101–143. DOI:10.1093/rfs/16.1.0101 |
| [13] | Bates D S. The crash of ’87: Was it expected? The evidence from options markets[J]. The Journal of Finance, 1991, 46(3): 1009–1044. DOI:10.1111/j.1540-6261.1991.tb03775.x |
| [14] | Black F, Scholes M. The pricing of options and corporate liabilities[J]. Journal of Political Economy, 1973, 81(3): 637–654. DOI:10.1086/260062 |
| [15] | Bollen N P B, Whaley R E. Does net buying pressure affect the shape of implied volatility functions?[J]. The Journal of Finance, 2004, 59(2): 711–753. DOI:10.1111/j.1540-6261.2004.00647.x |
| [16] | Bollerslev T, Todorov V. Tails, fears, and risk premia[J]. The Journal of Finance, 2011, 66(6): 2165–2211. DOI:10.1111/j.1540-6261.2011.01695.x |
| [17] | Chang B Y, Christoffersen P, Jacobs K. Market skewness risk and the cross section of stock returns[J]. Journal of Finan- cial Economics, 2013, 107(1): 46–68. DOI:10.1016/j.jfineco.2012.07.002 |
| [18] | Christoffersen P, Heston S, Jacobs K. The shape and term structure of the index option smirk: Why multifactor stochastic volatility models work so well[J]. Management Science, 2009, 55(12): 1914–1932. DOI:10.1287/mnsc.1090.1065 |
| [19] | Dennis P, Mayhew S. Risk-neutral skewness: Evidence from stock options[J]. The Journal of Financial and Quantita- tive Analysis, 2002, 37(3): 471–493. DOI:10.2307/3594989 |
| [20] | Ding C G, Wang H J, Lee M C, et al. How does the change in investor sentiment over time affect stock returns?[J]. Emerging Markets Finance and Trade, 2014, 50(S2): 144–158. DOI:10.2753/REE1540-496X5002S210 |
| [21] | Easley D, O’Hara M, Srinivas P S. Option volume and stock prices: Evidence on where informed traders trade[J]. The Journal of Finance, 1998, 53(2): 431–465. DOI:10.1111/0022-1082.194060 |
| [22] | Eraker B, Johannes M, Polson N. The impact of jumps in volatility and returns[J]. The Journal of Finance, 2003, 58(3): 1269–1300. DOI:10.1111/1540-6261.00566 |
| [23] | Fama E F, Macbeth J D. Risk, return, and equilibrium: Empirical tests[J]. Journal of Political Economy, 1973, 81(3): 607–636. DOI:10.1086/260061 |
| [24] | Foresi S, Wu L R. Crash-o-phobia: A domestic fear or a worldwide concern?[J]. The Journal of Derivatives, 2005, 13(2): 8–21. DOI:10.3905/jod.2005.605352 |
| [25] | Gârleanu N, Pedersen L H, Poteshman A M. Demand-based option pricing[J]. The Review of Financial Studies, 2009, 22(10): 4259–4299. DOI:10.1093/rfs/hhp005 |
| [26] | Ge L, Lin T C, Pearson N D. Why does the option to stock volume ratio predict stock returns?[J]. Journal of Financial Economics, 2016, 120(3): 601–622. DOI:10.1016/j.jfineco.2015.08.019 |
| [27] | Hayunga D K, Lung P P. Trading in the options market around financial analysts’ consensus revisions[J]. Journal of Financial and Quantitative Analysis, 2013, 49(3): 725–747. |
| [28] | Jin W, Livnat J, Zhang Y. Option prices leading equity prices: Do option traders have an information advantage?[J]. Journal of Accounting Research, 2012, 50(2): 401–432. DOI:10.1111/j.1475-679X.2012.00439.x |
| [29] | Johnson T L, So E C. The option to stock volume ratio and future returns[J]. Journal of Financial Economics, 2012, 106(2): 262–286. DOI:10.1016/j.jfineco.2012.05.008 |
| [30] | Kelly B, Jiang H. Tail risk and asset prices[J]. The Review of Financial Studies, 2014, 27(10): 2841–2871. DOI:10.1093/rfs/hhu039 |
| [31] | Merton R C. Option pricing when underlying stock returns are discontinuous[J]. Journal of Financial Economics, 1976, 3(1-2): 125–144. DOI:10.1016/0304-405X(76)90022-2 |
| [32] | Pan J. The jump-risk premia implicit in options: Evidence from an integrated time-series study[J]. Journal of Financial Economics, 2002, 63(1): 3–50. DOI:10.1016/S0304-405X(01)00088-5 |
| [33] | Pan J, Poteshman A M. The information in option volume for future stock prices[J]. The Review of Financial Studies, 2006, 19(3): 871–908. DOI:10.1093/rfs/hhj024 |
| [34] | Roll R, Schwartz E, Subrahmanyam A. O/S: The relative trading activity in options and stock[J]. Journal of Financial Economics, 2010, 96(1): 1–17. DOI:10.1016/j.jfineco.2009.11.004 |
| [35] | Rubinstein M. Nonparametric tests of alternative option pricing models using all reported trades and quotes on the 30 most active CBOE option classes from august 23, 1976 through august 31, 1978[J]. The Journal of Finance, 1985, 40(2): 455–480. DOI:10.1111/j.1540-6261.1985.tb04967.x |
| [36] | Xing Y H, Zhang X Y, Zhao R. What does the individual option volatility smirk tell us about future equity returns?[J]. The Journal of Financial and Quantitative Analysis, 2010, 45(3): 641–662. DOI:10.1017/S0022109010000220 |
| [37] | Yan S. Jump risk, stock returns, and slope of implied volatility smile[J]. Journal of Financial Economics, 2011, 99(1): 216–233. DOI:10.1016/j.jfineco.2010.08.011 |
| [38] | Zhang J E, Xiang Y. The implied volatility smirk[J]. Quantitative Finance, 2008, 8(3): 263–284. DOI:10.1080/14697680601173444 |


