
2020第46卷第2期
2. 成都银行 风险管理部,四川 成都 610000
2. Risk Management Department,Bank of Chengdu,Chengdu 610000,China
一、引 言
近年来,我国商业银行普遍存在监管套利、空转套利和关联套利等行为,资金“脱实向虚”现象明显,增加了资产泡沫风险。为了防范化解金融风险,2016年底我国中央经济工作会议提出,“要把防控金融风险放到更加重要的位置”,“着力防控资产泡沫”。2017年,银监会相继发布了《关于银行业风险防控工作的指导意见》《关于开展银行业专项治理工作的通知》等文件,旨在促进银行体系去杠杆。2018年,银监会发布《关于进一步深化整治银行业市场乱象的通知》,要求继续推进银行体系内部去杠杆、去通道、去链条。可见,杠杆率监管是当前及未来一段时期内我国防范金融风险的重要工作。
国际金融危机后,作为全球监管体系的重大改革举措,杠杆率监管被引入宏观审慎监管体系。参考《巴塞尔协议Ⅲ》,我国于2011年正式引入杠杆率监管指标。根据官方公布的数据,我国主要商业银行的杠杆率已高于最低4%的监管标准,而金融危机后我国银行体系风险持续集聚也是不争的事实。那么,杠杆率监管是否有效降低了银行体系的系统性风险?这对于评估宏观审慎监管的有效性具有重要意义。事实上,2007−2009年国际金融危机后,越来越多的国家开始使用各类宏观审慎监管工具,但我们对这些工具及其有效性的理解仍比较有限。因此,评估宏观审慎政策工具的有效性成为近年来的新兴课题(Akinci和Olmstead-Rumsey,2018)。然而,由于数据缺乏、经济金融系统复杂等,当前评估杠杆率工具有效性的文献尚不多见。
一些文献从理论上探讨了杠杆率监管对银行体系稳定性的影响,主要存在以下两种观点:一种认为杠杆率监管对于有效控制系统性风险是非常必要的(Mirza和Strobel,2013)。信息不对称条件下的杠杆率约束与风险加权资本要求相结合,可以减少银行过度的风险承担行为,并引导其报告自身风险的真实信息(Blum,2008)。另一种则认为杠杆率监管可能会降低银行的收益水平和竞争能力,激励其增加风险承担行为,从而不利于银行体系的稳定(Kiema和Jokivuolle,2014;Allahrakha等,2018)。
有关杠杆率监管对银行风险承担行为的影响,实证研究结果同样存在较大差异。比如,Kellermann和Schlag(2013)认为,最低杠杆率要求潜在地降低了银行风险资产的比重,从而激励其承担更多的风险。Smith等(2017)的分析表明,杠杆率约束会增加银行的风险承担行为,但同时损失吸收能力增强,最终金融体系会更加稳定。此外,上述研究通常没有量化银行体系的系统性风险,因而并不能准确评估杠杆率监管工具的有效性。
从国内研究看,当前仅有梁琪等(2015)、方意(2016)等少数学者基于GNSS模型或系统GMM等方法评估了贷款价值比、存贷比、存款准备金率等宏观审慎工具的有效性,而鲜有文献定量评估杠杆率监管的有效性。鉴于现有研究并没有明晰地回答杠杆率监管是否有效降低了银行体系的系统性风险,计量方法难以解决模型潜在的内生性问题和追踪风险传染过程,本文拟使用内生性网络模型来探讨杠杆率监管的有效性。
系统性风险的产生与金融体系的复杂网络结构相关,因此网络模型被广泛应用于系统性风险分析。银行间网络的构造通常有三种方法:第一种是使用银行间双边业务关联数据进行刻画(黄聪和贾彦东,2010),但公开渠道通常无法获取相关数据。第二种是已知银行某一关联业务的总头寸数据,基于假定的银行间网络拓扑结构进行估计(马君潞等,2007;唐振鹏等,2016),目前多数网络模型文献采用这种方法。第三种是基于银行主体行为来构造内生性网络。在前两种方法中,银行关联业务的头寸是外生的,且通常是某一时点的静态数据。而内生性网络则是通过模拟银行的投资决策过程得到的,这种方法较好地体现了金融体系网络具有内生性的特征,克服了银行间双边风险暴露数据通常无法获得的缺陷,因而近年来受到了国内外学者的重视(Bluhm等,2014;Haᴌaj和Kok,2015;李守伟等,2019)。
而遗憾的是,现有的内生性网络模型通常忽略了杠杆率监管对银行行为的影响。为此,本文在Bluhm等(2014)模型的基础上,构建了评估杠杆率监管效应的内生性网络模型。与原模型不同,本文引入了杠杆率监管约束条件,并加入了网络拓扑结构分析。此外,考虑到存款准备金率对我国商业银行资产配置的影响,本文在模型中加入了这一变量。本文可能的贡献在于:第一,将杠杆率监管条件引入内生性网络模型,考察了杠杆率约束对银行体系系统性风险的影响,从而有助于更好地理解杠杆率监管的作用机制;第二,比较分析了不同市场参数组合下的杠杆率监管效应,为政府相关部门制定更加有效的杠杆率监管策略提供了理论支撑。
二、模型构建
假设金融体系中有N家银行,每家银行用网络中的节点表示。在正常时期,每家银行在满足一系列监管约束和资产负债表约束下,基于利润最大化原则选择最优的银行间资产、银行间负债、非流动性资产以及现金资产的数量。各家银行基于邻近匹配原则在银行间市场上选择交易对手。当金融体系达到均衡时,银行间市场的内生关联网络和每家银行的资产配置将处于稳定状态。在危机时期,银行体系在正常时期的均衡将被打破,一些银行会通过调整资产配置来满足监管要求,进而引发非流动性资产抛售、违约清算等一系列市场连锁反应。当银行的资产配置不再发生变化时,银行体系将处于新的均衡。本文将比较引入杠杆率监管和不存在杠杆率监管时,银行在正常时期的资产配置以及危机时期的风险传染过程的差异,以说明杠杆率监管影响银行体系系统性风险的机制和效应。
(一)银行行为
借鉴Bluhm等(2014)的研究,本文将银行的资产分为现金(l)、非流动性资产(nl)、①银行间贷款(bl)、外部贷款(ml)以及存款准备金(d×h,h为法定存款准备金率),将负债分为吸收存款(d)和银行间借款(bb),资产和负债的差额定义为所有者权益或净值(e)。假设资产负债表中的ml、h、d和e均为外生变量,②银行在满足相应约束条件下选择其他资产和负债项目(l、nl、bl和bb)的最优数量。我们用i表示个体银行,j表示银行i的交易对手。银行i的目标函数为:③
| maxli,nli,bli,bbiE(πi)=bli×rrf+rip×nli−bbi×rrf×11−ε×pdi | (1) |
其中,E(πi)为银行i的期望利润,
| li⩾a×di | (2) |
此外,金融机构还需满足资本充足率和杠杆率监管要求,如式(3)和式(4)所示。其中,χ1、χ2和χ3分别为非流动性资产、银行间贷款和外部贷款的风险权重,τ为额外的资本缓冲比率要求,γ*和lev*分别为资本充足率和杠杆率的最低监管要求。如果不存在杠杆率监管,则不需要满足(4)式。
| li+p×nli+bli+mli+di×h−di−bbiχ1×p×nli+χ2×bli+χ3×mli⩾γ∗+τ | (3) |
| li+p×nli+bli+mli+di×h−di−bbili+p×nli+bli+mli+di×h⩾lev∗ | (4) |
银行的资产负债表约束和变量的非负约束如下:④
| li+p×nli+bli+di×h+mli−bbi=di+ei | (5) |
| nli⩾0,li⩾0,bli⩾0,bbi⩾0 | (6) |
我们可以使用线性规划方法来求解满足式(2)−式(6)的目标函数式(1)优化问题。
(二)银行间市场均衡
给定pd i和其他外生参数,银行i基于利润最大化原则确定bbi和bli,银行间市场利率自发调整至均衡水平。一旦银行间市场达到均衡,银行i在均衡利率下的最优银行间资产(bli)和负债(bbi)随之确定。为了得到每家银行对其他银行的双边风险暴露数据,我们使用邻近匹配算法来确定表示银行间借贷网络的邻接矩阵(N×N维)。pd i和邻接矩阵的具体算法可参考Bluhm等(2014)以及朱波和卢露(2016)。
在得到表示银行间网络的邻接矩阵后,我们使用度、入度、出度、聚类系数以及中介中心性指标来度量银行间网络的拓扑结构。定义一个新的邻接矩阵A,当网络中银行i与银行j存在债权债务关系(即blij或blji不为0)时,矩阵中的元素aij取值为1,否则为0。式(7)和式(8)给出了网络中节点i的度(DEi)、入度(DEiin)和出度(DEiout)。式中Mout(i)和Min(i)分别表示银行i的债务银行(如果blij≠0,j即为i的债务银行)和债权银行(如果bbij≠0,j即为i的债权银行)集合。M(i)表示与银行i存在债权债务关系的银行集合。
| DEi=∑j∈M(i)aij | (7) |
| DEouti=∑j∈Mout(i)aij,DEini=∑j∈Min(i)aij | (8) |
聚类系数(Ci)测度的是网络中节点i的关联度密度,如式(9)所示。如果两个存在关联的节点i和j均与第三个节点y存在联系,那么这三个节点可以构成一个三角,平均聚类系数度量了网络中三角的密度。平均聚类系数越高,银行间网络越接近群体结构。聚类系数为1(0)表明银行间网络是全(不)连通的,即任意两个相邻节点都直接(不)相连。
| Ci=2DEi(DEi−1)∑j,yaijaiyajy | (9) |
中介中心性指标衡量了节点作为其他节点间连接通道的能力,中介中心性指标越高,节点在网络中的“中介”作用越强,因而越处于网络的中心。使用σij表示节点i和j之间最短路径的数量,σij(v)表示节点i和j的最短路径中经过节点v的数量,V表示网络中所有节点的集合,则节点v的中介中心性(CB(v))可以表示:
| CB(ν)=∑i≠v≠j∈Vσij(ν)σij | (10) |
(三)非流动性资产市场均衡
在金融体系受到冲击后,假设银行无法通过增资扩股等方式增加自身的资本金。一些银行因资产受损而不再满足资本充足率或杠杆率监管要求时,将不得不变卖非流动性资产或者偿还部分存款债务。假设银行i在受到冲击后的资本充足率和杠杆率分别变为γi和levi。当γi<γ*时,为了满足资本充足率要求,银行i所需卖出的非流动性资产数量为
| γ∗=p×(nli−si1)+li+bli+mli+di×h+p×si1−bbi−diχ1×p×(nli−si1)+χ2×bli+χ3×mli | (11) |
| si1=nli×p×(χ1×γ∗−1)+bli×(χ2×γ∗−1)+mli×(χ3×γ∗−1)+di×(1−h)+bbi−liχ1×γ∗×p | (12) |
当levi<lev*时,为了满足杠杆率监管要求,银行将依次减少流动性资产和卖出非流动性资产以偿还部分存款债务。设所需减少的债务为Δdi(Δdi
| 1−di+bbi−Δdip×nli+li+bli+mli+di×h−Δdi=lev∗ | (13) |
| Δdi=min{di+bbi−(1−lev∗)(p×nli+li+bli+mli+di×h)lev∗,di} | (14) |
为了偿还债务Δd i,银行需使用的流动性资产Δai(现金和存款准备金)和卖出的非流动性资产
| Δai=h×Δdi+max(li−α×di+α×Δdi,0) | (15) |
| si2=Δdi−[h×Δdi+max(li−α×di+α×Δdi,0)]p | (16) |
在杠杆率和资本充足率双重监管下(用I=1表示),银行i最终实际卖出的非流动性资产数量
| siI=1={min[nli,max(si1,si2)]γi<γ∗,levi<lev∗min(nli,si2)γi⩾γ∗,levi<lev∗0γi⩾γ∗,levi⩾lev∗min(nli,si1)γi<γ∗,levi≥lev∗ | (17) |
在不需要满足式(4),即仅存在资本充足率约束时(用I=0表示),银行需要卖出的非流动性资产数量
| siI=0={min(nli,si1)γi<γ∗0γi⩾γ∗ | (18) |
如果卖出全部的非流动性资产后仍不满足资本监管要求,银行将被视为技术性违约而进行破产清算。具体的资产清算过程以及债务人偿付顺序和比例参考Eisenberg和Noe(2001)的做法。非流动性资产的售卖将导致其价格螺旋式下跌,使原本满足资本监管要求的银行净值下降,从而引发新一轮的非流动性资产抛售。由于si随着p的下降而增加,非流动性资产的总供给函数S(p)=∑isi(p)是p的减函数。非流动性资产的市场均衡价格满足S(p)=D(p)。借鉴Cifuentes等(2005)的研究,定义函数θ:[p,1]→[p,1],均衡价格为式(19)的定点求解。函数θ的含义是,当银行的非流动性资产以价格p进行估值时,其买方报价将变为θ(p)。
| θ(p)=D−1(S(p)) | (19) |
价格的收敛过程由如下的反需求函数保证:
| p=exp(−β∑isi(p)) |
其中,β(β>0)表示价格对非流动性资产卖出数量的反应程度或者说价格的调整速度。参考Cifuentes等(2005)的研究,我们选取金融体系卖出全部非流动性资产时价格下跌程度为20%的价格调整速度。非流动性资产价格的迭代过程如下:假设在受到冲击前,非流动性资产的市场均衡价格p0为1。此时,所有银行均满足资本监管要求,非流动性资产的卖出数量为0。在资产遭受一定损失后,不满足资本监管要求的银行将卖出一定数量的非流动性资产以提高自身的资本比率,此时非流动性资产的供给数量为S(1)。买方基于反需求函数的报价为p(S(1))bid,但卖方的报价为1,最终的市场清算价格p1为p(S(1))bid和p0的均值。由于市场价格下降,一些银行不得不卖出额外的非流动性资产以满足资本监管要求。这种价格调整过程将一直持续到p(S(t))bid等于pt−1(t表示迭代次数),或者市场中不再有新的非流动性资产出售。
(四)模型均衡
模型的均衡定义为:
1. (li,nli,bli,bbi)为满足式(2)−式(6)的目标函数式(1)优化问题的解,即银行的最优资产配置。
2. 在银行间市场价格rrf下,银行间市场资金的总供给等于总需求,即
3. 银行违约率为基于迭代算法得到的期望违约概率。
4. 非流动性资产市场达到均衡,市场均衡价格基于θ(p)=D−1(S(p))的定点求解得到。
(五)系统性风险度量
借鉴Bluhm等(2014)的定义,本文的系统性风险为受到外生冲击后违约银行的总资产占银行体系总资产的比重。违约银行最终的资产价值将变为0,所以这里其资产是受到冲击之前的。系统性风险
| ϕ=∑m∈φϕm×probm=∑m∈φ∑defassetsdef∑iassetsi×probm | (21) |
其中,def表示金融体系受到外生冲击后违约的银行,
三、模拟分析
(一)参数校准
假设N的初始值为16,e、d和ml的数据从我国16家上市银行的资产负债表中获得。⑥其中,ml使用发放贷款及垫款表示,e使用银行的所有者权益表示。我们选取银行在2010年第2季度至2018年第3季度的数据进行校准,参数取值见表1。需要指出的是,各个季度的系统性风险值并不是对银行体系实际风险的度量,仅是为了比较杠杆率监管和无杠杆率监管两种情况下银行体系风险的差异。
| 参数 | 定义 | 取值 | 参考依据 |
| N | 系统中银行的数量 | 16 | Haᴌaj和Kok(2015)、Aldasoro等(2017) |
| α | 流动性比率要求 | 0.05 | 朱波和卢露(2016) |
| h | 法定存款准备金率 | 0.175 | 朱波和卢露(2016) |
| χ1 | 非流动性资产的风险权重 | 1 | Bluhm等(2014)、Aldasoro等(2017) |
| χ2 | 银行间贷款的风险权重 | 0.2 | Haᴌaj和Kok(2015)、Aldasoro等(2017) |
| χ3 | 外部贷款的风险权重 | 0.4 | 朱波和卢露(2016) |
| r | 银行的非流动性资产回报率 | U(0,0.15) | Bluhm等(2014)、Aldasoro等(2017) |
| ε | 银行的违约损失率 | 0.76 | 朱波和卢露(2016) |
| γ* | 资本充足率要求 | 0.08 | Bluhm等(2014)、Aldasoro等(2017) |
| τ | 资本缓冲比率要求 | 0.01 | Bluhm等(2014)、Aldasoro等(2017) |
| lev* | 杠杆率监管要求 | 0.04 | 2015年修订的《我国商业银行杠杆率管理办法》 |
|
φ
|
对外部贷款的冲击 | −abs(N(5,25,0)) | Bluhm等(2014)、Bluhm和Krahnen(2014) |
| ml | 外部贷款 | 取自银行资产负债表 | Bluhm等(2014)、朱波和卢露(2016) |
| d | 吸收存款 | 取自银行资产负债表 | Haᴌaj和Kok(2015)、Aldasoro等(2017) |
| e | 资产净值 | 取自银行资产负债表 | Haᴌaj和Kok(2015)、Aldasoro等(2017) |
| m | 冲击情景数 | 1 000 | Bluhm等(2014)、Bluhm和Krahnen(2014) |
| pc | 银行外部贷款回收比例 | 0.9 | Bluhm等(2014)、朱波和卢露(2016) |
(二)杠杆率监管对正常时期银行资产配置的影响
表2给出了杠杆率监管(I=1)和无杠杆率监管(I=0)两种情况下的银行间网络结构特征指标。从中可以看出,无论是否存在杠杆率监管,平均度均在2.8左右,意味着每个银行在网络中平均与约2.8个的银行存在债权债务联系。平均聚类系数在两种情况下都较低,这与Aldasoro等(2017)的发现一致。在引入杠杆率监管后,平均度、平均入度和平均出度均有所下降,表明杠杆率监管在一定程度上减少了银行间的债权债务联系。此外,平均聚类系数由I=0时的0.1444降至I=1时的0.1341,但杠杆率监管使平均中介中心性有所上升。这表明,尽管杠杆率监管降低了银行间的平均关联程度,但是一些银行作为网络中心节点的地位却有所上升,最终导致整个网络的平均中介中心性上升。
| 平均度 | 平均入度 | 平均出度 | 平均聚类系数 | 平均中介中心性 | |
| I=0 | 2.8750 | 1.4375 | 1.4375 | 0.1444 | 20.3194 |
| I=1 | 2.7153 | 1.3576 | 1.3576 | 0.1341 | 24.7222 |
| 注:上述指标值为样本期间的季度均值。 | |||||
表3给出了样本期间I=1和I=0时银行体系的非流动性资产(nl)、银行间市场规模(bb或bl)、现金资产(l)以及总资产(ta)。由于外生变量与是否存在杠杆率监管无关,表中未给出存款和资产净值数据。对比I=1和I=0两种情况可以发现,nl和l基本上无差异,bb和ta则存在显著差异。这说明,对银行施加4%的杠杆率约束并不会显著影响其现金资产和非流动性资产的配置,银行将主要通过收缩银行间市场的借款和贷款规模来控制资产的过度扩张,从而银行体系的资产规模与I=0时相比有所下降。此外,由模型推出的银行体系总资产呈现上升态势,这与近年来银行业资产规模不断扩张的事实相符,表明本文的模型能够较好地反映现实。
| I=1 | I =0 | |||||||
| nl | bb或bl | l | ta | nl | bb或bl | l | ta | |
| 2010Q2 | 8.6044 | 5.0014 | 2.3886 | 55.8619 | 8.6044 | 6.7169 | 2.3886 | 57.5773 |
| 2011Q2 | 11.1651 | 8.6290 | 2.7445 | 67.5627 | 11.1651 | 9.2100 | 2.7445 | 68.1437 |
| 2012Q2 | 13.3750 | 10.7728 | 3.1111 | 77.8510 | 13.3750 | 11.9115 | 3.1111 | 78.9897 |
| 2013Q2 | 15.5083 | 12.2281 | 3.4577 | 87.0562 | 15.5083 | 13.0764 | 3.4577 | 87.9045 |
| 2014Q2 | 18.0325 | 14.3061 | 3.8567 | 98.0357 | 18.0325 | 15.3977 | 3.8567 | 99.1273 |
| 2015Q2 | 13.3793 | 17.9156 | 4.0359 | 106.5905 | 13.3793 | 21.6352 | 4.0359 | 110.3102 |
| 2016Q2 | 15.7945 | 20.0844 | 4.3527 | 116.2637 | 15.7940 | 23.0738 | 4.3527 | 119.2530 |
| 2017Q2 | 17.1428 | 18.7831 | 4.7487 | 123.8526 | 17.1421 | 22.4656 | 4.7487 | 127.5350 |
| 2018Q2 | 18.5433 | 18.0011 | 5.0445 | 130.0550 | 18.5433 | 21.4575 | 5.0445 | 133.5114 |
| 注:由于银行间市场实现了均衡,每个季度均有bb=bl。受篇幅限制,表中仅列出部分时期的数据。单位为万亿元。 | ||||||||
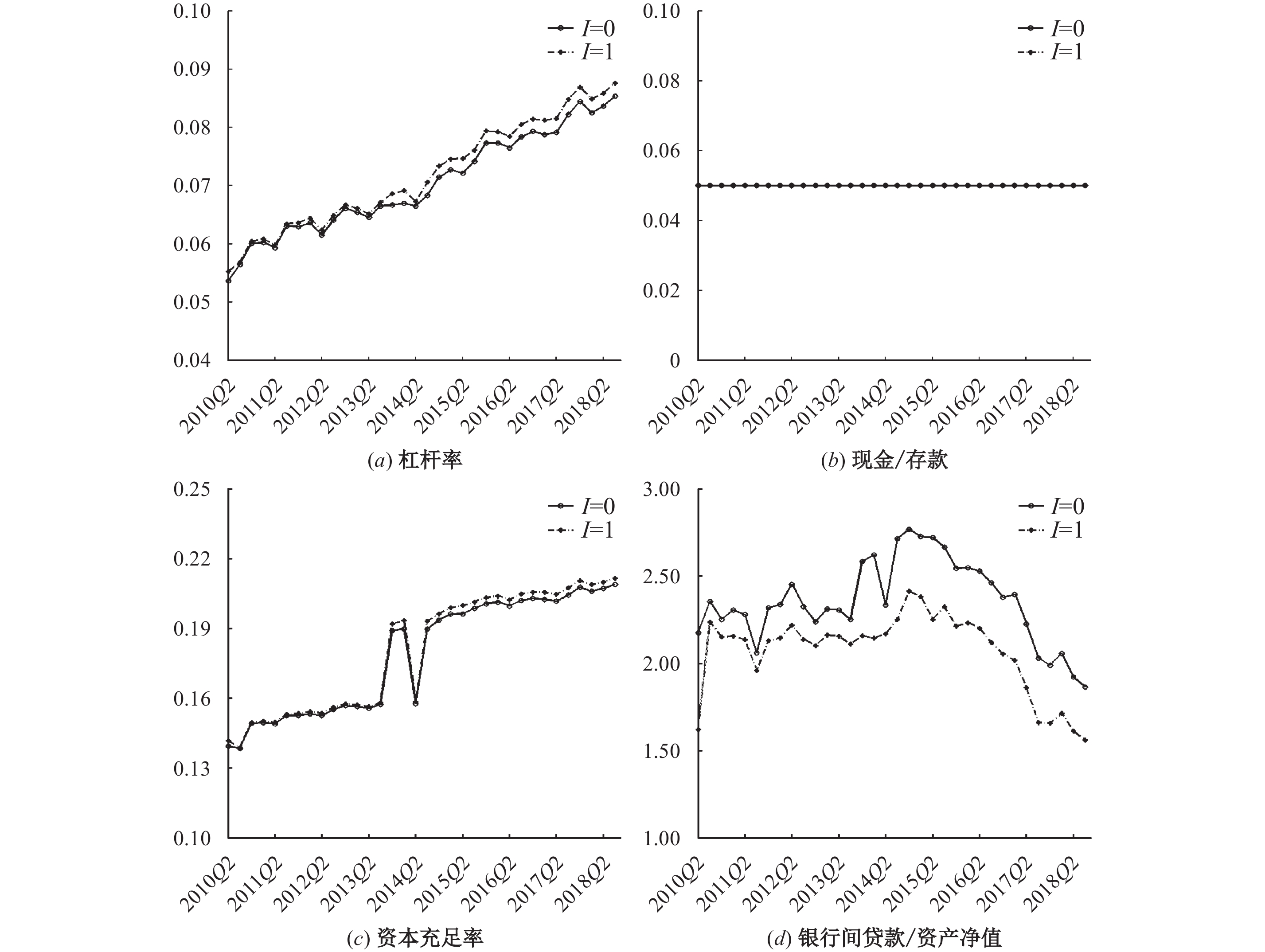
图1更直观地给出了两种情况下银行体系的相关指标。从中可以看出,银行体系的杠杆率和资本充足率在实施杠杆率监管后略有上升,这意味着杠杆率约束确实改善了银行的资本状况。由于银行持有现金资产并不会带来额外的收益,两种情况下银行所持有的现金占存款的比重均为最低监管要求5%。此外,银行间贷款占资产净值的比重在引入杠杆率监管后有所下降。这表明一些银行通过优先减少收益较低且风险较小的银行间贷款资产而不是非流动性资产来提升自身的杠杆率水平,即杠杆率监管增加了部分银行的风险承担激励。
表4给出了样本期间个体银行的杠杆率变化(Δlev)、杠杆率(levI=0)、资本充足率(γI=0)、银行规模(size)、非流动性资产收益率(r)以及资产结构(cs)之间的Pearson系数。其中,Δlev=levI=1−levI=0,银行规模等于资产净值与存款之和,资产结构使用存款与资产净值之比表示。由于e、d和r为模型的外生参数,size、r和cs与是否存在杠杆率监管无关。
|
| 图 1 杠杆率监管与无杠杆率监管下银行体系的资产配置 |
| Δlev | levI=0 | γI=0 | size | r | cs | |
| Δlev | 1.0000 | −0.2248*** | −0.0037 | 0.0957** | 0.0401 | 0.0543 |
| (1.0000) | (0.0000) | (0.3893) | (0.0256) | (0.3501) | (0.2060) | |
| levI=0 | −0.2248*** | 1.0000 | 0.8582*** | −0.1707*** | −0.0925** | −0.7928*** |
| (0.0000) | (1.0000) | (0.0000) | (0.0001) | (0.0311) | (0.0000) | |
| γI=0 | −0.0037 | 0.8582*** | 1.0000 | −0.3804*** | −0.0820** | −0.6811*** |
| (0.3893) | (0.0000) | (1.0000) | (0.0000) | (0.0559) | (0.0000) | |
| size | 0.0957** | −0.1707*** | −0.3804*** | 1.0000 | 0.0211 | 0.0019 |
| (0.0256) | (0.0001) | (0.0000) | (1.0000) | (0.6230) | (0.9640) | |
| r | 0.0401 | −0.0925** | −0.0820** | 0.0211 | 1.0000 | 0.0632 |
| (0.3501) | (0.0311) | (0.0559) | (0.6230) | (1.0000) | (0.1410) | |
| cs | 0.0543 | −0.7928*** | −0.6811*** | 0.0019 | 0.0632 | 1.0000 |
| (0.2060) | (0.0000) | (0.0000) | (0.9640) | (0.1410) | (1.0000) | |
| 注:***和**分别表示在1%和5%的水平上显著,括号内为p值。 | ||||||
表4显示,Δlev与levI=0显著负相关,表明杠杆率监管对无约束时杠杆率较低的银行有较大影响。此外,Δlev与size在5%的水平上显著正相关,意味着杠杆率监管对大银行有显著影响。⑦其原因在于,size与levI=0和γI=0均存在一定的负相关关系,表明大银行在I=0时的杠杆率和资本充足率通常处于较低的水平,因此施加杠杆率监管对这类银行会产生较大影响。这在一定程度上与王连军(2018)的研究结论相符,即在杠杆率监管前,资本补充能力强的大银行的杠杆率更低,从而对杠杆率监管政策的反应更大。
(三)杠杆率监管对危机时期风险传染的影响
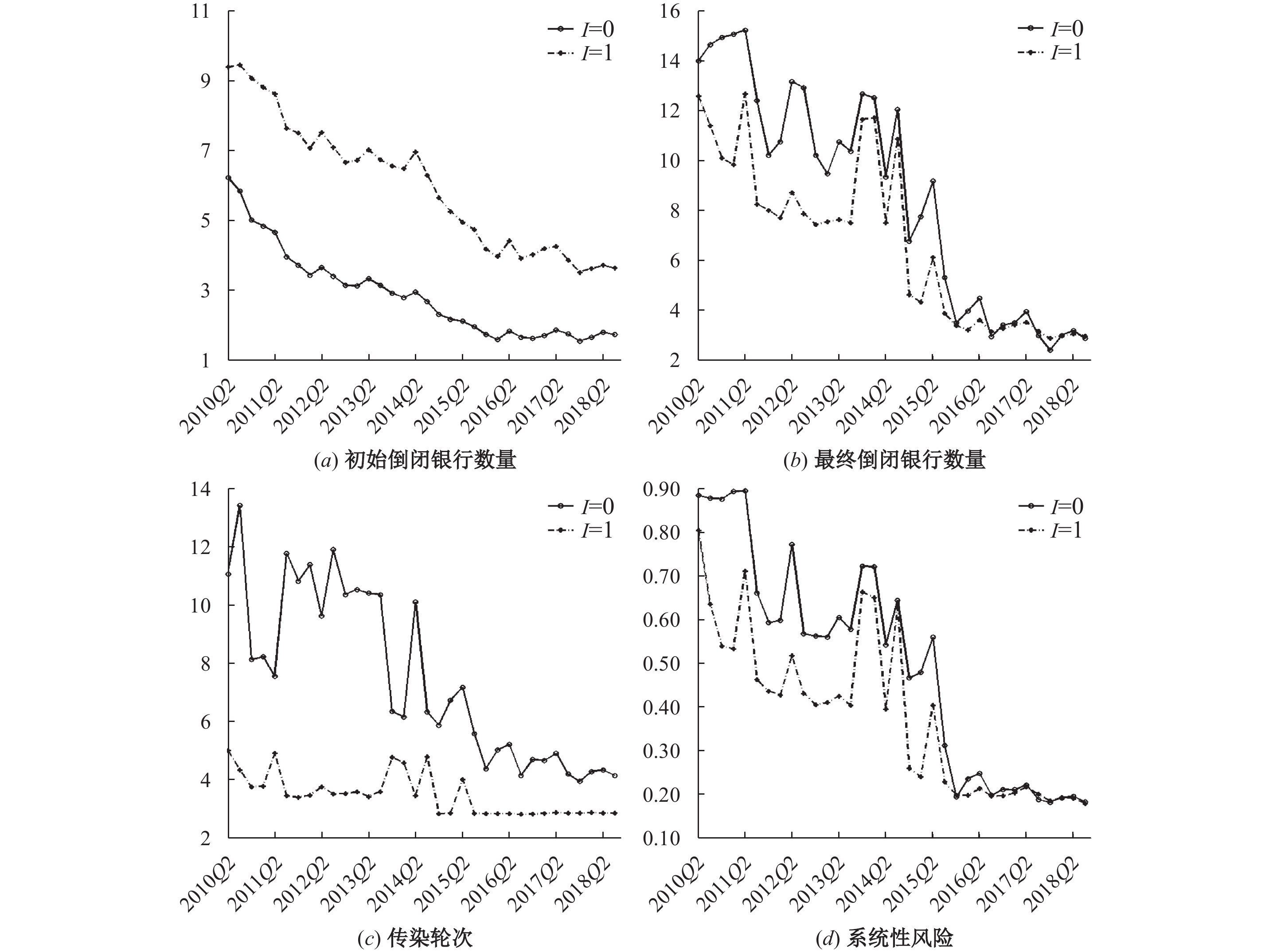
为了分析危机时期杠杆率监管如何影响银行的资产调整行为和风险传染程度,假设银行体系在受到外生冲击前,I=1时每家银行在均衡状态下的最优资产配置、银行间网络以及其他外生条件与I=0时均相同,即不考虑杠杆率监管对正常时期银行资产配置行为的影响。图2给出了两种情况下每个季度银行体系受到外生冲击时初始倒闭银行数量、最终倒闭银行数量、传染轮次以及系统性风险,每个季度的指标值为1 000次模拟结果的均值。
|
| 图 2 杠杆率监管与无杠杆率监管下的风险传染状况 |
从中可以看出,杠杆率监管会增加初始倒闭银行数量,这是因为更加严格的资本监管标准会使资本薄弱的银行在受到外生冲击时更容易低于技术偿付水平,从而被强制清算。尽管如此,杠杆率监管使最终倒闭的银行数量在绝大多数情况下低于无杠杆率监管时。从传染轮次与程度看,当存在杠杆率监管时,初始冲击所引发的传染轮次和系统性风险总体上更低。这表明,杠杆率监管在一定程度上通过加速脆弱性银行的倒闭,及时阻断了风险的进一步扩散;同时,更加严格的资本监管要求也增加了健康银行的风险抵御能力,从而最终降低了金融体系的损失。
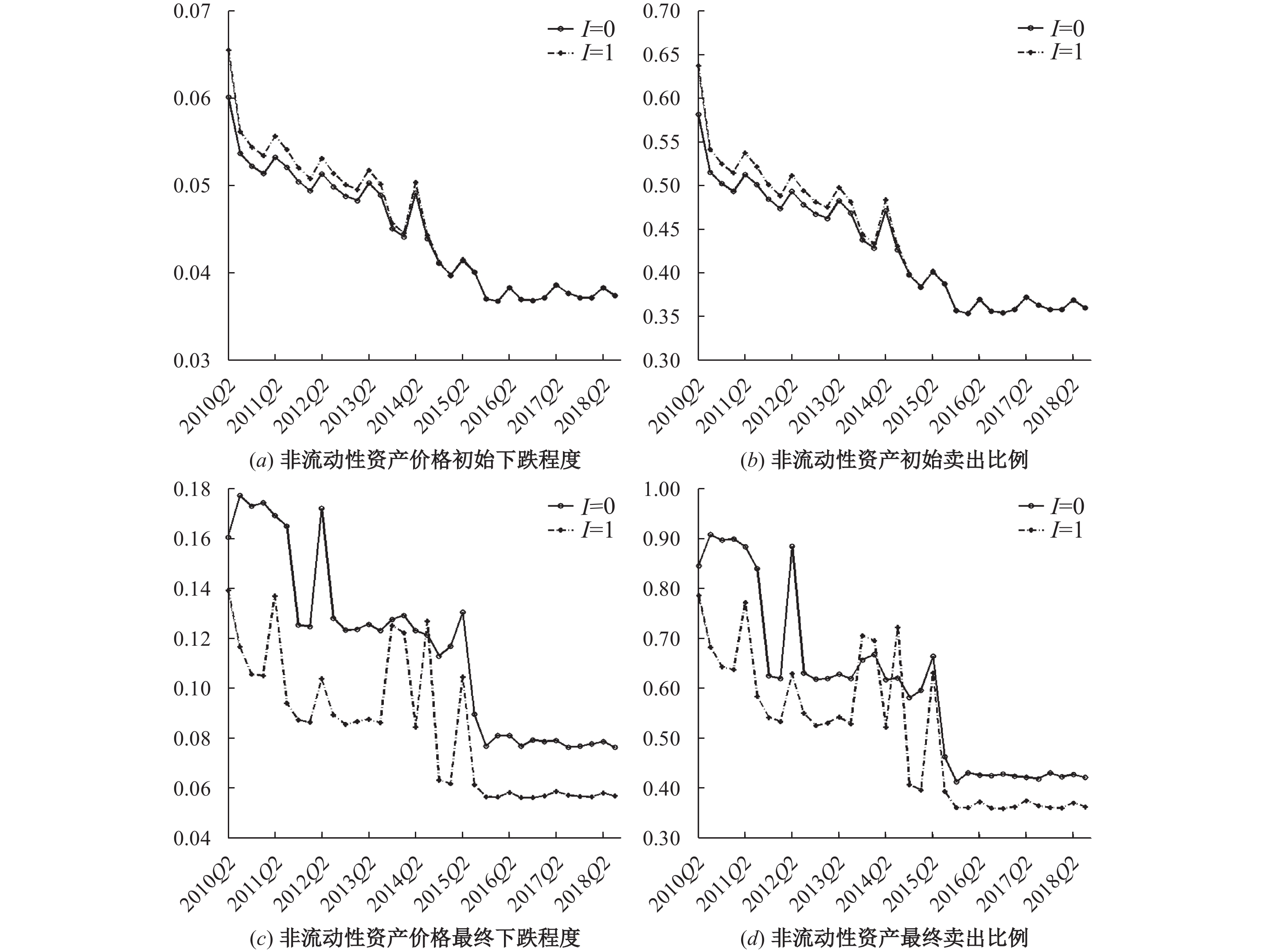
由于资产价格是风险传染的重要渠道之一,图3进一步对比了I=1和I=0时的非流动性资产市场指标。其中,非流动性资产价格初始(最终)下跌程度等于其初始价格减去第一轮(最终)传染结束时的价格,初始(最终)卖出比例等于第一轮(最终)传染结束时银行体系卖出的非流动性资产总数与受到冲击前总数之比。从中可以看出,杠杆率监管会增加银行体系在受到外生冲击时初始卖出的非流动性资产比例和价格下跌程度,但最终卖出的非流动性资产比例和价格下跌程度却有所下降。其原因在于,更加严格的资本监管要求会使资产负债结构脆弱的银行在受到冲击后的第一时间就减少风险较高的非流动性资产,从而增加市场中非流动性资产的初始抛售数量和价格下跌程度。但同时,这种及时的资产调整行为也增加了银行体系的风险抵御能力,减缓了风险的进一步扩散,从而非流动性资产最终的价格下跌程度和卖出数量有所下降。此外,非流动性资产的市场指标在样本期间总体上呈现下降趋势,这主要是因为银行体系总的资产净值在样本期间呈增长趋势,在面临相同的初始冲击时具有更强的风险抵御能力。
|
| 图 3 金融体系非流动性资产的变化情况 |
(四)杠杆率监管对系统性风险的综合影响效应
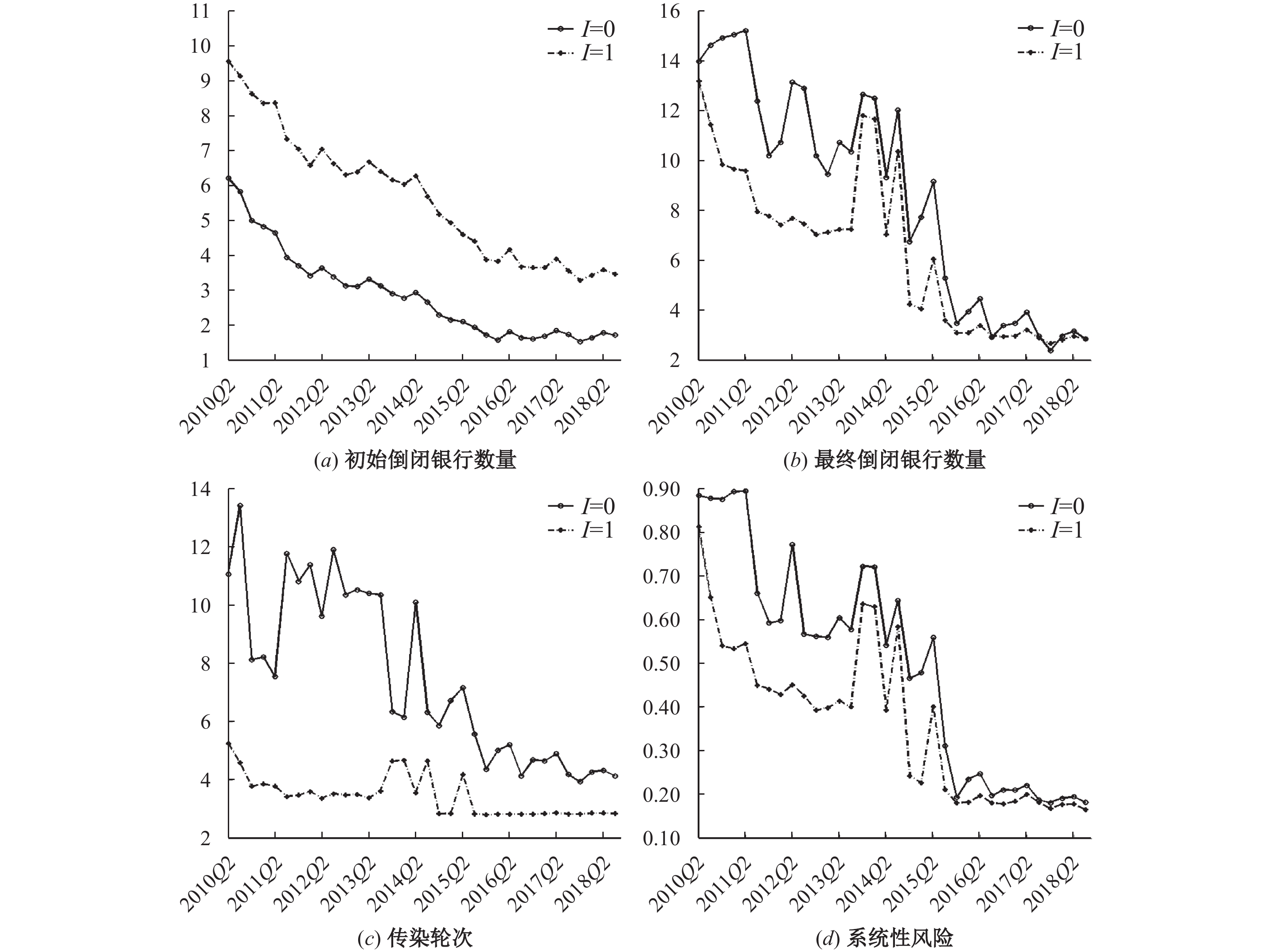
图4给出考虑了正常时期和危机时期影响后的综合效应。从中可以看出,I=1时金融体系初始倒闭银行数量比I=0时大约多4家,但最终倒闭银行数量总体上少于I=0时。I=1时的传染轮次低于I=0时,表明杠杆率监管通过影响银行的资产配置、银行间网络结构以及风险传染,最终降低了初始冲击在银行体系中扩散的广度和深度。此外,I=1时的系统性风险低于I=0时,表明对银行施加4%的杠杆率监管要求会带来更加稳定的银行体系。
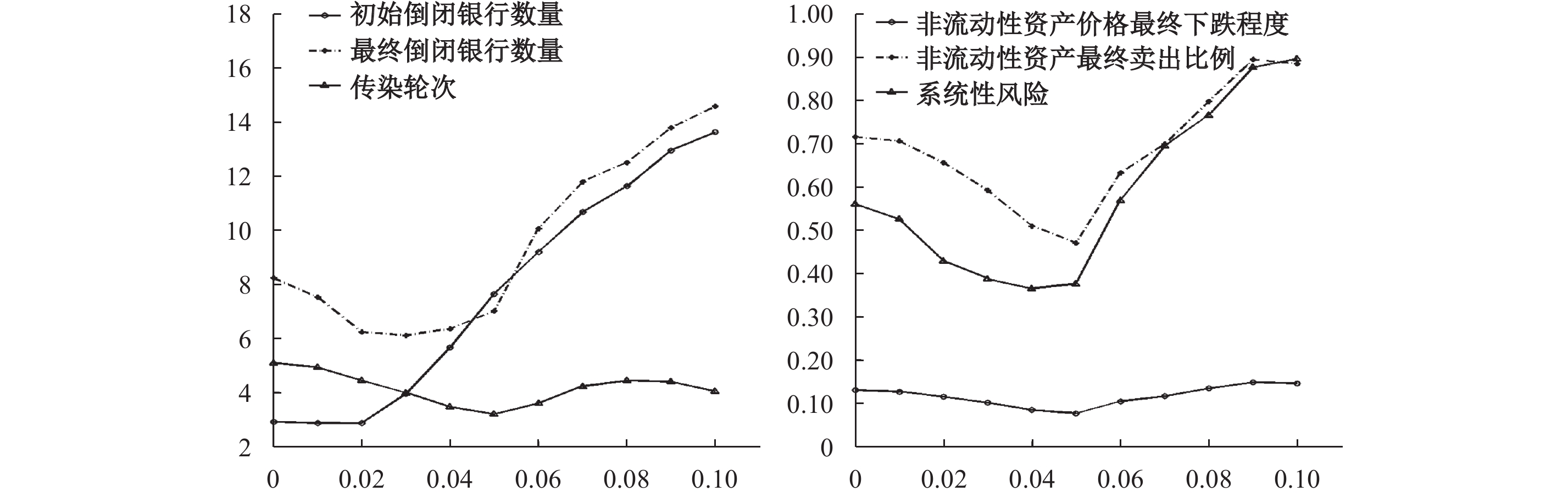
为了进一步说明杠杆率监管水平的影响,图5比较了lev*的不同取值下的银行体系风险状况,图中数值为样本期间所有季度的均值。从中可以看出,当lev*从0增至10%时,初始倒闭银行数量总体上呈上升趋势,lev*的提高将加速脆弱性银行的倒闭。在金融体系达到均衡时,最终倒闭银行数量呈先降后升的变化趋势,表明当lev*低于某一临界值时,提高lev*将有助于增强健康银行对初始倒闭银行风险传染的免疫力,从而银行体系最终倒闭银行数量下降。但一旦超过临界值,进一步提高lev*会使危机时期市场的流动性急剧枯竭,最终倒闭银行数量有所增加。此外,非流动性资产的价格最终下跌程度、卖出比例以及系统性风险指标的变化趋势也表明,提高lev*并不必然降低金融体系风险,在过高的杠杆率监管要求下,危机时期流动性紧缺的负面效应大于正常时期银行资产规模收缩和网络关联度下降的正面效应,最终系统性风险有所上升。
|
| 图 4 杠杆率监管对系统性风险的综合影响效应 |
|
| 图 5 不同杠杆率约束水平下的风险传染状况 |
(五)进一步分析
根据《巴塞尔协议III》的规定,各国商业银行需逐步建立2.5%的资本留存缓冲。为此,本文分析了提高资本缓冲比率(τ)是否有助于增强杠杆率监管的金融稳定效应。此外,考虑到金融市场在受到冲击时是否具有一定的弹性也会影响危机时期银行体系去杠杆的进程,本文进一步探讨了非流动性资产价格调整速度(β)和贷款回收比例(pc)对杠杆率监管下系统性风险的影响。与上文分析类似,下文图中的系统性风险为所有样本时点的均值。
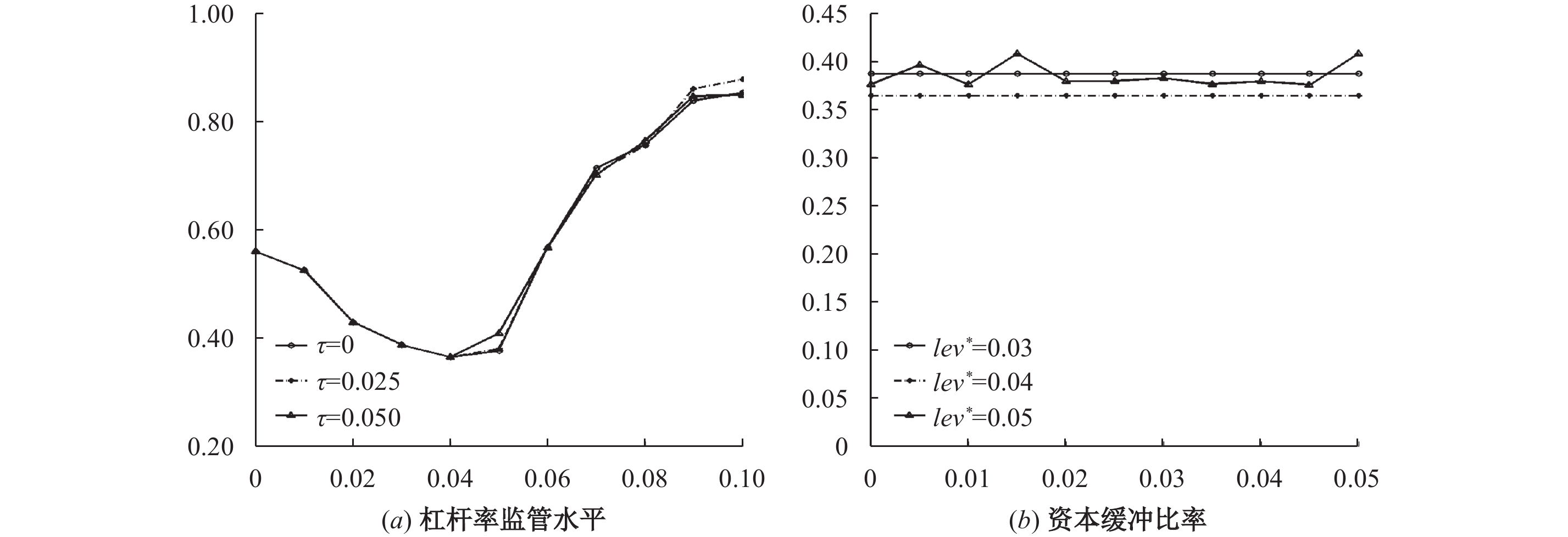
图6显示了不同的τ和lev*组合下的系统性风险。从图6(a) 中可以看出,在相同的lev*下,银行体系的系统性风险在τ取值为0、2.5%和5%时并不存在明显区别。图6(b) 进一步显示,当lev*为3%或4%时,银行体系的系统性风险并不会随着τ的提高而显著下降。当lev*为5%且τ在区间(1.5%,4.5%)时,系统性风险随着τ的提高而略有下降。总体而言,提高τ并不显著增强杠杆率监管的金融稳定效应。其原因在于,τ的提高仅对资本充足率在警戒线水平附近的银行有约束力,当系统中绝大多数银行的资本充足率远高于警戒线水平时,提高资本缓冲比率要求并不会显著降低银行体系的系统性风险。⑧
|
| 图 6 资本缓冲比率对系统性风险的影响 |
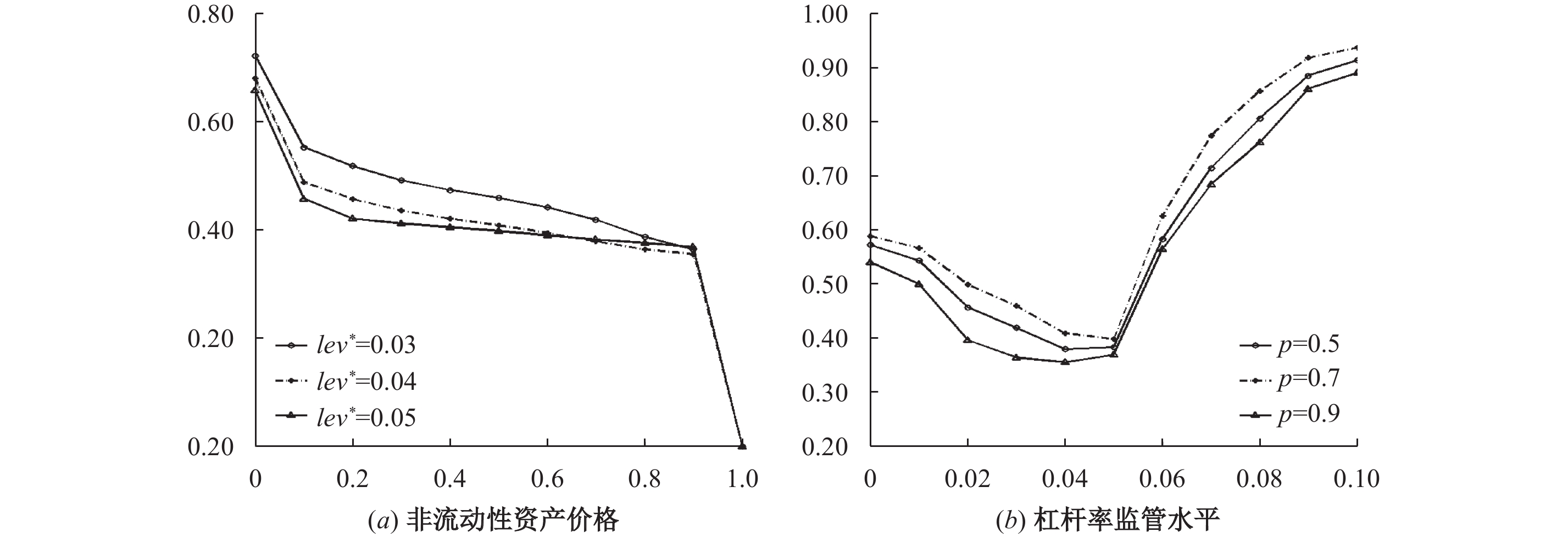
图7分析了非流动性资产价格调整速度β对不同lev*水平下系统性风险的影响,图中非流动性资产价格(p)为银行体系卖出全部非流动性资产时的价格,p越小意味着β越大。从图7(a) 中可以看出,随着β的取值变小(逐渐接近于0),不同lev*下的系统性风险降低,最终接近于0。特别是在p高于0.9时,系统性风险随着β的减小而急剧下降。图7(b) 显示,在相同的β下,系统性风险随着lev*的提高呈现出先降后升的趋势,这与上文分析类似。在不同的β下,系统性风险最低时的lev*略有差异。上述结果表明,非流动性资产价格调整速度越快,即市场越缺乏流动性时,在危机时期通过出售非流动性资产来满足监管要求会导致越高的系统性风险,这在一定程度上说明了危机时期央行对市场进行流动性救助的重要性。此外,在危机时期适当降低lev*也有助于减缓非流动性资产“抛售−价格下跌−抛售”这一恶性循环带来的金融体系脆弱性。
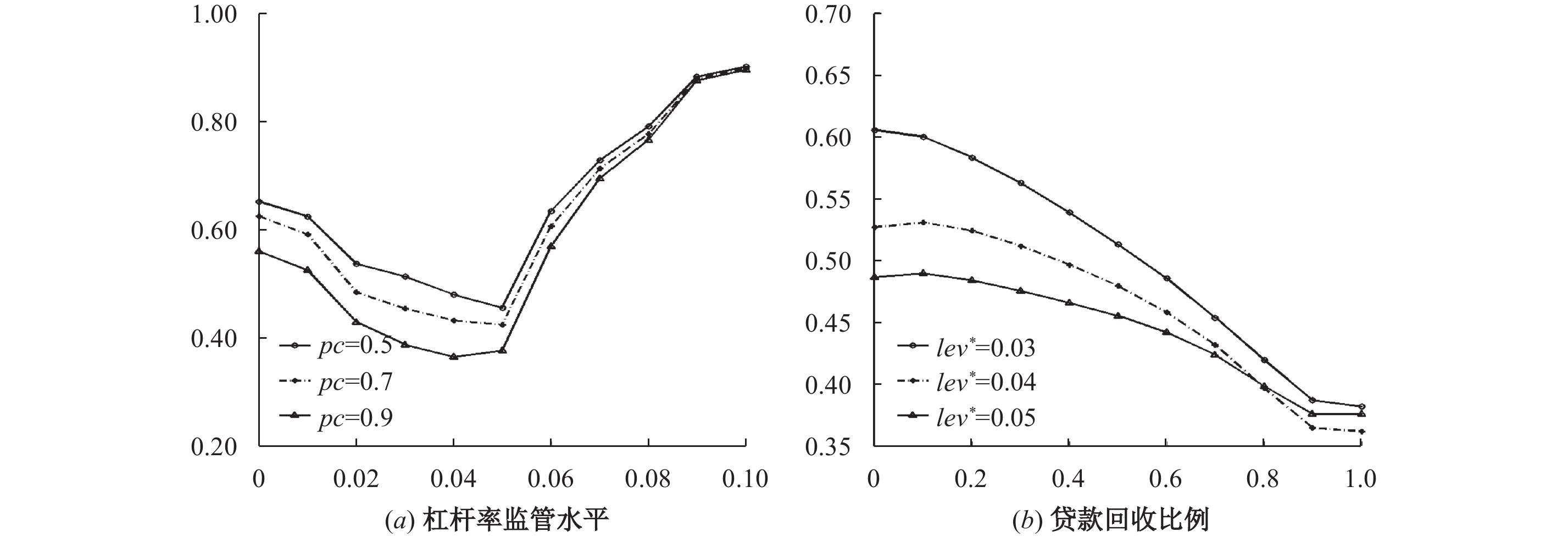
图8给出了贷款回收比例(pc)对杠杆率监管效应的影响。pc越高意味着当银行破产清算时,拍卖、收回或转让对外贷款资产的折价损失越小。图8(a) 的结果表明,当lev*在0和5%之间时,较高pc下的系统性风险明显较低。随着lev*的进一步提高,不同pc下的系统性风险差异逐渐变小。其原因在于,一旦lev*超过某一临界值,继续提高lev*所带来的最终倒闭银行数量下降的边际效应变小,因而不同pc下的系统性风险差异变小。图8(b) 显示,系统性风险随着pc的上升而呈现下降趋势。pc越高意味着银行在破产清算时的资产损失越小,从而对整个金融体系的风险溢出效应越小。上述结果意味着,提高破产银行的贷款回收比例将有助于增加杠杆率监管的金融稳定效应。
|
| 图 7 价格参数对系统性风险的影响 |
|
| 图 8 贷款回收比例对系统性风险的影响 |
四、结论与政策建议
银行体系去杠杆是当前我国金融体系供给侧结构性改革的重要内容,也是“三大攻坚战”中“防风险”的重要手段。本文基于内生性网络模型评估了杠杆率监管的有效性及作用机制。研究发现,引入杠杆率监管会增加正常时期部分银行的风险承担激励,降低银行间关联程度。在危机时期,杠杆率监管在短期内会增加倒闭银行的数量,加剧风险资产价值下跌,但从长期看会降低银行体系的系统性风险。总体而言,杠杆率监管会带来更加稳定的银行体系。
进一步研究发现,杠杆率监管要求并非越高越好,过高的杠杆率监管要求在正常时期会抑制银行资产的过度扩张,降低银行间网络关联程度,在危机时期则加剧银行体系的流动性紧缺。当后者的效应超过前者时,杠杆率监管降低系统性风险的作用将被弱化。此外,为市场补充流动性和提高贷款回收比例均有助于增强杠杆率监管政策的有效性,但提高资本缓冲比率要求对于改善杠杆率监管的空间非常有限。
本文的研究结论具有重要的政策启示。首先,当前的杠杆率监管政策总体上是有效的,应坚定不移地将杠杆率监管作为防控系统性金融风险的重要手段。为了满足杠杆率监管要求,一些银行会优先减少低风险资产。为了弱化这种激励,可以对不同类型银行实施差异化监管。其次,合理的杠杆率监管水平至关重要。当杠杆率监管在危机时期的流动性紧缩效应大于正常时期的银行资产扩张和银行间网络关联的抑制效应时,金融体系的脆弱性反而可能增加。因此,可以实施逆周期的杠杆率监管策略,在正常时期适度提高杠杆率监管水平以抑制银行资产规模的过度扩张,在危机时期则适度降低杠杆率监管要求以缓解市场流动性紧张所引发的风险传染。最后,在银行体系受到冲击后,及时对市场进行流动性救助以减缓资产价格的传染风险,并完善征信及司法拍卖机制以提高破产银行的贷款回收程度,对于有效发挥杠杆率监管的金融稳定效应同样重要。
① 本文中的非流动性资产是剔除外部贷款后的非流动性资产的统称。
② 上述项目被设置为外生变量的原因在于,银行对这些项目的支配性较弱,如外部贷款主要取决于贷款人的需求,存款取决于存款人的储蓄需求。而对于非流动性资产和银行间存贷款,银行则可以基于风险和收益来决定其最优数量,因此它们属于内生决策变量。
③ 资产负债表中的外生项目对银行来说是已发生或确定的,因此目标函数中不需要考虑其成本或收益。
④ 在不存在卖空机制的情况下,银行的非流动性资产需要大于等于0。
⑤ 金融体系稳定状态的定义请见Bluhm等(2014)。
⑥ 16家上市银行包括平安银行、宁波银行、浦发银行、华夏银行、中国民生银行、招商银行、南京银行、兴业银行、北京银行、中国农业银行、交通银行、中国工商银行、光大银行、中国建设银行、中国银行和中信银行。
⑦ 在分析引入杠杆率监管对金融体系的影响时,本文控制了模型的其他输入变量,这意味着I=0和I=1两种情况下相关指标的变化仅由杠杆率监管所引起。因此,根据表3中Δlev与银行其他指标的相关性,我们可以判断引入杠杆率监管对哪类银行杠杆率的影响更大。
⑧ 从图1中可以看出,在实现最优资产配置时,银行体系的资本充足率大致在14%以上。这意味着绝大多数银行的资本充足率远高于法定资本充足率加上缓冲资本比率的要求。
| [1] | 方意. 宏观审慎政策有效性研究[J]. 世界经济, 2016(8): 25–49. |
| [2] | 黄聪, 贾彦东. 金融网络视角下的宏观审慎管理——基于银行间支付结算数据的实证分析[J]. 金融研究, 2010(4): 1–14. |
| [3] | 李守伟, 马钱挺, 隋新, 等. 企业信用内生网络模型及其演化研究[J]. 中国管理科学, 2019(2): 53–60. |
| [4] | 梁琪, 李政, 卜林. 中国宏观审慎政策工具有效性研究[J]. 经济科学, 2015(2): 5–17. |
| [5] | 马君潞, 范小云, 曹元涛. 中国银行间市场双边传染的风险估测及其系统性特征分析[J]. 经济研究, 2007(1): 68–78. |
| [6] | 唐振鹏, 谢智超, 冉梦, 等. 网络视角下我国上市银行间市场系统性风险实证研究[J]. 中国管理科学, 2016(S1): 489–494. |
| [7] | 王连军. 去杠杆化与银行体系稳定性研究——基于中国银行业的实证[J]. 国际金融研究, 2018(10): 55–64. |
| [8] | 朱波, 卢露. 不同货币政策工具对系统性金融风险的影响研究[J]. 数量经济技术经济研究, 2016(1): 58–74. |
| [9] | Akinci O, Olmstead-Rumsey J. How effective are macroprudential policies? An empirical investigation[J]. Journal of Financial Intermediation, 2018, 33: 33–57. DOI:10.1016/j.jfi.2017.04.001 |
| [10] | Aldasoro I, Gatti D D, Faia E. Bank networks: Contagion, systemic risk and prudential policy[J]. Journal of Economic Behavior & Organization, 2017, 142: 164–188. |
| [11] | Allahrakha M, Cetina J, Munyan B. Do higher capital standards always reduce bank risk? The impact of the Basel leverage ratio on the U.S. triparty repo market[[J]. Journal of Financial Intermediation, 2018, 34: 3–16. DOI:10.1016/j.jfi.2018.01.008 |
| [12] | Bluhm M, Faia E, Krahnen J P. Monetary policy implementation in an interbank network: Effects on systemic risk[R]. SAFE Working Paper Series 46, 2014. |
| [13] | Bluhm M, Krahnen J P. Systemic risk in an interconnected banking system with endogenous asset markets[J]. Journal of Financial Stability, 2014, 13: 75–94. DOI:10.1016/j.jfs.2014.04.002 |
| [14] | Blum J M. Why ‘Basel II’ may need a leverage ratio restriction[J]. Journal of Banking & Finance, 2008, 32(8): 1699–1707. |
| [15] | Cifuentes R, Ferrucci G, Shin H S. Liquidity risk and contagion[J]. Journal of the European Economic Association, 2005, 3(2−3): 556–566. DOI:10.1162/jeea.2005.3.2-3.556 |
| [16] | Eisenberg L, Noe T H. Systemic risk in financial systems[J]. Management Science, 2001, 47(2): 236–249. DOI:10.1287/mnsc.47.2.236.9835 |
| [17] | Haᴌaj G, Kok C. Modelling the emergence of the interbank networks[J]. Quantitative Finance, 2015, 15(4): 653–671. DOI:10.1080/14697688.2014.968357 |
| [18] | Kellermann K, Schlag C. Occupy risk weighting: How the minimum leverage ratio dominates capital requirements: A Swiss example[J]. Journal of Financial Regulation and Compliance, 2013, 21(4): 353–372. DOI:10.1108/JFRC-06-2012-0019 |
| [19] | Kiema I, Jokivuolle E. Does a leverage ratio requirement increase bank stability?[J]. Journal of Banking & Finance, 2014, 39: 240–254. |
| [20] | Li S W, Sui X. Contagion risk in endogenous financial networks[J]. Chaos, Solitons & Fractals, 2016, 91: 591–597. |
| [21] | Mirza A, Strobel F. Leverage requirements and systemic risk[R]. Working Paper, 2013. |
| [22] | Smith J A, Grill M, Lang J H. The leverage ratio, risk-taking and bank stability[EB/OL]. https://pdfs.semanticscholar.org/4204/7966c824378f78ab012e92e98a051ca8443d.pdf, 2017. |


