2020第46卷第1期
一、引 言
中国政府自2003年起逐步在全国农村地区建立了新型农村合作医疗制度(简称:新农合),2012年进一步在新农合中引入了大病保险政策,该项政策的一个重要目标是,通过降低医疗服务价格,缓解“看病难、看病贵”现象,增强农村居民的医疗服务可及性,改善农村居民特别是贫困居民的健康水平。2003—2017年中国各级政府对新农合的财政补助,从每人20元提高到了450元,年均增长30%,仅2017年用于新农合的财政补贴就超过了3 000亿元。但是关于医疗保险存在的一个普遍担忧是:由于医疗保险领域的道德风险和信息不对称(Arrow,2001),医疗保险扭曲了供需双方的行为,在刺激医疗支出过度增长的同时,并未带来相应的健康改善。那么中国农村实施的医疗保险是否导致了医疗支出的过度增长,居民的身体健康是否有所改善?贫困居民是否受益更多?此类问题的回答,对中国政府提前采取预防和应对措施,完善现有的医疗保障和医疗服务供给制度,优化资源配置,化解财政风险,具有重要的理论和实践意义。
医疗保险对健康以及医疗支出的冲击效应,国内外的学者对此进行了大量的研究。例如,Hanratty(1996)研究发现加拿大的全民医保,显著降低了4%的婴儿死亡风险和1.3%的新生儿低体重发生风险。Wagstaff和Lindelow(2008)、Lei和Lin(2009)研究认为中国新农合产生了显著的健康收益,有效缓解了中国农村“因病致贫、因病返贫”现象。程令国和张晔(2012)研究发现新农合对老年人的医疗支出有明显的激励作用,但增长的医疗支出也相应改善了老年人的健康状况。黄枫和甘犁(2010)的研究认为,享受城镇居民医疗保险(简称:城居保)的老人按生存概率加权的平均总医疗支出明显大于无医疗保险老人的医疗支出,但医疗支出的边际效应较高。陈华和邓佩云(2016)对城镇职工医保的研究也得到类似的结论。与之相反,也有大量的文献认为医疗保险与健康之间的关系是脆弱的。例如,Skinner等(2001)的研究表明,用生存时间度量,将近有20%的医疗保险支出没有带来任何好处。仍然是针对中国新农合的研究,Chen和Jin(2012)并未发现新农合提高了参保农村居民(儿童)健康的证据。胡宏伟和刘国恩(2012)的研究则认为城居保虽然显著促进了低健康群体的健康水平,但没有显著改善城镇居民的总体健康水平。
综上所述,医疗保险对健康的影响究竟如何,已有的文献并未取得一致。实际上,此类研究存在两个问题会对研究结果产生较大冲击:一是参保状态的内生性问题;二是健康状况的度量问题。已有的研究多采用随机实验或自然实验方法解决内生性问题,其中兰德医疗保险实验最为著名,但是由于随机试验成本太高,更多的研究则是通过自然试验方法解决内生性问题。例如,Finkelstein和McKnight(2005)采用双重差分(Difference-In-Differences,DID)、Card等(2009)采用断点回归(Regression Discontinuity Design,RDD)对美国Medicare保险进行的研究。潘杰等(2013)、马超等(2015)采用工具变量法,估计城居保对城镇居民健康的影响。
不同健康度量指标同样会对研究结果带来很大的影响,有部分学者采用儿童年龄别身高评分(Height-for-age Z Score,HAZ)、健康体重指数(Body Mass Index,BMI)、婴幼儿死亡率、两周患病率以及老年人死亡风险等,度量人群的健康水平(宋月萍和张耀光,2009;Kelly和Markowitz,2009,2010;彭晓博和王天宇,2017),但是这些指标仅能反映健康的局部状况,难以概括研究群体的全面健康状况。因此,也有学者通过综合性的健康问卷,构建出诸如健康生活质量(Quality of Well-bing Index,QWB)、伤残调整生命质量年(Disablility -Adjusted-life-year,DALY)以及健康综合测量指数(Summary measure of Health,SMH)等全面反映人群健康水平的度量指标(赵忠和候振刚,2005;解垩,2009;李华和俞卫,2013),但是构建这些健康客观指标,需要详细的针对健康的专业问卷,获取和计算这类指标难度很大。①因此,更多的学者采用自评健康状况(Self-Assessed Health,SAH)作为健康的度量指标。Hays等(1996)认为SAH是一个更精确、更客观的健康测量方法,可以广泛概况生理认知和外界环境的信息,并形成对自身全面健康状况的认识,大量的文献也证明了健康自评数据与死亡率等客观指标高度相关,从而能够有效地反映被研究者的健康水平。同时SAH避免了诸如健康调整生命年等综合指标需要主观决定权重的难题。考虑到自评健康数据获得的成本低,因此在中国研究SAH更有意义,国内有许多学者在研究居民健康问题时,采用SAH度量居民健康(赵忠,2006;吴联灿和申曙光,2010;胡宏伟和刘国恩,2012;潘杰等,2013)。但是SAH是一个主观指标,个人对健康的判断标准存在差异,这种差异将导致SAH的测量误差,称之为SAH的报告异质性(Crossley和Kennedy,2002;Finkelstein等,2012),已有的文献主要基于受访者对他人健康虚拟场景的回答,对SAH的误差进行纠正(Lindeboom和van Doorslaer,2004;King等,2004)。总之,参保状态的内生性问题和健康状况的度量问题,是该领域研究者非常重视的问题,但是现有的医疗保险与健康关系的研究文献大多侧重于解决其中一种问题,不同程度地忽视了另一个问题,因此,这对研究结论的可靠性带来了诸多不利影响。
自2012年起,中国开始逐步在新农合中建立了大病保险制度,②新农合参保者无需额外缴费,自动享受大病保险。但各地大病保险实施的进程并不一致,这为我们提供了一个“自然实验”机会,对新农合大病保险的健康效应和医疗支出冲击效应进行估计和检验。基于SAH为定序数据这一情况,结合多重差分估计方法,本文提出一个统一的计量框架,在该框架内同时对政策的内生性和SAH报告的异质性进行纠正,以期获得更加稳健和可靠的结果。通过实证分析可以得到如下结论:一是新农合大病保险总体上提高了农村居民的健康水平,处理组居民的健康改善幅度在大病保险实施的次年即增加了10%—20%,且改善效应较为持久,在第三年依然显著。二是新农合大病保险对个人住院支出的激励作用最为明显,大病保险会使家庭人均医疗支出增长5%,个人住院支出增长接近30%,但对门诊支出没有任何作用,结合新农合对居民健康的促进作用,现在还难以得出医疗服务和医疗支出已呈现过度化倾向。三是新农合的上述效应具有异质性,低收入家庭并非最大受益者,中上等收入家庭的健康改善最为显著。四是医疗支出方面,低收入家庭、中等收入家庭和高收入家庭,大病保险对其住院支出的刺激效应逐次递增,分别为3 606元、3 661元和4 010元。医疗支出的分位数回归结果显示,家庭人均医疗支出和个人住院费用支出本来就多的居民,大病保险使他们的上述支出变得更多;而这两类支出本来就较少的居民,大病保险对其医疗支出的影响不大。医疗支出两部分模型的估计结果进一步表明,大病保险并没有提高医疗支出发生的概率,但是对已发生医疗支出的居民,大病保险对其医疗支出具有进一步的激励作用。上述结果表明,大病保险主要刺激了本来就有医疗需要的人,如老年人和有各种慢性病人群的医疗支出,因此,大病保险的建立促进了农村医疗服务有效需求的进一步释放,一定程度上改善了健康状况不佳人群的健康水平。总之,本文实证研究的结论,为我们设计更加有效的社会医疗保障制度,降低公共资源无效或低效消耗,为社会医疗保险制度的健康运行和可持续发展提供了实证依据。
二、健康效应估计
(一)数据来源。本研究所用的数据来自于北京大学中国社会科学调查中心实施的中国家庭追踪调查(China Family Panel Studies,CFPS)的农村样本,选用CFPS数据的理由有三:一是目前CFPS的数据有2010年、2012年、2014年和2016年共计四年的调查记录,时间跨度符合本研究所采用的估计方法的需要,2010年和2012年是基准年,2014年是部分省份(处理组)实施大病保险的第二年,2016年则是部分省份(处理组)实施大病保险的第四年;二是CFPS记载了较为详细的居民保险信息、健康信息和相应的医疗信息,并且收集了个体、家庭和社区三个层次的数据,从而使我们可以分别从家庭和个人两个方面,研究医疗保险对健康和医疗支出的政策效应;三是由于参加公费医疗和城镇职工医疗保险的群体不受此次大病保险政策的影响,而CFPS数据包括了农村和城镇居民,这为我们提供了使用三重差分方法估计大病保险效应的机会,因此我们选择了CFPS数据,而没有选择专门的农村微观调查数据。
本研究通过“户口”和“参保类型”这两个变量从CFPS中提取农村样本,由于CFPS数据没有收集西藏、青海、新疆、宁夏、台湾、香港和澳门的样本,并且北京、内蒙古和海南在2010年也没有相应的样本,因此本研究不包括上述地区。最后纳入研究的省份(自治区、直辖市)共有24个,其中作为处理组的省份(直辖市)是:辽宁、吉林、浙江、湖北、福建和重庆共计6个省份,其余省(直辖市、自治区)作为控制组。
表1给出了本研究采用的数据的描述性统计,其中医疗支出均指总的医疗花费,即包括个人自费部分和保险赔偿部分。因为2010年的CFPS调查数据没有记录个人门诊信息,因此门诊支出信息仅在2012年和2014年有相应数据。2016年的CFPS没有记录他人虚拟健康评价信息,因此在“定序模型与SAH纠正”一节的估计中,不包括2016年的样本。
| 变量 | 个数 | 均值 | 标准差 | 最小值 | 最大值 |
| A:被解释变量 | |||||
| 个人健康自评状况(Self_Health_Status) | 50 365 | 2.84 | 1.36 | 1 | 5 |
| 家庭人均医疗支出/年(Family_Health_Exp) | 26 597 | 1 189.41 | 3 947.89 | 0 | 246 666.7 |
| 个人住院支出/年(Adult_Hospitalized_Exp) | 45 129 | 1 118.79 | 7 746.64 | 0 | 400 000 |
| 个人门诊支出/年(Adult_Outpatient_Exp) | 31 151 | 784.92 | 2 967.06 | 0 | 130 000 |
| B:家庭特征变量 | |||||
| 人均年收入(F_Income) | 26 597 | 9 313.78 | 29 820.44 | 0 | 4 168 000 |
| 人均债务(F_Debt) | 26 597 | 1 160.06 | 5 808.36 | 0 | 333 333.3 |
| 人均资产(F_Assets) | 26 597 | 26 276.85 | 112 567.9 | 0 | 1.00e+07 |
| 未成年人个数(F_Age16) | 26 597 | 0.89 | 1.03 | 0 | 8 |
| 60岁老人个数(F_Age60) | 26 597 | 0.66 | 0.82 | 0 | 5 |
| C:个人特征变量 | |||||
| 年龄(Age) | 50 365 | 45.59 | 17.14 | 16 | 110 |
| 性别(Gender) | 50 365 | 0.32 | 1.23 | 0 | 1 |
| 受教育水平(Education) | 50 365 | 2.17 | 1.09 | 1 | 7 |
| 是否从事农业工作(Agriculture) | 50 215 | 0.20 | 0.41 | 0 | 1 |
| 是否独身(Single) | 50 365 | 0.79 | 0.41 | 0 | 1 |
| 是否是中共党员(CP) | 49 203 | 0.14 | 0.35 | 0 | 1 |
| 是否有慢性病(Chronic) | 50 365 | 0.156 | 0.363 | 0 | 1 |
| D:主观评价变量 | |||||
| 就医条件总体满意度(Satisfaction) | 41 862 | 2.43 | 0.68 | 1 | 5 |
| 他人健康评价1(Vig1) | 20 815 | 2.24 | 1.14 | 1 | 5 |
| 他人健康评价2(Vig2) | 20 815 | 4.08 | 1.13 | 1 | 5 |
| E:省份特征变量 | |||||
| 城镇化率%(Urbanization) | 50 365 | 0.49 | 0.13 | 0.30 | 0.90 |
| 人均GDP(Capita_GDP) | 50 365 | 37 909.73 | 17 194.77 | 13 401.61 | 107 960 |
| GDP增长率%(GDP_Inc) | 50 365 | 9.40 | 3.83 | −1.11 | 16.5 |
| 农村医疗保健服务价格指数(Price_ind) | 50 365 | 100.8 | 4.50 | 98.4 | 102.2 |
| 注:省份特征变量除农村医疗保健服务价格指数从《中国农村统计年鉴-农村市场与物价》中获取之外,其余变量从《中国统计年鉴》获取。本表数据不包括后继三重差分估计所用到的公费医疗和城镇职工医疗保险的样本。货币单位全部为元,且人均年收入、人均GDP和各类医疗支出按2015年可比价格计算得出。个人健康自评状况分别为:1-健康,2-一般,3-比较不健康,4-不健康,5-非常不健康。性别:0-女,1-男。教育水平:1-文盲/半文盲,2-小学,3-初中,4-高中/中专,5-大专,6-大学本科,7-硕士,8-博士。是否从事农业工作:0-否,1-是。是否中共党员:0-否,1-是。是否独身:未婚、离婚及丧偶为0,在婚以及同居为1。是否有慢性病:0-否,1-是。就医疗条件总体满意度:1-很满意,2-满意,3-一般,4-不满意,5-很不满意。他人健康评价是对2个虚拟场景所描述的虚拟人健康状况进行评价(具体描述见2.3节注释),具体取值为:1.非常健康,2.很健康,3.比较健康,4.一般,5.不健康。 | |||||
(二)多重差分估计。中国各个地区推行大病保险政策的进程并不一致。例如,福建省早在2010年便在三明市、莆田市试点新农合大病保险制度,并在2013年1月1日起在全省范围内全面实施。在2013年全省范围实施大病保险政策的除福建之外,还有辽宁、吉林、浙江、湖北、重庆、青海,其余省市则是在2014年之后在全省范围内实施。③由于健康的改善具有滞后性,大病保险的政策效应,应当在实施后一年才能充分体现,上述事实为本研究提供了一个“自然实验”机会,即将2013年在全省范围内实施大病保险的省份作为“处理组”(不包括青海),其余省份作为“控制组”,设定双重差分模型对大病保险的政策效应进行检验与估计。考虑到控制组的省份,虽然2013年未在全省范围内实施大病保险政策,但是2013年都存在一定的试点地区,试点地区的存在将会对政策效应估计带来干扰,由于CFPS只给出了省份信息,没有市县信息,因此无法在市县这一层级进行区分,为了尽可能地排除干扰,我们从控制组中剔除了试点地区较多的省份(江苏、安徽、江西、广东、陕西),④控制组的成员缩减为13个省份,基于此设定再次进行多重差分估计,并将结果与未删除五省份的估计结果进行对比,确保模型估计结果的稳健。由于此次大病保险改革仅适用于新农合和城居保,参加公费医疗或城镇职工医疗保险的居民则不受影响,因此本研究进一步在双重差分的基础上,进行了三重差分估计,为大病保险对农村居民的健康影响寻找更加可靠的结论。
基于以上研究思路,我们首先设定如下的双重差分模型:
| Yipt=α+γp+λt+τ=1∑τ=0δτ(Treatp×Tt+τ)+X′ptβ+Z′iptφ+εipt | (1) |
其中,
自2012年开始的大病保险改革仅适用于新农合和城居保,只有参加了新农合或城居保的居民方受此政策变更的影响,而参加公费医疗或城镇职工医疗保险的居民不受影响。这为DID方法提供了额外的第三个维度,即受影响的居民(affected group)和不受影响的居民(unaffected group),利用这一维度,可以进行三重差分估计,从而更加一致地估计大病保险对农村居民的健康冲击效应。我们在之前DID估计的农村样本中,加入参加公费医疗或城镇职工医疗保险的城镇居民,并设定如下的三重差分模型:
| yipt=α0+γp+λt+α1affected+α2Treat×affected+α3T×Treat+α4T×affected+1∑τ=0δτ(Treatp×Tt+τ×affectedp)+X′iptβ+Z′ptφ+εipt | (2) |
同(1)式比较,(2)式增加了
由于感兴趣的回归元只在省这一层面发生变动,同一省内的样本可能会存在相关性,数据表现出的这种群组结构,称之为聚类问题(Clustering Problem),⑦解决该类问题的方法之一是设定合适的聚类标准误,这里初步设定的聚类水平为省−年份,由于样本共有24个省4年的数据,因此共计有96个聚类。表2给出了在上述2种设置情况下的多重差分估计结果。
| 双重差分 | 三重差分 | 标准误类型 | |||||
| 滞后一期系数值 | 滞后三期系数值 | 滞后一期系数值 | 滞后三期系数值 | 稳健标准误 | 聚类标准误 | ||
| 控制组(18) | A | −0.127***(−2.67) | −0.238***(−4.54) | −0.137**(−2.44) | −0.172***(−5.33) | N | N |
| B | −0.127***(−2.48) | −0.238***(−3.99) | −0.137**(−2.55) | −0.172***(−5.40) | Y | N | |
| C | −0.127(−0.83) | −0.238*(−1.94) | −0.137**(−2.05) | −0.172***(−3.94) | N | Y | |
| 控制组(13) | A | −0.201***(−5.89) | −0.244***(−4.53) | −0.0995*(−1.72) | −0.169***(−4.69) | N | N |
| B | −0.201***(−5.50) | −0.244***(−4.00) | −0.0995*(−1.81) | −0.169***(−4.82) | Y | N | |
| C | −0.201*(−1.97) | −0.244*(−1.72) | −0.0995*(−1.59) | −0.169***(−3.51) | N | Y | |
| 注:控制组(18)是保留所有省份(控制组中共有18个省份)的回归结果,控制组(13)是剔除试点地区过多的5个省份(控制组中共有13个省份)的估计结果。A是采用普通标准误的估计结果,B是采用稳健标准误的估计结果,C是采用聚类标准误的估计结果。滞后一期、滞后三期系数值为相应的Treat×T的系数
δ
估计值(代表政策效应)。括号内为t值。***、**和*分别表示在1%、5%和10%的统计水平上显著。 |
|||||||
由表2可见,大病保险对健康冲击的滞后一期和滞后三期效应,在两类DID估计中全为负值,这表示大病保险总体上促进了处理组居民的身体健康,且具有显著的持久性。在未删除5省份的DID估计中,该政策效应在1%—10%的水平下显著,其系数估计值分别为−0.127与−0.238。在删除了5省份的DID估计中,系数估计结果在1%—10%的水平下高度显著,其系数估计值为−0.201与−0.244,滞后三期效应略大于滞后一期效应,表明大病保险的健康改善效应随着时间的推移在不断增强。从DDD的估价结果看,其系数在两类估计中也全为负值,但是DDD的估计的系数小于DID估计的系数值,并且其滞后三期效应明显强于滞后一期效应。总之,在设定的两种基准模型中,DID和DDD的估计结果可以相互验证,表明新农合大病保险政策对农村居民的健康具有实在的改善效应,并且这种改善效应随着大病保险实施时间的推移还在逐渐增强。
(三)定序模型与SAH纠正。基准模型中利用多重差分估计,较好地解决了政策变量的内生性问题,但是为了得到更为稳健的结论,尚有两个问题需要解决:一是SAH值是一个定序变量,各值之间并不等距,不能将SAH值作为基数处理;二是SAH存在一定的内生性,即个体的健康判断标准受自身特征的影响,导致其并不一致,文献中称之为个体健康报告异质性(Reporting Heterogeneity)。本研究尝试在一个统一的框架内,将DID模型内置于定序模型内,同时对政策效应的内生性和SAH的异质性进行纠正。该方法可称之为两步法估计:
第一步,估计出个体的异质性切点。假设个体报告的SAH值来自于一个健康潜变量模型,我们采用DID设定该模型如(3)式所示:
| Y∗ipt=α+γp+λt+δ(Treatp×Tt)+X′ptβ+Z′iptφ+εiptεipt∼N(0,1) | (3) |
其中,
在采用定序模型(ordered probit/logit)进行估计时,我们允许切点(cutoff-points)随个体而变化。利用CFPS提供的两个健康虚拟场景为切点建模,⑨假设个体对虚拟场景j(j=1,2)的健康潜变量的判断都是一致的,也即:
| hv∗ij=αj+εvij,εvij∼N(0,1) | (4) |
我们将
| hvij=kifμk−1i⩽hv∗ij<μki,k=1,⋯,5 | (5) |
其中,
| μki=γk0+Xiγk,k=1,⋯,5 | (6) |
| Pvijk=Pr | (7) |
第二步,采用区间回归(Interval Regression)估计大病保险健康效应。个体对自己的健康估计值与其健康潜变量之间有以下关系:
| {h_{it}} = k \Leftrightarrow \mu _{it}^{k - 1} \leqslant h_{it}^* < \mu _{it}^k,\;\mu _{it}^1 < \mu _{it}^2 < ... < \mu _{it}^5,\mu _{it}^0 = - \infty ,\mu _{it}^5 = \infty | (8) |
则个体评估其健康为
| \begin{aligned} \Pr [{h_{it}} = k] = & \Phi [\frac{{\mu _{it}^k - y_{it}^*}}{\sigma }] - \Phi [\frac{{\mu _{it}^{k - 1} - y_{it}^*}}{\sigma }] = \Phi [\dfrac{{\mu _{it}^k - (\alpha + {\gamma _p} + {\lambda _t} + \delta (trea{t_p} \times {T_t}) + {{X'}_{ipt}}\beta + Z_{pt}'\varphi )}}{\sigma }] \\ & - \Phi [\dfrac{{\mu _{it}^{k - 1} - (\alpha + {\gamma _p} + {\lambda _t} + \delta (trea{t_p} \times {T_t}) + {{X'}_{ipt}}\beta + Z_{pt}'\varphi )}}{\sigma }] \end{aligned} | (9) |
基于计算出的个体切点
由于两步法估计,第一步产生的误差会影响第二步的估计结果,因此为了提高估计效率,可以建立如下模型,采用极大似然估计方法实现一步估计:
| \ln L = \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^5 {{h_{itk}}\ln {P_{itk}} + \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^2 {\sum\limits_{k = 1}^5 {h_{ijkt}^v\ln P_{ijkt}^v} } } } } | (10) |
其中,
我们采用与基准模型中同样的变量设置,利用STATA编程实现对上述两步法和一步法的估计,由于CFPS在2016年没有采集虚拟场景评估信息,所以实证中不包括2016年的数据,⑩由于没有2016年的数据,因此这里只能估计滞后一期的政策效应,具体结果如表3所示。⑪
由表3给出的结果可见,无论是原始定序模型还是两种纠正后的定序模型,在控制组(18)和控制组(13)的估计中,系数估计结果均为负数,并都在1%—10%的水平上显著。表3也显示出在纠正了主观健康报告的异质性后,仍然得出了大病保险对健康具有显著改善效应的结论。总之,表2与表3的估计结果相互验证,表明大病保险政策对农村居民健康确实具有正向改善效应,此结论具有较强的稳健性。
三、进一步研究
(一)医疗支出。下面进一步分析,更加慷慨的新农合保险政策是否促进了农村居民的医疗支出,我们仍然采用DID方法进行估计。这里首先研究医疗支出大于0的样本,设定的基准模型是医疗支出为水平值的DID线性模型,并采用OLS进行估计。⑫考虑到医疗支出的分布具有非正态、偏斜分布和异方差的特征,有很长的右拖尾等问题,我们进一步设定了医疗支出对数变换线性模型和医疗支出平方根变换线性模型,⑬但是上述两个模型,其政策效应需要在系数估计结果的基础上求出边际效应,我们以对数变换线性模型举例:⑭
| E[{y_i}|{x_i}] = E[\exp ({x_i}\beta + {\varepsilon _i})|{x_i}] = \exp ({x_i}\beta )E[\exp ({\varepsilon _i})|{x_i}] | (11) |
其中,
| \frac{{\Delta E[{y_i}|{x_i}]}}{{\Delta {x_{ki}}}} = [(\exp {x_i}{\beta ^{|{x_k} = 1}}) - (\exp {x_i}{\beta ^{|{x_k} = 0}})]\exp (0.5\sigma _\varepsilon ^2) | (12) |
其中,
如果干扰项不服从正态分布(这是更为常见的情况),那么在同方差假设下可以对拖尾因子进行估计,然后再利用(11)式计算边际效应。⑮
| E[{e^{{{\hat \varepsilon }_i}}}|{x_i}] = {N^{ - 1}}\sum\limits_i {\exp ({{\hat \varepsilon }_i})} ,({\hat \varepsilon _i} = \ln {y_i} - {x_i}\hat \beta ) | (13) |
模型的线性部分设定同(1)式,这里的被解释变量分别为家庭人均医疗支出(Family_Health_Exp)、个人门诊支出(Adult_Hospitalized_Exp)和个人住院支出(Adult_Outpatient_Exp),三种医疗支出指的都是总支出,即包括个人自费部分和报销部分。上述三种方程,选用共同的省级特征向量
由表4可见,水平值与平方根变换的Ramsey检验均在1%的水平上拒绝了方程形式设定的假设,但是对数变换的个人医疗支出无法拒绝原假设,说明对数变换形式相对合理。从估计值来看,个人门诊支出在三种变换下均不显著,而个人住院支出在三种变换形式下均高度显著。对数变换显示大病保险使个人住院支出增长了30%,从边际效应看,对数变换显示大病保险的实施使处理组的个人医疗支出增长3 606—4 011元,远远小于水平估计值7 739元。上述估计结果符合直觉,因为门诊费用一般不属于大病保险的保障范围,大病保险所产生的政策冲击主要作用于住院支出上,这也验证了之前的假设:医疗服务价格的降低激励人们更多地使用该类医疗服务,因为门诊费用的价格没有降低,导致门诊支出没有显著变化。从基于人均收入分组的边际效应看,高收入组的边际效应最大,这表明大病保险对高收入人群医疗支出的激励作用最大,其次为中等收入组,而低收入组最小。
| 因变量
估计值 变换类型 |
个人住院支出 | 个人门诊支出 | 家庭人均医疗支出 | |||||
| 稳健标准误 | 聚类标准误 | 稳健标准误 | 聚类标准误 | 稳健标准误 | 聚类标准误 | |||
| 水平值 | 系数值 | 7 739.9*(1.90) | 7 739.9**(2.16) | 129.8(0.28) | 129.8(0.24) | 153.60*(1.86) | 153.60(1.62) | |
| Ramsey检验 | 41.13*** | 17.03*** | 13.00*** | |||||
| 对数变换 | 系数值 | 0.294*(1.80) | 0.294**(2.10) | 0.045(0.47) | 0.045(0.51) | 0.046(0.82) | 0.046(1.19) | |
| 边际效应 | 低收入 | 3 606.84 | 74.83 | 56.80 | ||||
| 中收入 | 3 661.72 | 78.13 | 58.71 | |||||
| 高收入 | 4 010.88 | 55.32 | 70.16 | |||||
| Ramsey检验 | 0.31 | 16.66*** | 12.32*** | |||||
| 平方根变换 | 系数值 | 18.52*(1.90) | 18.52*(2.31) | 0.073(0.04) | 0.073(0.03) | 0.348(0.33) | 0.348(0.46) | |
| 边际效应 | 低收入 | 3 505.02 | 4.03 | 18.30 | ||||
| 中收入 | 3 468.94 | 4.00 | 18.67 | |||||
| 高收入 | 3 617.25 | 3.53 | 19.99 | |||||
| Ramsey检验 | 41.04*** | 3.90*** | 17.91*** | |||||
| 注:表4给出了个人住院支出、个人门诊支出和家庭人均医疗支出的估计结果,上述支出均包括个人自费部分和医疗保险支付部分,支出金额根据历年医疗保健服务价格指数进行调整。系数值为
Treat \times T
的系数估计值,括号内为t值。Ramsey检验显示的为F值。边际效应计算的是
Treat \times T
在干扰项不服从正态分布但为同方差的假设下,按家庭人均收入分组计算出的组内平均边际效应。***、**和*分别表示在1%、5%和10%的统计水平上显著。 |
||||||||
表4的估计仅包括实际发生医疗支出的样本,没有包括全年医疗支出为0的样本,下面采用文献中常用的研究医疗支出的二部分模型(Two-parts Models),估计全样本的大病保险的冲击效应。⑰我们在第一部分使用Logit模型,第二部分仍然使用对数变换线性模型,二个模型均使用与表4估计相同的协变量,具体结果如表5所示,⑱由表5给出的第一部分估计结果可见,大病保险并没有提高医疗支出发生的概率(估计值均不显著);由第二部分估计结果可见,在个人住院支出大于0的条件下,大病保险能进一步刺激个人住院支出。
| 个人住院支出 | 个人门诊支出 | 家庭人均医疗支出 | |
| 第一部分 | −0.140(−0.97) | 0.222(1.12) | −0.164(−1.33) |
| 第二部分 | 0.316**(2.05) | 0.029(0.32) | −0.046(0.82) |
| 注:表5给出了个人住院支出、个人门诊支出和家庭人均医疗支出的两部分模型的估计结果,上述支出均包括个人自费部分和医疗保险支付部分,支出金额根据历年医疗保健服务价格指数进行调整。表中数据为
Treat \times T
的系数估计值,括号内为z值。**表示在5%的统计水平上显著。 |
|||
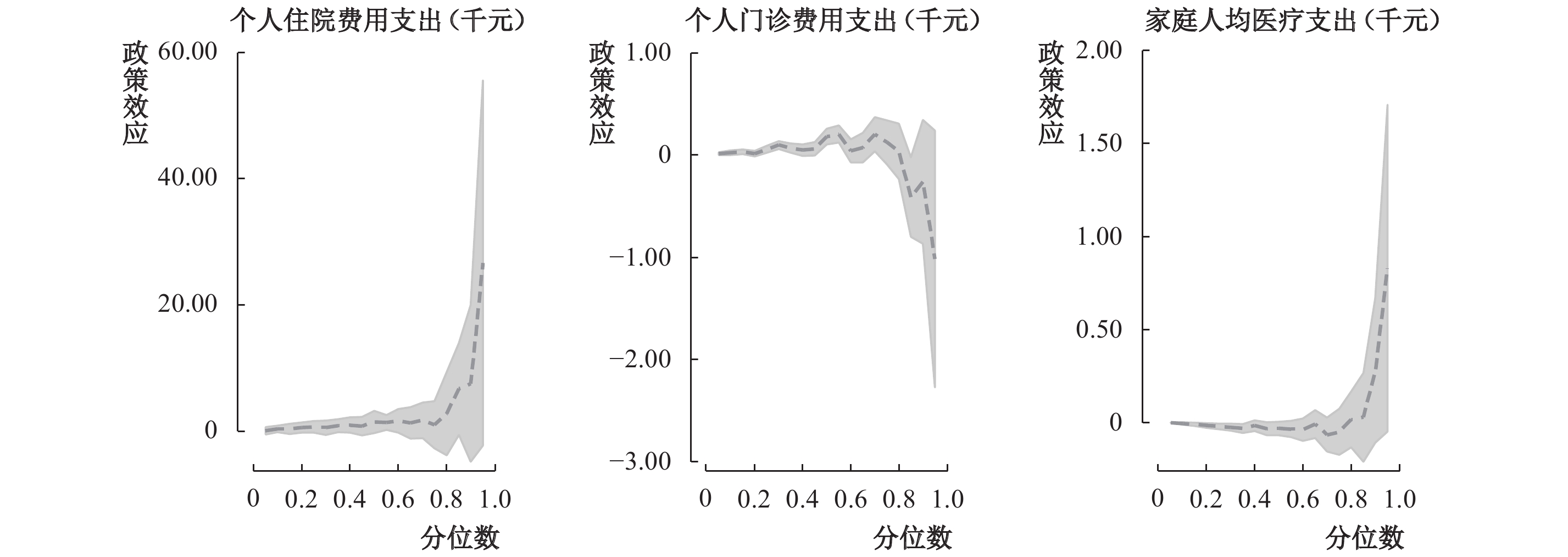
虽然上述结果验证了大病保险对农村居民的医疗支出具有促进作用,但这仅是对平均医疗支出的影响,我们想进一步了解大病保险的政策效应对整个医疗支出分布的影响,这里选择与表5同样的方程设定,对医疗支出进行条件分位数回归,结果如图1所示。⑲
图1显示了大病保险对三类医疗支出分布的冲击效应,家庭人均医疗支出和个人住院费用支出,在0.8分位点之后显著上升,但是个人门诊费用支出在0.6分位点后变为负值,且逐渐下降,从95%的置信区间覆盖0值看,统计上也不显著。因此,由图1可以得出以下结论:家庭人均医疗支出和个人住院费用支出本来就多的家庭(居民),大病保险政策使他们的上述支出变得更多;而这两类支出原本就较少的居民,大病保险政策对其医疗支出的影响不大。大病保险政策对农村居民的个人门诊费用支出的影响不明显。
(二)异质性效应。健康问题是导致农民贫困的一个重要原因,2016年全国建档立卡贫困户中,因病致贫、因病返贫的贫困户占比达到44.1%,⑳因此,在中国农村建立有效的医疗保险制度,特别是向农村低收入人口倾斜的医疗保险制度,对中国农村实施的精准脱贫战略起了非常关键的作用。那么新农合大病保险,对不同收入水平的农户有怎样的影响?是否改善了农村中最低收入群体的健康水平?我们按照家庭人均收入将样本分为三组,对不同的收入组分别按照(1)式与(10)式设定的模型进行估计,其中控制向量的选用同表2。表6给出了二种模型的估计结果。㉑
| OLS | SAH纠正定序模型(Probit) | |||||
| 1nd | 2nd | 3nd | 1nd | 2nd | 3nd | |
| 滞后一期 | 0.0386(0.37) | −0.338**(−1.99) | −0.213(−0.82) | −0.126(−0.18) | −0.477***(−2.63) | −0.430***(−2.80) |
| 滞后三期 | −0.136**(−2.49) | −0.180**(−2.10) | −0.184**(−1.93) | −0.308*(−1.75) | −0.314***(−2.72) | −0.411(−1.50) |
| 注:表6数据分别是政策效应(Treat×T)的滞后一期与滞后三期系数估计值。1nd、2nd和3nd分别是按家庭人均收入由低到高分组对应的低收入组、中等收入组和高收入组。采用聚类标准误进行估计,聚类水平为省-年份。家庭人均收入按照2010年可比价格进行了调整。括号内为t值。***、**和*分别表示在1%、5%和10%的统计水平上显著。 | ||||||
由表6可见,二种计量模型估计结果显示:中高收入人群的健康水平的改善更为明显。具体而言,两种模型的滞后一期效应显示中高收入人群的健康改善明显,而最低收入人群的健康改善不明显。滞后三期效应估计结果显示,最低收入人群的健康改善效应有较大提升,但仍然低于中上收入人群。总之,基于以上估计结果可见,新农合大病保险对农村居民的健康改善效应具有异质性:其对农村上等收入群体的健康水平具有积极的提升作用,但是对农村最低收入群体健康的改善比较有限。
四、稳健性检验
(一)聚类问题检验。同一地区的居民,由于受气候、风俗习惯和地理环境等共同因素的影响,可能在健康方面表现出一定的相关性,及
| \frac{{v(\hat \delta )}}{{{v_c}(\hat \delta )}} = 1 + \left[\frac{{v({n_g})}}{{\bar n}} + \bar n - 1\right]{\rho _x}{\rho _e} | (14) |
其中,
| 聚类数 | 自评健康状态 | 家庭人均医疗支出 | 个人门诊费用 | 个人住院费用 | |
| 聚类水平:省−年 | 96 | (−2.67)*** | (1.62) | (0.24) | (2.16)** |
| 聚类水平:省 | 24 | (−1.37) | (1.61) | (−1.31) | (2.24)** |
| 聚类水平:区县 | 358 | (−1.41) | (1.03) | (−1.18) | (1.92)** |
| 注:自评健康状态采用OLS方法估计滞后一期效应,医疗支出均采用水平值进行估计,括号内为T值。**和***分别表示在5%和1%的统计水平上显著。 | |||||
(二)DID-PSM稳健性检验。本研究采用DID-PSM方法,对上述的结论进行稳健性检验,具体估计时,使用核估计匹配策略,采用Logit函数估计倾向得分,仅使用有共同取值范围内的观测值进行匹配,对应不同的因变量,协变量的选取与正文中相应模型的协变量相同,具体估计结果如表8所示。由表8可见,DID-PSM方法的估计结果,同原有的结论基本一致,“自评健康”的系数为−0.406,并且高度显著。家庭医疗人均支出和个人住院费用支出分别增加了54.86元和1 819.72元,而个人门诊费用支出减少了259元,但在统计上依然不显著。总之,DID-PSM方法给出的结果与之前的主要结论高度一致,这进一步证明了本文结论的可靠性。
| Base Line | Follow-up | Diff-in-Diff | |||||
| 控制组 | 处理组 | Diff(T-C) | 控制组 | 处理组 | Diff(T-C) | ||
| 自评健康 | 1.783 | 2.155 | 0.037***(18.84) | 3.259 | 3.225 | −0.034(0.73) | −0.406***(7.97) |
| 家庭医疗人均支出 | 1 198.04 | 1 119.56 | −78.48(−1.18) | 1 636.17 | 1 612.48 | −23.67(0.33) | 54.80(0.56) |
| 个人住院费用支出 | 1 388.80 | 943.82 | −444.98(−1.77) | 1 487.89 | 2 862.62 | 1 374.73***(3.13) | 1 819.72***(3.59) |
| 个人门诊费用支出 | 1 849.20 | 1 194.41 | −654.79(−2.78) | 2 710.95 | 1 797.58 | −913.38**(2.40) | −258.58(0.58) |
| 注:上述各类医疗支出均包括个人自费部分和医疗保险支付部分,金额根据历年医疗保健服务价格指数进行调整。其中最后一列为DID-PSM估计的政策效应。括号内为T值。**和***分别表示在5%和1%的统计水平上显著。 | |||||||
五、结 论
本文在对大病保险政策内生性和SAH报告异质性进行纠正的基础上,实证研究了更加慷慨的新农合大病保险政策,是否改善了农村居民的健康水平,刺激了医疗卫生支出。实证结果证实大病保险对农村居民的健康起到了改善作用,大病保险使处理组居民的健康改善幅度达到10%—20%。并且这种改善效应较为持久,在大病保险实施后的第三年仍然显著。同时,大病保险也刺激了居民医疗支出的大幅增长,其使得家庭人均医疗支出增长了5%,而个人住院支出则增长接近30%。但是上述效应在不同人群中存在显著差异,从健康改善效应看,最低收入群体并不是最大受益群体,中上等收入群体的健康改善幅度最大。从医疗支出的激励效应看,低收入家庭、中等收入家庭和高收入家庭,其个人住院支出逐次递增,分别为3 606元、3 661元和4 010元,这也部分解释了为何中上等收入群体的健康改善最显著。医疗支出的条件分位数估计结果显示,家庭人均医疗支出和个人住院费用支出本来就多的居民,大病保险对其医疗支出的刺激效应最大;而这两类支出本来就较少的居民,该政策对其医疗支出的影响甚微。医疗支出两部分模型的估计结果进一步表明,大病保险并没有提高医疗支出发生的概率,但是对已发生医疗支出的居民而言,大病保险具有进一步的支出激励作用。
综上结果,虽然大病保险刺激了医疗支出,但是农村居民的健康水平也得到了较大改善。因此,由中国政府主导的农村医疗保险,并未向西方国家一样,由于严重的道德风险,医疗支出已经处于边际收益递减的区域;相反,中国农村地区由于长期缺乏有效的医疗保障,大病保险的建立促进了医疗服务有效需求的释放,本文对不同医疗支出群体的异质性效应检验也证明了这样一个事实:大病保险主要刺激了本来就有医疗需要的人,如老年人和有各种慢性病人群的医疗支出,因此,当前农村的医疗保险对居民健康的影响仍然处于政策红利阶段。本文的研究结果为中国政府继续加大对农村医疗保险的财政补助,提高农村医疗保障水平,提供了一定的决策支持。本文的研究也表明,大病保险对农村最低收入群体的医疗支出激励效应最弱,其健康改善幅度相对中高收入群体也最低,因此作为有一定福利性质的农村医疗保险,如何向农村贫困人口倾斜,从而使最低收入群体成为最大受益者,还需要更有针对性的制度安排。需要指出的是,本文主要采用多重差分方法检验大病保险的政策效应,由于CFPS的数据限制,处理组与控制组无法在县级层面进行控制,因此控制组存在一定的试点地区,这对多重差分估计带来了一定程度的干扰。此外,本研究的时间跨度比较短,而大病保险的影响需要较长时间才能充分发挥作用。因此,大病保险的政策效应究竟怎样,其长期趋势如何,仍需要在未来做进一步的深入研究。
① 中国健康与营养调查(China Health and Nutrition Survey,CHNS)是一个专门的面向健康方向的调查数据库,但即便像CHNS这样的专业数据库,其中给出的健康问卷信息也较难生成令人满意的综合指标。
② 2012年8月,国家发改委联合卫生部、财政部等六部委发布《关于开展城乡居民大病保险工作的指导意见》,针对城居保、新农合参保人,建立大病保险制度,减轻城乡居民的大病负担,大病报销比例不低于50%。《指导意见》明确规定城居保和新农合的参保人无需额外支付任何费用,自动享有大病保险待遇,大病保险的实施标志着中国农村医疗保障制度的工作重点已从“制度建立”阶段向“质量建设”阶段转变。
③ 我们判断的依据是根据各省颁布的实施方案或实施意见加以确定,例如:《河南省新型农村合作医疗大病保险实施方案(试行)》(豫政办〔2013〕22号)。
④ 江苏、江西2013年在每个省辖市选择一个县(区)开展试点。安徽2013年共有11个县开展试点。广东2013年在16个市开展试点。陕西2013年在西安、宝鸡、延安、汉中四个省辖市开展试点。
⑤ 人均GDP按照2000年的不变价格进行调整。
⑥ 进一步的解释:加入这些变量后回归估计的是(为了说明问题起见,假设不存在其他控制向量):
⑦ 聚类问题又称为Moulton问题,用以纪念Moulton对这个问题作出的开创性贡献。
⑧ 由于篇幅所限,我们没有给出完整的估计结果,备索。
⑨ “他人健康评价1”:孙军/李梅在走路、跑步、活动四肢上毫无问题。他/她每周慢跑2次,每次跑5公里。他/她记不得最近一次感到身体疼痛是什么时候,因为最近一年里他/她都从未感到过疼痛。即使在体力劳动或者锻炼后,他/她也不曾感到任何身体疼痛。您认为,孙军/李梅的健康状况如何?1.非常健康 2.很健康 3.比较健康 4.一般 5.不健康。“他人健康评价2”:赵刚/王丽走200米的路毫无困难。但走完一公里或爬完几层楼后,会觉得累。他/她的日常活动没有问题,比如从市场上买完菜拎回家。他/她每月都有一次头痛,吃药之后会有所缓解。头痛时,他/她能继续做日常工作。您认为,赵刚/王丽的健康状况如何?1.非常健康 2.很健康 3.比较健康 4.一般 5.不健康。
⑩ 为了对比起见,表4定序模型的估计也只包括2010年、2012年和2014年的数据。后继异质性效应分析中表8的定序模型,包括2016年的样本。
⑪ 由于篇幅所限,我们只给出了
⑫ 原始因变量线性模型其优点是简单,估计直接在“原始”的数据上进行,其偏效应易于解释,无需进行逆变换。考虑到异方差问题,这里一律采用聚类稳健型标准误。
⑬ 选择平方根变换模型的原因是,同对数变换模型一样,平方根模型也可以对分布偏斜进行修正,并且可以估计医疗支出为0的样本,在计算偏效应的时候不受拖尾因子的影响,因此在研究医疗支出问题中,它也是常用模型。
⑭ 对数线性变换估计的系数有一个简单的直观解释,即半弹性,本文后继讨论中也将采用这一解释。
⑮ 表4计算的边际效应均值,是对每个农村居民样本根据(13)式计算出大病保险的边际效应,然后基于家庭人均收入分组计算组内边际效应的样本均值。
⑯ 这里给出的是控制组(18)的回归结果,控制组(13)的回归结果与表4类似,由于篇幅所限这里没有给出,备索。
⑰ 由于篇幅所限,本文没有对二部分模型的原理给予说明,Mihaylova等(2011)对二部分模型在医疗支出研究中的应用给予了详细的解释。
⑱ 表5使用了stata命令“twopm”进行估计。
⑲ 由于篇幅所限,本文没有给出具体的估计结果,备索。
⑳ 数据来源于国家卫生计生委等15个部门联合印发的《关于实施健康扶贫工程的指导意见》。
㉑ 由于篇幅所限,本文没有给出具体的估计结果,备索。
| [1] | 陈华, 邓佩云. 城镇职工基本医疗保险的健康绩效研究——基于CHNS数据[J]. 社会保障研究, 2016(4): 44–52. DOI:10.3969/j.issn.1674-4802.2016.04.007 |
| [2] | 程令国, 张晔. " 新农合”: 经济绩效还是健康绩效?[J]. 经济研究, 2012(1): 120–133. |
| [3] | 胡宏伟, 刘国恩. 城镇居民医疗保险对国民健康的影响效应与机制[J]. 南方经济, 2012(10): 186–199. DOI:10.3969/j.issn.1000-6249.2012.10.016 |
| [4] | 黄枫, 甘犁. 过度需求还是有效需求? ——城镇老人健康与医疗保险的实证分析[J]. 经济研究, 2010(6): 105–119. |
| [5] | 李华, 俞卫. 政府卫生支出对中国农村居民健康的影响[J]. 中国社会科学, 2013(10): 41–60,205. |
| [6] | 马超, 顾海, 孙徐辉. 参合更高档次的医疗保险能促进健康吗? ——来自城乡医保统筹自然实验的证据[J]. 公共管理学报, 2015(2): 106–118. |
| [7] | 潘杰, 雷晓燕, 刘国恩. 医疗保险促进健康吗? ——基于中国城镇居民基本医疗保险的实证分析[J]. 经济研究, 2013(4): 130–142. |
| [8] | 彭晓博, 王天宇. 社会医疗保险缓解了未成年人健康不平等吗[J]. 中国工业经济, 2017(12): 59–77. |
| [9] | 解垩. 与收入相关的健康及医疗服务利用不平等研究[J]. 经济研究, 2009(2): 92–105. |
| [10] | 赵忠, 侯振刚. 我国城镇居民的健康需求与Grossman模型——来自截面数据的证据[J]. 经济研究, 2005(10): 79–90. |
| [11] | 赵忠. 我国农村人口的健康状况及影响因素[J]. 管理世界, 2006(3): 78–85. |
| [12] | Angrist J D, Pischke J S. Mostly harmless econometrics: An empiricist's companion[M]. New Jersey: Princeton University Press, 2008. |
| [13] | Arrow K J. Uncertainty and the welfare economics of medical care(American Economic Review, 1963)[J]. Journal of Health Politics, Policy and Law, 2001, 26(5): 851–883. DOI:10.1215/03616878-26-5-851 |
| [14] | Beck T, Levine R, Levkov A. Big bad banks? The winners and losers from bank deregulation in the united states[J]. The Journal of Finance, 2010, 65(5): 1637–1667. DOI:10.1111/j.1540-6261.2010.01589.x |
| [15] | Card D, Dobkin C, Maestas N. Does medicare save lives?[J]. The Quarterly Journal of Economics, 2009, 124(2): 597–636. DOI:10.1162/qjec.2009.124.2.597 |
| [16] | Chen Y Y, Jin G Z. Does health insurance coverage lead to better health and educational outcomes? Evidence from rural China[J]. Journal of Health Economics, 2012, 31(1): 1–14. DOI:10.1016/j.jhealeco.2011.11.001 |
| [17] | Finkelstein A, McKnight R. What did medicare do(and was it worth it)? [R]. NBER Working Paper No. w11609, 2005. |
| [18] | Finkelstein A, Taubman S, Wright B, et al. The Oregon health insurance experiment: evidence from the first Year[J]. The Quarterly Journal of Economics, 2012, 127(3): 1057–1106. DOI:10.1093/qje/qjs020 |
| [19] | Kelly I R, Markowitz S. Incentives in obesity and health insurance[J]. Inquiry, 2009-2010, 46(4): 418–432. DOI:10.5034/inquiryjrnl_46.4.418 |
| [20] | Lei X Y, Lin W C. The new cooperative medical scheme in rural China: Does more coverage mean more service and better health?[J]. Health Economics, 2009, 18(S2): S25–S46. DOI:10.1002/hec.1501 |
| [21] | Lindeboom M, van Doorslaer E. Cut-point shift and index shift in self-reported health[J]. Journal of Health Economics, 2004, 23(6): 1083–1099. DOI:10.1016/j.jhealeco.2004.01.002 |
| [22] | Mihaylova B, Briggs A, O’Hagan A, et al. Review of statistical methods for analysing healthcare resources and costs[J]. Health Economics, 2011, 20(8): 897–916. DOI:10.1002/hec.1653 |
| [23] | Skinner J S, Fisher E, Wennberg J E. The efficiency of medicare[R]. NBER Working Paper No. w8395, 2001. |
| [24] | Tanaka S. Environmental regulations on air pollution in China and their impact on infant mortality[J]. Journal of Health Economics, 2015, 42: 90–103. DOI:10.1016/j.jhealeco.2015.02.004 |
| [25] | Wagstaff A, Lindelow M. Can insurance increase financial risk? : The curious case of health insurance in China[J]. Journal of Health Economics, 2008, 27(4): 990–1005. DOI:10.1016/j.jhealeco.2008.02.002 |