
2019第45卷第9期
2. 中国海洋大学 经济学院,山东 青岛 266100;
3. 苏州大学 东吴商学院,江苏 苏州 215012;
4. 中国农业大学 经济管理学院,北京 100083
2. School of Economics, Ocean University of China, Qingdao 266100, China;
3. Dongwu Business School, Soochow University, Suzhou 215012, China;
4. College of Economics and Management, China Agricultural University, Beijing 100083, China
一、引 言
党的十九大报告及2018年中央经济工作会议均明确指出要“保持人民币汇率在合理均衡水平上的基本稳定”,因此,在增强汇率弹性的同时,维持人民币汇率在合意均衡水平上的有序波动是货币当局现阶段关注的重要问题。为避免汇率剧烈波动及其扰乱经济运行,货币当局经验性地采取入市干预的操作手段进行调控,在外汇市场上通过购买(卖出)外汇以释放(回笼)流动性的方式维持人民币汇率稳定。其中,2015年8月所进行的旨在推进人民币汇率市场化的改革,引发了国际资本大量流出,此后人民币汇率一度呈现大幅贬值情形。为弱化人民币汇率贬值预期,中国人民银行除了采取冲销式干预之外,还采取了上调中期借贷便利利率、逆回购利率和常备借贷便利利率以及在中间报价机制中引入逆周期调节因子等非常规货币政策进行调控。但需指出的是,伴随着我国外汇市场运行机制的深刻变化,汇率频繁剧烈波动的特征事实依然明显且表现为 “常态化”,这隐含着我国逆周期调控政策的有效性尚未得到充分体现。
为此,本文力求从一个新的框架阐释人民币汇率的动态变化特征及其波动成因,旨在从历史演进视角揭示人民币汇率波动的特征异质性,并重点剖析特征异质性背后的潜在影响因素及其所隐含的经济学含义。显然,对于上述命题的进一步研究,不仅能为回答经典汇率决定理论模型无法准确捕捉人民币汇率变动特征提供理论解释,还有助于从既有的改革与发展进程中探索人民币汇率的波动根源。更为重要的是,厘清上述问题还能为完善货币政策调控以推进汇率市场化改革提供启示,这对于优化人民币汇率形成机制并维持其在合意均衡的区间内有序波动具有重要的理论与现实意义。
长期以来,关于采用何种理论框架刻画汇率的动态变化特征及其波动成因,学术界始终存有争议(Beckmann和Schussler, 2016)。受严格假设的影响,传统的经典汇率决定理论(如购买力平价理论、利率平价理论、弹性价格货币模型及汇率超调模型等)并没有在解释汇率波动成因上得出准确的先验结论,甚至其预测效果低于简单的随机游走模型。尽管有学者尝试放松假设并对其形式进行修正,但这些解释的能效依然未有充分改观(Meese和Rogoff,1983;Meese等,1983;Obstfeld和Rogoff,2000;Evans和Lyons,2005;江春和刘春华,2007;范立夫,2011;潘锡泉,2013;司登奎等,2016)。
在关于汇率决定的文献中,不乏学者从经济基本面探索汇率波动的成因,而其中以采用具有内生特征的货币政策规则为主。泰勒规则作为内生货币政策的典型形式,在汇率决定中备受学者关注,且研究观点基本形成共识,即具有内生特征的泰勒规则能够较好地解释汇率变动成因。例如,Engel和West(2005)研究发现,泰勒规则汇率模型能够较好地拟合1978—2001年间美元汇率的动态变化特征;Mark(2009)发现将泰勒规则与利率平价理论模型结合起来,纳入利差的泰勒规则模型对汇率的动态变化具有较好的解释;陈平和李凯(2010)对汇改后人民币汇率变动进行预测,结果发现泰勒规则模型能够较好地解释人民币汇率变动;陈创练和杨子晖(2012)也从泰勒规则出发,并结合中国转轨经济的特点,构建资本流动管制下汇率和通货膨胀率决定的动态理论模型,并在此基础上采用多种动态方法对人民币实际汇率波动的影响因素进行了分析;江春等(2018b)发现,在泰勒规则模型之中纳入资产价格(股价)能够实现对传统“股票导向”模型和资产组合平衡模型的补充。
需要指出的是,随着中国金融双向开放的不断推进,尤其是资本账户的进一步开放和“沪港通”的开通,资本市场与外汇市场之间的联系也更加紧密。在这一现实背景下,从学理层面刻画国际资本流动对汇率的影响引起了学界的关注。例如,Filer II(2004)认为大量资本流入会导致经济过热,从而增加通货膨胀的压力,引发本币升值;Caballero和Krishnamurthy(2006)指出国际资本的快速流入是引起汇率剧烈波动的重要原因;朱孟楠和刘林(2010)发现,短期国际资本流入会导致人民币汇率升值以及市场对人民币升值的预期,而且资本流出对人民币汇率的影响也较为显著;周爱民和遥远(2015)将资本流动分为流入实体经济从事生产活动的资本和有投机性质的资本流动,研究发现前者在短期内不会造成实际汇率升值,而后者则会造成实际汇率升值;司登奎等(2018)以国际资本流动为媒介,在包含投资者情绪的开放框架下对汇率的变动成因进行实证分析,结果发现投资者情绪不仅会对汇率产生直接影响,还会通过影响国际资本流动而对汇率产生“叠加”的间接影响;查尔斯•恩格尔(2019)研究发现,中国实行资本管制制度对于稳定汇率波动具有重要的作用,且能够带来福利改进。
诚然,尽管上述研究在汇率波动成因层面进行了一系列解释,但现有研究还存在如下待于拓展之处:第一,由于传统汇率决定模型存在较为严格的假设,因而无法准确地解释汇率波动的成因,其分析结果与现实尚存在一定的偏差,甚至得出的结果与经济现象相悖。虽有学者尝试对其进行修正,但缺乏基于模型内生化思想的改进,使得解释能效并未得到根本体现。第二,尽管已有研究分析国际资本流动在汇率决定中所扮演的重要角色,但它们将国际资本流动视为外生冲击的处理方式颇为不妥,因而并不利于准确分析国际资本流动影响汇率变动的具体机理。第三,鉴于人民币汇率的形成机制在不同的经济环境下所表现的特点可能不同,也即具有潜在的非线性特征,而已有研究在线性假定的框架下解释人民币汇率波动的成因显然有失偏颇,这并不利于准确识别人民币汇率的动态变化特征。
鉴于此,本文在已有汇率决定研究成果的基础上,将国际资本流动内生地植入泰勒规则汇率模型之中,并从理论上刻画汇率的动态决定机制,同时采用含随机波动的时变贝叶斯向量自回归模型(TVP-SV-BVAR)实证分析人民币汇率波动成因的非线性特征。理论分析表明,国际资本流动、汇率预期、利差、通胀差、产出缺口差对即期汇率的影响均取决于利率平滑操作程度、本国与外国货币政策对汇率偏离的相对敏感程度,而且国际资本流动、产出缺口差及通胀差对汇率的影响还与货币政策的反应程度有关。进一步采用TVP-SV-BVAR模型分别从不同时点和不同时期进行多维实证分析的结果显示,包含国际资本流动的泰勒规则对人民币汇率的影响具有显著的时变性,且包含国际资本流动的泰勒规则在短期和长期内对汇率变动的影响具有显著的异质性,具体表现为:(1)国际资本流入以及利差扩大在短期和长期内均会助推人民币汇率升值,但短期影响大于长期影响,且该影响在2015年“汇改”后明显增强;(2)通胀率上升在短期和长期内均会引发人民币汇率升值,但该效应相对较小;(3)产出增加在短期内会引发人民币贬值,但长期内会助推人民币升值,而且产出缺口差对汇率的影响最大,且较为稳定;(4)汇率预期对人民币即期汇率的影响在短期内为正向,但长期内会因为货币当局进行外汇干预而变为负向,且该影响在2015年“汇改”后也明显增强。
相较于已有的研究,本文的边际贡献及主要工作体现于:第一,以泰勒规则货币政策为研究框架,在纳入汇率预期并适当放宽假设的基础上进一步拓展至开放形式,这有利于解决中国货币政策与汇率政策之间的潜在冲突,进而为完善货币政策调控体系提供参考。第二,将国际资本流动内生地植入泰勒规则模型以刻画人民币汇率的动态决定机制,有利于准确识别人民币汇率波动成因的微观机制,进而能为分析汇率的动态决定提供一种新的思路。第三,基于TVP-SV-BVAR模型实证分析人民币汇率波动的成因,有利于从历史演进视角识别人民币汇率变动的冲击源,因而能为维持人民币汇率在合理均衡水平上的基本稳定提供经验支持。
二、理论分析
长期以来,学术界关于货币政策应是“规则行事”还是“相机抉择行事”一直存在争议,这主要与当时的历史背景和理论指导有关。①从全球货币政策的演化特征看,数量型向价格型工具的转变已是不争的事实。基于这一现实背景,Taylor(1993)提出锚定产出缺口与通胀缺口的利率政策有利于发挥货币政策调控目标的有效性。其中,泰勒规则的标准形式如下:
| $ i_{t}^{*}=r^{*}+\pi_{t}+\alpha_{0}\left(\pi_{t}-\pi^{*}\right)+\alpha_{2} y_{t} $ | (1) |
其中,
如前文所言,随着经济全球化及金融一体化格局的日益凸显,国际资本流动也会对一国货币政策产生影响,而且历史经验也表明国际资本流动会对外汇市场产生一定的冲击。因此,为避免遗漏重要变量,并提高模型对经济现象的解释力,本文将国际资本流动内生地植入泰勒规则之中,其形式如下:
| $ i_t^* = {r^*} + {\pi _t} + {\alpha _0}({\pi _t} - {\pi ^*}) + {\alpha _2}{y_t} + {\alpha _3}c{f_t} $ | (2) |
其中,
| $ i_t^* = \mu {\rm{ + }}{\alpha _1}{\pi _t} + {\alpha _2}{y_t} + {\alpha _3}c{f_t} + {\alpha _4}({e_t} - {\bar e_t}) $ | (3) |
其中,
| $ {i_t} = \rho {i_{t - 1}} + (1 - \rho )i_t^{\rm{*}} + {\varepsilon _t} $ | (4) |
在式(4)中,ρ用来刻画利率平滑程度,取值范围为(0,1),
| $ {i_t} = \rho {i_{t - 1}} + (1 - \rho )\left[ {{\alpha _1}{\pi _t} + {\alpha _2}{y_t} + {\alpha _3}c{f_t} + {\alpha _4}({e_t} - {{\bar e}_t}) + \mu } \right] + {\varepsilon _t} $ | (5) |
参照江春等(2018a, b)的研究,我们假设国外货币政策同样遵循泰勒规则,并假设国外货币当局对通胀、产出缺口的反应与国内一致,②但对汇率的反应与本国不同。基于此,我们将国外的货币政策规则表达如下:
| $ i_t^f = \rho i_{t - 1}^f + (1 - \rho )[{\alpha _1}\pi _t^f + {\alpha _2}y_t^f + \alpha _4^*({e_t} - {\bar e_t}) + {\mu ^f}] + \varepsilon _t^f $ | (6) |
将式(5)与式(6)相减,可得:
| $ \begin{aligned} {i_t} - i_t^f =& \rho ({i_{t - 1}} - i_{t - 1}^f) + (1 - \rho ){\alpha _1}({\pi _t} - \pi _t^f) + (1 - \rho ){\alpha _2}({y_t} - y_t^f)\\ & + (1 - \rho ){\alpha _3}c{f_t} + (1 - \rho )({\alpha _4} - \alpha _4^*)({e_t} - {{\bar e}_t})\\ & + (1 - \rho )(\mu - {\mu ^f}) + {\varepsilon _t} - \varepsilon _t^f \end{aligned} $ | (7) |
值得注意是,在式(7)中,由于
依据无抛补利率平价与购买力平价条件,我们可分别得到:
| $ {E_t}{e_{t + 1}} = {e_t} + {i_t} - i_t^f $ | (8) |
| $ {\bar e_t} = {p_t} - p_t^f $ | (9) |
其中,
将式(8)与式(9)代入式(7)中,整理可得:
| $ \begin{aligned} [1 + (1 - \rho )({\alpha _4} - \alpha _4^*)]{e_t} =& {E_t}{e_{t + 1}} - \rho ({i_{t - 1}} - i_{t - 1}^f) - (1 - \rho ){\alpha _1}({\pi _t} - \pi _t^f)\\ & - (1 - \rho ){\alpha _2}({y_t} - y_t^f) + (1 - \rho )({\alpha _4} - \alpha _4^*)({p_t} - p_t^f)\\ & - (1 - \rho ){\alpha _3}c{f_t} - (1 - \rho )(\mu - {\mu ^f}) - ({\varepsilon _t} - \varepsilon _t^f) \end{aligned} $ | (10) |
此时,令
| $ \begin{aligned} {e_t} = &s{E_t}{e_{t + 1}} - s\rho ({i_{t - 1}} - i_{t - 1}^f) - s({\varepsilon _t} - \varepsilon _t^f) - s(1 - \rho )(\mu - {\mu ^f})\\ & - s(1 - \rho )[{\alpha _1}({\pi _t} - \pi _t^f) + {\alpha _2}({y_t} - y_t^f) + {\alpha _3}c{f_t} - ({\alpha _4} - \alpha _4^*)({p_t} - p_t^f)] \end{aligned} $ | (11) |
进一步地,我们将
| $ \begin{aligned} {e_t} =& s{E_t}{e_{t + 1}} - s\rho ({i_{t - 1}} - i_{t - 1}^f) - s({\varepsilon _t} - \varepsilon _t^f) - s(1 - \rho )(\mu - {\mu ^f})\\ & - s(1 - \rho )\{ [{\alpha _1} - ({\alpha _4} - \alpha _4^*)]({p_t} - p_t^f) - {\alpha _1}({p_{t - 1}} - p_{t - 1}^f) + {\alpha _2}({y_t} - y_t^f) + {\alpha _3}c{f_t}\} \end{aligned} $ | (12) |
其中,
需要特别提及的是,从式(12)中还可以推演出一个基本结论,即在异质性经济环境和不同时期(短期、中期和长期)下,拓展型泰勒规则中不同因素间的相互作用方向和程度很有可能会发生变化。特别地,本国与外国货币当局不仅在货币政策本身的平滑操作上不尽一致,而且两国货币政策在锚定汇率与国际资本流动的方向与力度上也可能因时而异,这隐含着包含国际资本流动的泰勒规则对汇率的影响并非一成不变,而是在不同的经济环境以及异质性阶段中表现为时变性特征。
三、变量选取及相关检验
依据本文研究目的,并结合前文的理论分析,我们将直接标价法下的人民币兑美元期末汇率(ER)作为本文的核心被解释变量。在测算中美利差(ID)时,本文借鉴江春等(2018a, b)的研究,采用中国银行间同业拆借隔夜利率(id)与美国联邦基金利率(if)之差表示。类似地,我们将通货膨胀表示为居民消费者价格指数的环比增长率,因此中美通胀差为两国的居民消费者价格指数环比增长率之差。需要提及的是,在测度产出缺口时,由于我国并没有对GDP的月度数据进行统计,为了充分利用数据的有效信息并提高研究的时效性,我们采用工业增加值作为GDP的代理变量,并以此测算中国的产出缺口。类似地,采用美国工业增加值作为美国产出的代理变量,同样将该工业增加值缺口近似替代美国的产出缺口,并将两者之差记为中美产出缺口差。关于人民币汇率预期的衡量,考虑到离岸市场中人民币兑美元汇率更接近市场化,且受政策干预的影响较小,因此我们借鉴江春等(2018a, b)及司登奎等(2018)的研究,采用离岸市场中直接标价法下的人民币兑美元一年期无本金交割协议价(Non-deliverable Forward,NDF)表示。由于我国并未直接公布国际资本流动的具体数据,且学界较多地采用间接法进行近似估计,因此,我们借鉴张明(2011)、李小林等(2018)的研究,将央行外汇占款增量与净出口及实际利用FDI之差来近似衡量短期国际资本流动。上述数据来源于FRED及Wind数据库。考虑到2005年7月以来,人民币汇率波动更具弹性,因此本文的样本期间设定为2005年7月至2018年10月。
在对变量间的关系进行刻画时,为避免出现虚假回归并导致参数估计结果非一致情形,同时考虑到本文所涉及的经济金融变量易受非预期外部冲击及政策调整的影响而具有结构突变特征,特别是在不同的时间区间及区制环境下,上述变量的动态变化特征很有可能存在差异。鉴于此,我们借鉴司登奎等(2017)的研究,采用能同时捕捉结构突变和平滑渐变的分位数单位根方法对变量的非线性动态变化进行平稳性检验,结果如表1所示。
| τ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| ER |
$ {\alpha _1}(\tau )$
|
−1.133 | −3.301 | −4.146 | −3.922 | −3.818 | −4.327 | −3.540 | −2.452 | −0.259 |
| p | 0.276 | 0.004 | 0.000 | 0.000 | 0.006 | 0.000 | 0.004 | 0.056 | 0.734 | |
| QKS | 9.004*** | K | 1 | F | 467.574*** | |||||
| CF |
$ {\alpha _1}(\tau )$
|
−2.906 | −2.856 | −3.820 | −3.742 | −3.700 | −3.952 | −3.205 | −7.537 | −5.197 |
| p | 0.028 | 0.016 | 0.004 | 0.006 | 0.012 | 0.002 | 0.012 | 0.000 | 0.000 | |
| QKS | 7.451*** | K | 2 | F | 19.458*** | |||||
| ID |
$ {\alpha _1}(\tau )$
|
−5.402 | −5.958 | −5.362 | −7.596 | −10.316 | −9.050 | −9.308 | −4.129 | −2.598 |
| p | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.048 | |
| QKS | 8.726*** | K | 1 | F | 254.374*** | |||||
| GDP |
${\alpha _1}(\tau ) $
|
−3.772 | −7.024 | −5.438 | −7.487 | −10.113 | −8.666 | −7.878 | −3.923 | −0.824 |
| p | 0.006 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.012 | 0.398 | |
| QKS | 6.462*** | 2 | F | 29.387*** | ||||||
| CPI |
${\alpha _1}(\tau ) $
|
−1.321 | −1.663 | −2.544 | −2.900 | −2.607 | −2.312 | −3.173 | −2.596 | −2.225 |
| p | 0.270 | 0.236 | 0.042 | 0.024 | 0.054 | 0.108 | 0.008 | 0.026 | 0.094 | |
| QKS | 5.943* | K | 3 | F | 47.151*** | |||||
| NDF |
${\alpha _1}(\tau ) $
|
−1.348 | −1.849 | −2.439 | −3.422 | −3.848 | −4.115 | −3.129 | −2.095 | −0.498 |
| p | 0.292 | 0.206 | 0.068 | 0.006 | 0.000 | 0.000 | 0.012 | 0.128 | 0.730 | |
| QKS | 7.427*** | K | 1 | F | 229.660*** | |||||
| 结构突变点位置 | ||||||||||
| 突变点1 | 突变点2 | 突变点3 | 突变点4 | 突变点5 | ||||||
| ER | 2008M1 | 2009M10 | 2011M9 | 2013M1 | 2015M7 | |||||
| CF | 2012M3 | 2013M8 | 2015M7 | 2017M6 | ||||||
| ID | 2007M4 | 2008M11 | 2010M11 | 2013M4 | ||||||
| GDP | 2008M9 | 2010M1 | ||||||||
| CPI | 2008M6 | 2010M11 | 2012M8 | 2013M12 | 2015M4 | |||||
| NDF | 2006M12 | 2008M8 | 2011M3 | 2013M2 | 2015M7 | |||||
| 注:***和*分别表示1%和10%的显著性水平;
$ {\alpha _1}(\tau )$
表示在不同分位数水平
$\tau $
下对变量的残差序列进行平稳性检验时的自回归系数;p 为检验
$ {\alpha _1}(\tau )$
是否显著时的伴随概率;QKS为含傅里叶级数的分位数单位根检验统计量,其原假设为变量在全局内非平稳,其临界值根据5 000次用bootstrap算法获得;K表示平滑渐变点的个数;F统计量用来检验变量是否为线性形式,原假设为“变量为线性”,此时拟合变量数据生成过程的傅里叶级数中的正弦(sine)与余弦(cosine)项均不显著。 |
||||||||||
从表1中的检验结果可以看出,QKS统计量在至少10%的显著性水平上拒绝了“序列为非平稳”的原假设,这意味着上述所有变量均为平稳序列。从平滑渐变点检验结果(K)可以发现,中美通胀差含有3个平滑渐变点,国际资本流动与产出缺口均含有2个平滑渐变点,而汇率、中美利差及汇率预期均含有1个平滑渐变点。同时,结构突变点检验结果表明,人民币即期汇率、中美通胀差及汇率预期均含有5个结构突变点,资本流动、利差均含有4个结构突变点,而产出缺口差则含有2个结构突变点。此外,所有变量的F统计量在至少10%的显著性水平上拒绝了“变量为线性”的原假设,这意味着变量的数据生产过程(Data Generating Process,DGP)均呈现非线性特征,这在一定程度上印证了采用非线性方法刻画变量间动态关系的必要性。
四、实证分析
(一)参数估计
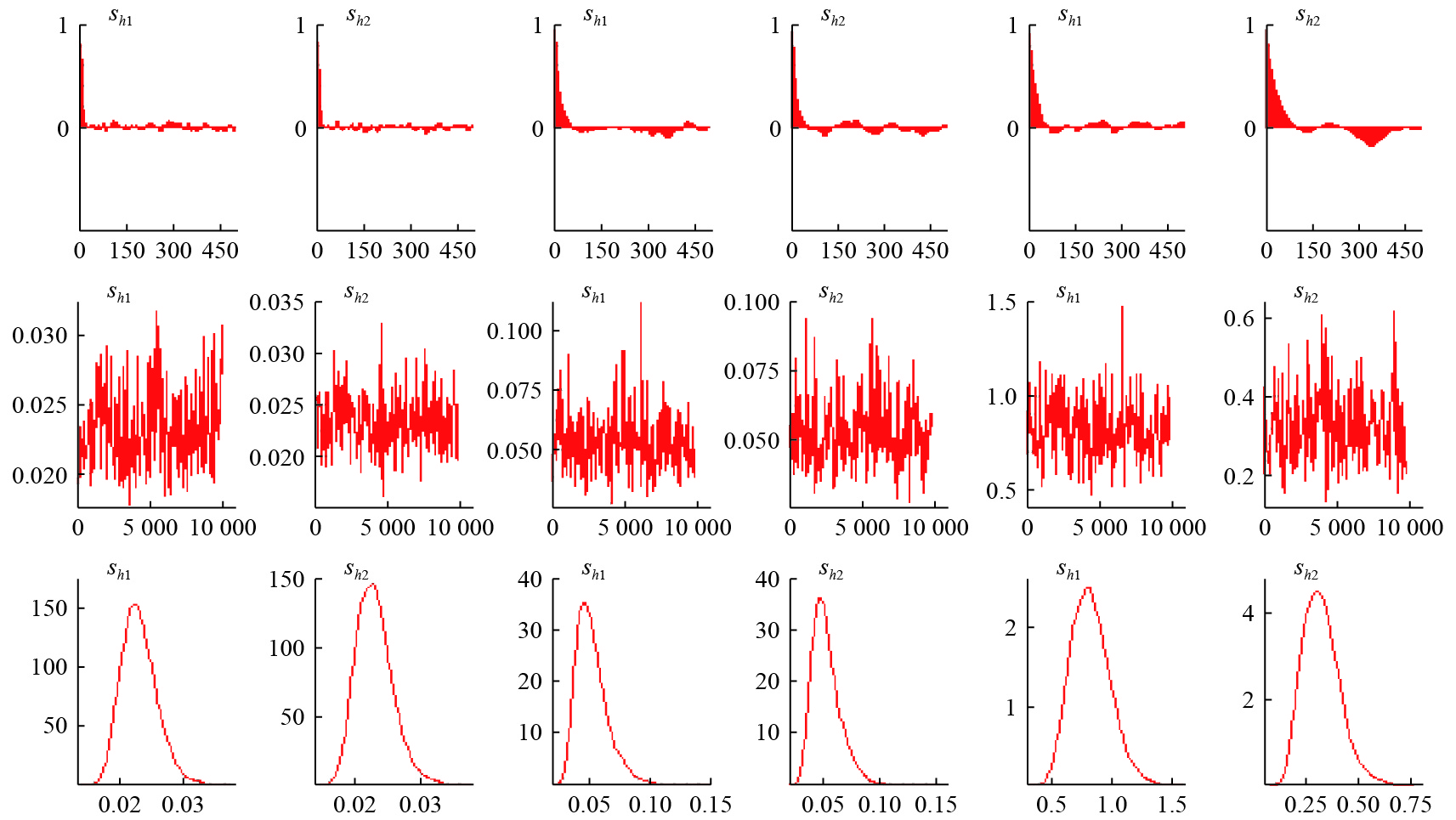
为考察纳入国际资本流动的泰勒规则对汇率影响的时变性特征,我们借鉴Primiceri(2005)、Franta等(2014)与江春等(2018a, b)的研究,采用TVP-SV-BVAR模型从动态演进视角对人民币汇率的时变性特征予以刻画。③需要特别提及的是,为了保证参数估计的有效性,我们采用贝叶斯多步移动Gibbs抽样方法进行分析。其中,我们设定抽样次数为11 000次,并将前1 000次结果作为“预烧”(burn-in)以避免初始值对参数估计的影响,其参数估计结果分别见表2与图1。不难发现,剔除预烧期的抽样样本自相关性明显下降,样本的取值路径趋于平稳,这意味着抽样之后所产生的样本具有一定的有效性。同时从表2中的参数回归结果还可以发现,CD检验统计量的伴随概率均大于10%,这说明表中所有参数均无法拒绝收敛于后验分布的原假设,并意味着迭代周期中预烧期能够有效使得马尔科夫链趋于集中。此外,表2中最后一列的无效因子普遍较低,最大值仅为54.62,这表示通过MCMC抽取样本至少可获得183(=10 000/54.62)个有效样本数,从而可进一步表明该参数估计结果具有较高的有效性。
| 参数 | 均值 | 标准差 | 95%置信区间 | CD检验 | 无效因子 |
|
${\left( {\sum\nolimits_\beta } \right)_1} $
|
0.0232 | 0.0027 | [0.0186,0.0291] | 0.1320 | 13.09 |
|
$ {\left( {\sum\nolimits_\beta } \right)_2} $
|
0.0230 | 0.0028 | [0.0183,0.0292] | 0.7810 | 8.86 |
|
${\left( {\sum\nolimits_\alpha } \right)_1} $
|
0.0525 | 0.0129 | [0.0339,0.0834] | 0.7510 | 25.34 |
|
$ {\left( {\sum\nolimits_\alpha } \right)_2}$
|
0.0523 | 0.0125 | [0.0338,0.0818] | 0.2480 | 25.51 |
|
${\left( {\sum\nolimits_h {} } \right)_1} $
|
0.8297 | 0.1583 | [0.5572,1.1742] | 0.5010 | 35.82 |
|
$ {\left( {\sum\nolimits_h {} } \right)_2}$
|
0.3240 | 0.0874 | [0.1833,0.5237] | 0.3460 | 54.62 |
| 注:α、β和h (i, j, k= 1, 2, 3)分别表示Σα、Σβ和Σh的第i、j和k个对角元素,并且Σα和Σβ的估计值和标准差都乘以100。CD检验为Geweke (1992)提出的收敛性检验(Convergence diagnostics),其原假设为参数收敛于后验分布。无效因子是经过11 000次MCMC抽样后计算得到的结果,主要用来判断MCMC抽取样本的有效性。 | |||||
(二)不同时点下的实证结果
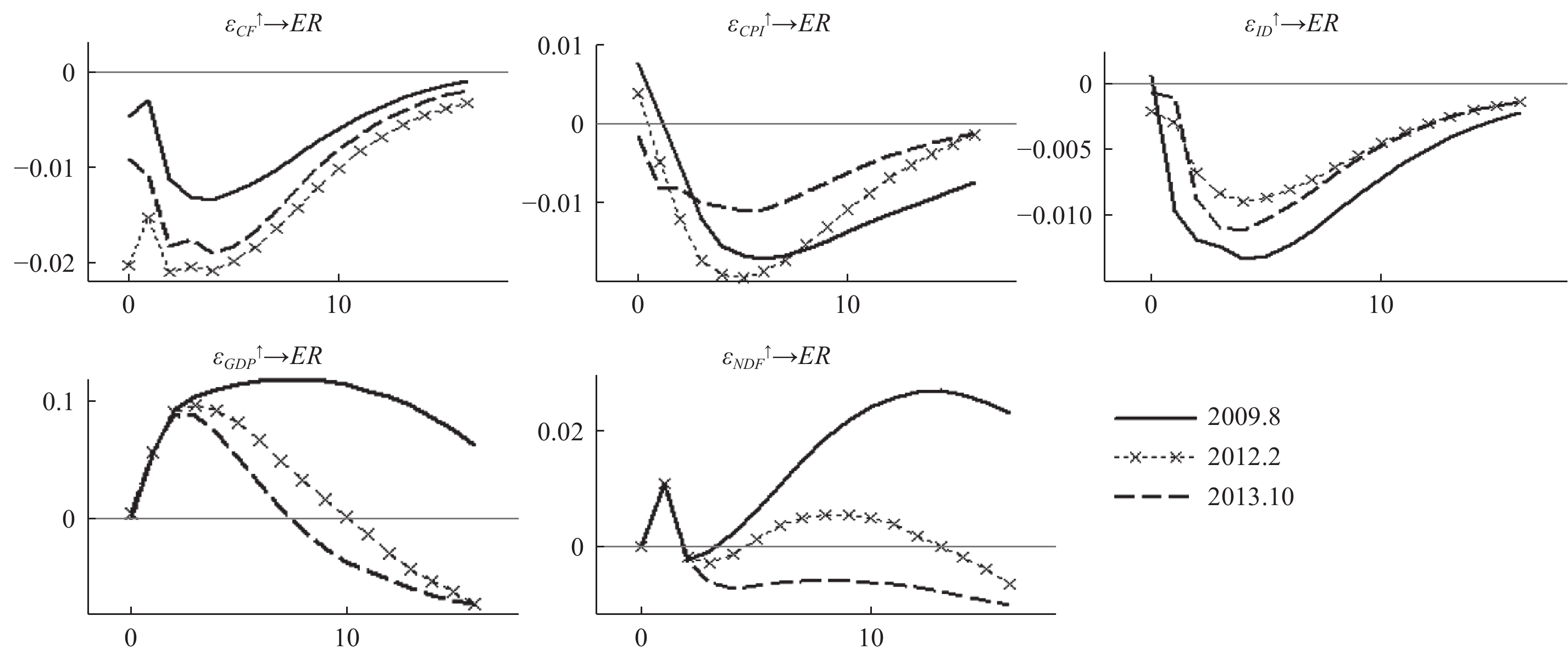
依据TVP-SV-BVAR模型的贝叶斯后验分布,我们可以得到每个时点下的参数估计结果,并进而得出不同时点和不同时期下的时变冲击,其脉冲响应结果分别如图2和图3所示。
|
| 图 1 TVP-SV-VAR 参数估计结果 |
|
| 图 2 不同时点下的脉冲响应 |
|
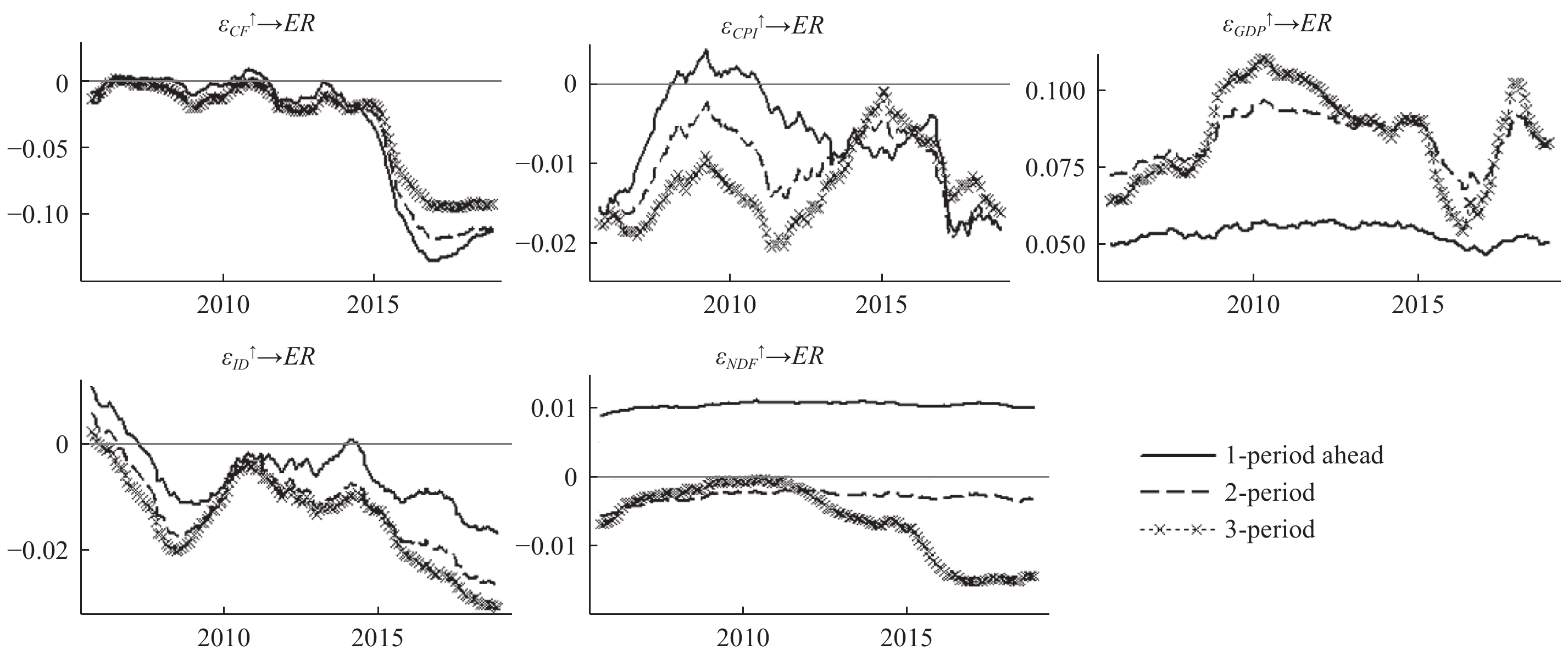
| 图 3 不同时期下的脉冲响应结果 |
依据图2中不同时点下的研究结果,我们可以得到如下发现:国际资本流动对汇率的冲击效应(
需要指出的是,包含国际资本流动的泰勒规则对汇率的影响与购买力平价理论及利率平价理论所阐释的观点不尽相同。特别地,当中国的通货膨胀较美国明显时,人民币兑美元汇率倾向于升值。④类似地,人民币利率较美元利率增加时,人民币汇率表现为升值态势。⑤这是因为,泰勒规则属于内生化利率规则,当物价上涨时,货币当局则会内生性地采取提高利率的紧缩性货币政策进行调控。从中国的现实来看,自2008年4月至2013年底,中美利差持续扩大后随之维持在高位,人民币升值预期逐渐显现,这在一定程度上加速了国际资本流入,并进一步加剧了人民币升值压力。与此同时,自2015年8月人民币汇率实行中间报价机制的制度改革以来,中美利差的持续降低使得人民币汇率呈现明显的贬值预期,这无疑会引发国际资本流出,从而使得人民币汇率呈现潜在的贬值特征。因此,相对于利率平价与购买力平价理论而言,包含国际资本流动的泰勒规则更能体现出近年来中国货币政策的操作经验,同时也印证了泰勒规则汇率模型能够较好地解释人民币汇率的动态演化特征。
此外,包含国际资本流动的泰勒规则模型在解释产出缺口对汇率的影响方面,其结论与粘性价格货币模型、实际利差模型以及巴拉萨-萨缪尔森效应的结论基本一致,即产出相对于外国增加时,本国货币长期内将趋向于升值。然而应注意的是,由于异质性环境的存在,人民币汇率对产出缺口的响应在不同的时点下会产生非一致的结果。其中,2008年国际金融危机爆发后,我国对人民币汇率制度做出了与美元紧密挂钩的“稳定化安排”。无独有偶,汇率预期对即期汇率的影响与产出缺口冲击下的动态走势基本相似,且汇率贬值预期在短期内会加剧汇率的进一步贬值,并呈现“相互印证、相互实现”的特点;但从长期来看,汇率贬值预期的格局并不能持续,这在一定程度上与外部冲击有关。⑥从货币当局的实践操作经验来看,一旦人民币汇率形成贬值预期并进一步加剧汇率贬值时,货币当局会实施冲销式干预操作进行调控,特别是在外汇市场上卖出外汇并回笼人民币资产以遏制人民币汇率的进一步贬值,伴随着货币当局冲销式干预效果的逐渐显现,人民币汇率的贬值预期会得到抑制。
(三)不同时期下的实证结果
为了比较包含国际资本流动的泰勒规则与人民币汇率的联动效应在不同时期下的潜在差异,我们将预测步长设定为h={1,2,3},并以此从相对视角刻画不同提前期下的脉冲响应走势,⑦其结果如图3所示。我们发现,国际资本流动对汇率的冲击(
进一步从泰勒规则中的核心变量对汇率的冲击效应来看,人民币利率的相对提高倾向于引发人民币兑美元汇率升值,这与不同时点下汇率对利差的响应结果保持一致。需要指出的是,在2008—2014年间,利差对汇率的冲击效应明显回落,但随后又开始快速增大,且一直持续至样本期末。这可能与2014年3月央行扩大人民币兑美元汇率的波动幅度后,人民币兑美元汇率的弹性增强有关。同时,我国货币政策的调控框架也积极地从数量型向价格型转变,此时汇率对利差的响应增强也在一定程度上可以说明价格型货币政策在维持人民币汇率水平的基本稳定上具有一定的有效性,而且伴随人民币汇率形成机制的不断完善以及我国货币政策调控框架的不断成熟,利率政策在外汇市场上调控的有效性将会进一步增强。
需要指出的是,在不同时期,包含国际资本流动的泰勒规则都能够稳健地刻画通胀与汇率之间的动态机制,且通货膨胀差的相对变大会引发人民币汇率升值。除了2008—2011年期间外,通胀差对汇率的冲击效应在短期内表现为正,其余样本期内则表现为负向效应。该结果表明,在2008—2011年间,中国通货膨胀的相对增加在短期内会导致人民币汇率贬值。这是因为,受全球金融危机的影响,美国出台了多轮量化宽松政策并通过向市场注入流动性的形式刺激经济增长,而在此期间有大量的外资流入中国,此时中国的通货膨胀逐渐显现。正如前文所言,为抑制资本进一步流入国内并造成不利冲击,决策当局将会采取入市干预的形式进行逆向冲销操作,此时人民币汇率升值的态势不断弱化,甚至会出现贬值预期并进而引发即期汇率贬值的态势。这与前文在不同时点下的脉冲响应结果相印证,其潜在机制可由泰勒规则的本质思想所解释,即当国内出现偏离均衡水平的通胀时,货币当局会通过采取提高利率的方式来收紧银根,并以此降低流动性,此时利率的提高将会助推人民币汇率的升值。
在包含国际资本流动的泰勒规则模型中,当中国产出缺口相对美国增加时,在三个不同提前期下,人民币汇率均呈现贬值态势。这一结果与前文不同时点下汇率在前8期内表现为正向响应的结论相印证,其潜在的原因可能为,当中国产出增速相对美国较高时,通常会伴随相对较高的通货膨胀率,因此人民币名义汇率表现为贬值态势。需要指出的是,在2015—2016年期间,产出缺口对汇率的冲击效应还具有下降的趋势,但随后产出缺口对汇率的冲击又进一步增大。其原因还可归结为2015年8月所进行的人民币汇率报价机制改革,虽然这次改革提高了人民币汇率的市场化程度,但在这一过程中,贬值预期的不断强化加剧了人民币汇率变动。伴随着货币当局政策调控的逐渐奏效,人民币汇率贬值预期的态势也有所弱化,预期的平稳格局使得经济基本面对汇率变动的冲击仍然发挥着主导作用,而且该结果还验证了经济基本面是影响汇率变动的长期决定因素。
还需提及的是,提前1期的汇率贬值预期冲击会导致即期汇率贬值,而提前2期和3期的贬值预期冲击则会导致即期汇率升值,这进一步印证了不同时点下的脉冲响应结果不同。而从时变视角来看,在2015年之前,提前1期的贬值预期对汇率的冲击效应最大,提前2期和3期的冲击效应均较小,而之后提前3期的贬值预期的冲击效应显著增大。这些结果意味着,汇率预期对即期汇率的影响在2015年前主要表现为短期影响;而在2015年后,该影响的持续性和强度均有所增加。这一结果背后所隐含的潜在原因可概述为:自2015年“8•11”汇改之后,人民币汇率的形成机制更加市场化,而这会使得汇率预期在即期汇率的动态决定中所发挥的作用更加重要,同时也会使得汇率预期对即期汇率的影响具有长期性。
五、结论与启示
本文以泰勒规则货币政策为研究框架,并内生地植入国际资本流动以考察汇率动态决定机制。理论分析表明,国际资本流动、汇率预期、利差、通胀差、产出缺口差对即期汇率的影响均取决于利率平滑操作程度,以及本国与外国货币政策对汇率偏离的相对敏感程度,而且国际资本流动、产出缺口差及通胀差对汇率的影响还与货币政策的反应程度有关。此外,在不同的时点及时期下,本国与外国货币当局不仅在货币政策的平滑操作上会发生变化,而且两国货币政策在锚定汇率与国际资本流动的方向与力度上也可能因时而异,这表明包含国际资本流动的泰勒规则对汇率的影响很有可能具有时变性特征。
鉴于此,本文以2005年7月至2018年10月为研究样本期,采用TVP-SV-BVAR模型分别从不同时点和不同时期的双重视角实证刻画了包含国际资本流动的泰勒规则对人民币汇率影响的特征。实证研究表明,包含国际资本流动的泰勒规则对人民币汇率的影响具有显著的时变性特征,且包含国际资本流动的泰勒规则在短期和长期视角下对汇率变动的影响具有显著的异质性,具体表现为:(1)国际资本流入以及利差扩大在短期和长期内均会助推人民币汇率升值,但短期影响大于长期影响,且该影响在2015年“汇改”后明显增强;(2)通胀率相对上升在短期和长期内均会引发人民币汇率升值,但该效应在大多数时期内相对较小,仅在样本期末有所增强;(3)产出相对增加在短期内会引发人民币贬值,但长期内会助推人民币升值,而且相对于其他变量,产出缺口差对汇率的影响最大,且在大多数样本期内均较为稳定;(4)汇率预期对人民币即期汇率的影响在短期内为正向,但长期内会因为货币当局进行外汇干预而变为负向,且该影响的持续性和强度在2015年“汇改”后也明显增加。
基于上述研究结论,本文可以得到以下政策启示:第一,考虑国际资本流动的货币政策规则能够有效锚定汇率的动态变化,因此中国在推进资本账户开放的过程中,货币政策对于汇率的锚定应注重防范国际资本流动的急剧变动及其对汇率所产生的不利冲击,这有利于提高货币政策调控的有效性。第二,由于国际资本流动的异常剧烈波动会对人民币汇率及经济稳定产生重要的不利冲击,并且考虑到资本账户的进一步开放会对国际资本流动产生更加深刻的影响,因此决策当局对国际资本流动要实施一体化监管,避免出现大规模资本流动而形成风险甚至危机,否则将不利于我国经济的平稳健康增长。第三,为抑制国际资本流入所引起的通货膨胀,并弱化其对外汇市场的冲击,货币当局可考虑将包含国际资本流动的泰勒规则作为逆周期调控的一种思路框架和参照系。特别地,由于包含国际资本流动的泰勒规则能够同时锚定通胀与汇率,因而能为货币当局稳定经济环境并进而推进汇率和利率市场化具有重要的启示。第四,由于维持经济的平稳增长并合理引导预期能够避免人民币汇率的剧烈波动,因此,当局在完善货币政策调控时,可考虑在货币政策规则中纳入预期因子,这有利于提高货币政策操作的前瞻性,避免偏离基本面而出现“超调”及多重市场均衡的情形,进而完善货币政策调控体系。
① 早在19世纪末,瑞典经济学家魏克塞尔(Wicksell, 1898)提出魏克塞尔利率规则,认为政策目标利率需围绕均衡利率波动,这一理论被瑞典国家银行于1931年采纳;Friedman(1968)提出弗里德曼规则,认为应采取与潜在产出增速相等的单一固定货币供给规则;在此基础上,McCallum(1987)提出麦卡勒姆规则,认为基础货币增长率应根据目标名义GDP增长率、货币流通速度变化进行调整。20世纪80年代金融创新和金融脱媒的迅速发展也对货币数量规则带来了巨大挑战。理论和实践的双重挑战使各国中央银行在20世纪80年代中期开始逐步放弃货币数量目标制。
② 我们也可假设国外货币当局对通胀、产出缺口反应与国内不一致,虽然模型形式会发生变动,但并不影响研究结论。因此,我们基于“简单模型说明问题”的原则,做出“国外货币当局对通胀、产出缺口反应与国内一致”的假设。
③ 限于篇幅,我们未报告TVP-SV-BVAR的具体公式,感兴趣的读者可向作者索取。
④ 当通货膨胀差受到1单位的正向冲击时,人民币汇率的响应路径仍大致呈现为逆“驼峰”形,最大响应值发生在第5期,约为−0.016,并于第16期收敛至稳态。
⑤ 当利差受到1个单位的正向冲击时,人民币汇率会表现出升值态势,且最大响应值发生在第4期,约为−0.015,并于第17期收敛至稳态。
⑥ 面对2009年8月这一时点下1个单位的汇率预期正向冲击(即贬值预期冲击)时,人民币即期汇率的响应在短期和长期内均表现为正向响应;而在最近的两个时点下,人民币即期汇率的响应先是表现为正,最大响应值发生在第1.5期,约为0.010,但在第2期后开始转为负向响应。
⑦ 在划分短期、中期和长期的依据上,不同学者所选取的步长不尽相同。本文设定预测步长h={1,2,3},并意指短期、中期和长期,是从相对意义而言的。
| [1] | 查尔斯•恩格尔. 关于国际资本流动管理和汇率政策的几点思考[J]. 经济学(季刊), 2019(1): 415–440. |
| [2] | 陈创练, 杨子晖. " 泰勒规则”、资本流动与汇率波动研究[J]. 金融研究, 2012(11): 60–73. DOI:10.3969/j.issn.1009-4350.2012.11.018 |
| [3] | 陈平, 李凯. 人民币汇率与宏观基本面: 来自汇改后的证据[J]. 世界经济, 2010(9): 28–45. |
| [4] | 范立夫. 我国利率政策与汇率政策协调问题研究——基于资产加权收益率平价模型的分析[J]. 财贸经济, 2011(7): 48–54. DOI:10.3969/j.issn.1005-913X.2011.07.029 |
| [5] | 江春, 刘春华. 利率平价理论的分析与探讨[J]. 经济管理, 2007(20): 18–23. |
| [6] | 江春, 司登奎, 李小林. 基于拓展泰勒规则汇率模型的人民币汇率动态决定: 理论分析与经验研究[J]. 金融研究, 2018a(2): 82–99. |
| [7] | 江春, 司登奎, 李小林. 泰勒规则、股价波动与人民币汇率动态决定[J]. 国际金融研究, 2018b(1): 65–74. |
| [8] | 李小林, 司登奎, 江春. 扩展型泰勒规则与人民币汇率变动: 理论机理与实证检验[J]. 统计研究, 2018(3): 14–22. |
| [9] | 潘锡泉. 中美利率和汇率动态效应研究: 理论与实证——基于拓展的非抛补利率平价模型的研究[J]. 国际贸易问题, 2013(6): 76–87. |
| [10] | 司登奎, 江春, 李小林. 基于汇率预期与央行外汇干预的汇率动态决定: 理论分析与经验研究[J]. 统计研究, 2016(9): 13–21. |
| [11] | 司登奎, 李小林, 江春. 央行外汇干预、投资者情绪与汇率变动[J]. 统计研究, 2018(11): 58–70. |
| [12] | 司登奎, 李小林, 张仓耀. 分位数单位根检验的拓展及其应用研究[J]. 统计研究, 2017(5): 102–117. |
| [13] | 张明. 中国面临的短期国际资本流动: 不同方法与口径的规模测算[J]. 世界经济, 2011(2): 39–56. |
| [14] | 周爱民, 遥远. 资本流动对实际汇率的结构性冲击[J]. 世界经济研究, 2015(10): 3–12. |
| [15] | 朱孟楠, 刘林. 短期国际资本流动、汇率与资产价格——基于汇改后数据的实证研究[J]. 财贸经济, 2010(5): 5–13. |
| [16] | Caballero R J, Krishnamurthy A. Bubbles and capital flow volatility: Causes and risk management[J]. Journal of Monetary Economics, 2006, 53(1): 35–53. DOI:10.1016/j.jmoneco.2005.10.005 |
| [17] | Engel C, West K D. Exchange rates and fundamentals[J]. Journal of Political Economy, 2005, 113(3): 485–517. DOI:10.1086/429137 |
| [18] | Evans M D D, Lyons R K. Meese-Rogoff redux: Micro-based exchange-rate forecasting[J]. American Economic Review, 2005, 95(2): 405–414. DOI:10.1257/000282805774669934 |
| [19] | Filer II L H. Large capital inflows to Korea: The traditional developing economy story?[J]. Journal of Asian Economics, 2004, 15(1): 99–110. DOI:10.1016/j.asieco.2003.11.002 |
| [20] | Franta M, Horvath R, Rusnak M. Evaluating changes in the monetary transmission mechanism in the Czech Republic[J]. Empirical Economics, 2014, 46(3): 827–842. DOI:10.1007/s00181-013-0699-0 |
| [21] | Friedman M. The role of monetary policy[J]. The American Economic Review, 1968, 58(1): 1–17. |
| [22] | McCallum B T. The case for rules in the conduct of monetary policy: a concrete example[J]. Weltwirtschaftliches Archives, 1987, 123(3): 415–429. DOI:10.1007/BF02707752 |
| [23] | Mark N C. Changing monetary policy rules, learning, and real exchange rate dynamics[J]. Journal of Money, Credit and Banking, 2009, 41(6): 1047–1070. DOI:10.1111/jmcb.2009.41.issue-6 |
| [24] | Meese R A, Rogoff K. Empirical exchange rate models of the seventies: Do they fit out of sample?[J]. Journal of International Economics, 1983, 14(1-2): 3–24. DOI:10.1016/0022-1996(83)90017-X |
| [25] | Meese R A, Rogoff K, Frenkel J. The out-of-sample failure of empirical exchange rate models: Sampling error or misspecification?[M]. Exchange Rates and International Macroeconomics, Chicago: University of Chicago Press and NBER, 1983. |
| [26] | Obstfeld M, Rogoff K. The six major puzzles in international macroeconomics: Is there a common cause?[R]. NBER Working Paper, No. 7777, 2000. |
| [27] | Primiceri G E. Time varying structural vector autoregressions and Monetary Policy[J]. The Review of Economic Studies, 2005, 72(3): 821–852. DOI:10.1111/j.1467-937X.2005.00353.x |
| [28] | Taylor J B. Discretion versus policy rules in practice[J]. Carnegie-Rochester Conference Series on Public Policy, 1993, 39: 195–214. DOI:10.1016/0167-2231(93)90009-L |
| [29] | Wicksell K. Interest and prices[M]. London: MacMillan Press, 1898. |


