
2019第45卷第7期
2. 清华大学 中国经济社会数据研究中心,北京 100084;
3. 北京师范大学 统计学院,北京 100875
2. China Data Center,Tsinghua University,Beijing 100084,China;
3. School of Statistics,Beijing Normal University,Beijing 100875,China
一、引 言
随着中国特色社会主义进入新时代,我国社会主要矛盾已经转化为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾。当前,我国区域发展的不平衡不充分,正是这一主要矛盾在发展空间布局方面的具体表现。为此,党的十九大报告首次提出了要实施区域协调发展战略。其中,缓解区域收入差距不仅是实现区域协调发展战略的主要内容,也是实现社会主义社会共同富裕的本质特征。与多数工业化国家的发展历程相似,改革开放和社会主义市场经济体制的建立在促进我国经济发展的同时,也使财富空前累积。同时,受不同地区历史条件、自然环境和政策差异等因素的影响,我国区域发展不平衡与区域收入差距矛盾不断恶化。根据人口加权估算的我国四大区域人均GDP变动趋势显示,自20世纪90年代初期以来,伴随我国实施全方位对外开放战略与社会主义市场经济体制的进一步确立,我国东、中、西部及东北地区人均GDP呈增速上涨趋势。但是,不同区域人均GDP的增速变化不一。东部地区显著高于其他区域。其中,2016年中部、西部、东北地区的人均GDP分别相当于东部地区的56.49%、54.11%和62.01%;居民人均可支配收入分别相当于东部地区的65.29%、59.94%和72.96%。以赫芬达尔—赫希曼指数(Herfindahl-Hirschman Index,HHI)刻画的地区经济差距从20世纪90年代起快速上涨。虽然,受国际金融危机的影响,HHI指数自2007年以来有所下降,但是依然处于相对高位。大量研究显示,区域收入差距已成为我国整体收入差距的重要内容(李实等,2008),是阻碍我国区域协调发展,实现共同富裕的主要矛盾之一。
已有文献从教育投入、要素禀赋、市场开放、金融发展及税收等多个角度对导致区域收入差距扩大的原因进行了研究,均得到上述因素与区域收入差距扩大且具有显著相关性的结论。然而,相比其他因素,教育或是影响我国区域收入差距不断扩大的最重要的因素−根据巴黎经济学院发布的2018年《世界不均等报告》,总结各国自20世纪80年代以来收入差距演变的历史经验发现,教育是导致包括发达国家和发展中国家收入差距扩大的主要原因。其中,增加教育投入、改革教育政策、促进受教育机会平等性是避免各国收入与贫富差距加剧的关键政策。然而,在探讨教育对收入差距影响的具体机制方面,存在两种截然不同的观点:一种基于新古典理论框架,指出在市场经济条件下,只要存在区域收入差距和就业机会差异,人力资本和劳动力就不可避免地从边际劳动生产率低的地区向边际劳动生产率高的地区流动,从而提高经济效率,缩小区域间收入差距(姚枝仲和周素芳,2003;王小鲁,2004;Heuchemer,2016);一种基于新经济地理学理论框架,研究认为教育促进人力资本积累并流动,会导致人力资本集聚和地区间人力资本存量差异的不断增大,从而恶化地区间收入差距,甚至造成收入差距的持续扩大与恶性循环(De Gregorio和 Lee,2002;许召元和李善同,2006;杨俊等,2008;Coady和Dizioli,2017)。针对上述研究,本文拟从以下两方面对已有文献进行改进:
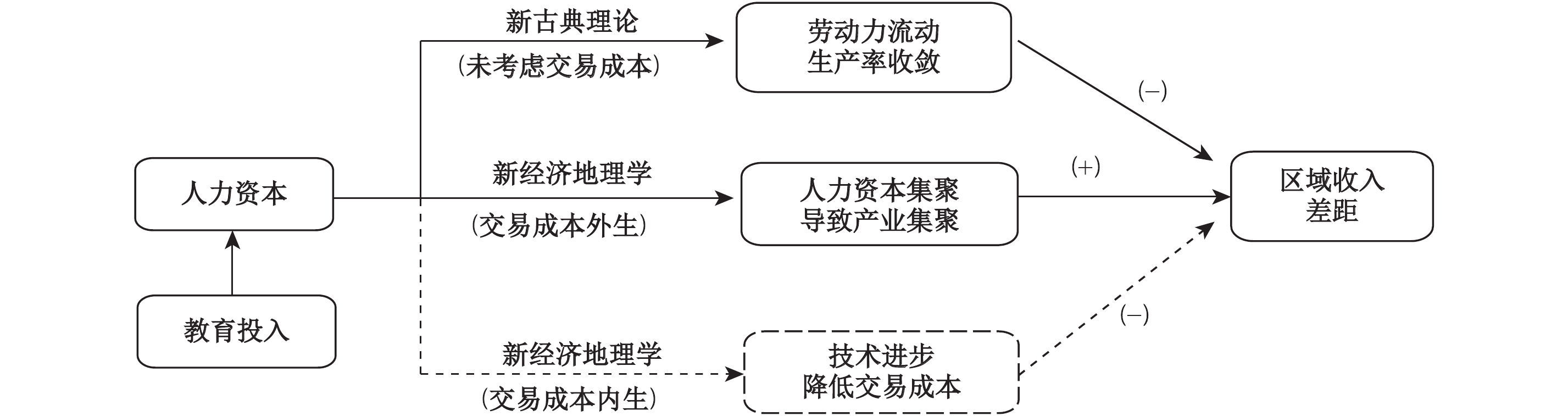
第一,针对文献指出,教育对区域收入差距的影响是不确定的,存在两种不同的作用机制。一是基于新古典理论,在不考虑交易成本的情况下,研究教育通过增加人力资本积累从而提高劳动生产率水平,在促进劳动者流动的同时缩小了区域间收入差距;一是基于新经济地理学理论,在引入外生交易成本的情况下,研究教育通过增加人力资本积累导致产业集聚,从而扩大了区域收入差距。在两种理论机制下,教育对区域收入差距的影响效果并不相同。本文基于新经济地理学理论框架,在前人研究基础上,通过放松有关交易成本外生的假设,将其作为内生因素引入一般均衡框架,并采用中介效应模型实证检验了教育对区域收入差距的影响机制。得到了前者能通过促进技术进步降低交易成本,从而有利于缩小区域收入差距的结论。以往文献仅将“交易成本”视为简单的运输成本,因此在模型框架中外生处理。然而,“交易成本”泛指除直接生产之外,为促成交易发生而形成的所有成本。既包括产品销售过程中所发生的实际运输费用等显性成本,也包括地区贸易保护壁垒和市场分割等形成的各种隐性成本,还包括产品生产过程中阻碍劳动力、资本和土地等生产要素在区域间合理自由流动的各种体制性障碍。因此,简单将“交易成本”视为运输成本会低估交易成本对区域收入差距的影响。本研究完善了新经济地理学有关教育对区域收入差距影响的研究,为在该理论体系下讨论两者的关系提供了一个新的可能视角,并进一步澄清了无论基于新古典理论框架还是新经济地理学理论框架,教育有助于促进人力资本积累并缩小区域收入差距是一个较强且稳健的结论。(见图1)
|
| 图 1 有关人力资本因素对区域收入差距研究的机制概述 |
第二,针对文献指出,地区间教育投入差异是导致地区间收入差距扩大的主要原因。本文从理论推导与实证检验两方面证明了教育投入的地区差异并不会导致区域收入差距的扩大,即教育投入对缓解区域收入差距不存在空间异质性。①但不同地区教育投入的增加会对缩小区域间收入差距产生不同程度的影响。相比较而言,增加低收入地区教育投入对缓解区域收入差距的效果更加显著。因此,教育投入对缓解区域收入差距可视为一种帕累托改进。更进一步,在比较各级教育投入对区域收入差距影响后发现,义务教育相对于其他各级教育对缓解区域收入差距的作用更加显著。
二、理论模型
本文通过将教育因素引入Krugman(1991)新经济地理学理论框架,并在此基础上内生化区域交易成本,探讨教育投入对区域收入差距的不同作用机制。
(一)消费者需求。假定消费者对差异化产品显示多样性偏好,其效用函数取决于消费产品的数量及种类。消费者效用函数满足以下柯布-道格拉斯(C-D)效应函数形式:
| $U = C_M^\pi C_N^{1 - \pi },0 < \pi < 1$ | (1) |
其中:CN表示农产品的消费量。CM表示消费者消费的不同工业产品组合的数量指数。设其为不变替代弹性(Constant Elasticity of Substitution,CES)效应函数:
| $\text{消费者预算月数为:}{P_N}{C_N} + \mathop \sum \nolimits_{i = 1}^n {p_i}{c_i} = Y$ | (2) |
其中:Y为收入水平,PN为农产品价格,pi为第i种工业产品价格。
求解消费者效用最大化可转化为求解消费CM成本最小化问题。也即:
| $Min \mathop \sum \nolimits_{i = 1}^n {p_i}{c_i},s.t.{\left[\mathop \sum \nolimits_{i = 1}^n c_i^{\textstyle\frac{{\sigma - 1}}{\sigma }}\right]^{\textstyle\frac{\sigma }{{\sigma - 1}}}} = {C_M}$ | (3) |
构造拉格朗日函数,求解一阶条件,可解得:
| $\begin{aligned} {C_M} = {\left[\displaystyle\mathop \sum \nolimits_{i = 1}^n {\left( {{c_j}{{[\frac{{{p_i}}}{{{p_j}}}]}^{ - \sigma }}} \right)^{\textstyle\frac{{\sigma - 1}}{\sigma }}}\right]^{\textstyle\frac{\sigma }{{\sigma - 1}}}} = {c_j}{p_j}^\sigma {\left( {\mathop \sum \nolimits_{i = 1}^n {p_i}^{1 - \sigma }} \right)^{\textstyle\frac{\sigma }{{\sigma - 1}}}}; \; {c_j} = {p_j}^{ - \sigma }{\left( {\mathop \sum \nolimits_{i = 1}^n {p_i}^{1 - \sigma }} \right)^{\textstyle\frac{\sigma }{{1 - \sigma }}}}{C_M} \end{aligned}$ |
定义
| $Max U = C_M^\pi C_N^{1 - \pi },s.t.{P_M}{C_M} + {P_N}{C_N} = Y$ | (4) |
| ${C_N} = \frac{{\left( {1 - \pi } \right)Y}}{{{P_N}}},{C_M} = \frac{{\pi Y}}{{{P_M}}},{c_i} = {p_i}^{ - \sigma }P_M^\sigma {C_M}$ | (5) |
选择合适的度量单位可省去常数项,将消费者对第i种工业品的需求函数表示为:xi=pi−σ。其中:xi为第i种工业产品需求量,pi为其价格。
(二)生产者供给。假设一个经济体包含两个地区:A和B。每个地区均拥有传统农业生产部门和现代非农生产部门(或称工业生产部门),分别生产农产品和工业品。假定农业生产部门生产同质产品,生产技术为规模报酬不变,市场结构为完全竞争。工业生产部门生产差异化工业产品,且每种工业产品的生产都具有规模经济,市场结构为垄断竞争。其中,农业劳动力在A、B两个地区均匀分布且不可流动。由于农业部门的生产技术具有规模报酬不变特征,假设单位农产品产出需要单位农业劳动力投入。又由于农业部门是完全竞争部门,两个地区的农产品价格相等。为简化分析,将农产品视为计价物,两个地区的价格均为1个单位。根据要素最优使用原则,一单位劳动力投入的边际产品价值等于一单位劳动投入的工资报酬,可得:PN=WN=1。其中:PN和WN分别表示农产品价格和农业劳动力工资水平,且当整个农产品市场出清时,农产品供给等于需求。
相比之下,工业部门的劳动力在A、B两个地区之间可相互流动,且在A、B两个地区的初始配置数量分别为LA和LB。参考赵伟和李芬(2007)的研究,假设教育投入通过人力资本积累和知识技术外溢效应提高劳动生产率,使得系统中有效劳动力的占比提高,则A、B两个地区工业部门的有效劳动力数量或人力资本分别为HA=LAEA和HB=LBEB,其中HA、HB和EA、EB分别表示A、B两个地区的人力资本和教育投入。
在此,本文使用生产中存在固定成本来刻画生产技术的规模收益递增特征。②即厂商扩大生产会促进单位产出固定成本的降低,从而使得平均成本随产出增加而减少,实现生产技术的规模报酬递增。假设生产每种工业品的固定成本和边际成本都相同,反映劳动和产出关系的生产函数可用如下线性成本函数可表示为li=α+βxi。其中:li表示生产第i种工业品所需要的有效劳动力投入量,xi为第i种工业品的产出量。α是以有效劳动力投入为度量的固定成本,β为边际成本。
由于有许多潜在的工业制造品,且每一种工业产品的生产都存在规模经济,因此厂商倾向于生产自身具有相对比较优势的产品,即各自生产不同种类的异质性产品,生产过程具有垄断性。假定每个厂商与产品存在一一对应关系,企业数量等于产品种类数,整个产品市场上消费品种类多种多样。
地区A第i个厂商利润函数为:πAi=pAixAi-wA(α+βxAi),其中wA为地区A工业部门单位有效劳动力的工资水平。且地区A第i个厂商利润最大化的供给决策和价格决策满足下列条件:
| $Max \{ {p_{Ai}}{x_{Ai}} - {w_A}\left( {\alpha + \beta {x_{Ai}}} \right)\} ,s.t.{x_{Ai}} = {p_{Ai}}^{ - \sigma }$ | (6) |
假设地区A第i个垄断厂商最优定价策略满足“边际成本加成定价法”,也即
| ${n_A} = \frac{{{L_A}{E_A}}}{{{l_i}}} = \frac{{{L_A}{E_A}}}{{\alpha + \beta x}} = \frac{{{L_A}{E_A}}}{{\alpha \sigma }} = \frac{{{H_A}}}{{\alpha \sigma }},{n_B} = \frac{{{L_B}{E_B}}}{{{l_i}}} = \frac{{{L_B}{E_B}}}{{\alpha + \beta x}} = \frac{{{L_B}{E_B}}}{{\alpha + \beta x}} = \frac{{{H_B}}}{{\alpha \sigma }}$ | (7) |
综上,工业产品种类数n是一个内生变量,与产品替代弹性和有效劳动力地区分布有关。一方面,不同工业品之间替代弹性越小,消费者多样性偏好程度越大,工业品种类数就越多。另一方面,由于假设每一种工业产品的生产函数和面对的需求曲线相同,故每个厂商投入的有效劳动力和产出量都相等,每个地区工业厂商个数或产品种类数与有效劳动力数量或人力资本成正比,即有效劳动力数量或人力资本越多的地区产品种类数也越多。因此,生产企业的空间分布等价于人力资本的空间分布,地区间人力资本的流动就意味着生产企业的转移。
(三)交易成本和区域均衡条件。为简化分析,假设两个地区之间农产品贸易没有成本,农产品价格和农业劳动力工资水平在两个地区没有差别。同时假设,同一区域内工业品贸易也没有交易成本,而两个地区间工业产品的贸易存在交易成本,参考萨缪尔森“冰山成本”对其进行刻画。也即,如果1单位产品从地区A运输到地区B,则只剩下τ单位(其中,τ<1),其余(1−τ)单位产品在运输途中被“融化”掉。③为了补偿运输过程中存在的损失,厂商在地区B就要制定更高的销售价格,如地区A售价为1个单位的产品在地区B价格将提高到
教育投入通过增加整个社会的人力资本积累,对促进技术进步发挥重要作用。而技术进步一方面可以通过改善区域间交通物流条件直接降低区域间运输成本;另一方面可以通过解决信息不对称问题,降低搜寻成本、谈判成本和履约成本来改善区域间贸易环境间接降低交易成本。
第一,教育投入通过促进技术的创新和发展,能够降低显性的交通运输成本。一方面,技术进步使得高铁等交通基础设施条件得到大幅改善,在降低运输成本的同时也促进了产品跨区域流动与区域间贸易。另一方面,互联网+交通平台技术,能够通过为物流运输服务的需求者和供给者提供大数据匹配信息解决信息不对称的问题,从而降低运输成本,提高生产效率。
第二,教育投入通过促进技术的创新和发展,打破了地区封锁和垄断等体制障碍,改善了市场环境,间接降低了交易成本。区域市场封锁和地方保护主义等体制障碍会妨碍产品和要素的跨区域流动,导致市场分割。然而,随着移动互联网、大数据、云计算等现代信息通讯技术的快速发展,网络购物、移动支付、共享经济等新业态、新模式蓬勃发展,许多产品(尤其是服务)从原本的“不可贸易”根本性地转变为“可贸易”,对推动区域间市场一体化发挥了重要作用。同时,微信、支付宝的广泛使用对传统通讯和金融等垄断行业形成了巨大冲击,逐渐倒逼原有的不合理制度进行改革,可见,技术进步对整个社会交易成本的降低发挥了重要作用。
鉴于增加系统中的教育投入可以促进技术进步,而技术进步一方面可以通过改善区域间交通物流条件直接降低区域间运输成本,另一方面可以通过降低搜寻成本、谈判成本和履约成本来改善区域间贸易环境间接降低交易成本。因此,设定
地区A和地区B的消费者面对的工业品价格指数分别为:
| ${P_A} = {\left[{n_A}{p_{Ai}}^{1 - \sigma } + {n_B}{\left(\frac{{{p_{Bi}}}}{\tau }\right)^{1 - \sigma }}\right]^{1/\left( {1 - \sigma } \right)}},{P_B} = {\left[{n_A}{\left(\frac{{{p_{Ai}}}}{\tau }\right)^{1 - \sigma }} + {n_B}{p_{Bi}}^{1 - \sigma }\right]^{1/\left( {1 - \sigma } \right)}}$ | (8) |
将工业产品种类数和价格表达式代入,并简化部分常量后可得:
| ${P_A} = {\left[{L_A}{E_A}{w_A}^{1 - \sigma } + {L_B}{E_B}{\left(\frac{{{w_B}}}{\tau }\right)^{1 - \sigma }}\right]^{1/\left( {1 - \sigma } \right)}},{P_B} = {\left[{L_A}{E_A}{\left(\frac{{{w_A}}}{\tau }\right)^{1 - \sigma }} + {L_B}{E_B}{({w_B})^{1 - \sigma }}\right]^{1/\left( {1 - \sigma } \right)}}$ | (9) |
假定:消费者面对的全部消费品的总价格指数是农产品与工业产品价格的几何平均,因此,地区A和地区B的完全价格指数可分别表示为:
| ${p_A} = P_A^\pi {P_N}^{\left( {1 - \pi } \right)} = P_A^\pi ,{p_B} = P_B^\pi {P_N}^{\left( {1 - \pi } \right)} = P_B^\pi $ | (10) |
以货币购买力反映的两地区单位有效劳动力的实际工资分别为:
| ${\omega _A} = \frac{{{w_A}}}{{{p_A}}} = \frac{{{w_A}}}{{P_A^\pi }} = {{{w_A}}}\biggr/{{{{\left[{L_A}{E_A}{w_A}^{1 - \sigma } + {L_B}{E_B}{{\left(\displaystyle\frac{{{w_B}}}{\tau }\right)}^{1 - \sigma }}\right]}^{\pi /\left( {1 - \sigma } \right)}}}}$ | (11) |
| ${\omega _B} = \frac{{{w_B}}}{{{p_B}}} = \frac{{{w_B}}}{{P_B^\pi }} = {{{w_B}}}\biggr/{{{{\left[{L_A}{E_A}{{\left(\displaystyle\frac{{{w_A}}}{\tau }\right)}^{1 - \sigma }} + {L_B}{E_B}{{({w_B})}^{1 - \sigma }}\right]}^{\pi /\left( {1 - \sigma } \right)}}}}$ | (12) |
地区间工资差距为:
| $\frac{{{\omega _A}}}{{{\omega _B}}} = \frac{{{w_A}}}{{{w_B}}}{{{{\left[{L_A}{E_A}{{\left(\displaystyle\frac{{{w_A}}}{\tau }\right)}^{1 - \sigma }} + {L_B}{E_B}{{({w_B})}^{1 - \sigma }}\right]}^{\pi /\left( {1 - \sigma } \right)}}}}\biggr/{{{{\left[{L_A}{E_A}{w_A}^{1 - \sigma } + {L_B}{E_B}{{\left(\displaystyle\frac{{{w_B}}}{\tau }\right)}^{1 - \sigma }}\right]}^{\pi /\left( {1 - \sigma } \right)}}}}$ | (13) |
为更加直观地刻画教育投入、交易成本与地区收入差距之间的关系,本文对经济系统做进一步简化。由于两个地区各种工业产品生产函数均相同,故假定两个地区每单位工业有效劳动力的边际产出相同、名义工资也相等。若将名义工资标准化为1个单位,则两地区实际工资和地区间工资差距的表达式为:
| ${\omega _A} = {[{L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}}]^{\pi /\left( {\sigma - 1} \right)}},{\omega _B} = {[{L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B}]^{\pi /\left( {\sigma - 1} \right)}}$ | (14) |
| $\frac{{{\omega _A}}}{{{\omega _B}}} = \frac{{{{[{L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B}]}^{\pi /\left( {1 - \sigma } \right)}}}}{{{{[{L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}}]}^{\pi /\left( {1 - \sigma } \right)}}}}$ | (15) |
可以看出,地区A和地区B的实际工资及地区间的工资差距均与两个地区的工业劳动力数量、教育投入、地区间交易成本有关,④即与人力资本的地区分布和交易成本相关。短期看,可以认为各地区人力资本的空间分布是给定的。长期看,劳动力在地区间的流动和教育投入的变化会导致人力资本的空间分布发生变化,或会改变各地区的实际收入和地区间收入差距。
(四)教育投入影响区域收入差距的作用机制。
命题1 :交易成本是导致地区间收入差距扩大的主要诱因。
证明:由于地区间交易成本的存在,厂商为补偿该部分损失将通过在非生产地区制定更高的产品销售价格,将交易成本转嫁给消费者。因此,交易成本的存在会降低各地区消费者的实际收入(如式(16)、(17)所示)。然而,人力资本高的核心地区生产的消费品种类和数量相对较多,需从其他边缘地区输入的产品较少,故消费者所承担的交易成本比人力资本或产品种类相对稀缺的地区要小,即生活成本相对较低,以货币购买力衡量的实际收入相对较高,从而导致地区间收入差距扩大(如式(18)、(19)所示)。交易成本导致的价格指数效应或生活成本效应对人力资本和产业形成巨大吸引力,促使其不断向核心区集聚,从而导致核心区(高收入地区)形成“低交易成本−人力资本集聚(产业集聚)−实际收入增加的”循环累积因果,进而促进高收入地区收入上涨,扩大了区域间收入差距(如式(20)所示)。因此,交易成本或是影响区域收入差距形成并进一步扩大的主要矛盾。
| $\frac{{\partial {\omega _A}}}{{\partial \left( {1 - \tau } \right)}} = \frac{{\partial {\omega _A}}}{{\partial \left( \tau \right)}}\frac{{\partial \left( \tau \right)}}{{\partial \left( {1 - \tau } \right)}} = - \pi {\tau ^{\sigma - 2}}{({L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_B}{E_B}{\rm{ < 0}}$ | (16) |
| $\frac{{\partial {\omega _B}}}{{\partial \left( {1 - \tau } \right)}} = \frac{{\partial {\omega _B}}}{{\partial \left( \tau \right)}}\frac{{\partial \left( \tau \right)}}{{\partial \left( {1 - \tau } \right)}} = - \pi {\tau ^{\sigma - 2}}{({L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_A}{E_A}{\rm{ < 0}}$ | (17) |
| $\frac{{\partial {\omega _B}}}{{\partial \left( {1 - \tau } \right)}}\bigg/\frac{{\partial {\omega _A}}}{{\partial \left( {1 - \tau } \right)}} = \frac{{\partial {\omega _B}}}{{\partial \left( \tau \right)}}\bigg/\frac{{\partial {\omega _A}}}{{\partial \left( \tau \right)}} = \frac{{{{({L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B})}^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_A}{E_A}}}{{{{({L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}})}^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_B}{E_B}}}{\rm{ > 1}}$ | (18) |
| $\frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( {1 - \tau } \right)}} = \frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( \tau \right)}}\frac{{\partial \left( \tau \right)}}{{\partial \left( {1 - \tau } \right)}} = - \frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( \tau \right)}} > 0$ | (19) |
| $\frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( {{H_A}} \right)}} = \frac{\pi }{{1 - \sigma }}{\left(\frac{{{L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B}}}{{{L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}}}}\right)^{{\textstyle\frac{\pi }{{1 - \sigma }}} - 1}}\frac{{{L_B}{E_B}\left( {{\tau ^{2\left( {\sigma - 1} \right)}} - 1} \right)}}{{{{({L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}})}^2}}} > 0$ | (20) |
数值模拟也在一定程度上印证了以上理论推导结论的成立。假设,先天自然地理条件、历史社会变革等外生因素的空间差异使得地区间人力资本的初始状态不同。人力资本在A、B地区的集聚比例分别为hA、hB,hA+hB=1,则区域收入差距可表示为:
| $\frac{{{\omega _A}}}{{{\omega _B}}} ={{{{[{h_A}{\tau ^{\sigma - 1}} + {h_B}]}^{\pi /\left( {1 - \sigma } \right)}}}}\Big/{{{{[{h_A} + {h_B}{\tau ^{\sigma - 1}}]}^{\pi /\left( {1 - \sigma } \right)}}}}$ | (21) |
参照赵伟和李芬(2007)有关新经济地理学框架的应用,设定参数π=0.4、σ=5,模拟本文讨论的有关人力资本集聚在各种不同取值下地区收入差距对交易成本的演变路径。结果显示,无论地区间人力资本集聚的初始状态如何,随着交易成本的逐渐下降((1−τ)→0,即τ→1),区域间收入差距呈逐渐递减趋势,并最终收敛到0。特别地,当(1−τ)=0或τ=1时,ωA=ωB,
因此,理论推导和数值模拟结果均显示,无论人力资本集聚的初始状态如何,随着交易成本的下降,区域收入差距会逐渐收敛并趋于0。即交易成本,而非人力资本集聚或产业集聚,是导致区域收入差距形成的主要诱因。因此,已有文献中,无论是利用不考虑交易成本的新古典经济学框架,还是利用交易成本外生的新经济地理学框架,均无法较好地对导致区域收入差距扩大的根本原因进行全面的刻画。本文将内生的交易成本引入新经济地理学框架,是对文献的有益补充。
命题2:教育投入对缓解区域收入差距不存在空间异质性,是一种帕累托改进。也即无论增加哪一地区的教育投入均有利于缓解区域间收入差距。
根据上文理论框架,可以证明:
| $\frac{{\partial {\omega _A}}}{{\partial {E_A}}} = \frac{\pi }{{\sigma - 1}}{({L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_A}{\rm{ > 0}}$ | (22) |
| $\frac{{\partial {\omega _A}}}{{\partial {E_B}}} = \frac{\pi }{{\sigma - 1}}{({L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_B}{\tau ^{\sigma - 1}}{\rm{ > 0}}$ | (23) |
| $\frac{{\partial {\omega _B}}}{{\partial {E_A}}} = \frac{\pi }{{\sigma - 1}}{({L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_A}{\tau ^{\sigma - 1}}{\rm{ > 0}}$ | (24) |
| $\frac{{\partial {\omega _B}}}{{\partial {E_B}}} = \frac{\pi }{{\sigma - 1}}{({L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_B}{\rm{ > 0}}$ | (25) |
| $\text{也即} \frac{{\partial {\omega _A}}}{{\partial {E_A}}}{\rm{ > 0}}\frac{{\partial {\omega _A}}}{{\partial {E_B}}}{\rm{ > 0}}\frac{{\partial {\omega _B}}}{{\partial {E_A}}}{\rm{ > 0}}\frac{{\partial {\omega _B}}}{{\partial {E_B}}}{\rm{ > 0}}$ | (26) |
由式(26)可见,无论是增加A地区的教育投入还是增加B地区的教育投入,均可促进两地区实际工资收入水平的提高。这是由于教育投入增加了系统中的人力资本积累,为产品市场上创造了更加多样化的产品,丰富的产品种类通过价格指数效应降低了产品的相对价格,从而提高了各地区劳动力的实际工资水平。
假定地区A的实际工资水平高于地区B,地区间存在收入差距。
| $\text{由}\frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( {1 - \tau } \right)}} > 0\text{、}\frac{{\partial \left( {1 - \tau } \right)}}{{\partial E}} < 0,\text{可得}\frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( E \right)}} = \frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( {1 - \tau } \right)}}\frac{{\partial \left( {1 - \tau } \right)}}{{\partial \left( E \right)}} < 0$ | (27) |
| $\frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( {{E_A}} \right)}} = \frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( E \right)}}\frac{{\partial \left( E \right)}}{{\partial \left( {{E_A}} \right)}} < 0\frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( {{E_B}} \right)}} = \frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( E \right)}}\frac{{\partial \left( E \right)}}{{\partial \left( {{E_B}} \right)}} < 0$ | (28) |
如式(27)所示,教育投入与交易成本负相关,交易成本与地区收入差距正相关。因此,增加教育投入可以通过促进技术进步、改善交通运输条件或贸易环境降低地区间交易成本,从而缩小地区间收入差距。由式(28)可看出,无论增加低收入地区还是高收入地区的教育投入,均有助于缓解两地区的收入差距。教育投入对缓解区域收入差距不存在空间异质性。然而,由于地区间交易成本的存在,各地区教育投入的增加使得本地区实际收入水平较其他地区提高得更快(如式(31)所示)。
| $\frac{{\partial {\omega _A}}}{{\partial {E_A}}} - \frac{{\partial {\omega _B}}}{{\partial {E_A}}} = \frac{\pi }{{\sigma - 1}}{({L_A}{E_A} + {L_B}{E_B}{\tau ^{\sigma - 1}})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_A}\left( {1 - {\tau ^{\sigma - 1}}} \right){\rm{ > 0}}$ | (29) |
| $\frac{{\partial {\omega _B}}}{{\partial {E_B}}} - \frac{{\partial {\omega _A}}}{{\partial {E_B}}} = \frac{\pi }{{\sigma - 1}}{({L_A}{E_A}{\tau ^{\sigma - 1}} + {L_B}{E_B})^{{\textstyle\frac{\pi }{{\sigma - 1}}} - 1}}{L_B}\left( {1 - {\tau ^{\sigma - 1}}} \right){\rm{ > 0}}$ | (30) |
| $\text{也即} \frac{{\partial {\omega _A}}}{{\partial {E_A}}} - \frac{{\partial {\omega _B}}}{{\partial {E_A}}}{\rm{ > 0}}\frac{{\partial {\omega _B}}}{{\partial {E_B}}} - \frac{{\partial {\omega _A}}}{{\partial {E_B}}}{\rm{ > 0}}$ | (31) |
假定地区A的实际工资水平高于地区B,教育资源在地区A和地区B的配置比例分别为eA和 eB,且eA+eB=1。
| $\frac{{\partial \left( {\displaystyle\frac{{{\omega _A}}}{{{\omega _B}}}} \right)}}{{\partial \left( {{e_B}} \right)}} = \frac{\pi }{{1 - \sigma }}{\left(\frac{{{L_A}{e_A}{\tau ^{\sigma - 1}} + {L_B}{e_B}}}{{{L_A}{e_A} + {L_B}{e_B}{\tau ^{\sigma - 1}}}}\right)^{{\textstyle\frac{\pi }{{1 - \sigma }}} - 1}}\frac{{{L_B}\left( {1 - {\tau ^{\left( {\sigma - 1} \right)}}} \right) + {L_A}{e_B}}}{{{{({L_A}{e_A} + {L_B}{e_B}{\tau ^{\sigma - 1}})}^2}}}{L_A}\left( {1 - {\tau ^{\sigma - 1}}} \right) < 0$ | (32) |
因此,在交易成本存在且教育资源有限的情况下,优化教育资源配置结构使教育经费投入向低收入落后地区倾斜,可以缩小其与高收入地区人力资本的差异,对缓解区域收入差距效果更好。
综上,人力资本集聚本身并不是导致区域收入差距扩大的根本诱因,其只在交易成本导致地区间收入差距扩大的过程中起到“催化剂”的作用。降低交易成本是缓解地区间收入差距的有效途径。而增加教育投入,既可以通过增加系统中的人力资本积累提高各地区收入水平,又可以通过降低交易成本来缓解区域间收入差距(见图2),属于效率与公平兼顾的帕累托改进。

|
| 图 2 教育投入缓解区域收入差距的作用机制 |
三、实证分析
本部分拟对以上理论推导的两个命题进行实证检验。具体通过构建空间面板计量模型验证教育投入对地区收入差距的影响机制。并在此基础上,进一步细分各级教育进行比较分析。
(一)变量选取与数据说明。本文的核心变量包括教育投入、交易成本和区域收入差距。其他控制变量参考已有文献选择对外开放程度、金融效率、国有企业比重、城镇化率和经济发展水平等。具体而言:
1. 区域收入差距(Ginc)。本文使用基尼系数作为反映区域收入差距的被解释变量,测算方法参考Sundrum(1992)提出的“分组加权法”公式进行估算:
| $Ginc = P_u^2\frac{{{Y_u}}}{Y}Gin{c_u} + P_r^2\frac{{{Y_r}}}{Y}Gin{c_r} + {P_u}{P_r}\frac{{{Y_u} - {Y_r}}}{Y}$ | (33) |
其中:Pu和Pr分别为各省的城镇人口比重和农村人口比重;Yu和 Yr分别为各省的城镇居民人均可支配收入与农村居民人均纯收入;Y代表全省所有居民的人均收入,计算公式为:Y=PrYr+PuYu。原始数据均来自《中国统计年鉴》。Gincu和 Gincr分别为城镇居民可支配收入基尼系数和农村居民纯收入基尼系数,采用“积分法”公式
2. 教育投入(Edu)。教育投入采用各级教育生均经费投入表示,具体细分为普通小学(Primary)、普通初中(Lower)、普通高中(Upper)、普通高等学校(College)等。数据来自历年《中国教育经费统计年鉴》。其中:整体生均教育经费支出(Edu)为小学、普通初中、普通高中、普通本专科等各级教育的教育经费总支出与在校生人数的加权平均值。
3. 交易成本(TC)。由于交易成本泛指任何不牵涉直接生产的机会成本,不同的交易往往就涉及不同种类的交易成本,很难界定及量化。因此,直接测度地区间交易成本难度较大。然而,一价定律指出,当各地间开放贸易且交易费用为0时,相同产品无论在何地销售,其价格都应相等。地区之间贸易一体化程度越高,物价水平差异越小;否则说明区域间交易成本升高,市场一体化有恶化的迹象。鉴于此,本文从交易成本导致不同地区产品价格的差异出发,利用各地区工业品价格指数PPI作为间接衡量区域间交易成本的替代指标。⑥
4. 人力资本存量(HR)。人力资本存量使用各省就业人口中高技能劳动力占比表示。其中,高技能劳动力占比为就业人口中具有大学专科、大学本科、研究生及以上受教育程度的人数比上各地区总就业人口。数据来源于《中国人口和就业统计年鉴》。
除教育投入、交易成本影响地区收入差距外,其他反映经济基本面情况的宏观变量也会不同程度地影响收入差距。参考已有文献,本文选择对外开放程度、金融效率、国有企业占比、城镇化率、人均国内生产总值等指标作为影响地区收入差距的其他控制变量。其中,对外开放程度采用外商直接投资占国内生产总值的比重表示(FDI)。一般认为,对外开放有助于促进可贸易品价格的相对上升,从而促进该类产品密集使用的生产要素价格的上涨,对地区收入差距具有负向影响;金融效率(Finance)采用金融机构人民币贷款总额与金融机构人民币存款总额的比值衡量,数据来源于《新中国六十年统计资料汇编》和各省市统计年鉴。金融效率越高一定程度上增加了劳动者获得资本性回报的机会,从而有利于增加收入;国有企业比重(SOE)选取规模以上国有控股工业企业总产出与规模以上工业企业总产出的比重表示,数据来自《中国统计年鉴》。现阶段,我国仍属于多种所有制形式并存的混合经济,不同地区所有制结构会对要素资源配置产生影响,从而影响地区间收入差距;人均GDP水平(Gdppc)反映一个地区的经济发展水平。美国经济学家库兹涅茨指出,伴随经济发展收入水平逐渐增加,在发展效率与公平的转化过程中,收入不平等或随着经济社会的发展呈现先增加后下降的倒U形曲线变化趋势;城镇化率(Urban)为城镇人口占总人口的比重。通常,城镇化率越高,由此带动的投资、消费需求为经济高速增长提供动力,居民收入也会快速增长。城镇化率数据来自《中国人口统计年鉴》;各省人口抚养比(AGE)反映劳动力市场上的供需矛盾,从而影响收入差距。
(二)实证检验。
1. 教育投入、交易成本与地区收入差距。伴随着交通条件的日益改善和体制障碍的逐步消除,我国各省份之间的社会经济联系愈加紧密,若仅考虑当地教育投入对收入差距的影响,而忽略其他地区经济的空间溢出效应,所估计的教育投入与地区收入差距模型很可能产生结果偏误。根据空间自相关性检验结果显示2003-2014年区域间收入差距和教育投入的全局Moran’s I指数均为正值,尽管不同年份的相关指数表现出一定波动性,但均在1%水平下呈现显著的统计相关关系。因此,回归模型应考虑数据间的空间自相关性。本文采用空间计量分析方法且同时选用空间自回归模型(Spatial Autoregressive Model,SAR)和空间误差项模型(Spatial Error Model,SEM)对各级教育投入影响地区收入差距的效果进行实证检验。空间自回归模型和空间误差项模型的具体形式分别如下所示:
| $\begin{aligned} Gin{c_{it}} =& \alpha {\rm{ + }}\lambda WGin{c_{it}} + {\beta _1}Ln{(edu)_{it}} + {\beta _2}T{C_{it}} + {\beta _3}T{C_{it}} \times {\rm{Ln}}{(edu)_{it}} + {\beta _4}FD{I_{it}} + {\beta _5}Financ{e_{it}} + \\ & {\beta _6}SO{E_{it}} + {\beta _7}Urba{n_{it}} + {\beta _8}AG{E_{it}} + {\beta _9}{\rm{Ln}}{(Gdppc)_{it}} + {\beta _{10}}lagGin{c_{i,t}} + {\varepsilon _{it}} \\ \end{aligned} $ |
| $\begin{aligned} Gin{c_{it}} =& \alpha + {\beta _1}{\rm{Ln}}{(edu)_{it}} + {\beta _2}T{C_{it}} + {\beta _3}T{C_{it}} \times {\rm{Ln}}{(edu)_{it}} + {\beta _4}FD{I_{it}} + {\beta _5}Financ{e_{it}} + \\ & {\beta _6}SO{E_{it}} + {\beta _7}Urba{n_{it}} + {\beta _8}AG{E_{it}} + {\beta _9}{\rm{Ln}}{(Gdppc)_{it}} + {\beta _{10}}lagGin{c_{i,t}} + {\mu _{it}} \\ \end{aligned} $ |
| ${\mu _{it}} = \rho W{\mu _{it}} + {\varepsilon _{it}}$ | (34) |
其中:Gincit为省份i(i=1,…,N)在时期t(t=1,…,T)的收入基尼系数。W为空间权重矩阵,WGincit即为空间关联省份收入差距的空间加权自相关变量。λ度量空间自相关变量WGincit对Gincit的影响。λ>0说明空间关联地区收入基尼系数对本地区收入基尼系数有正向影响;反之,表示有负向影响。lagGinci,t-1为滞后一期的地区收入差距,既可表示除以上控制变量之外的其他诸如历史背景、人文环境、风俗习惯及政治制度等潜在遗漏变量的影响,也可作为工具变量并控制动态时滞,一定程度上解决教育投入与地区收入差距可能存在互为因果的模型内生性问题,β为对应解释变量的系数,ε为随机误差项,ρ表示误差项的空间自相关系数,衡量了空间关联省份收入差距随机扰动项中的误差冲击对本省的收入差距的影响。
为检验教育投入通过降低交易成本缓解地区收入差距的作用机制(教育投入→交易成本→收入差距),本文采用中介效应模型逐步进行检验:第一步,检验教育投入对地区收入差距的总效应;第二步,检验教育投入对中介变量交易成本的效应和中介变量交易成本对地区收入差距的效应;第三步,检验中介变量交易成本是教育投入影响地区收入差距的完全中介还是部分中介。表1为具体结果:
| 解释变量 | 被解释变量 | |||||
| 区域收入差距 | 交易成本 | 区域收入差距 | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | |
| SAR | SEM | SAR | SEM | SAR | SEM | |
| Lnedu | −0.012**(−2.287) | −0.018***(−3.029) | −7.177***(−4.854) | −4.939***(−4.030) | −0.019***(−4.030) | −0.022***(−3.994) |
| TC | 0.006***(4.073) | 0.006***(3.958) | ||||
| Lnedu×TC | 0.001***(4.209) | 0.001***(4.100) | ||||
| FDI | −1.024*(−1.866) | −1.160*(−1.822) | −16.860(−0.086) | 34.101(0.202) | −0.331(−0.553) | −0.665(−0.977) |
| Finance | 0.017 5**(2.067) | 0.026 0***(2.598) | −8.294 8***(−2.817) | −5.352 0**(−2.167) | 0.009 5(1.087) | 0.007(0.687) |
| SOE | −0.004(−0.452) | −0.009(−0.802) | 7.513**(2.166) | 5.950**(1.998) | −0.000 3(−0.032) | −0.007(−0.585) |
| Urban | −0.000 5**(12.411) | −0.000 4(−1.284) | 0.060(1.157) | 0.025(0.610) | −0.000 1(−0.709) | −0.000 1(−0.597) |
| AGE | 0.000 6***(2.372) | 0.000 7***(2.365) | −0.090(−1.073) | −0.088(−1.226) | 0.000 3(1.273) | 0.000 7**(2.265) |
| Gdppc | 0.156***(2.471) | 0.127*(1.668) | 33.815*(1.610) | 17.678(0.993) | 0.062(0.932) | 0.079(1.047) |
| Lagy | 0.242***(7.430) | 0.239***(7.101) | −0.044(−1.334) | −0.014(−0.415) | 0.266***(9.086) | 0.262***(8.790) |
|
$\lambda $
|
0.324***(6.149) | −0.481***(−6.634) | 0.263***(5.293) | |||
|
$\rho $
|
0.351*** | −0.447*** | 0.299*** | |||
| (5.470) | (−5.652) | (4.477) | ||||
| Moran I | 0.187*** | 0.187*** | −0.260*** | −0.260*** | 0.209*** | 0.209*** |
|
${R^2}$
|
0.948 | 0.938 | 0.457 | 0.284 | 0.928 | 0.918 |
| Log−L | 871.46 | 864.42 | −853.88 | −859.30 | 827.58 | 821.31 |
| 观测数 | 288 | 288 | 288 | 288 | 288 | 288 |
| 说明:Moran I指数为空间相关性检验结果。R2和Log-L反映模型的拟合优度。λ、ρ为空间自回归模型(SAR)和空间误差模型(SEM)的空间相关系数。***、**和*分别表示在1%、5%和10%的显著性水平上显著。括号内为估计参数的t值。空间面板数据模型控制了个体固定效应和时间固定效应。 | ||||||
整体而言,表1模型的空间相关系数均通过了1%的显著性检验,且空间自相关模型和空间误差模型均通过了传统拉格朗日乘子检验和稳健的拉格朗日乘子检验。从R2和Log-L统计量结果看,各个模型均具有较好的拟合优度,说明本文构建的空间面板数据模型较合理地刻画了教育投入对地区收入差距的作用机制。具体而言:第一,SAR和SEM模型结果显示,增加教育投入有助于缩小区域收入差距。第二,教育投入与交易成本呈显著负相关关系,增加教育投入可降低交易成本;同时,交易成本与地区收入差距显著正相关,⑦说明交易成本是导致地区收入差距扩大的重要原因。因此,交易成本对教育投入缓解地区收入差距具有显著的中介效应。第三,在控制中介变量−交易成本影响后,教育投入对地区收入差距的直接效应依然显著为负。说明交易成本在教育投入缓解区域收入差距的机制中并非完全中介,而是部分中介。教育投入对区域收入差距另具其他影响渠道。
其他控制变量对地区收入差距的具体影响也大致符合预期。其中,对外开放程度的系数为负,说明加大对外开放力度可以缩小地区收入差距。积极参与国际贸易和引进外资可以促使地区具有比较优势的产业快速发展,增加对中低端劳动力的需求,提高劳动力收入,缩小收入差距;金融效率的系数显著大于0,说明虽然金融效率提高有利于居民享有更多的金融服务,增加资本性回报和收入水平,但不同地区所获金融服务差异越大,会导致地区收入差距扩大;人口抚养比的影响系数显著为正,说明劳动力市场上非劳动年龄人口比重越大,劳动力供需矛盾越突出,不同个体之间的收入差距越大;人均国内生产总值的估计系数显著大于0,对地区收入差距的影响作用为正,说明我国尚未越过库兹涅茨“倒U形”曲线的拐点,还处于左侧的上升阶段;滞后一期的地区收入差距系数也通过了显著性检验,说明地区收入差距在相当程度上受到历史背景、人文环境、风俗习惯等潜在因素的影响。
本文进一步对各级教育缓解区域收入差距的效果进行了比较。比较分析结果显示,第一,各级教育投入均有助于缩小地区收入差距,且各级教育投入均通过降低交易成本这一中介变量来缓解地区收入差距。一定程度上反映了教育投入对缓解区域收入差距具有系统稳健性。第二,从区分各级教育投入降低交易成本从而缓解地区收入差距的效果看,义务教育相较于其他各级教育的作用更加明显。
2. 教育投入、人力资本与地区收入水平。本部分拟利用不同空间回归模型对教育投入的空间异质性进行讨论。空间自回归模型和空间误差项模型的具体形式分别如下所示:
| $\begin{aligned} {\rm{Ln}}{(Income)_{it}} =& \alpha {\rm{ + }}\lambda W{\rm{Ln}}{(Income)_{it}} + {\beta _1}{\rm{Ln}}{(edu)_{it}} + {\beta _2}H{R_{it}} + {\beta _3}H{R_{it}}\times{\rm{Ln}}{(edu)_{it}} + {\beta _4}FD{I_{it}} + {\beta _5}Financ{e_{it}} + \\ & {\beta _6}SO{E_{it}} + {\beta _7}Urba{n_{it}} + {\beta _8}{\rm{Ln}}{(Gdppc)_{it}} + {\beta _9}lag{\rm{Ln}}{(Income)_{i,t}} + {\varepsilon _{it}} \\ \end{aligned} $ |
| $\begin{aligned} {\rm{Ln}}{(Income)_{it}} =& \alpha + {\beta _1}{\rm{Ln}}{(edu)_{it}} + {\beta _2}H{R_{it}} + {\beta _3}H{R_{it}}\times {\rm{Ln}}{(edu)_{it}} + {\beta _4}FD{I_{it}} + {\beta _5}Financ{e_{it}} + \\ & {\beta _6}SO{E_{it}} + {\beta _7}Urba{n_{it}} + {\beta _8}{\rm{Ln}}{(Gdppc)_{it}} + {\beta _9}lag{\rm{Ln}}{(Income)_{i,t}} + {\mu _{it}} \\ \end{aligned} $ |
| ${\mu _{it}} = \rho W{\mu _{it}} + {\varepsilon _{it}}$ | (35) |
其中:Ln(Income)it为省份i(i=1,…,N)在时期t(t=1,…,T)的收入水平。W为空间权重矩阵,WLn(Income)it即为空间关联省份收入水平的空间加权自相关变量。HR表示各省人力资本存量。其他控制变量解释同上。
由表2可见,整体而言,空间自相关模型和空间误差模型均通过了稳健拉格朗日乘子检验,模型均具有较好的拟合优度,说明本文构建的空间动态面板数据模型较合理地刻画了各级教育投入对区域收入差距的影响机制,模型中各解释变量系数的估计结果显著性较高。具体而言:第一,各级生均教育经费投入和人力资本积累均有助于提高各地区的收入水平。第二,增加各级教育投入可以通过增加人力资本积累来促进各地区收入水平的提高。这一结论与前文的理论框架分析结果一致。第三,从区分各级教育投入影响地区收入水平的效果看,义务教育相比其他各级教育对增加地区收入水平的作用更加显著。
| 解释变量 | 被解释变量:区域人均收入水平 | |||||||||
| 整体教育 | 小学教育 | 初中教育 | 高中教育 | 大学教育 | ||||||
| SAR | SEM | SAR | SEM | SAR | SEM | SAR | SEM | SAR | SEM | |
| Lnedu | 0.159*** (5.624) |
0.168*** (5.968) |
0.146*** (5.393) |
0.176*** (7.240) |
0.162*** (6.708) |
0.168*** (7.529) |
0.126*** (4.045) |
0.099*** (3.677) |
0.086*** (2.780) |
0.043* (1.529) |
| HR | 0.003
(1.092) |
0.004* (1.700) |
0.005** (2.074) |
0.004** (2.134) |
0.004* (1.764) |
0.004*** (1.830) |
0.004* (1.578) |
0.003* (1.690) |
0.003* (1.515) |
0.004** (1.947) |
| HR×Lnedu | 0.003*** (3.396) |
0.003*** (3.058) |
0.003*** (3.260) |
0.003***(3.420) | 0.003*** (2.890) |
0.003*** (2.992) |
0.003*** (3.186) |
0.004*** (4.130) |
0.008*** (4.850) |
0.009*** (5.478) |
| FDI | −7.145*** (−2.423) |
−11.633*** (−3.927) |
−7.305*** (−2.462) |
−10.606*** (−3.625) |
−8.988*** (−3.116) |
−12.180*** (−4.223) |
−9.464*** (−3.179) |
−12.845*** (−4.255) |
−7.079** (−2.329) |
−12.403*** (−4.068) |
| Finance | 0.248*** (5.039) |
0.191*** (3.726) |
0.181*** (3.878) |
0.148*** (3.049) |
0.192*** (4.172) |
0.164*** (3.397) |
0.173*** (3.660) |
0.140*** (2.755) |
0.195*** (4.033) |
0.149*** (2.908) |
| SOE | −0.032
(−0.555) |
−0.049
(−0.830) |
−0.040
(−0.682) |
−0.055
(−0.942) |
−0.042
(−0.736) |
−0.025
(−0.444) |
0.043
(0.755) |
0.023
(0.386) |
0.075
(1.308) |
0.025
(0.427) |
| Urban | 0.002** (1.840) |
0.003*** (2.491) |
0.003** (3.054) |
0.004*** (3.933) |
0.004*** (3.652) |
0.004*** (3.874) |
0.002** (1.937) |
0.002** (1.986) |
0.008
(0.795) |
0.001
(1.177) |
| LnGdppc | 6.198*** | 6.189*** | 6.026*** | 5.811*** | 5.760*** | 5.950*** | 7.051*** | 7.481*** | 7.885*** | 8.184*** |
| (15.073) | (14.320) | (13.802) | (14.013) | (14.346) | (15.547) | (21.499) | (23.152) | (34.090) | (35.696) | |
| Lag
Ln(Income) |
0.026*** (3.017) |
0.012* (1.742) |
0.020*** (2.347) |
0.010* (1.628) |
0.019** (2.212) |
0.009
(1.379) |
0.021*** (2.392) |
0.012* (1.803) |
0.025*** (2.858) |
0.017*** (2.442) |
| λ | −0.037** (−2.071) |
−0.033* (−1.836) |
−0.031* (−1.756) |
−0.038** (−2.096) |
−0.039** (−2.134) |
|||||
| ρ | 0.627*** | 0.656*** | 0.626*** | 0.618*** | 0.620*** | |||||
| (14.794) | (16.297) | (14.745) | (14.365) | (14.458) | ||||||
| Moran I | 0.470*** | 0. 470*** | 0.492*** | 0.492*** | 0.478*** | 0.478*** | 0.464*** | 0.464*** | 0.472*** | 0.472*** |
| R2 | 0.975 | 0.973 | 0.974 | 0.973 | 0.969 | 0.974 | 0.974 | 0.973 | 0.974 | 0.973 |
| Log−L | 367.15 | 422.83 | 364.96 | 429.25 | 372.49 | 431.82 | 360.11 | 413.46 | 360.11 | 412.00 |
| 观测数 | 403 | 403 | 403 | 403 | 403 | 403 | 403 | 403 | 403 | 403 |
近年来,我国教育经费投入增长显著。其中:2016年全国教育经费总投入3.9万亿元,在不考虑价格因素的情况下较1995年0.2万亿元的教育经费投入扩大了近20倍,年均增速高达40%。国家财政性教育经费占国内生产总值的比重更是从1995年的2.3%增加到2016年的4.2%。然而,国际横向比较而言,我国仍属于公共财政教育经费投入偏低的国家。根据世界银行全球发展指数(World Development Indicators,WDI),2012年瑞典、挪威、芬兰等国的公共教育支出占GDP的比重分别为7.66%、7.37%和7.19%,显著高于我国的4.28%。同时,我国教育经费投入,特别是义务教育经费投入的地区差异较大。根据上文的理论研究和实证检验结果,教育是降低交易成本,促进人力资本积累,从而缓解区域收入差距的有效手段。其中:相对于其他各级教育,义务教育对缓解区域收入差距的作用更加显著。因此,十九大报告提出“优先发展教育事业”、“推动城乡义务教育一体化发展”等,正是缓解当前我国发展不平衡矛盾,特别是缓解区域发展不平衡矛盾的主要推动力。
四、结 论
本文通过文献回顾发现,在不同理论框架下,已有文献关于教育通过人力资本积累对区域发展不平衡问题的研究存在不一致的结论。一种研究结论认为,在新古典有关完全市场假说条件下,当不考虑交易成本时,教育可以通过增加人力资本积累提高劳动生产率水平并促进劳动力在区域间流动,从而缩小区域间收入差距。另一种研究结论认为,在新经济地理学框架下,通过引入外生交易成本,研究得到教育不仅无助于缓解区域收入差距,反而会通过增加人力资本积累导致产业集聚,从而扩大区域收入差距。在两种理论机制下,教育对区域收入差距的影响效果并不相同。在前人研究基础上,本文对相关问题研究进行了两方面的探索,一是基于新经济地理学框架,通过放松有关交易成本外生的假设,将其作为内生因素引入一般均衡框架,并采用含中介效应的空间自回归模型和空间误差模型对理论部分进行实证检验,探讨导致区域收入差距扩大的根本诱因。二是检验地区教育投入差异是否为导致地区间收入差距扩大的主要原因,并在此基础上进一步比较分析了各级教育投入对缓解区域收入差距的不同作用。结果显示:
第一,并非人力资本集聚或产业集聚而是交易成本,是导致地区间收入差距扩大的主要诱因。交易成本的存在导致了各地实际收入水平的下降,但其对欠发达地区收入下降的影响程度更大,从而扩大了地区收入差距。人力资本集聚只是在交易成本导致地区间收入差距扩大的过程中起了“催化剂”作用。因此,缓解地区间收入差距的根本途径并非是人力资本集聚或产业集聚,而是降低交易成本。从世界发展经验看,几乎所有发达国家在经济发展过程中,均不同程度地呈现人口和产业向少数地区集聚的趋势,但与之带来的不是地区收入差距扩大而是经济繁荣。若将地区间平衡发展简单理解为是人口和经济在地域空间上的均匀分布,误将地区发展不平衡归结为是人力资本集聚或产业集聚导致的结果,从而违背市场发展规律,试图通过扭曲的行政干预手段人为地将经济集聚地区的人口或产业强制疏解出去,往往只会造成地区间资源配置无效甚至影响经济可持续增长(陆铭,2017)。鉴于交易成本在区域发展不平衡中所起的关键作用,因此,降低交易成本,促进劳动力资本等生产要素和产品合理自由流动,使市场在资源配置中起决定性作用,是解决地区发展不平衡矛盾推动区域协调发展的重要渠道。⑧
第二,教育投入对缓解区域收入差距不存在空间异质性,即无论增加哪一地区的教育投入均有利于缓解区域间收入差距。本文从理论框架与实证检验两方面证明了地区间教育投入的差异并不会导致地区间收入差距的扩大,但不同地区教育投入的增加对缩小区域间收入差距产生不同程度的正向影响。因此,教育投入对缓解区域收入差距可视为一种帕累托改进。
第三,各级教育投入对缓解区域收入差距的影响程度不同。相比较而言,增加义务教育投入对缓解区域收入差距的效果更加显著。未来随着我国经济的减速调整,各级政府财政收入的增速回落,进一步合理配置教育经费投入资源以实现国民经济整体效益的最大化,是跨越中等收入陷阱和全面建成小康社会战略目标的重要保障。为此,各级部门应进一步提高教育经费投入,尤其是义务阶段的教育投入,既可减缓短期私人部门投资减少对宏观经济的冲击,平滑经济增速波动,又有利于增加人力资本积累,提高我国长期潜在的经济增速。
综上,通过增加教育投入降低交易成本,促进要素合理自由流动,是有效缓解我国地区收入差距矛盾,实现效率与公平兼顾的包容性增长目标的重要途径。
① 本文空间异质性具体指,利用空间计量模型检验不同地区教育投入对缓解区域间收入差距是否存在相异结论。后文理论与实证结果显示,无论增加低收入地区还是高收入地区教育投入,均有助于缓解两地区收入差距。因此,教育投入对缓解区域收入差距这一结论不具有空间差异性。
② 此处刻画的是内部规模经济,即厂商的平均生产成本随其自身生产规模扩大而下降;规模经济还包括外部规模经济,即平均成本与单个厂商的生产规模无关,但与整个行业的规模有关。在其他条件相同的情况下,大量企业集中在同一地区后行业规模扩大,由于“干中学”等外部性,结果使得行业规模较大的地区比行业规模较小的地区生产成本更低、生产效率更高、规模收益递增。
③ 萨缪尔森“冰山成本”实际上是将交易成本从被运输产品中直接扣除掉。本文所述交易成本泛指除直接生产之外的为促成交易发生而形成的所有成本。
④ 鉴于本文的主要研究目的是探讨教育投入通过降低交易成本影响区域收入差距的作用机制。为简化分析,此处假定消费者在工业品上的支出比例和工业品间的替代弹性等其他决定区域经济活动空间分布与收入差距分化或收敛的参数均为确定的常数。一般而言,由于交易成本的存在,工业品间替代弹性越小,经济活动集聚程度越大,区域收入差距越大;消费者在工业品上的支出比例越大,工业化程度越高,越有利于产业集聚,促进区域间收入分化。
⑤ 鉴于基尼系数受系统中收入分配结构的影响,短期内与收入的相对变化较为稳定。因此,对某些省份仅个别年份缺失住户调查数据的,基尼系数的计算采用近三年其对人均收入相对变化的弧弹性进行估算。
⑥ 需要指出的是,此处对交易成本的刻画仍存在较大的局限性。如何更好地衡量交易成本,是未来可以继续深入研究的课题。
⑦ 本文回归模型中将教育投入与交易成本的交互项进行了中心化处理(即减去了各自的平均数),目的是使此处主要项的解释更符合经济意义。比如,控制教育投入为其平均水平时,教育投入与交易成本呈显著负相关关系;控制交易成本为其平均水平时,教育投入与地区收入差距为负向相关关系。若交互项不进行中心化处理,则应解释为控制教育投入和交易成本为0,显然不符合客观经济实际。
⑧ 王一鸣:“十三五”时期推动区域协调发展的几点思考。http://news.xinhuanet.com/politics/2016-02/03/c_128698017.htm
| [1] | 高连水. 什么因素在多大程度上影响了居民地区收入差距水平?−基于1987~2005年省际面板数据的分析[J]. 数量经济技术经济研究, 2011(1): 130–139. |
| [2] | 教育部财务司, 北京师范大学中国教育经济信息研究中心. " 十二五”中国教育经费发展报告[M]. 北京: 人民教育出版社, 2017. |
| [3] | 李实, 史泰丽, 别雍·古斯塔夫森. 中国居民收入分配研究-III[M]. 北京: 北京师范出版社, 2008. |
| [4] | 陆铭. 城市、区域和国家发展−空间政治经济学的现在与未来[J]. 经济学(季刊), 2017(4): 1499–1532. |
| [5] | 许召元, 李善同. 近年来中国地区差距的变化趋势[J]. 经济研究, 2006(7): 106–116. DOI:10.3969/j.issn.1005-913X.2006.07.049 |
| [6] | 许召元, 李善同. 区域间劳动力迁移对地区差距的影响[J]. 经济学(季刊), 2009(1): 53–76. |
| [7] | 杨俊, 黄潇, 李晓羽. 教育不平等与收入分配差距: 中国的实证分析[J]. 管理世界, 2008(1): 38–47. |
| [8] | 姚枝仲, 周素芳. 劳动力流动与地区差距[J]. 世界经济, 2003(4): 35–44. DOI:10.3969/j.issn.1007-6964.2003.04.007 |
| [9] | 赵伟, 李芬. 异质性劳动力流动与区域收入差距: 新经济地理学模型的扩展分析[J]. 中国人口科学, 2007(1): 27–35. DOI:10.3969/j.issn.1000-7881.2007.01.004 |
| [10] | Cheung S N S. The transaction costs paradigm: 1998 presidential address, western economic association[J]. Economic Inquiry, 1998, 36(4): 514–521. DOI:10.1111/ecin.1998.36.issue-4 |
| [11] | Coady D, Dizioli A. Income inequality and education revisited: Persistence, endogeneity, and heterogeneity[R]. IMF Working Papers WP/17/126, 2017. |
| [12] | De Gregorio J, Lee J W. Education and income inequality: New evidence from cross-country data[J]. Review of Income and Wealth, 2002, 48(3): 395–416. DOI:10.1111/roiw.2002.48.issue-3 |
| [13] | Duranton G, Puga D. Micro-foundations of urban agglomeration economies[J]. Handbook of Regional and Urban Economics, 2004, 4: 2063–2117. DOI:10.1016/S1574-0080(04)80005-1 |
| [14] | Heuchemer M. The relation between income inequality, education and social structure: Panel data analysis of the european union[EB/OL]. http://hdl.handle.net/2105/34001, 2016-07-06. |
| [15] | Krugman P. Increasing returns and economic geography[J]. Journal of Political Economy, 1991, 99(3): 483–499. DOI:10.1086/261763 |


