公开市场操作、利率走廊与市场拆借利率

《财经研究》
2019第45卷第7期

文章浏览量：[]

引用本文

黄志刚, 刘郭方. 公开市场操作、利率走廊与市场拆借利率[J]. 财经研究, 2019, 45(7): 31-44. 复制到剪切板

Huang Zhigang, Liu Guofang. Open market operations, interest rate corridors and the inter-bank offered rate[J]. Journal of Finance and Economics, 2019, 45(7): 31-44. 复制到剪切板

公开市场操作、利率走廊与市场拆借利率

黄志刚 , 刘郭方

中央财经大学金融学院，北京 100081

收稿日期: 2019-02-06

作者简介: 黄志刚（1982—），男，浙江富阳人，中央财经大学金融学院教授，硕士生导师;
刘郭方（1981—）（通讯作者），男，河南安阳人，中央财经大学金融学院博士研究生。

摘要: 文章构建了一个银行同业拆借市场的三期模型，为分析公开市场操作和利率走廊两种货币政策工具提供了一个理论框架。理论分析发现，公开市场操作和利率走廊都会影响拆借利率，但利率走廊稳定拆借利率的效果要优于公开市场操作。公开市场操作对拆借利率的影响大小取决于其是否被预期到，与基本面不一致的未预期到的公开市场操作会引起拆借利率的异常波动。而无论是预期到的还是未预期到的利率走廊，都能起到稳定拆借利率的作用。但具有严格抵押要求的利率走廊会减弱政策效果，抵押溢价会导致拆借利率突破政策利率上限。数值模拟分析进一步证实了上述结论。

关键词: 公开市场操作利率走廊拆借利率

Open Market Operations, Interest Rate Corridors and the Inter-bank Offered Rate

Huang Zhigang, Liu Guofang

School of Finance, Central University of Finance and Economics, Beijing 100081, China

Summary: In recent years, there have been sharp fluctuations in short-term interest rates in China’s financial markets, posing challenges to the implementation of monetary policies and the stability of financial markets. There was a similar phenomenon in LIBOR rates of major currencies during the financial crisis. After the financial crisis, the " interest rate corridor” gradually became a new trend of monetary policies, and the central bank of China gradually introduced a similar mechanism to implement monetary policies.　　This paper sets up a three-phase model of the inter-bank market, expanding the traditional analytical framework into a peer-to-peer market with OTC market attributes. This approach enables the model of this paper to characterize the heterogeneous characteristics of the bank’s liquidity, and distinguish between banks which need interest rate corridors and those which have no need of the corridors, so that the unique mechanism that interest rate corridors affect market liquidity can be reflected. The establishment of the interest rate corridor mechanism will affect the liquidity position of commercial banks by affecting the expected liquidity management costs and benefits of commercial banks. Thus, the inter-bank offered rate can be impacted and it will be stable within interest rate corridors. In order to highlight the unique mechanism of the interest rate corridor mechanism, this paper first analyzes the impact of open market operations with characteristics of quantitative regulation on market interest rates, and demonstrates the advantages and disadvantages of the interest rate corridor mechanism through comparison.　　The theoretical analysis shows that open market operations and interest rate corridors have their own advantages and disadvantages in regulating interest rate fluctuations. First, open market operations regulate interest rate volatility by regulating the liquidity of the whole interbank market. Interest rate corridors only need to adjust the liquidity of part of the banks to regulate interest rate fluctuations, so interest rate corridors affect market activities from the margin, and the regulation has less disturbance to the market. Second, in terms of regulating short-term interest rates, both the expected open market operations and interest rate corridor adjustments will be constrained by the " liquidity substitution effect”. Because of the liquidity substitution effect, the adjustment of open market operations may be completely offset, but that of interest rate corridors cannot be. In terms of stabilizing interest rates, open market operations rely on the judgment of the central bank, while interest rate corridors can be more independently implemented. Finally, under the interest rate corridor mechanism, a tight mortgage policy may cause the inter-bank offered rate to break through the interest rate corridor ceiling. However, the central bank can adjust the mortgage policy, using the camera selection strategy and the cooperation with macro-prudential management, which can respectively achieve different purposes for post-hoc response and pre-existing prevention.

Key words: open market operations interest rate corridors inter-bank offered rate

一、引　言

近年来，我国金融市场中出现了短期利率的剧烈波动，对货币政策的实施和金融的稳定提出了挑战。SHIBOR数据显示，2011−2015年，我国短期利率出现了持续的大幅波动，2013年6月甚至出现了“钱荒”风波，隔夜利率飙升至13.4%。在金融危机期间，各主要货币的LIBOR利率也出现类似的现象。如何有效地稳定短期利率成为各国央行面临的政策挑战。金融危机之后，“利率走廊”逐渐成为货币政策的新潮流，我国央行也逐渐引入了类似的机制。那么，如何设计行之有效的“利率走廊”制度？本文将对此进行理论探讨。

对于利率走廊调控短期利率波动的机制，现有研究大致有两种不同的观点：一种是利率走廊通过调节货币资金的需求来调控短期利率波动。这种观点认为，利率走廊可以控制货币资金的机会成本。由于银行以利润最大化为目标，机会成本变化会影响其对货币资金的需求。在央行外生供给货币资金的条件下，影响需求就可以调节均衡利率（Clinton，1997；Whitesell，2006；Berentsen和Monnet，2008；Martin和Monnet，2008；Berentsen等，2010，2014）。另一种是利率走廊通过管理商业银行预期来调控短期利率波动。这种观点认为，利率走廊为银行提供了一个及时应对未预期的流动性冲击的手段，减弱了预防性货币资金需求对短期利率的冲击，从而使短期利率稳定（Quirós等，2009；Bindseil和Jabłecki，2011；孙国峰和蔡春春，2014；牛慕鸿等，2017）。

这些研究从宏观角度阐释了利率走廊调控短期利率波动的机制，但是基本都假设银行体系的流动性由央行外生供给，且银行间市场是完全竞争的。在这样的假设下，银行是同质的，央行通过利率走廊向任何一家银行贷款就是对整个同业市场注入流动性。这些假设使其研究框架与研究传统货币政策工具（如公开市场操作）的理论框架并无实质性区别，因而不能凸显利率走廊调控同业利率的本质特征。

有文献通过对比利率走廊和公开市场操作来分析利率走廊的特点，主要发现包括：第一，公开市场操作在应对技术冲击方面更有优势（Woodford，2001）；第二，利率走廊能实现更高的福利水平（Martin和Monnet，2008）；第三，利率走廊能以更低的成本来实施货币政策（牛慕鸿等，2017）。但这些发现并没有抓住利率走廊的本质特征。与公开市场操作为代表的传统货币政策工具相比，利率走廊的本质特征是根据银行的流动性异质特征来提供便利工具。若要清晰地刻画这一特点，首先应构建一个能够体现银行流动性异质特征的模型框架。

为了刻画利率走廊的本质特征以及弥补已有理论的不足，本文借鉴Heider等（2015）的流动性内生模型，将其拓展成具有OTC（Over The Counter）市场属性的同业拆借市场。^①这样，本文的模型就可以刻画银行的流动性异质特征，区分需要与不需要利率走廊的银行，从而体现出利率走廊影响市场流动性的独特机制。利率走廊机制会通过影响商业银行的流动性头寸来影响拆借利率，使其稳定在利率走廊内。为了突出利率走廊机制的独特机制，本文首先分析了以数量调控为特点的公开市场操作对市场利率的影响，然后通过对比来论证利率走廊机制的优势与不足。

本文主要有5点发现：第一，公开市场操作通过调节整个同业拆借市场的流动性来调控利率波动。而利率走廊只需调节部分银行的流动性，就可以调控利率波动，从而对市场的扰动更小。第二，预期到的公开市场操作对拆借利率的调控受到“流动性替代效应”的约束。在特定环境下，流动性替代效应会完全抵消公开市场操作对拆借利率的影响。未预期到的公开市场操作不受“流动性替代效应”影响，因而相机抉择的公开市场操作能更好地调控利率波动，但要以央行对经济形势的准确判断为前提。央行判断失误可能导致利率异常波动，出现类似于“钱荒”的风波。第三，下调利率走廊和收窄限宽的政策是扩张性货币政策。利率走廊调控利率也会受到“流动性替代效应”的制约，但这种效应不会完全抵消利率走廊对短期利率的影响，因此政策效果优于公开市场操作。第四，贷款便利工具的过于严格的抵押要求可能会导致拆借利率突破利率走廊上限。央行可以通过相机抉择策略和结合宏观审慎管理两种方式来应对这种利率异常升高，两者存在事后应对和事前预防的差异。第五，数值模拟分析证实了上述结论，并进一步说明：只有央行能够较准确地判断市场状况，公开市场操作才能有效减小拆借利率波动；反之，若央行反应过于滞后，反而会加大市场利率波动。然而，央行往往受到过往信息的影响，很难通过公开市场操作来及时补充流动性，利率走廊则可以克服这一不足。

本文的创新主要有：第一，从微观视角构建了一个同业拆借市场局部均衡模型。该模型刻画了同业拆借市场上商业银行流动性供求的异质性特征，为分析银行间市场行为及货币政策工具的调控机制提供了理论框架。第二，本文从调控利率波动的视角拓展了主要货币政策工具（如公开市场操作和利率走廊）的调控机制研究，区分了全面的流动性投放和有针对性的流动性调节。第三，本文的模型为回答在中国如何有效执行利率走廊提供了理论分析框架。

二、模型设定

假设经济中存在三个时期，

$t = 0,1,2$

，其中

$t = 1$

表示短期，

$t = 2$

表示长期。假设经济中在连续统

$[0,1]$

上存在风险中性的银行。在第0期，每家银行获得1单位存款，通过投资不同期限的资产来获取收益并管理流动性。银行有两种资产选择：长期资产和短期资产。长期资产持有到第2期的收益率为R，但流动性低。短期资产收益为1，但具有完全的流动性，可用来应对流动性冲击。银行投资长期资产的比例为

$\alpha $

，投资短期资产的比例为

$1 - \alpha $

。

银行的资金来源于大量储户的存款，储户可能提前提取存款，进而形成对银行的流动性冲击。储户在

$t = 0$

期的1单位存款，若在

$t = 1$

期取款，银行需支付

$\mathop d\nolimits_1 $

；若在

$t = 2$

期取款，银行则需支付

$\mathop d\nolimits_2 $

。假设银行

$i$

有

$\mathop \lambda \nolimits_i $

比例的储户要在

$t = 1$

期取款，则将面临

$\mathop \lambda \nolimits_i \mathop d\nolimits_1 $

的流动性冲击。设

$\mathop \lambda \nolimits_i $

是一个随机变量，

$\mathop \lambda \nolimits_i \in [0,1]$

，其密度函数为

$f\left( {\mathop \lambda \nolimits_i } \right)$

，

$E\left( {\mathop \lambda \nolimits_i } \right) = 0.5$

。与已有文献不同，本文假设流动性冲击是异质性的，这样就可以刻画银行的流动性异质特征和差异化的流动性需求。

在

$t = 1$

期，银行有两种方式管理流动性：同业拆借与出售长期资产。假设同业拆借市场是OTC市场。每家银行在该市场上与另一家银行展开双边谈判，以确定借贷利率与数量。假设资产市场是外生的，银行可以通过出售长期资产获得流动性。出售长期资产的价格为

${z_m}$

，但存在流动性调整成本，设为出售资产规模的函数：

${c_i} = 0.5\phi A_i^2$

，其中

${A_i}$

为长期资产出售量。银行会权衡以上两种流动性管理方式的成本。

求解该经济的均衡，需要分两步：第一步，在

$t = 1$

期，考虑流动性冲击，求解最优的银行同业借贷和资产交易决策；第二步，在

$t = 0$

期，银行根据未来收益和长期资产调整成本来决定资产配置，即长期资产和短期资产的投资比例。下面我们将分析不同货币政策工具下的市场均衡。

三、公开市场操作

1999年以来，公开市场操作已成为我国央行货币政策日常操作的重要工具。人民银行利用该工具吞吐流动性。与欧美国家不同，我国的公开市场操作具有数量型中介目标（戴根有，2003；伍戈和李斌，2016）。为了刻画这一特点，假设央行通过公开市场向每家银行注入流动性

$\eta $

，则向整个市场投放的流动性为

$m = \int \eta di$

。

（一）同业拆借市场中银行的决策。在

$t = 1$

期，银行有两种方式管理流动性：同业拆借与出售长期资产。那么，有两种情况需要考虑。第一，银行

$i$

与银行

$k$

相遇时，他们的总体流动性冲击较高，流动资产之和小于流动性冲击之和：

$({\lambda _i} + {\lambda _k}){d_1} > 2(1 - \alpha + \eta )$

。管理流动性时，双方会在出售长期资产和同业拆借之间进行权衡。银行

$i$

的利润函数为：

${\Pi _i} = R(\alpha - {A_i}) - 0.5\phi A_i^2 - (1 + {r_{ik}}){B_i} - (1 - {\lambda _i}){d_2}$

(1)

其中，

${A_i}$

为银行

$i$

的长期资产出售量，

${A_i} > 0$

。

${B_i}$

为银行

$i$

的同业市场借贷量，

${B_i} = {\lambda _i}{d_1} - (1 - \alpha ) - {z_m}{A_i} - \eta $

。该式表明，银行

$i$

同业拆入的流动性（

${B_i} < 0$

则为拆出的流动性）等于流动性冲击

${\lambda _i}{d_1}$

减去自有流动性资产

$1 - \alpha $

、出售长期资产获得的流动性

${z_m}{A_i}$

以及央行注入的流动性

$\eta $

。

${r_{ik}}$

为银行

$i$

与银行

$k$

之间达成的成交利率。那么，成交利率为（求解过程留存备索）：

$1 + {r_{ik}} = \frac{R}{{{z_m}}} + \frac{\phi }{{z_m^2}}(D - 1 + \alpha - \eta )$

(2)

设

$D = 0.5({\lambda _i} + {\lambda _k}){d_1}$

，表示两家相遇银行的平均流动性冲击水平（简称流动性冲击水平）。

第二，银行

$i$

与银行

$k$

相遇时，他们的流动性冲击水平较低（

$D \in [0,1 - \alpha + \eta ]$

）。他们的整体流动性剩余较多，交易的机会成本为

$R/{z_m}$

。此时，银行

$i$

的利润函数为：

${\Pi '_i} = R\alpha + 1 - \alpha + \eta - {\lambda _i}{d_1} - (1 - {\lambda _i}){d_2}$

(3)

（二）银行资产配置决策。在

$t = 0$

期，银行有1单位资金，配置短期资产和长期资产，以实现期望利润最大化。银行

$i$

的目标函数为：

$\mathop {\rm{Max}}\limits_\alpha \int_{D \in [1 - \alpha + \eta ,{d_1}]} {{\Pi _i}dF\left( D \right)} + \int_{D \in [0,1 - \alpha + \eta ]} {{\Pi '_i}dF\left( D \right)} - 0.5\psi {(\alpha - {\alpha _0})^2}$

(4)

其中，第一项为两家高流动性冲击银行匹配时银行

$i$

的预期收益，第二项为两家低流动性冲击银行匹配时银行

$i$

的预期收益，第三项为长期资产调整成本。本文借鉴马骏等（2016）的研究，假设银行投资长期资产时会发生成本

$0.5\psi {(\alpha - {\alpha _0})^2}$

。

${\alpha _0}$

为一个常数，

$\psi $

为反映长期资产投资成本大小的系数。这个成本函数用于刻画银行调整资产结构的难易程度。

我们需要求解银行

$i$

的最优资产配置，进而得到其对公开市场操作的反应程度。由式（4）关于

$\alpha $

的一阶条件可得（求解过程留存备索）：

$\frac{{\partial \alpha }}{{\partial \eta }} = 1 - \frac{\psi }{{\psi + \displaystyle\frac{\phi }{{z_m^2}}\tilde X + \frac{\phi }{{z_m^2}}\tilde Y + \frac{2}{{{d_1}}}(R - 1)\tilde Z}}$

(5)

其中，

$\tilde X$

、

$\tilde Y$

和

$\tilde Z$

为密度函数

$f\left( {\mathop \lambda \nolimits_i } \right)$

和

$f\left( {\mathop \lambda \nolimits_j } \right)$

的积分，均大于零，显然

${{\partial \alpha }/{\partial \eta }} \in [0,1]$

。式（5）表明，银行的长期资产投资与央行的公开市场操作正相关（

$\partial \alpha /\partial \eta > 0$

）。这意味着央行的流动性投放会减弱银行持有流动性资产的动机，从而增加银行的长期资产投资。产生这种效果的原因是，央行的公开市场操作是预期到的。在预期到的公开市场操作下，央行增加流动性时，银行会用央行提供的流动性来替代自己的流动性，本文将这种特征称为“流动性替代效应”。

（三）公开市场操作与同业拆借利率。综合以上分析，成交利率为：

$1 + {r_{ik}} = \left\{ \begin{aligned} & \frac{R}{{{z_m}}} + \frac{\phi }{{z_m^2}}[D - 1 + \alpha - \eta ]{\rm{ }} & 1 - \alpha + \eta \leqslant D \leqslant {d_1} \\ & \frac{R}{{{z_m}}} & 0 \leqslant D \leqslant 1 - \alpha + \eta \; \\ \end{aligned} \right.$

(6)

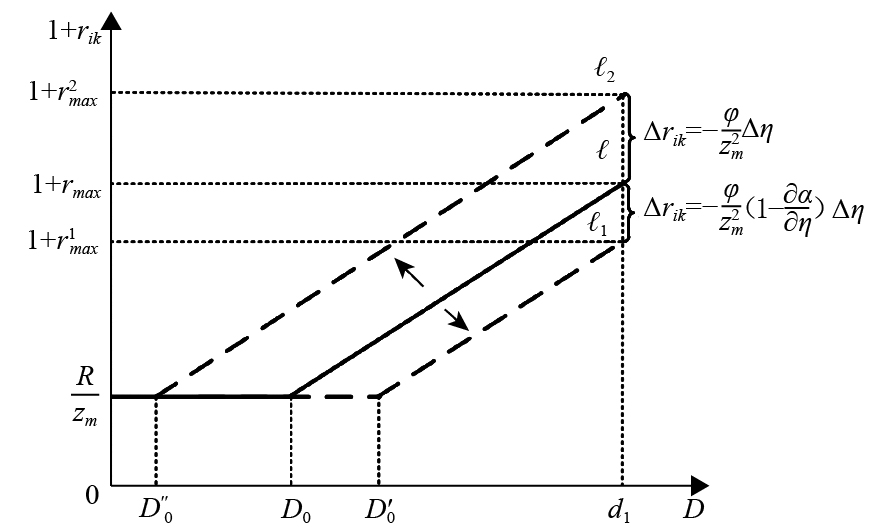
给定其他变量和参数，成交利率是流动性冲击水平（D的函数，如图1所示的

$\ell $

曲线。式（6）表明，公开市场操作能够影响拆借利率水平，进而调控拆借利率波动。然而，其政策效果会受到长期资产调整成本的影响，与之呈正相关关系。因此，未预期到的公开市场操作的政策效果要优于预期到的。其中的原因可以借助图1分析。

图 1 公开市场操作对同业拆借利率的影响

图选项

假设央行在第1期通过公开市场投放流动性

${\eta _1}$

，银行在第0期的预期为

${\eta _0}$

。那么，

${\eta _0}$

为预期到的公开市场操作，

${\eta _1} - {\eta _0}$

为未预期到的公开市场操作。

1. 预期到的公开市场操作。假设为了降低拆借利率水平和利率波动，央行通过公开市场增加流动性投放，且银行预期到了这一操作。此时，

$\Delta \eta {\rm{ = }}{\eta '_0} - {\eta _0} > 0$

，曲线

$\ell $

向右平移（

$\ell \to {\ell _{\rm{1}}}$

），成交利率下降，

$\Delta {r_{ik}} = - {\phi /{z_m^2}}(1 - {{\partial \alpha }/{\partial \eta }})\Delta \eta $

。因此，拆借利率下降，其分布区间收窄，从

$[{R/{{z_m}}},1 + {r_{max}}]$

变为

$[{R/{{z_m}}},1 + r_{max}^1]$

。

公开市场操作对拆借利率的影响有两种效应，分别为收入效应和替代效应，而拆借利率下降是两种效应的综合结果。流动性收入效应是指央行投放流动性增加了同业市场的供给，降低了拆借利率。流动性替代效应是指，由于预期到央行投放流动性，银行在第0期减少了流动性资产投资，导致同业市场供给下降，拆借利率上升。因为收入效应大于替代效应，所以拆借利率下降。此时，央行投放流动性的目的是抑制利率升高，而替代效应会削弱政策效果。进一步分析发现，流动性替代效应产生的原因是，银行可以预期到公开市场操作，进而反向调整资产配置。但银行调整资产配置时需要付出成本，流动性替代效应与长期资产调整成本负相关。因此，公开市场操作对拆借利率的作用大小受到长期资产调整成本的影响，与之呈正相关关系。

2. 未预期到的公开市场操作。当央行实际投放的流动性低于银行的预期投放（

$\Delta \eta {\rm{ = }}{\eta _1} - {\eta _0} < 0$

）时，

$\Delta {r_{ik}} = - ({\phi /{z_m^2}})\Delta \eta > 0$

，拆借利率上升。曲线

$\ell $

向左平移（

$\ell \to {\ell _2}$

），拆借利率波动也大幅上升，分布区间从

$[{R/{{z_m}}},1 + {r_{max}}]$

变为

$[{R/{{z_m}}},1 + r_{max}^2]$

。

未预期到的公开市场操作对利率的影响显著大于预期到的公开市场操作。计算发现，即使初期资产调整成本为0，未预期到的公开市场操作也能显著影响拆借利率，而预期到的公开市场操作则不能。其原因在于，公开市场操作是否被预期到，对银行资产组合的选择具有不同的影响。当公开市场操作被预期到时，银行会调整资产组合，流动性替代效应发挥作用，使公开市场操作对市场利率的影响有限。而当公开市场操作没有被预期到时，流动性替代效应不起作用，银行初期会选择持有更多的流动性资产以预防未来的流动性冲击，这种流动性持有动机与未预期到的公开市场规模无关。因此，未预期到的公开市场操作能够有效改变市场中的流动性总量，进而影响市场利率。由于存在流动性替代效应，要有效发挥公开市场操作的作用，应使用相机抉择的操作方式。

3. “钱荒”的形成机制。2013年6月，在我国银行间市场发生了“钱荒”，本文的模型可以对此进行分析。美国“次贷”危机之后，为了缓解外需疲弱所带来的经济下滑，我国开始采取宽松的货币政策，在很长一段时间内，源源不断地给市场提供流动性。在这种情况下，银行预期央行会持续提供流动性，所以

${\eta _0}$

非常高，结果就发生了“流动性替代效应”。在“次贷”危机之后，我国银行业的资产负债期限错配愈加严重，信贷资产长期化，流动资产比重下降，从而增加了银行间市场的脆弱性。不过，由于存在大量的国际收支盈余，央行通过外汇市场给银行业输送着流动性，问题并没有很快暴露。

在2013年年中，我国国际收支盈余快速下降，通过增加外汇占款方式来投放流动性的规模迅速减少。然而，由于央行对经济金融形势判断的滞后，未及时通过其他方式补充流动性，结果发生了一次异常的央行供给流动性的下降。央行实际提供的流动性远远低于预期的流动性供给，在模型中体现为

${\eta _1} < {\eta _0}$

。根据上述分析，这种未预期到的公开市场操作会带来整个银行间市场流动性的紧张。因此，当央行流动性供给枯竭时，银行自身的流动性也非常少，结果必然出现“钱荒”现象。这里的分析不同于已有文献对“钱荒”的解释，如“货币空转说”（朱孟楠和侯哲，2014；杨光和孙浦阳，2015）和“QE退出说”（董小君，2013；张明，2013；张明等，2016）。本文认为，货币在金融系统中空转和美国QE政策宣布退出等是导致银行间市场流动性减少的原因，但央行未及时采用公开市场操作来调节流动性供给、保持流动性稳定，从而引发了“钱荒”。

综合上述分析，可以得到如下结论：（1）被预期到的公开市场操作对拆借利率的调控作用受到“流动性替代效应”的制约。当银行能够灵活调整资产结构时，流动性替代效应会完全抵消被预期到的公开市场操作的作用，市场利率不受公开市场操作影响；银行调整资产结构越困难，流动性替代效应越弱，预期到的公开市场操作对拆借利率的影响就越大。（2）未预期到的公开市场操作不受流动性替代效应影响，对拆借利率的影响大。因此，相机抉择的公开市场操作的政策效果更优。但相机抉择需要以央行对经济走势的准确判断为前提。一旦央行的判断失误，公开市场操作不仅不能实现其调控目标，反而会导致利率异常波动。

四、利率走廊

从2010年开始，我国同业拆借市场频繁发生利率异常波动现象。同时，M₂存量过多使公开市场操作的调控空间受限，难以应对货币供求结构性失衡。在这一背景下，中国人民银行于2013年初推出SLF，并于2016年1月被官方确认为“利率走廊”。利率走廊包括存款便利工具和贷款便利工具。存款便利工具是指央行对银行的超额存款准备金支付利息，设其利率为

${r^s}$

；而贷款便利工具是指银行可以随时自由地向央行贷款，设其利率为

${r^f}$

。

（一）同业拆借市场中银行的决策。引入利率走廊之后，除了同业拆借和出售长期资产外，银行还可以利用利率走廊来管理流动性。利率走廊将同业拆借市场中银行的双边谈判区分为三种情况。第一，当银行

$i$

与银行

$k$

相遇时，他们的流动性冲击水平较高。如果不从央行融资，双边谈判的结果会使成交利率高于利率走廊上限，即

$1 + {r_{ik}} > 1 + {r^f}$

。此时，资金短缺的银行可以通过拆入流动性、出售长期资产和向央行借钱这三种方式来管理流动性，最优决策须满足三者的边际成本相等。而资金相对充裕的银行也会出售一些长期资产，使得资金的边际成本等于边际收益。此时，银行

$i$

的利润函数为：

$\Pi _i^f = R(\alpha - {A_i}) - 0.5\phi {A_i^2} - (1 + {r^f}){B_i} - (1 - {\lambda _i}){d_2}$

(7)

银行

$i$

与银行

$k$

的成交利率为（求解过程留存备索）：

$1 + {r_{ik}} = 1 + {r^f}$

(8)

第二，当银行

$i$

与银行

$k$

相遇时，他们的流动性冲击水平较低。如果不在央行存款，双边谈判的结果会使成交利率低于利率走廊下限，即

$1 + {r_{ik}} < 1 + {r^s}$

。此时，资金充裕的银行可以拆出流动性，也可以将其存入央行，同时会出售一些长期资产，使得资金的边际成本等于边际收益。而资金短缺银行的最优流动性管理决策须满足出售长期资产和同业拆借的边际成本相等。此时，银行

$i$

的利润函数为：

$\Pi _i^s = R(\alpha - {A_i}) - 0.5\phi {A_i^2} + (1 + {r^s}){B_i} - (1 - {\lambda _i}){d_2}$

(9)

银行

$i$

与银行

$k$

的成交利率为（求解过程留存备索）：

$1 + {r_{ik}} = 1 + {r^s}$

(10)

第三，当银行

$i$

与银行

$k$

相遇时，他们的总体流动性冲击水平中等大小，双边谈判的结果是：

$1 + {r^s} < 1 + {r_{ik}} < 1 + {r^f}$

。银行不使用走廊，双方根据竞价结果达成交易。银行

$i$

利润函数为：

${\Pi _i} = R(\alpha - {A_i}) - 0.5\phi A_i^2 - (1 + {r_{ik}}){B_i} - (1 - {\lambda _i}){d_2}$

(11)

银行

$i$

与银行

$k$

的成交利率为：

$1 + {r_{ik}} = \frac{R}{{{z_m}}} + \frac{\phi }{{z_m^2}}\left( {D - 1 + \alpha } \right)$

(12)

（二）银行资产配置决策。在

$t = 0$

期，银行有1单位资金，配置短期资产和长期资产以实现期望利润最大化。银行

$i$

在第0期的期望利润函数为：

$\mathop {\rm{Max}}\limits_\alpha \int_{D \in [1 - \alpha + \kappa ,{d_1}]} {\Pi _i^fdF\left( D \right)} + \int_{D \in [0,1 - \alpha + \nu ]} {\Pi _i^sdF\left( D \right)} + \int_{D \in [1 - \alpha + \nu ,1 - \alpha + \kappa ]} {{\Pi _i}dF\left( D \right)} - 0.5\psi {(\alpha - {\alpha _0})^2}$

(13)

其中，第一项是使用贷款便利工具时的期望收益，第二项是使用存款便利工具时的期望收益，第三项是不使用利率走廊便利工具时的期望收益。与公开市场操作类似，我们先求

$\alpha $

的一阶最优条件，然后对一阶最优条件等式两边分别求

${r^f}$

和

${r^s}$

的一阶导数，求解可得（求解过程留存备索）：

$\frac{{\partial \alpha }}{{\partial {r^f}}} = - \frac{{\tilde S}}{{\psi + {{\phi \tilde V}/{z_m^2}}}},\frac{{\partial \alpha }}{{\partial {r^s}}} = - \frac{{\tilde H}}{{\psi + {{\phi \tilde V}/{z_m^2}}}}$

(14)

其中，

$\tilde S$

、

$\tilde V$

和

$\tilde H$

为密度函数

$f\left( {\mathop \lambda \nolimits_i } \right)$

和

$f\left( {\mathop \lambda \nolimits_j } \right)$

的积分，均大于零。显然，

${{\partial \alpha }/{\partial {r^f}}} < 0$

，

${{\partial \alpha }/{\partial {r^s}}} < 0$

。式（14）表明，银行的长期资产投资与贷款便利利率负相关，即贷款便利利率越高，银行会持有越多的流动性资产、越少的长期资产。其原因在于，贷款便利利率越高，银行预期到未来面临流动性冲击时的融资成本越高，从而会投资越多的流动性资产。另外，银行的长期资产投资与存款便利利率也负相关，即存款便利利率越高，银行也会持有越多的流动性资产、越少的长期资产。其原因在于，存款便利利率越高，期望拆借利率越高，融资成本也就越高，从而银行会投资越多的流动性资产。式（14）还表明，银行的长期资产投资对存贷款便利利率变化的敏感程度与长期资产调整成本参数（

$\psi $

）负相关。

另外，我们还可以考察核心利率不变时，利率走廊限宽变化对银行资产配置的影响。假设核心利率为

$\bar r = \left( {{r^f} + {r^s}} \right)/2$

，走廊限宽为

$\delta $

，则

${r^f} = \bar r + \delta /2$

，

${r^s} = \bar r - \delta /2$

。将其代入式（13），并经过上述优化分析可得：

$\frac{{\partial \alpha }}{{\partial \delta }} = - \frac{{\tilde S - \tilde H}}{{2(\psi + {{\phi \tilde V}/{z_m^2}})}}$

(15)

式（15）表明，银行的长期资产投资与利率走廊限宽变化的关系并不明确，因为

${{\partial \alpha }/{\partial \delta }}$

的符号取决于高流动性冲击银行与低流动性冲击银行的相对分布情况（证明留存备索）。当央行放宽走廊限宽时，贷款便利利率上升会使银行减少长期资产投资、增持流动性资产，存款便利利率下降则会使银行进行相反的资产配置。如果高流动性冲击银行较多，则前一种效应更大，限宽放宽导致银行的长期资产投资减少（

${{\partial \alpha }/{\partial \delta }} < 0$

）；如果低流动性冲击银行较多，则后一种效应更大，限宽放宽导致银行的长期资产投资增加（

${{\partial \alpha }/{\partial \delta }} > 0$

）。这与Whitesell（2006）及Bindseil和Jabłecki（2011）的研究结论一致。但这些研究并没有指出产生这一结果的原因，本文则发现这是由银行流动性异质特征所致。

（三）利率走廊与同业拆借利率。结合式（8）、式（10）和式（12），在利率走廊背景下，同业成交利率为（计算过程留存备索）：

$1 + {r_{ik}} = \left\{ \begin{aligned} &\;1 + {r^f} \quad\quad\quad\quad\quad\quad \ \,1 - \alpha + \kappa \leqslant D \leqslant {d_1}\\ &\;\frac{R}{{{z_m}}} + \frac{\phi }{{z_m^2}}[D - 1 + \alpha ] \quad\; 1 - \alpha + \nu < {\rm{ }}D < 1 - \alpha + \kappa\\ &\; 1 + {r^s} \quad\quad\quad\quad\quad\quad \ \,\, 1 - \alpha < {\rm{ }}D \leqslant 1 - \alpha + \nu \quad \end{aligned} \right.$

(16)

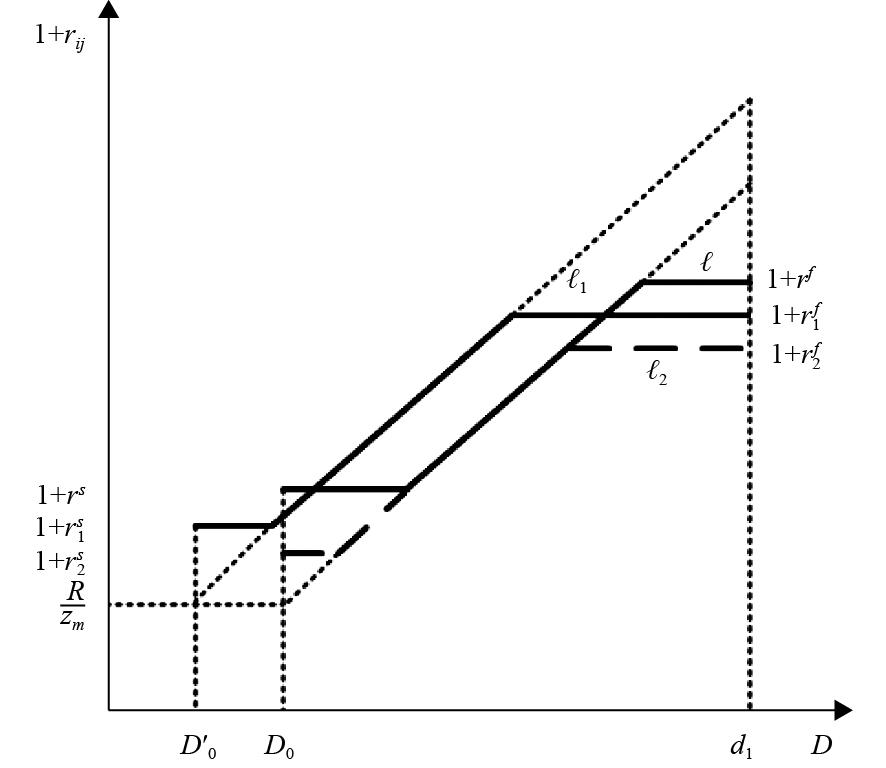
式（16）表明，成交利率是流动性冲击水平的分段函数。利率走廊可以较好地控制利率分布的区间，但调控利率的效果受到流动性替代效应的制约。产生这一结果的原因可以借助图2和图3分析。另外，本文集中分析利率走廊执行实践中常用的两种调控手段：调节走廊上下限和调节走廊限宽。

图 2 利率走廊上下限对同业拆借利率的影响

图选项

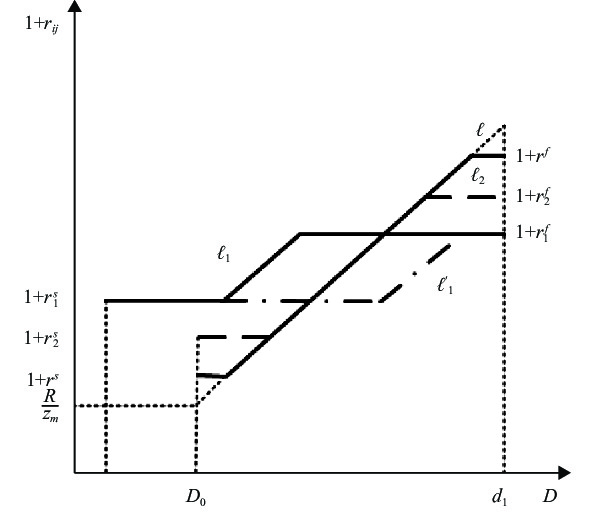
图 3 利率走廊限宽对同业拆借利率的影响

图选项

1. 利率走廊上下限同幅调整对拆借利率的影响

（1）预期到的利率走廊上下限调整。假设为降低利率和维持利率波动稳定，央行同时下调走廊上下限。成交利率曲线

$\ell $

向左平移（

$\ell \to {\ell _1}$

），拆借利率的分布区间从

$[1 + {r^s},1 + {r^f}]$

变为

$[1 + r_1^s,1 + r_1^f]$

，如图2所示。产生这一结果的主要原因是，在成交利率为

$1 + {r_{ik}} \in [1 + r_1^s,1 + r_1^f]$

的交易中，由于存贷款便利利率下降降低了银行的融资成本，银行会减持流动性资产，因此当面临相同的流动性冲击时，成交利率上升。与走廊调整之前相比，由于银行持有的流动性资产减少，原本一些流动性冲击较大的银行（D较大）从无需贷款便利转向贷款便利，原本一些流动性冲击较小的银行（D较小）则从存款便利变为不再需要存款便利。总体而言，由于利率走廊下调，银行间的流动性降低，银行更加依赖央行的流动性供给。因此，预期到的利率走廊调整也存在“流动性替代效应”。这种特征恰好符合政策意图，因为下调利率走廊的意图就是实施宽松的货币政策。从数量上讲，宽松的货币政策还要有数量宽松的含义。当下调利率走廊时，银行从央行拆借的资金增多，从而实现了数量上的宽松。同时，在银行的资产配置中，长期资产比例上升，这就增加了银行向实体经济提供的信贷规模。

此时，虽然央行增加了货币供给，但是银行减少了流动性资产（流动性替代效应）。两者综合的结果是，银行系统的流动性总量增加（证明留存备索）。可见，央行下调利率走廊增加了市场的货币总量，属于扩张性货币政策。同时，同业拆借加权平均利率也会下降。从调控方向来说，央行能够实现政策意图。

与公开市场操作相比，利率走廊下的流动性替代效应对拆借利率的影响存在明显的差异。式（6）表明，公开市场操作提供流动性（

$\eta $

上升），流动性替代效应使流动性资产减少（

$\alpha $

上升），结果拆借利率下降，但下降幅度部分被流动性替代效应所抵消。式（16）表明，当利率走廊下调时，流动性替代效应也会使流动性资产减少，对于不依赖利率走廊的银行，他们的拆借利率反而上升。利率走廊下调只会降低依赖走廊的银行的短期资金利率。因此，在利率走廊下，流动性替代效应对不同银行的短期资金利率的影响方向是相反的，并不像公开市场操作那样会降低每类银行的拆借利率。此外，当资产结构调整成本为零时，流动性替代效应会完全抵消公开市场操作对拆借利率的影响，但不会完全抵消利率走廊调整对拆借利率的影响。从这个角度看，利率走廊的政策效果比公开市场操作具有更好的稳健性。

（2）未预期到的利率走廊上下限调整。如果走廊上下限下调是未预期到的，成交利率曲线

$\ell $

向下移动（

$\ell \to {\ell _2}$

），拆借利率的分布区间从

$[1 + {r^s},1 + {r^f}]$

变为

$[1 + r_2^s,1 + r_2^f]$

，如图2所示。由于利率走廊调整未预期到，银行的资产配置维持在原来的状态，持有的流动性资产不受利率走廊调整的影响，因此不依赖利率走廊的银行的拆借利率不受影响。但有三类银行会受影响：第一类是原本就依赖利率走廊的银行。对于原来依赖贷款便利的银行（D很大），由于利率走廊下调，资金成本降低；对于原来依赖存款便利的银行（D很小），由于利率走廊下调，央行存款收益下降。第二类是原来不依赖走廊、现在依赖走廊的银行（D较大）。这些银行原来通过拆借市场融资的利率较高，贷款便利利率下调后，他们转向依赖央行融资，从而融资成本下降。第三类是原来依赖走廊、现在不依赖走廊的银行（D较小）。这些银行原来将多余的资金存在央行，收益率较高；存款便利利率下降后，他们将以高于此的利率拆出资金。

这种未预期到的利率走廊下调会降低银行间的平均拆借利率水平。由于一些流动性冲击低的银行不选择在央行存款而回到拆借市场，另一些流动性冲击高的银行选择向央行借款而离开拆借市场，这样低流动性冲击的交易替代了高流动性冲击的交易，或者低成交利率取代了高成交利率。因此，成交利率在各部分都有所下降，加权平均的拆借利率也会下降。

2. 利率走廊限宽调整对拆借利率的影响

（1）预期到的利率走廊限宽调整。假设为抑制利率波动和保持目标利率不变，央行决定收窄走廊的限宽。如果该政策是被预期到的，成交利率曲线

$\ell $

可能向左平移（

$\ell \to {\ell _1}$

），也可能向右平移（

$\ell \to {\ell '_1}$

），因为

${{\partial \alpha }/{\partial \delta }}$

的符号不确定。也就是说，存在“流动性替代效应”，但该效应的大小和方向不确定。拆借利率的分布区间变小，从

$[1 + {r^s},1 + {r^f}]$

变为

$[1 + r_1^s,1 + r_1^f]$

，如图3所示。

此时，我们不能确定银行系统的流动性总量的变化情况（证明留存备索），也就不能确定加权平均拆借利率的波动方向，因为“流动性替代效应”的大小和方向不确定。利率走廊的执行经验支持这一结论。比如，2006年4月，英格兰银行收窄了利率走廊限宽，SONIA从低于目标利率5个基点上升为高于5个基点。2008年10月，欧洲央行也收窄了利率走廊限宽，而EOIAR却呈现长期下跌趋势。

（2）未预期到的利率走廊限宽调整。如果是未预期的走廊限宽收窄，成交利率曲线

$\ell $

没有移动，只是水平部分向中间收缩（

${\ell _2}$

）。拆借利率的分布区间从

$[1 + {r^s},1 + {r^f}]$

变为

$[1 + r_2^s,1 + r_2^f]$

，如图3所示。由于未预期到限宽调整，银行不会调整资产配置，因此不存在“流动性替代效应”。那么，同业市场货币数量变动等于央行货币释放。此时，同业市场货币数量增加，加权平均拆借利率下降。央行较好地实现了扩张性货币政策的意图。

综合上述分析，可以得到如下结论：（1）同幅度下调利率走廊上下限的政策属于扩张性货币政策，反之则为紧缩性货币政策。若是预期到的，由于存在“流动性替代效应”，该政策对拆借利率的调控作用较小；若是未预期到的，其对拆借利率的调控作用较大。（2）收窄利率走廊限宽的政策属于扩张性货币政策，反之则为紧缩性货币政策。若是预期到的，由于存在“流动性替代效应”，该政策对拆借利率的调控方向并不明确；若是未预期到的，则可以有效调控拆借利率。（3）利率走廊在稳定利率波动方面优于公开市场操作。无论是预期到还是未预期到的，利率走廊都能较好地控制拆借利率波动区间。

五、利率走廊抵押约束与同业拆借利率

抵押要求是指银行使用央行贷款便利工具时需要提供合格的抵押品。这是一种风险规避机制，但客观上会对银行的信用扩张行为产生影响，进而影响拆借利率。已有文献大多将抵押率作为内生变量，根据抵押品的成本等特征来决定最优抵押率（Berentsen和Monnet，2008；Martin和Monnet，2008；Berentsen等，2010）。本文认为抵押率由央行决定，是重要的政策变量。在“次贷”危机期间，执行利率走廊的国家几乎都上调了抵押率。为了刻画抵押要求及其影响，本文引入如下的抵押约束：

${L_i} \leqslant \rho \alpha $

(17)

其中，

${L_i}$

为银行

$i$

利用贷款便利工具贷款的数量，

$\rho $

为央行规定的长期资产抵押率（

$0 \leqslant \rho \leqslant 1$

）。

（一）银行决策。在

$t = {\rm{1}}$

期，抵押要求将银行使用贷款便利的同业交易区分为两种情况：一种是银行的流动性需求较小，其从央行融资不受抵押要求的约束；另一种是银行的流动性需求较大，其从央行融资受到抵押要求的约束。第一种情况与上述利率走廊的分析相同。下面我们分析第二种情况。假设银行

$i$

与银行

$k$

相遇，他们的总体流动性冲击很高，需要大量的流动性，但无法提供足够的抵押品，因此只能以更高的利率拆借。银行

$i$

的利润函数为：

$\Pi _i^{'f} = R(\alpha - {A'_i}) - 0.5\phi A_i^{'2} - (1 + {r'_{ik}}){B_i} - (1 + {r^f})\rho \alpha - (1 - {\lambda _i}){d_2}$

(18)

两家银行的成交利率为（求解过程留存备索）：

$1 + {r'_{ik}} = \frac{R}{{{z_m}}} + \frac{\phi }{{z_m^2}}[D - 1 + (1 - \rho )\alpha ]$

(19)

在

$t = 0$

期，银行依然以预期收益减去长期资产调整成本最大化为目标来决定资产配置。使用与上文类似的优化过程可得（求解过程留存备索）：

$\frac{{\partial \alpha }}{{\partial \rho }} > 0$

式（20）表明，银行的长期资产投资与贷款便利工具抵押率正相关。其原因在于，在有抵押要求的情况下，银行持有的长期资产具有抵押价值，其大小由参数

$\rho $

决定。

$\rho $

越大，长期资产的抵押价值越高，银行的持有意愿越强。

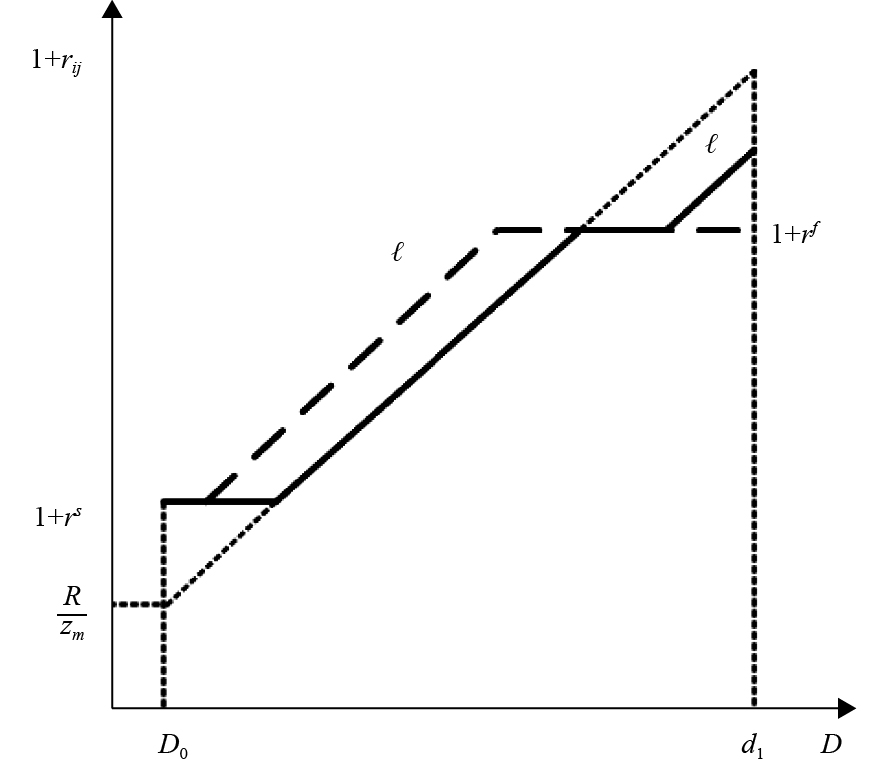
（二）抵押政策与同业拆借利率。结合式（8）、式（10）、式（12）和式（19）得到成交利率（留存备索）。如图4所示，当银行从央行融资受到利率走廊抵押要求的约束时，成交利率会突破利率走廊上限。其原因在于，银行虽然有意愿从央行融资，但是没有足够的抵押品，因此只能在同业市场上拆借；同时，由于银行的流动性需求较大，而对方银行提供流动性资金的边际成本递增，因此成交利率超过走廊上限水平。

图 4 抵押约束对同业拆借利率的影响

图选项

为了应对这种利率的异常升高，央行可以采取相机抉择的策略来调节抵押政策，或者结合宏观审慎管理来制定抵押政策。后一种应对方式与牛慕鸿（2018）的观点相同，但其没有给出具体做法。如果采用相机抉择策略来调节抵押政策，那么在第1期，当发现部分交易的成交利率高于走廊上限时，央行可以及时提高抵押率。具体来说，央行应将抵押率提高为

$\bar \rho {\rm{ = }}{{z_m^2}/{\phi \alpha }} \times $

$ [{R/{{z_m}}} + {\phi /{z_m^2}} \times ({d_1} - 1 + \alpha ) - (1 + {r^f})]$

。因为是相机抉择，银行没有预期到，所以提高抵押率不会影响银行的资产配置（

$\alpha $

），成交利率曲线

$\ell $

不发生移动。而由于抵押率提高，高流动性冲击银行可以使用贷款便利工具来满足流动性需求，因此较高的成交利率下降至贷款便利利率水平。

如果将抵押政策和宏观审慎管理相结合，那么央行应根据银行体系的流动性供求状况来逆周期制定抵押政策，银行此时可以预期到央行提高抵押率。具体来说，央行可以根据宏观审慎评估（MPA）体系中的流动性指标来判断银行体系的流动性变化周期。如果银行体系出现流动性短缺趋势，央行可以考虑将抵押率提高为

$\bar \rho $

，以保证高流动性冲击发生时，拆借利率不会突破利率走廊上限。另外，与相机抉择策略不同，由于可以预期到抵押率提高，银行会增加其长期资产投资，导致成交利率曲线向左平移（

$\ell \to \ell '$

），但其分布区间不会超出走廊范围。

综合上述分析，可以得到如下结论：（1）抵押要求过于严格会约束银行从央行融资，导致拆借利率异常升高，可能会突破利率走廊上限。（2）为了应对抵押约束所导致的拆借利率异常升高，央行可以采取相机抉择策略来调节抵押政策，也可以将抵押政策与宏观审慎管理相结合。相机抉择策略可以使拆借利率异常升高后回归利率走廊范围，结合宏观审慎管理则可以避免这种利率的异常升高。

六、数值模拟分析

为使上述结论更加直观，本文利用式（6）、式（16）和式（19）进行了数值模拟分析。为了观察货币市场利率的波动，我们将上文的模型扩展成一个更多期限的模型。假设模型中设定的3期发生在同一天，第0期设为上午，第1期设为中午，第2期设为下午。下面我们模拟每天的均衡拆借利率的变化情况。模型中的基础参数取值为：

$R{\rm{ = }} 1.6$

，

${z_m} = 100$

，

$\phi = 300$

。另外，为了动态模拟市场利率的变化情况，我们将银行面临的冲击分解为两类：异质性冲击和系统性冲击，则可令

$\Phi = {D_{ik}} + D'(t) - 1 + \alpha $

，其中

$D'(t)$

为系统性冲击。由于银行的货币持有量（

$1 - \alpha $

）在上午已经决定，而流动性冲击（D）发生在中午，因此可将

$\Phi $

理解为拆借市场的流动性缺口或剩余（

$\Phi > 0$

为短缺，

$\Phi < 0$

为剩余）。货币政策主要通过应对每个时点上的

$\Phi (t)$

（t表示第t天中午的流动性状况）来调控拆借利率。数值模拟过程为：首先，根据式（6）、式（16）和式（19），在同一时点求得成交利率的市场均值，即拆借利率；然后，根据拆借利率的不同波动形态，分析三种政策（公开市场操作、利率走廊与抵押政策）的调控效果。

公开市场操作主要根据

$\Phi (t)$

来确定货币投放量。考虑到信息不完美，假设央行的货币投放量具有“向后看”的特征，即

$\eta = \theta \Phi (t) + (1 - \theta ) \Phi (t - 1)$

，其中

$\theta \in [0,1]$

为央行对市场流动性状况的判断准确度。

$\theta $

越高表示央行的判断越准确。由于

$\eta $

还取决于前一时点的流动性状况，

$\theta $

越高还表示央行应对流动性冲击越及时，反之则说明央行的调控越依赖滞后信息。

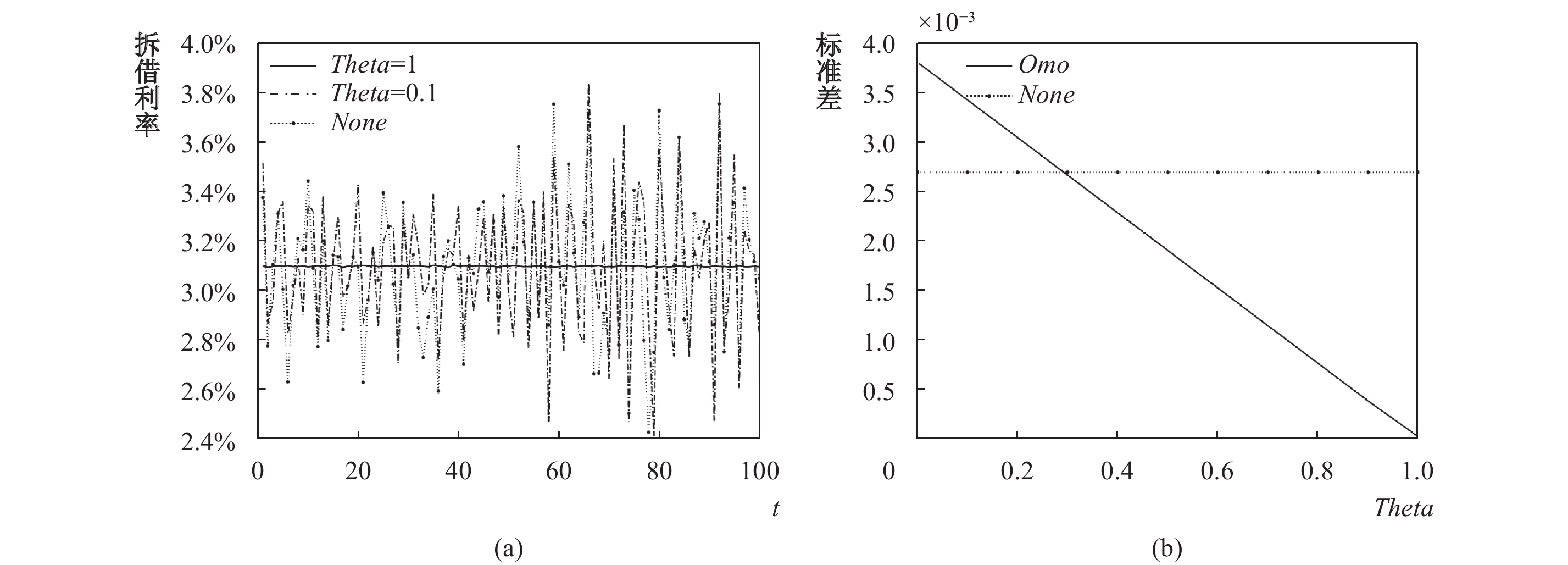
对于公开市场操作，本文模拟了

$\theta = 1 $

和

$\theta = 0.1 $

这两种央行判断准确度下，以及没有货币政策调控时（none）的拆借利率波动情况。模拟结果如图5所示。图5（a）表明，当央行能够准确了解流动性的系统性变化时（

$\theta = 1 $

），恰当的公开市场操作能够实现市场利率的完全稳定。但当公开市场操作具有明显的滞后特点时（

$\theta = 0.1 $

），市场利率的波动没有明显改善。图5（b）进一步证实了这一结果。图5（b）模拟了

$\theta $

与拆借利率波动（纵轴为标准差）之间的关系，包括公开市场操作（omo）和无政策调控（none）两种情况。在公开市场操作下，随着

$\theta $

的增加，拆借利率的波动性下降。这说明在公开市场操作下，央行对市场流动性状况的判断越准确，拆借利率的波动幅度下降越大。图中omo和none有一个交点，说明

$\theta $

达到一定数值后，公开市场操作才能减弱拆借利率的波动。

图 5 公开市场操作与拆借利率波动

图选项

上述结果证实了上文的结论，即公开市场操作对拆借利率的调控效果依赖于央行对当前市场状况的判断。一旦央行判断失误，公开市场操作不仅不能实现央行的调控目标，反而会导致利率异常波动。同时，模拟结果与上文对“钱荒”的分析也吻合。模拟结果还说明，央行往往根据历史和当前的信息来判断拆借市场的流动性缺口，很难及时补充流动性。因此，在公开市场操作下，拆借利率往往呈现更大的波动性。而利率走廊可以利用其便利工具来及时调节流动性，即对于较高的拆借利率自动补充流动性，对于较低的拆借利率则自动吸纳流动性，从而可以克服公开市场操作的上述不足。

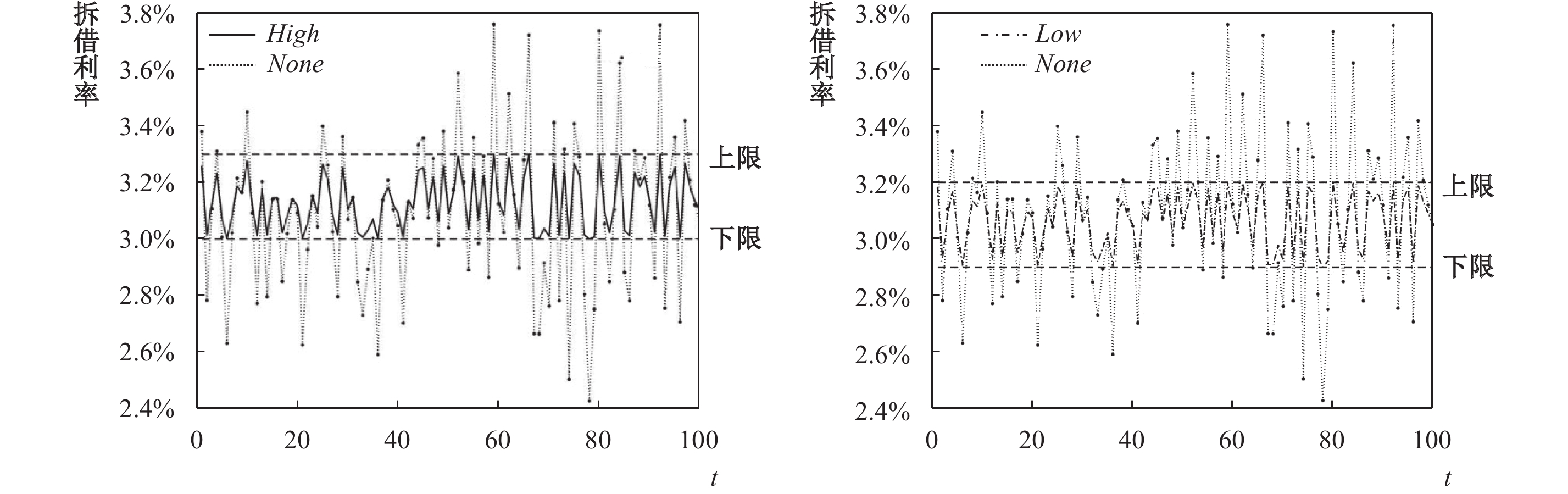
对于利率走廊，本文模拟了没有货币政策调控时（none），以及较高位置（high）与较低位置（low）的利率走廊下拆借利率的波动情况。模拟结果如图6所示。从中可以看出，利率走廊可以将拆借利率控制在其范围内，并主要通过影响高于上限的拆借利率和低于下限的拆借利率来实现调控。这与上文所揭示的利率走廊机制一致。此外，利率走廊同幅度下调后（

$ high \to low $

），拆借利率降低，且其政策效果与央行的判断无关。这证实了上文的结论，即同幅度下调利率走廊上下限的政策属于扩张性货币政策。

图 6 利率走廊与拆借利率波动

图选项

结合图5和图6，利率走廊在稳定利率波动方面优于公开市场操作，能较好地控制拆借利率的波动区间。但当利率走廊的抵押政策过紧时，银行从央行融资会受到约束，拆借利率也可能突破利率走廊上限。

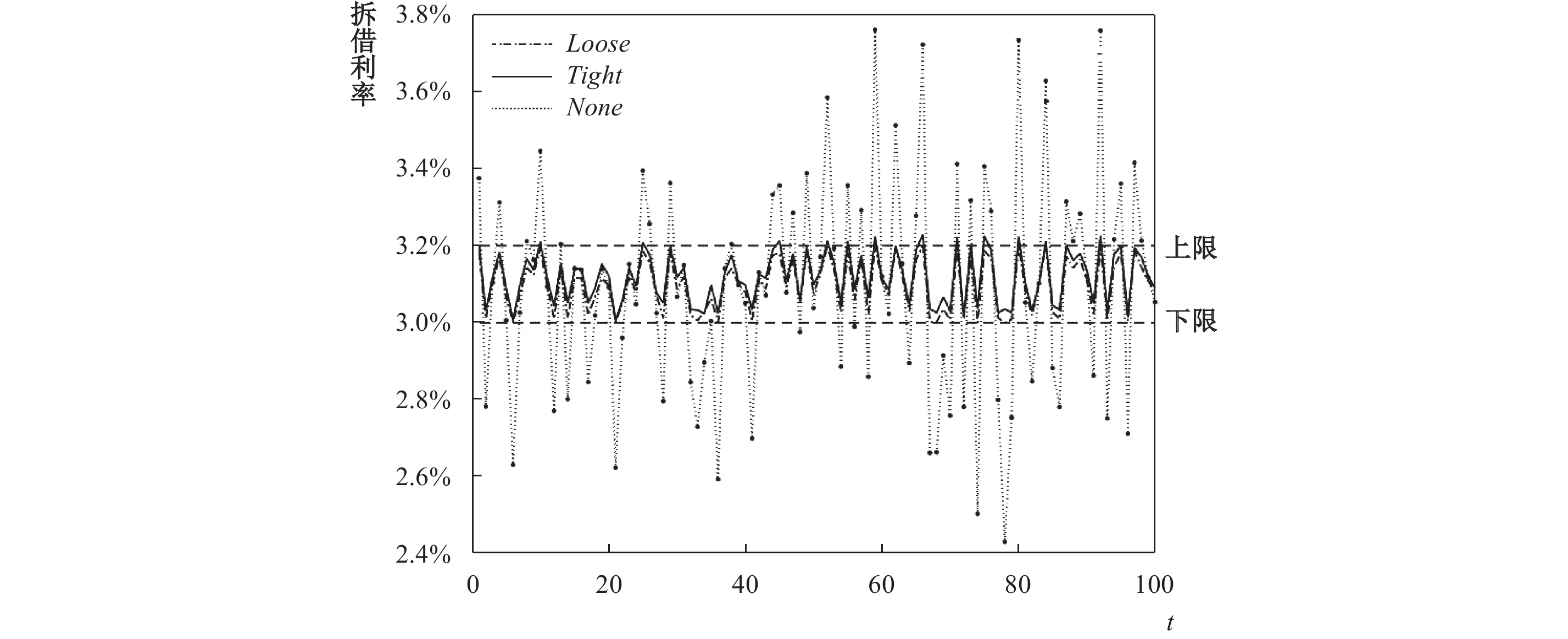
本文对利率走廊的抵押政策也进行了数值模拟分析，选取

$\rho {\rm{ = }} 0.5$

与

$\rho {\rm{ = }} 1$

分别表示抵押政策过紧（tight）和宽松（loose）的情况。模拟结果如图7所示。从中可以看出，当抵押政策过紧时，拆借利率多次突破利率走廊上限。但与没有利率走廊调控（none）时相比，拆借利率还是有所下降。这与上文的结论相符，即当银行从央行融资受到抵押要求的约束时，流动性需求较高的银行虽然有意愿从央行融资，但是没有足够的抵押品，而只能接受同业市场较高的利率。此时，抵押品虽然不能满足银行的需要，但是也可为其获得一些央行贷款，因此拆借利率比没有利率走廊时有所下降。央行放松抵押政策后，拆借利率回到利率走廊范围内波动。此时，流动性需求较高的银行从央行融资不再受到抵押政策的约束，利率走廊恢复自动、及时调节拆借利率的能力。

图 7 抵押政策与拆借利率波动

图选项

七、结　论

本文刻画了一个具有OTC市场属性的同业拆借市场，在这个市场上，具有异质流动性特征的银行两两匹配交易，进而构建了一个银行间市场的局部均衡模型。本文的模型深入刻画了银行间市场形成拆借利率的过程，为分析公开市场操作和利率走廊提供了一个统一的理论框架。研究发现，公开市场操作和利率走廊在调控利率波动方面各有优势和不足。首先，公开市场操作通过调节整个同业拆借市场的流动性来调控利率波动。而利率走廊只需调节部分银行的流动性就可以调控利率波动，从而利率走廊调控对市场的扰动较小。其次，在调控短期利率方面，预期到的公开市场操作和利率走廊调整都会受到“流动性替代效应”的约束，流动性替代效应可能会完全抵消公开市场操作对短期利率的调节作用，而不会完全抵消利率走廊的调控作用。在稳定利率方面，公开市场操作依赖于央行的判断，而利率走廊更具有独立性，政策效果更稳健。最后，在利率走廊机制下，过紧的抵押政策可能会导致拆借利率突破走廊上限。不过，央行可以通过相机抉择策略和结合宏观审慎管理两种方式来调节抵押政策，以分别实现事后应对和事前预防的不同目的。

　　* 感谢匿名审稿人及“中央财经大学宏观金融组”各位成员提出的宝贵意见与建议。文责自负。

① 一些文献已经证实，包括我国在内的世界上大多数国家的银行间市场是OTC市场（Ashcraft等, 2011；周荣芳，2015）。另外，中国人民银行制定的《同业拆借管理办法》第十五条规定，同业拆借交易以询价方式进行，自主谈判、逐笔成交；第十六条规定，同业拆借利率由交易双方自行商定。

主要参考文献

[1]	董小君. 从" 热钱”到" 钱荒”: 形势逆转的原因、影响及应对之策[J]. 经济学动态, 2013(7): 94–98.

[2]	马骏, 施康, 王红林, 等. 利率传导机制的动态研究[J]. 金融研究, 2016(1): 31–49.

[3]	牛慕鸿. 利率走廊运行机理再认识[J]. 中国金融, 2018(9): 25–27.

[4]	牛慕鸿, 张黎娜, 张翔. 利率走廊、利率稳定性和调控成本[J]. 金融研究, 2017(7): 16–28. DOI:10.3969/j.issn.1006-169X.2017.07.004

[5]	孙国峰, 蔡春春. 货币市场利率、流动性供求与中央银行流动性管理——对货币市场利率波动的新分析框架[J]. 经济研究, 2014(12): 33–44. DOI:10.3969/j.issn.2095-3151.2014.12.033

[6]	伍戈, 李斌. 货币数量、利率调控与政策转型[M]. 北京: 中国金融出版社, 2016.

[7]	杨光, 孙浦阳. 流动性过剩是否造成了" 钱荒”现象−基于异质性DSGE框架的分析[J]. 南开经济研究, 2015(5): 59–73.

[8]	张明. 银行间市场" 钱荒”的根源及政策含义[J]. 金融市场研究, 2013(7): 30–33.

[9]	张明, 郭子睿, 何帆. " 钱荒”为什么会发生? −上海银行间同业拆放利率的影响因素分析[J]. 国际金融研究, 2016(12): 84–93.

[10]	朱孟楠, 侯哲. 中国商业银行资金错配问题研究−基于" 钱荒”背景下的思考[J]. 国际金融研究, 2014(4): 62–69.

[11]	Ashcraft A, McAndrews J, Skeie D. Precautionary reserves and the interbank market[J]. Journal of Money, Credit and Banking, 2011, 43: 311–348. DOI:10.1111/jmcb.2011.43.issue-s2

[12]	Berentsen A, Monnet C. Monetary policy in a channel system[J]. Journal of Monetary Economics, 2008, 55(6): 1067–1080. DOI:10.1016/j.jmoneco.2008.07.002

[13]	Berentsen A, Marchesiani A, Waller C J. Channel systems: Why is there a positive spread? [R]. CESifo Working Paper No.3251, 2010. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1713686

[14]	Berentsen A, Marchesiani A, Waller C J. Floor systems for implementing monetary policy: Some unpleasant fiscal arithmetic[J]. Review of Economic Dynamics, 2014, 17(3): 523–542. DOI:10.1016/j.red.2013.09.001

[15]	Heider F, Hoerova M, Holthausen C. Liquidity hoarding and interbank market rates: The role of counterparty risk[J]. Journal of Financial Economics, 2015, 118(2): 336–354. DOI:10.1016/j.jfineco.2015.07.002

[16]	Whitesell W. Interest rate corridors and reserves[J]. Journal of Monetary Economics, 2006, 53(6): 1177–1195. DOI:10.1016/j.jmoneco.2005.03.013