
2019第45卷第3期
2. 中国社会科学院 财经战略研究院,北京 100028
2. National Academy of Economic Strategy,Chinese Academy of Social Science,Beijing 100028,China
一、引 言
自2008年国际金融危机爆发以来,房地产价格与企业投资的演变成为刻画中国经济运行的重要特征。国家统计局数据显示,2009—2016年,我国全社会固定资产投资增速出现了趋势性的下降:2009年固定资产投资增速高达30.1%,而到了2016年,投资增速仅为7.9%。但同期房地产价格增速却呈现“V”形走势:2009—2013年,全国商品房增速稳定在7.5%以上,而2014—2016年,房价增速却从1.4%快速上升至10.1%。按照中国人民银行公布的数据,2016年新增贷款的45.6%与房地产贷款相关,资金“脱实向虚”问题引起社会各界广泛讨论。随着政府持续加大对房地产市场的宏观调控,2017年房地产价格快速上涨的势头得到一定程度的控制,同时外需改善与供给侧结构性改革的加快推进改善了工业企业的生产经营状况,全社会固定资产投资增速出现一定程度的回升。尽管当前企业投资增速下行与房地产价格大幅上涨的状况有所缓解,但该问题产生的根源并未彻底消除,如房价上涨从一二线向三四线城市转移,实体投资尤其是民间投资增速仍不容乐观。因此,2017年12月中央经济工作会议明确强调“加快建立多主体供应、多渠道保障、租购并举的住房制度”和“促进有效投资特别是民间投资合理增长”。鉴于此,清晰地认识房地产价格与企业投资之间的内在联系,对于防范化解我国系统性金融风险和出台更有效的宏观调控政策具有重要意义。
房地产价格与企业投资之间是否存在关联?这个问题一直以来就受到学术界的高度重视。该问题的一个重要研究视角体现在房地产的资产与生产要素属性上。作为一种资产,企业购买房地产除了提供资金收入外,还能作为一种融资抵押物(Barro,1976),缓解企业外部融资压力。Chaney等(2012)采用1993—2007年美国微观数据研究发现,这段时期美国企业持有的房地产价值对企业投资具有正向促进作用。张成思和张步昙(2016)将传统金融与房地产行业统称为“泛金融部门”(Krippner, 2005),而金融、房地产之外的其他行业定义为实体经济。他们的实证研究(样本期间为2006—2014年)表明,企业金融化尽管会带来充裕资金,但是会使其更加依赖金融渠道获利,减少对固定资产的投资。Wang等(2017)构建了一个民营与国有企业的DSGE模型,将融资约束机制引入模型中,发现民营企业投资与房地产价格正相关,而国有企业投资与房地产价格负相关。
房地产的另一个属性是作为生产的投入要素之一。土地、房地产价格上涨,租赁或自建营业用房的成本上升,这将提高企业生产成本、压缩利润,对企业投资产生影响。吴海民(2012)分析了沿海地区民营工业数据,发现房地产价格上涨对民营投资具有明显的“挤出效应”,加剧了民营工业的“规模空心化”。罗时空和周亚虹(2013)拓展了Iacoviello(2005)的模型,认为房地产具有生产要素与资产的双重属性。他们发现,稳定房价从长远看有利于降低企业投资成本,促进企业投资。
作为国民经济的一个重要部门,房地产也将对上下游产业发展产生重要影响。原鹏飞和冯蕾(2014)考察了房地产价格上涨对全社会投资的影响,发现房价上涨带动了建筑业、重工业等房地产相关行业的发展,但会对农业、轻工业等非住房投资产生挤出效应。许宪春等(2015)采用投入产出等国民经济核算理论和方法对统计数据进行了细致分析,发现1998—2013年房地产开发企业的国内贷款增速比制造业企业高出1.3%,导致房地产贷款占国内全部贷款的比重高出制造业的水平从5.8%扩大到11.6%。他们的研究证实了房地产经济过热时,市场经济中资本的逐利性会导致大量资本进入房地产市场,助推房价进一步上涨,对实体经济产生“抽血效应”。
以往的文献从不同侧面研究了企业投资与房地产价格之间的关系,产生了大量有意义的成果,但仍存在一些不足:第一,部分研究工作集中于实证检验,理论机制分析不够充分,不利于厘清关键变量之间的传导机理;第二,已有文献对2008年之后企业资产负债表机制的研究不够,未考虑当前我国企业债务高企,企业资产负债表对自身投资决策的影响,即企业主动修复资产负债表过程;第三,绝大部分研究对金融危机之后我国经济典型特征的刻画不充分,同时缺乏对房地产价格与实体投资间关系共同影响因素的分析。
本文以2008年以来我国经济运行的典型特征为出发点,构建了含有“资产负债表衰退”机制的新凯恩斯动态随机一般均衡模型,重点考察了房地产偏好冲击和企业资产负债表冲击对房地产价格与企业投资之间关系的影响。研究表明,房地产偏好正向冲击在提高房价的同时,小幅挤入企业投资;企业资产负债表负向冲击则降低企业投资,导致盈余资金转入房地产市场,推高房价。进一步研究发现,在企业资产负债表负向冲击时,政府降低企业税负有助于刺激企业投资,缓解资金的“脱实向虚”。
本文的主要贡献体现在:一是在理论上,重视企业资产负债表传导机制,将Koo(2011)的“资产负债表衰退”理论引入新凯恩斯动态随机一般均衡模型中。目前,这方面的研究十分匮乏,本文拓展了企业资产负债表问题的理论研究。二是在研究视角上,重视对中国经济现实特征的刻画,重点分析当前我国房地产需求刚性与外需疲软对房地产价格与企业投资之间关系的作用机理。三是在政策涵义上,针对企业的不同税负情形,考察了房地产偏好冲击与企业资产负债表冲击对房地产价格与企业投资关系的影响,为政府决策部门出台相应的宏观调控政策提供了一定的参考依据。
二、模型构建
本文依据Koo(2011)的资产负债表衰退理论,构建了含有“资产负债表衰退”特征的NK-DSGE模型。该模型由耐心家庭、非耐心家庭、企业、资本品生产商、零售商、银行家、政府与中央银行构成。“资产负债表衰退”理论的核心在于企业部门。通常情形下,企业的经营目标是利润最大化。但当外部不利因素导致企业资产负债表严重恶化时,为了继续在市场上存活,企业经营决策的重心开始转向负债最小化。本文借鉴Cevallos-Fujiy(2015)模型思想,依据企业净资产与均衡净资产的相对水平来构建一个logistic函数,将两种经营目标统一在一个复合目标函数中。
(一)耐心家庭。参考Yu等(2013)的设定,耐心家庭对消费、房地产自用量和劳动做出决策,最大化其终生效用贴现值。目标函数为:
| $ \max \;\;{E_0}\sum\limits_{t = 0}^\infty {\beta _P^t [\ln ({C_{P,t}} - \eta {C_{P,t - 1}}) + {j_t}\ln \left( {\kappa {H_{P,t}}} \right) - \nu \frac{{L_{P,t}^{1 + \chi }}}{{1 + \chi }}} ] $ |
其中,
| ${C_{P,t}} + Q_t^H({H_{P,t}} - {H_{P,t - 1}}) + {B_{P,t}} \leqslant \frac{{{R_{t - 1}}{B_{P,t - 1}}}}{{{\pi _t}}} + {W_{P,t}}{L_{P,t}} + R_t^H(1 - \kappa )Q_t^H{H_{P,t}} + {F_t} + Div{i_t}$ | (1) |
其中,
(二)非耐心家庭。非耐心家庭不出租房地产,效用函数由消费、房地产持有量与劳动共同决定。除了提供劳动获得收入外,非耐心家庭还利用房地产抵押贷款,以平滑各期消费。非耐心家庭的目标函数、预算约束与抵押贷款约束分别为:
| $\max \;\;{E_0}\sum\limits_{t = 0}^\infty {\beta _{IP}^t [\ln ({C_{IP,t}} - \eta {C_{IP,t - 1}}) + {j_t}\ln {H_{IP,t}} - \nu \frac{{L_{IP,t}^{1 + \chi }}}{{1 + \chi }}} ]$ |
| ${C_{IP,t}} + Q_t^H({H_{IP,t}} - {H_{IP,t - 1}}) + \frac{{{R_{IP,t - 1}}{B_{IP,t - 1}}}}{{{\pi _t}}} \leqslant {B_{IP,t}} + {W_{IP,t}}{L_{IP,t}}$ | (2) |
| ${B_{IP,t}} \leqslant m{E_t}\frac{{Q_{t + 1}^H{H_{IP,t}}{\pi _{t + 1}}}}{{{R_{IP,t}}}}$ | (3) |
其中,
(三)企业。与通常的新凯恩斯模型不同,本文模型中企业的决策目标服从logistic分布,其概率分布是一个关于企业净资产相对水平的函数,即企业的决策目标是利润最大化与债务最小化的复合函数。企业的决策目标函数为:
| $\max \;\;{Pr _t}{\Pi _t} - (1 - {Pr _t}){E_t}{D_{t + 1}}$ |
其中,
| ${s_t}Q_t^K{K_t} = {D_t} + {N_t}$ | (4) |
其中,
在正常情形下,企业经营以利润最大化为目标,其表达式为:
| ${\Pi _t}{\rm{ = (1 - }}\tau {\rm{)}}\frac{{{Y_t}}}{{{X_t}}} - {W_{P,t}}{L_{p,t}} - {W_{IP,t}}{L_{Ip,t}} - R_t^H(1 - \kappa )Q_t^H{H_{P,t}} - \delta Q_t^K{K_t}$ | (5) |
其中,
| ${D_{t{\rm{ + }}1}}{\rm{ = }}{R_{E,t}}{D_t} + Q_{t{\rm{ + 1}}}^K({K_{t{\rm{ + 1}}}} - {K_t}) - (1 - \xi ){\Pi _t}$ | (6) |
企业投资
| ${I_t}{\rm{ = }}{K_t} - (1 - \delta ){K_{t - 1}}$ | (7) |
企业投入劳动、资本和房地产进行生产,生产函数为:
| ${Y_t}{\rm{ = }}{A_t}{K_t}^\alpha {(L_{P,t}^\phi L_{IP,t}^{1 - \phi })^\beta }{[(1 - \kappa ){H_{P,t}}]^\gamma }$ | (8) |
为了保证扣除成本之后还留存一部分收益,企业生产函数参数满足
参考Koo(2011)以及汪勇等(2018),本文假定在正常时期,企业倾向于利润最大化目标;但在特殊时期,如资产净值大幅下降时,企业会更加重视经营风险,侧重于债务最小化决策。企业决策目标的概率分布函数
| ${Pr _t}{\rm{ = }}\frac{{{e^{\psi {n_{t - 1}}}}}}{{1{\rm{ + }}{e^{\psi {n_{t - 1}}}}}}$ | (9) |
其中,
| $\alpha (1 - \tau )\frac{{{Y_t}}}{{{X_t}K{}_t}} = \delta Q_t^K + \frac{{{N^\psi }}}{{N_{t - 1}^\psi + (1 - \xi ){N^\psi }}}({R_{E,t}}Q_t^K - {E_t}Q_{t + 1}^K)$ | (10) |
| $\gamma (1 - \tau )\frac{{{Y_t}}}{{{X_t}{H_{P,t}}}} = R_t^H(1 - \kappa )Q_t^H$ | (11) |
| $\beta \phi (1 - \tau )\frac{{{Y_t}}}{{{X_t}L{}_{P,t}}} = {W_{P,t}}$ | (12) |
| $\beta (1 - \phi )(1 - \tau )\frac{{{Y_t}}}{{{X_t}L{}_{IP,t}}} = {W_{IP,t}}$ | (13) |
式(13)为企业对资本需求的最优条件,即资本的边际收益等于相应的边际成本。引入“资产负债表衰退”机制之后,企业对资本的需求除了受到资本折旧率的影响外,还受到自身资产净值的影响。企业资产净值通常具有顺周期性,即资产净值在经济形势好时上升,这将增大企业投资的顺周期性。进一步地,这将使外部冲击通过企业资产负债表渠道对宏观经济波动的影响扩大。式(14)为企业对房产需求的最优条件,左侧为使用房产的边际收益,右侧衡量相应的边际成本。房产的租赁价格
(四)资本品生产商。资本品生产商从企业购买已使用的资本和投资新资本,修复旧资本、生产新资本,同时以价格
| $\mathop {\max }\limits_{{I_t}} \;\;{E_t}\sum\limits_{i = 0}^\infty {{\Lambda _{t,t + i}}[Q_{t + i}^K{I_{t + i}} - (1 + f(\displaystyle\frac{{{I_{t + i}}}}{{{I_{t + i - 1}}}}){I_{t + i}})]} $ |
其中,
| $Q_t^K = 1 + f(\displaystyle\frac{{{I_t}}}{{{I_{t{\rm{ - }}1}}}}) + f'(\frac{{{I_t}}}{{{I_{t{\rm{ - }}1}}}})\frac{{{I_t}}}{{{I_{t{\rm{ - }}1}}}} - {\beta _P}{E_t}f''(\frac{{{I_{t + 1}}}}{{{I_t}}}){(\frac{{{I_{t + 1}}}}{{{I_t}}})^2}$ | (14) |
(五)零售商。参考Bernanke等(1999),本文假定零售商购买中间品,无成本地生产最终品,其利润全部归耐心家庭所有。零售商的目标函数为:
| $\mathop {\max }\limits_{P_t^*(j)} \;\;{E_t}\sum\limits_{i = 0}^\infty {{\theta ^i}{\Lambda _{t,t + i}}\left( {\displaystyle\frac{{P_t^*(j)}}{{{P_{t + i}}}} - \displaystyle\frac{1}{{{X_{t + i}}}}} \right)Y_{t + i}^*(j)} $ |
其中,
| ${E_t}\sum\limits_{i = 0}^\infty {{\theta ^i}{\Lambda _{t,t + i}}\left( {\displaystyle\frac{{P_t^*(j)}}{{{P_{t + i}}}} - \frac{X}{{{X_{t + i}}}}} \right)Y_{t + i}^*(j)} = 0$ | (15) |
其中,
(六)银行家。参考Iacoviello(2015),银行家的目标是终生效用最大化,其具体形式为:
| $\max \;\;{E_0}\sum\limits_{i = 0}^\infty {\beta _B^t\ln ({C_{B,t}} - \eta {C_{B,t - 1}})} $ |
其中,
| ${B_{P,t}} \leqslant \rho ({B_{P,t{\rm{ - 1}}}} - {D_{t - 1}} - {B_{IP,t{\rm{ - 1}}}} - {B_{G,t - 1}}) + (1 - \rho )({\gamma _E}{D_t} + {\gamma _{IP}}{B_{IP,t}} + {\gamma _G}{B_{G,t}})$ | (16) |
其中,
| $\begin{gathered} {C_{B,t}} + \frac{{{R_{t - 1}}{B_{p,t - 1}}}}{{{\pi _t}}} + {D_t} + {B_{IP,t}} + {B_{G,t}} + ad{j_{BP,t}} + ad{j_{BE,t}} + ad{j_{BG,t}} + ad{j_{BIP,t}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \leqslant {B_{P,t}} + \frac{{{R_{E,t - 1}}{D_{t - 1}}}}{{{\pi _t}}} + \frac{{{R_{IP,t - 1}}{B_{IP,t - 1}}}}{{{\pi _t}}} + \frac{{{R_{G,t - 1}}{B_{G,t - 1}}}}{{{\pi _t}}} \hfill \\ \end{gathered} $ | (17) |
其中,
| $ad{j_{P,t}}{\rm{ = }}\frac{{{\phi _P}}}{2}\frac{{{{({B_{P,t}} - {B_{P,t - 1}})}^2}}}{{{B_P}}}$ |
| $ad{j_{BE,t}}{\rm{ = }}\frac{{{\phi _E}}}{2}\frac{{{{({D_t} - {D_{t - 1}})}^2}}}{D}$ |
| $ad{j_{BG,t}}{\rm{ = }}\frac{{{\phi _G}}}{2}\frac{{{{({B_{G,t}} - {B_{G,t - 1}})}^2}}}{{{B_G}}}$ |
| $ad{j_{BIP,t}}{\rm{ = }}\frac{{{\phi _{IP}}}}{2}\frac{{{{({B_{IP,t}} - {B_{IP,t - 1}})}^2}}}{{{B_{IP}}}}$ |
(七)政府和中央银行。政府支出来自企业税收②和发行的政府债券,预算约束方程为:
| ${G_t} + \frac{{{R_{G,t - 1}}{B_{G,t - 1}}}}{{{\pi _t}}} \leqslant {B_{G,t}} + \tau \frac{{{Y_t}}}{{{X_t}}}$ | (18) |
其中,
| $\frac{{{G_t}}}{G} = {\left( {\frac{{{G_{t - 1}}}}{G}} \right)^{{\rho _G}}}{\left( {\frac{{{Y_t}}}{Y}} \right)^{{\phi _Y}}}{e^{\varepsilon _t^G}}$ | (19) |
其中,
中央银行的货币政策设定为常规的Taylor规则形式:
| $\frac{{{R_t}}}{R} = {\left( {\frac{{{R_{t - 1}}}}{R}} \right)^{{r_R}}}{\left[ {{{\left( {\frac{{{\pi _t}}}{\pi }} \right)}^{{r_\pi }}}{{\left( {\frac{{{Y_t}}}{Y}} \right)}^{{r_Y}}}} \right]^{1 - {r_R}}}{e^{\varepsilon _t^R}}$ | (20) |
其中,
(八)一般均衡条件。本文模型的一般均衡要求劳动力、商品、资本与房地产市场同时出清。鉴于模型已有的一些约束条件,劳动力市场自动出清,剩下三个市场只需要两个市场出清即可。本文将房地产供给标准化为1,即:
| ${H_{P,t}} + {H_{IP,t}} = 1$ | (21) |
商品市场均衡条件为:
| ${Y_t} = {C_{P,t}} + {C_{IP,t}} + {C_{B,t}} + {G_t} + \left[ 1 + f(\frac{{{I_t}}}{{{I_{t{\rm{ - }}1}}}}) \right]{I_t}$ | (22) |
该经济体共存在5种类型冲击。参照主流DSGE文献做法,本文假定家庭住房需求冲击、企业资产负债表冲击和生产率冲击均服从AR(1)过程,③即
三、参数校准与贝叶斯估计
本文使用的数据来自中经网宏观数据库和Wind数据库。由于Shibor从2007年1月开始正式运行,本文选取了2007年第1季度至2016年第4季度的数据。本文选择了GDP(扣除净出口)、政府投资支出、房地产价格、固定资产投资完成额和上海银行间同业拆借利率Shibor这5个变量。参考汪勇等(2018),本文对上述变量进行了相应处理。
(一)模型参数校准与贝叶斯估计。模型中的参数分为两类:一类是与稳态相关的参数,利用已有研究或可观测变量矩条件进行校准;另一类是与转移动态相关的参数,采用贝叶斯方法进行估计。对于家庭部门,参数包括
对于第二类参数,本文采用贝叶斯估计方法确定,这些参数包括
| 参数符号 | 参数名称 | 先验分布 | 后验分布 | ||||
| 分布类型 | 均值 | 标准差 | 5% | 均值 | 95% | ||
|
|
Calvo定价粘性系数 | Beta | 0.75 | 0.20 | 0.684 | 0.736 | 0.815 |
|
|
投资品调整成本系数 | Gamma | 1.50 | 0.10 | 1.133 | 1.586 | 2.022 |
|
|
利率规则中的利率粘性系数 | Beta | 0.80 | 0.10 | 0.592 | 0.745 | 0.865 |
|
|
利率规则中的通胀反应系数 | Gamma | 1.52 | 0.10 | 1.313 | 1.461 | 1.640 |
|
|
利率规则中的产出反应系数 | Gamma | 0.36 | 0.10 | 0.330 | 0.496 | 0.658 |
|
|
财政政策冲击AR(1)系数 | Beta | 0.80 | 0.10 | 0.541 | 0.680 | 0.795 |
|
|
企业技术冲击AR(1)系数 | Beta | 0.80 | 0.10 | 0.969 | 0.985 | 0.999 |
|
|
房产需求冲击AR(1)系数 | Beta | 0.80 | 0.10 | 0.949 | 0.973 | 0.997 |
|
|
资产负债冲击AR(1)系数 | Beta | 0.80 | 0.10 | 0.659 | 0.790 | 0.880 |
|
|
货币政策冲击标准差 | IG | 0.01 | 0.2 | 0.003 | 0.008 | 0.012 |
|
|
财政政策冲击标准差 | IG | 0.01 | 0.2 | 0.016 | 0.023 | 0.042 |
|
|
企业技术冲击标准差 | IG | 0.01 | 0.2 | 0.012 | 0.018 | 0.023 |
|
|
房产需求冲击标准差 | IG | 0.01 | 0.2 | 0.009 | 0.022 | 0.032 |
|
|
资产负债冲击标准差 | IG | 0.01 | 0.2 | 0.008 | 0.010 | 0.012 |
(二)模型适用性分析。从总体上看,模型经济与现实经济的宏观变量标准差较为接近,说明模型的适用性较好。表2表明,模型经济中的利率标准差与现实经济相同,产出、政府支出和房地产价格的标准差稍低于现实经济,而投资的标准差略高于现实经济,同时各变量标准差与产出标准差的相对大小方向与现实经济保持一致。
| 变量 | 产出 | 投资 | 政府支出 | 房地产价格 | 利率 |
| 现实经济 | 0.018 | 0.030 | 0.046 | 0.028 | 0.002 |
| 模型经济 | 0.017 | 0.036 | 0.044 | 0.025 | 0.002 |
四、脉冲分析与方差分解
我们在这部分首先探讨房地产偏好正向冲击与企业资产负债表负向冲击对房地产价格与企业投资之间关系的影响,然后对企业的不同税负情形做多重情景分析,最后对企业投资、房地产价格等主要经济变量进行方差分解。
(一)房地产偏好正向冲击的宏观经济效应。现阶段,房地产价格上涨与居民住房需求刚性紧密相关(王立平,2013)。图1模拟了居民家庭住房偏好1个百分点的正向冲击对房地产价格、企业投资等内生经济变量的影响。居民住房偏好上升在推动房地产价格上涨的同时,抑制了社会总消费,④带来了企业投资⑤和产出的增加。从房地产市场来看,政府控制土地供应,房地产供给缺乏弹性,居民家庭对住房需求的增加使房地产价格出现较大幅度上升。尽管房地产价格上涨会通过“财富效应”对居民家庭消费起到刺激作用,但是此时家庭需将更大一部分的收入用于购置房地产,这又会抑制居民家庭的消费。在这两种作用下,居民家庭总消费出现小幅下降,进而引起社会总消费下降。对企业而言,房地产具有生产要素属性,房地产价格上升增加了生产成本(如厂房租赁成本),这会减少企业对房地产要素的需求。而房地产要素与固定资产投资之间存在一定的替代性,企业此时会增加要素价格相对低廉的固定资产投资。⑥投资作为社会总需求的一部分,投资上升将引起产出小幅上升。
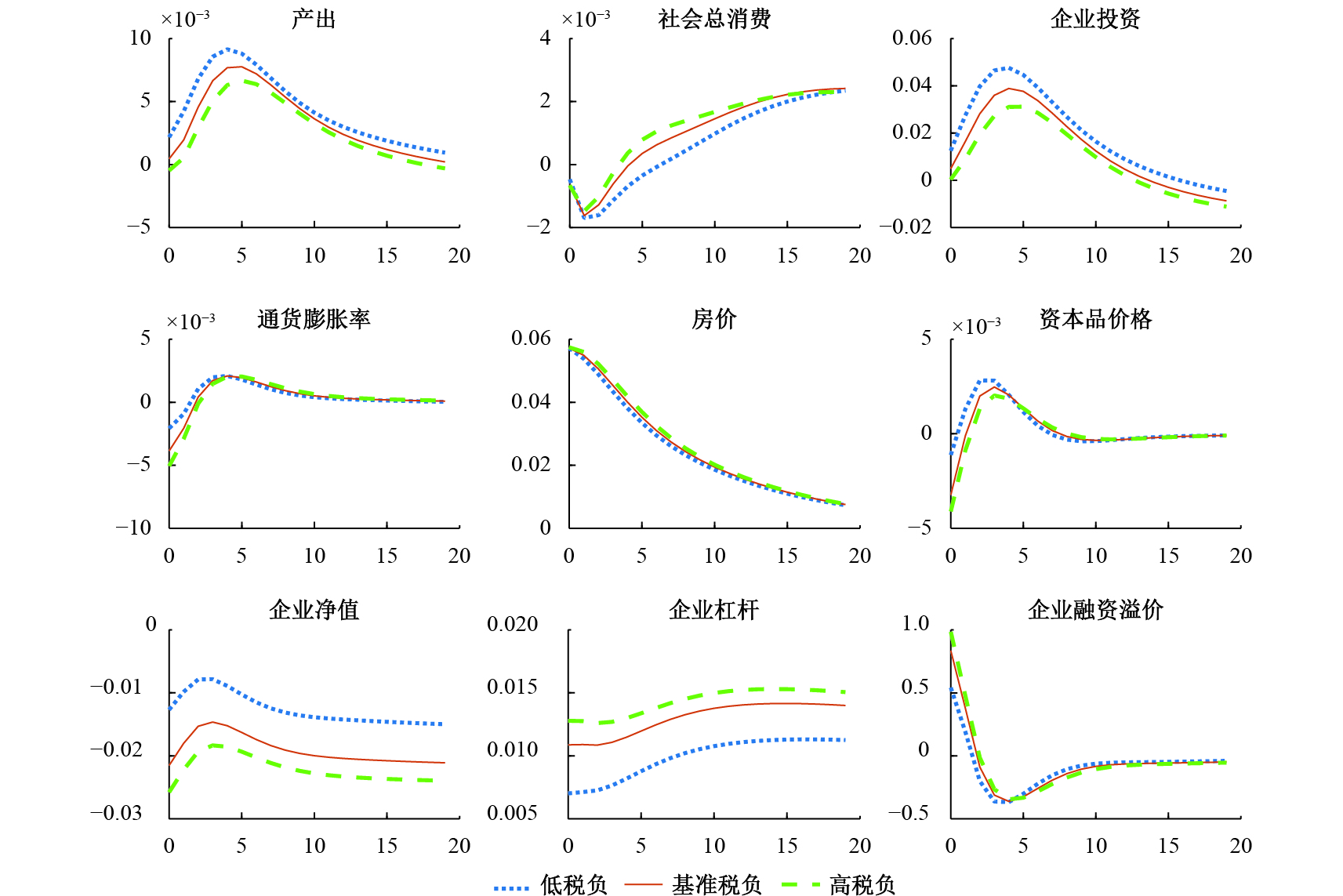
|
| 图 1 不同企业税负下房地产偏好正向冲击的宏观经济效应 |
(二)企业资产负债表负向冲击的宏观经济效应。国际金融危机以来,外部需求不振给我国企业(尤其是出口企业)产品需求形成了巨大压力,导致企业利润明显下滑,资产负债表恶化。本文模型中未加入进出口部门,是一个封闭经济模型,不能直接考察外部需求冲击的影响。理论上看,我国企业资产负债表受到国内外需求的共同影响。但一方面,长期以来我国经济外向依存度高,我国企业资产负债表受到外部需求的影响很大;另一方面,近些年我国政府强调转变经济发展方式,突出内需对经济的拉动作用,促使国内消费对经济增长的贡献稳步提升。综合来看,2008年金融危机以来,外需疲软是我国企业资产负债表不利变化的最重要来源。鉴于此,本文将施加在企业资产负债表上的负向冲击近似为外部需求负向冲击。
图2模拟了企业资产负债表1个百分点的负向冲击对房地产价格、企业投资等内生经济变量的影响。经济受到企业资产负债表负向冲击时,企业投资下滑,产出下降,房地产价格上升,社会总消费增加。不利的外部需求冲击使企业利润下滑,资产净值大幅下降。这会加大企业还债压力,引起企业杠杆率大幅上升,导致企业资产负债表恶化。一方面,由于企业还债压力加大,基于风险收益考虑,银行会提高企业的外部融资溢价,“融资溢价效应”会抑制企业投资热情;另一方面,资产净值大幅下降导致企业资产负债表恶化,出于经营风险和外部声誉考虑,企业的去杠杆动机增强,更倾向于债务最小化目标,启动“资产负债表衰退”机制,优先偿还债务,减少投资。企业投资下滑造成资本品价格下跌,进一步强化这两种效应的反馈机制,增大投资下滑幅度。实体经济不景气会改变居民家庭的投资策略,在银行中介的作用下,储蓄资金会进入房地产市场,引起房地产价格出现较大幅度上涨,资金“脱实向虚”显现。由于房地产价格上升带来的“财富效应”,国内消费需求受到刺激,对经济总需求产生一定的拉动作用。

|
| 图 2 不同企业税负下企业资产负债表负向冲击的宏观经济效应 |
在我国,居民家庭可选的投资渠道较少,投资房地产是一种重要的投资形式。从实践来看,2008年至今,我国股票市场的平均收益率低,但投资房地产市场却能带来数倍的回报。因此,当实体经济不景气时,居民家庭通过银行中介将闲余资金投资于房地产市场是比较理性。在图2中,本文考察的是企业资产负债表负向冲击所引起的房地产价格短期波动,研究结果与中国现实基本吻合,这在一定程度上验证了本文研究结论的可靠性。
(三)不同企业税负情形的情景分析。随着美联储启动新一轮加息,加之我国宏观杠杆率高企,为防范化解系统性金融风险,我国央行实施了稳健中性的货币政策。在去杠杆的大背景下,实体企业(尤其是民营和中小微企业)面临融资难、融资贵等问题。为切实缓解实体企业的生产经营压力,党中央和国务院先后多次出台和落实降低企业税负的政策。为此,本文模拟了不同企业税负下房地产偏好正向冲击与企业资产负债表负向冲击对房地产价格与企业投资关系的影响。
政府降低企业税负会增强房地产偏好上升冲击对企业投资的“挤入效应”,促使产出进一步上升,但对房地产价格没有明显影响。图1显示了房地产偏好正向冲击在低税负、基准税负和高税负下对企业投资、产出、房地产价格等内生经济变量的影响。政府降低企业税率2个百分点,企业投资和产出相对于基准税负情形分别增加22.5%和17.8%。出现这一结果的主要原因是,税负降低会增加企业利润和固定资产投资力度,从而企业投资的上升幅度增大。作为社会总需求的一部分,投资更大幅度的上升将带来产出更大幅度的上升。房地产价格更多地受到房地产需求与供给的作用,而企业税负的变化对房地产市场的供给和需求没有直接的影响,因此房地产价格与基准税负情形相比没有明显变化。
本文也模拟了企业资产负债表负向冲击在不同税负下对企业投资、产出、房地产价格等内生经济变量的影响。图2表明,企业税负降低使资产负债表负向冲击对企业投资的不利影响变小,房地产价格上升势头有所缓解,社会资金“脱实向虚”倾向减弱。与基准税负情形相比,税负下降2个百分点,企业投资和产出的下滑幅度分别减少17.5%和15.4%,房地产价格的上升幅度下降5.6%。从传导机制上看,政府降低企业税负之后,企业资产负债表负向冲击的不利影响会减弱。此时,“融资溢价效应”与“资产负债表衰退效应”的反馈力度也会减弱,从而企业投资的下降幅度减小。作为社会总需求的一部分,投资下降幅度的减小将引起产出下降幅度的减小。与基准税负情形相比,实体企业的经济景气度有所提高,使得居民家庭资金流入房地产市场的额度减少,房地产价格的上升幅度也会减小。
(四)方差分解。上文分析了房地产偏好冲击与企业资产负债表冲击对企业投资与房地产价格之间关系的影响,不同冲击的持续性和波动性存在很大差异,要细致讨论不同冲击对企业投资、房地产价格等变量的作用,本文需要考虑各个冲击的特征,并对这些经济变量进行方差分解。表3给出了模型中企业投资、房地产价格和产出的方差分解结果。
| 变量 | 生产技术 | 住房偏好 | 企业资产负债表 | 政府支出 | 货币政策 |
| 企业投资 | 41.98% | 4.58% | 45.08% | 6.7% | 1.66% |
| 房地产价格 | 34.89% | 49.05% | 7.16% | 8.75% | 0.13% |
| 产出 | 90.08% | 0.19% | 5.76% | 3.85% | 0.14% |
在企业投资波动方面,企业资产负债表冲击的影响最大,房地产偏好冲击与企业资产负债表冲击能解释企业投资波动的近50%。在房地产价格波动方面,房地产偏好冲击的影响最大,企业资产负债表冲击和房地产偏好冲击对房地产价格波动的解释比例达到56%。在产出波动方面,生产技术冲击的影响占绝对优势,能解释产出波动的90%以上,这与国内外主流文献的研究结论一致。因此,房地产偏好冲击和企业资产负债表冲击是影响我国企业投资和房地产价格波动的主要因素。
五、结 论
近年来,我国企业投资疲软与房地产价格大幅上涨现象并存。本文借鉴Koo(2011)的理论,构建了一个含有“资产负债表衰退”特征的新凯恩斯DSGE模型,重点考察了房地产需求刚性与外部需求疲软对企业投资与房地产价格之间关系的影响。本文模型的重点在于企业部门,在企业资产负债表受到冲击时,除了“融资溢价”机制外,“资产负债表衰退”机制会使企业的去杠杆动机增强,减少投资、偿还债务以修复自身资产负债表。本文得到了三个主要结论:
第一,房地产需求刚性所产生的房地产偏好正向冲击小幅提升了企业投资。由于房地产要素与固定资产投资之间存在一定的替代性,房地产价格上升增加了企业经营成本,促使企业增加要素价格相对低廉的固定资产投资。
第二,外部需求收缩所引致的企业资产负债表负向冲击对企业投资形成不利影响,促使社会盈余资金转入房地产市场,推动房价上涨,导致社会资金的“脱实向虚”。外部需求下降导致企业利润和资本回报率下降,在减弱企业投资需求的同时,也恶化了其资产负债表。这进一步通过“融资溢价效应”和“资产负债表衰退效应”抑制企业投资。
第三,政府降低企业税负会增强房地产偏好正向冲击对企业投资的“挤入效应”,减弱企业资产负债表负向冲击对企业投资的不利影响。企业税率下降2个百分点,房地产偏好正向冲击将推动企业投资与基准税负情形相比上升22.5%,资产负债表负向冲击则使企业投资与基准税负情形相比下降幅度减少17.5%,从而缓解了社会资金的“脱实向虚”问题。
① 本文考虑了可变资本折旧率情形,模拟了房地产需求冲击与企业资产负债表冲击,发现这两类冲击对企业投资、房地产价格与产出的影响与不变折旧率模型相比在数值上有所增大,但影响方向与走势没有变化,即引入可变折旧率对本文的基本结果没有影响。感谢匿名评审专家的建议性意见!
② 本文基于两点理由对政府税收做了简化:其一,本文考虑的是针对企业的增值税,这是一种总量税,在一定程度上已经考虑了工资税;其二,本文模拟的是针对企业的税率变化,而没有模拟针对家庭工资的税收变化,因此理论上引入家庭工资税不会显著改变本文的基本结果。
③ 本文也考虑了家庭住房需求冲击与企业资产负债表冲击服从AR(2)的情况,发现改变冲击的设定形式并不改变本文的基本结果。感谢匿名评审专家的宝贵意见!
④ 社会总消费包含政府支出。
⑤ 本文中的企业投资指除房地产要素之外的企业固定资产投资。
⑥ 需要说明的是,房地产偏好冲击发生时,企业资产负债表也会出现一定程度的不利变化,相应地通过“资产负债表衰退”和“融资溢价”渠道影响企业投资,但影响程度很小,对企业实体投资的总体影响不大。
| [1] | 冯根福, 郑冠群. 中国货币政策非对称干预资产价格波动的宏观经济效应——基于分段线性新凯恩斯动态随机一般均衡模型的模拟和评价[J]. 中国工业经济, 2016(10): 5–22. |
| [2] | 黄志刚, 许伟. 住房市场波动与宏观经济政策的有效性[J]. 经济研究, 2017(5): 103–116. DOI:10.3969/j.issn.1005-913X.2017.05.047 |
| [3] | 栗亮, 刘元春. 经济波动的变异与中国宏观经济政策框架的重构[J]. 管理世界, 2014(12): 38–50. |
| [4] | 罗时空, 周亚虹. 房价影响企业投资吗: 理论与实证[J]. 财经研究, 2013(8): 133–144. |
| [5] | 王君斌, 王文甫. 非完全竞争市场、技术冲击和中国劳动就业——动态新凯恩斯主义视角[J]. 管理世界, 2010(1): 23–35. |
| [6] | 王立平. 我国房地产价格" 稳健性”影响因素实证研究[J]. 管理世界, 2013(10): 184–185. |
| [7] | 汪勇, 马新彬, 周俊仰. 货币政策与异质性企业杠杆率——基于纵向产业结构的视角[J]. 金融研究, 2018(5): 47–64. DOI:10.3969/j.issn.1009-3109.2018.05.009 |
| [8] | 王云清, 朱启贵, 谈正达. 中国房地产市场波动研究——基于贝叶斯估计的两部门DSGE模型[J]. 金融研究, 2013(3): 101–113. |
| [9] | 吴海民. 资产价格波动、通货膨胀与产业" 空心化”——基于我国沿海地区民营工业面板数据的实证研究[J]. 中国工业经济, 2012(1): 46–56. |
| [10] | 许宪春, 贾海, 李皎, 等. 房地产经济对中国国民经济增长的作用研究[J]. 中国社会科学, 2015(1): 84–101. |
| [11] | 原鹏飞, 冯蕾. 经济增长、收入分配与贫富分化——基于DCGE模型的房地产价格上涨效应研究[J]. 经济研究, 2014(9): 77–90. DOI:10.3969/j.issn.1002-5863.2014.09.032 |
| [12] | 张成思, 张步昙. 中国实业投资率下降之谜: 经济金融化视角[J]. 经济研究, 2016(12): 32–46. DOI:10.3969/j.issn.1002-5863.2016.12.012 |
| [13] | Barro R J. The loan market, collateral, and rates of interest[J]. Journal of Money, Credit and Banking, 1976, 8(4): 439–456. DOI:10.2307/1991690 |
| [14] | Bernanke B S, Gertler M, Gilchrist S. The financial accelerator in a quantitative business cycle framework[A]. Taylor J B, Woodford M. Handbook of macroeconomics[C]. Elsevier, 1999. |
| [15] | Cevallos-Fujiy B. A model of the balance sheet recession[R]. Working Paper, 2015. |
| [16] | Chaney T, Sraer D, Thesmar D. The collateral channel: How real estate shocks affect corporate investment[J]. The American Economic Review, 2012, 102(6): 2381–2409. DOI:10.1257/aer.102.6.2381 |
| [17] | Christiano L J, Eichenbaum M, Evans C L. Nominal rigidities and the dynamic effects of a shock to monetary policy[J]. Journal of Political Economy, 2005, 113(1): 1–45. DOI:10.1086/426038 |
| [18] | Coenen G, Straub R, Trabandt M. Gauging the effects of fiscal stimulus packages in the euro area[J]. Journal of Economic Dynamics and Control, 2013, 37(2): 367–386. DOI:10.1016/j.jedc.2012.09.006 |
| [19] | Falagiarda M, Saia A. Credit, endogenous collateral and risky assets: A DSGE model[J]. International Review of Economics & Finance, 2017, 49: 125–148. |
| [20] | Fernández-Villaverde J. The econometrics of DSGE models[J]. SERIEs, 2010, 1(1−2): 3–49. DOI:10.1007/s13209-009-0014-7 |
| [21] | Iacoviello M. House prices, borrowing constraints, and monetary policy in the business cycle[J]. The American Economic Review, 2005, 95(3): 739–764. DOI:10.1257/0002828054201477 |
| [22] | Iacoviello M. Financial business cycles[J]. Review of Economic Dynamics, 2015, 18(1): 140–163. DOI:10.1016/j.red.2014.09.003 |
| [23] | Koo R C. The holy grail of macroeconomics: Lessons from Japan’s great recession[M]. John Wiley & Sons, 2011. |
| [24] | Krippner G R. The financialization of the American economy[J]. Socio-Economic Review, 2005, 3(2): 173–208. DOI:10.1093/SER/mwi008 |
| [25] | Wang R, Hou J, He X B. Real estate price and heterogeneous investment behavior in China[J]. Economic Modelling, 2017, 60: 271–280. DOI:10.1016/j.econmod.2016.09.020 |
| [26] | Yu S X. Evaluating macroprudential policy in a DSGE framework with financial frictions[R]. Working Paper, Division of Social Science, New College of Florida, 2013. |


