
2019第45卷第3期
一、引 言
气候变化已经成为世界性环境问题,正在对全球生态系统和社会经济发展造成深远影响。全球二氧化碳(CO2)排放总量在经历了短暂的稳定期后又呈现出较强的上升趋势,2017年世界能源相关的二氧化碳排放总量约为325亿吨,较2016年增长1.4%,中国排放量增长率为1.7%,高于全球平均水平。二氧化碳等温室气体排放的不断上升加快了全球气候变暖的速度,以中国为例,2016年我国年平均气温为10.36 ℃,较1981—2010年平均气温提高了0.81 ℃,新的气候环境下极端高温越来越普遍。目前各国在国际碳排放中的努力不足以实现《巴黎协定》中设定的目标,遏制碳排放继续上升的形势依然十分严峻。
一国产生的碳排放不仅会对本国产生影响,还会扩散到大气层中,进而影响全球气候变化。碳排放的负外部性导致各个国家在全球气候变化的过程中并不能独善其身,即碳减排需要世界各国的共同努力,对碳排放的研究也应在国际视角下进行。并且,碳排放主要是由经济生产活动导致的,控制碳排放不可避免地会对经济发展形成一定的阻碍。在美国宣布退出《巴黎协定》等一系列重大事件的影响下,各国对碳减排冲击本国经济发展和就业增长的担忧不断上升,国际碳减排进程中的不确定性也在增加。因此,在国际视角下,探究国家间碳排放关联的结构特征,研究国家间经济发展与碳排放之间的相互影响关系十分必要。
现有文献对国际碳排放问题的研究主要集中于国际贸易隐含碳、国际碳泄漏、经济发展与碳排放之间的关系三个方面,对贸易隐含碳问题的早期研究侧重于国际贸易碳转移对碳排放的影响渠道分析(Grossman和Krueger,1993;Copeland和Taylor,1995;Antweiler等,2001)。随着国际投入产出数据库的开发和完善,许多学者采用投入产出法对国际贸易隐含碳进行了更为精确的测度(Wyckoff和Roop,1994;Machado等,2001;齐晔等,2008;Peters等,2011)。王文举和向其凤(2011)验证了发达国家向发展中国家转移碳排放的现象,蒋雪梅和刘轶芳(2013)指出了国际碳转移主要是由于各国技术差异导致的。
由于各国采取不同强度的碳减排政策,可能会导致碳泄漏现象,即采取相对严格碳减排政策的国家碳排放减少的同时,会使碳减排政策较为宽松的其他国家碳排放增加(彭水军和张文城,2016)。Copeland和Taylor(2005)通过构建新古典一般均衡模型对国际碳泄漏形成的理论机制进行了研究,认为碳泄漏的发生与否取决于贸易条件、收入效应和消费替代效应等;牛玉静等(2012)则基于可计算一般均衡模型,对全球碳泄漏程度进行了估算,认为美国参与碳减排可显著减少国际碳泄漏。对于碳泄漏问题测度及形成机制的研究已经较为全面,但是大多数研究忽视了国家间碳排放的结构特征。
在经济发展与碳排放之间关系的研究方面,环境库兹涅茨曲线(Environmental Kuznets Curve,EKC)是重要的理论基础(Grossman和Krueger,1993),很多学者对于这一理论在各国的适用性进行了检验(Holtz-Eakin和Selden,1995;Zhang和Cheng,2009)。然而,Coondoo和Dinda(2002)指出,环境库兹涅茨曲线假说没有充分考虑经济增长与碳排放之间的双向影响,导致模型存在内生性问题。此后,格兰杰因果关系检验和向量自回归(VAR)模型在经济增长与碳排放关系的研究中得到了广泛应用。然而,大多数研究主要是对单个国家进行分析,在国际视角下针对各国经济增长与碳排放的双向冲击效应及传导路径的研究并不充分。
国家间的经济联系使得各国之间的碳排放产生了关联,一国的碳排放不仅受到国内生产活动的影响,还通过进出口活动形成了国际碳排放的流入和流出效应,应充分捕捉国家间的经济及碳排放联系,合理描述国际碳排放关系的网络特征。网络分析是系统研究社会结构的方法,主要应用于社会学和管理学中,近期也被频繁应用于政治学和经济学等领域(徐振宇,2013),运用网络分析方法可以更好地揭示国家间网络的全局性特征及各经济体在网络中的地位等(Rauch和Watson,2004;刘华军等,2015;李敬等,2017)。
国家之间的经济联系使得各国间的碳排放产生了相互影响,进而产生了复杂的碳排放关联,并且碳排放的关联性已经超出地理范围的限制,并逐渐形成了多节点、多路径的网络形态。因此,本文使用社会网络分析方法,对国际碳排放的网络结构进行分析,不仅符合现实的碳关联特征,而且为各国间碳排放关系的研究提供了新的研究视角和研究方法。
国家间经济增长与碳排放的相互冲击效应通过错综复杂的多路径实现传导,应充分考虑各国经济产出与碳排放的联立关系。全球向量自回归(Global Vector Auto-Regression,GVAR)方法对经典向量自回归模型进行了扩展(Granger和Jeon,2007),其将各国的经济联系设置为连接矩阵,是研究国际经济问题的有效工具(张延群,2012)。张红等(2014)、王美昌和徐康宁(2015)基于GVAR方法研究了中国经济增长对国际碳排放的动态影响,分析了不同开放程度下经济增长与碳排放动态关系的传导路径等。
本文还在国家间碳排放关联矩阵的基础上,构建权重矩阵并嵌入到全球向量自回归(GVAR)模型中,对各国之间经济增长与碳排放的关系进行了更为准确的测度,深入挖掘了国际经济增长与碳排放的内在联系,准确识别了经济发展对碳排放影响的传导渠道和动态关系,这有助于各个国家特别是我国协调经济增长、国际贸易与碳排放的关系,进而实现经济高质量发展与达成碳减排的约束目标。
二、“国际贸易—碳排放”矩阵的构建及网络分析方法
(一)国际碳排放矩阵的构建。为表述世界各国之间经济增长与碳排放的紧密关联,参照Chang和Shih(2005)、Montresor和Marzetti(2009)的研究,本文基于国际多区域投入产出(International Multi-Region Input-Output,IMRIO)表和各国碳排放量数据构建国家间“国际贸易—碳排放”矩阵,简称国际碳排放矩阵。国际多区域投入产出表如式(1)所示。
| $\left( {\begin{array}{*{20}{c}} {{x_1}} \\ \vdots \\ {{x_n}} \end{array}} \right){\rm{ = }}\left( {\begin{array}{*{20}{c}} {{a_{11}}}& \cdots &{{a_{1n}}} \\ \vdots & \ddots & \vdots \\ {{a_{n1}}}& \cdots &{{a_{nn}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}} \\ \vdots \\ {{x_n}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {\sum\nolimits_{j = 1}^n {{y_{1j}}} } \\ \vdots \\ {\sum\nolimits_{j = 1}^n {{y_{nj}}} } \end{array}} \right)$ | (1) |
其中,xi是国家i的总产出,aij为国家j对国家i的直接消耗系数,yij为国家j对国家i的最终需求,
多区域投入产出表是各国行业之间中间产品投入和使用关系的重要体现形式,将其与碳排放数据相结合,能够合理地测度国家间和行业间的碳排放量和碳转移量。本文以各个国家为节点,得到国际碳排放矩阵:
| $P = \left( {\hat c} \right){\left( {\hat x} \right)^{ - 1}}{\left( {I - A} \right)^{ - 1}}Y$ | (2) |
其中,
本文采用的国际多区域投入产出表来自于世界投入产出数据库(World Input-Output Database,WIOD),该投入产出表由欧盟27个成员国和欧盟之外的12个重要经济体组成,其他国家和地区被放入ROW区域,数据区间为1995年至2014年。碳排放数据来自世界发展指标(World Development Indicators,WDI)数据库,为与WIOD中的数据相匹配,本文选取了WDI数据库中39个经济体1995—2014年的二氧化碳排放量。进一步地,为便于分析,本文将27个欧盟成员国合并为1个欧盟地区,对投入产出表和碳排放数据逐年进行了合并,再运用式(2)计算得到每一年的国际碳排放矩阵。
为使用网络分析方法研究国际碳排放关系网络的结构特征,首先需要选择一个适当的门限值m,将国际碳排放矩阵P二值化为D,即选择m值使国际碳排放矩阵满足:
| ${d_{ijt}} = \left\{ {\begin{array}{*{20}{c}} {1,\;\;\;{P_{ijt}} \geqslant m}\\ {0,\;\;\;{P_{ijt}} < m} \end{array}} \right.$ | (3) |
其中,Pijt为第t年国际碳排放矩阵第i行j列的元素,dijt为二值化碳排放矩阵D中对应的元素。
在对国际碳排放矩阵进行二值化处理时,关键的一步是选取门限值m,本文首先通过初步的灵敏度测试确定合适的门限值范围,即在门限值由低到高变化的过程中,二值化矩阵的整体特征相对稳定。例如,随着国家间生产关系和经济联系日益密切,反映国际碳排放矩阵整体性的网络密度应逐渐增大且波动程度较小,同时还应保证各个年份国际碳排放网络的结构特征显著等。因此,本文设定门限值在0至10的区间内变动,步长为0.01,选取门限值m=3.1,在二值化的国际碳排放网络中保留了足够多的联系,且省略了微弱的碳排放关联,便于分析碳排放网络显著的结构特征。
(二)网络结构分析方法。本文主要从刻画个体位置特征的中心性方面对国际碳排放网络的结构特征进行分析。根据中心国家对其他国家碳排放影响渠道的不同,中心度又可以划分为度数中心度、中间中心度及接近中心度三类。
1. 度数中心度:在国际碳排放网络中,一国的度数中心度指的是与该国家存在直接碳排放联系的国家数量,度数中心度越高,则该国与其他国家之间的联系越多,越处于网络的中心位置。每个国家的度数中心度可基于点入度和点出度计算得到,其中点入度指的是一国通过进口将本应属于该国的碳排放转移到其他国家的关系数量,点出度则是一国出口而为其他国家承担的碳排放,是其他国家转移到本国的关系数量。在二值化的国际碳排放矩阵中,第t年第i国家的点入度(IIndit)和点出度(IOutdit)的计算公式分别为式(4)和式(5)。
| $IIn{d_{it}} = \sum\nolimits_{j\left( {i \ne j} \right)} {{d_{jit}}} ,\;\;0 \leqslant IIn{d_{it}} \leqslant n - 1$ | (4) |
| $IOut{d_{it}} = \sum\nolimits_{j\left( {i \ne j} \right)} {{d_{ijt}}} ,\;\;0 \leqslant IOut{d_{it}}\leqslant n - 1$ | (5) |
由于点入度和点出度是绝对量,对于不同年份、不同规模的碳排放网络而言,不能直接进行比较。在两者的基础上综合形成的度数中心度,不仅完整地体现了国际碳排放的关联特征,而且是相对量可以用于多维比较。本文用国际碳排放网络中一国的出度、入度之和与最大可能的度数之比表示国家度数中心度,第t年国家i度数中心度(IDeit)的计算方法为:
| $I{D_{eit}} = {{\left( {IIn{d_{it}} + IOut{d_{it}}} \right)}/{\left( {2n - 2} \right)}}$ | (6) |
产品流动是国际碳排放网络中点入度和点出度的经济载体,点入度衡量一国将碳排放转移到其他国家的程度,而点出度则衡量承担来自其他国家的碳转移程度,二者的综合度数中心度则反映了一国通过经济关联对其他国家碳排放的直接影响力。
2. 中间中心度:中间中心度是反映一国在国际碳排放网络中“中介”或“桥梁”作用的指标,第t年国家i对于国家j和国家k而言的中间中心度为:
| ${b_{jkt}}\left( i \right) = {{{g_{jkt}}\left( i \right)}/{{g_{jkt}}}}$ | (7) |
其中,gjkt为第t年国家j和国家k之间存在的捷径数量,即国家j通过碳排放网络与国家k建立联系所需要经过的最短关系链的数目,gjkt(i)为gjkt中经过国家i的捷径数目,则bjkt(i)可以表示第t年国家i控制国家j和国家k碳排放关联的能力。
将国家i相对于网络中所有国家的中间度相加,得到第t年第i国家的中间中心度(ICABit):
| $I{C_{ABit}} = \sum\nolimits_j {\sum\nolimits_k {{b_{jkt}}\left( i \right)} } ,\;\;i \ne k \ne j,j < k$ | (8) |
中间中心度表示在产品流动引致的国际碳转移关系网络中,一国处于各条碳转移关系链上中间环节的程度,衡量对于其他国家之间碳排放关联的控制力和影响力,其值越高意味着该国控制其他国家碳排放关系的能力越强。
3. 接近中心度:接近中心度利用国家间捷径的“距离”来表示一国在国际碳排放网络中的中心性,如果国家在碳排放网络中与其他国家的捷径“距离”都很短,则该国在网络中处于中心行动者位置。一国的接近中心度是国家与网络中其他国家的捷径距离之和,第t年国家i的接近中心度(ICAPit)定义为:
| $I{C_{APit}} = {{\left( {\sum\nolimits_j {{f_{jit}}} + \sum\nolimits_j {{f_{ijt}}} } \right)}/{\left( {2n - 2} \right)}}$ | (9) |
其中,fijt为第t年国家i到国家j的捷径距离。
一国的接近中心度衡量的是该国与其他国家建立碳排放联系的难易程度,反映了与各个国家之间存在经济联系进而产生碳排放联系的行动力,接近中心度越低,该国通过经济联系与其他国家取得碳排放联系就越容易。
三、“国际贸易—碳排放”网络的结构分析:基于节点的视角
本文计算个体的网络结构指标,对各国在国际碳排放网络中的位置等进行刻画,计算得到1995年、2014年各国的点出度、点入度和度数中心度,绘制了散点图如图1所示,其中虚线为45度分割线。

|
| 图 1 代表性经济体的出入度与度数中心度 |
在图1中,将1995—2014年各个国家的点入度和点出度进行对比可得,入度大于出度的国家主要为美国、日本、欧盟等发达经济体,而出度高于入度的国家则多为金砖国家和新兴经济体国家,如中国、俄罗斯、印度和巴西等。基于资源禀赋的视角分析,发达国家对基础性原材料、初级产品和能源资源的需求量较大,需要从发展中国家进口较多的资源密集型和劳动密集型产品,通过产品进口与发展中国家建立经济和碳排放联系,因而在国际碳排放网络中,发达国家的入度较大。不同的是,发展中国家依靠资源禀赋生产了大量的要素密集型中间产品供给发达国家使用,通过向发达国家进行产品出口的同时,接收了来自发达国家的碳输入,因而其出度较高。
如前所述,在国际碳排放网络中,一国的度数中心性衡量的是与此国家存在直接碳转移关系的国家数量,在图1中大部分国家都位于45度线以上,反映出网络中国家个体的中心性提高。其中,中国的入度、出度和度数中心度均较大。原因在于,中国经济实现高速增长的过程中,在其市场规模、劳动力低成本优势的作用下,中国也融入世界生产网络并嵌入全球价值链中,通过中间品贸易和加工贸易等途径与其他国家建立了大量的生产联系,碳排放关联随之建立。特别是2013年实施“一带一路”发展战略后,中国更为迅速地融入了世界经济体系中,生产关联及碳排放关联的网络密度进一步加大。
与之相对,部分发达国家如美国、欧盟、日本等,1995—2014年上述发达经济体的度数中心度基本处于45度线左右,中心性没有明显提升,在国际碳排放网络中的位置相对稳定。与发达经济体不同,一些发展中国家或新兴经济体国家如印度、巴西、土耳其、墨西哥等,其度数中心度均有显著提升,然而由于经济规模或地理位置等因素的限制,其度数中心度很低,大多处于碳排放网络的边缘位置。
除了度数中心度之外,本文还根据式(8)和式(9)计算了各个经济体的中间中心度、接近中心度,以充分反映一国在国际碳排放网络中的中心性特征,如图2和图3所示。

|
| 图 2 代表性经济体的中间中心度 |

|
| 图 3 代表性经济体的接近中心度 |
图2显示,中国、俄罗斯、美国及欧盟等经济体具有较高的中间中心度,上述国家在国际碳排放网络中控制其他国家之间生产及碳排放关联的能力较强,在国际碳排放网络中属于关键的节点。这也充分表明,国际商品贸易经由中国、美国等国家的路径多、概率高,这些国家由于产品生产和国际贸易所引致的碳排放在世界碳排放总量中占有很高比重。1995—2014年,中国的中间中心度增长幅度最大且远超过其他国家,这与中国的对外贸易结构紧密相关。作为“世界工厂”,中国的国际贸易结构表现为“中间在内、两头在外”的特征,即从发达国家进口零部件经加工组装后再返回到发达国家和流向第三国,加工贸易占贸易总额的比重较高使得中国在国际碳排放网络中的“桥梁”位置十分突出。
与中间中心度的结果类似,通过对图3中接近中心度的测度结果分析可得,美国、俄罗斯以及欧盟等国家和地区的接近中心性较小,上述国家与其他国家之间构建碳排放联系所经由的国家数相对较少,属于国际碳排放网络的中心行动者,处于碳排放网络的核心位置。此外,图3显示,1995—2014年所有经济体的接近中心度均处在45度线以下,说明网络中国家之间碳排放联系的路径更短,碳排放伴随着产品流动能够更为快速地转移到网络中的其他国家,在国际碳排放网络中处于中心位置,与边缘位置的国家建立了更为直接的碳排放联系。
四、国际经济增长对碳排放的传导分析:基于路径的视角
本文在对国际碳排放矩阵的网络结构特征进行研究的基础上,再次使用国际碳排放矩阵作为国家之间的动态关联矩阵,从网络关联的角度探究一国经济增长通过碳排放网络的传导对其他国家碳排放所产生的影响。与第三部分不同,这一部分充分利用了国际碳排放网络中的关联路径,因此本文第三部分和第四部分分别突出的是国际碳排放网络中“点”和“线”的特征。本文基于Pesaran等(2004)提出的全球向量自回归(GVAR)模型,选取中国以及美国、欧盟、日本、俄罗斯等代表性经济体,探究中国经济增长对其他国家碳排放的影响路径,分析其他国家经济增长对中国碳排放的冲击效应。
(一)GVAR模型的构建。参照张延群(2012)对全球向量自回归(GVAR)模型理论及方法的描述,本文设定了国际碳排放问题的GVAR模型,首先设定各个国家的VARX *模型为:
| ${X_{it}} = {\alpha _{i0}} + {\alpha _{i1}}t + {\varPhi _i}{X_{it - 1}}{\rm{ + }}{\varLambda _{i\,0}}X_{it}^* + {\varLambda _{i1}}X_{it - 1}^* + {\varepsilon _{it}}$ | (10) |
其中,Xit为第t时期第i个国家的国内变量向量,其元素个数为ki,Xit*为与Xit相对应的国外变量,元素个数为ki*,并且假定Xit*具有弱外生性。
其次,设定表示各国之间关系的连接矩阵,将各个国家的VARX *模型连接为全球模型。基于Boschi和Girardi(2011)、Eickmeier和Ng(2015)的研究可知,连接矩阵可以选取贸易、投资和地理距离等反映国家间联系的变量进行构建,大多数文献中也广泛采用了上述变量构造连接矩阵。本文基于计算得到的1995—2014年每一年的“国际贸易—碳排放”矩阵构造连接矩阵,动态国际碳排放矩阵更加符合国家间经济增长与碳排放关系变动的现实。在国际碳排放矩阵的基础上,计算得到国家j转移给国家i的碳排放占世界各国转移给国家i总碳排放的比重wij,对应的国外变量可通过wij加权计算得到。例如,国外产出变量Yit*的计算方法为:
| $Y_{it}^{\rm{*}} = \sum\nolimits_{j = 0}^N {w_{ij}^Y{Y_{jt}}} $ | (11) |
然后,需要对国家之间经济增长对碳排放影响的传导途径加以设定,可设置国外变量Xit*的当期值和滞后值都会对国内变量Xit产生影响,各国变量Xit都会受到全球外生变量的冲击,误差协方差矩阵的存在意味着各国之间存在当期冲击的相互影响。
最后,对VARX *模型检验变量间的协整关系,构建相应的WECMX *模型,并通过连接矩阵将各个国家的WECMX *模型整合为GVAR模型。将式(10)改写为:
| ${A_i}{Z_{it}} = {\alpha _{i0}} + {\alpha _{i1}}t + {B_i}{Z_{it - 1}} + {\varepsilon _{it}}$ | (12) |
其中,
假设
| ${Z_{it}} = {W_i}{X_t}$ | (13) |
综合式(12)和式(13),得到式(14):
| ${A_i}{W_i}{X_t} = {\alpha _{i0}} + {\alpha _{i1}}t + {B_i}{W_i}{X_{t - 1}} + {\varepsilon _{it}}$ | (14) |
将式(14)改写为上下叠加的形式,得到GVAR模型的基本表达形式:
| $G{X_t} = {\alpha _0} + {\alpha _1}t + H{X_{t - 1}} + {\varepsilon _t}$ | (15) |
其中,
将全球共同外生变量加到GVAR模型中,得到扩展的VARX *模型如式(16)所示。
| ${X_{it}} = {\alpha _{i0}} + {\alpha _{i1}}t + {\varPhi _i}{X_{it - 1}} + {\varLambda _{i0}}X_{it}^* + {\varLambda _{i1}}X_{it - 1}^* + {\psi _{i0}}{d_t} + {\psi _{i1}}{d_{t - 1}} + {\varepsilon _{it}}$ | (16) |
其中,dt为全球共同变量向量,元素个数为全球外生变量的个数,共同变量具有弱外生性。
在式(15)和式(16)的基础上,最终得到扩展的GVAR模型为:
| $G{X_t} = {\alpha _0} + {\alpha _1}t + H{X_{t - 1}} + {\psi _0}{d_t} + {\psi _1}{d_{t - 1}} + {\varepsilon _t}$ | (17) |
本文中的GVAR模型由欧盟和其他12个国家共13个经济体的VARX *模型组合而成,基于世界发展指标(WDI)数据库的计算可知,2014年模型中13个经济体的GDP之和占世界GDP总量的83%,碳排放量占世界碳排放总量的比例为75%,因而能够反映全球经济发展及碳排放的整体特征。
参照Prell(2016)中有关控制变量的选取方法,从影响一个国家碳排放的经济发展、产业结构、贸易水平、能源消耗四个重要方面进行变量选取,对于单个国家和地区的VARX *模型,国内变量选择二氧化碳排放量、实际GDP、工业增加值占GDP比重、进出口贸易总额占GDP比重及能源变量,数据均来自于世界发展指标(WDI)数据库。为保证全球向量自回归模型的收敛性,并得到准确的估计结果,本文采用EViews 9.0软件将部分年度数据转化为季度数据。全球共同变量为国际石油价格,记为poil,石油价格的季度数据来自美国能源信息署网站,样本区间为1995年第1季度到2014年第4季度。
(二)经济增长对碳排放的影响路径分析。广义脉冲响应函数(Generalized Impulse Response Function,GIRF)是全球向量自回归模型中的一种重要方法,能够反映模型中经济产出变量与碳排放变量之间的动态冲击效应。本文对GVAR模型进行估计后,采用GIRF方法对中国与代表性经济体经济增长和碳排放的影响关系进行分析,一方面研究中国经济增长对其他经济体碳排放的冲击效应,另一方面分析其他国家和地区经济增长对中国碳排放的影响效应。为简化起见,本文仅选取了与中国经济联系最为紧密的9个代表性经济体进行分析,按照经济体类型可以划分为发达国家、金砖国家及部分新兴经济体国家三组,其中发达经济体包括美国、日本、欧盟;金砖国家包括俄罗斯、巴西、印度;部分新兴经济体国家包括韩国、印度尼西亚、墨西哥。
1. 中国经济增长对代表性经济体碳排放的冲击效应与传导路径。对中国实际GDP进行一个标准差的正向冲击,得到9个代表性经济体碳排放量的响应函数值,结果如图4所示。
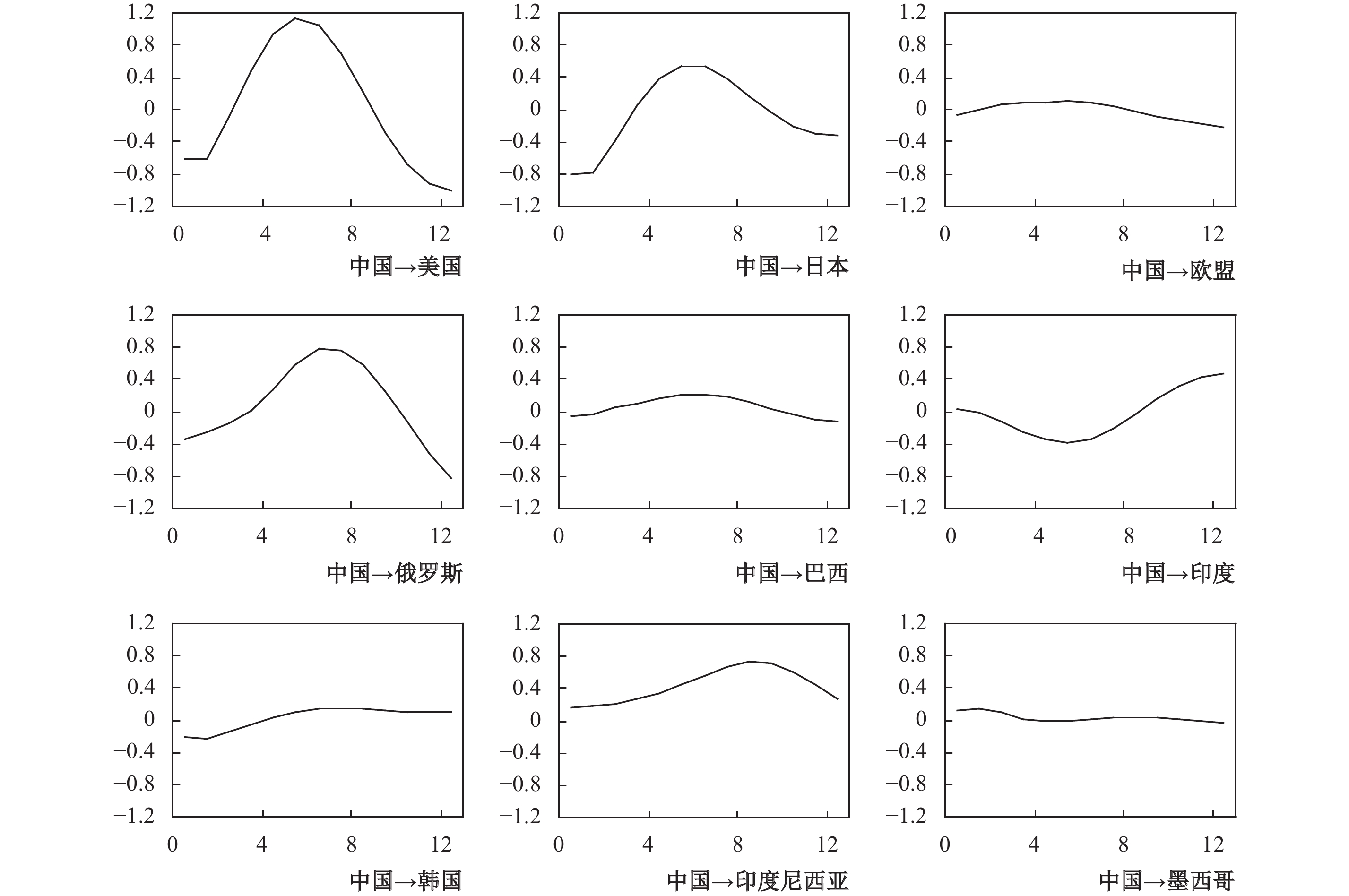
|
| 图 4 中国经济增长对代表性经济体碳排放的影响 |
在图4中,中国经济增长冲击下代表性经济体碳排放脉冲响应函数的变动趋势显示,除印度表现出“U”形特征外,其他各经济体基本表现出倒“U”形特征。对美国、日本、欧盟等发达经济体和俄罗斯、韩国而言,中国经济产出的增加在初期能够显著降低其碳排放,在国际化分工的背景下,中国生产的污染型初级产品出口到上述国家中,为其生产提供了必需的中间品,降低了其高能耗和高排放中间产品的生产水平,从而减少了本国的碳排放。当中国生产的中间产品输入到上述国家后,还会使得相关行业的生产规模扩大,规模效应引发的能源消耗和产出增加对碳排放具有促进作用,当其逐渐抵消了产品输入导致的碳排放减少幅度时,上述国家碳排放出现了增长的趋势,图4显示,在第2—3期左右,美国、日本、俄罗斯和韩国的脉冲响应函数开始由负转正。随着中间产品完全消耗和经济产出规模趋向平稳,上述国家的碳排放量增速逐渐回落。特别是在第9期以后,美国、日本等国家碳排放的脉冲响应函数又低于零值,一个可能的解释是发达国家在中国经济增长的冲击后实现了产业和碳排放的共同转移,进而使碳排放出现了负增长。
根据图4可得,中国经济增长对印度尼西亚、墨西哥等部分新兴经济体国家的冲击效应也呈现出倒“U”形的变动趋势,但两个国家的脉冲响应函数一直大于零,并没有表现出碳排放增长量正负交替的特征。原因在于,中国经济增长对部分新兴经济体国家的影响主要不体现在产品出口上,而是表现在产业转移中,新兴经济体国家经济发展对资本的依赖程度较大,并利用资本边际回报率较高的优势积极引进外资和承接国家产业转移,中国经济增长与部分新兴经济体国家的经济生产实现了优势互补和良性互动,促使其碳排放量上升。
需要指出的是,印度碳排放量对中国经济增长的初期响应是负向的,这与两国的经济结构和对外贸易结构相关。由于劳动力要素禀赋和经济发展阶段的高度近似,中国和印度在国际产业分工中存在着很大程度的重合,例如加工贸易在贸易总额中占有较高比重以及低附加值劳动密集型产品在出口中的占比较大等,两国在国际市场上具有高度的竞争关系,因此中国的经济增长会导致国际市场上对印度产品的需求缩减,对其经济产出具有抑制作用,导致印度的碳排放量也随之减少。但是,图4显示,在第8期之后,印度碳排放对中国经济增长冲击的脉冲响应函数由负转正,来自中国的竞争效应促使印度加大了中间品的生产和输出,从而使得印度的碳排放逐渐回升。
此外,在中国经济增长冲击下9个代表性经济体的碳排放在响应大小和响应时滞上存在一定差异,其中美国碳排放脉冲响应函数的波动幅度和响应速度均是最为突出的。中国与美国的经济联系较为密切,对美国的进出口呈现相对稳定且快速增长的特征,2014年中国对美国的进出口额同比增长6.6%,中国进出口总额中美国占比高达11.2%。①更为重要的是,中国与美国在全球价值链产业分工中的互补性很强,中国参与全球价值链的重要方式是加工贸易,即从事加工、组装等活动,一般处于全球价值链的中游水平,而美国则处在全球价值链的高端环节,中国经济产出冲击沿着全球价值链自下而上传导,引致美国碳排放波动较为明显。
2. 代表性经济体产出增长对中国碳排放的影响效应与传导路径。本文分别对9个代表性经济体的实际GDP进行一个标准差的正向冲击后,得到中国碳排放量的脉冲响应图形。
如图5所示,美国和欧盟经济增长对中国碳排放呈现倒“U”形的正向冲击效应,而日本经济增长对中国碳排放则具有“U”形的负向冲击特征。如前所述,由于美国、欧盟两大发达经济体产出增长对中国高能耗、高污染中间产品的需求直接促进了中国经济的增长和碳排放量的增加,中国碳排放的脉冲响应函数开始上升。在美国、欧盟对来自中国的中间品消耗完成后,即产品的生产周期结束后,两大经济体对中国经济产出的刺激效应减弱,中国碳排放的脉冲响应函数逐渐回落。对于日本而言,与其他发达国家不同,中国大量进口了原产自日本的中间产品,将其加工后又出口到美国和欧盟,“中国制造”中含有一定程度的“日本成分”,这一点也在中国对日本贸易长期以来的持续逆差中得以体现,特别是日本向中国出口和输入了大量高技术含量和高增加值的中间品,大幅减少了中国同类和相关产品的生产活动,使得碳排放量出现了一定程度的下降。
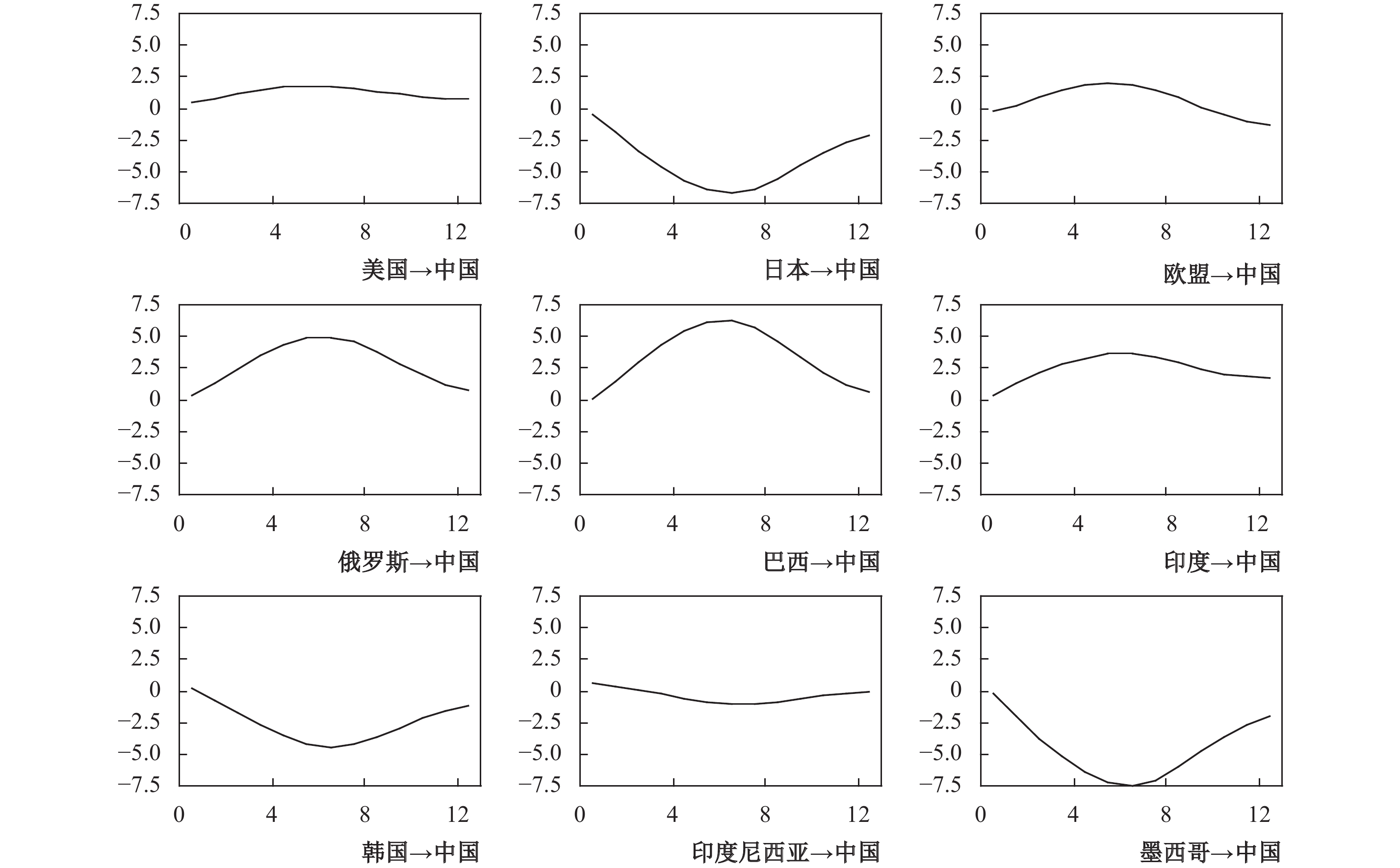
|
| 图 5 代表性经济体产出增长对中国碳排放的影响 |
在俄罗斯、巴西和印度等金砖国家经济增长的冲击下,中国碳排放的脉冲响应函数表现出明显的倒“U”形特征,且响应函数值均为正。金砖国家与中国经济的贸易合作十分紧密,2009—2014年,在全球经济增速放缓的情形下,金砖国家国际贸易总额年均增速超过30%,各金砖国家之间的年均贸易额超过3 000亿美元。中国与金砖国家之间的贸易规模持续扩大,贸易合作的深化促进了各国以扩大进口的形式拉动中国的产品需求,对中国经济增长进而对碳排放产生了正向冲击效应。金砖国家经济增长对中国碳排放的冲击效应在第5期左右达到峰值后开始呈现下降趋势,一个可能的解释是中国以对外投资的方式向市场潜力较大的金砖国家实现了部分产业的转移和碳输出,国内的碳排放量增速下降。
与金砖国家的冲击效应相反,中国碳排放对韩国、印度尼西亚、墨西哥等新兴经济体经济增长冲击的响应函数呈现“U”形变动趋势,且响应函数值基本为负。在国际贸易中,中国与部分新兴经济体国家呈现出相互依赖性,特别是在进口方面,新兴经济体中印度尼西亚、墨西哥丰富的矿产品等自然资源及橡胶塑料等初级产品等为中国经济发展提供了重要的物质保障,并且印尼等国是中国产业转移和对外直接投资的重要目的国,因此其经济增长有助于中国碳排放的输出和国内碳排放量的降低。韩国向中国出口的机电产品、光学产品和集成电路产品较多,在与韩国的贸易往来中,中国通过“进口中学”和“出口中学”引进先进技术,激发了创新动力,获得部分清洁型或环境友好型生产技术,使得自身碳排放量逐渐减低。
在代表性经济体经济发展对中国碳排放冲击效应的幅度方面,日本和墨西哥对中国的负向冲击效应最大,巴西对中国的正向冲击效应最大,这在一定程度上是由其向中国出口中间产品的类型决定的。日本、墨西哥主要向中国出口机电产品和运输设备等,会对中国国内同类产品的生产形成替代效应,进而减少中国的碳排放。与之不同,巴西的铁矿石、有色金属等自然资源的丰裕度很高,通过将其出口到中国后,推动了中国高耗能和高排放行业的发展,进而促使中国的碳排放量快速上升。因此,出口贸易商品结构是导致代表性经济体经济增长对中国碳排放影响程度差异的主要因素。
五、结 论
本文基于国际投入产出数据构建“国际贸易—碳排放”矩阵,将网络分析方法与全球向量自回归方法相结合,厘清了国际碳排放网络的结构特征,采用动态的碳排放连接矩阵识别了国家间经济增长对碳排放的传导路径,得到研究结论如下:在国际碳排放网络中,发达经济体通过大量进口中间产品实现了碳转移,在国际碳排放网络中的点入度较大,金砖国家和新兴经济体国家进行产品出口的同时接收了来自发达国家的碳输入,导致其点出度较高。发达国家实现了“产品输入和碳输出”,发展中国家则呈现出“产品输出和碳输入”的特征。中国通过加工贸易等途径与其他国家建立了大量的生产及碳排放联系,碳排放关联随之建立并日益密切。总体而言,发达经济体的中心度在国际碳排放网络中的位置相对稳定,与之相对,发展中国家或新兴经济体国家度数中心度均有显著提升。在国家个体网络位置特征分析的基础上,本文进一步从网络关联的角度研究国家间经济增长与碳排放的冲击效应,基于全球向量自回归模型的研究结果显示,在中国经济增长的冲击下,除印度外代表性经济体的碳排放呈现出倒“U”形的变动特征,中国生产的中间产品输入导致的碳排放减少效应与刺激生产规模扩大引发碳排放增长效应的大小关系决定了代表性经济体碳排放的变动方向。除日本外的发达经济体及金砖国家产出增长对中国碳排放呈现倒“U”形的正向冲击效应,而新兴经济体经济增长对中国碳排放则具有“U”形的负向冲击特征,国际产业分工地位和出口贸易商品结构能够在很大程度上解释代表性经济体与中国之间经济增长与碳排放冲击效应的差异。
基于本文的研究,我们认为,应充分考虑各国在国际碳排放网络中的关联特征,根据各自的发展阶段、要素禀赋及生产结构特点制定差异化的减排策略,充分体现“共同但有区别责任”的原则。发达国家应率先减排并对金砖国家、新兴经济体国家输出减排技术和进行减排援助等,在应对全球气候变化中承担更多的国际责任。对于中国而言,在推动经济增长模式由要素驱动向创新驱动转变的过程中,加大碳减排技术或清洁生产技术的引进、消化和吸收,特别是煤炭清洁高效利用技术的创新,不仅是从根本上降低中间品生产中的碳排放进而减少国际间碳转移量的关键所在,而且是发挥中国对世界碳减排贡献的重要方式。
① 数据来源于《2014年中国对外贸易发展情况》,中华人民共和国商务部综合司,网址:http://zhs.mofcom.gov.cn/。
| [1] | 蒋雪梅, 刘轶芳. 全球贸易隐含碳排放格局的变动及其影响因素[J]. 统计研究, 2013(9): 29–36. DOI:10.3969/j.issn.1002-4565.2013.09.005 |
| [2] | 李敬, 陈旎, 万广华, 等. " 一带一路”沿线国家货物贸易的竞争互补关系及动态变化——基于网络分析方法[J]. 管理世界, 2017(4): 10–19. |
| [3] | 刘华军, 刘传明, 孙亚男. 中国能源消费的空间关联网络结构特征及其效应研究[J]. 中国工业经济, 2015(5): 83–95. |
| [4] | 牛玉静, 陈文颖, 吴宗鑫. 全球多区域CGE模型的构建及碳泄漏问题模拟分析[J]. 数量经济技术经济研究, 2012(11): 34–50. |
| [5] | 彭水军, 张文城. 国际贸易与气候变化问题: 一个文献综述[J]. 世界经济, 2016(2): 167–192. |
| [6] | 齐晔, 李惠民, 徐明. 中国进出口贸易中的隐含碳估算[J]. 中国人口·资源与环境, 2008(3): 8–13. DOI:10.3969/j.issn.1002-2104.2008.03.002 |
| [7] | 王美昌, 徐康宁. 贸易开放、经济增长与中国二氧化碳排放的动态关系——基于全球向量自回归模型的实证研究[J]. 中国人口·资源与环境, 2015(11): 52–58. DOI:10.3969/j.issn.1002-2104.2015.11.007 |
| [8] | 王文举, 向其凤. 国际贸易中的隐含碳排放核算及责任分配[J]. 中国工业经济, 2011(10): 56–64. |
| [9] | 徐振宇. 社会网络分析在经济学领域的应用进展[J]. 经济学动态, 2013(10): 61–72. |
| [10] | 张红, 李洋, 张洋. 中国经济增长对国际能源消费和碳排放的动态影响: 基于33个国家GVAR模型的实证研究[J]. 清华大学学报(哲学社会科学版), 2014(1): 14–25. |
| [11] | 张延群. 全球向量自回归模型的理论、方法及其应用[J]. 数量经济技术经济研究, 2012(4): 136–149. |
| [12] | Antweiler W, Copeland B R, Taylor M S. Is free trade good for the environment?[J]. The American Economic Review, 2001, 91(4): 877–908. DOI:10.1257/aer.91.4.877 |
| [13] | Boschi M, Girardi A. The contribution of domestic, regional and international factors to Latin America’s business cycle[J]. Economic Modelling, 2011, 28(3): 1235–1246. DOI:10.1016/j.econmod.2011.01.002 |
| [14] | Chang P L, Shih H Y. Comparing patterns of intersectoral innovation diffusion in Taiwan and China: A network analysis[J]. Technovation, 2005, 25(2): 155–169. DOI:10.1016/S0166-4972(03)00077-4 |
| [15] | Coondoo D, Dinda S. Causality between income and emission: A country group-specific econometric analysis[J]. Ecological Economics, 2002, 40(3): 351–367. DOI:10.1016/S0921-8009(01)00280-4 |
| [16] | Copeland B R, Taylor M S. Trade and transboundary pollution[J]. The American Economic Review, 1995, 85(4): 716–737. |
| [17] | Copeland B R, Taylor M S. Free trade and global warming: A trade theory view of the Kyoto protocol[J]. Journal of Environmental Economics and Management, 2005, 49(2): 205–234. DOI:10.1016/j.jeem.2004.04.006 |
| [18] | Eickmeier S, Ng T. How do US credit supply shocks propagate internationally? A GVAR approach[J]. European Economic Review, 2015, 74: 128–145. DOI:10.1016/j.euroecorev.2014.11.011 |
| [19] | Granger C W J, Jeon Y. Evaluation of global models[J]. Economic Modelling, 2007, 24(6): 980–989. DOI:10.1016/j.econmod.2007.03.008 |
| [20] | Grossman G M, Krueger A B. Environmental impacts of a north American free trade agreement[A]. Garber P M. The Mexico-US free trade agreement[C]. Cambridge MA: MIT Press, 1993: 223−250. |
| [21] | Holtz-Eakin D, Selden T M. Stoking the fires? CO2 emissions and economic growth [J]. Journal of Public Economics, 1995, 57(1): 85–101. DOI:10.1016/0047-2727(94)01449-X |
| [22] | Jorgenson A K, Clark B. Are the economy and the environment decoupling? A comparative international study, 1960—2005[J]. American Journal of Sociology, 2012, 118(1): 1–44. DOI:10.1086/665990 |
| [23] | Machado G, Schaeffer R, Worrell E. Energy and carbon embodied in the international trade of Brazil: An input-output approach[J]. Ecological Economics, 2001, 39(3): 409–424. DOI:10.1016/S0921-8009(01)00230-0 |
| [24] | Montresor S, Marzetti G V. Applying social network analysis to input–output based innovation matrices: An illustrative application to six OECD technological systems for the middle 1990s[J]. Economic Systems Research, 2009, 21(2): 129–149. DOI:10.1080/09535310902940228 |
| [25] | Pesaran M H, Schuermann T, Weiner S M. Modeling regional interdependencies using a global error-correcting macroeconometric model[J]. Journal of Business & Economic Statistics, 2004, 22(2): 129–162. |
| [26] | Peters G P, Minx J C, Weber C L, et al. Growth in emission transfers via international trade from 1990 to 2008[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(21): 8903–8908. DOI:10.1073/pnas.1006388108 |
| [27] | Prell C. Wealth and pollution inequalities of global trade: A network and input-output approach[J]. Social Science Journal, 2016, 53(1): 111–121. DOI:10.1016/j.soscij.2015.08.003 |
| [28] | Rauch J E, Watson J. Network intermediaries in international trade[J]. Journal of Economics & Management Strategy, 2004, 13(1): 69–93. |
| [29] | Wyckoff A W, Roop J M. The embodiment of carbon in imports of manufactured products: Implications for international agreements on greenhouse gas emissions[J]. Energy Policy, 1994, 22(3): 187–194. DOI:10.1016/0301-4215(94)90158-9 |
| [30] | Zhang X P, Cheng X M. Energy consumption, carbon emissions, and economic growth in China[J]. Ecological Economics, 2009, 68(10): 2706–2712. DOI:10.1016/j.ecolecon.2009.05.011 |

