一、引　言

经济的发展和医疗水平的改善使得世界人口的平均寿命持续增加，与之伴随的是各国普遍存在的受教育年限的延长和劳动供给年限的缩短。从20世纪50年代至今，世界平均受教育年限从1950年的3.12年上升到了2010年的7.89年（Barro 和 Lee，2013），但很多国家的老年劳动参与率则持续降低，劳动供给时间逐渐减少（Gruber 和 Wise，1998；Hazan 和 Zoabi，2006；Hazan，2009；Cervellati 和 Sunde，2013）。中国也存在这种情况，从1982年到2010年，人均受教育年限由6.8年升高至10.8年，起始劳动年龄从14.8岁增至18.8岁，工作年限却从42.7年减少至38.8年（邵国栋等，2007），老年劳动参与率具有明显的下降趋势（张川川和赵耀辉，2014）。

预期寿命增加伴随着人力资本投资增加和劳动供给减少的现象引起了学术界广泛的关注。对该现象的产生，现有文献大多围绕Ben-Porath（1967）提出的理论（Ben-Porath机制）来解释。该机制认为，更长的生命期将延长个人教育投入的回报期，促使个人增加人力资本投资以获得更多收入，因此预期寿命的增加会导致受教育年限的增加。然而，Ben-Porath机制对劳动供给和退休行为的预测并没有与现实非常吻合。Hazan（2009）指出，基于Ben-Porath理论，预期寿命增加引起受教育年限延长的必要条件是预期终生劳动供给也增加，即只有教育回报时间（工作时间）变长，增加人力资本投资才是合理的。Hazan（2009）通过研究1840—1970年美国男性预期平均劳动小时数的数据，观察到了相反的结论，发现预期寿命增加的同时，消费者的终生预期工作小时数在逐渐降低，与Ben-Porath机制的结论相悖，由此引发了学术界的“Ben-Porath机制之争”。

此后，有不少研究围绕Hazan（2009）提出的质疑展开了讨论。张熠（2015）梳理了相关文献，对国内外学术界有关Ben-Porath机制的争论进行了详细的比较与归纳。有学者认为，人口预期寿命增加、退休年龄提前与教育年限增加都是经济发展的结果，工资提高引起的收入效应使得个人对教育和闲暇的需求都有所增加，而预期寿命增加本身对教育和劳动供给并没有直接的影响（Bloom 等，2014）。有文献通过放宽和改变Hazan（2009）的模型设定，提出退休年龄延迟并不是Ben-Porath机制成立的必要条件（Strulik 和 Werner，2012；Cai 和 Lau，2012；Cervellati 和 Sunde，2013）。此外，还有学者试图构建与经验数据相符合的理论模型，比如Hansen 和 Lønstrup（2012）通过引入不完善金融市场，得出了预期寿命增加可以同时引起受教育年限增加和退休提前的结论。

在试图引入市场摩擦而使得理论与经验数据相吻合的文献中，大部分研究往往将不完善市场作为外生给定的经济背景条件，并且大多数考虑的是极端情况，比如经济中完全不存在年金市场（Hansen 和 Lønstrup，2012）。但是当市场的摩擦程度不同时，预期寿命增加带来的经济效应也可能是不尽相同的，而市场的发展和完善过程本身对消费者行为也可能会产生重要的影响。本文从与预期寿命及退休行为紧密联系的年金市场的角度出发，讨论当经济中存在年金市场时，预期寿命增加会如何影响消费者的人力资本投资和劳动供给行为，并讨论年金市场的发展对消费者行为会产生怎样的影响。

在我国，研究预期寿命增加、年金市场发展和消费者经济行为之间的关系显得尤为重要。中国日益严峻的老龄化形势和劳动人口的提前退休趋势使得我国人口和社会保障制度内的抚养比持续上升，给我国社会和经济发展带来了很大的压力。年金作为养老保障的三大支柱之一，不管是企业年金还是商业年金，其需求在不断增大，年金市场的健康发展迫在眉睫（孙祁祥等，2013）。近年来政府为了鼓励年金市场发展，出台了一系列相关政策。1991年，国务院发布了《企业职工养老保险制度改革的决定》，提出“逐步建立起基本养老保险与企业补充养老保险和职工个人储蓄性养老保险相结合的制度”。2004年，原劳动和社会保障部颁发了《企业年金试行办法》，规范企业为个人进行的补充型养老保险福利，并大力推行此类型的养老保险。2017年人力资源社会保障部和财政部公布了《企业年金办法》，进一步完善了我国的企业年金制度。

在这样的需求和政策环境下，我国年金保险发展势头迅猛。根据人社部发布的《2017年度全国企业年金基金业务数据摘要》，2017年企业年金基金规模达12 880亿，较2016年增速16.3%，覆盖8万企业和2 331万个人。而中国保险行业协会发布的《2017年度互联网人身保险市场运行情况报告》也显示我国年金保险发展迅速，2017年全年累计实现规模保费461.4亿元，同比增长86.4%，占互联网人身保险总保费的33.4%，为仅次于寿险的第二大互联网人身保险险种。考虑到在我国，年金市场正处于起步和探索阶段，随着其发展规模的不断壮大，其产生的直接和间接效应非常值得关注和探索。基于此，本文将通过构建生命周期模型，讨论预期寿命增加和年金市场发展对消费者人力资本投资、储蓄和退休行为的影响。

本文的主要探索是：（1）在讨论预期寿命增加对人力资本投资、储蓄行为和退休决策行为的影响时，强调了年金市场的存在和完善程度对上述经济效应的影响，以及年金市场发展本身对消费者行为的直接影响；（2）相比现有文献大多讨论预期寿命增加对退休行为的影响，本文还关注了预期寿命增加如何影响消费者一生的预期劳动供给，从而使本文的结论与Hazan（2009）的经验结果具有可比性。本文的主要结论是：随着预期寿命的增加，典型消费者会增加人力资本投资、增加储蓄率，但退休行为和预期终生劳动供给的变化不确定。当年金市场不完善或市场利率水平较低时，预期寿命增加会引起消费者提前退出劳动力市场。本文还发现，如果预期寿命不变，那么随着年金市场的不断完善，消费者会提前退休。

本文余下部分是：第二部分构建了包含年金市场的三期生命周期模型并求解了典型消费者的最优行为；第三部分通过比较静态分析，讨论了当存在不同完善程度的年金市场时，预期寿命增加对消费者受教育年限、储蓄、退休决策和预期终生劳动供给的影响，以及年金市场的发展对消费者行为的影响；第四部分利用数值方法对本文的结论进行了稳健性检验；第五部分总结，并提出了相关政策建议。部分证明在附录中。

二、模型基本结构

本文在Hansen 和 Lønstrup（2012）模型的基础上，构建了一个开放经济条件下的三期生命周期模型。每个典型消费者最多存活三期：青年（y）、中年（m）和老年（o），每期的存活概率为φ^y=1、φ^m=1和φ^o=φ<1，即每个人一定能存活到中年期，但是在老年期期初面临生存风险。消费者在每个存活期都可获得1单位时间。在青年期，消费者将1单位时间用于接受教育（e）和工作（1−e）。假设消费者的初始人力资本为1，接受e单位时间教育后，其人力资本水平增加为h（e），并且在后两期保持不变。h（e）函数满足h′（e）>0，h′′（e）<0，h₀=1。在获得人力资本水平h（e）后，消费者每单位工作时间的工资收入为wh（e），其中w外生给定。假设信贷市场存在约束，年轻人不能通过贷款的方式提前消费。那么典型消费者在青年期的消费（c₁）将全部来自于当期的工资收入：^①

若消费者在教育上投入越多时间，那么其人力资本水平越高，会增加当期和未来两期每单位劳动时间的收入，但同时使青年期用于工作的时间减少。由于存在借贷约束，不能通过向未来借钱来平滑三期的消费，更多的人力资本投资将使消费者青年期的工资收入和消费水平降低。

消费者在中年期工作1单位时间，其工资收入被用于当期的消费c₂和储蓄。本文只考虑消费者在中年期期末储蓄值为正（S>0）的情况。消费者在中年期的预算约束为：

典型消费者从中年期到老年期的生存概率为φ<1。在本文模型中，预期寿命增加来自于生存概率φ的提高。^②我们在模型中引入年金市场，如果消费者在中年期期末将储蓄存入年金市场，那么其实际回报率受生存概率φ的影响。^③随着年金市场的不断完善，由于一部分消费者不能存活到老年期而非自愿遗留下来的储蓄将更大程度地被转移给存活到老年期的消费者，从而对存活到老年期的消费者而言，他们从年金市场获得的回报率会随着年金市场的不断发展而提高。参考Kalemli-Ozcan和 Weil（2010）以及Hansen 和 Lønstrup（2012）的做法，我们对由于不存在年金市场或年金市场不完善情况下没有被转移和分配的那部分偶发遗赠不作讨论，可以假设这部分遗赠被用于支付年金市场的管理成本，或用作不影响消费者福利的其他用途。另外，偶发遗赠在代际的转移也不在本文讨论范围。以R表示外生给定的市场利率，用参数δ∈[0，1]衡量年金市场的完善性，假定年金市场上中年期储蓄的实际回报率为 $\tilde R \equiv R/$ $\left( {1 - \delta + \delta \varphi } \right)$ ，参数δ取值越大，年金市场越完善，实际回报率 ${\tilde R}$ 越高。当δ=0时， $\tilde R = R$ ，该经济体中不存在年金市场；当δ=1时， $\tilde R = R/\varphi $ ，该经济体中存在完善的年金市场；当0<δ<1时，该经济体中存在不完善的年金市场。

对存活到老年期的消费者，他们将根据期初财富（ $S\tilde R$ ）和工资水平（wh（e））内生选择退休的时间，记闲暇（退休）时长为l∈[0，1]，则老年期工作时长为1−l。老年期的消费为：

消费者的效用取决于每期的消费水平和老年期的闲暇时长。假设如下对数形式的效用函数：

其中：β>0是时间偏好因子，θ衡量了个人对闲暇的偏好程度。典型消费者在式（1）至式（3）约束下，通过选择人力资本投入、各期消费水平和退休时长来最大化终生效用（4）。定义：

Kuhn-Tucker条件为：

表1给出了消费者问题的最优解。具体求解过程见附录A。

由于本模型只考虑消费者中年期储蓄为正（s₁>0）的情况，我们做如下假设：

假设1. $\tilde R > \displaystyle\frac{1}{{\varphi \beta \left( {1 + \theta } \right)}}$ （等价于 $R > \displaystyle\frac{{1 - \delta + \delta \varphi }}{{\varphi \beta \left( {1 + \theta } \right)}}$ ）。

由表1可知，消费者的最优选择可根据在老年期是否工作划分为两种情况：一是在老年期工作一段时间后再退休（内点解），二是老年期完全不工作直接退休（端点解）。消费者在老年期是否工作受年金市场实际回报率的影响。当储蓄的实际回报率较高时 $\left( {\tilde R > \displaystyle\frac{{1 + \varphi \beta }}{{\varphi \beta \theta }}} \right)$ ，由于中年期和老年期之间可以通过储蓄来平滑消费，收入效应将使消费者在中年期和老年期的消费水平都较高，由于边际效用递减，当老年期消费水平较高时，在老年期多工作1单位时间带来的消费增加引起的边际效用的增加将小于闲暇减少引起的边际效用的减少。这种情况下，消费者选择在老年期不工作（l=1），老年期的所有消费来自于年金市场的收入。由于中年期和老年期之间不存在借贷约束，因此这两种情况下，我们均有 $u'\left( {{c_2}} \right)/u'\left( {{c_3}} \right) = \varphi \beta \tilde R$ 。

三、比较静态分析

这里，我们分别讨论预期寿命和年金市场对消费者受教育年限、储蓄行为和劳动供给行为的影响。具体地，首先假定预期寿命不变，考虑年金市场发展对消费者行为的直接影响。然后，讨论预期寿命增加对消费者行为的影响，并指出年金市场的完善程度如何影响这些效应。

（一）年金市场对消费者行为的直接影响

在本文的模型框架下，年金市场的完善程度体现在参数δ的取值上，其对消费者行为的影响主要通过对实际回报率 $\left( {\tilde R = R/\left( {1 - \delta + \delta \varphi } \right)} \right)$ 的影响。年金市场越完善，其实际回报率越大。

首先，我们发现在对数效用函数假设条件下，年金市场回报率对消费者受教育年限e没有影响，从而年金市场的完善程度对受教育年限没有影响。增加受教育年限的成本是青年期的工作时间，当存在信贷约束时，直接影响消费者在青年期的工资收入和消费，而收益是整个工作期的工资率水平。对储蓄者而言，当实际利率水平增加，一方面，其带来的收入效应将促使消费者增加在每期的消费水平，由于青年期存在借贷约束，为了使青年期和后两期的消费相对平滑，消费者会减少受教育时长，通过在青年期多工作来增加青年期的消费水平；另一方面，实际利率增加引起的替代效应将增强消费者的储蓄动机，由于中年期期末的储蓄全部来自于中年期的工作收入，而中年期工作时间固定为1，因此消费者会在青年期接受更多教育以增加每单位工作时间的工资率。当假设对数效用函数形式时，这两种效应恰好互相抵消，从而实际利率的变化对受教育年限没有产生影响。在下文的稳健性检验中，当我们假设更一般的效用函数形式后，年金市场的发展和完善将会对消费者的人力资本投资行为产生影响。

再看年金市场发展对储蓄率的影响。将储蓄率s₁的表达式写为：

可得 $\partial {s_1}/\partial \tilde R > 0$ ，从而 $\partial {s_1}/\partial \delta > 0$ 。随着年金市场的不断完善，实际利率上升会同时产生收入效应和替代效应。当假设了对数效用函数形式，而且消费者在老年期仍然有劳动供给和劳动收入，那么储蓄回报率增加产生的替代效应将强于收入效应，会促使消费者储蓄更多。如果老年期完全退休，除年金外没有额外的收入，那么 $\partial {s_2}/\partial \delta =0$ ，利率变化产生的替代效应恰好与收入效应抵消，储蓄率不受年金市场完善程度的影响。这些结论与两期Diamond（1965）模型框架下的结论一致（Liu和Thøgersen，2019）。

年金市场发展还会直接影响消费者的老年期劳动供给行为。易证 $\partial {l_1}/\partial \tilde R > 0$ ，从而 $\partial {l_1}/\partial \delta > 0$ ，即其他条件不变时，随着年金市场的不断完善，消费者将减少劳动供给，提前退休。这是因为年金市场回报率增加所产生的收入效应促使消费者对闲暇的需求增加。

以上我们讨论了年金市场发展本身对消费者最优决策的影响。接下来我们主要分析预期寿命增加对消费者的人力资本投资、储蓄和退休决策的影响，并强调年金市场的完善程度如何影响这些经济效应。预期寿命增加对消费者行为的影响主要通过两个渠道：一是消费者老年期存活概率增加，老年期的消费和闲暇被赋予更多的权重；二是通过对年金市场回报率的影响，如果更多的人能存活到老年期，那么更少的偶发遗赠被分配给更多的老年期生存者，因此实际回报率会降低：

而且年金市场越完善，回报率降低的幅度越大：

（二）预期寿命对接受教育年限的影响

在对数效用函数假设条件下，由上文可知，实际利率的变化对消费者受教育年限没有影响，因此预期寿命增加对消费者人力资本投资决策的影响来自于老年期在整个生命周期中重要性的增加。根据表1中受教育年限的表达式，由隐函数定理，可计算：

当生存概率增加，消费者受教育年限将增加。直观地讲，当预期寿命变长，人力资本投资的预期回报期将延长，从而使个人倾向于在工作前积累更多的人力资本。这也是Ben-Porath机制的主要解释。但是，由下文的结论可知，消费者终生劳动供给时长的变化并不确定。即使工作时长变短，人力资本投资的回报期变短，消费者仍然愿意提高教育水平。这是由于当模型引入青年期借贷约束后，教育时长的选择不再独立于消费水平的选择，还直接决定了青年期的消费水平，是平滑青年期消费和未来两期消费的一种方式。因此，即使人力资本投资的回报期变短，消费者也可能增加受教育年限。

由于在对数效用函数假设条件下，年金市场对受教育年限（e）没有影响，因此年金市场是否完善对预期寿命增加带来的人力资本投资效应（de/dφ）也没有影响。

（三）预期寿命增加对储蓄率的影响

消费者在中年期期末的储蓄行为受预期寿命变化的影响主要通过生存概率增加和实际利率减少这两个渠道：

我们按消费者在老年期是否工作分两种情况讨论。

1. 消费者在老年期先工作再退休（内点解）。由表1中储蓄率的表达式可计算：

当生存概率增加时，一方面，偶发遗赠的风险减少，老年期在整个生命周期中的重要性增加，因而消费者储蓄动机增加，将通过多储蓄的方式满足有更大概率发生的老年期的消费需求；另一方面，当假设了对数效用函数形式，如果消费者在老年期仍然有劳动供给和劳动收入，那么储蓄回报率降低产生的替代效应将强于收入效应，会促使消费者减少储蓄。综合以上两种效应，可得：

即在对数效用函数假设条件下，生存概率增加产生的正向效应更强。证明过程见附录B。

再看年金市场的完善程度如何影响这种储蓄效应。可计算：

随着年金市场的不断完善，预期寿命增加引起储蓄率增加的程度会被削弱。由上文分析可知，年金市场越完善，生存概率增加引起的实际利率降低的幅度越大，从而使由回报率产生的负向效应加强，削弱了预期寿命增加引发的总的正向储蓄效应。

2. 消费者在老年期完全退休（端点解）。如果消费者在老年期没有劳动供给，当假设对数效用函数时，实际利率变化引起的收入效应和替代效应互相抵消，不影响消费者储蓄行为。消费者储蓄行为的改变全部来自于正向效应：

在这种情况下，由于储蓄率不受实际利率变化的影响，因此，年金市场是否完善不改变预期寿命增加对储蓄行为的影响。

（四）预期寿命增加对退休决策的影响

这里我们主要讨论消费者在老年期存在劳动供给（内点解）的情形。在本文的框架设定下，退休行为的决定发生在老年期，而不确定性在老年期期初便得以消除，因此对存活到老年期的每一个消费者而言，其退休行为并不会受长寿风险的直接影响，长寿风险通过改变中年期储蓄行为来间接影响老年期的劳动供给行为。^④对在老年期存活下来的消费者来说，其老年期期初的财富水平（W^old）来自于年金收入。给定期初财富 ${W^{old}} = S\tilde R = swh\left( e \right)\tilde R$ 和当期工资率wh（e），我们求解如下老年期效用最大化问题：

可得 $l = \displaystyle\frac{\theta }{{1 + \theta }}\left( {1 + s\tilde R} \right)$ 。

由于效用函数为对数形式，而且期初财富是工资率wh（e）的线性函数，因此，老年期的工资水平变化引起的替代效应和收入效应恰好抵消，退休决定并不受老年期工资率wh（e）的影响，仅受老年期期初财富的影响。期初财富水平越高，根据收入效应，消费者将同时消费更多的消费品和闲暇，提前退休。

消费者老年期期初的财富水平取决于中年期的储蓄行为和年金市场回报率。定义：

从而有：

由（11）式和（16）式可知，随着预期寿命的增加，消费者储蓄动机增强，但同时年金市场回报率变低。老年期期初财富水平的变化取决于这两种效应的相对大小。这种因为储蓄增加而引起的提前退休在Kalemli-Ozcan 和 Weil（2010）中被讨论过，^⑤但是本文的模型还考虑了因生存概率增加引起年金市场回报率下降所产生的负向作用。

通过求解 $\displaystyle\frac{{d{w^{old}}}}{{d\varphi }}$ 并判断其符号（见附录C），我们有以下结论：

（1）如果 $\delta {\text{≤}} \displaystyle\frac{1}{{1 + \beta {\varphi ^2}}}$ ，那么 $\displaystyle\frac{{d{l_1}}}{{d\varphi }} > 0$ ；

（2）如果 $\delta > \displaystyle\frac{1}{{1 + {\varphi ^2}\beta }}$ ，那么当 $R < \displaystyle\frac{{{{\left( {1 - \delta + \delta \varphi } \right)}^2}}}{{\delta + \delta \beta {\varphi ^2} + \delta \theta \beta {\varphi ^2} - 1}}$ 时，^⑥ $\displaystyle\frac{{d{l_1}}}{{d\varphi }} > 0$ ；当 $R > \displaystyle\frac{{{{\left( {1 - \delta + \delta \varphi } \right)}^2}}}{{\delta + \delta \beta {\varphi ^2} + \delta \theta \beta {\varphi ^2} - 1}}$ 时， $\displaystyle\frac{{d{l_1}}}{{d\varphi }} < 0$ 。

当经济中不存在年金市场或年金市场较不完善，预期寿命增加将引起消费者提前退休；如果年金市场较完善，那么当外生利率水平较低时，预期寿命增加会引起退休提前，外生利率水平较高时，预期寿命增加会引起退休延迟。Hansen 和 Lønstrup（2012）只考虑了经济中不存在年金市场（δ=0）的情形，并得出预期寿命增加引起退休提前的结论，这在结论（1）中有所体现。但是即使放宽了他们强调的市场摩擦条件之一，即不存在年金市场，在不完全年金市场假设条件下，只要外生利率水平较低，预期寿命增加仍然会引起退休提前。

预期寿命增加引起的退休决策变化之所以受年金市场完善程度的影响，是因为随着年金市场的不断发展，预期寿命增加引起储蓄率增加的程度会被削弱（见（17）式），同时，实际回报率降低会随着年金市场的完善和外生利率水平R的提高而增强（见（12）式和（23）式）：

因此当年金市场较不完善或外生利率水平较低时，生存概率增加更容易引起老年期期初的财富增加，促使消费者提前退休。

（五）预期寿命增加对预期终生劳动供给的影响

Hazan（2009）指出，预期寿命增加引起受教育年限延长的同时，消费者预期终生劳动供给（Expected Total Working Hours，ETWH）在下降。由上文的讨论可知，随着老年期生存概率的增加，消费者因为受教育年限增加而推迟进入劳动力市场，并且在一定条件下会提前退休，但是这并不一定验证了Hazan（2009）的经验发现。退休提前是每一个存活到老年期的消费者所选择的行为，而预期终生劳动供给不仅受实际退休时长的影响，还受生存概率的影响。因此，为了验证本文的模型能否得出与Hazan（2009）经验发现相匹配的结论，我们讨论预期寿命增加对预期终生劳动供给的影响。在本文模型中，预期终生劳动供给可定义为：

如果是端点解（l=1），那么由于 $\displaystyle\frac{{de}}{{d\varphi }} > 0$ ，一定有 $\displaystyle\frac{{dETWH}}{{d\varphi }} < 0$ ，即随着预期寿命的增加，预期终生劳动供给在减少。

如果是内点解，那么即使 $\displaystyle\frac{{dl}}{{d\varphi }} > 0$ ，但是φ也在增加，我们无法判断预期终生劳动供给的变化。具体地有：

其中： $\displaystyle\frac{{de}}{{d\varphi }} > 0$ ， $1 - {l_1} > 0$ ， $\displaystyle\frac{{d{l_1}}}{{d\varphi }}$ 的符号不确定。当且仅当 $\displaystyle\frac{{de}}{{d\varphi }} > \left( {1 - {l_1}} \right) - \varphi \displaystyle\frac{{d{l_1}}}{{d\varphi }}$ 时，有 $\displaystyle\frac{{dETWH}}{{d\varphi }} < 0$ 。

如果假设函数h（e）满足 $\displaystyle\frac{{h'\left( e \right)e}}{{h\left( e \right)}} = \mu $ ，即人力资本投资函数不变弹性，那么由 $\left( {1 + \beta + \varphi {\beta ^2}} \right)\displaystyle\frac{{h'\left( e \right)}}{{h\left( e \right)}} - $ $ \displaystyle\frac{1}{{1 - e}} = 0$ ，可得：

通过求解 $\displaystyle\frac{{dETWH}}{{d\varphi }}$ 并判断其符号（见附录D），我们有以下结论：

预期寿命增加对消费者预期终生劳动供给的影响不确定。存在临界值：

当 $R > \hat R$ 时，随着预期寿命的增加，消费者预期终生的劳动供给减少。

该结论看似与预期寿命增加对退休决策影响的结论相矛盾。之前我们发现，如果经济中年金市场较完善，那么当外生利率水平较低时，预期寿命增加会引起退休提前，却更容易引起预期终生劳动供给增加。这是因为当外生利率水平R较高时，消费者在老年期的工作时长较少（ $\displaystyle\frac{{\partial {l_1}}}{{\partial R}} > 0$ ），因而（25）式中（1−l₁）较小。综合其他效应（ $\displaystyle\frac{{de}}{{d\varphi }} > 0$ ， $\displaystyle\frac{{d{l_1}}}{{d\varphi }}$ 符号不确定），预期终生劳动供给更有可能减小。这也强调了在分析退休行为和预期劳动供给时应区别对待。即使我们观察到一个经济中消费者平均进入劳动力市场的时间推迟，平均退出劳动力市场时间提前，但是由于生存概率的增加，整个社会中平均劳动力供给的变化并不确定。

我们将以上结论总结如下：

在一个存在信贷约束和（不完善）年金市场的三期生命周期理论模型中，如果假设效用函数为对数函数形式，而且消费者在中年期期末储蓄为正，那么有：（1）如果预期寿命不变，那么随着年金市场的不断完善，消费者受教育年限不受影响，但是储蓄率会增加，退休提前。（2）当预期寿命增加，消费者在青年期接受教育年限会增加。年金市场的完善程度不影响该效应。（3）当预期寿命增加，消费者在中年期的储蓄率会增加。当消费者在老年期仍然有劳动供给时，随着年金市场的不断完善，该正向效应会被削弱；当消费者在老年期没有劳动供给时，年金市场的完善程度不影响该效应。（4）当预期寿命增加，消费者在老年期退休行为的变化不确定。如果消费者在老年期仍然有劳动供给，当年金市场较不完善或外生利率水平较低时，预期寿命增加会引起退休提前。（5）当预期寿命增加，消费者终生预期劳动供给的变化不确定。当外生利率水平较高时，终生预期劳动供给会减少。

四、稳健性检验

在理论模型分析过程中，我们假设效用函数为对数形式，为了检验结果的稳健性，我们采用更一般的不变跨期替代弹性（CIES）函数形式：^⑦

并假设人力资本积累函数为 $h\left( e \right) = 1 + A{e^\mu },0 < \mu < 1$ 。

参考现有文献，我们对各参数赋值如下：关于效用函数，对时间偏好率的估计，国内外经验研究一般认为年贴现率在0.01—0.03之间，如Auerbach 和 Kotlikoff（1987）、Barro 和Sali-i-Martin（2003）。在三期模型中，一般假定每期代表25年，因此文中我们取β=1/1.02²⁵=0.61。对消费跨期替代弹性的估计，现有文献中关于σ取值大于1或小于1存在较大的争议（Thimme，2017）。为了检验理论部分结论的稳健性，我们分别讨论以下五种情况：σ₁=0.5，σ₂=0.8，σ₃=1.0，σ₄=2.5，σ₅=5.0，使得跨期替代弹性范围在0.2至2之间变化。关于人力资本积累函数，我们参考Tang 和 Zhang（2007）以及Hansen 和Lønstrup（2012）的做法，设定μ=1/3，A=3。关于外生给定的利率和工资水平，我们设定R=（1+0.03）²⁵=2.09，w=1。参考历年《中国人口统计年鉴》和《中国人口与就业统计年鉴》，根据中国2012年分年龄死亡率，估算出在2012年50岁的人能存活到75岁的概率约为0.68。我们将φ的范围设定在0.6—0.95之间，其中基准模型中设定φ=0.68。对衡量效用函数中闲暇权重的参数θ的取值，文献中关注很少，我们分别针对不同的σ值设定相应的θ值，使得当不存在年金市场（δ=0）时，基准模型（φ=0.68）下老年期的劳动力供给为0.2，即l=0.8，以每期25年计算，相当于在55岁左右退休。表2给出了不同σ值对应的θ值。

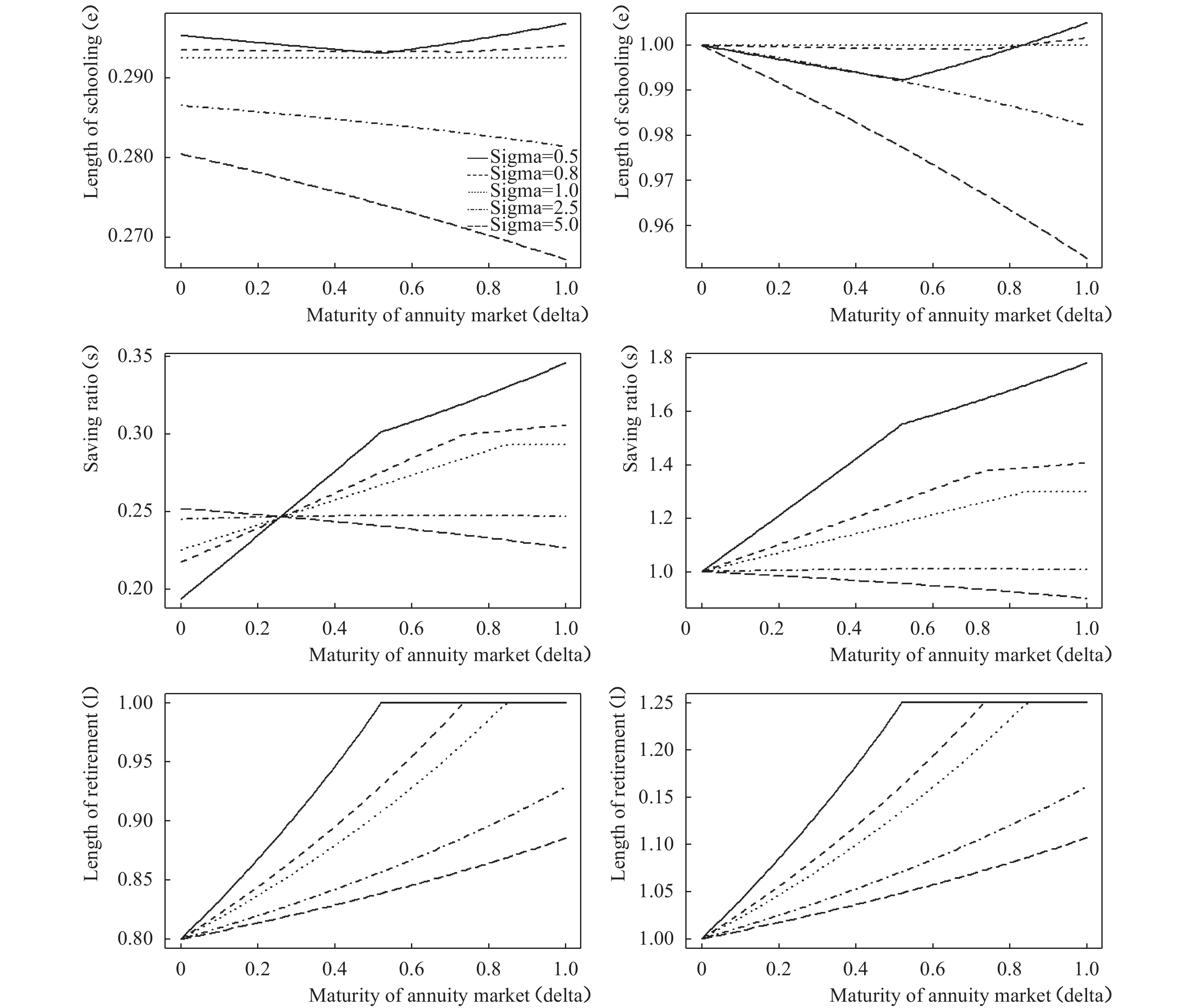
我们首先假定预期寿命不变，讨论年金市场发展本身对人力资本投资、储蓄率和退休行为的影响。图1描绘了在生存概率保持不变（φ=0.68）的情况下，面对不同完善程度年金市场时消费者的最优选择。其中左列的图是各变量（受教育年限、储蓄率和退休时长）在不同年金市场和不同跨期替代弹性情形下的取值，右列的图是各变量相对于不存在年金市场（δ=0）时取值的百分比。稳健性检验中我们考虑了端点解的情形，在图中表现为不平滑的转折点，具体取值可根据退休时间点（图1第3行）判断。^⑧

由图1可知，如果预期寿命保持不变，而且消费者在老年期仍有劳动供给，那么当σ≠1时，年金市场的不断完善将引起人力资本投资的降低。年金市场变化对储蓄率的影响不确定，取决于消费者的偏好，随着消费跨期替代弹性不断变小（σ变大），实际利率增加引起的替代效应逐渐减弱，消费者储蓄动机减小，在σ=2.5和σ=5.0两种情形下，年金市场的不断完善引起储蓄率降低。消费者的退休决策与上文的理论分析结果相一致，随着年金市场的不断完善，消费者在老年期提前退休。

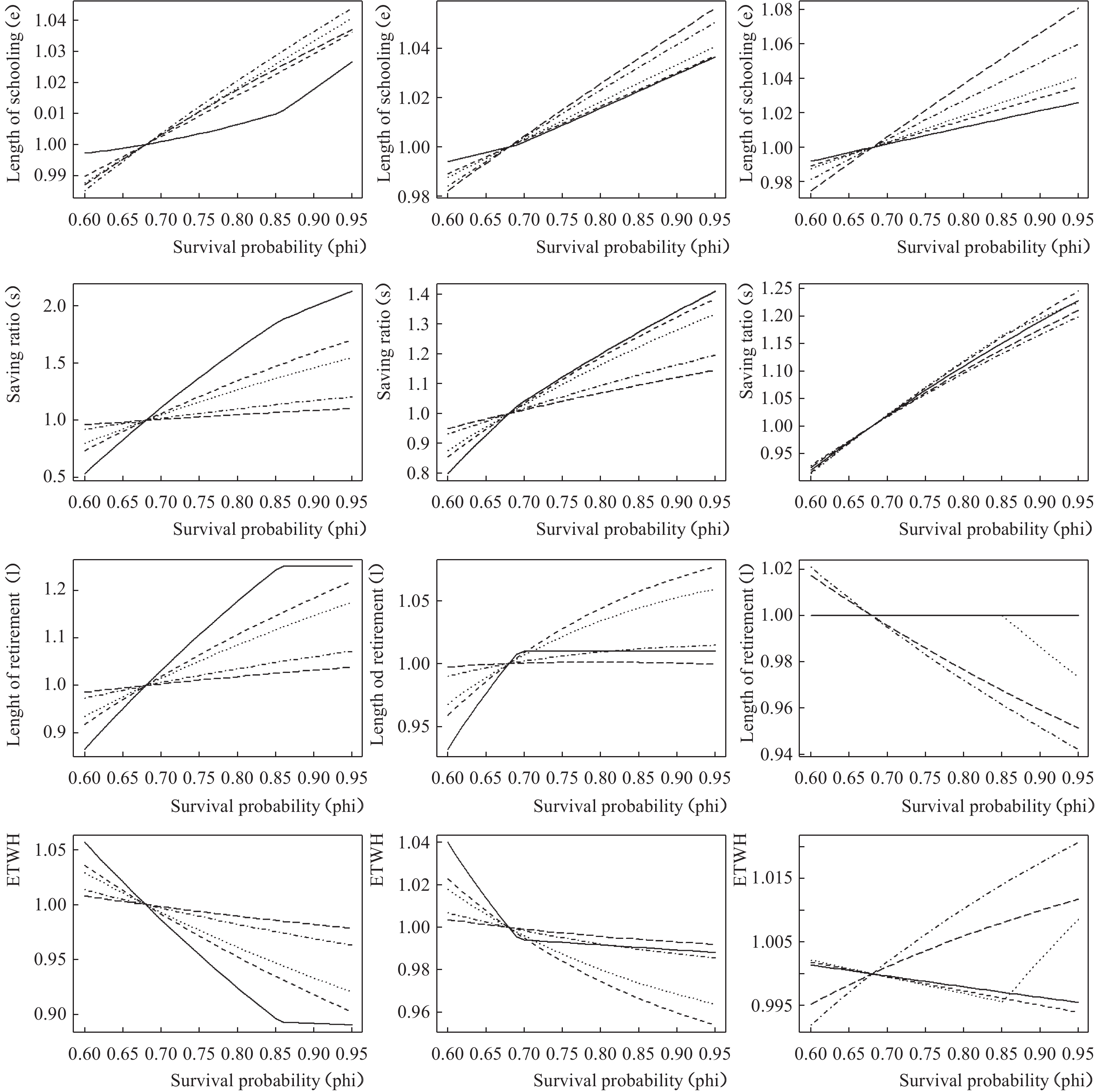
接下来，我们讨论预期寿命增加对消费者行为的影响。为了比较年金市场完善程度对结果的影响，我们在分析预期寿命增加引起消费者行为变化时，分别讨论以下三种情况：δ₁=0（不存在年金市场）、δ₂=0.5（存在不完善年金市场）和δ₃=1（存在完善年金市场）。图2描绘了在三种年金市场假设条件下，当从中年期进入老年期的生存概率在0.5—0.95之间变化时，消费者受教育年限、储蓄率、退休时长和预期终生劳动供给的变化。限于篇幅，我们仅在图2中描绘了各变量相对于基准模型（φ=0.68）取值的大小，以相对百分比衡量，图2与图1相同，其中左、中、右列分别对应于δ₁=0、δ₂=0.5和δ₃=1的情形。

由图2可知，不管年金市场的完善程度如何，随着预期寿命的增加，消费者都倾向于在青年期积累更多的人力资本，即使教育投资回报率的时间会减少（提前退休）。其次，预期寿命增加会引起储蓄率提高，通过对比不同年金市场情况下储蓄率提高的幅度，可以发现随着年金市场的不断完善，这种正向效应被逐渐削弱。预期寿命增加如何影响退休行为与年金市场的完善程度相关，当经济中存在较完善的年金市场时，生存概率增加可能会引起消费者推迟退休。预期寿命增加对预期终生劳动供给的影响也不确定，在完全年金市场假设条件下，由于消费者可能推迟退休，而生存概率也在增加，这两者引起的预期劳动供给增加可能会超过人力资本投资增加引起的进入劳动力市场推迟，从而引起预期终生劳动供给增加。这些结论与理论部分的分析基本一致。

五、结论与政策建议

世界各国普遍存在着预期寿命增加伴随着人力资本投资增加和退休提前的现象。本文构建了一个三期的生命周期模型，通过引入信贷约束和（不完全）年金市场，分析了生存概率增加和年金市场发展对消费者的人力资本投资、储蓄、退休决策和预期终生劳动供给的影响。本文从理论上详细讨论了预期寿命和年金市场对消费者各阶段行为产生影响的作用机制，并通过数值模拟的方法验证了相关结论。

研究发现，随着预期寿命增加，消费者会增加人力资本投资和储蓄率，但其退休行为和预期终生劳动供给的变化不确定。当年金市场不完善或市场利率较低时，预期寿命增加会促使消费者提前退休；如果年金市场较完善，并且利率较高，预期寿命增加会引起退休延迟。但是即使进入劳动力市场时间推迟，退出劳动力市场时间提前，由于生存概率的增加，预期终生劳动供给的变化并不确定。本文还发现，如果预期寿命不变，那么随着年金市场的不断完善，消费者会提前退休，但是受教育年限和储蓄率的变化不确定。

本文从年金市场的角度，对过去几十年里观测到的“教育年限增加和提前退休之谜”的现象进行了可能的解释。对一些发展中国家而言，该现象可能是由信贷市场摩擦和缺乏年金市场引起的。而对一些已经具有较完善年金市场的发达国家，教育年限增加和提前退休同时发生，一方面的原因可能是该经济体的利率水平较低，那么预期寿命增加会引起退休提前；另一方面的原因在于，年金市场从开始出现到不断完善这个过程本身也会引起退休提前。

近年来，随着我国人口老龄化压力的不断增大，政府积极推行养老年金市场的发展，并将延迟法定退休年龄提上日程。随着经济的发展，预期寿命在增加，年金市场也在不断完善，政府在制定相关政策时，应该同时考虑这两个变化对消费者行为尤其是劳动者就业意愿的影响。我国年金市场尚处于起步阶段，在大力发展年金市场的同时，还可以采取一些其他政策，比如不断完善资本信贷市场，以尽量减少提前退休现象的发生。

① 这里没有限制消费者在青年期的存款，但是正如Hansen和Lønstrup（2012）指出，在生命周期模型中，消费者一般在青年期选择向未来借钱而不是储蓄。

② 张熠（2015）指出，从各国的数据来看，死亡率下降存在“老龄化”趋势。对比中国第五次和第六次人口普查结果可发现，在我国主要的死亡率下降已经转移到退休后年龄段中。因此，本文模型中主要考察从中年期过渡到老年期的生存概率的提高，而没有考虑从青年期到中年期的生存概率的变化。

③ 这里的实际回报率是指年金市场中由于生存风险而产生的高于经济中其他资产回报率的利率水平，并不是指文献中常见的对名义利率和实际利率的区分。

④ 感谢审稿人指出本文的模型框架在刻画长寿风险影响退休行为作用机制方面的局限性。

⑤ Kalemli-Ozcan和Weil（2010）指出，当生存概率较低时，偶发遗赠风险较高，消费者倾向于不储蓄而一直工作以满足消费需求；随着生存概率的上升，储蓄被浪费的概率减小，因而消费者会考虑通过储蓄的方式满足退休后的消费需求，并提前退休。

⑥ 假设1要求 $ {R > \displaystyle\frac{{1 - \delta + \delta \varphi }}{{\varphi \beta \left( {1 + \theta } \right)}}}$ 。易证 $ {\displaystyle\frac{{{{\left( {1 - \delta + \delta \varphi } \right)}^2}}}{{\delta + \delta \beta {\varphi ^2} + \delta \theta \beta {\varphi ^2} - 1}} - \frac{{1 - \delta + \delta \varphi }}{{\varphi \beta \left( {1 + \theta } \right)}} = \frac{{\left( {1 - \delta + \delta \varphi } \right)\left( {1 - \delta } \right)\left[ {\varphi \beta \left( {1 + \theta } \right) + 1} \right]}}{{\left( {\delta + \delta \beta {\varphi ^2} + \delta \theta \beta {\varphi ^2} - 1} \right)\varphi \beta \left( {1 + \theta } \right)}} \geqslant 0}$ ，因此只要 $ {\delta < 1}$ ，在假设1条件下，一定存在外生利率水平满足该条件。在完全年金市场条件 $ {\left( {\delta = 1} \right)}$ 下，预期寿命增加引起退休提前要求外生利率水平需满足 $ {R < \displaystyle\frac{1}{{\beta \left( {1 + \theta } \right)}}}$ ，与假设1的条件 $ {R > \displaystyle\frac{1}{{\beta \left( {1 + \theta } \right)}}}$ 相矛盾。因此在假设1条件下，如果存在完全年金市场，预期寿命增加一定引起消费者推迟退休。

⑦ 当存在不确定时，该效用函数又称为CRRA函数。当 ${\sigma = 1}$ ，函数为对数形式。

⑧ 由于生存概率不变，预期终生劳动供给的变化取决于消费者进入和退出劳动力市场的时间点。因此这里不讨论预期寿命不变时年金市场完善程度对消费者预期终生劳动供给的影响。