文章信息
 | 财经研究 2018年44卷第12期 |
- 田海燕, 李秀敏,
- Tian Haiyan, Li Xiumin.
- 财政科教支出、技术进步与区域经济协调发展——基于引致技术进步动态多区域CGE模型
- Fiscal spending on science and education, technical progress and regional economic coordinated development:based on a dynamic multi-regional cge model incorporating induced technical change
- 财经研究, 2018, 44(12): 85-99
- Journal of Finance and Economics, 2018, 44(12): 85-99.
-
文章历史
- 收稿日期:2018-05-17

2018第44卷第12期
一、引 言
习总书记在“十九大报告”中两次提到“创新、协调、绿色、开放、共享”五大发展理念,将创新和协调放在了突出的位置。创新促进技术进步,使技术进步成为驱动经济增长的主要动力;协调的含义包括区域经济协调发展,但同时实现创新和协调两大目标则并非易事。创新源自一系列因素的支撑(如高科技企业、研究机构、高等教育机构),这些支撑在我国各地区间存在着显著的差异,从而使这些地区间的科技创新能力存在严重失衡(李国平和王春阳,2012)。如何保证创新能力较弱地区在创新驱动模式下有更好的发展,以促进区域经济协调发展,将成为政府部门制定政策需要重点考虑的问题。
内生经济增长理论认为,经济的长期增长是由人力资本、技术进步等内生变量决定。因此,区域竞争力主要依赖于区域内的人才数量和规模、企业创新能力和技术水平。为了提高落后地区的竞争力,政府可以借助财政支出手段来影响个人或企业行为,达到加快落后区域人力资本积累和技术进步的目的,进而促进落后地区的经济增长(Garau和Lecca,2008)。问题是中国幅员辽阔,内部差异大,东北、西部和广大中部地区经济都相对落后,有限的财政科教资金应该投往何处?当资金投向不同区域时,是否会促进这些地区的技术进步和经济增长?其他没有获得扶持政策的区域的技术水平和经济增长将如何发展?此外,增加财政科教资金的投入对技术进步与经济增长的促进作用是否持久?如果不改变财政支出的规模,是否可以通过调整财政各项支出的比例来实现创新和协调?这些问题都受到了社会各界的广泛关注。
目前关于财政科教支出对经济增长影响的理论和实证研究主要是在内生经济增长的框架下,将研发和教育作为企业和居民的内生决策行为,刻画技术进步的微观机制。关于财政研发支出对经济增长影响的理论研究,学者们将财政研发支出引入增长模型,分析财政研发支出对经济增长的影响机制(Glomm和 Ravikumar,1994;Pelloni,1997;Park,1998;Morales,2004;杨朝峰和贾小峰,2008;胡志国等,2013),都得出了政府公共研发投入能提高经济增长率的结论。关于财政教育支出对经济增长影响的理论和实证研究都未得出一致结论。一些研究认为,财政教育支出规模的增加有助于促进经济增长并缩小区域经济差距(Glomm和 Ravikumar,1992;Viaene和 Zilcha,2006)。另一些研究认为,财政教育支出对经济增长的影响不显著(Easterly和Rebelo,1993;Devarajan等,1996;郭庆旺和贾俊雪,2009)。此外,Blankenau等(2007)的研究表明,在经济发展水平不同的国家,政府教育支出对经济增长的影响存在较大区别,政府教育支出对发达国家的经济增长具有促进作用,对发展中国家的经济增长没有显著影响。
内生经济增长的理论模型复杂,模型无法得到显示解,只能进行数值模拟,而数值模拟的结果又很难利用实际数据加以验证。并且模型中包括的外生参数众多,参数值选取存在较大随意性和不规范之处,因而数值模拟结果的可靠性一直颇受质疑。
相比内生经济增长模型,CGE模型同样有着坚实的微观经济理论基础,并且模型服从真实经济数据,是非常有效的政策分析工具。以往大部分CGE模型的应用研究都以不发生技术进步或技术进步参数外生为假设前提。董万好和刘兰娟(2012)、刘兰娟等(2013)在假设不存在技术进步的前提下,利用CGE模型模拟财政科教支出对就业和产业结构的影响。财政科教支出不影响技术进步显然与现实不符,这种设定可能导致政策效应低估而受到质疑。
将内生经济增长理论的思想引入CGE模型,技术水平不再外生决定,考虑微观主体行为对技术水平的影响,称为引致技术进步CGE模型。Garau和Lecca(2008)构建了引致技术进步动态单区域CGE模型,研究政府对意大利撒丁区研发补贴政策的经济增长效应;Křístková(2012)构建了同样的CGE模型,研究研发投资政策对捷克经济增长的影响。娄峰(2017)构建了中国引致技术进步静态CGE模型对科技研发投入的政策效应进行了模拟分析。在Garau和Lecca(2008)、Křístková(2012)和娄峰(2017)的研究中,将知识作为一种生产要素引入生产函数,其思想为:知识类似于物质资本,研发活动作为知识积累活动,知识存量会随着R&D投入的增加而增加,并随着时间的推移发生折旧而减少。这种将技术进步引入CGE模型的方式存在三种缺陷:其一,将知识与物质资本以相同方式引入生产函数不准确,因为知识和物质资本不同,物质资本存在竞争的排他性,在生产过程中不能被多个产业同时使用,而现实中同一种知识可以被多个产业同时使用。所以,这样的模型设置不能反映知识的外溢效应,可能低估政策效果。其二,仅关注研发投入对技术进步的影响,没有考虑教育投入对人力资本积累进而对经济增长的影响。其三,研究中采用希克斯中性技术进步假定,在有偏技术进步得到广泛证实的情况下,这种设定并不合理。
总体而言,以引致技术进步CGE模型研究财政研发政策的成果很少,学者们建立的基本都是单区域模型,引入技术进步的方式也有诸多缺陷。因此,本文研究有以下探索:一是在模型构建中放松希克斯中性技术进步的常见假设,允许不同生产要素有不同的效率水平变化,并检验本文模型能很好地拟合现实经济;二是将研究与实验发展行业和教育行业的投入都作为技术进步的影响因素,更全面地分析技术进步产生的原因;三是将知识要素视作公共产品,技术进步可以同时提高多个生产部门的生产效率,即体现知识的外溢效应,防止政策效应低估;四是基于动态多区域模型,可用于比较分析不同地区增加财政科教支出的规模和调整财政科教支出比例的长期影响及其区域效应,为探寻技术进步和区域经济协调发展的双赢策略提供经验证据。
二、引致技术进步动态多区域CGE模型构建
动态多区域CGE模型适合分析政策冲击的长期影响和区域传递效应及反馈效应。本文以生产要素效率变化反映技术进步水平,用增加知识生产函数使要素效率内生的方式将技术进步引入标准的动态多区域CGE模型。为突出研究重点和建模需要,本文模型将全国划分为8大地区。①将产业划分为研究与实验发展业、教育业和其他产业。主要包括三大模块:即生产模块、收入储蓄及需求模块、贸易及区域间商品流动模块。该模型的逻辑结构如图1所示。
(一)生产模块。投入包括初始要素和中间投入,假定两者之间不可替代。其方程为:
| $QIN{T_{r, j, t}} = \sum\limits_i^n {{a_{i, j}} * {X_{r, j, t}}} $ | (1) |
| $V{A_{r, j, t}} = {X_{r, j, t}} - QIN{T_{r, j, t}}$ | (2) |
其中:下标r代表地区,t代表时期,j代表部门,i代表商品;QINT、X、VA和aij分别表示中间投入、总产出、增加值和直接消耗系数。
初始要素由劳动和资本组成,CGE模型一般以标准CES生产函数描述增加值的生产过程:
| $\displaystyle V{A_{r, j, t}} = {A^{VA}}_{r, j, t} {\left[ {{\delta ^{VA}}_{r, j, t} {L_{r, j, t}}^{ - {\rho ^{VA}}_r} + \left( {1 - {\delta ^{VA}}_{r, j, t}} \right) {K_{r, j, t}}^{ - {\rho ^{VA}}_r}} \right]^{ - \frac{1}{{{\rho ^{VA}}_r}}}}$ | (3) |
其中:A、L和K分别代表全要素生产率、劳动和资本,
| $V{A_{r, j, t}} = {\left[ {{{\left( {E_{r, j, t}^L {L_{r, j, t}}} \right)}^{\frac{{{\sigma ^{VA}}_r - 1}}{{{\sigma ^{VA}}_r}}}} + {{\left( {E_{r, j, t}^K {K_{r, j, t}}} \right)}^{\frac{{{\sigma ^{VA}}_r - 1}}{{{\sigma ^{VA}}_r}}}}} \right]^{\frac{{{\sigma ^{VA}}_r}}{{{\sigma ^{VA}}_r - 1}}}}$ | (4) |
其中:
生产者追求成本最小化,合理选择资本和劳动的投入比例。既定产量下,企业的最优化选择为:
| ${\rm{Min}}\;\;{C_{r, j, t}} = dist{L_{r, j}} \times W{L_t} \times {L_{r, j, t}} + W{K_{r, j, t}} \times {K_{r, j, t}}$ |
| ${\rm{S.T.}}\;\;V{A_{r, j, t}} = {\left[ {{{\left( {E_{r, j, t}^L \times {L_{r, j, t}}} \right)}^{\frac{{{\sigma ^{VA}}_r - 1}}{{{\sigma ^{VA}}_r}}}} + {{\left( {E_{r, j, t}^K \times {K_{r, j, t}}} \right)}^{\frac{{{\sigma ^{VA}}{{^{}}_r} - 1}}{{{\sigma ^{VA}}_r}}}}} \right]^{\frac{{{\sigma ^{VA}}_r}}{{{\sigma ^{VA}}_r - 1}}}}$ |
其中:C代表成本,WL、distL和WK分别代表全国平均工资水平、劳动力价格在不同地区和行业间的扭曲系数以及资本报酬。拉格朗日求解如下:
| ${\rm{Min}}\;\;L{\rm{ = dist}}{{\rm{L}}_{r, j}} \times W{L_t} \times {L_{r, j, t}} + W{K_{r, j, t}}\times {K_{r, j, t}} - \lambda \left\{ {V{A_{r, j, t}} - {{\left[ {{{\left( {E_{r, j, t}^L {L_{r, j, t}}} \right)}^{\frac{{{\sigma ^{VA}}_r - 1}}{{{\sigma ^{VA}}_r}}}} + {{\left( {E_{r, j, t}^K {K_{r, j, t}}} \right)}^{\frac{{{\sigma ^{VA}}_r - 1}}{{{\sigma ^{VA}}_r}}}}} \right]}^{\frac{{{\sigma ^{VA}}_r}}{{{\sigma ^{VA}}_r - 1}}}}} \right\}$ |
对相应变量求导,一阶条件为:
| $\frac{{\partial L}}{{\partial {K_{r, j, t}}}} = W{K_{r, j, t}} - \lambda \frac{{{\sigma _r}}}{{{\sigma _r} - 1}} {\left[ {{{\left( {E_{r, j, t}^L {L_{r, j, t}}} \right)}^{\frac{{{\sigma _r} - 1}}{{{\sigma _r}}}}} + {{\left( {E_{r, j, t}^K {K_{r, j, t}}} \right)}^{\frac{{{\sigma _r} - 1}}{{{\sigma _r}}}}}} \right]^{\frac{1}{{{\sigma _r} - 1}}}} \frac{{{\sigma _r} - 1}}{{{\sigma _r}}} {\left( {E_{r, j, t}^K {K_{r, j, t}}} \right)^{ - \frac{1}{{{\sigma _r}}}}} E_{r, j, t}^K = 0$ |
| $\frac{{\partial L}}{{\partial {L_{r, j, t}}}} = dist{L_{r, j}} \times W{L_t} - \lambda \frac{{{\sigma _r}}}{{{\sigma _r} - 1}} {\left[ {{{\left( {E_{r, j, t}^L {L_{r, j, t}}} \right)}^{\frac{{{\sigma _r} - 1}}{{{\sigma _r}}}}} + {{\left( {E_{r, j, t}^K {K_{r, j, t}}} \right)}^{\frac{{{\sigma _r} - 1}}{{{\sigma _r}}}}}} \right]^{\frac{1}{{{\sigma _r} - 1}}}} \frac{{{\sigma _r} - 1}}{{{\sigma _r}}} {\left( {E_{r, j, t}^L {L_{r, j, t}}} \right)^{ - \frac{1}{{{\sigma _r}}}}}E_{r, j, t}^L = 0$ |
对上述两式合并得到生产者的要素选择方程:
| $\frac{{W{K_{r, j, t}}}}{{dist{L_{r, j}} \times W{L_t}}} = {\left( {\frac{{E_{r, j, t}^K}}{{E_{r, j, t}^L}}} \right)^{\frac{{{\sigma ^{VA}}_r - 1}}{{{\sigma ^{VA}}_r}}}}{\left( {\frac{{{K_{r, j, t}}}}{{{L_{r, j, t}}}}} \right)^{ - \frac{1}{{{\sigma ^{VA}}_r}}}}$ | (5) |
标准CGE模型中要素效率外生,为了反映技术进步,资本效率和劳动效率设为内生变量,需要在标准模型基础上增加其决定方程,劳动和资本效率有不同的影响因素,如:教育业的发展会提高劳动力的整体素质,从而提高劳动生产效率;研究与实验发展业的发展会促进新产品、新工艺的研制,从而提高资本的生产效率。从本质上讲,教育业和研究实验发展业可以被看作技术进步的“原料生产”环节,引入知识生产函数(Jones,1995),用以描述教育业、研究实验发展业与劳动力效率和资本效率的投入产出关系。设定如下:
| $E_{r, j, t}^K = \eta _{r, j}^K{\left[ {\frac{{X_{r, t}^{RD}}}{{{L_{r, t}}}}} \right]^{{\phi _{r, j}}^{RD}}}{\left[ {E_{r, j, t{\rm{ - }}{1_{}}}^K} \right]^{1 - {\phi _{r, j}}^{RD}}}\gamma _{r, j}^K$ | (6) |
| $E_{r, j, t}^L = \eta _{r, j}^L{\left[ {\frac{{X_{r, t}^{EDU}}}{{{L_{r, t}}}}} \right]^{{\phi _{r, j}}^{EDU}}}{\left[ {E_{r, j, t{\rm{ - }}{1_{}}}^L} \right]^{1 - {\phi _{r, j}}^{EDU}}}\gamma _{r, j}^L$ | (7) |
其中:
以上设定有一点需要说明,在生产函数中采用劳动力数量对教育业和研究与实验发展业的投入进行调整,是为了消除知识生产的规模效应,可以理解为:随着人口规模的扩大,教育、研究与实验发展需要更多的投入,新投入用于新增就业人口的技术学习,在不存在政策冲击的情况下,经济增长在长期处于平衡增长路径(Jones,1995)。
(二)收入、储蓄及需求模块。居民和企业是生产活动中资本和劳动要素的提供者,要素报酬按一定比例分配给居民和企业。政府通过向生产者征收直接税,向居民和企业征收所得税获取收入,税率外生。居民收入以固定份额形成储蓄。企业收入全部用于储蓄。政府收入扣除政府消费形成政府储蓄。国外部门在各地区的储蓄为各地区进口额与出口额的差额。各地区居民、企业、国外部门和政府的储蓄形成全国总储蓄。
居民收入除去储蓄部分用于私人消费,假设居民的消费习惯固定,即各种商品的消费占总消费的比例固定。生产活动对中间投入的消耗决定中间产品需求,政府对各地区产品的消费需求外生。全国总储蓄全部转化为投资。投资在各地区的分配遵循Jung和Thorbecke(2003)的投资分配理论,(简称J-T规则)方程为:
| $IN{D_{r, j, t}} = \phi _{r, j}^{INV} {\left[ {\frac{{W{K_{r, j, t}}}}{{P{K_{r, j, t}}\left( {{\delta ^z} + I{R_t}} \right)}}} \right]^{\sigma _{r, j}^{INV}}} {K_{r, j, t}}$ | (8) |
其中:IND、PK、WK、
因为各种投资商品存在技术性关系,使用Leontief函数来决定各地区投资对各部门投资商品的需求量。其方程为:
| $QIN{V_{r, i, t}} = \sum\limits_j {{b_{i, j}}} IN{D_{r, j, t}}$ | (9) |
其中:QINV为投资需求品,bij为转换矩阵。
(三)贸易及区域间商品流动模块。各地区的居民消费需求、中间投入需求和投资需求既可由本地生产的商品满足,又可由进口品和外地调入品满足,以CES函数描述他们之间的替代关系,如图2所示。CES上两层嵌套的是两种商品的复合,其CES函数形式和需求者选择的最优化方程推导和生产模块中完全一致,这里不再赘述。以私人需求为例,最下层的多种商品复合的CES方程为:
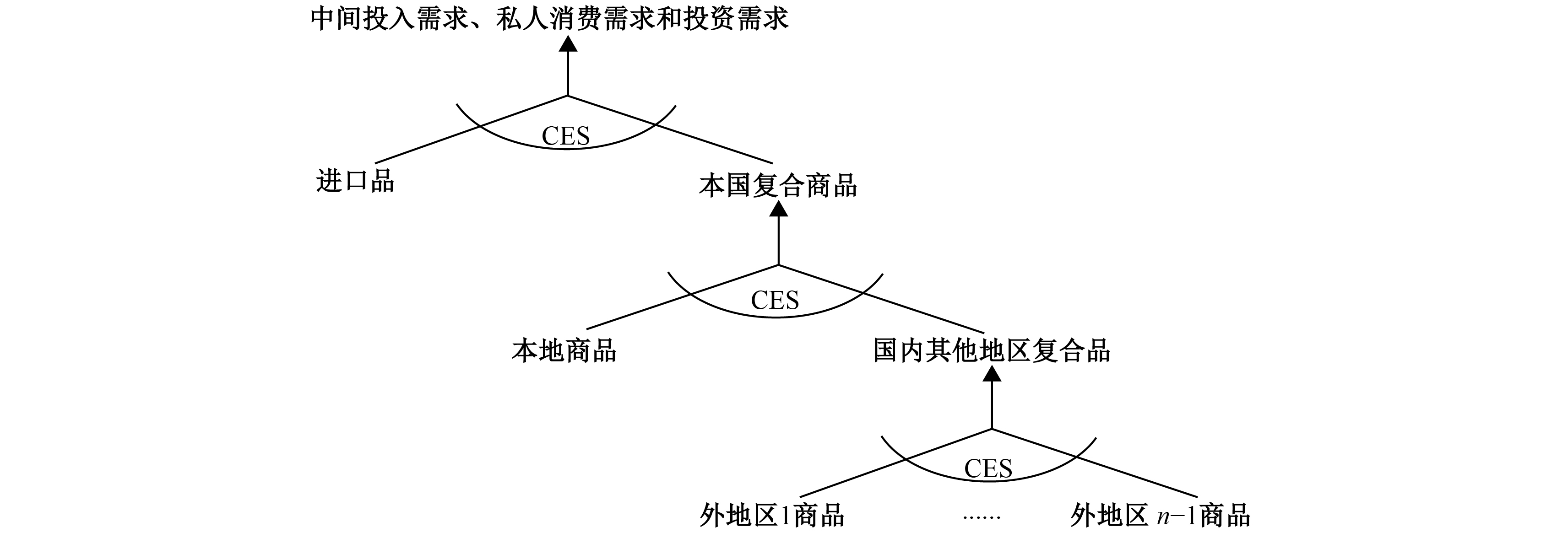
|
| 图 2 模型的需求结构 |
| $QHM{T_{r, i, t}} = A_{r, i}^{QHMT}{\left[ {\sum\limits_{rp} {\beta _{rp, i}^{QHMT}QHM_{rp, i, t}^{ - {\rho ^{QHMT}}}} } \right]^{ - \frac{1}{{{\rho ^{QHMT}}}}}} \left( {r \ne rp} \right) $ | (10) |
其中:
需求者根据不同地区商品的价格,以成本最小化原则选择在各地区调入商品数量。方程为:
| $QH{M_{rp, i, t}} = {\left[ {\frac{{{\beta _{r, i}}^{QHMT}PHM{T_{r, i, t}}}}{{P{L_{rp, i, t}}}}} \right]^{{\sigma ^{QHMT}}}}{\left( {A_{r, i}^{QHMT}} \right)^{{\sigma ^{QHMT}} - 1}}QHM{T_{r, i, t}}$ | (11) |
其中:
本文模型的供给结构反映本地生产产品在出口、本地销售和国内其他地区销售之间的关系。逻辑关系见图3所示。各地区在生产活动中产出的产品在国外和国内销售,以CET函数反映两者间的替代关系。其方程为:

|
| 图 3 模型的供给结构 |
| ${X_{r, i, t}} = A_{r, i}^X{\left[ {\beta _{r, i}^XE_{r, i, t}^{{\rho ^X}} + \left( {1 - \beta _{r, i}^X} \right)D_{r, i, t}^{{\rho ^X}}} \right]^{\frac{1}{{{\rho ^X}}}}}$ | (12) |
其中:E代表出口品数量,D代表国内销售品数量,
生产者以利润最大化原则根据出口产品价格和产品本国销售价格的不同调整出口量和国内销售产品数量间的比例关系。其方程为:
| $\frac{{{E_{r, i, t}}}}{{{D_{r, i, t}}}} = {\left[ {\frac{{1 - \beta _{r, i}^X}}{{\beta _{r, i}^X}}\frac{{P{E_{r, i, t}}}}{{P{L_{r, i, t}}}}} \right]^{{\sigma ^X}}}$ | (13) |
(18)式的推导过程与生产模块CES函数最优条件的推导过程一致。其中:PE代表出口品价格,PL表示本国销售价格,
因为本地生产的商品如果调出其他地区,其价格和在本地出售的价格相同,所以不用通过对比价格进行最优化选择,国内供给商品数量等于本地供给与调出商品数量之和。本地商品供给等于中间投入对本地商品需求、投资对本地商品需求、私人消费和政府消费对本地商品需求之和。调出商品数量等于其他地区从本地区调入的中间商品、私人消费品和投资商品之和,由此实现商品供给和需求的平衡。
此外,模型还包括区域间的劳动力分配,假定区域间的劳动力不完全自由流动,全国平均工资水平内生,但各地区、各行业存在工资扭曲,各地区、各行业的就业量内生,总就业量外生。价格方面,汇率外生,采用小国假设,进口品和出口品的价格外生,居民平均消费价格为基准价格,除以上外生价格变量外的其他价格变量都内生。本文模型为递推动态模型,动态化过程主要通过人口增长、资本积累和技术进步实现。当期资本存量由上期资本存量扣除折旧再加上投资决定,技术进步水平内生决定。
三、数据来源及模型检验
(一)数据来源及参数取值。模型所需数据主要来自作者编制的2010年SAM表,该表根据中国科学院地理科学与资源研究所和国家统计局核算司合作出版的2010年区域间投入产出表和各省统计年鉴编制。模型中各外生和内生变量的初始值来自SAM表。弹性参数外生给定,各地区资本和劳动的替代弹性取值参考陈晓玲和连玉君(2013)的估计结果,各地区取值分别为东北0.329、京津1.14、北部沿海1.522、华东沿海1.639、南部沿海1.924、中部0.304、西北0.709和西南0.54。资本和劳动效率的初始值由(3)式和(4)式组成的联立方程组校准得到。模型需求结构三层嵌套CES函数的替代弹性取值为2.5。供给结构中CET函数的替代弹性取值为3.5。投资需求的弹性参数取值为2。折旧率取值0.04。各类分配参数、规模参数利用方程平衡关系校准得到。
(二)历史拟合与模型有效性检验。2011—2015年为模型检验的历史拟合期。各地区劳动力增长率按各年各地区的实际值设置。资本积累内生变化。以2011—2015年统计年鉴各地区收入法GDP中劳动者报酬和资本收入(固定资产折旧、营业盈余、生产税净额之和)为外生变量对劳动和资本效率进行再校准,再以劳动和资本效率为外生变量对模型中各内生变量进行预测。
根据模型预测消费和投资变量的数值,并与各地区统计年鉴中的真实数据进行对照。选择评价指标对模型预测效果进行评价。预测评价的常用指标有均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和希尔不等系数(TIC),考虑到本文的消费和投资数据较大,而均方根误差和平均绝对误差的取值大小受初始值影响,因此,本文选择绝对百分比误差和希尔不等系数两个相对评价指标对模型的历史拟合效果进行评价。指标的计算结果见表1。一般认为平均绝对百分比误差小于10%,希尔不等系数最好小于0.05,为可接受的预测误差范围。表1中模型预测误差较大的变量有东北、中部和西部地区的投资,京津和西南地区的消费。出现预测误差的部分原因是区域间投入产出表和统计年鉴之间的数据差异所致。表2中显示了区域间投入产出表和统计年鉴之间的数据差距。对比表1和表2,区域间投入产出表和统计年鉴中京津和西南地区的消费存在很大差距,误差分别为11%和6%,除去统计误差,两变量预测误差在可接受范围。东北、中部和西部地区的投资数据误差很大,部分是统计误差造成,还有部分是非经济因素使总投资在各地区的分配过程没有遵循J-T规则,国家的政策引导,使投资更多向东北、中部和西部地区分配。为了提高投资效率,非经济因素影响将逐渐变小。除此之外,其他模型的预测值和真实值之间的误差在可接受的范围内,模型的可信度可以接受。
| 东北 | 京津 | 北部沿海 | 华东沿海 | 南部沿海 | 中部 | 西北 | 西南 | ||
| 投资 | MAPE(%) | 10.422 | 5.812 | 5.217 | 5.603 | 8.222 | 12.047 | 17.429 | 11.831 |
| TIC | 0.055 | 0.032 | 0.028 | 0.039 | 0.051 | 0.065 | 0.102 | 0.063 | |
| 消费 | MAPE(%) | 4.602 | 9.052 | 2.634 | 3.458 | 2.406 | 4.833 | 8.654 | 9.931 |
| TIC | 0.024 | 0.041 | 0.014 | 0.022 | 0.019 | 0.027 | 0.045 | 0.056 |
| 东北 | 京津 | 北部沿海 | 华东沿海 | 南部沿海 | 中部 | 西北 | 西南 | |
| 投资 | −0.09 | −0.04 | −0.05 | −0.06 | −0.04 | −0.06 | −0.06 | −0.06 |
| 消费 | −0.07 | 0.11 | −0.04 | −0.05 | −0.07 | −0.04 | −0.07 | −0.06 |
之前检验说明,在资本和劳动效率外生的情况下模型整体有效,但本文引入了知识生产函数,各部门的资本和劳动效率内生,模型中知识生产函数的参数应合理取值,方程设计的合理性也需进行检验。以物质资本效率的生产方程为例,对(6)式两端取对数再求导得:
| $\frac{{E_{r, j, t}^K - E_{r, j, t - 1}^K}}{{E_{r, j, t}^K}} = \phi _{r, j}^{RD}\frac{{X_{r, t}^{RD} - X_{r, t - 1}^{RD}}}{{X_{r, t}^{RD}}} - \phi _{r, j}^{RD}\frac{{{L_{r, t}} - {L_{r, t - 1}}}}{{{L_{r, t}}}} + (1 - \phi _{r, j}^{RD})\frac{{E_{r, j, t - 1}^K - E_{r, j, t - 2}^K}}{{E_{r, j, t - 1}^K}}$ | (14) |
根据(19)式,最理想的方法是利用回归分析对
| 东北 | 京津 | 北部沿海 | 华东沿海 | 南部沿海 | 中部 | 西北 | 西南 | ||
| 资本效率 | MAPE(%) | 1.372 | 1.783 | 1.464 | 1.694 | 1.701 | 1.454 | 1.436 | 1.478 |
| TIC | 0.007 | 0.009 | 0.007 | 0.008 | 0.008 | 0.007 | 0.007 | 0.007 | |
| 劳动效率 | MAPE(%) | 1.236 | 1.987 | 1.688 | 1.833 | 1.793 | 1.352 | 1.457 | 1.466 |
| TIC | 0.006 | 0.010 | 0.008 | 0.009 | 0.009 | 0.007 | 0.007 | 0.007 |
由表3可知,模型求解值与真实值之间的误差很小,各地区要素效率预测的平均绝对误差都在2%以内,希尔不等系数均小于0.01。说明知识生产函数中的参数取值和方程设置的合理性均在可接受范围。
(三)政策模拟期基准情景预测。2015—2025年为政策模拟期。政策实施前的基准情景设计为,S0:各地区人口增长率按各地区的历史发展趋势设置;在整个模拟期内,资本积累内生变化;假设不发生技术进步,各地区经济运行处于平衡增长路径,预测结果见表4。
| 年份 | 东北 | 京津 | 北部沿海 | 华东沿海 | 南部沿海 | 中部 | 西北 | 西南 |
| 2015 | 0.080 | 0.055 | 0.128 | 0.191 | 0.142 | 0.203 | 0.079 | 0.121 |
| 2020 | 0.077 | 0.058 | 0.128 | 0.187 | 0.144 | 0.203 | 0.080 | 0.122 |
| 2025 | 0.075 | 0.061 | 0.129 | 0.185 | 0.146 | 0.202 | 0.080 | 0.122 |
在基准情景下,地区差距不断扩大。京津及沿海发达地区的GDP份额快速上升,经济地位不断增强。西部地区在全国的经济地位缓慢增强,东北地区的经济地位快速下降,中部地区的经济地位缓慢下降。在没有政策冲击、不发生技术进步的情况下,受人口流失和投资减少的影响,东北和中部地区的经济发展不容乐观,“新东北现象”和“中部塌陷”有其形成的必然性。西部地区经济地位虽然缓慢提升,但经济基础薄弱,缓慢的经济增长不足以摆脱贫困。在实施创新驱动政策的情况下,科教资源丰富的京津和沿海发达地区会加速发展,如果东北、中部和西部地区不能获得政策扶持,实现技术进步,地区差距会进一步扩大。
四、增加财政科教支出规模效果的模拟及分析
(一)增加受援区域财政研发支出规模效果的模拟。2015年分别对东北(S1情景)、中部(S2情景)和西部地区(S3情景)增加财政研发支出100亿。情景设计主要是考虑我国未来将继续实施西部大开发、东北老工业基地振兴和中部崛起等区域政策,评估财政研发支出政策在促进区域技术进步和经济发展中的作用。模拟结果见表5所示。
| 情景 | 地区 | 2020年 | 2025年 | ||||||
| 物质资本效率 | 人力资本效率 | GDP | GDP份额 | 物质资本效率 | 人力资本效率 | GDP | GDP份额 | ||
| S1 | 东北 | 0.802 | −0.034 | 1.041 | 0.950 | 0.626 | −0.028 | 1.038 | 0.954 |
| 京津 | 0.006 | −0.001 | −0.002 | −0.092 | 0.005 | −0.001 | −0.008 | −0.091 | |
| 北部沿海 | 0.000 | −0.001 | −0.004 | −0.094 | 0.000 | −0.002 | −0.011 | −0.094 | |
| 华东沿海 | 0.007 | 0.001 | −0.008 | −0.098 | 0.007 | 0.001 | −0.014 | −0.097 | |
| 南部沿海 | 0.004 | 0.002 | −0.016 | −0.106 | 0.005 | 0.002 | −0.021 | −0.105 | |
| 中部 | 0.004 | 0.001 | −0.018 | −0.108 | 0.005 | 0.001 | −0.028 | −0.111 | |
| 西北 | 0.002 | 0.000 | 0.002 | −0.088 | 0.001 | 0.000 | −0.004 | −0.087 | |
| 西南 | 0.005 | 0.002 | −0.029 | −0.120 | 0.008 | 0.003 | −0.038 | −0.121 | |
| S2 | 东北 | 0.005 | 0.001 | −0.014 | −0.117 | 0.006 | 0.001 | −0.023 | −0.121 |
| 京津 | 0.015 | −0.001 | 0.005 | −0.098 | 0.013 | 0.000 | −0.001 | −0.098 | |
| 北部沿海 | 0.008 | 0.001 | −0.010 | −0.113 | 0.008 | 0.002 | −0.015 | −0.112 | |
| 华东沿海 | 0.010 | 0.000 | 0.005 | −0.098 | 0.008 | 0.000 | −0.001 | −0.098 | |
| 南部沿海 | 0.003 | 0.000 | −0.006 | −0.108 | 0.003 | −0.001 | −0.011 | −0.109 | |
| 中部 | 0.409 | −0.009 | 0.494 | 0.390 | 0.333 | −0.006 | 0.493 | 0.395 | |
| 西北 | 0.030 | 0.000 | 0.018 | −0.085 | 0.026 | 0.001 | 0.010 | −0.088 | |
| 西南 | 0.006 | 0.001 | −0.018 | −0.121 | 0.007 | 0.002 | −0.026 | −0.124 | |
| S3 | 东北 | 0.006 | 0.001 | −0.023 | −0.129 | 0.008 | 0.001 | −0.036 | −0.132 |
| 京津 | 0.019 | −0.001 | 0.009 | −0.097 | 0.016 | −0.001 | 0.001 | −0.095 | |
| 北部沿海 | 0.010 | 0.002 | −0.016 | −0.122 | 0.012 | 0.003 | −0.023 | −0.119 | |
| 华东沿海 | 0.014 | 0.000 | 0.002 | −0.104 | 0.013 | 0.000 | −0.007 | −0.103 | |
| 南部沿海 | 0.002 | −0.001 | −0.005 | −0.111 | 0.001 | −0.002 | −0.015 | −0.111 | |
| 中部 | 0.008 | 0.000 | −0.014 | −0.120 | 0.008 | 0.001 | −0.026 | −0.123 | |
| 西北 | 0.407 | −0.007 | 0.466 | 0.360 | 0.327 | −0.002 | 0.454 | 0.357 | |
| 西南 | 0.410 | −0.012 | 0.494 | 0.388 | 0.332 | −0.008 | 0.489 | 0.392 | |
增加财政研发支出,受援区域的物质资本效率显著提高,但区域间差异较大;2020年,东北地区的物质资本效率提高幅度最大(0.802%);中部和西部地区的物质资本效率提高幅度相近,在0.407%—0.410%之间。在没有持续性财政研发支出增长的情况下,受援区域物质资本效率的提高幅度缓慢下降;2020—2025年,东北地区的物质资本效率提高幅度由0.802%下降为0.626%,降幅低于0.2%。受援区域的人力资本效率下降,并且区域间差距较大;2020年,东北地区的人力资本效率下降0.034%,中部和西部地区的人力资本效率下降幅度在0.007%—0.012%之间。与受援区域物质资本效率的提高幅度相比,人力资本效率下降的幅度较小;物质资本效率的提高幅度均大于0.4%,人力资本效率的下降幅度均小于0.04%。
增加财政研发支出,受援区域GDP和GDP份额的上升幅度显著提高,但地区间差距较大;东北地区GDP和GDP份额的上升幅度最大(2020年分别为1.041%和0.95%),中部和西部地区GDP和GDP份额的上升幅度差距较小(2020年分别为0.466%—0.494%和0.36%—0.39%)。在没有进一步增加受援区域财政研发支出规模的情况下,受援区域GDP的提高幅度逐渐下降;其中西部地区GDP的提高幅度下降最快(分别为0.466%—0.454%和0.494%—0.489%),其次是东北地区(1.041%—1.038%),最后是中部地区(0.494%—0.493%)。东北、中部和西南地区GDP份额的上升幅度持续提高(分别为0.95%—0.954%、0.390%—0.395%和0.388%—0.392%),而西北地区GDP份额的上升幅度则缓慢下降(0.360%—0.357%)。
对受援区域增加研发支出,非受援区域物质资本效率提高,但提高幅度较小(≤0.03%)。人力资本的效率变化几乎可以忽略不计(≤±0.002%)。GDP变化具有不确定性,部分非受援区域的GDP发生了较大幅度下降;如:S1情景下,西南和中部地区的GDP下降幅度最大;S2情景下,西南和东北地区GDP的下降幅度最大;S3情景下,东北、北部沿海和中部地区GDP的下降幅度最大。即使在不对受援区域进一步增加财政研发支出的情况下,非受援区域GDP的下降幅度也在逐年增加或上升幅度逐年下降。与2020年相比,2025年各非受援地区GDP的上升幅度减小或下降幅度增加。
由前(11)式和(12)式可知,物质资本效率、人力资本效率受研发投入、教育投入和就业的影响,只有研发投入和教育投入的增长幅度大于就业增长的幅度时,要素效率才能提高。由图1可知,政府财政支出的变化影响居民消费和企业投资,而政府、居民和企业对研发和教育的需求共同决定着研发和教育的投入。财政研发支出规模增加促进受援区域物质资本效率提升的原因是财政研发支出的“杠杆效应”,即促进受援区域企业研发投资的增加,虽然总需求扩大会导致受援区域就业的增加,但研发投入的增长幅度大于就业增长幅度。由于(11)式的“知识积累”效应,故要素效率提高的持续性较好。受援区域人力资本效率的下降是受就业增加的影响。在促进受援区域物质资本效率和经济地位的提升方面,对东北地区增加财政支出的效果最明显,东北地区的经济总量和人口规模都小于中部和西部地区,相同数量财政资金的投入对东北地区的影响更大。非受援区域物质资本效率提升的原因是非受援区域就业下降。由(4)式可知,受援区域GDP的增长是受物质资本效率提升和就业增加的推动。由图1可知,部分非受援区域GDP的下降是政府对受援地区增加支出,导致政府储蓄减少,进而总储蓄下降使非受援区域投资减少。
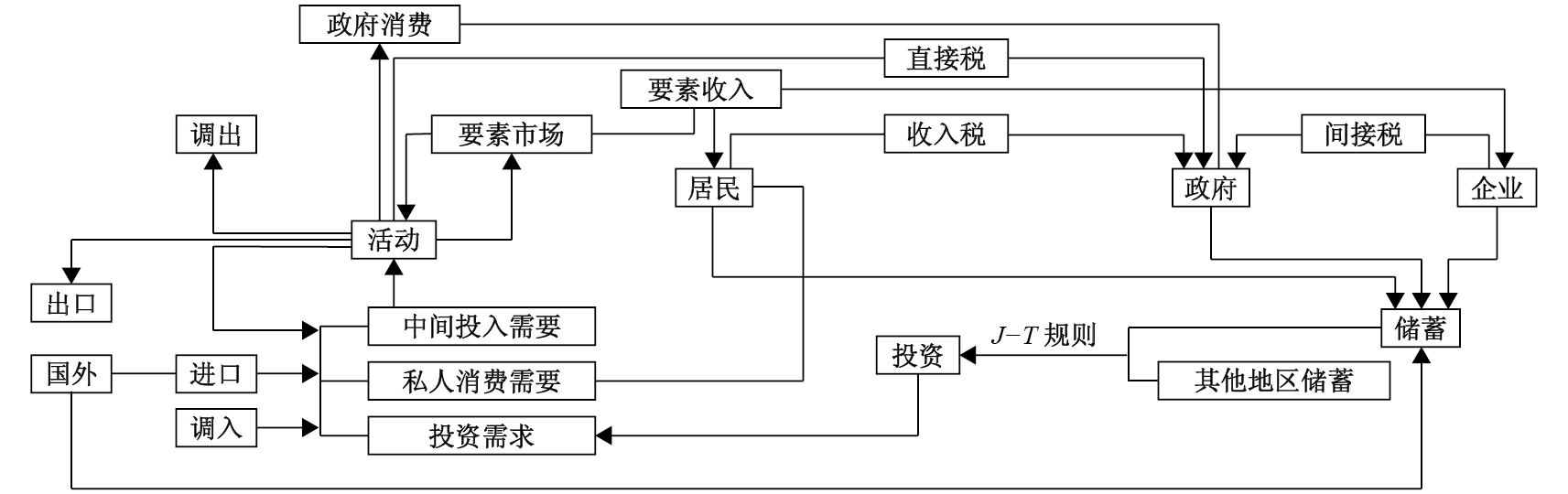
|
| 图 1 8区域中一个区域的结构 |
(二)增加受援区域财政教育支出规模效果的模拟。2015年分别对东北(SS1情景)、中部(SS2情景)和西部地区(SS3情景)增加财政教育经费100亿。这种情景设置是考虑了我国教育资源分配不均的情况下,评估政府对教育资源贫乏地区增加教育支出的影响。相同规模的教育支出变化也便于与财政研发支出政策效果进行对比。模拟结果见表6所示。
| 情景 | 地区 | 2020年 | 2025年 | ||||||
| 物质资本效率 | 人力资本效率 | GDP | GDP份额 | 物质资本效率 | 人力资本效率 | GDP | GDP份额 | ||
| SS1 | 东北 | −0.010 | −0.003 | 0.020 | 0.025 | −0.009 | −0.003 | 0.013 | 0.019 |
| 京津 | 0.002 | 0.000 | −0.007 | −0.002 | 0.002 | 0.000 | −0.006 | −0.001 | |
| 北部沿海 | 0.001 | 0.001 | −0.007 | −0.001 | 0.001 | 0.000 | −0.006 | −0.001 | |
| 华东沿海 | 0.002 | 0.001 | −0.007 | −0.001 | 0.002 | 0.001 | −0.006 | −0.001 | |
| 南部沿海 | 0.002 | 0.001 | −0.007 | −0.001 | 0.002 | 0.001 | −0.006 | −0.001 | |
| 中部 | 0.001 | 0.000 | −0.010 | −0.005 | 0.001 | 0.000 | −0.009 | −0.004 | |
| 西北 | 0.001 | 0.000 | −0.008 | −0.002 | 0.001 | 0.000 | −0.007 | −0.002 | |
| 西南 | 0.002 | 0.001 | −0.010 | −0.005 | 0.002 | 0.001 | −0.009 | −0.004 | |
| SS2 | 东北 | 0.001 | 0.000 | −0.009 | −0.004 | 0.001 | 0.000 | −0.008 | −0.003 |
| 京津 | 0.001 | 0.000 | −0.007 | −0.002 | 0.002 | 0.000 | −0.007 | −0.001 | |
| 北部沿海 | 0.001 | 0.001 | −0.007 | −0.002 | 0.002 | 0.001 | −0.007 | −0.001 | |
| 华东沿海 | 0.001 | 0.001 | −0.007 | −0.001 | 0.001 | 0.000 | −0.006 | −0.001 | |
| 南部沿海 | 0.001 | 0.001 | −0.007 | −0.001 | 0.001 | 0.000 | −0.006 | −0.001 | |
| 中部 | −0.003 | −0.001 | 0.002 | 0.008 | −0.002 | −0.001 | 0.000 | 0.006 | |
| 西北 | 0.001 | 0.000 | −0.008 | −0.002 | 0.001 | 0.000 | −0.007 | −0.002 | |
| 西南 | 0.001 | 0.000 | −0.009 | −0.004 | 0.001 | 0.000 | −0.008 | −0.003 | |
| SS3 | 东北 | 0.001 | 0.000 | −0.010 | −0.004 | 0.002 | 0.000 | −0.009 | −0.002 |
| 京津 | 0.003 | 0.001 | −0.008 | −0.001 | 0.003 | 0.001 | −0.006 | 0.000 | |
| 北部沿海 | 0.001 | 0.001 | −0.007 | −0.001 | 0.002 | 0.001 | −0.007 | −0.000 | |
| 华东沿海 | 0.001 | 0.000 | −0.007 | −0.001 | 0.002 | 0.000 | −0.007 | −0.000 | |
| 南部沿海 | 0.001 | 0.000 | −0.007 | −0.001 | 0.001 | 0.000 | −0.007 | −0.000 | |
| 中部 | 0.001 | 0.000 | −0.009 | −0.002 | 0.001 | 0.000 | −0.008 | −0.002 | |
| 西北 | −0.004 | 0.000 | −0.004 | 0.002 | −0.003 | 0.000 | −0.005 | 0.002 | |
| 西南 | −0.005 | −0.002 | −0.000 | 0.007 | −0.004 | −0.002 | −0.002 | 0.004 | |
由表6可见,增加财政教育支出,受援区域要素效率均下降,但下降幅度很小(≤0.01%),区域间差距较小。东北和中部地区GDP和GDP的份额小幅度上升,但两地区间差距较大;2020年,东北GDP上升幅度为0.02%,而中部地区GDP仅上升0.002%。西部地区GDP小幅度下降,西北和西南地区GDP的下降幅度均小于0.005%,GDP份额小幅度上升,西北和西南GDP份额上升幅度小于0.007%。非受援区域的要素效率小幅度上升(≤0.002%),GDP和GDP的份额小幅度下降(≤0.01%,≤0.005%),并且区域间差距较小。
财政教育支出规模的增加会促进受援区域总需求的增加,并改善就业状况,但财政教育支出并未表现出“杠杆效应”,研发投入和教育投入的增长幅度小于就业的增长幅度,受援区域要素效率降低。此时,部分受援区域虽然能实现经济增长,但增长速度缓慢,且主要依赖就业增长的拉动,属于外延式经济增长。而非受援区域则需求不足,就业减少,促使其要素效率发生小幅度上升(≤0.002%),但不足以弥补就业下降对经济的影响,因此非受援区域GDP下降。总体而言,对受援区域增加财政教育支出导致的各地区要素效率和GDP变化的幅度很小,因为在基准情形中,财政教育支出规模较大,相对较小规模的财政教育支出变化对各地区居民和企业行为的变化影响不显著。
五、调整财政科教支出比例效果的模拟及分析
由前文模拟结果可知,增加财政科教支出规模不能形成技术进步和区域经济协调发展的双赢局面,但可以为政策进一步优化提供设计思路。首先,对受援区域增加财政科教支出,会使政府储蓄减少,总储蓄减少导致部分非受援区域投资减少,GDP下降;促进区域经济协调发展不应以牺牲非受援区域的经济增长为代价。因此,控制对受援区域财政支出的总规模,可能会达到降低非受援区域经济损失的目的。其次,增加财政研发支出比增加教育支出对受援区域要素效率和经济增长的影响程度更大,研发支出在财政总支出中占比小,小规模增加研发支出的同时减少对其他产业的支出,对政府运转不产生太大影响,而教育支出在财政总支出中占比大,小规模增加教育支出效果不明显,大规模增加教育支出的同时缩减其他产业的支出不具有现实性。最后,基准情形下,东北和中部地区的经济地位明显下降;财政研发支出对东北地区经济地位提升的效果最明显,中西部地区间人均财政研发投入的差距很大,中部地区的人均财政研发经费更匮乏,2015年中西部地区的人均财政研发经费分别为90.48和171.67。
因此,本文的政策情景设计为:2015—2025年,每年分别对东北(SSS1)和中部地区(SSS2)增加财政研发支出10亿元,②不改变财政教育支出规模,政府对其他产业的支出减少10亿元,保持财政对两地区的支出规模不变;东北和中部地区(SSS3)同时增加财政研发支出10亿元,不改变两地区的财政教育支出规模,政府对两地区其他产业的支出分别减少10亿元,保持财政对两地区的支出规模不变。政策模拟结果见表7所示。
| 情景 | 地区 | 2020年 | 2025年 | ||||||
| 物质资本效率 | 人力资本效率 | GDP | GDP份额 | 物质资本效率 | 人力资本效率 | GDP | GDP份额 | ||
| SSS1 | 东北 | 0.614 | 0.006 | 0.701 | 0.643 | 0.929 | 0.008 | 1.205 | 1.105 |
| 京津 | 0.003 | 0.000 | 0.001 | −0.056 | 0.004 | 0.000 | 0.001 | −0.097 | |
| 北部沿海 | 0.000 | 0.000 | 0.001 | −0.056 | 0.000 | 0.001 | 0.001 | −0.097 | |
| 华东沿海 | 0.003 | 0.000 | 0.002 | −0.055 | 0.005 | 0.001 | 0.004 | −0.094 | |
| 南部沿海 | 0.001 | 0.000 | 0.001 | −0.056 | 0.004 | 0.001 | 0.002 | −0.096 | |
| 中部 | 0.002 | 0.000 | 0.001 | −0.055 | 0.004 | 0.001 | 0.002 | −0.096 | |
| 西北 | 0.007 | 0.000 | 0.002 | −0.055 | 0.012 | 0.000 | 0.003 | −0.095 | |
| 西南 | 0.002 | 0.001 | 0.001 | −0.056 | 0.005 | 0.002 | 0.002 | −0.096 | |
| SSS2 | 东北 | 0.004 | 0.000 | 0.002 | −0.068 | 0.007 | 0.000 | 0.003 | −0.115 |
| 京津 | 0.011 | 0.000 | 0.003 | −0.067 | 0.018 | 0.000 | 0.006 | −0.112 | |
| 北部沿海 | 0.005 | 0.000 | 0.003 | −0.067 | 0.009 | 0.001 | 0.005 | −0.113 | |
| 华东沿海 | 0.008 | 0.001 | 0.008 | −0.062 | 0.012 | 0.000 | 0.009 | −0.110 | |
| 南部沿海 | 0.002 | 0.000 | 0.001 | −0.068 | 0.004 | 0.000 | 0.002 | −0.116 | |
| 中部 | 0.299 | 0.002 | 0.328 | 0.258 | 0.461 | 0.003 | 0.559 | 0.441 | |
| 西北 | 0.021 | 0.000 | 0.006 | −0.064 | 0.037 | 0.000 | 0.009 | −0.109 | |
| 西南 | 0.004 | 0.000 | 0.002 | −0.068 | 0.007 | 0.001 | 0.004 | −0.114 | |
| SSS3 | 东北 | 0.617 | 0.006 | 0.704 | 0.576 | 0.936 | 0.008 | 1.208 | 0.989 |
| 京津 | 0.014 | 0.000 | 0.004 | −0.123 | 0.022 | 0.000 | 0.007 | −0.209 | |
| 北部沿海 | 0.005 | 0.000 | 0.004 | −0.123 | 0.009 | 0.002 | 0.006 | −0.210 | |
| 华东沿海 | 0.010 | 0.001 | 0.010 | −0.117 | 0.017 | 0.001 | 0.012 | −0.204 | |
| 南部沿海 | 0.003 | 0.000 | 0.002 | −0.125 | 0.008 | 0.001 | 0.004 | −0.212 | |
| 中部 | 0.301 | 0.002 | 0.329 | 0.202 | 0.465 | 0.003 | 0.561 | 0.344 | |
| 西北 | 0.029 | 0.000 | 0.009 | −0.118 | 0.049 | 0.000 | 0.013 | −0.203 | |
| 西南 | 0.006 | 0.001 | 0.003 | −0.124 | 0.012 | 0.003 | 0.006 | −0.210 | |
提高财政研发支出比例,东北和中部地区的要素效率提高;其中,物质资本效率显著提升,但东北和中部提升幅度的差距较大。2020年,东北地区物质资本效率提高0.614%,而中部地区物质资本效率提高0.299%。人力资本效率上升幅度相对较小,2020年,东北地区人力资本效率上升0.006%,中部地区人力资本效率仅上升0.002%。随着政策的实施,东北和中部地区要素效率提高的幅度逐年增加;其中,物质资本效率提高幅度增长较快,五年间,东北和中部地区物质资本效率提高的幅度分别由0.613%和0.299%上升为0.929%和0.461%;人力资本效率提高幅度增长较慢,五年间,东北和中部地区人力资本效率提高的幅度分别由0.006%和0.002%上升到0.008%和0.003%。东北和中部地区GDP和GDP份额提高的幅度逐年显著上升,但东北和中部之间存在一定差距;2020—2025年,东北和中部地区GDP的增长幅度分别由0.701%和0.328%上升到1.205%和0.559%。
对财政研发支出比例不变的地区而言,物质资本效率提高幅度较小,但地区间存在一定差距;如:在SSS1情景下,2020年北部沿海物质资本效率几乎不变,而西北地区物质资本效率提高0.007%。随着政策的实施,财政研发支出比例不变地区物质资本效率提高的幅度也会逐年增加,但增长速度较慢,各地区人力资本效率的提高幅度几乎不发生变化(≤0.002%)。财政研发支出比例不变地区GDP提高的幅度较小,上升速度缓慢;GDP份额显著下降,并且下降速度较快。
同时提高东北和中部地区的研发支出比例,各地区要素效率、GDP和GDP份额的变化幅度相当于单独提高东北或中部地区财政研发支出比例引致的要素效率、GDP和GDP份额的变化幅度之和;SSS3情景下,要素效率、GDP和GDP份额的变化幅度是SSS1和SSS2情景下相应指标的求和(差距
提高东北和中部地区财政研发支出比例而不改变财政支出规模,可以防止其他地区投资减少和经济增长速度下降;同时,东北和中部地区的要素效率和经济增长都提高会促进其他地区商品调入的增加,从而促进其他地区的经济增长和技术进步。
六、结论及启示
本文基于自主构建的引致技术进步动态多区域CGE模型,模拟了对东北、中部和西部地区增加财政科教支出和调整东北、中部地区财政支出结构的影响。结论为:
1. 东北、中部或西部地区增加财政研发支出规模,对三个地区的物质资本效率、经济增长和经济地位的提高都有显著的促进作用;其中对东北物质资本效率提升和经济增长促进的作用最明显,其次是中部,最后是西部。在没有进一步增加财政研发支出规模的情况下,三地区物质资本效率和GDP的提高幅度缓慢下降,而且增加财政支出规模还不利于三地区人力资本效率的提升。增加财政支出规模会降低政府储蓄,非受援区域投资规模下降,从而导致部分非受援区域GDP下降。其中,对东北地区增加财政研发支出,西南和中部地区GDP下降的幅度最大;对中部地区增加财政研发支出,西南和东北GDP下降的幅度最大;对西部增加财政研发支出,东北、北部沿海和中部地区GDP下降的幅度最大。所以,增加财政研发支出的规模不能同时促进三地区的经济增长,不利于东北、中部和西部地区之间的协调发展;即使同时增加三地区的财政研发支出规模,政策效果也会互相抵消而减弱,而其他地区则因为投资减少导致的GDP下降幅度会进一步扩大。
2. 对东北、中部和西部地区增加财政教育支出规模,在短期可以促进三地区的总需求增加和就业改善,有利于三地区的经济增长和经济地位提升。对东北、中部和西部地区增加财政教育支出规模,在长期对三地区的人力资本积累和经济增长的影响很小。根据内生增长理论,教育是人力资本形成的最重要影响因素,教育投入在长期可以促进人力资本积累和经济增长。财政教育支出是教育投入非常重要的组成部分,对受援区域增加财政教育支出本应促进该区域的人力资本积累和经济增长。然而,本文的模拟结果并没有支持这一观点。其可能原因是:一是受援地区财政教育支出增加,对区域内居民的教育投入产生了较大的挤出作用,从而教育总投入增长的幅度较小;二是总需求增加促进了就业的增加,新增就业占用更多的教育资源,从而抵消了部分教育投入增加的成果;三是由前文模型方程设定,各地区间的工资水平存在扭曲,受援区域工资水平低,总需求增加促进的就业增长主要体现为非熟练劳动力的增加,而受援区域教育业发展培训的大量熟练劳动力更容易流向发达地区。非受援区域总需求不足,就业减少,经济增长速度小幅度下降。
3. 提高东北或中部地区的财政研发支出比例,可以持续促进八大地区的技术进步和区域经济协调发展。提高东北或中部地区的财政研发支出比例,能够促进东北和中部地区的物质资本效率提高。随着政策的实施,东北和中部地区物质资本效率提高的幅度逐年增加,人力资本效率小幅度提高;其他未提高财政研发支出比例地区的物质资本效率小幅度提升,人力资本效率基本没有变化。在不改变各地区财政支出规模的情况下,提高东北和中部地区的财政研发支出比例不仅可以防止其他地区投资减少导致的经济增长速度下降,而且可以带动其他地区实现小幅度经济增长和技术进步。同时提高这两个地区的财政研发支出比例,各地区要素效率和GDP的提高幅度相当于单独提高东北或中部地区研发支出比例引致的各地区要素效率和GDP提高幅度的合计,政策效果不会互相抵消,从而更有利于各地区的技术进步和经济协调发展。
以上结论表明,财政科教支出对各地区的技术进步和经济增长的影响存在很大差异。为促进技术进步和区域协调发展,在短期可以大规模增加东北、中部和西部地区的财政科教支出规模,进而促进三地区的总需求增加,就业水平提高,加快经济增长和经济地位提升。然而,值得注意的是,对受援地区增加财政科教支出规模,可能导致非受援区域的总需求下降,并影响经济增长速度。在长期,政府应在控制东北或中部地区投资规模的基础上,提高这两个地区的研发支出比例,还可以同时提高两地区的财政研发支出比例。一方面,在平衡增长路径下,东北和中部地区在全国的经济地位会不断下降,影响区域经济协调发展;另一方面,提高两地区的财政研发支出比例可以持续地促进东北和中部地区的技术进步和经济地位提升,可以作为培养这两个地区内生增长动力的重要手段,破解“新东北现象”和“中部塌陷”的区域发展难题;另外,提高两地区的财政研发支出比例不会对其他地区的经济带来负面影响,而且有利于其他地区的技术进步。财政研发支出的政策虽然可以促进东北、中部和西部地区的物质资本效率提高和经济增长,但对三地区人力资本效率的影响非常小,为促进三地区人力资本效率的提高,还需结合财政教育支出政策。为使财政教育支出政策取得较理想的效果,需要相关的政策配套。一是在对东北、中部和西部地区增加财政教育支出的同时,对区域内居民的教育投入给予补贴,以减小财政教育支出的挤出效应。二是进一步研究各地区工资扭曲的影响因素,缩小东北、中部和西部地区与其他发达地区工资扭曲的差距;进一步研究制定受援区域留住人才、吸引人才的相关政策。
① 8大地区名称及具体包括的省份分别为,(1)东北:黑龙江、吉林、辽宁;(2)京津:北京、天津;(3)北部沿海:河北、山东;(4)华东沿海:江苏、上海、浙江;(5)南部沿海:福建、广东、海南;(6)中部:山西、河南、安徽、湖南、江西、湖北;(7)西北:内蒙古、青海、新疆、甘肃、陕西、宁夏;(8)西南:四川、广西、重庆、西藏、云南、贵州。
② 本文的动态递推模型各外生变量按人口比例增长,这里增加10亿元是指随人口自然增长的基础上再增加10亿元,下同。
| [1] | 陈晓玲, 连玉君. 资本-劳动替代弹性与地区经济增长−德拉格兰德维尔假说的检验[J]. 经济学(季刊), 2013(1): 93–118. |
| [2] | 董万好, 刘兰娟. 财政科教支出对就业及产业结构调整的影响−基于CGE模拟分析[J]. 上海经济研究, 2012(2): 41–52. |
| [3] | 郭庆旺, 贾俊雪. 公共教育政策、经济增长与人力资本溢价[J]. 经济研究, 2009(10): 22–35. DOI:10.3969/j.issn.1002-5863.2009.10.011 |
| [4] | 胡志国, 严成樑, 龚六堂. 政府研发政策的经济增长效应与福利效应[J]. 财贸经济, 2013(9): 112–120. |
| [5] | 李国平, 王春杨. 我国省域创新产出的空间特征和时空演化−基于探索性空间数据分析的实证[J]. 地理研究, 2012(1): 95–106. |
| [6] | 刘兰娟, 董万好, 徐鑫. 财政科技投入对产业结构的影响−城镇化过程中劳动报酬占比的视角[J]. 上海财经大学学报, 2013(4): 73–80. |
| [7] | 娄峰. 科技研发投入政策模拟分析: 基于中国科技CGE模型[J]. 重庆理工大学学报(社会科学版), 2017(1): 59–66. |
| [8] | 杨朝峰, 贾小峰. 政府公共R&D影响经济增长的机制研究[J]. 中国软科学, 2008(8): 37–42,109. DOI:10.3969/j.issn.1002-9753.2008.08.006 |
| [9] | Blankenau W F, Simpson N B, Tomljanovich M. Public education expenditures, taxation, and growth: Linking data to theory[J]. The American Economic Review, 2007, 97(2): 393–397. DOI:10.1257/aer.97.2.393 |
| [10] | Devarajan S, Swaroop V, Zou H F. The composition of public expenditure and economic growth[J]. Journal of Monetary Economics, 1996, 37(2): 313–344. DOI:10.1016/S0304-3932(96)90039-2 |
| [11] | Jones C I. R&D-based models of economic growth[J]. The Journal of Political Economy, 1995, 103(4): 759–784. DOI:10.1086/262002 |
| [12] | Jung H S, Thorbecke E. The impact of public education expenditure on human capital, growth, and poverty in Tanzania and Zambia: A general equilibrium approach[J]. Journal of Policy Modeling, 2003, 25(8): 701–725. DOI:10.1016/S0161-8938(03)00060-7 |
| [13] | Křístková Z. Impact of R&D investment on the economic growth of the Czech Republic-a recursively dynamic CGE Approach[J]. Prague Economic Papers, 2012, 2012(4): 412–433. |
| [14] | Morales M F. Research policy and endogenous growth[J]. Spanish Economic Review, 2004, 6(3): 179–209. |
| [15] | Park W G. A theoretical model of government research and growth[J]. Journal of Economic Behavior & Organization, 1998, 34(1): 69–85. |
 2018, Vol. 44
2018, Vol. 44


