
一、引 言
党的十九大报告提出,创新是引领发展的第一动力,是建设现代化经济体系的战略支撑。创新贯穿于整个产业转型过程中,已成为产业实现转型升级的核心力量。尽管技术创新对产业升级的促进效应在政府和学术界已经达成了共识,但关于技术进步以及新技术应用的来源却有着不同的观点。部分学者从劳动要素价格与技术创新之间关系的角度展开了理论和实证研究。基于要素替代角度,David(1975)、Van Reenen(1996)等研究发现工资的上升会使企业用技术替代劳动力进行生产,且这种替代效应会推动企业的发展。基于效率工资角度,Shapiro和Stiglitz(1984)认为高工资不仅可以降低企业的监督成本,还会使工人失业的机会成本提高,从而激励工人努力工作,提高劳动生产率。基于需求创造角度,Murphy等(1989)通过对“大推进”理论的进一步研究,理论上认为工资上升不仅会增加当地消费,引起劳动力由非正规部门转移至正规部门,而且还会加快其他行业的产业升级步伐。基于创造性破坏角度,在熊彼特的“创造性破坏”理论的基础上,Kleinknecht和Naastepad(2001)通过对荷兰企业进行研究,发现较低的工资会抑制企业创新能力的发挥,使得市场上大量的低生产率企业生存下来,熊彼特的“创造性破坏”效应得到削弱。在中国,林炜(2013)利用1998—2007年中国工业企业的微观数据库研究劳动力成本与创新之间的关系,发现劳动力成本的上升会倒逼企业进行研发与创新,打破部分制造业企业一直以来对低劳动力成本优势的依赖。王雷(2017)用2001—2014年沪深A股制造业上市公司的样本,也从实证层面证明了劳动力成本上升对企业创新的倒逼影响。
然而,透过劳动力成本,直接研究外生的政府所定最低工资制度对企业创新升级造成冲击的却很少。目前,国内外对最低工资的产业升级效应的研究还缺乏相应的实证支撑。一部分学者的实证研究表明,最低工资标准的提高会带动工资水平的普遍上升(Brown等,1982;Belman和Wolfson,1997;马双等,2012;孙楚仁等,2013a;邸俊鹏和韩清,2015)。除此之外,已有少部分学者从劳动力市场的外生冲击−最低工资标准的角度间接考察了企业的技术创新,如Webb(1912)(在对法定最低工资制度的经济学理论进行阐述时)认为最低工资的上升会提高企业的生产效率。理论上,Acemoglu(2003)认为在存在工资议价、租金分享的情形下,由最低工资、劳动力市场管制等引起的工资上升会鼓励企业进行技术创新与研发,并使用新技术。他通过构建内生的技术增长理论模型,验证了劳动需求下降是20世纪技术进步的一个重要因素,劳动力短缺会激发劳动节约型技术创新,而外生的工资上升会通过降低企业对劳动力的需求而刺激其进行劳动节约型技术的研发(Acemoglu,2010)。Aaronson和Phelan(2017)从要素替代的视角,发现短期内最低工资上升导致的低技能劳动力成本增加会促使企业更多地使用技术替代工人来执行手工的常规任务。那么,在现实社会中,政府对最低工资的调整是否会刺激企业创新,进而促进产业升级呢?
本文通过直接效应和间接效应两个渠道来分析最低工资的上升是如何加快产业升级的步伐的,并提出了两个相应的研究假说。
1. 最低工资调整影响企业技术创新的直接效应。这主要体现在以下三个方面:第一,最低工资上升通过替代效应倒逼企业进行技术创新。Hicks(1932)在《工资理论》中提到,企业进行生产活动主要依靠资本和劳动这两种生产要素,而这两种要素在一定程度上存在着替代关系。当一种生产要素相对于另一种要素的价格上升时,企业对该要素的需求量就会下降,反过来通过增加另一种要素的使用来达到预定的产出量。理论上,最低工资是高于市场均衡水平的工资,其上升会导致低于最低工资水平的工人工资上升,进而提高企业的劳动力成本。面临劳动力价格上升时,企业会降低对劳动力的需求,进而加大研发创新,用技术和资本替代劳动。第二,最低工资上升通过效率工资效应激励企业进行技术创新。最低工资具有类似于效率工资的作用:一方面,怠工模型(Shirking Model)(Shapiro和Stiglitz,1984)表明,在劳动力市场没有充分就业的情况下,最低工资的上升提高了工人不努力工作的机会成本,这可能会倒逼劳动者提高其生产效率,为企业的创新创造了前提条件;另一方面,逆向选择模型(Adverse Selection Model)(Leonard,1987)认为高工资会激励工人积极接受教育和培训,从而吸引更多高素质的劳动者来企业工作,为企业创新积累人力资本。第三,最低工资上升通过需求创造效应促进企业创新。Marglin和Bhaduri(1990)、Bowles和Boyer(1995)、Onaran和Galanis(2012)等的研究表明,工资获得者的消费倾向明显高于利润获得者,因此最低工资的上升会增加整个社会的消费,需求上升会带来企业产品的创新和产出的扩张。进一步地,根据Murphy等(1989)提出的“大推进”理论,创新可以通过经济体中不同行业相互作用产生的潜在市场规模效应发挥作用,从而实现产业的转型升级。综上所述,本文提出如下研究假说:
假说1:最低工资的上升会直接导致企业生产成本的上升,降低企业的劳动力需求,刺激企业进行技术创新,即最低工资上升对产业升级存在直接的促进效应。
本文通过Heckman两阶段模型对上述直接效应进行实证检验。结果表明,最低工资上升确实会提高企业的创新意愿、增加创新成果,并且该结果在改变创新水平的衡量指标、估计方法、子样本区间后依然是稳健的。
2. 最低工资调整促进产业升级的间接效应。1912年熊彼特在《经济发展理论》中重点突出了创新给经济带来的破坏性进步,即所谓的“创造性破坏”(Creative Destruction)理论。该理论主要研究企业如何通过创新淘汰旧的技术,建立一套新的生产体系来刺激经济的创造性增长(Schumpeter,1934)。从这一角度看,较低的劳动力成本抑制了熊彼特“创造性破坏”效应的发挥,而最低工资的上升事实上创造了一种破坏机制,形成创新驱动的一个推手。在当下中国面临产业结构调整和产品转型升级的背景下,这会倒逼一部分企业进行技术的研发与创新。长期以来,中国一些企业特别是劳动密集型企业对“低工资”过分依赖,这在一定程度上延缓了企业的技术升级。最低工资的上升挤压了这部分企业的利润空间,如果这些落后的传统劳动密集型企业不能承受这样的劳动力成本压力,要么退出市场,要么通过加快技术创新而提高产品生产效率,或者开发新的产品,提升自身产品的附加值。因此,本文提出如下研究假说:
假说2:最低工资标准的不断提高,会淘汰掉行业内部分产品附加值低、生产率低的企业,倒逼企业在现有产能的基础上寻求技术创新,提高生产效率,即最低工资上升会间接带来产业升级的效应。
本文通过面板Probit模型回归对上述间接效应进行实证检验。结果表明,最低工资上升确实会淘汰掉行业内低生产率的企业。因此生产率高的企业生存下来,这不仅优化了行业的资源配置,还可以通过创新刺激企业加快转型升级的步伐。除此之外,本文借助2004年《最低工资规定》实施这一准自然实验的双重差分检验也印证了以上结论。
二、数据来源与变量说明
(一)变量说明
1. 企业的创新水平。借鉴以前文献的做法(Aghion等,2009;Hu和Jefferson,2009;Hashmi,2013),本文采用企业每年申请的专利数量来衡量该指标。之所以选择专利作为测度企业创新能力的一个指标,是因为它很好地捕获了企业创新投入的效率(不论是可观测到的还是不可观测到的);另外,专利还可以反映企业产品的更新换代速度、产品质量等。除了专利数据以外,还存在一些其他变量可对创新进行测度,如研发支出(R&D),其大小反映了企业创新投入的多少,但它只能从可观测到的角度衡量创新投入,且无法测度创新质量。同时,研发投入仅有2005—2007年的数据,数据不连续,没法很好地实现本文的研究设想。因此,为了得到较好的实证研究结果,本文主要采用企业申请专利数作为创新水平的衡量指标。
2. 城市最低工资标准。这是本文的核心解释变量。最低工资是政府旨在保护劳动者基本生存权益,保障居民基本生活需求而制定的一项工资标准,世界上大多数国家或地区先后建立了最低工资制度。就我国而言,1993年政府正式出台了《企业最低工资规定》,并在2004年颁布的《最低工资规定》中做了进一步修订。自此之后,最低工资制度在全国各个省份全面铺开。近几年,最低工资的实施力度在不断加大。人力资源和社会保障部公布的数据表明,2011年全国有24个省份调整了最低工资标准,平均增幅为22%;2012年有25个省份调整最低工资标准,平均增幅为20.2%;2013年全国有27个省份调整了最低工资标准,平均调增幅度为17%。
3. 其他控制变量。通过对现有关于企业创新的文献进行梳理,本文首先控制了企业年龄(lnage)、资本密集度(lnkl)、融资能力(lnfin)、利润率(lnprofit)、就业人数(lnemp)、是否出口(export)等企业层面的特征对创新的影响;其次,由于技术创新具有显著的累积效应,越是经济发达、对外开放程度越高的地区,知识的集聚效应越明显,企业的创新研发活动就越多。因此,本文也引入了城市层面的这些变量来控制其对企业创新的影响,这些变量包括城市人均GDP指标(lngdpper)、城市居民消费价格指数(CPI)、城市就业水平(jobrate)、城市就业工资水平(lncitywage)、城市社会保障水平(lnwelfare)、市场竞争强度(hhi)。①考虑到这些变量也是影响地区最低工资标准的因素,并且最低工资标准的调整主要是参照地区上一年度的经济与就业信息,因此以上城市层面的变量均取一阶滞后项后再加入到模型当中。
(二)数据来源
以上分析表明,本文的实证检验主要依赖于企业层面的数据。中国工业企业数据库是中国国家统计局对国有工业企业以及规模以上(年销售收入达500万元及以上)的非国有企业每年进行调查所获取的数据,②包括1998—2007年企业层面的微观数据。该数据库调查的企业数目从20世纪90年代末的14万增长到2007年的30多万;同时,该数据库提供了每个企业的详细信息,包括企业名称、代码、所在行业、所在地区等基本信息,以及企业注册年份、从业人数、资本、中间投入品、新产品产值、所有权特征等经营信息和财务信息。这些都为本文对最低工资上升与企业创新之间关系的研究提供了详实的企业微观数据支撑。借鉴Cai和Liu(2009)的做法,并根据国际通用的会计准则,本文对该数据库内的数据进行了初步处理。本文剔除了流动资产规模大于总资产规模、固定资产规模大于总资产规模、固定资产净值大于总资产规模等存在异常值问题的企业样本数据;同时,参照Brandt等(2012)的做法,本文将企业从业人数少于8人、公司成立年份明显错误(晚于2007年或早于1900年)、非制造业行业的企业从样本中剔除。
本文的被解释变量是企业每年的专利申请数,该数据来自于国家知识产权局安全出版社发行的《中国专利数据库文摘1985—2012(光碟版)》。这一数据库提供了1985年以来每家企业每个专利的详细信息,有专利申请号、申请日期、专利名称、摘要、分类号、申请人、发明人、优先权等,这为本文将工业企业数据库与专利数据库进行匹配提供了可能。本文将中国工业企业数据库和企业专利申请数据,按照企业代码和企业名称两个关键识别信息进行了一对一匹配。由于中国工业企业数据库中2008年和2009年的部分数据缺失,因此本文将样本区间设定为2002—2007年。最终,在样本区间内,匹配成功的企业达到专利数据库企业的70%以上。本文将企业每年的专利申请总数看作企业的总体创新成果。此外,由于研发投入、研发周期、技术水平等方面的差异,我们还按照国际通行的专利分类,将专利划分为发明、实用新型、外观设计等,并以此衡量企业不同技术水平的创新成果。
除此之外,本文还从国泰安城市数据库中获取了2002—2007年城市层面的详细数据,并按照城市名称和年份,将这些数据与工业企业数据库、专利数据库进行匹配,得到微观综合数据并进行整理,其中,地区的最低工资数据通过浏览当地政府网站、政策法规、统计公报等途径进行收集。最终,本文得到了样本区间为2002—2007年,包含33万多家企业、29个制造业行业、160个地区,共639 553个样本的非平衡面板数据。
三、最低工资上升对产业升级的直接效应
(一)基本模型构建
本文的被解释变量−企业专利申请数是非负整数,但有些企业在某些年份的专利申请数为0,如果在回归时将专利申请数为0的非创新企业包括在内,将在一定程度上使本文的估计结果存在一定的偏差(Westerlund和Wilhelmsson,2009)。此外,现实社会中企业的创新决策并非随机事件,往往那些地处工资和社会保障制度相对完善的地区的企业才更有可能选择创新,因此剔除专利申请为0的企业,或仅对创新企业进行回归都会存在样本选择偏差问题(Coe和Hoffmaister,1998)。③为了更好地对最低工资与企业技术创新之间的关系进行研究,本文采用Heckman两阶段模型对样本进行估计。基本估计模型如下:
| $\mathop {P(Innovation}\nolimits_{icjt} = 1) = \varPhi (\mathop \alpha \nolimits_0 + \mathop \alpha \nolimits_1 \mathop {{\rm ln}minwage}\nolimits_{ct} + \beta \mathop X\nolimits_{icjt} + \gamma \mathop Z\nolimits_{ct} + \mathop \phi \nolimits_j + \mathop \theta \nolimits_t )$ | (1) |
| $\mathop {T\!ech}\nolimits_{icjt} = \mathop \eta \nolimits_0 + \mathop \eta \nolimits_1 \mathop {{\rm ln}minwage}\nolimits_{ct} + \mathop {\varphi X}\nolimits_{icjt} + \chi \mathop Z\nolimits_{ct} + \delta \mathop \lambda \nolimits_{icjt} + \mathop \phi \nolimits_j + \mathop \theta \nolimits_t + \mathop u\nolimits_{icjt} $ | (2) |
其中,下标i、c、j和t分别代表企业、城市、行业和时间。方程(1)是企业是否创新的选择方程,采用Probit模型进行估计;Innovationicjt是企业是否创新的哑变量,企业选择创新则取值为1,否则取值为0。方程(2)是创新成果方程,采用面板固定效应模型进行估计。Techicjt不仅代表企业的创新成果,还反映企业的创新技术水平,用企业每年专利申请总数来表示;lnminwagect是最低工资标准的对数值,该指标是本文分析的关键解释变量;如前文所述,预期系数α1和η1的符号都为正,即最低工资标准的上升会刺激企业进行研发创新;Xicjt和Zct分别是企业层面和城市层面的控制变量。另外,模型还加入了行业和时间固定效应,以控制行业和时间层面的不可观测的异质性;uicjt是方程的随机扰动项。Heckman两阶段估计的关键在于在第二阶段估计中加入了从第一阶段估计中得到的λicjt项(逆米尔斯比,inverse mill’s ratio),用于克服样本的选择性偏差。
(二)最低工资上升刺激企业创新
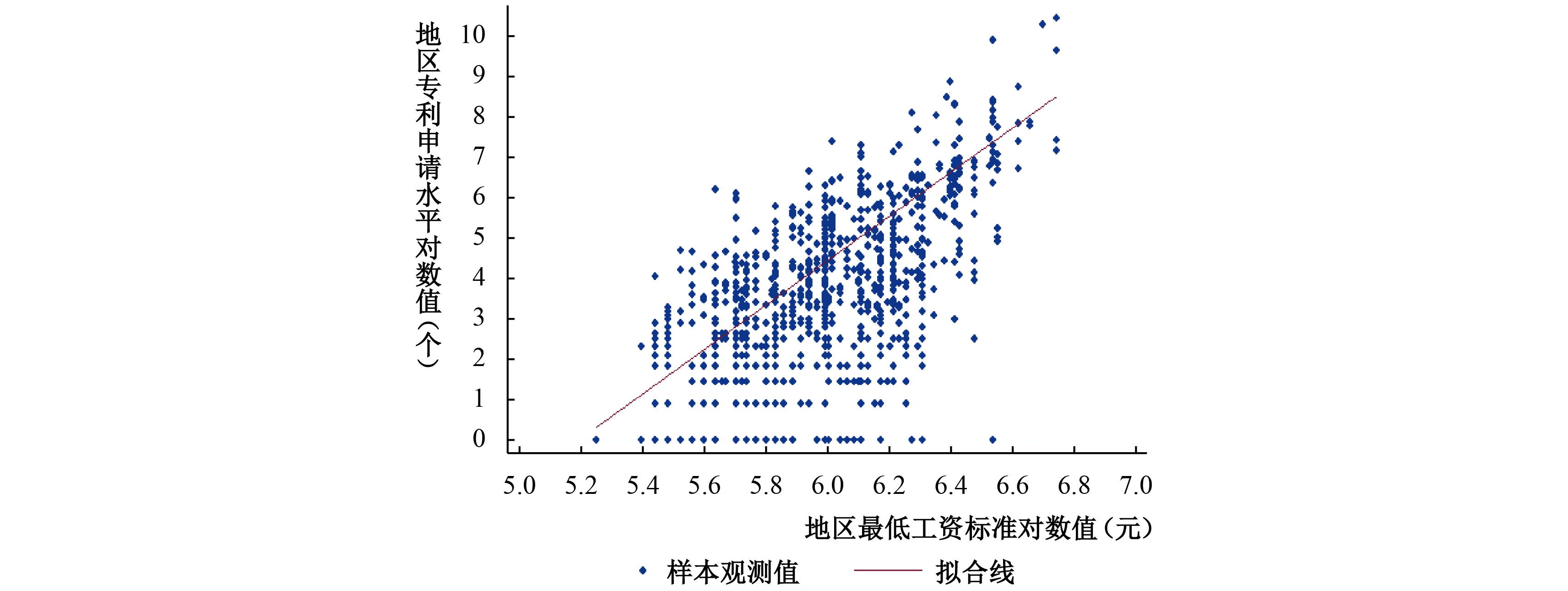
为了更直观地揭示最低工资与企业创新之间的关系,本文首先利用样本数据对最低工资与地区的专利申请总数作了一个简单的二维散点图。④从图1中线性拟合线的斜率为正可以看出,最低工资的上升会带来创新成果的增加。当然,这是在没有控制其他变量影响的情况下得到的基本相关性描述结果,对两者关系更精确的检验将在下文展开详细讨论。
|
| 图 1 地区最低工资与创新成果之间关系 |
通过不断地在模型中加入控制变量,表1给出了模型(1)的基本估计结果,所有的结果均表明最低工资的上升会刺激企业进行技术创新,并带来企业创新成果的增加,即存在最低工资上升对产业升级的直接促进效应。表1中的列(1)和列(2)只加入了企业层面控制变量,并包含时间和行业固定效应,结果表明最低工资的系数显著为正,这暗示着当最低工资上升时,企业在劳动力成本上升的压力下,会被迫加大技术创新的力度。企业层面的其他变量(如企业年龄、规模、资本密集度、盈利能力、是否出口等)的结果显示,规模越大、资本密集度越高、盈利能力越强、市场竞争强度较低、越倾向于出口的企业,创新的概率越大,这与现有研究的结论一致(Liu和Qiu,2016);同时,本文发现企业年龄与创新成果呈现倒“U”形关系。列(3)和列(4)进一步加入了城市层面的控制变量,结果和预期一致,即平均工资水平越高、社会福利保障水平越好的城市,企业创新的可能性越大,创新的成果也越多。选择方程表明,最低工资的上升会提高企业进行创新的可能;边际效应的结果显示,月最低工资每上升10%,企业创新的可能性会提高0.23个百分点;⑤成果方程表明,月最低工资每上升10%,企业的创新成果将上升0.41个百分点。此外,在模型第二阶段的估计中,λicjt项的估计系数显著不为0,表明样本选择问题确实存在,因此采用Heckman两阶段模型进行估计是有效且恰当的。
| 被解释变量 | (1) | (2) | (3) | (4) |
| 创新决策 | 创新成果 | 创新决策 | 创新成果 | |
| lnmw | 0.592***(0.019) | 0.047***(0.003) | 0.369***(0.035) | 0.041***(0.005) |
| imesr | 0.679***(0.004) | 0.699***(0.005) | ||
| 企业层面控制变量 | 控制 | 控制 | 控制 | 控制 |
| 城市层面控制变量 | 控制 | 控制 | ||
| 行业/时间 | 控制 | 控制 | 控制 | 控制 |
| Observations | 639 548 | 639 548 | 391 667 | 391 667 |
| R2 | 0.170 | 0.663 | 0.174 | 0.660 |
| 注:(1)括号内为行业-地区层面的稳健标准差,***表示在1%的水平上显著。(2)所有方程均控制了企业、城市层面控制变量,以及行业和时间固定效应;限于篇幅,这里没有汇报其回归结果。下同。 | ||||
考虑到当期最低工资上升可能并不会立即逼迫企业进行研发创新,为此,本文进一步在模型中加入了最低工资水平以及其他变量的滞后项,观察前期最低工资的调整对本期企业创新的影响是否更大,即最低工资对企业创新的影响是否存在较强的滞后性。最低工资滞后一期(l.lnmw)的估计结果见于表2,⑥通过观察最低工资的滞后项系数,发现前一期最低工资的调整对企业创新的影响变小,说明最低工资上升对企业创新的刺激效应会随时间而减弱。
| 被解释变量 | (1) | (2) |
| 创新决策 | 创新成果 | |
| l.lnmw | 0.266***(0.043) | 0.018***(0.006) |
| imesr | 0.713***(0.006) | |
| 企业/城市层面控制变量 | 控制 | 控制 |
| 行业/时间 | 控制 | 控制 |
| Observations | 240 285 | 240 285 |
| R2 | 0.166 | 0.663 |
(三)稳健性检验⑦
本文的初步回归结果表明,最低工资上升会增强企业的创新意愿,增加企业的创新成果。为了进一步得到更可靠、更稳健的结论,本文接下来分别从不同创新水平、不同估计方法、不同类型企业等角度来验证以上得出的结论。
1. 不同创新指标的检验。很多研究将研发投入作为企业创新活动的指标(Griliches,1979;Klette,1994;Hall,1996;Hall等,2007;毛其淋和许家云,2014)。为了验证本文的基本结论不受特定创新指标的影响,我们采用研发投入作为企业创新水平的代理变量,重新对本文的基本模型进行了检验。除此之外,由经济学常识可知,资源的稀缺性决定了一个社会都必须通过一定的方式把有限的资源合理分配到社会的各个领域中去,以实现资源的最佳利用,即用最少的资源耗费生产出最适用的商品和劳务,以获取最佳的效益。创新是一项企业将有限的资金、资源投入到技术研发当中,以求通过技术创新来获得更大收益的活动。当企业的研发资源得到有效利用,即企业创新行为的投入产出比较大时,企业的创新活动则是有效率的。因此,为了进一步验证最低工资调整对企业创新效率的影响,本文用专利申请数与企业研发投入金额代表的创新效率来代替方程(2)中的企业创新水平,重新对模型进行了估计。经过对创新指标的更换,本文发现最低工资上升不仅会增强企业的创新意愿,增加企业的创新成果,而且还将提高企业的创新效率:最低工资每上升10%,每单位投入的企业专利产出将提高大约8.76个百分点。
2. 不同估计方法的检验。在前面的模型估计中,我们主要采用Heckman两阶段模型对最低工资与企业创新的关系进行实证检验。现在,我们采用可替代的其他模型的估计方法对本文的理论假说加以进一步验证,以排除特定估计方法对结论产生的干扰。本文的被解释变量是企业创新水平,衡量该指标的专利申请数是一系列非负整数,属于计数数据。通常,计数数据一般采用泊松回归的方法对经济变量进行实证分析。但是,泊松回归的使用受限于变量泊松分布的期望和方差基本相等,而本文统计分析的结果表明,每年专利申请数的期望和方差显然不可能相等,方差明显大大高于期望,存在过度分散问题。由于过度分散问题的存在,本文最终又采用了负二项回归对样本重新进行实证检验,结果表明最低工资的系数显著性和绝对值大小与表1相差不大,说明本文的基本结论不受特定估计方法的影响。
(四)异质性检验
以上分析已经对本文的基本假说进行了稳健性验证,为了更清晰地看到本文结论的可靠性,根据实际情况,本文将进一步对最低工资上升影响不同创新技术水平、不同企业的创新行为进行分样本的异质性考察,以使本文结论具有更丰富的现实意义。
1. 不同创新技术水平的检验。根据企业的专利申请类型,本文将专利按研发投入、研发周期、技术水平等方面的差异划分为三种,即发明、实用新型和外观设计,并分别进行了检验。分专利申请类型的估计结果表明,相对于实用新型与发明,最低工资上升对企业进行外观设计创新的刺激效应似乎更大。通常来说,发明的创新价值最高,因为其对创新的技术水平要求最为严格,从而研发投入、研发周期比较长,是典型的革命性创新,可能颠覆以往的生产方式,实现产业升级的可能性更大。较发明而言,实用新型的技术性要求较低,主要注重实用性的设计方案与新创造,故称之为“小发明”,其创新价值相对偏低。而与发明、实用新型不同,外观设计更侧重于产品的新颖性,不管是形状、图案,还是色彩与形状、图案的结合,这种创新的成本都不高,短期内较容易实现,不需要太高的技术水平。技术创新不等于大投入、大项目,一些技术细节的改进也能带来巨大效益。虽然企业的微创新、小创新的水平不高,但在短期内也能给企业带来利润水平的提高,削弱成本上升带来的压力。
2. 不同企业的检验。由于受行业要素密集度、最低工资标准实施强度、地区经济发展水平差异的影响,不同行业、不同所有制、不同地区的企业对最低工资调整的反应可能存在一定的差异,因此本文将全部样本区分为不同资本密集度、不同所有制类型、不同地区,并进行了进一步验证。最终的检验结果显示:第一,与资本密集型企业相比,最低工资上升对劳动密集型企业的创新激励效应更大,但由于受行业竞争压力的影响,其利润空间挤压较严重,从而创新的成果并不多。第二,最低工资制度作为一种引自西方发达国家(地区)的制度,深深地影响着这些国家(地区)的企业,因此最低工资上升对外资企业创新的刺激作用最大,同时最低工资上升对国有企业创新成果的影响并不显著,这可能是受到国有企业人才缺乏、创新激励机制缺失的影响。第三,最低工资上升对东部地区企业创新的刺激作用较大,即东部地区企业对最低工资的上升更为敏感;然而,西部地区的结果不显著,甚至为负,这可能是由东部地区本身的工资标准较高导致的。
四、最低工资对产业升级的间接效应
结合熊彼特的“创造性破坏”理论,本文认为最低工资的不断上调实质上创造了一种破坏机制,倒逼部分企业尽快进行技术研发与创新,刺激企业尽早实现产品转型升级。当整体的工资水平较低时,市场上大量的低生产率企业生存下来,企业创新能力的发挥被抑制,产业升级进行缓慢;伴随着最低工资标准的不断提高,企业整体的工资水平被迫提升,只有生产率高的企业才能生存下来,而生产率低的企业会被淘汰,这不仅优化了行业的资源配置,还可以通过创新刺激企业加快转型升级的步伐。接下来,本文将从企业退出的角度,研究最低工资上升是否会提高企业退出市场的概率,哪些企业退出市场的风险会更大,以及加大研发创新是否是企业避免退出市场的重要出路。
(一)创造性破坏效应的初步检验
现实社会中,企业退出市场意味着该企业已经停止经营。退出是指一个企业从原来的业务领域中撤退出来,即放弃生产或提供某一特定市场上的产品或服务。但由于本文利用的是中国工业企业数据库中的调查数据,该数据库并没有对企业是否退出市场进行调查;因此,对于中国工业企业数据库中企业退出指标的定义,本文参照Brandt等(2012,2014)的做法,根据每年企业是否在调查范围内来衡量:若一个企业t期从数据库中退出,可能是其在t-1期的规模超过以上标准,但t期却没能达到该统计标准。⑧因此,与现实中的企业退出相比,本文关于企业退出的标准可能会大大高估市场上企业的退出比例,毕竟只有符合一定经营规模的企业才会被持续调查,尽管Brandt等(2014)认为规模以上标准这一门槛对企业退出造成的影响并不大。从本文的研究意义的角度看,这一定义在一定程度上会导致对最低工资上升影响企业退出水平的高估,但该指标仅仅是为了从侧面检验最低工资上升对产业升级的影响,因此利用该指标可以间接达到本文的研究目的。如果想准确得到有哪些企业退出市场,或对退出市场的企业进行进一步研究,则还需要结合该企业在现实中的经营情况进行判断。
借鉴以往文献研究企业退出问题时利用Probit模型对假设进行估计的方法(Zingales,1998;Greenaway等,2008;Eslava等,2009;马光荣和李力行,2014),并进一步考虑到面板内序列相关性的存在,本文采用了Probit的面板随机效应模型对以上问题进行实证检验,以期得到大样本下更有效的估计结果。具体模型设定如下:
| $ P(\mathop {exit}\nolimits_{icjt} = 1) = \varPhi (\mathop \alpha \nolimits_0 + \mathop \alpha \nolimits_1 \mathop {{\rm ln}minwage}\nolimits_{ct} + \beta \mathop X\nolimits_{icjt} + \gamma \mathop Z\nolimits_{ct} + \mathop \phi \nolimits_j + \mathop \theta \nolimits_t ) $ | (3) |
其中,exiticjt是一个二值变量,如果t期企业退出市场,则取值为1,否则为0
最低工资上升给产业升级带来的间接效应的检验结果报告于表3。总体的回归结果表明,最低工资上升会降低样本期间内企业退出的概率。进一步参考Liu和Qiu(2016)的做法,本文将样本按照不同行业的不同生产率水平分为3个不同的子样本。分样本回归的结果与本文的预期一致,即最低工资上升确实会提高低生产率企业的退出概率,而对于生产率较高的企业,最低工资上升反而降低了其退出风险。
| 被解释变量 | (1) | (2) | (3) | (4) |
| 总样本 | tfp<25% | 25%≤tfp<75% | tfp≥75% | |
| lnmw | −0.075*** (0.018) |
0.126*** (0.031) |
−0.181*** (0.029) |
−0.169*** (0.042) |
| 企业/城市层面控制变量 | 控制 | 控制 | 控制 | 控制 |
| 行业/时间 | 控制 | 控制 | 控制 | 控制 |
| Observations | 628 789 | 157 049 | 314 112 | 157 628 |
(二)进一步检验
2004年,政府正式出台了修订后的《最低工资规定》,之后最低工资制度在全国范围内广泛实施,最低工资政策的实施力度、范围、调整频次都进一步加大。根据蒋灵多和陆毅(2017)对中国1998—2007年地区月最低工资与企业月平均工资的研究发现,大部分时间里月最低工资标准的年增长速度快于企业月平均工资的年增长速度,特别是2004年《最低工资规定》颁布之后,最低工资标准以年平均14%的速率在增长。本文的样本信息也显示,企业平均工资水平在不断提高:1998年月平均工资低于月最低工资标准的企业约占到全部样本的20%,这一比例在2003年下降到了13%,而2007年该比例仅有8%左右。现有研究表明,最低工资制度的实施会显著提高企业的平均工资(Draca等,2011),尤其是那些平均工资水平低于最低工资标准的企业,在最低工资上升时,这些企业的反应最为敏感。因此,本文认为最低工资的上升会加大那些月平均工资水平低于最低工资标准的企业被市场淘汰的风险。基于此,本文参考Draca等(2011)的做法,借助2004年《最低工资规定》的推行实施“准自然实验”,利用双重差分的思想重新认识最低工资的上升是否会提高这部分企业的退出风险。双重差分模型设定如下:
| $ P(\mathop {exit}\nolimits_{icjt} = 1) = \varPhi (\mathop \alpha \nolimits_0 + \mathop \alpha \nolimits_1 treat \times post04 + \mathop \alpha \nolimits_2 treat + \beta \mathop X\nolimits_{icjt} + \gamma \mathop Z\nolimits_{ct} + \mathop \phi \nolimits_j + \mathop \theta \nolimits_t ) $ | (4) |
其中,α1是该部分估计的核心系数。实验组是2004年《最低工资规定》实行以前企业月平均工资低于最低工资标准的那部分企业,这部分企业的treat值设定为1;剩下的企业设定为对照组,treat取值为0。post04是最低工资政策冲击的时间,本文借鉴Lu等(2017)的处理方法,将2004年之前取值为0,2004年之后取值为1,而2004年当年取值为5/6。
表4给出了模型(4)的双重差分估计结果。列(1)中α1的系数显著为正,这说明相对于对照组,2004年以后实验组企业的退出风险明显上升。同时,本文分样本回归的结果还表明,2004年以后实验组中生产率低的企业的退出风险明显高于其他生产率水平的企业。
| 被解释变量 | (1) | (2) | (3) | (4) |
| 总样本 | tfp<25% | 25%≤tfp<75% | tfp≥75% | |
| treat×post04 | 2.784*** (0.107) |
3.080*** (0.198) |
2.811*** (0.161) |
2.420*** (0.222) |
| treat | −2.646*** (0.102) |
−2.838*** (0.188) |
−2.710*** (0.152) |
−2.336*** (0.211) |
| 企业/城市层面控制变量 | 控制 | 控制 | 控制 | 控制 |
| 行业/时间 | 控制 | 控制 | 控制 | 控制 |
| Observations | 628 789 | 157 049 | 314 112 | 157 628 |
(三)机制检验⑨
根据本文的研究思路,本文猜想在最低工资上升的压力下,技术创新可以在一定程度上降低企业被市场淘汰的风险,逼迫存活企业提高生产效率。为了进一步验证创造性破坏效应的存在,本文在模型(3)中引入了企业专利申请数与最低工资的交叉项,估计结果表明,无论总样本还是分样本,交叉项的系数均显著为负,这表明技术创新会显著降低因最低工资上升所引致的竞争淘汰效应。另外,对存活企业(exit=0)全要素生产率(LP法)及其增速的估计显示,⑩最低工资上升会显著提高存活企业的生产效率及其增长速度。该结论与本文的预期一致,即频繁调整的最低工资会加剧行业内企业的竞争。为了保持原有的竞争优势,避免被市场淘汰,在位企业会加大产品的研发创新,改进生产技术,从而提高自身的生产效率。综上所述,本文认为最低工资上升会倒逼生产率低的企业退出市场,而剩余企业为了在行业内生存下来必须加大产品的研发创新,以缓解由此带来的竞争淘汰压力。
五、结论与建议
最低工资制度的出台对就业、工资等的影响,在很长一段时间内得到了学界和政策制定者的广泛关注,但很少有人研究最低工资的调整会对产业升级产生怎样的影响。本文通过对现有文献的梳理,从理论和实证两个方面详细分析了最低工资标准的实施与不断调整是否会直接激励企业加大研发创新的力度,淘汰行业内低效率的企业,优化社会资源配置,推动产业升级,从而实现中国经济又好有快的发展。
政府出台最低工资制度的初衷是保障人民的基本生活,伴随着最低工资制度的不断完善与成熟,最低工资的实施监管力度越来越大,该政策对微观企业的影响也越来越明显。本文利用中国工业企业微观数据与企业专利申请数据、地区最低工资数据进行匹配后的综合数据库,从两个层面对最低工资上升引起的产业升级效应进行了验证。一方面,最低工资上升会激励企业创新而直接促进产业升级。通过对Heckman两阶段模型进行实证检验,初步结果发现最低工资上升不仅会显著刺激企业加大研发创新力度,增加企业的创新成果,而且还会提高企业的研发创新效率。这一结论不受创新指标、估计方法、子样本区间等变化的影响。另一方面,最低工资上升会提高企业的生产成本,挤压企业的利润空间,倒逼低生产率的企业退出市场,鼓励企业加大研发创新力度,从而间接实现产业的转型升级。通过构建企业退出指标,本文的Probit面板随机效应模型估计结果表明,最低工资上升确实会提高生产率低的企业被市场淘汰的风险。另外,针对2004年《最低工资规定》出台这一“准自然实验”,本文利用双重差分模型的估计结果进一步证实了上述结论。
本文的研究结论能够为政府进一步完善最低工资制度以及中国经济的结构转型提供有意义的解决思路。第一,最低工资标准的制定要综合考虑当地经济发展状况与产业结构等因素。随着经济发展水平的提高,政府需要逐步提高最低工资标准,但这一调整应当适度、稳定、可控,要本着实事求是、因地制宜的原则,致力于当地的产业发展现状,以及对未来发展的影响。对于依赖劳动密集型产业发展的地区,要注意从现有产业发展动力、潜力等维度进行分析,决定最低工资标准的调整幅度与频率;对于西部地区,最低工资的调整幅度不宜过高,频率不宜过快。第二,进一步完善最低工资制度,既有利于改善收入不平等状况,也有利于转变对出口导向型经济增长模式的依赖。在新一轮经济增速换挡的背景下,通过工资增长的收入分配政策来引导国内消费,进而拉动经济的增长。在以后的研究当中,我们将进一步探讨最低工资上升对生产率水平、资源配置和经济增长等方面的深远影响。
① 限于篇幅,这里没有汇报所有变量的描述性统计结果;有需要的读者可以向作者索取。
② 2011年之前,规模以上工业企业是指年主营业务收入在500万元及以上的法人工业企业;2011年之后(包括2011年),规模以上工业企业是指年主营业务收入在2 000万元及以上的法人工业企业。
③ 感谢匿名审稿人的宝贵意见。本文在参考Heckman(1979)研究的基础上,采用计量上最为常见的Heckman两阶段估计方法来解决样本回归可能存在的选择性偏差问题,该方法被广泛运用于国际贸易(盛丹等,2011)、技术创新(武力超等,2015)等领域。
④ 其中,地区专利申请总数是由该地区所有企业的专利申请数简单加总得到。
⑤ 受篇幅限制,本文在这里没有汇报Probit回归系数的边际效应值;有需要的读者可向作者索取。
⑥ 在这里,城市层面的控制变量将取滞后两期。
⑦ 限于篇幅,本文没有汇报模型的稳健性检验和异质性检验结果;有需要的读者可向作者索取。
⑧ 对于退出又进入的样本,即在数据库内表现为企业在某年消失而后又出现的情形,本文统一将这些企业视为存活企业。这很有可能是由企业规模变动导致的。若非如此,可能会高估企业的退出率。对于那些在统计年度内曾经改变过企业代码,而实际上并没有退出市场的企业,本文参照马光荣和李力行(2014)的方法,对样本进行了重新匹配。
⑨ 限于篇幅,本文没有汇报机制检验和存活企业的进一步估计结果;有需要的读者可向作者索取。
⑩ 全要素生产率的测算采用的是LP方法(Levinsohn和Petrin,2003)。
| [1] | 邸俊鹏, 韩清. 最低工资标准提升的收入效应研究[J]. 数量经济技术经济研究, 2015(7): 90–103. |
| [2] | 林炜. 企业创新激励: 来自中国劳动力成本上升的解释[J]. 管理世界, 2013(10): 95–105. |
| [3] | 孙楚仁, 田国强, 章韬. 最低工资标准与中国企业的出口行为[J]. 经济研究, 2013(2): 42–54. DOI:10.3969/j.issn.2095-0977.2013.02.013 |
| [4] | 王雷. 劳动力成本、就业保护与企业技术创新[J]. 中国人口科学, 2017(1): 71–80. |
| [5] | Aaronson D, Phelan B J. Wage shocks and the technological substitution of low-wage jobs[J]. The Economic Journal, 2017. DOI:10.1111/ecoj.12529 |
| [6] | Acemoglu D. When does labor scarcity encourage innovation?[J]. Journal of Political Economy, 2010, 118(6): 1037–1078. DOI:10.1086/658160 |
| [7] | David P A. Technical choice innovation and economic growth: Essays on american and british experience in the nineteenth century[M]. Cambridge: Cambridge University Press, 1975. |
| [8] | Draca M, Machin S, Van Reenen J. Minimum wages and firm profitability[J]. American Economic Journal: Applied Economics, 2011, 3(1): 129–151. DOI:10.1257/app.3.1.129 |
| [9] | Hicks J R. The theory of wages[M]. London: Macmillan, 1932. |
| [10] | Hu A G, Jefferson G H. A great wall of patents: What is behind China’s recent patent explosion?[J]. Journal of Development Economics, 2009, 90(1): 57–68. DOI:10.1016/j.jdeveco.2008.11.004 |
| [11] | Liu Q, Qiu L D. Intermediate input imports and innovations: Evidence from Chinese firms’ patent filings[J]. Journal of International Economics, 2016, 103: 166–183. DOI:10.1016/j.jinteco.2016.09.009 |
| [12] | Schumpeter J A. The theory of economic development: An inquiry into profits, capital, credit, interest, and the business cycle[M]. Piscataway, NJ: Transaction Publishers, 1934. |
| [13] | Van Reenen J. The creation and capture of rents: Wages and innovation in a panel of U. K. companies[J]. The Quarterly Journal of Economics, 1996, 111(1): 195–226. DOI:10.2307/2946662 |
| [14] | Webb S. The economic theory of a legal minimum wage[J]. Journal of Political Economy, 1912, 20(10): 973–998. DOI:10.1086/252125 |
 2018, Vol. 44
2018, Vol. 44




