文章信息
 | 财经研究 2018年44卷第10期 |
- 陈达飞, 邵宇, 杨小海,
- Chen Dafei, Shao Yu, Yang Xiaohai.
- 再平衡:去杠杆与稳增长——基于存量-流量一致模型的分析
- Rebalance: deleveraging and stabilizing economic growth — based on an analysis of the stock-flow consistent model
- 财经研究, 2018, 44(10): 4-23
- Journal of Finance and Economics, 2018, 44(10): 4-23.
-
文章历史
- 收稿日期:2017-09-08

2018第44卷第10期
2. 清华大学 国家金融研究院,北京 100083
2. National Institute of Financial Research,Tsinghua University,Beijing 100083,China
一、引 言
面对金融危机,债务驱动型经济增长模式成为中国应对挑战的方略。首先是2009—2010年的“4万亿”计划,传统银行机构天文量级的信贷投放使M2存量和M2/GDP快速增加。2010年以后,中国贸易顺差急剧收缩,传统货币投放渠道受阻,央行开始下调存款准备金率,以对冲流动性收缩。2009—2013年的强刺激不仅降低了资金利用效率,还加剧了金融系统的脆弱性。2013年6月,银行业的“钱荒”事件是强刺激政策后遗症的集中体现,开始引起监管部门的注意。而“加杠杆”进程并没有因此停止。巨大的息差激励银行进行监管套利,中国式影子银行从无到有,由弱到强,资金脱媒拉长了资金链条,也使金融杠杆越来越高。资金在金融机构间“空转”不仅提高了金融系统性风险,也使金融服务实体经济的效率下降。因此,2015年底,中央将“去杠杆”列为供给侧结构性改革的五大任务之一,突出了“去杠杆”任务的紧迫性和艰巨性。从2016年10月开始,金融整顿成为经济政策的主要议题,金融去杠杆也成为去杠杆的手段。
中国的杠杆既有总量问题,又有结构问题,而且结构问题才是核心。据BIS的数据,截至2017年6月,中国宏观杠杆率(总债务/GDP)为255.9%,高于新兴市场的平均水平190%,也高于美国的249.5%。从结构来看,中国非金融企业部门的杠杆率为163.4%,在主要经济体中位列第一,远高于欧元区的103.4%、日本的102.1%和美国的73.3%,更高于印度等新兴市场经济体。中国居民部门和政府部门的杠杆率分别为46.8%和45.7%,都处于较低水平,但居民部门的杠杆增速较快。因此,宏观杠杆高企与结构失衡都是严峻的挑战。
Fisher(1933)在探讨经济周期问题时认为,繁荣与萧条周期性更替的主要扰动因素是过度负债和通缩,它不仅增加了金融风险,也拖累了实体经济。但他同时也强调,债务−通缩循环是可以通过再通胀和一些稳定政策来预防的。2017年中央经济工作会议强调,未来几年“防范重大风险”是“三大攻坚战”之一,而杠杆问题是连接实体部门与金融部门的“枢纽”。
去杠杆并非孤立,它与经济增长密切相关。在中国特有的经济增长模式和金融市场结构中,债务杠杆的累积是2008年以来各项稳增长政策的结果。简单逆向思维认为,去杠杆一定伴随着经济增速的下行。比如,20世纪日本等国家的经验表明,如果去杠杆的方式不当,经济将会陷入“资产负债表衰退”(辜朝明,2003)。中国能否避免重演日本的历史,关键在于如何选择去杠杆的措施,以应对不断出现的国内外挑战。辜朝明(2003)的研究表明,在债务引发的“资产负债表衰退”过程中,行为人的目标函数转变为“债务最小化”,而非主流经济学所设定的效用或利润最大化。金融危机以来,主流宏观模型受到多方面的批评,除了关键假设脱离现实,更重要的是忽视了货币、资产价格与金融市场的作用,从而使其解释世界的能力有所下降。宏观模型实际上是一种理解世界的方法论。与主流方法论不同,本文利用后凯恩斯学派的存量—流量一致(Stock-Flow Consistent,SFC)模型,对包括实体和金融在内的宏观经济部门进行建模,研究中国如何平衡去杠杆与稳增长的问题。
本文通过构建五部门SFC模型,考察了货币政策、财政政策以及公司微观政策对去杠杆与稳增长的影响。结果表明,紧缩性货币政策,特别是提高基准利率,短期内会增加企业的债务利息负担,迫使其加杠杆,同时还会减少企业投资,对GDP增速产生较大的负面影响;提高政府支出增速和减税都能在一定程度上降低企业部门杠杆,但减税能够更好地平衡去杠杆与稳增长;企业提高内源融资比例不仅有助于自身降杠杆,还会带动政府和居民降杠杆,对宏观经济的负面影响也相对温和。
本文的结构安排如下:第二部分为文献综述,梳理了国内外关于去杠杆的影响及政策措施效果的文献;第三部分基于宏观各部门的资产负债—存量表和交易—资金流量表,构建了一个封闭的五部门SFC模型,并对参数进行了校准;第四部分模拟了不同的政策及政策组合对企业、居民和政府去杠杆的效应,并考察了其对国民经济及其构成以及就业状况的影响;最后总结全文。
二、文献综述
债务累积与信贷泡沫和金融监管放松密切相关。Rainhart和Rogoff(2009)认为,“我们关于危机的阐述有一个共同的话题,那就是过度举债”。债务危机的一个表现就是信贷膨胀,如Kindleberger和Aliber(2001)开门见山所说,“每一轮金融危机都伴随着信贷泡沫”。Minsky(1986)阐述了金融不稳定的内生机制,认为在经济上升周期,人们基于乐观的预期会过度借债,但当银行收缩信贷时,泡沫就会破裂。Edison等(2000)构建理论模型考察了亚洲金融危机期间泰国和印度尼西亚等国家金融杠杆与资产泡沫的问题,认为金融自由化和监管缺位是资产泡沫愈演愈烈的重要原因。
如何去杠杆是研究的落脚点。Ueda(2012)对比了房地产泡沫破裂后日本央行和美联储在去杠杆过程中的货币政策,认为美联储的快速应对是美国经济快速复苏的关键原因。Ueda(2012)基于日本的案例研究认为,如果由市场自发地去杠杆,则可能出现信贷危机和投降式抛售,使得资产价格进一步下跌,杠杆率不降反升。Eggertsson和Krugman(2012)从理论上分析了在弹性与粘性价格下,政府通过扩张资产负债表来缓解信贷约束的去杠杆进程对经济产生的负面影响。他们强调了不同部门债务的异质性,认为债务结构才是问题的核心。但Palley(2010)认为,政府通过债务融资的方式进行需求管理意味着赤字货币化,从而会导致通货膨胀。他认为经济增长还是应回归到生产率驱动模式上。另外,Edison等(2000)认为金融冻结、注资和兼并重组是资产价格泡沫破裂后缓解金融动荡的有效措施。整体而言,关于如何去杠杆,大多数学者还是支持政府逆周期的需求管理政策;但大量文献都是考察危机发生后的被动去杠杆过程,与中国当前的情况有些差异。
国内目前关于去杠杆主题的文献主要分为三类:首先是描述中国杠杆的总体与结构性特征。例如,钟宁桦等(2016)分析了中国400万个工业企业1998—2013年的面板数据,发现样本期内企业杠杆率整体上呈现下降趋势,但下降幅度因企业的产权属性、规模和空间布局等而存在显著差异。谭小芬(2016)基于中国2 500家非金融上市企业2006—2015年数据,发现国有企业与私营企业杠杆的剪刀差正在逐步扩大(前者高,后者低)。
其次,对于企业债务杠杆率的决定因素,现有文献从宏观与微观两个角度展开分析。在宏观方面,马建堂等(2016)基于资产负债表数据的分析认为,中国企业债务杠杆快速增加主要源于融资方式单一、资金利用率低以及产能过剩行业对信贷资金的挤占。钟宁桦等(2016)检验了国有企业和私营企业债务杠杆率的决定因素,发现信贷资源配置对于国有企业表现出显著的非市场化原则,且在金融危机后,国有僵尸企业的贷款可得性大大提高。在微观方面,肖泽忠和邹宏(2008)研究了中国上市公司资本结构的影响因素,发现债务杠杆与企业规模和有形资产率成正比,与成长机会和获利能力成反比。
最后,在政策研究方面,谭海鸣等(2016)在CGE框架下探讨了金融杠杆与经济增长、人口迁移与出生率之间的关系,认为适度可控的杠杆有利于经济增长。胡志鹏(2014)在DSGE框架下考察了去杠杆与稳增长双重目标下的央行货币政策最优选择,认为单纯依靠货币政策去杠杆是不够的。但模型仅仅考虑了数量型工具,且将货币供应量视为外生,而当前央行思路正在向价格型调控转变。吕炜等(2016)基于DSGE模型考察了财政政策在去杠杆方面的效应,认为增加政府投资建设性支出会显著提高国有企业的杠杆率,而增加保障性支出则会相对提高民营企业的杠杆率,同时国企杠杆率温和上升,因此在当前国企高杠杆的背景下,增加保障性支出要优于增加投资性支出。
去杠杆会加重经济下行的压力,并可能引发长期萧条。Koo (2008)从资产负债表衰退角度理解“大萧条”和去杠杆,认为日本“失去的二十年”和美国次贷危机都可以从这个视角来诠释。Fukao和Kwon (2006)认为,日本的长期萧条源于僵尸企业的存在导致银行信贷配置无效率,很多利润较高的企业不得不退出。
已有文献大多基于DSGE模型或CGE模型来考察各种外生的政策冲击对去杠杆的效应及其传导机制。但在金融危机后,以DSGE模型为代表的一般均衡模型对现实的偏离及其可靠性备受争议(Solow,2008;Bezemer,2010)。比如,它并未考虑“肥尾”现象,将金融危机等小概率事件排除在模型之外,从而容易犯“第二类错误”。此外,Bezemer(2011)总结了12篇正确预测金融危机论文的建模方法,并将其与主流的DSGE模型进行了对比,认为这些模型均强调金融资产、负债、资金流量表和资产负债表约束、不确定性与非最优化行为,而对这些特征的描述在金融危机以前的DSGE模型中都比较缺乏。
Minsky(1992)认为,宏观经济的运行可以用一系列相互联系的资产负债表与现金流量表来描述。该方法的一个主要代表是基于资产负债表(Balance Sheet-Stock Table,BSST)和现金流量表(Transaction-Flow Table,TFT)约束的存量−流量一致(Stock-Flow Consistent,SFC)模型(Godley,1996;Godley和Lavoie,2007)。主流方法将宏观模型建立在理性行为人最优化选择的基础上,将货币看作一层“面纱”,将商业银行仅看作借贷的媒介,或将金融体系的运作排除在模型之外。而SFC方法从“环流”的视角看经济运行,将货币看作交易媒介与记账手段,将商业银行看作信贷创造的主体,区分了不同的金融资产,采用部门分析法将金融体系与实体经济纳入统一的框架下研究,而且没有理性人和信息约束。SFC模型在国际上已被广泛用于分析金融危机、财政和货币政策、流动性偏好、产能利用率和影子银行等问题,而在中国,这方面的研究相对欠缺。①本文旨在构建一个基准模型,分析各种政策的去杠杆(或移杠杆)和稳增长效应。
三、SFC模型构建与参数设定
本文基于五部门国民账户体系,构建一个完整的SFC模型。金融资产包括基础货币(现金和准备金)、存款、贷款、国库券、长期国债、股票等,非金融资产包括物质资本与存货。建模步骤如下:(1)构建五部门的BSST;(2)基于BSST构建TFT;(3)基于BSST和TFT,构建由BSST约束、TFT约束和行为方程构成的联立方程模型;(4)校准参数,设定变量初始值,并求稳态解;(5)通过改变参数或外生变量值,做脉冲响应分析,考察政策或政策组合的去杠杆和稳增长效应。
(一)资产负债−存量表
表1为五部门合并资产负债−存量表。“+”表示资产项,“−”表示负债项;小写下标表示部门,大写下标表示相应的科目。②除了实物资产(物质资本与存货)外,各行之和均为0,因为金融资产与金融负债是对应的。例如,贷款是商业银行的资产,同时是居民与企业的负债,在数量上相等。同时,各部门的资产负债表是平衡的,所以各列之和为0。③对于各项金融资产,以带下标的方式标出需求方。以基础货币为例,家庭的基础现金需求为MBh,商业银行的准备金需求为MBb,央行的基础货币总供给为MB。各部门均满足会计恒等式:资产=负债+净资产。
表1反映了各部门的以下行为:(1)家庭对5项资产(现金MBh、存款Dh、国库券Bh、长期国债PBLBLh和股票PEEh)④进行组合管理,并通过贷款Lh为消费(或投资组合)融资,净资产为Vh;(2)企业拥有物质资本K,并通过贷款Lf和发行股票PEE为投资行为(包括存货投资IN)融资,净资产为Vf;(3)商业银行吸收存款D,发放贷款L,并向央行缴纳准备金MBb,同时购买数量为Bb的国库券;(4)政府通过发行国库券B和长期国债PBLBL来弥补财政赤字,净资产为Vg;(5)央行吸收MB,并购买数量为Bcb的国库券。
| 家庭 | 企业 | 商业银行 | 政府 | 中央银行 | 总计 | |
| 1. 物质资本 | +K | +K | ||||
| 2. 存货 | +IN | +IN | ||||
| 3. 基础货币 | +MBh | +MBb | −MB | 0 | ||
| 4. 存款 | +Dh | −D | 0 | |||
| 5. 贷款 | −Lh | −Lf | +L | 0 | ||
| 6. 国库券 | +Bh | +Bb | −B | +Bcb | 0 | |
| 7. 长期国债 | +PBLBLh | −PBLBL | 0 | |||
| 8. 股票 | +PEEh | −PEE | 0 | |||
| 9. 净资产 | −Vh | −Vf | 0 | −Vg | 0 | −(K+IN) |
| 10. 总计 | 0 | 0 | 0 | 0 | 0 | 0 |
(二)交易−流量表
表2构建了各部门在一段时间内(通常指一年)的资金(交易)流量表。与表1不同的是,“+”表示资金流入,“−”表示资金流出。表2可分为三部分:1—3行表示生产循环,决定总产出;4—12行表示金融循环,主要记录要素报酬和利润分配;13—18行表示存量变动所引起的价值重估。
生产循环以企业为核心。在封闭经济体中,总产出由消费C、投资
| 家庭 | 企业 | 商业银行 | 政府 | 中央银行 | 总计 | ||||
| 资本账户 | 经常账户 | 资本账户 | 经常账户 | 资本账户 | 经常账户 | ||||
| 1. 消费 | −C | +C | 0 | ||||||
| 2. 投资 | +(I+ΔIN) | −(I+ΔIN) | 0 | ||||||
| 3. 政府支出 | +G | −G | 0 | ||||||
| 4. 税收 | −T | +T | 0 | ||||||
| 5. 工资 | +WB | −WB | 0 | ||||||
| 6. 库存融资成本 |
|
|
0 | ||||||
| 7. 存款利息 |
|
|
0 | ||||||
| 8. 贷款利息 |
|
|
|
0 | |||||
| 9. 国库券利息 |
|
|
|
|
0 | ||||
| 10. 长期国债利息 |
|
|
0 | ||||||
| 11. 企业利润 | +FDf | −Ff | +REf | 0 | |||||
| 12. 银行利润 | +Fb | −Fb | +Fcb | −Fcb | 0 | ||||
| 13. Δ 基础货币 | −ΔMBh | −ΔMBb | +ΔMBcb | 0 | |||||
| 14. Δ 存款 | −ΔDh | +ΔD | 0 | ||||||
| 15. Δ 贷款 | +ΔLh | +ΔLf | −ΔL | 0 | |||||
| 16. Δ 国库券 | −ΔBh | −ΔBb | +ΔB | −ΔBcb | 0 | ||||
| 17. Δ 长期国债 | −ΔBLhPBL | +ΔBLPBL | 0 | ||||||
| 18. Δ 股票 | −ΔEhPE | +ΔEhPE | 0 | ||||||
| 19. 总计 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
价值重估部分与表1资产负债−存量表中金融资产(负债)是一一对应的。需要强调的是,第17行记录长期国债存量变动所引起的价值重估,第18行记录股票份额变动所引起的存量变化。这里应与价格变化所引起的价值重估区别开来,若考虑价格涨跌的存量变化效应,前者应表示为ΔPBLBLh-1,后者为ΔPEEh-1,即当期价格变化与上期期末存量的乘积。因此,由价格变化与资产组合调整所引起的价值重估总量为两者之和,以长期国债为例,
表1是表2的基础,表1与表2共同构成了SFC模型联立方程组的依据。由以上描述与说明可以看出,表1与表2共同构建了一个存量与流量一致、金融循环与产业循环互联的动态国民账户体系。
(三)SFC模型构建
SFC模型中的方程主要分为约束方程和行为方程两类。下文将分部门阐述方程的构建及其含义。除了利率变量外,小写字母表示真实值,大写字母表示名义值,上标e表示期望值,上标T表示目标值,下标-1表示前期值。
1. 企业
(1)生产与投资
企业主要从事生产与投资活动,表3描述了总产出与投资决定方程及其派生的方程。方程1表示真实产出y等于预期真实总销售额与预期存货增量
| 1.
|
10.
|
| 2.
|
11.
|
| 3.
|
12.
|
| 4.
|
13.
|
| 5.
|
14.
|
| 6.
|
15.
|
| 7.
|
16.
|
| 8.
|
17.
|
| 9.
|
18.
|
(2)工资与就业
表4描述了工资与就业决定方程。方程19定义真实目标工资水平与劳动生产率pr成正比,与就业率ER存在非线性关系(Tobin,1995),即就业率在区间[1-Bot,1+Top]内不影响工资。方程20为就业率,等于前期就业人数N−1与劳动总人数之比。方程21定义了劳动生产率的变动情况,设它以grpr的速度增加。方程22为名义工资变动方程,定义当期工资等于上期工资加上当期目标工资与上期工资之差的一个比例。方程23定义总工资等于就业人数与工资率的乘积。方程24为就业人数变动(N−N−1)方程,等于当期目标就业人数与上期就业人数之差的一个固定比例。方程25定义目标就业人数为真实总产出与劳动生产率之比。
| 19.
|
| 20.
|
| 21.
|
| 22.
|
| 23.
|
| 24.
|
| 25.
|
(3)定价
表5描述了企业定价行为。方程26为典型的后凯恩斯学派定价方程,设定为一般历史单位成本NHUC上的一个加成φ。方程27设定NHUC为当期与前期一般单位成本NUC的加权平均值,其中σN为外生的存货销售比。方程28定义NUC为名义工资率与劳动生产率之比。
| 26.
|
| 27.
|
| 28.
|
(4)利润及分配
表6描述了企业的利润及分配行为。基于企业的经常项目约束,方程29为企业的利润方程,利润Ff等于总销售额与存货投资增量之和再减去工资和贷款利息。方程30定义了企业贷款需求Lfd的变动情况,新增贷款(Lfd−Lfd-1)等于总投资(I+ΔIN)减去留存收益REf与新增股票融资总额ΔEsPE,这符合融资优序理论。方程31设定股票红利为上期利润的一个固定比例φD。方程32中的REf为扣除股利后的利润,公司可以减少派息以增加内源融资比例。方程33表示目标新增股票融资总额
| 29.
|
34.
|
| 30.
|
35.
|
| 31.
|
36.
|
| 32.
|
37.
|
| 33.
|
非金融企业是实体经济的依托,方程1—方程37完整描述了企业的生产投资等行为,可以研究总产出的决定、企业的融资决策、工资及就业的决定等问题。其中,企业的投资与融资决策是实体经济与金融市场联系的纽带,工资和就业又与居民部门密切相关。下面介绍居民部门的行为方程和约束方程。
2. 居民
(1)收入与消费
在该经济体中,居民的活动主要表现在收入与消费、组合投资与融资等方面,表7定义了居民的收入与消费行为。方程38为居民名义收入总额YP,等于工资总额WB、股利FDf、银行利润Fb和各项利息收入(储蓄存款Dhd−1、国库券Bhd−1和长期国债BLd−1)之和。方程39为居民可支配收入,等于YP减去税收T和居民贷款利息rL−1Lhd−1后的余额。方程40定义税收为YP的固定比例θ。方程41为Haig-Simons口径的可支配收入(Haig,1921;Simons,1938),它考虑了资本利得CG的影响。方程42定义CG等于股票与长期国债价格变动的损益。方程43定义名义财富增量(V−V−1)为YDHS与消费C之差。方程44为经价格调整的真实财富水平。方程45设定名义消费为真实消费c与物价水平的乘积。方程46设定了居民真实消费函数,它与居民预期可支配的真实收入ydre、真实净贷款nl以及上期的真实财富存量v−1正相关。方程47为nl与名义净贷款NL的关系。方程48定义NL为YP的一个比例
| 38.
|
|
| 39.
|
47.
|
| 40.
|
48.
|
| 41.
|
49.
|
| 42.
|
50.
|
| 43.
|
51.
|
| 44.
|
52.
|
| 45.
|
53.
|
| 46.
|
54.
|
(2)资产组合选择⑦
表8描述了居民的资产组合选择行为。方程55−方程58A为托宾式的资产组合方程,各项资产的需求与自身收益率成正比,与其他资产的收益率成反比。以方程55为例,居民的国库券需求与国库券利率rB成正比,与存款利率rD、股息率rDY和长期国债利率rBL成反比。最后一项刻画居民可支配收入的变化对其金融资产配置的影响。方程58表明居民存款需求为财富分配的余项。居民财富分配的基数为其可支配的资金VFA,方程59揭示了它的构成,即财富水平V加上居民贷款减去现金需求MBhd。方程60设定居民的现金需求为名义消费额的一个外生比例λc。
| 55.
|
| 56.
|
| 57.
|
| 58A.
|
| 58.
|
| 59.
|
| 60.
|
3. 政府:支出、赤字与债务
表9描述了政府支出、财政赤字与政府债务。方程61为名义政府支出总额,等于实际支出与价格水平的乘积。方程62设定实际政府支出g以外生设定的增长率grg增长。方程63为政府财政赤字GFD方程,来源于政府的资金流量表约束,它等于政府购买与债务利息之和减去税收收入和央行利润的转移。方程64刻画了国库券增量(Bs−Bs−1),等于财政赤字减去长期国债的融资额。方程65表明国库券的发行量BLs等于居民部门的债券需求BLhd。方程66为政府债务总额,等于短期的国库券加上长期国债。方程67定义长期国债价格为收益率的倒数。方程68定义了政府的利息负担,等于利息支出与总收入(税收T加上央行利润Fcb)之比。
| 61. G=g×P | 65. BLs=BLhd |
| 62. g=g-1(1+grg) | 66. GD=Bs+BLsPBL |
| 63. GFD=G+rB-1Bs-1+rBL-1BLs-1−T−Fcb | 67.
|
| 64. Bs=Bs-1+GFD−ΔBLs-1PBL | 68.
|
4. 中央银行:基准利率与货币发行
表10描述了央行的基本方程。在模型中,我们对央行的行为进行了一定的简化,其主要制定基准利率并作为国库券的剩余购买者;在基础货币供给方面,央行制定准备金率。方程69为央行购买的国库券的利息收入,即央行利润Fcb,模型假设央行利润是政府收入的一部分。方程70表明央行购买的国库券是居民与银行购买后余下的部分。方程71为基础货币供求恒等式,MBhd和MBbd分别为居民的现金需求与商业银行的准备金需求,由方程60和方程77决定。方程72为央行的资产负债表约束。方程73设定国库券利率rB为央行决定的常数
| 69. Fcb=rB-1Bcbd-1 | 72. Bcbd=MBs |
| 70. Bcbd=Bs−Bhd−Bbd | 73.
|
| 71. MBs=MBhd+MBbd | 74. rBL=rB+addBL |
5. 商业银行:存贷款利率及利润
表11描述了商业银行的存贷款利率决定方程及利润,在描述居民与企业行为时其实反映了商业银行的存贷款决策,所以表11只是对其进行补充。基于商业银行经常账户约束,方程75描述了商业银行的利润Fb,等于贷款利息与国库券利息之和减去存款利息。方程76为商业银行的资产负债约束,即商业银行的国库券购买额等于存款总额与贷款总额(Lfd+Lhd)、准备金需求MBbd之差。方程77设定商业银行的准备金需求MBbd为存款的固定比率ρ。方程78为存款的供求均衡方程,也可以看作货币供求均衡,这是典型的后凯恩斯视角下的货币供给方程。即货币供给决定于货币需求,而货币需求又取决于储户的资产组合选择行为。因此,货币供给是内生的,而非央行控制的外生变量。方程79设定存款利率为外生设定的常数
| 75. Fb=rL-1(Lfd-1+Lhd-1)+rB-1Bbd-1−rD-1Ds-1 | 78. Ds=Dhd |
| 76. Bbd=Ds−Lfd−Lhd−MBbd | 79.
|
| 77. MBbd=ρDs | 80. rL=rD+addL |
方程1—方程80组成的联立方程体系完整描述了封闭经济条件下一国宏观经济五部门的行为与约束。可以看出,部门内与部门间都是紧密相连的。用局部均衡与比较静态分析方法观察宏观经济的运行往往顾此失彼,而SFC模型恰恰能克服这种弊端。以上方程的构建运用了一个技巧,即一旦出现了内生变量,紧接着就对其进行定义,环环相扣,防止出现遗漏而使联立方程体系难以识别。
(四)参数设定与稳态解
在SFC模型中,参数设定一般有估计和校准两种方法。估计法基于时间序列数据对参数进行估计。以利维(Levy)研究所为代表的模型被称为完全实证模型(Fully empirical models),Godley和Zezza(1986)最早采用该方法,构建了一个简化的SFC模型,以丹麦为例进行了模拟。该方法的问题在于,预测的基本前提是参数保持不变,而这正是卢卡斯批判的主要内容。与之不同,利默里克(Limerick)模型(Kinsella和Tiou-Tagba Aliti,2012)仅基于已有的存量数据对关键方程的参数进行估计,其他参数则基于校准得到。该模型的主要用途并非预测,而是对历史进行模拟,如模拟某项政策的实施效果等。
整体而言,估计法比较复杂,且模型估计误差较大,因而使用相对较少,大多数文章基于特征事实或经验法则对参数进行校准。校准的一个优点在于方程设定方面的弹性,特别是对于SFC模型这样庞大的体系,校准法更具可操作性,可根据研究问题设定行为方程。本文基于变量的时间序列数据对参数进行校准,因数据缺失而无法测算的参数则参考国内外已有文献(见附表1)。变量初始值选定为2016年初值。
SFC模型的求解有两种途径。对于相对简单的模型,可以求得解析解,并通过比较静态分析来研究变量的动态特征和相互关系,或者通过代入参数与变量初始值,获得稳态解。为了获得解析解,要求构建简化的模型,但这样做必须省略某些现实特征,有损模型的完整性。对于相对复杂的模型,一般的做法是利用计算机模拟求得稳态解。本文的模型比较复杂,因而直接利用计算机模拟求得稳态解,并以此为参照系,⑧通过重新设定单个或多个参数来考察模型的脉冲响应。
四、模拟分析⑨
下文将对去杠杆的各项政策(或政策组合)进行模拟,考察其去杠杆和稳增长效应。针对中国杠杆总水平较高与结构差异性较大的特征,一方面应当去杠杆,因为高杠杆会挤压企业利润并增加系统性风险;另一方面可以移杠杆,将地方政府和非金融企业的过高杠杆向中央政府与居民部门转移,这也正是中国采取债务置换和债转股的逻辑。
(一)货币政策
金融危机以来,中国企业的加杠杆进程伴随着货币政策的宽松,那么紧缩货币是否可以去杠杆?目前在这个问题上还存在较大的分歧。支持方认为中国企业债务主要表现为银行信贷,去杠杆就要收缩信贷。但也有持相反意见的,谭小芬(2016)认为货币政策的杠杆效应存在显著的不对称性,货币政策宽松有利于企业加杠杆,但是在债务存量高企时,紧缩货币将导致利息上升,从而加重企业负担。按照明斯基金融不稳定假说对融资的分类,这将促使企业由对冲融资转向投机融资或庞氏融资,企业的杠杆率会越来越高,使得金融体系更加不稳定。另外,留存收益减少会降低内源融资的可获得性,且企业上市和股权融资存在严格限制,因此企业更加依赖债务融资,导致杠杆率上升,这与融资优序理论⑩是一致的。
图1(a)—图1(c) 显示了紧缩性货币政策(准备金率与基准利率同时上升1个百分点)对企业、居民和政府的利息负担与债务杠杆的影响。如图1(a) 所示,紧缩性货币政策将大幅增加企业的利息负担,最高达到稳态时的2.2倍。企业将举借新的贷款支付利息,从而导致企业债务与GDP比率及债务与权益比率分别上升至稳态时的1.4倍和1.2倍。整个期限内企业的债务杠杆率维持在稳态之上。居民部门的情形略有不同,如图1(b) 所示,贷款利率上升导致居民部门的利息负担迅速增加,但次年开始逐步下降。其原因在于,贷款是利率的减函数,储蓄是利率的增函数,利率上升促使居民增加储蓄、减少贷款,所以居民的杠杆水平(债务/净财富)在冲击发生时小幅下降,随后小幅反弹到1.05倍的位置,2020年即开始了真实的去杠杆进程。政府利息负担与债务杠杆的表现与企业一致,如图1(c) 所示,由于债券利率上升,政府的利息负担迅速增加到稳态时的1.3—1.4倍,政府赤字增加,通过发行新债来偿还旧债利息。政府债务增加使其杠杆率也稳步上升,于2033年达到最高值1.13。⑪综合而言,在去杠杆方面,紧缩性货币政策将会使企业和政府的杠杆不降反升,同时也会增加居民的利息负担。
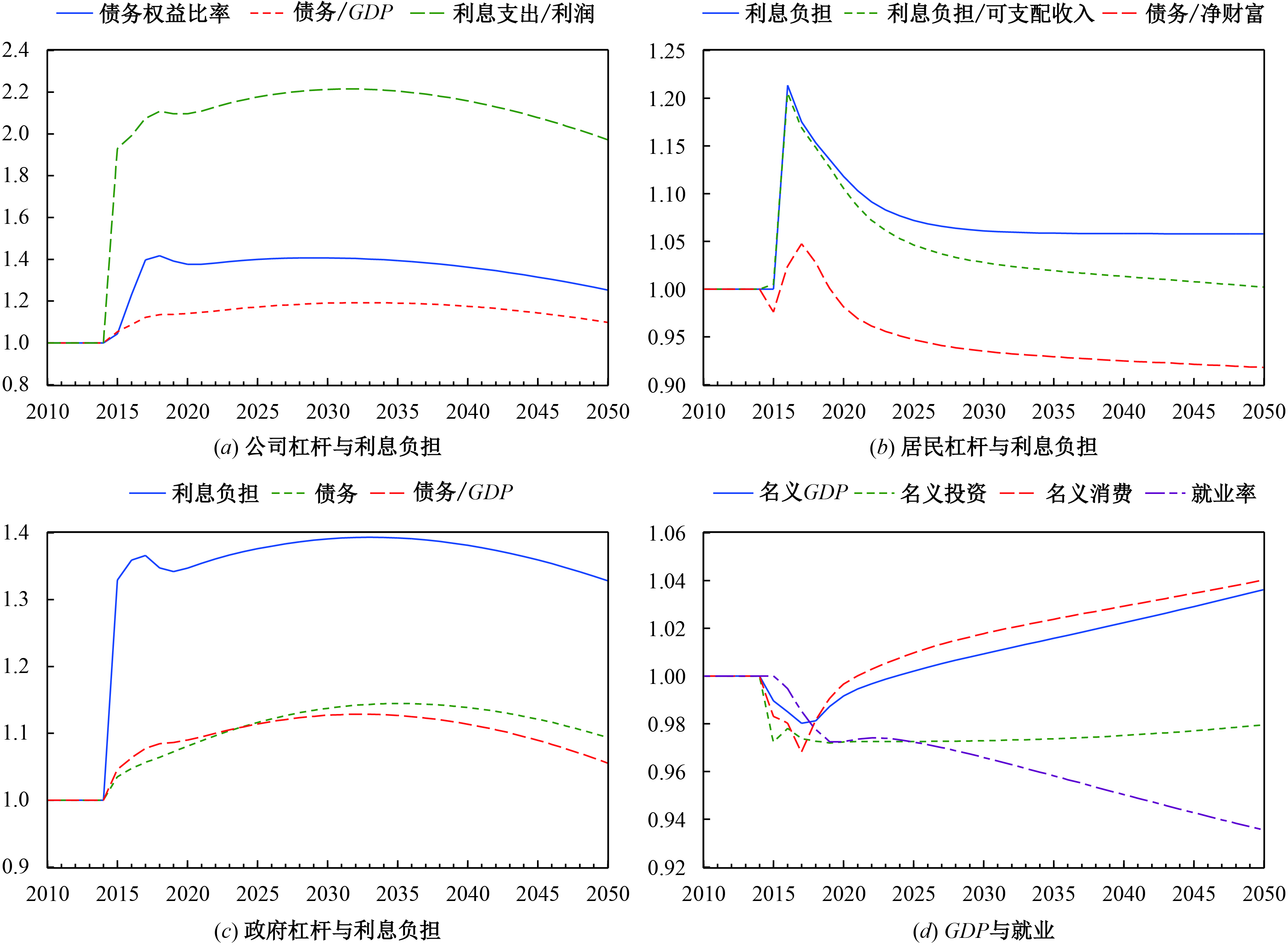
|
| 图 1 紧缩性货币政策对各部门杠杆与宏观经济的影响 |
紧缩性货币政策对宏观经济的影响如图1(d) 所示,相对于稳态时,名义GDP先逐渐下降,最低时为2017年的0.98,随后逐渐上升,在2023年恢复到冲击前的水平。名义GDP的下降源于消费和投资的双双下降,随后的上升主要是因为消费稳步增加和企业投资企稳。图1(d) 还显示,由于企业投资成本上升,就业水平逐步下降。可见,紧缩性货币政策对经济增长的负面效应是相对温和的。
(二)财政政策
图2为政府支出增速提高1个百分点的脉冲响应图。图2(a) 显示,企业的利息负担与债务杠杆同步下跌,到2050年下降到稳态时的34%。其原因在于,政府购买是企业收入的一部分,政府购买增加会提升企业的利润,从而增加内部融资来源,减少其贷款需求。图2(b) 显示,居民部门的利息负担与稳态时基本持平,杠杆率小幅下降,而利息负担与可支配收入的比值稳步下降,2050年降到了82.2%(这主要源于居民收入的增加,一方面,企业扣除留存收益后的股票红利增加;另一方面,就业率提高,如图2(d) 所示)。图2(c) 刻画了政府的情形,出乎意料的是,政府增加支出反而降低了债务水平和利息负担,这与模型设置有关。由方程63可知,政府赤字与支出成正比,与税收T和央行利润Fcb成反比。由于总支出的增加幅度小于收入的增加幅度(如附图1所示),政府赤字和债务存量反而会减少。图2(d) 显示了财政政策的刺激作用,就业、投资、消费和名义GDP都缓慢增加。
扩张性财政政策还可以通过减税来实施,图3为个人所得税率下降1个百分点的脉冲响应图。⑫图3(a) 显示,企业的利息负担与债务杠杆同步下降,原因在于居民的可支配收入增加带来了消费需求,改善了企业的盈利状况。居民部门呈现出分化情形,如图3(b) 所示,债务与财富比率小幅增加,最高上升0.6%,随后稳定在1.002的水平(原因在于居民的净贷款需求为可支配收入的增函数)。利息负担相对于稳态时小幅下降,最低时下降了1.3%,随后收敛到稳态水平。由于税收的减少对可支配收入的影响更直接,利息负担与可支配收入的比值下降较多,最多降低了4%,且稳定在96.8%的水平。图3(c) 为政府的脉冲响应图,政府减税减少了其收入,一开始会增加利息负担,但由于企业和居民的资产负债表改善,且如图3(d) 所示,消费和投资增加带动了名义GDP上升(政府支出下降,使得GDP上升的幅度小于消费增加的幅度),就业率也有所提高,因此政府税收在中长期反而会增加,赤字减少,从而债务存量与杠杆水平降低。可见,减税能达到去杠杆与稳增长的双重效果。
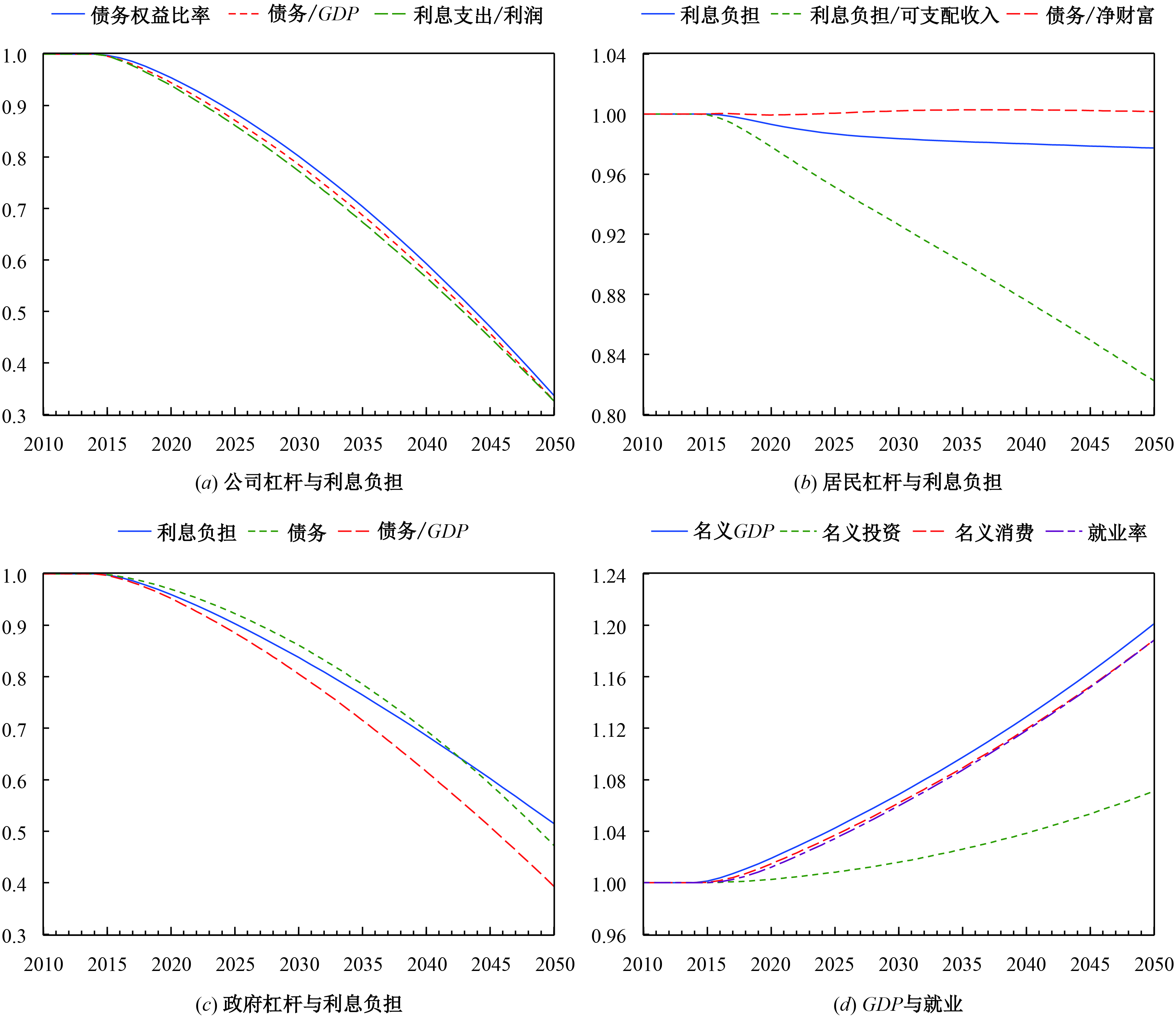
|
| 图 2 提高政府支出增速对各部门杠杆与宏观经济的影响 |
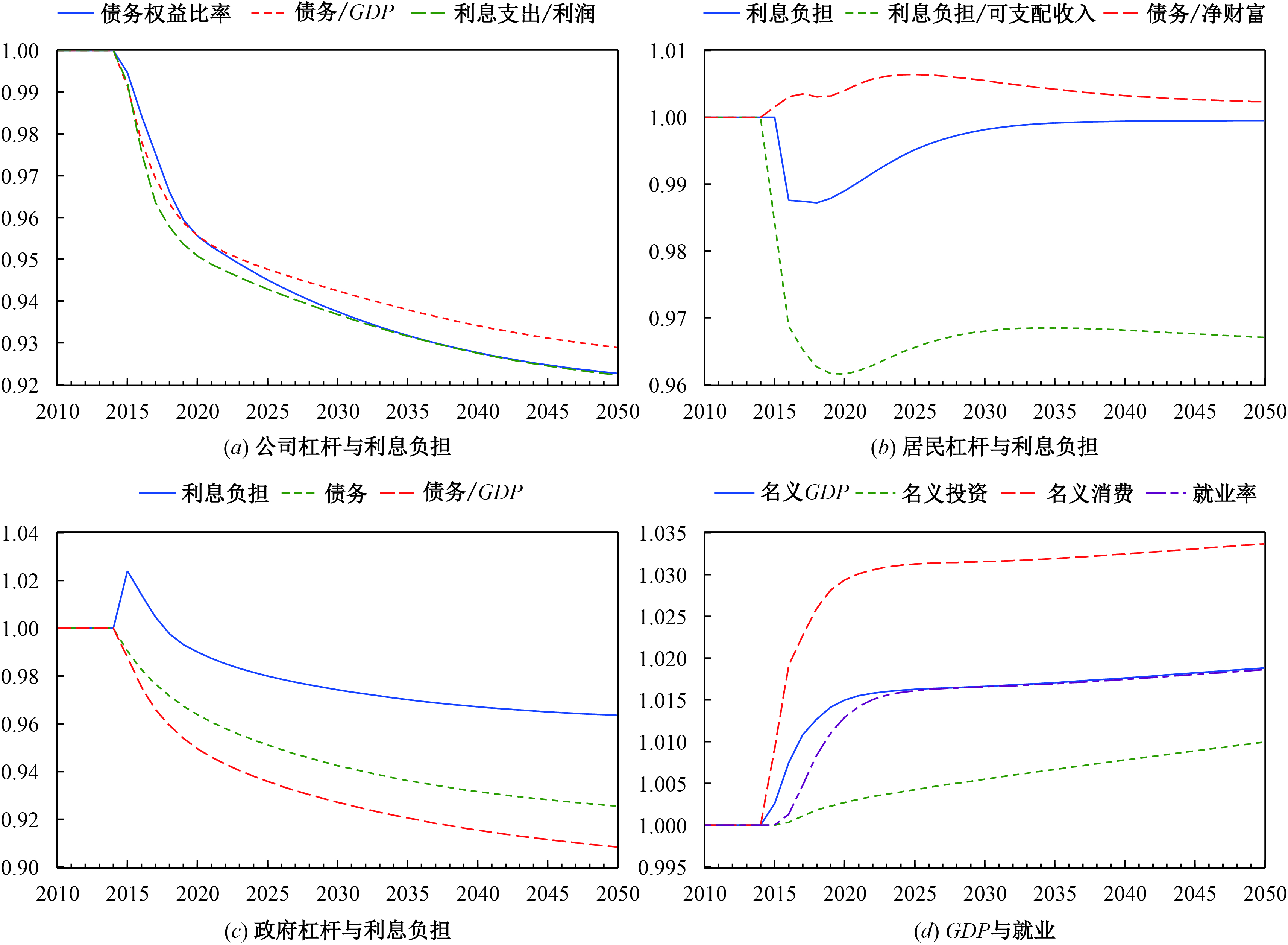
|
| 图 3 减税对各部门杠杆与宏观经济的影响 |
(三)股权融资
对中国而言,一个基本共识是,股权融资有助于减弱企业对银行贷款的依赖,是解决融资难、融资贵问题的可选途径。在本文的模型中,企业遵循融资优序理论,在留存收益和股票融资仍不能满足投资需求时才会向银行贷款。为了模拟股权融资的去杠杆效应,可以提高股权融资占比,即降低内源融资占比
图4为增加股权融资的脉冲响应图。图4(a) 与预期一致,企业的利息负担和债务杠杆稳步下降。⑬图4(b) 显示,居民部门的利息负担和杠杆率出现了一定的分化,利息负担与可支配收入的比值小幅增加,这源于居民可支配收入的下降和资产组合的调整。居民是企业股票的唯一购买者,股票需求的增加会降低居民的储蓄,而且可支配收入和储蓄的下降幅度要大于贷款的下降幅度(附图2)。图4(c) 显示,政府的债务杠杆率和利息负担均下降,但幅度并不大。其原因在于,企业的股权融资主要是与居民部门的交易,对政府资产负债表的影响相对有限。图4(d) 显示了主要宏观经济变量,如名义GDP、投资、消费和就业的变化情况。相对于稳态时,它们都有小幅下降,但比较温和。可见,股权融资是非金融企业去杠杆的有效途径,同时对居民和政府的杠杆也可以起到一定的改善作用,⑭对经济增长的负面影响比较温和。
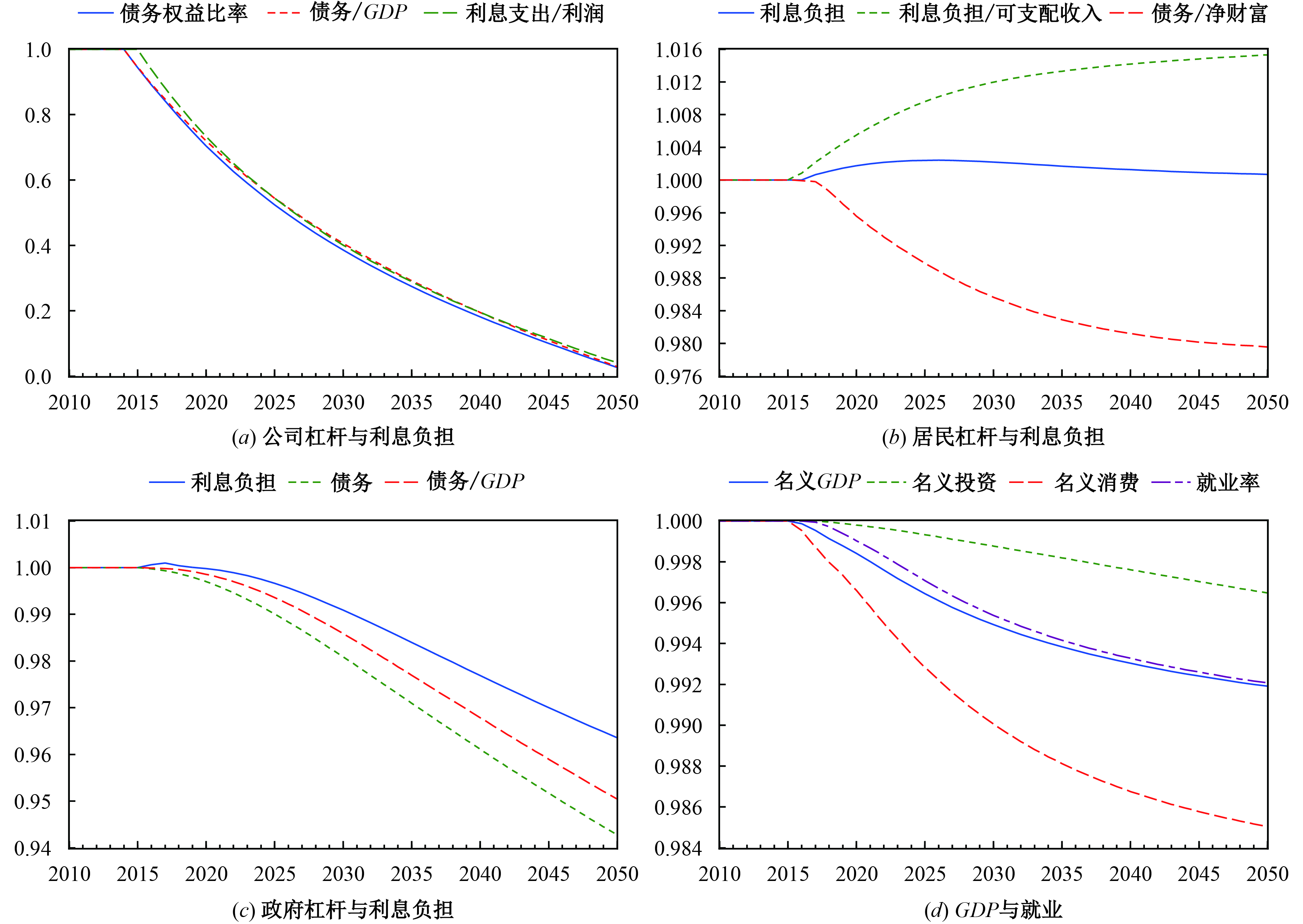
|
| 图 4 股权融资对各部门杠杆与宏观经济的影响 |
(四)经济增长模式转变
中国非金融企业(特别是国有制造企业)杠杆高的原因之一是政府主导的投资拉动型经济增长模式。本节模拟中国从投资驱动型向消费驱动型发展模式转变的去杠杆效应。我们可以通过企业投资增速下降和居民部门减税来刻画。
图5为减税和投资减速下降的脉冲响应分析,结论与预期一致。图5(a) 显示,企业的杠杆和利息负担以先快后慢的速度下降,在5年内都下降了40%左右。图5(b) 显示,居民部门的杠杆并没有大幅上升,且利息负担有了较大幅度的下降。居民的债务杠杆最高时在2023年上升了7%,随后稳步下降。相对于稳态时,利息负担在冲击之初就下降了15%,随后稳步上升,并逐渐收敛到稳态。相对于可支配收入,利息负担有较大幅度的下降。图5(c) 显示,在减税之初,政府不得不减少开支,债务存量下降。同时,由于利息支出取决于前一期的债务存量,政府的利息负担在冲击发生时迅速上升到稳态时的1.16倍,随后随着债务存量的下降而逐步降低,到2050年相对降低了38%。随着债务存量的下降和GDP的增加(见图5(d) ),政府债务与GDP比率稳步下降。可以看出,政府主导的投资驱动型向消费驱动型经济增长模式转变,有助于降低非金融企业和政府的杠杆水平。⑮
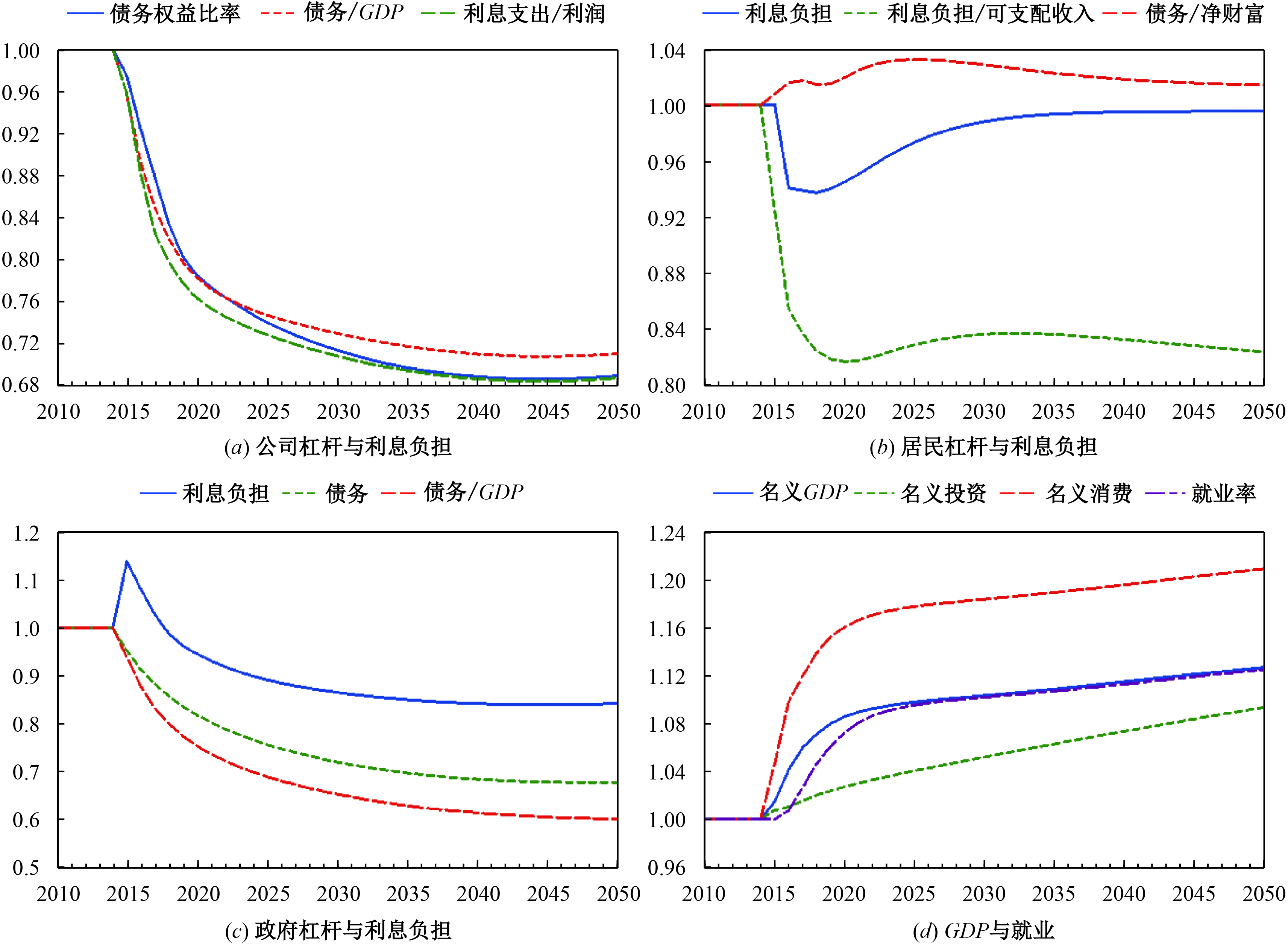
|
| 图 5 投资驱动向消费驱动转变(减税)对各部门杠杆与宏观经济的影响 |
(五)去杠杆的微观视角
上文都是从宏观层面讨论去杠杆问题,虽然各项政策对去杠杆与稳增长都有一定作用,但是由于中国各部门内部存在显著的结构性差异,需要进一步从微观层面探讨如何去杠杆。考虑到中国杠杆最严重的是非金融企业,我们专门讨论非金融企业去杠杆的微观措施。Ruscher和Wolff(2013)总结到,企业去杠杆的常用措施主要有降低工资、削减投资、降低派息率等。本文着重针对降低派息率进行分析。
图6考察了降低派息率(下降5个百分点)对企业自身杠杆率和宏观经济的影响。⑯图6(a) 显示,企业债务权益比率先上升后下降,这是因为:居民的股票需求与股息率成正比,股息率下降一开始会降低企业的股权融资能力,因而债务权益比率在初期迅速上升;随后逐渐下降,主要源于股票市值在期初波动之后逐渐稳定,同时由于股息率的下跌会减少居民消费,企业投资增速也逐渐下跌,从而贷款需求减少(见图6(b) )。图6(a) 中企业债务与GDP之比也有所改善,由图6(c) 可以看出,这主要是因为贷款下降的速度要快于GDP下降的速度。由于投资和消费都下跌,GDP和就业相对于稳态时也逐渐下跌。但需要注意的是,图6(d) 中各指标的下降都比较温和,消费最多下降2%。
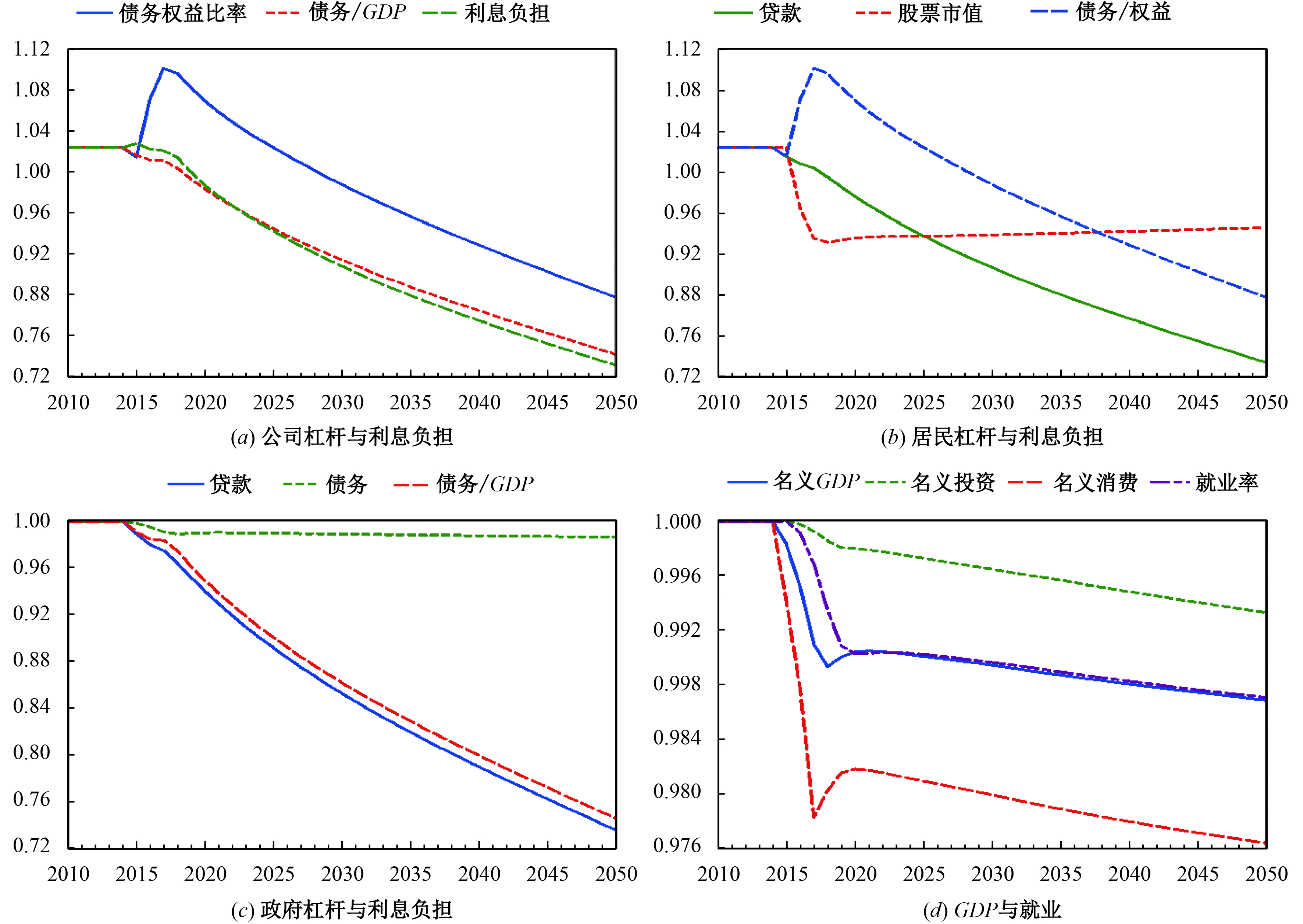
|
| 图 6 降低派息率对各部门杠杆与宏观经济的影响 |
基于统一的SFC框架,图1—图6考察了不同的宏观(货币政策、财政政策等)和微观(利润分配)措施的组合在去杠杆和稳增长方面的效果。我们还通过修正部分参数或内生变量初始值,做了一些稳健性检验,上文结论保持不变。
五、结 论
本文基于宏观经济各部门的资产负债表与资金流量表之间的依存关系、存量与流量的共生关系以及不同部门的行为模式,构建了一个涵盖企业、居民、商业银行、政府与中央银行的五部门SFC模型,考察了各项政策在去杠杆和稳增长方面的效果。本文得到以下结论:第一,提高利率和准备金率使企业和政府的杠杆不降反升,同时也会增加居民的利息负担。GDP呈现先下降后上升的趋势,且比较温和。第二,减税和提高政府支出增速都能平衡去杠杆和稳增长,但增加政府支出对于去杠杆的效果更加明显。第三,提高股权融资比重能够有效实现企业部门去杠杆,而且与其他几种方式相比,股权融资的效果最明显。第四,投资驱动型向消费驱动型增长模式转变,当降低企业投资增速和居民部门减税时,可以实现企业去杠杆与稳增长的平衡。第五,当企业提高内源融资比例时,债务权益比率不降反升,但债务与GDP之比略有改善,对宏观经济运行的负面影响相对温和;当企业降低投资增速时,自身杠杆先上升后下降,且对稳增长有一定的负面影响。
危机以来,宏观经济研究如同全球宏观经济一样,站在新周期的拐点,以新古典为代表的主流方法备受争议。主流阵营的代表者,如Solow(2008)、Krugman和Rogoff(2009)等,也开始反思其方法论的弊端。而本文正是对宏观研究方法的一种回归。⑰本文基于传统的SFC方法,对中国当下面临的去杠杆与稳增长任务进行分析,希望能够与DSGE模型开展良性对话。本文的分析仍是基础性的,文中模型可看作一个基准模型。针对中国杠杆的结构性特征,未来可以进一步将企业分为国有部门和私营部门,对它们的异质性行为分别建模,这一点对中国而言有相当重要的意义。
| 参数 | 含义 | 数值 | 校准依据 |
| β | 预期销售额方程中当期真实销售额的权重系数 | 0.5 | Godley和Lavoie(2007) |
| grpr | 劳动生产率增长率 | 0.093 | 2008—2016年均值(世界劳工组织) |
| γ | 预期库存调整系数 | 0.15 | Godley和Lavoie(2007) |
| σT | 目标库存占预期销售的比例 | 0.09 | 工业企业库存率历史均值 |
| γo | 自发固定资本投资增速 | 0.025 | Lavoie和Zhao(2010) |
| γu | 固定资本投资增速对产能利用率的敏感系数 | 0.05 | Godley和Lavoie(2007) |
| γr | 固定资本投资增速对真实利率的敏感系数 | 1 | Lavoie和Zhao(2010) |
| δk | 固定资本折旧率 | 0.125 | 文献中资本年折旧率一般在0.1和0.15之间,本文取均值 |
| Ω0 | 目标工资率函数中的常数项 | −0.21 | Godley和Lavoie(2007) |
| Ω1 | 目标工资率对劳动生产率的敏感系数 | 1 | Godley和Lavoie(2007) |
| Ω2 | 目标工资率对就业率的敏感系数 | 2 | Godley和Lavoie(2007) |
| Ω3 | 名义工资率调整系数 | 0.46 | Godley和Lavoie(2007) |
| Ω4 | 就业人数调整系数 | 0.6 | Godley和Lavoie(2007) |
| Nfe-1 | 总劳动力人口 | 83.18 | 由就业人数与失业率序列推算得到 |
| φ | 价格加成比例 | 0.1 | 根据陈昆亭等(2004)以及黄志刚和陈晓杰(2010)校准 |
| σN | 历史的单位成本调整系数 | 0.17 | Godley和Lavoie(2007) |
| φD | 派息率 | 0.35 | 根据上市公司年派息率均值校准 |
| φRET | 留存收益率 | 0.65 | 根据上市公司留存收益率均值校准 |
| θ | 个人收入所得税 | 0.25 | 个人收入所得税率中位数 |
| ε1 | 居民净贷款对个人收入的敏感系数 | 0.074 | AR(1)回归系数 |
| ε2 | 居民净贷款对真实利率的敏感系数 | 0.4 | AR(1)回归系数 |
| ε3 | 预期真实可支配收入调整的权重系数 | 0.5 | Godley和Lavoie(2007) |
| ε4 | 贷款偿还额占贷款存量的比例 | 0.25 | 根据贷款存量及新增量数据测算 |
| α1 | 预期真实可支配收入的边际消费倾向 | 0.8 | Lavoie和Zhao(2010) |
| α2 | 真实财富的边际消费倾向 | 0.05 | Lavoie和Zhao(2010) |
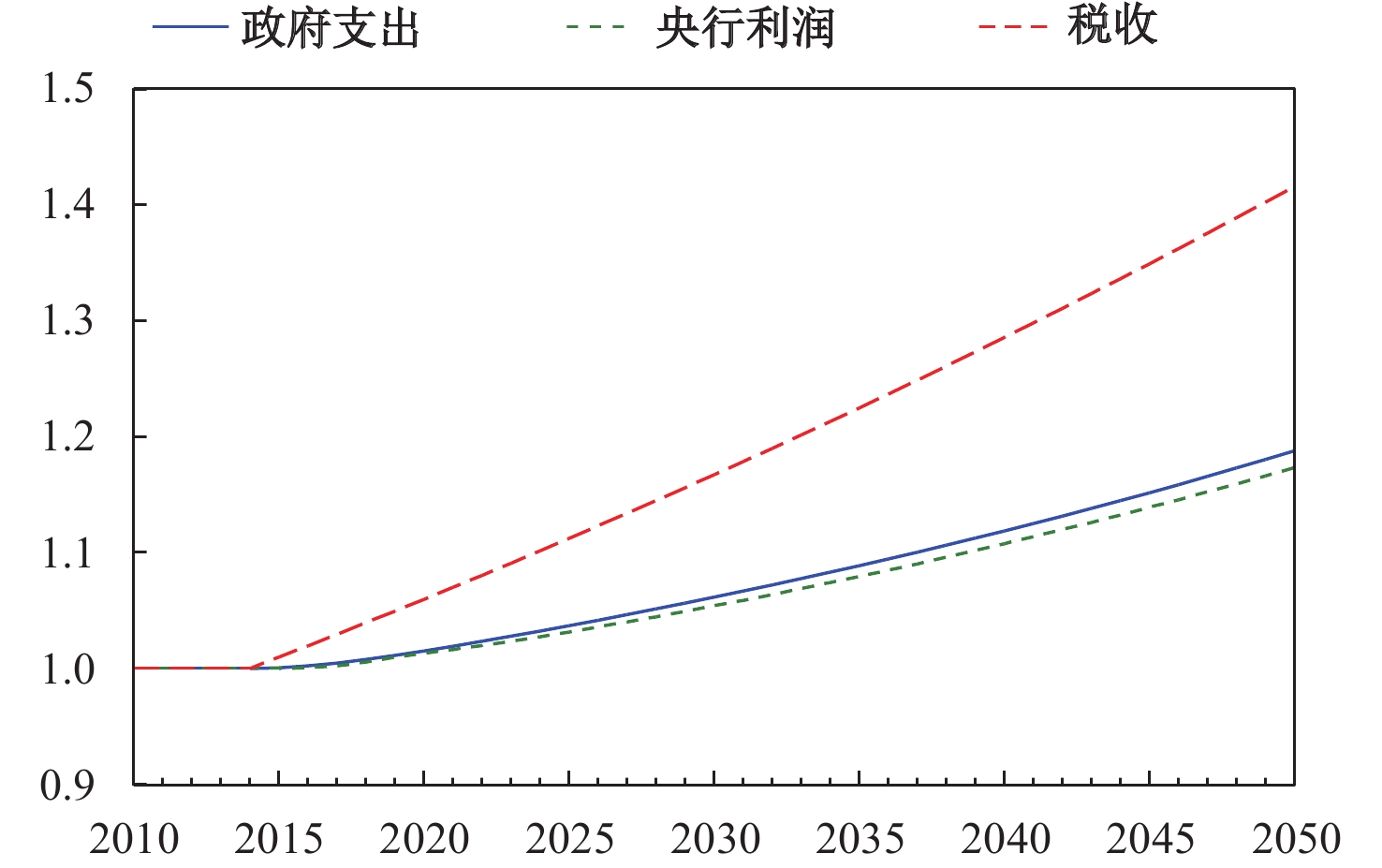
|
| 附图 1 政府支出、央行利润与税收 |
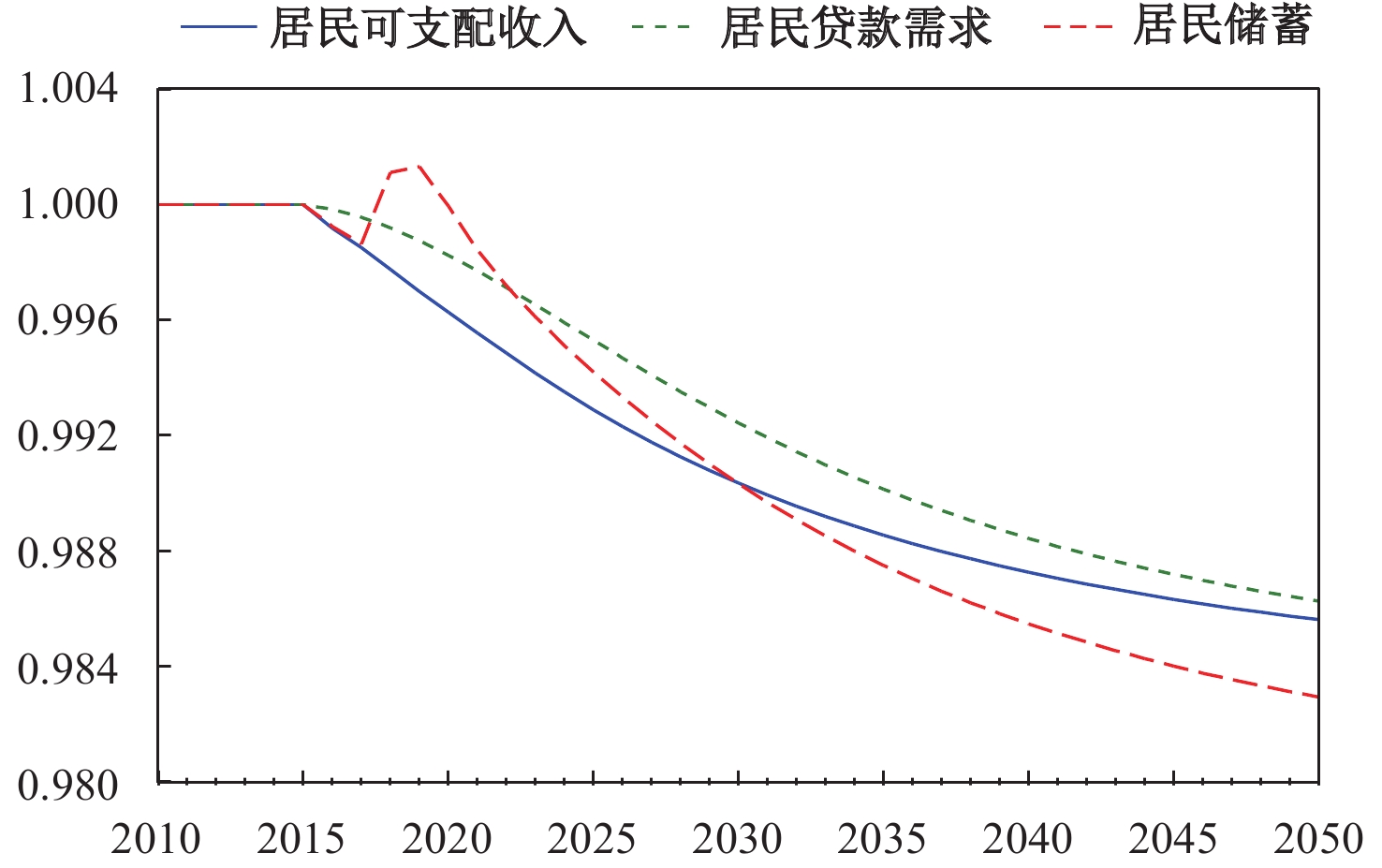
|
| 附图 2 居民可支配收入与资产组合管理 |
① 柳欣等(2012,2013)曾对SFC方法做过简要介绍,而建立五部门SFC模型并进行数值模拟的研究还是空白。
② h表示居民,f表示非金融企业,b表示商业银行,g表示政府,cb表示中央银行;E表示企业发行的股票,BL表示政府长期债券。
③ 净资产项均为负值,因为可以将其理解为“所有者权益”,在会计报表中与负债记在同列。
④ PBL为长期国债价格,BL为国债存量。PE为股票市场价格,Eh为股票份额。
⑤ 对我国而言,国债的购买主体是券商资管、专户和私募等,由于本文并没有对大金融行业进行细分,这里将居民看作长期国债的最终拥有人。
⑥ 长期国债与股票账面价值的变动有两个原因:一是市场价格的变动,二是存量的变动。表2中的价值重估是指第二种原因所引起的账面价值变动。它与一个部门的收支行为是串联起来的,如果生产循环和金融循环表示某部门收大于支,则它将表现为该部门某项(或几项)金融资产数量的增加(假定其他不变)。价格变动所引起的变化将在后文中由资本利得方程表示。
⑦ 方程55−方程58A的参数设置需满足垂直约束与对称约束,具体可参见Godley和Lavoie(2007)第5章。
⑧ 下文的脉冲响应均以稳态为参照系。
⑨ 受篇幅限制,除了一些预期之外的结论,各种政策冲击的脉冲响应图都只有4幅,分别为企业、居民和政府的利息负担和债务杠杆及其对宏观经济的冲击。
⑩ 融资优序理论认为企业的融资偏好排序是内源融资(留存收益)、股权融资和债务融资。但肖泽忠和邹宏(2008)认为我国上市公司具有显著的股权融资偏好。
⑪ 在脉冲分析时需要更加关注短期效应,这是因为如“卢卡斯批判”所言,长期来看,经济结构和政策等都会变化,参数也会发生变化。因此,本文分析长期效应仅提供一个参照系。
⑫ 我们还考察了税率一次性降到25%时的脉冲响应,基本结论保持不变,但冲击效应变大。可见,减税的去杠杆效应随减税力度的增大而增强。
⑬ 读者无需在意2050年的债务杠杆几乎为0的情形,在内源融资与股权融资能够满足投资需求时,企业不存在债务融资需求,因而债务杠杆趋向于0,这与融资优序理论是一致的。
⑭ 在现有的模型中,考察企业的融资选择行为对杠杆的影响,还可以通过降低股息率φD来增加留存收益。基本结论与图4一致。
⑮ 本文还模拟了企业投资增速下降和居民部门消费倾向上升的情形,去杠杆的效果更加明显,但对经济增长有一定的负面影响。
⑯ 由于函数的非线性特征,削减工资的脉冲响应图呈现出非平滑的特征。由于数字变化非常小,基本可以忽略其影响。为节省篇幅,这里未展示。
⑰ 在20世纪70年代,诺贝尔奖得主Tobin在耶鲁大学的研究团队及Godley在剑桥大学的团队都是SFC模型的研究中心。只是新凯恩斯学派和理性预期学派兴起以后,这种方法逐渐被遗忘了。
| [1] | 陈昆亭, 龚六堂, 邹恒甫. 什么造成了经济增长的波动, 供给还是需求: 中国经济的RBC分析[J]. 世界经济, 2004(4): 3–11. |
| [2] | 胡志鹏. " 稳增长”与" 控杠杆”双重目标下的货币当局最优政策设定[J]. 经济研究, 2014(12): 60–71. |
| [3] | 黄志刚, 陈晓杰. 人民币汇率波动弹性空间评估[J]. 经济研究, 2010(5): 41–54. |
| [4] | 李杨, 张晓晶, 常欣, 等. 中国国家资产负债表2015——杠杆调整与风险管理[M]. 北京: 中国社会科学出版社, 2015. |
| [5] | 柳欣, 赵雷, 吕元祥. 我国经济增长中的需求结构失衡探源——基于存量−流量均衡的分析视角[J]. 经济学动态, 2012(7): 57–63. |
| [6] | 柳欣, 赵雷, 吕元祥. 宏观经济学的存量流量一致模型研究述评[J]. 经济学动态, 2013(12): 15–23. |
| [7] | 吕炜, 高帅雄, 周潮. 投资建设性支出还是保障性支出——去杠杆背景下的财政政策实施研究[J]. 中国工业经济, 2016(8): 5–22. |
| [8] | 马建堂, 董小君, 时红秀, 等. 中国的杠杆率与系统性金融风险防范[J]. 财贸经济, 2016(1): 5–21. |
| [9] | 谭海鸣, 姚余栋, 郭树强, 等. 老龄化、人口迁移、金融杠杆与经济长周期[J]. 经济研究, 2016(2): 69–81. |
| [10] | 谭小芬. 中国企业杠杆率现状、影响及去杠杆的对策[A]. 潘英丽, 黄益平. 激辩去杠杆——如何避免债务−通缩[C]. 北京: 中信出版社, 2016. |
| [11] | 肖泽忠, 邹宏. 中国上市公司资本结构的影响因素和股权融资偏好[J]. 经济研究, 2008(6): 119–134. DOI:10.3969/j.issn.1005-913X.2008.06.052 |
| [12] | 钟宁桦, 刘志阔, 何嘉鑫, 等. 我国企业债务的结构性问题[J]. 经济研究, 2016(7): 102–117. |
| [13] | Bezemer D J. Understanding financial crisis through accounting models[J]. Accounting, Organizations and Society, 2010, 35(7): 676–688. DOI:10.1016/j.aos.2010.07.002 |
| [14] | Bezemer D J. The credit crisis and recession as a paradigm test[J]. Journal of Economic Issues, 2011, 45(1): 1–18. DOI:10.2753/JEI0021-3624450101 |
| [15] | Edison H J, Luangaram P, Miller M. Asset bubbles, leverage and ‘lifeboats’: Elements of the east Asian crisis[J]. The Economic Journal, 2000, 110(460): 309–334. DOI:10.1111/ecoj.2000.110.issue-460 |
| [16] | Eggertsson G B, Krugman P. Debt, deleveraging, and the liquidity trap: A Fisher-Minsky-Koo approach[J]. The Quarterly Journal of Economics, 2012, 127(3): 1469–1513. DOI:10.1093/qje/qjs023 |
| [17] | Fisher I. The debt-deflation theory of great depressions[J]. Econometrica, 1933, 1(4): 337–357. DOI:10.2307/1907327 |
| [18] | Fukao K, Kwon H U. Why did Japan’s TFP growth slow down in the last decade? An empirical analysis based on firm-level data of manufacturing firms[J]. Japanese Economic Review, 2006, 57(2): 195–228. DOI:10.1111/jere.2006.57.issue-2 |
| [19] | Godley W. Money, finance, and national income determination: An integrated approach[R]. Working Paper No. 167, 1996. |
| [20] | Godley W, Lavoie M. Monetary economics: An integrated approach to credit, money, income, production and wealth[M]. London: Palgrave Macmillan, 2007. |
| [21] | Kindleberg C P, Aliber R Z. Manias, panics, and crashes: A history of financial crises(4th ed.)[M]. London: Palgrave Macmillan, 2001. |
| [22] | Kinsella S, Tiou-Tagba Aliti G. Towards a stock flow consistent model for Ireland[R]. SSRN E-Library, 2012. |
| [23] | Koo R C. The holy grail of macroeconomics: Lessons from Japan’s Great Recession[M]. Singapore: John Wiley & Sons (Asia) Pte. Ltd., 2008. |
| [24] | Krugman P R, Dominquez K M, Rogoff K. It’s Baaack: Japan’s slump and the return of the liquidity trap[J]. Brookings Papers on Economic Activity, 1998, 1998(2): 137–205. DOI:10.2307/2534694 |
| [25] | Lavoie M, Zhao J. A study of the diversification of China’s foreign reserves within a three-country stock-flow consistent model[J]. Metroeconomica, 2010, 61(3): 558–592. |
| [26] | Minsky H P. Stabilizing an unstable economy[M]. New Haven: Yale University Press, 1986. |
| [27] | Minsky H P. Reconstituting the United States’ financial structure: Some fundamental issues[R]. Working Paper No. 69, 1992. |
| [28] | Ueda K. Deleveraging and monetary policy: Japan since the 1990s and the United States since 2007[J]. Journal of Economic Perspectives, 2012, 26(3): 177–201. DOI:10.1257/jep.26.3.177 |
| [29] | Palley T I. The economics of deleveraging: The aftermath of financialization[J]. European Journal of Economics and Economic Policies: Intervention, 2010, 7(2): 401–413. DOI:10.4337/ejeep |
| [30] | Rainhart C M, Rogoff K S. This time is different: Eight centuries of financial folly[M]. Princeton: Princeton University Press, 2009. |
| [31] | Ruscher E, Wolff G B. Corporate balance sheet adjustment: Stylized facts, causes and consequences[J]. Review of Economics, 2013, 64(2): 117–138. |
| [32] | Solow R M. The state of macroeconomics[J]. The Journal of Economic Perspectives, 2008, 22(1): 243–246. DOI:10.1257/jep.22.1.243 |
 2018, Vol. 44
2018, Vol. 44


