
一、问题的提出
“北上广深”是中国广大年轻人追逐梦想的地方,但随着一线城市人口的逐渐饱和,定居成本的不断攀升,人们逃离“北上广”的呼声越来越强烈。是选择在“北上广”打拼,还是到二三线城市过较为轻松的生活?这是广大“北漂”和“海漂”内心都在挣扎的问题。一方面,一线城市的就业机会多、工资待遇高、教育和医疗条件更好,生活设施也便利;另一方面,大城市的交通拥堵、工作压力大、近年来房价飙升,加上最近几年北方雾霾天气严重,户口和购车摇号的门槛越来越高不可攀,定居在一线城市的压力从来没有像今天这么大,承受不住生活压力的年轻人很多选择了离开。如果选择逃离“北上广深”,到家乡的二三线城市定居,相比留在“北上广”,一生会损失多少福利?这是本文尝试回答的问题。
通常人们采用GDP来衡量一个地区的经济发展水平。单纯从人均GDP看,天津市的人均GDP在2012年已经超越了北京,但在大众的认知中天津的吸引力远不如北京;如果以人均收入作为衡量指标,浙江省的人均收入十分接近北京,但同样浙江也未能吸引比北京更多的人才。我们所认为的一线城市的高福利究竟是什么并有多高?以下几个方面是显而易见的,首先,丰富的经济资源,一线城市汇集了大量知名公司的总部和中小型的创业公司,提供了大量各种层次的就业岗位;其次,集中的高水平教育资源,能为自己将来深造和孩子上学等都提供更好的平台;齐全的医疗资源,一线城市的医院集中了几乎全国最好的医生和医疗设备,很多在地方无法治愈的疾病在这里都能够得到很好的治疗;便利的基础设施,公共交通工具,让生活更加方便。综合以上几个方面,我们发现现有的统计方法很难综合考虑这么多指标,更无法具体得出相应的福利水平。
当前测算福利指数的方法大多有一定的缺陷。通过消费商品获得效用是经济学最基本的定义,因此,早期的福利经济学都集中于测算商品的消费。Sen(1980和1992)认为消费的商品基于个人能力所带来的机会和活动才是创造福利的源泉,提出了可行能力理论,这一定义打破了以往福利经济学仅仅关注通过消费商品获得效用的局限,扩展了福利经济学的研究范围,并且Sen还引入基尼系数,提出了广为采用的福利指数。目前的福利经济学研究已经扩展到了可行能力方面,测算福利指数最为广为人知的是联合国发布的人类发展指数HDI,该指数采用预期寿命、成人识字率和人均GDP对数共三个指标,分别对应人的寿命水平、知识水平和生活水平。该指数由联合国开发计划署从1990年开始提出并沿用至今,有广泛的影响力。但是该指标测算的范围太过狭窄,比如生活在压力大、环境差的都市,大量时间用于工作,几乎没有自己的闲暇时间,这样的地区尽管HDI指数很高,但是生活的福利并不一定高。而且该模型仅仅是将某些数据进行一定比例的加权求和,并没有微观经济学基础,因而被Ravallion(2011)等学者所诟病。这种采取不同的指标,并赋予相应权重,最终得到一个综合指数的方法具有测算方便和覆盖范围广的优点,纳入一个新的因素只需要将反映该因素的指标进行初步处理,并调整相应权重就可以得到新的指数,而且计算方便,公式简单明了,国内很多的大学排名、机构排名等等都热衷于这类方法。但是这种方法有着十分致命的缺点,就是其权重的赋予十分随意,选取的指标也十分随意,看似合理的指数,排名者经过适当权重和指标的修改,被排名者根据公式的指标针对性地提高,就能够达到想要的结果,因而很容易被人为操纵,并且由于公式的随意性,导致其没有相应的理论基础,被攻击时使用者也无法合理反驳。
很多学者试图基于不同的指标来衡量社会福利,其中选取收入还是消费作为居民福利的指标尚有争议。Becker等(2005) 采用结合收入和预期寿命的效用函数,不是简单将两个指标赋予一定权重,而是根据微观经济理论将寿命和收入结合,计算了一个人的终身效用,但是这个测度方法过度强调了收入的作用,并没有考虑其他影响福利的因素。Fleurbaey和Gaulier(2009)采用了收入为主,包含了寿命、闲暇和不平等作为福利衡量指标,和Jones和Klenow(2016)采用的指标十分接近,只是后者采用消费,而不是收入作为衡量标准。Nordhaus和Tobin(1972) 很早就提出了一个采用消费和闲暇的福利衡量方法,并以此衡量了美国城镇居民福利水平,Córdoba和Verdier(2008)采用了类似Lucas的模型,比较了国家内和国家间的终身消费不平等对福利的影响。有很多学者探讨了收入和消费之间的关系,Aguiar和Mark(2015)通过需求系统模型研究了消费不平等和收入不平等的关系,发现消费不平等和收入不平等高度相关,以往通过Engle模型得出的结论低估了两者的相关性。本文采用了消费作为影响效用的主要指标,一方面,只有消费才能够得到相应的效用,收入如果没有被消费掉只是存款,而不能带来实际的效用;另一方面,中国的储蓄率很高,很多地区由于社会保障体系不健全,居民不敢过度消费,只能把大量收入储蓄起来,用于结婚买房、养老和预防大病等情况,这样反而降低了相应的福利。本文采用了消费而没有采用人均可支配收入的原因也是基于此。需要注意的是,本文测算的是福利水平,而不是主观幸福感,或许高收入和高储蓄能够给人带来一定的幸福感,但是实际享受到的才是福利。
国内测算福利水平的文章在指标选取、数据范围和构建方法等方面很难做到较好的权衡。首先,数据的选取大多为宏观层面,比如余谦和高萍(2011)基于收入分配与公平、医疗保障、教育文化、农业生产四个方面构造中国农村社会福利指数,其中医疗保障采用的数据为人均寿命、人均床位、人均卫生员数和人均老年收养福利机构数量。此外,国内对福利水平的研究很多基于上文介绍的Sen的可行能力理论,方福前和吕文慧(2009)基于Sen的理论,利用问卷调查获得的数据对我国城镇居民功能空间内的福利状况进行了实证分析,发现收入和学历,休闲状况、住房状况和工作状况对福利水平的实现具有显著的影响。但是该研究的数据仅来源于几个城镇的问卷调查。杨爱婷和宋德勇(2012)研究了国家层面的数据,但是缺少地区间的变化,他们同样采用了Sen的方法,用集对分析法对我国改革开放以来的国家福利水平进行了分析,并发现我国的福利水平明显低于经济发展水平,而且与主要国家的对比中发现我国的福利发展质量明显落后。除了采用Sen的方法进行福利测算,还有利用需求系统模型对家庭消费的福利进行分析。李连友等(2014)采用了需求系统模型,对2002年和2007年CHIPS中国流动人口数据进行了分析,根据不同消费类别的价格弹性对居民的福利水平进行了研究,并认为医保、教育和保障性住房对福利的影响更大。除此之外,一线城市农民工群体的福利水平也是学者关注的重点,袁方和史清华(2013)重点研究了不平等对农民工福利的影响,通过收入不平等和可行能力不平等,对2009年上海农民工这一特殊群体进行了考察,结果发现低收入的农民工福利受到不平等的损害最大。叶静怡和王琼(2014)以2008年和2012年北京市进城务工人员调查数据为样本,使用模糊集理论和因子分析方法,对福利水平进行了评价,发现务工人员的福利水平处于低水平状态,防护性保障和社会资本对福利的影响最大。
综上所述,本文试图在以下几个方面有所探索:首先,之前国内福利的测度大多基于Sen的方法,将反映福利的指标进行处理后再赋予一定的权重进行求和,人为地构造一个福利指数,没有经济学理论基础,本文基于Lucas模型所构建的终身效用模型建立在成熟的宏观经济学模型之上,具有很强的理论基础;其次,以往指数采用的大多是宏观数据,不能反应个体真实的生存状况,本文采用的家庭微观调查数据能够提供详尽的个人消费和工作时间信息;此外,以往测度福利所采用的无论收入或消费指标都比较片面,无法涵盖隐性福利,本文在消费中加入了所有家庭的“房租”用来衡量居住条件和所在地区的教育、医疗和交通等资源,并用政府消费来衡量公共物品和基础设施等,能够更加全面地衡量地区福利;最后,我国目前基本还没有区域性的福利水平测度,现有的文献大多是国家层面或某一个地区的研究,缺少区域之间福利水平的对比,本文采用的CFPS数据涵盖了全国绝大多数省份,能够提供十分详尽的区域对比数据。
本文其他内容结构如下:第二部分提出测算福利的理论模型;第三部分进行数据整理和选取指标的分析;第四部分对不同区域福利水平进行分解,并进行区域比较,对不同年份福利增长率进行了分析;第五部分进行了稳健性检验,最后得出结论。
二、模型的建立
找到一份“活少钱多离家近”的工作对所有人都是最梦寐以求的,“活少”即工作时间短,有足够的闲暇来享受生活;“钱多”即工资高,能够买得起想要的东西,房子车子都不是问题,能够体面地生活;“离家近”能够照顾孩子和老人,生活的环境卫生,教育医疗条件齐全。这三点综合起来就是闲暇、消费和寿命。本文主要参考了Jones和Klenow(2016)的模型,该模型基于经济学中经典的Lucas模型,具有简单易懂和理论基础扎实的优点。模型综合考虑了寿命、消费、闲暇和不平等一共四个因素,需要特别指出的是本文的消费包含了个人消费性支出、房租和人均政府消费。这四个因素涵盖了居民生活的主要部分,反映了福利的各个方面,比如生存环境和医疗条件可以反映在寿命中,同样受到雾霾的困扰,北京的人均寿命平均比河北高4岁,这和北京丰富的医疗资源不无关系;教育资源、居住条件和地理位置等可以反映在房价中,“学区房”的高价以及市中心和郊区的区别都可以通过房价体现,我们将住房价值乘以租售比得出了所有人的“房租”;基础设施可以通过政府消费体现。当然本文也有一些方面没有考虑到,比如地域文化、自然环境和人口流动等等。
基本设定:C代表个人的年消费,l代表闲暇和家务的时间,预计的终身效用为:
| $U = E\mathop \sum \limits_{a = 1}^{100} {\beta ^a}u\left( {{C_a},{l_a}} \right)S\left( a \right)$ | (1) |
其中:S(a)代表个人生存到年龄a的概率,期望E处理消费和闲暇的不确定性。该效用函数衡量的是一个人从年龄岁数1到100岁的效用加总,每一岁的效用函数取决于消费和闲暇,并乘以该年龄的折现因子βa和生存到这一年龄的概率S(a)。
为了衡量不同地区的福利水平,我们定义Ui(λ)为在地区i的预计终身效用,其中消费被乘以一个因子λ:
| ${U_i}\left( \lambda \right) = {E_i}\mathop \sum \limits_{a = 1}^{100} {\beta ^a}u\left( {\lambda {C_{ai}},{l_{ai}}} \right){S_i}\left( a \right)$ | (2) |
本文采取北京市作为对照地区,通过因子λ调整消费水平,使得生活在北京的某人将其消费乘以因子λ之后,预期终身效用等于生活在其他省份i的预计终身效用水平。
| ${U_{bj}}\left( {{\lambda _i}} \right) = {U_i}\left( 1 \right)$ | (3) |
接下来进入函数形式的具体分析,先定义效用函数的形式,效用函数依赖于消费和闲暇:
| $u\left( {C,l} \right) = \bar u + logc + v\left( l \right)$ | (4) |
其中:v(l)代表闲暇的效用,本文采用的v(l)具体形式为:
| $v\left( l \right) = - \frac{{\theta \epsilon }}{{1 + \epsilon }}{\left( {1 - l} \right)^{\frac{{1 + \epsilon }}{\epsilon }}}$ | (5) |
其中:
| $\bar \omega _{ja}^j = \frac{{\omega _{ja}^j}}{{\mathop \sum \nolimits_{j = 1}^{N_a^i} \omega _{ja}^i}}$ | (6) |
生活在地区i的人预期效用水平为:
| ${U_i} = \mathop \sum \limits_{a = 1}^{100} {\beta ^a}S_a^i\mathop \sum \limits_{j = 1}^{N_a^i} \bar \omega _{ja}^ju\left( {c_{ja}^i{e^{ga}},l_{ja}^i} \right)$ | (7) |
其中:Sai为在地区i的人生存到年龄a的概率,每个年龄段的效用水平都乘以该年龄段的生存率Sai。本文测算的是一个刚出生人从现在起一生的效用水平,因此当这个人到了a岁时,距离统计数据的年份已经过去了a年,所以这个人a岁时的消费水平是通过现在a岁的人乘以每年消费的增长率g得到,假设消费的增长率为恒定的速率g,即
我们定义生活在北京的人预期效用水平如下:
| ${U_{bj}}\left( {{\lambda _i}} \right) = \mathop \sum \limits_{a = 1}^{100} {\beta ^a}S_a^{bj}\left[ {u_a^{bj} + log\left( {{\lambda _i}} \right)} \right]$ | (8) |
其中:uabj的定义列如下所示。
| $u_a^{bj} = \bar u + ga + \mathop \sum \limits_{j = 1}^{N_a^{bj}} \bar \omega _{ja}^{bj}\left[ {{\rm log}\left( {c_{ja}^{bj}} \right) + v\left( {l_{ja}^{bj}} \right)} \right]$ | (9) |
根据Ubj(λi)=Ui(1),计算得到λi如下:
| ${\rm log}\left( {{\lambda _i}} \right) = \frac{1}{{\mathop \sum \nolimits_a {\beta ^a}S_a^{bj}}}\mathop \sum \limits_a {\beta ^a}\left[ {\left( {S_a^i - S_a^{bj}} \right)u_a^i + S_a^{bj}\left( {u_a^i - u_a^{bj}} \right)} \right]$ | (10) |
简化公式,定义如下的生存率:
| $s_a^{bj} = \frac{{{\beta ^a}S_a^{bj}}}{{\mathop \sum \nolimits^ {\beta ^a}S_a^{bj}}}$ |
| $\Delta s_a^i = \frac{{{\beta ^a}\left( {S_a^i - S_a^{bj}} \right)}}{{\mathop \sum \nolimits^ {\beta ^a}S_a^{bj}}}$ |
将定义的sabj和Δsai代入λi的公式后,得到简化的λi如下:
| ${\rm log}\left( {{\lambda _i}} \right) = \sum\nolimits_a {\Delta s_a^iu_a^i} + \sum\nolimits_a {s_a^{bj}} \left( {u_a^i - u_a^{bj}} \right)$ | (11) |
将效用函数u代入公式:
| ${\rm log}\left( {{\lambda _i}} \right) = \mathop \sum \limits_a \Delta s_a^iu_a^i + \mathop \sum \limits_a s_a^{bj}\left( {\mathop \sum \limits_{j = q}^{N_a^i} \bar \omega _{ja}^i\left[ {{\rm log}\left( {c_{ja}^i} \right) + v\left( {l_{ja}^i} \right)} \right] - \mathop \sum \limits_{j = q}^{N_a^{bj}} \bar \omega _{ja}^{bj}\left[ {{\rm log}\left( {c_{ja}^{bj}} \right) + v\left( {l_{ja}^{bj}} \right)} \right]} \right)$ |
为了进一步简化公式和明确公式中各部分的意义,定义平均消费和平均闲暇,以及通过消费和闲暇得到的效用如下:
| ${{\bar c}_i} = \mathop \sum \limits_a s_a^{bj}\mathop \sum \limits_{j = 1}^{N_a^i} \bar \omega _{ja}^ic_{ja}^i{e^{ga}}$ |
| ${{\bar l}_i} = \mathop \sum \limits_a s_a^{bj}\mathop \sum \limits_{j = 1}^{N_a^i} \bar \omega _{ja}^il_{ja}^i$ |
| $E{\rm log}{c_i} = \mathop \sum \limits_a s_a^{bj}\mathop \sum \limits_{j = 1}^{N_a^i} \bar \omega _{ja}^i{\rm log}\left( {c_{ja}^i{e^{ga}}} \right)$ |
| $Ev\left( {{l_i}} \right) = \mathop \sum \limits_a s_a^{bj}\mathop \sum \limits_{j = 1}^{N_a^i} \bar \omega _{ja}^iv\left( {l_{ja}^i} \right)$ |
| ${\rm log}\left( {{\lambda _i}} \right) = \sum\nolimits_a {\Delta s_a^iu_a^i} + E{\rm log}{c_i} - E{\rm log}{c_{bj}} + Ev\left( {{l_i}} \right) - Ev\left( {{l_{bj}}} \right)$ | (12) |
以上消费和闲暇代入公式,因为log的可加性,我们得到一个分解的福利水平:
| $\begin{aligned}{{\rm log}\frac{{{\lambda _i}}}{{\widetilde {{y_i}}}} = }&{\mathop \sum \limits_a \Delta s_a^iu_a^i} \quad \quad \quad \quad\quad \; \quad \quad \quad \quad \quad \quad \text{生命}\\{}&{ + \log \frac{{{{\bar c}_i}}}{{{y_i}}} - \log \frac{{{{\bar c}_{bj}}}}{{{y_{bj}}}}} \quad \quad \quad \quad\quad \; \quad \quad\quad \text{消费}\\{}&{ + v\left( {{{\bar l}_i}} \right) - v\left( {{{\bar l}_{bj}}} \right)} \quad \quad \quad \quad \quad \quad \quad \ \, \quad\quad\text{闲暇}\\{}&{ + E{\rm log}{c_i} - {\rm log}{{\bar c}_i} - \left( {E{\rm log}{c_{bj}} - {\rm log}{{\bar c}_{bj}}} \right)} \quad \text{消费不平等}\\{}&{ + Ev\left( {{l_i}} \right) - v\left( {{{\bar l}_i}} \right) - \left( {Ev\left( {{l_{bj}}} \right) - v\left( {{{\bar l}_{bj}}} \right)} \right)} \quad \quad \text{闲暇不平等}\end{aligned}$ | (13) |
其中:
三、数据来源和处理
本文采用的数据为中国家庭追踪调查CFPS 2010年、2012年和2014年共三年的数据,该数据为北京大学中国社会科学调查中心实施,覆盖了25个省市自治区,每年的样本规模大约为16 000户,包含有丰富的消费和工作信息,而且每个样本均赋予了权重,具有全国代表性。除此之外,还采用了2010年中国人口普查数据来计算预期生命值和生存概率,同时采用中国统计年鉴中各省份政府消费数据来加总到个人消费,还采用各省份的CPI来调整微观数据中的消费。由于数据保密需要,CFPS不提供市级代码,因而广州和深圳等一线城市,还有大量二线城市无法直接比较。此外,CFPS数据还缺少新疆、西藏、内蒙古、青海、海南、中国台湾和中国香港等地区的数据。
本文的数据主要有生命、消费和闲暇三个部分。生命数据通过人口普查数据编制的简略寿命表得到,寿命表反映不同年龄的人口死亡概率,并且具有不同年龄段的预期寿命。联合国世界卫生组织每年都会发布各个国家的寿命表,但是国内并没有公开发布分省份的简略寿命表,因此本文根据2010年人口普查数据中各省份城镇居民不同年龄段人口数量等信息,编制了不同省份城镇居民不同性别的简略寿命表,对应到微观数据中每个不同年龄观测值的生存概率。由于我国人口普查采用5年一小普,10年一大普的规律,因而在2012年和2014年没有相应的普查数据,所以本文采用的不同年龄的生存概率都是由2010年人口普查得到的,为此假设在2010—2014年之间,中国各省份城镇居民的生存率没有发生显著的变化。
消费数据采用的是人均年消费性支出,包含了房租和人均政府消费。本文采用的是个人层面的数据,但是消费数据都是以家庭为单位统计,因此采用了简单平均的方法,将家庭消费性支出除以家庭人口得到个人消费。将房租包含在消费中是很有必要的,住房条件是衡量生存状况的关键指标之一,而且房租也能够反映当地的教育资源、医疗资源和区位优势等影响个人福利的因素。中国住房自有率高达80%左右,绝大部分家庭都没有租房,对没有房租的家庭通过住房的价值乘以租售比得到其“房租”。租售比是通过不同市级地区、城乡的租房家庭的房租除以房屋价值,取其中位数得到。政府消费支出是指政府部门为全社会提供的公共服务的消费支出和免费或以较低的价格向居民住户提供的货物和服务的净支出,政府消费大多用于当地的软硬件建设上,最终被所在地的人享受,因而加入政府消费同样重要。人均政府消费通过中国统计年鉴中不同省份政府的消费除以人口得到的人均政府消费,然后通过其与微观数据进行一定比例的转换加总到个人总消费中。为了统一统计口径,转换的比例为年鉴中不同省份人均消费除以微观数据中省级人均消费的平均值。为了便于对比,根据不同省份的CPI对不同年份的消费数据进行了平减处理,确保对比结果的准确性。
闲暇的数据是通过1减去每年的工作小时数除以最多工作时间。本文采用每天最多16个小时的工作时间,一年365天就是5 840小时,根据CFPS数据中提供的丰富的工作时间信息,包含工作的月份,每周工作时间等等,计算一年的总工作时间,除以最多工作时间5 840小时,然后用1减去该比值,得到介于0到1之间的小数,代表闲暇。
四、测算结果
本文采用CFPS 2010年、2012年和2014年三年的数据进行了测度,得出该三年分省份城镇居民的福利水平。采用上文的模型,以北京作为对比,其他省份的福利水平表示为北京的百分比,并且对福利水平构成因素进行分解,得出的福利水平结果见表1。①
| 省份 | 福利 | 收入 | 福利/收入对数 | 福利分解 | ||||
| 寿命 | 消费/收入 | 闲暇 | 消费不平等 | 闲暇不平等 | ||||
| 北京市 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 83.481 | 1.166 | 0.867 | 1.498 | 0.211 | ||||
| 天津市 | 0.699 | 1.052 | −0.409 | −0.049 | −0.448 | 0.014 | 0.061 | 0.013 |
| 83.051 | 0.745 | 0.874 | 1.458 | 0.208 | ||||
| 河北省 | 0.178 | 0.4 | −0.809 | −0.408 | −0.306 | −0.02 | −0.025 | −0.051 |
| 80.316 | 0.858 | 0.857 | 1.402 | 0.228 | ||||
| 山西省 | 0.13 | 0.351 | −0.989 | −0.391 | −0.301 | −0.029 | −0.188 | −0.08 |
| 80.406 | 0.863 | 0.852 | 1.407 | 0.238 | ||||
| 辽宁省 | 0.32 | 0.652 | −0.713 | −0.325 | −0.305 | −0.019 | −0.024 | −0.039 |
| 81.11 | 0.86 | 0.857 | 1.454 | 0.225 | ||||
| 吉林省 | 0.219 | 0.502 | −0.831 | −0.204 | −0.42 | −0.04 | −0.07 | −0.098 |
| 81.903 | 0.766 | 0.847 | 1.368 | 0.242 | ||||
| 黑龙江省 | 0.278 | 0.392 | −0.346 | −0.325 | 0.102 | 0.023 | −0.132 | −0.014 |
| 81.12 | 1.291 | 0.879 | 1.384 | 0.215 | ||||
| 上海市 | 0.91 | 0.974 | −0.068 | −0.055 | 0.006 | −0.007 | −0.027 | 0.015 |
| 83.26 | 1.173 | 0.863 | 1.491 | 0.205 | ||||
| 江苏省 | 0.457 | 0.819 | −0.584 | −0.218 | −0.209 | −0.063 | −0.029 | −0.065 |
| 81.865 | 0.946 | 0.837 | 1.483 | 0.233 | ||||
| 浙江省 | 0.44 | 0.73 | −0.507 | −0.155 | −0.215 | −0.047 | −0.018 | −0.073 |
| 82.454 | 0.94 | 0.844 | 1.445 | 0.234 | ||||
| 安徽省 | 0.163 | 0.344 | −0.75 | −0.23 | −0.243 | −0.085 | −0.062 | −0.129 |
| 81.686 | 0.914 | 0.827 | 1.398 | 0.251 | ||||
| 福建省 | 0.261 | 0.635 | −0.888 | −0.195 | −0.504 | −0.062 | −0.081 | −0.047 |
| 81.976 | 0.705 | 0.837 | 1.433 | 0.227 | ||||
| 江西省 | 0.161 | 0.347 | −0.768 | −0.425 | −0.275 | −0.07 | 0.039 | −0.038 |
| 80.278 | 0.886 | 0.834 | 1.336 | 0.223 | ||||
| 山东省 | 0.273 | 0.609 | −0.802 | −0.283 | −0.394 | −0.042 | −0.023 | −0.059 |
| 81.335 | 0.786 | 0.846 | 1.415 | 0.23 | ||||
| 河南省 | 0.193 | 0.371 | −0.651 | −0.324 | −0.224 | −0.015 | −0.062 | −0.026 |
| 80.959 | 0.932 | 0.859 | 1.398 | 0.22 | ||||
| 湖北省 | 0.287 | 0.471 | −0.496 | −0.169 | −0.243 | −0.019 | −0.017 | −0.048 |
| 82.258 | 0.914 | 0.857 | 1.41 | 0.227 | ||||
| 湖南省 | 0.232 | 0.403 | −0.553 | −0.256 | −0.268 | 0.011 | −0.045 | 0.005 |
| 81.497 | 0.892 | 0.872 | 1.464 | 0.212 | ||||
| 广东省 | 0.377 | 0.635 | −0.521 | −0.248 | −0.151 | −0.023 | −0.054 | −0.045 |
| 81.703 | 1.002 | 0.855 | 1.462 | 0.225 | ||||
| 广西 | 0.203 | 0.331 | −0.487 | −0.208 | −0.086 | −0.118 | −0.047 | −0.027 |
| 81.879 | 1.069 | 0.814 | 1.437 | 0.222 | ||||
| 重庆市 | 0.355 | 0.479 | −0.298 | −0.118 | −0.16 | 0.002 | −0.017 | −0.005 |
| 82.628 | 0.994 | 0.868 | 1.459 | 0.215 | ||||
| 四川省 | 0.21 | 0.351 | −0.513 | −0.139 | −0.12 | −0.016 | −0.183 | −0.055 |
| 82.441 | 1.034 | 0.859 | 1.455 | 0.231 | ||||
| 贵州省 | 0.14 | 0.264 | −0.634 | −0.329 | −0.05 | −0.07 | −0.107 | −0.079 |
| 81.147 | 1.109 | 0.834 | 1.419 | 0.236 | ||||
| 云南省 | 0.109 | 0.273 | −0.915 | −0.75 | 0.021 | −0.128 | 0.003 | −0.06 |
| 78.032 | 1.19 | 0.811 | 1.393 | 0.232 | ||||
| 陕西省 | 0.28 | 0.469 | −0.516 | −0.196 | −0.225 | −0.009 | −0.052 | −0.034 |
| 81.907 | 0.931 | 0.862 | 1.474 | 0.225 | ||||
| 甘肃省 | 0.185 | 0.264 | −0.359 | −0.264 | −0.002 | −0.019 | −0.015 | −0.058 |
| 81.547 | 1.163 | 0.857 | 1.402 | 0.231 | ||||
(一)城镇居民福利水平分解及分区域比较
表1的收入采用的是人均GDP,第四列反映的是福利水平和人均GDP的差异,后五列是对测算的福利水平进行分解,分别是寿命、消费/收入、闲暇、消费不平等和闲暇不平等。分解部分每个省份第一行是与北京对比的差异,第二行是测算的具体数据,如北京寿命第一行是与自己的对比,因此为0,第二行寿命83.49是北京的预期寿命,以此类推。需要注意的是,福利分解的第二列消费/收入一项,很多省份的消费除以人均GDP都超过了1,根据支出法得到的GDP本不应该低于居民消费,但是由于本文将虚拟的房租加入到个人消费中,房价上涨导致“房租”也跟着上涨,而且还有政府支出,国内的政府支出包含政府的转移支付,低收入地区得到的财政转移支付也多,因而本文计算的很多省份消费上涨,最终导致消费收入比超过1。
首先从福利水平看,北京作为对比的基础,福利为1;上海仅次于北京,为0.91;天津为0.699。作为前三甲,这三个都是直辖市,经济发达而且兼具各自的区位优势。不过这三个市虽然人均GDP十分接近,但福利水平相差巨大,特别是天津市福利水平只有北京的70%,这也符合我们的直觉,毕竟天津的福利水平和北京还是相差甚远。北京、上海作为一线城市,福利水平远超其他省市至少一倍以上,难怪一线城市会吸引那么多的年轻人去奋斗。作为第二梯队的浙江、江苏和广东,其各自的福利水平仅为北京的1/3多一点,但是三省的人均GDP则为北京的60%—80%,其福利水平相对北京缩水了近一半(见图1)。
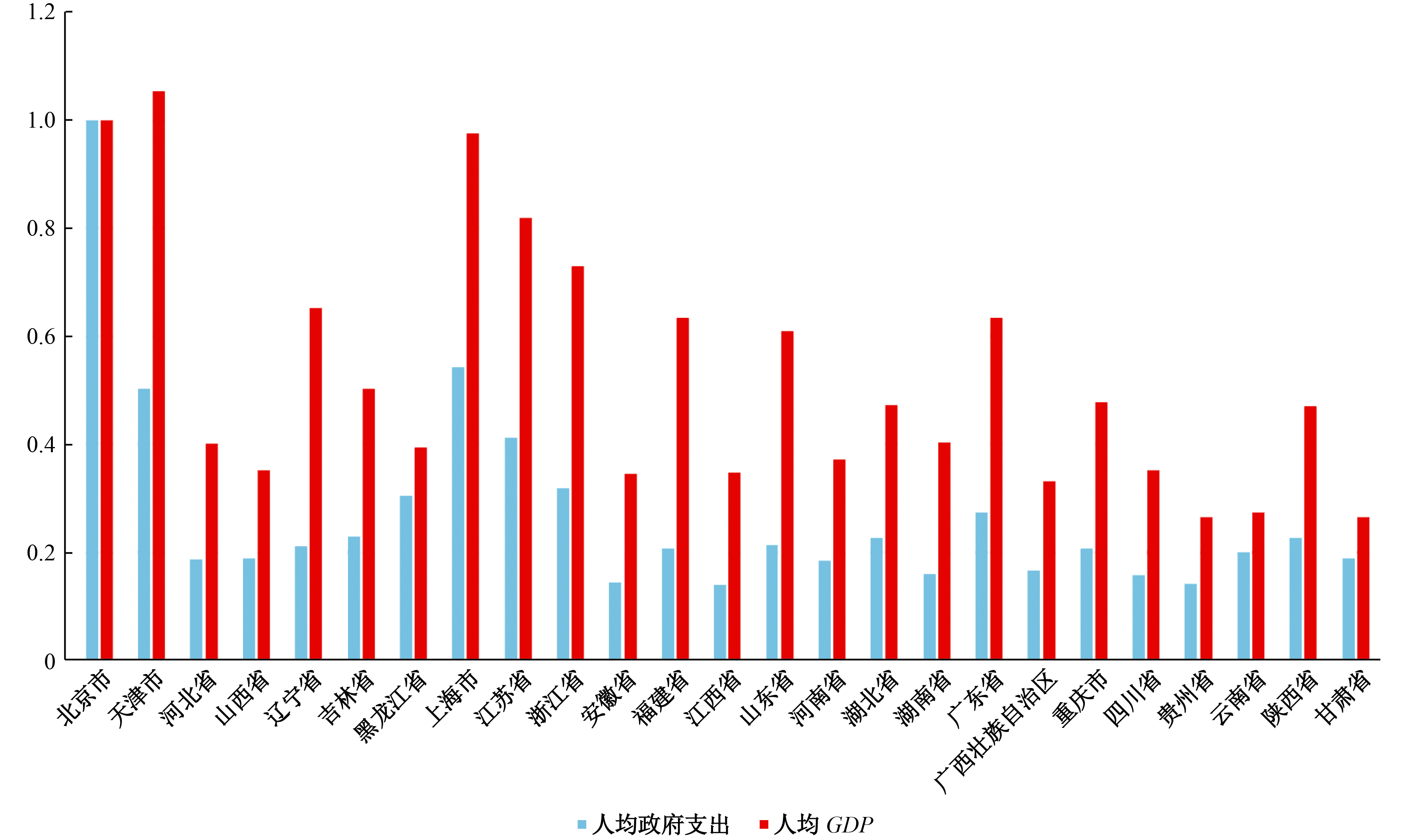
|
| 图 1 2014年中国各省份人均政府消费和人均GDP |
政府转移支付降低了收入不平等。东三省的福利水平很接近,其中黑龙江和吉林的闲暇水平在全国最高,尽管辽宁省的人均GDP高于吉林,吉林又高于黑龙江,但是来自政府的转移支付导致了三个省份的最终消费十分接近。由此可见,政府通常是采用财政转移支付来降低收入不平等的。同样在低收入的甘肃、贵州、云南和陕西等省份,政府的支出相对更高,从而导致了其最终总支出水平更高,因而拉高了福利水平,这使得全国不同区域的福利水平更趋接近。但是北京作为首都,其政府支出水平远高于其他省市,反而加剧了福利水平的不平等程度(见图1)。
通过福利分解,能够更清楚地看出各个省市在哪些方面具有优势和劣势。北京的人均期望寿命和消费水平都很高,但是工作时间和消费不平等水平也很高。而与北京相邻的河北省同样遭受雾霾的困扰,但是其城镇居民的预期寿命仅为80.3岁,平均比北京少活3岁,北京丰富的医疗资源和优越的生活条件是造成这种差异的主要原因,这对生活在北京的人是很高的福利。
闲暇方面,全国的闲暇水平差距并不大,大多围绕在0.85左右,经济水平较发达的地区闲暇水平也较低。由于本文验证的是一生的综合效用,考虑了所有人的综合闲暇,其中孩子、无业人员和退休的老人都是闲暇为1,过多的老人或无业人员会导致闲暇水平上升,因而预期寿命过高也会提高闲暇水平。
北京市的消费不平等位居全国首位,上海第二,江苏第三。消费不平等对福利的影响很大,袁方和史清华(2013)发现收入不平等对农民工的福利有损害,而且对低收入的农民工损害更大。消费的不平等对低收入者的伤害巨大,甚至会造成社会的不稳定,而且高收入者的高消费容易给身边的人造成自己“变穷”了的感觉,从而降低幸福感,损害绝大部分人的福利水平。“北上广”虽然福利水平全国最高,但是消费不平等同样最高,而且工作者的闲暇水平也很低,因而生活在一线城市人的幸福感并不高,但是一线城市高消费带来的福利是实实在在的。
为了进一步比较区域福利水平差异,本文采用R软件绘制了中国城镇居民福利水平地图。
图2左边为福利,右边为人均GDP,通过地图,我们可以清晰地看出一线城市的福利和其他省份的差距,除了北京、上海和天津颜色比较深,其他省份都是浅灰色。东部沿海地区的福利水平略高于内地省份,浙江、江苏和广东的颜色明显更深,但是东部地区和内地的区别并不大。中部地区的福利水平大多十分接近,云贵地区是福利最低的地区,主要原因是云贵地区的预期寿命太短,拉低了终身的福利水平。而通过人均GDP图解可以看出北京、上海和东部沿海省份的差距并不大,广东和江浙地区已经十分接近北京和上海,无法体现出一线城市的高福利。并且中国的GDP分为明显的东部最高,中部其次,西部最低这三个阶梯区域。本文测算的福利水平在区域上的不平等水平要比人均GDP低很多。
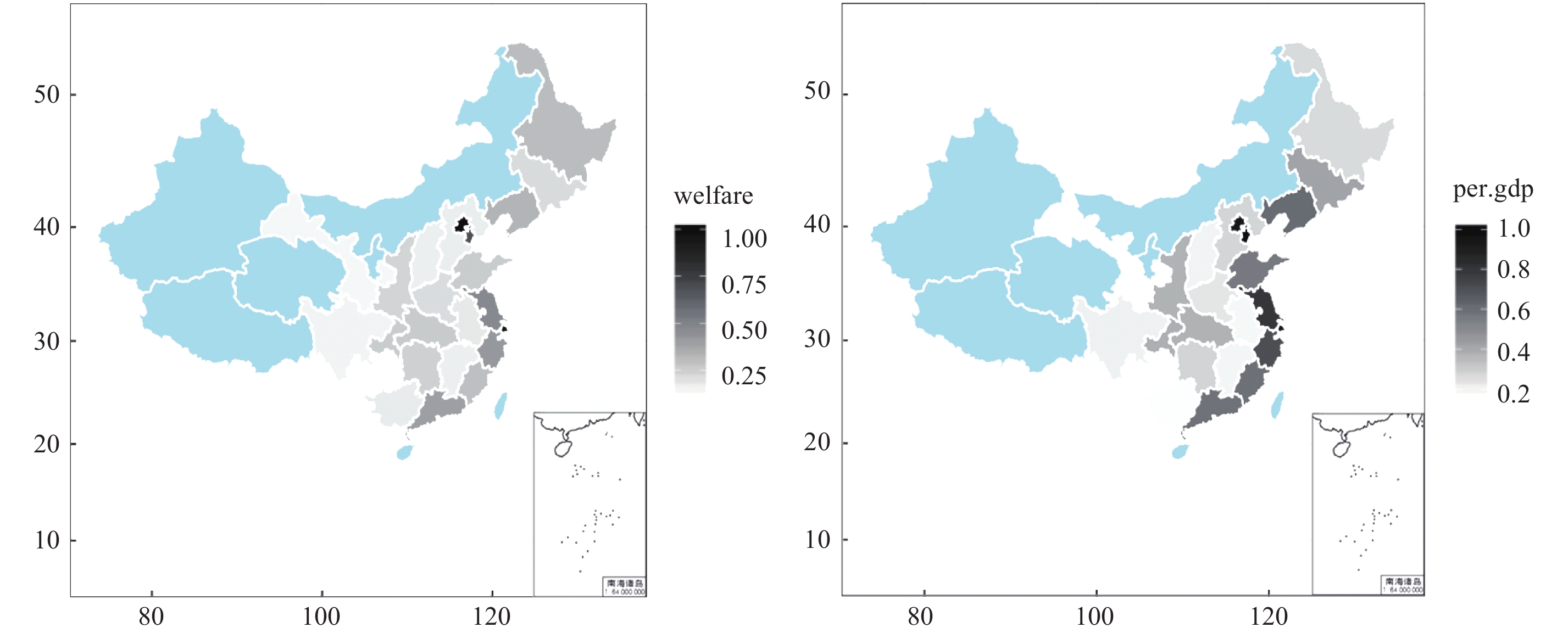
|
| 图 2 2014年中国分区域城镇居民的福利和人均GDP地图 |
对比中国的福利和人均GDP地图,最明显的特征是一线城市的福利水平特别高,人均GDP为北京80%左右的江浙,福利水平仅为北京45%左右,降了几乎一半。结合表1,我们定义GDP的“水分“为人均GDP和福利水平差距,GDP水平并不能完全反映居民的生活福利,两者相差越大,表示GDP并没有使当地居民生活得到相应的福利,从而表明GDP的“水分”越大。“水分”最大的是山西省,由人均GDP0.351降为福利水平0.13,山西省城镇居民的人均寿命仅为80.4岁,比北京少3年,这背后是空气污染加剧和医疗条件落后的现实,并且山西省的消费水平低,消费不平等水平高,拉低了山西省的福利水平。“水分”第二和第三的分别是云南省和福建省还有吉林、河北和山东等省份的福利和人均GDP差距也较大。这些省份中,云南省城镇居民的人均寿命为78左右,在统计的省份中最低,直接拉低了福利水平;河北省的人均寿命和山西接近,但是远低于北京和天津,并且比东三省也要少活一年左右。北方的雾霾天气最严重的就是山西、河北和京津地区,但是没有京津优越的医疗条件和生存环境,河北和山西遭受雾霾的危害更大。不过河北和山西的工作时间并不多,不平等水平也较低。
(二)城镇居民福利增长率
GDP增长率是衡量地区经济发展的重要指标,而经济的发展是否转化为居民真实的福利则更为重要。很多人抱怨收入跑不过CPI,福利增速比不上经济增速,本文对2010年、2012年和2014年共三年的数据进行了福利水平测算,得出这三年福利水平增长的柱状图见图3。
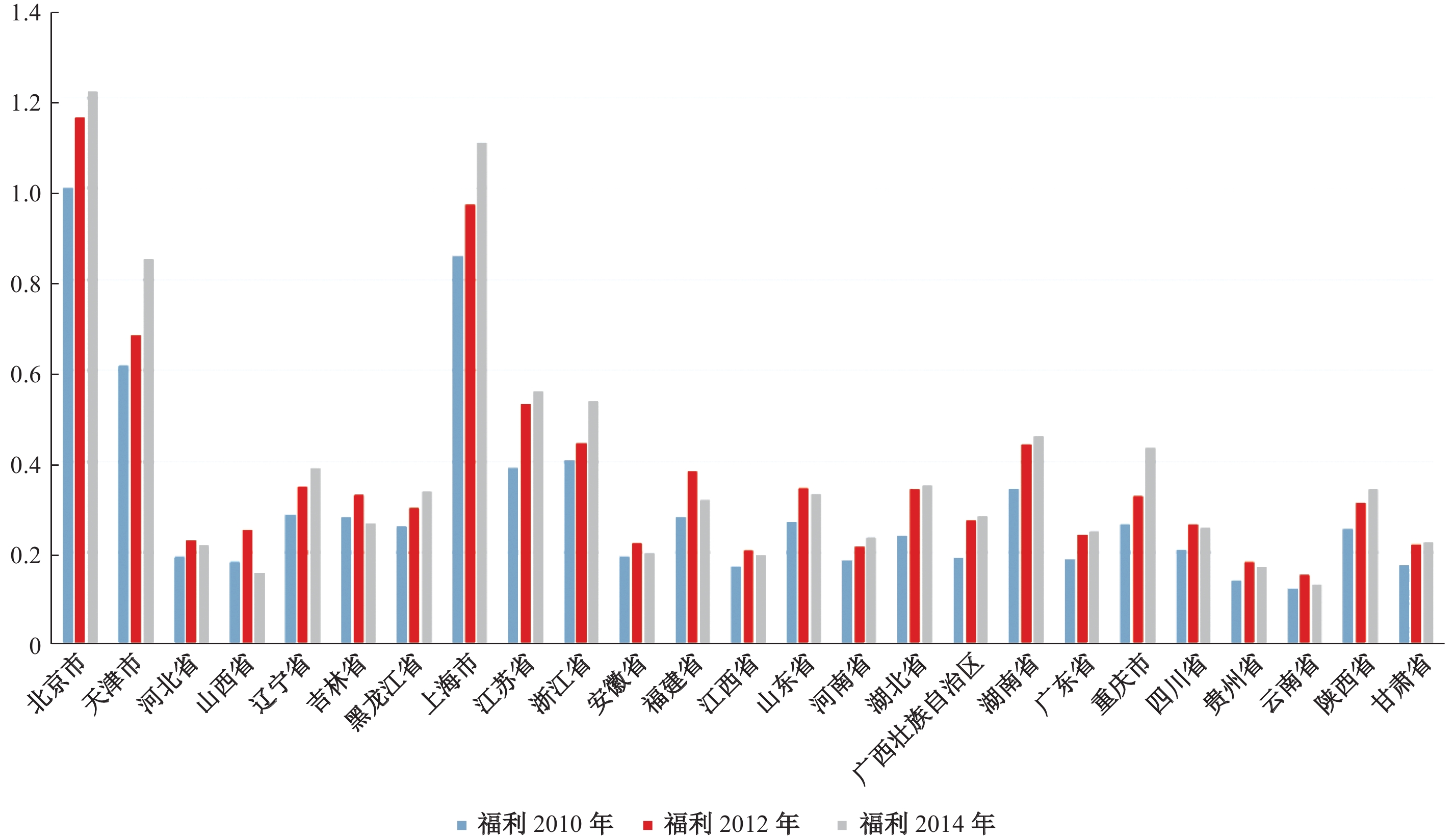
|
| 图 3 中国2010年、2012年和2014年分区域的城镇居民福利指数 |
通过图3可以直观感受到一线城市的福利水平增长迅速,而中低收入省市的福利增长缓慢,北京、上海和天津本身的福利水平已经遥遥领先,福利水平增加的幅度也远超其他省份,而其他省份的福利增长水平增速缓慢。随着时间的推移,一线城市的福利水平正在和其他省份拉开差距,特别是一线城市本身的福利水平已经很高,还在维持高增长,使资源越来越集中,从而导致了大量年轻人涌入“北上广”。2010—2012年,全国各省市的福利均有所增长,而2012—2014年平均增长率有所降低,但整体上我国的福利水平仍保持较高的增长速度。2010—2014年之间我国的居民寿命水平、工作闲暇并没有发生显著变化,最主要的变化是经济增速在2010—2012年保持在10%,而2012—2014年降低到了7%,经济增速的下降直接导致了福利水平的大幅降低,部分省份甚至还出现了负增长。由此可见,福利水平高度依赖经济发展,福利水平的增长速度比GDP增速更缓慢,因而经济下行对居民福利的负面影响也更大。
为了更好地比较不同省份福利的增长率,以及和GDP的差异,图4列出了2010—2014年各省份的福利水平增长率,以及相应的实际GDP增长率和名义GDP增长率。整体上看,福利水平的增长率低于GDP的增长率。通过图4,可以看出重庆的福利增长率最高,而湖南、湖北、江苏、天津、广东和辽宁等省份的增长率次之;山西省和吉林省的福利增长率为负,即2014年的福利水平竟然低于2010年,经过4年的发展,城镇居民的生活水平不升反降,令人震惊。福利增长率的高低表明该省市的居民生活水平提高的快慢,通过福利增长率,我们并没有发现地域分布上的显著区别。
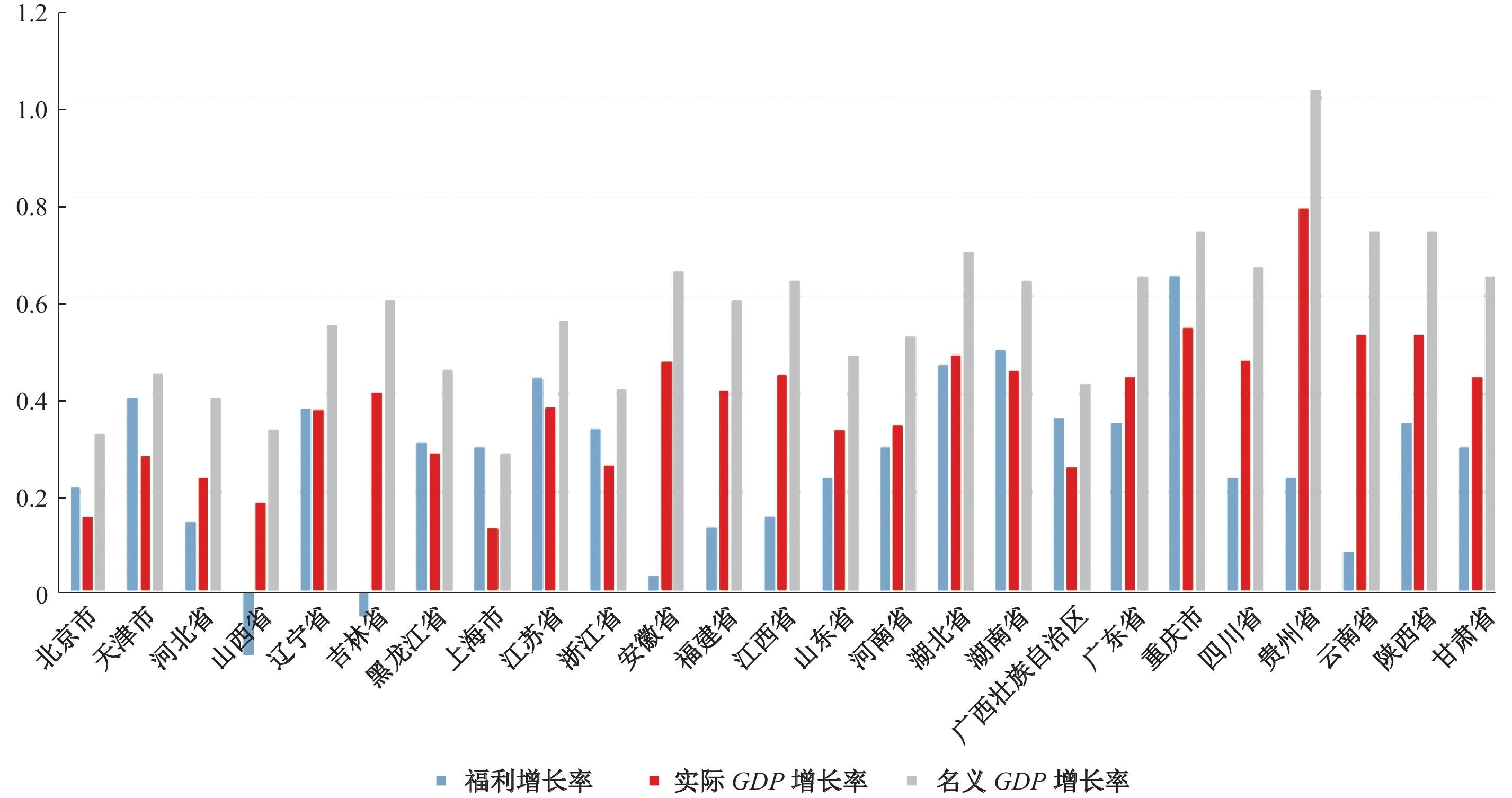
|
| 图 4 中国2010−2014年分区域城镇居民福利指数增长率和GDP增长率对比 |
城镇居民福利水平的增长率和实际GDP增长率相关性很高,但不完全一致。其中,“北上广”、江苏、浙江和重庆等发达省市的福利水平增长率大大超过了GDP增长率,而山西、吉林、安徽和云南等省份的福利增长率则远远落后于GDP增长率,这表明GDP增长率并不能完全反映福利水平的增长,它低估了“北上广”等一线城市的福利增长,而高估了经济欠发达省市的福利增长。
五、稳健性检验
由于中国的特殊国情,根据我国实际情况更改模型中的参数十分必要。经济学人智库发布的《中国消费者2030年面貌前瞻》(The Chinese consumer in 2030)中预计未来2016—2030年个人消费的平均增长率为5.5%,因此模型中假设的消费的固定年增长率g可以被赋值为5%;此外,适当调低人们对未来的重视程度,把折现因子β从0.99调整到0.98;绝大多数人口迁移发生在大学生毕业找工作或农民工进城打工,这时候的人已经度过了青少年时期,所以把起始的年龄从0岁重新设为20岁,即测算20岁以后的终身效用水平;去除个人消费中有一些异常值,只选取个人消费和房租在0.1%和99.9%之间的观测值,其他保持不变。
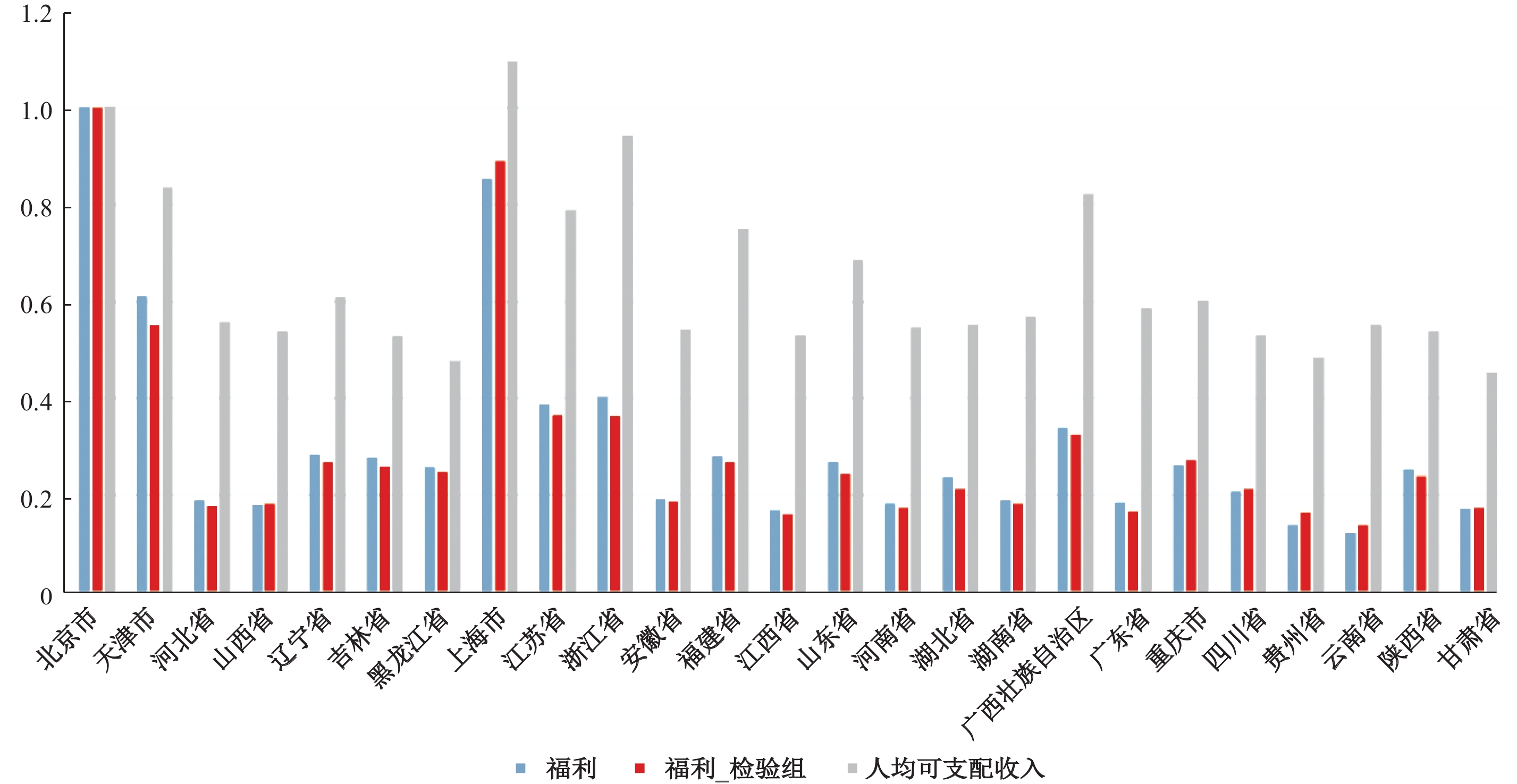
采用更改后的参数,对2010年的城镇居民进行再次估计,得到新的福利水平作为检验组,并与之前的结果进行对比。此外,由于人均可支配收入代表了居民的实际收入,能够比人均GDP更好地衡量居民财富水平,所以在对比图中加入了人均可支配收入。
根据图5,前两个柱状图分别代表前述测算的福利指数和这里修改了大量参数之后得到的福利指数,可以看出两者的变化非常小,并且前文得出的结论也同样适用,因此本文的模型十分稳健。
|
| 图 5 2010年城镇居民福利稳健性检验和人均可支配收入对比 |
柱状图的第三个是人均可支配收入,可以明显看出,除了北京、上海和东部沿海省份的人均可支配收入较高外,其他省份都十分接近,变化很小,因此人均可支配收入同样无法解释一线城市的高福利水平,而且和福利水平的相关性也不高,甚至不如人均GDP能够更好地衡量城镇居民的社会福利水平。
六、结 论
本文试图说明从随机性角度看,一个生活在北京的人需要减少多大比例的消费,能够和生活在其他省份的某人拥有一样的终生福利,并以此指标作为该省份对比北京的福利水平。该指标涵盖了寿命、消费、闲暇和不平等四个主要部分。根据计算的福利水平,我们发现:尽管人均GDP和城镇居民福利水平相关性很高,但仅凭GDP无法解释一线城市的高福利,并且人均GDP和福利水平有一定的差距;北京、上海等一线城市的福利水平远超其他省市,即使东部江、浙省份的福利水平也仅达到北京的1/3左右,而且这个差距有扩大的趋势,但是北京、上海的工作时间和收入不平等都位居全国前列;在其他省市,相较于人均GDP的差异,福利水平的区域不平等相对较小,特别是政府通过财政的转移支付降低了不平等程度;福利水平的增速显著慢于GDP的增速,而经济下行会导致福利水平的迅速降低。这些结论对如何更准确地刻画人民日益增长的美好生活需要与不平衡、不充分的发展之间的矛盾,如何探索更有质量、更有效率、更为公平的增长方式等论题具有重要的理论和实践意义。
① 因篇幅限制,2010年和2012年福利水平分解结果未予列出,如有需要可向作者索取。
| [1] | 方福前, 吕文慧. 中国城镇居民福利水平影响因素分析——基于阿马蒂亚•森的能力方法和结构方程模型[J]. 管理世界, 2009(4): 17–26. |
| [2] | 李连友, 宋泽, 刘子兰. 城镇移民生活福利水平研究[J]. 中国人口科学, 2014(6): 62–70. |
| [3] | 杨爱婷, 宋德勇. 中国社会福利水平的测度及对低福利增长的分析——基于功能与能力的视角[J]. 数量经济技术经济研究, 2012(11): 3–17. |
| [4] | 叶静怡, 王琼. 进城务工人员福利水平的一个评价——基于Sen的可行能力理论[J]. 经济学(季刊), 2014(4): 1323–1344. |
| [5] | 余谦, 高萍. 中国农村社会福利指数的构造及实测分析[J]. 中国农村经济, 2011(7): 63–71. |
| [6] | 袁方, 史清华. 不平等之再检验: 可行能力和收入不平等与农民工福利[J]. 管理世界, 2013(10): 49–61. |
| [7] | Aguiar M, Mark B. Has consumption inequality mirrored income inequality?[J]. American Economic Review, 2015, 105(9): 2725–2756. DOI:10.1257/aer.20120599 |
| [8] | Becker G S, Philipson T J, Soares R R. The quantity and quality of life and the evolution of world inequality[J]. The American Economic Review, 2005, 95(1): 277–291. DOI:10.1257/0002828053828563 |
| [9] | Córdoba J C, Verdier G. Inequality and growth: Some welfare calculations[J]. Journal of Economic Dynamics and Control, 2008, 32(6): 1812–1829. DOI:10.1016/j.jedc.2007.06.015 |
| [10] | Fleurbaey M, Gaulier G. International comparisons of living standards by equivalent incomes[J]. The Scandinavian Journal of Economics, 2009, 111(3): 597–624. DOI:10.1111/sjoe.2009.111.issue-3 |
| [11] | Jones C I, Klenow P J. Beyond GDP? Welfare across countries and time[J]. The American Economic Review, 2016, 106(9): 2426–2457. DOI:10.1257/aer.20110236 |
| [12] | Nordhaus W D, Tobin J. Is growth obsolete?[A]. Nordhaus W D, Tobin J. Economic research: Retrospect and prospect: Economic growth[M]. New York: National Bureau of Economic Research, 1972: 1—80. |
| [13] | Ravallion M. Mashup indices of development[J]. The World Bank Research Observer, 2011, 27(1): 1–32. |
| [14] | Sen A. Equality of what?[A]. McMurrin S M. Tanner Lectures on Human Values[M]. Cambridge: Cambridge University Press, 1980. |
| [15] | Sen A. Inequality Reexamined[M]. Oxford: Oxford University Press, 1992. |
 2018, Vol. 44
2018, Vol. 44





