一、引　言

在过去相当长的时期内，国内债券市场保持了无实质性违约的“世界纪录”。在债务濒临兑付危机时，总有机构合乎预期地充当接盘侠或神乎其神地找到兜底人，从而将兑付危机消弭于无形，成就了中国债券市场长期“零违约”的丰功伟绩。中国式兜底预期广泛存在于经济金融业态中，其典型形态有两种：第一，基于借款主体的隐性担保预期，如中央政府对地方政府债务的隐性担保、地方政府对融资平台债务的隐性担保、各级政府对辖属国企的隐性担保等；第二，基于借款项目的刚性兑付，如信托业的刚性兑付惯例、银行业抽屉协议式回购承诺、P2P等新兴行业的刚兑窠臼等。在基于借款主体的隐性担保形态中，借款人往往是地方政府、融资平台和国有企业，其偿债能力由借款人自身的资产价值（或自偿能力）和第三方的兜底预期共同构成及保障。在基于借款项目的刚性兑付实践中，借款资金通常对接于特定项目，且借款人承诺以项目现金流进行债务自偿；当其不足以偿债时，项目发起人等关联方的刚性兑付预期将深刻影响债权人的估值模式。^①

中国式兜底有着复杂和深刻的根源（详见第二部分的阐释）。中国式兜底预期模糊了风险资产和无风险资产的差异性，导致债务融资市场的风险定价机制失效或扭曲（陈道富，2015）。当存在刚性兑付预期时，市场无风险收益绑定于信托、理财等目标或承诺收益，银行存款也将日趋“理财化”和“同业化”（鲁政委，2015）。当存在中国式兜底预期时，债权人对借款人的风险状态、项目发起人的运营能力和其他关联人的风控能力可能不敏感，并倾向于挂钩风险资产的目标收益，提高对低风险借款人的信用风险补偿要求，进而推升其债务融资的理论成本（或其债务价值的隐含到期收益率水平）。那么，中国式兜底预期对高风险借款人的债务融资成本有何影响？其对不同风险状态借款人的债务估值体系有着怎样的结构性影响？

为了解构和回答上述问题，本文基于前述两种中国式兜底预期形态，将借款主体或借款项目都人格化为借款人，^②将借款人的资产价值视为其自偿能力。假设借款人以发债方式融资，当资产价值低于债务价值时，借款人将对债权人违约，并触发第三方的兜底或代偿预期，这将确保借款人的预期偿债能力（包括借款人自偿能力和第三方兜底预期）总是高于待偿债务价值。在此结构范式的基础上，本文对兜底预期下的借款人预期偿债能力进行了动态相依的随机刻画，在结构化模型框架内对其债务融资的理论成本进行了定价解析。模型的敏感性测算表明，在中国式兜底预期下，债权人倾向于“高估”低风险借款人的债务融资成本，而“低估”高风险借款人的债务融资成本，从而形成了结构分化的债务估值体系；其将间接推升低风险资产（或“无风险”资金）价格及预期，增强高风险借款人的风险承担倾向，诱导社会资本向高风险部门、行业或项目流动与配置，进而形成广泛的资本误配或资金错配。

从金融资产定价角度看，本文属于经济学范畴的公司债估值模型。在债券估值或债务估值体系中，利率债估值和公司债估值是两种主流范式。在固定收益证券的定价和投资决策过程中，一般使用利率债估值模型对国债等低信用风险品种进行估值。^③而在债务估值的经济学分析框架内，公司债估值模型属流行范式。利率债估值模型普遍假设债券价格由特定因子驱动，在对各因子随机刻画的基础上求解债券价格（Duffie和Kan，1996）。公司债估值模型假设公司债务价值由其资产价值（或现金流量）的随机运动驱动，在特定资本结构下界定公司债务的现金流结构，对其进行定价解析，相关文献及进展可参阅Wang等（2014）。利率债估值模型假设利率是时变或随机的，其仅考虑了市场风险因素；而公司债估值模型通常假设利率是常数，且内嵌了借款人的信用风险因素。从模型的兼容性来看，本文属于公司债估值模型范畴，共性特征包括：假设借款人的债务价值由其资产价值的随机运动驱动；借款人的资产价值服从几何布朗运动过程；风险中性测度下的利率是常数；借款人的资本结构或债务结构给定。本文对借款人自偿能力的模型刻画与公司债估值模型相似。而不同的是，本文考虑了中国式兜底预期对借款人预期偿债能力的动态相依影响，显性刻画了中国式兜底预期对借款人债务估值的潜在和复杂影响，此属中国经济金融之“常态”但久被学术讨论所忽略之现象。^④

从相关文献的分布情况看，与本文主题相关的是政府隐性担保（其属中国式隐性兜底预期的一种特例），刚性兑付相关文献相当罕见。政府隐性担保相关研究主要有：政府隐性担保的存在性及存在形式（罗荣华和刘劲劲，2016；钟辉勇等，2016）；政府隐性担保对有关主体的风险承担倾向（孙铮等，2006）和资金配置（王钰等，2015）的影响；政府隐性担保是否向有关借款人提供了融资便利，以及是否改善了其融资条件（方红星等，2013；罗荣华和刘劲劲，2016；钟辉勇等，2016）。现有文献仅经验考察了政府隐性担保是否对借款人的融资成本产生影响，而没有关注其对不同风险状态借款人债务融资成本的结构性影响。与现有研究不同，本文中的中国式兜底预期包括隐性担保和刚性兑付等丰富形态，且模型刻画了中国式兜底预期对不同风险状态借款人债务融资成本的结构性影响。本文的结论适用于中国式兜底预期下的债务估值问题，其适用范围更加广泛。

本文的行文结构安排如下：第二部分阐释了中国式兜底预期的典型形态及其现实根源；第三部分对兜底预期下的借款人债务融资成本进行了定价解析，将其与无兜底预期下的债务融资成本进行了对比分析，讨论了中国式兜底预期对高风险和低风险借款人的复杂影响；第四部分数值计算了借款人的风险状态与其债务融资成本之间的结构性关系，逻辑推演了其对资金误配的潜在影响；最后是全文结论及其政策启示。

二、中国式兜底预期的典型形态及其现实根源

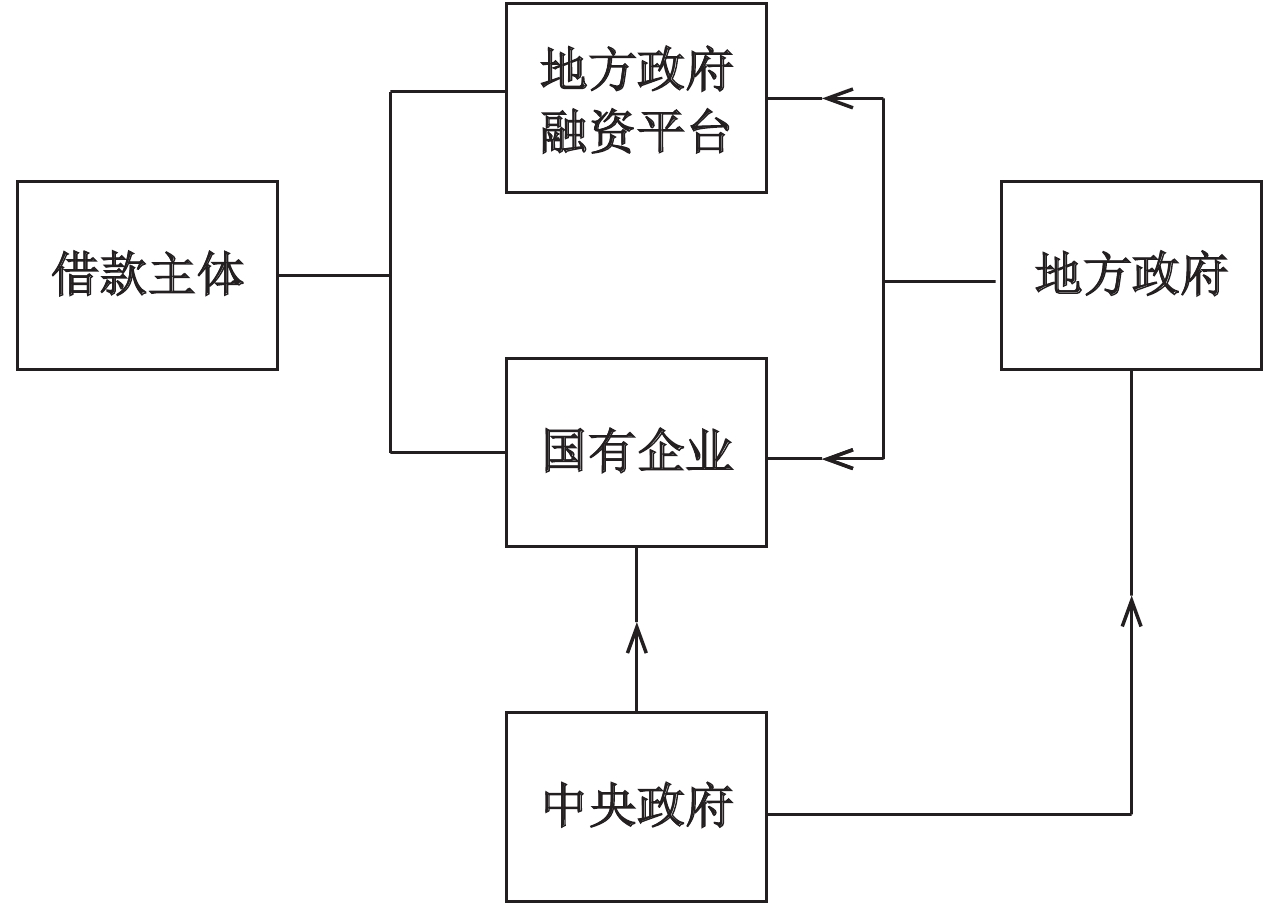
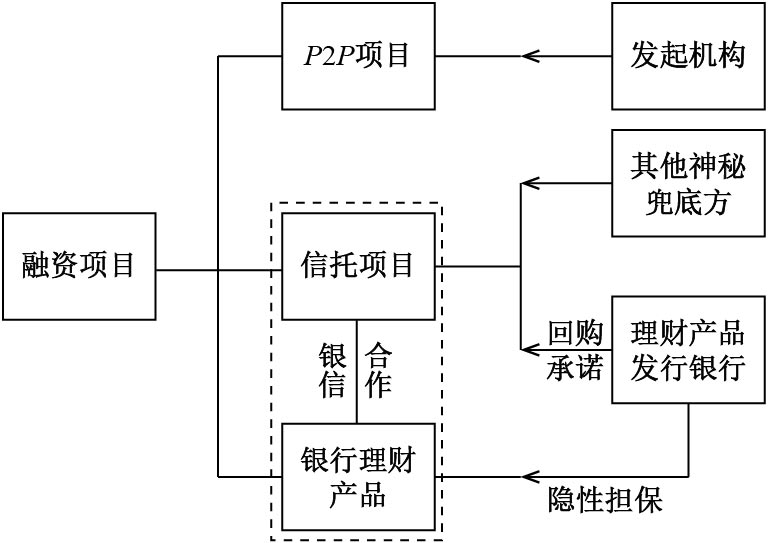
基于借款主体的隐性担保和借款项目的刚性兑付是中国式兜底预期的两种典型形态，图1和图2分别简要揭示了这两种兜底预期的常见形态。

（一）基于借款主体的隐性担保。我国久已形成了以“中央政府为核心、地方政府为主体”的隐性担保体系。中央政府向地方政府提供隐性担保的逻辑是：在非对称性财政分权模式下，地方政府仅有有限的财权，且常非债务发行主体，其责任空间较为模糊；地方政府是软预算约束主体，缺乏外部监督的制约机制；地方政府不能被破产清算，没有相应的债权保障机制；地方政府债务非纯粹的市场借贷关系，危机处置过程掺杂着维稳和其他诉求。中央政府对地方债务的隐性担保预期使政府债务风险不断上移和过度累积，进而“倒逼”中央政府提供事实上的“兜底”。在中央政府坚守不发生系统性和区域性风险的底线控制下，地方政府债务的信用下沉和风险上移将持续并存，上级政府的信用风险不断累积和凸显，刚性兑付仍将是市场普遍预期的一项政策选择（闫文涛和李燕，2014）。

地方政府提供公共服务的投资缺口巨大，为了满足职能需要，符合银行授信标准及监管要求，地方政府纷纷设立融资平台，以企业名义向银行业金融机构借款。融资平台为地方公益性或准公益性项目进行投融资服务，地方政府普遍向融资平台提供信用担保等融资便利，具体形式包括但不限于：地方人大等权力机构出具担保函，承诺将融资平台债务纳入预算安排；地方政府及其部门出具承诺函、安慰函、知悉函等进行暗示性兜底；地方政府不直接向银行债权提供信用担保，而是向信托投资标的等提供间接担保，以规避财预〔2012〕463号文等约束。在地方政府的各种隐性兜底下，融资平台债务构成了地方政府的隐性和有限承诺债务（刘红忠和许友传，2017）。

（二）基于借款项目的刚性兑付。刚性兑付是源自信托业的一种特殊现象。信托业的“刚性兑付术”可谓五花八门，如信托发起机构以自营资金向借款人发放信托贷款、认购信托计划受益权、垫付信托计划等，以确保原信托债务的及时兑付；信托发起机构滚动发行信托计划，构筑信托资金池和接盘原信托财产；信托计划关联方或其他神秘人出资购买或有条件兑付原信托计划。信托业的刚性兑付有着复杂的现实根源。在信托业重新登记和“一法两规”实施后，有关部门曾警告“谁出风险就停谁的业务”，使得“保兑付”成为行业性“市场惯例”。信托业刚性兑付的其他诱因包括：激烈市场竞争下的自适性反应；信托机构防范或有监管处罚的调适；监管干预和维稳关切下的应急举措。在信托计划濒临兑付危机时，监管机构总是在尊重市场规则和避免群体事件之间摇摆，但平衡强势主体和保护弱势群体的“天平”却时常偏向前者，用刚性兑付来约束信托无疑是有效法宝。

刚性兑付也是银行业财富管理领域的一大“潜规则”。中国相当部分的银行理财产品通过银信合作方式与企业或项目对接，其典型交易结构如下：银行发行理财产品募集资金，用其购买或投资信托计划，并指示信托机构向指定客户发放信托贷款或认购其表内信贷资产，银行承诺在信托投资标的到期前回购，银行对信托计划的底层资产提供了事实上的信用背书。即使在非银信合作式理财产品的兜售和兑付管理中，抽屉协议式隐性兜底也相当流行。据财政部公布的《龙江银行违规向村镇银行出售理财产品的会计信息质量检查公告》披露，龙江银行以出售理财产品方式做同业业务，向村镇银行出具了抽屉协议式兜底函，后者获得了龙江银行的信用背书，前者则隐匿信用风险和少提监管资本。^⑤

国内还存在其他形形色色的刚兑操作，P2P平台就始终难逃隐性兜底的宿命。从本质上讲，P2P平台是信息中介而非信用中介，其不应对投资项目进行兜底。然而，中国式P2P平台以信息中介之名行信用中介之实，其含糊报告投资项目、资金投向等关键信息，且不甘于赚取有限的中介费，豪取巧夺投资者的息差收入，这是后者要求其兜底的“蛮横”和“正当”理由。

三、中国式兜底预期与借款人的债务融资成本

（一）无兜底预期下的借款人债务融资成本。在风险中性概率测度Ω下，假设借款人的资产价值（或自偿能力）V_t服从几何布朗运动 $d{V_t} = $ $ r{V_t}dt + \sigma {V_t}dW_t^\Omega $ ，其中r表示无风险利率，σ表示借款人的资产波动性， $d{W_t} \sim N\left( {0,dt} \right)$ ，则借款人资产价值V_T的动态随机运动规律可表示为 ${V_T} = $ $ {V_t}\exp \left\{ {\left. {\left( {r - \displaystyle\frac{{{\sigma ^2}}}{2}} \right)dt + \sigma dW_t^\Omega } \right\}} \right.$ （t<T，t和T可分别视为当前时点和债务到期时点）。

假设借款人以发债方式融资，时点T的待偿债务规模为D_T。在时点T，若借款人的资产价值大于其待偿债务规模，则借款人能够充分偿债，债权人能收回全部债权；若借款人的资产价值小于其待偿债务规模，且无第三方的兜底或代偿预期，则借款人以资产价值为限进行债务偿付，债权人仅能收回V_T部分的债权，故借款人的债务价值D_1t（即在无兜底预期下，借款人的待偿债务在当前时点的预期价值）为：

${D_{1t}} = {e^{ - r\Delta T}}E_t^\Omega \left[ {\left( {{D_T}|{V_T} {\text{≥}} {D_T}} \right) + \left( {{V_T}|{V_T} < {D_T}} \right)} \right]$

(1)

其中， $E_t^\Omega \left[ \cdot \right]$ 表示在Ω测度下对括号内变量在时点t求条件期望，由标准的期权定价范式可知：

${D_{1t}} = {V_t}\Phi \left( { - {d_1}} \right) + {D_T}{e^{ - r\Delta T}}\Phi \left( {{d_2}} \right)$

(2)

其中， ${d_1} = \displaystyle\frac{{{\rm{Ln}}\left( {\displaystyle\frac{{{V_t}}}{{{D_T}}}} \right) + \left( {r + \displaystyle\frac{{{\sigma ^2}}}{2}} \right)\Delta T}}{{\sigma \sqrt {\Delta T} }}$ ， ${d_2} = {d_1} - \sigma \sqrt {\Delta T} $ ， $\Delta T = T - t$ ， $\Phi \left( \cdot \right)$ 表示标准正态累积分布函数。^⑥

设借款人债务价值的隐含到期收益率为y₁，则借款人的债务现值 ${D_{1t}} = {D_T}{e^{ - {y_1}\Delta T}}$ ，其与 ${y_1} = $ $\displaystyle\frac{1}{{\Delta T}}{\rm{Ln}}(\displaystyle\frac{D_T}{D_{1t}})$ 相互等价，将式（2）代入化简得：

${y_1} = r - \frac{1}{{\Delta T}}{\rm{Ln}}\left[ {\Phi \left( {{d_2}} \right) + \frac{{{V_t}}}{{{D_T}{e^{ - r\Delta T}}}}\Phi \left( { - {d_1}} \right)} \right]$

(3)

式（3）即为无兜底预期（或正常情景）下的借款人债务价值的隐含到期收益率，其中y₁−r相当于借款人的信用风险溢价或信用风险补偿要求。^⑦

需要指出的是，借款人债务融资的理论成本与其债务价值的隐含到期收益率相当（由市场无风险利率和借款人的信用风险溢价等构成，债权人的市场定价行为主要体现在如何确定借款人的信用风险溢价上），而借款人债务融资的实际成本由债券票面利率或息票利率等反映，后者指借款人向债权人承诺的定期付息水平。仅当以平价发行时，债券到期收益率才与票面利率相等，此时债券融资的实际付息成本与其理论估值一致。本文借款人的债务融资成本均指其理论成本，这是从债权人估值角度而言的。

（二）兜底预期下的借款人债务融资成本。当存在第三方兜底预期时，若借款人的资产价值大于其待偿债务规模，则借款人的自偿能力即能保证充分偿债；若借款人的资产价值小于其待偿债务规模，这将触发第三方的兜底或代偿预期，债权人预期第三方会对借款人未能清偿部分进行代偿，从而将借款人的预期偿债能力 $\widetilde {{V_T}}$ 提高至具备还款能力，其可用下式近似逼近：

$\widetilde {{V_T}} = {V_T} \max\left\{ {\left. {1,\frac{{{D_T}}}{{\mathop {\min }\limits_{\tau \in \left[ {t,T} \right]} \left( {{V_\tau }} \right)}}} \right\}} \right.$

(4)

显然，当 $\mathop {\min }\limits_\tau \left( {{V_\tau }} \right) {\text{≥}} {D_T}$ （ $\tau \in \left[ {t,T} \right]$ ）时，即借款人在[t，T]期间的资产价值始终大于其待偿债务，不会触发第三方的兜底或代偿预期，借款人的预期偿债能力等于其资产价值；而当 $\mathop {\min }\limits_\tau \left( {{V_\tau }} \right) < $ $ {D_T}$ 时，即在任意时点τ，只要借款人的资产价值低于其待偿债务规模，将触发第三方的兜底或代偿预期，并确保借款人的预期偿债能力始终大于待偿债务规模。^⑧可见，当不存在兜底预期时，借款人的债务价值仅由其资产价值驱动；而当存在中国式兜底预期时，借款人的债务价值将由预期偿债能力驱动，后者由借款人的资产价值和兜底方的代偿预期共同构成。当借款人的预期偿债能力服从式（4）随机过程时，其债务价值D_2t如下：

${D_{2t}} = {D_T}{e^{ - r\Delta T}}\left[ {P_t^\Omega \left( {\frac{{\widetilde {{V_T}}}}{{{D_T}}} {\text{≥}} 1} \right) + E_t^\Omega \left( {\frac{{\widetilde {{V_T}}}}{{{D_T}}}\left|\frac{{\widetilde {{V_T}}}}{{{D_T}}}\right. < 1} \right)} \right]$

(5)

其中， $P_t^\Omega \left[ \cdot \right]$ 表示在Ω测度下对括号内变量在时点t求条件概率。不妨令 $X = {\rm{Ln}}\left( {\displaystyle\frac{{\widetilde {{V_T}}}}{{{D_T}}}} \right)$ ，则有：

${D_{2t}} = {D_T}{e^{ - r\Delta T}}\left[ {P_t^\Omega \left( {X {\text{≥}} 0} \right) + E_t^\Omega \left( {{e^X}|X < 0} \right)} \right]$

(6)

其中，随机变量X的概率密度函数为 ${f_X}\left( x \right) = \varphi \left( {x;{\rm{Ln}}\left( {\displaystyle\frac{{{V_t}}}{{{D_T}}}} \right) + {\mu ^*}\Delta T,{\sigma ^2}\Delta T} \right) + $ ${\left( {\displaystyle\frac{{{D_T}}}{{{V_t}}}} \right)^{R - 1}} \varphi \Bigg( {x; - {\rm{Ln}}\left( {\displaystyle\frac{{{V_t}}}{{{D_T}}}} \right) + } $ ${\mu ^*}\Delta T,{\sigma ^2}\Delta T \Bigg)- $ $\left( {R - 1} \right){e^{\left( {R - 1} \right)x}} \left[ {1 - \Phi \left( {\displaystyle\frac{{x + {\rm{Ln}}\left( {{V_t}/{D_T}} \right) + {\mu ^*}\Delta T}}{{\sigma \sqrt {\Delta T} }}} \right)} \right]$ ，其中 ${\mu ^*} = r - \displaystyle\frac{{{\sigma ^2}}}{2}$ ， $R = \displaystyle\frac{{2r}}{{{\sigma ^2}}}$ ， $\varphi \left( {x;{\mu _1},\sigma _1^2} \right)$ 表示随机变量X服从期望为μ₁、方差为 $\sigma _1^2$ 的正态分布（Cox和Miller，1965），将其代入 $P_t^\Omega \left( {x {\text{≥}} 0} \right)$ 和 $E_t^\Omega \left( {{e^x}|x < 0} \right)$ 分别有：

$P_t^\Omega \left( {x {\text{≥}} 0} \right) = 1 + {\left( {\frac{{{D_T}}}{{{V_t}}}} \right)^{R - 1}}\Phi \left( { - {d_3}} \right)\left( {1 - \frac{1}{{\sigma \sqrt {\Delta T} }}} \right)$

(7)

$E_t^\Omega \left( {{e^x}|x < 0} \right) = \frac{{{V_t}{e^{r\Delta T}}}}{{{D_T}}}\Phi \left( { - {d_1}} \right) - \left( {1 - \frac{1}{R}} \right)\Phi \left( { - {d_2}} \right) + {\left( {\frac{{{D_T}}}{{{V_t}}}} \right)^R}{e^{r\Delta T}}\Phi \left( {{d_4}} \right)\left[ {1 - \frac{1}{{\sigma \sqrt {\Delta T} }}\left( {1 - \frac{1}{R}} \right)} \right]$

(8)

其中， ${d_3} = \displaystyle\frac{{{\rm{Ln}}\left( {\displaystyle\frac{{{V_t}}}{{{D_T}}}} \right) - \left( {r - \displaystyle\frac{{{\sigma ^2}}}{2}} \right)\Delta T}}{{\sigma \sqrt {\Delta T} }}$ ， ${d_4} = {d_3} - \sigma \sqrt {\Delta T} $ 。^⑨由式（6）至式（8）可知，兜底预期下的债务融资的理论成本为：^⑩

$\begin{aligned}{y_2} =& r - \displaystyle\frac{1}{{\Delta T}}{\rm{Ln}}\left\{ {\left[ {\Phi \left( {{d_2}} \right) + \frac{{{V_t}}}{{{D_T}{e^{ - r\Delta T}}}}\Phi \left( { - {d_1}} \right)} \right] + \frac{1}{R}\Phi \left( { - {d_2}} \right) + {{\left( {\frac{{{D_T}}}{{{V_t}}}} \right)}^{R - 1}}\left( {1 - \frac{1}{{\sigma \sqrt {\Delta T} }}} \right)}\Phi \left( { - {d_3}} \right) \right.\\& \left. { + {{\left( {\displaystyle\frac{{{D_T}}}{{{V_t}}}} \right)}^R}{e^{r\Delta T}}\left[ {1 - \frac{1}{{\sigma \sqrt {\Delta T} }}\left( {1 - \frac{1}{R}} \right)} \right]\Phi \left( {{d_4}} \right)} \right\}\end{aligned}$

(9)

（三）兜底预期对借款人债务融资成本的复杂影响。不妨令 $\eta = \displaystyle\frac{{{D_T}}}{{{V_t}}}$ 和 $\varepsilon = 1 - \displaystyle\frac{1}{R} = \frac{1}{r}\left( {r - \frac{{{\sigma ^2}}}{2}} \right)$ ，它们分别反映了借款人的债务杠杆状况和资产价值的运动趋势（如当ε>0时，借款人资产价值的确定性成分呈趋势向上的指数运动），则式（9）可简化为：

$\begin{aligned}{y_2} = & r - \displaystyle\frac{1}{{\Delta T}}{\rm{Ln}}\left\{ {\left[ {\Phi \left( {{d_2}} \right) + \frac{{{e^{r\Delta T}}}}{\eta }\Phi \left( { - {d_1}} \right)} \right] + \left( {1 - \varepsilon } \right)\Phi \left( { - {d_2}} \right) + {\eta ^{R - 1}}\left( {1 - \frac{1}{{\sigma \sqrt {\Delta T} }}} \right)}\Phi \left( { - {d_3}} \right) \right.\\& \left. { + {\eta ^R}{e^{r\Delta T}}\left( {1 - \displaystyle\frac{\varepsilon }{{\sigma \sqrt {\Delta T} }}} \right)\Phi \left( {{d_4}} \right)} \right\}\end{aligned}$

(10)

其中， ${d_1} = \displaystyle\frac{{ - {\rm{Ln}}\left( \eta \right) + r\left( {2 - \varepsilon } \right)\Delta T}}{{\sigma \sqrt {\Delta T} }}$ ， ${d_2} = {d_1} - \sigma \sqrt {\Delta T} $ ， ${d_3} = \displaystyle\frac{{ - {\rm{Ln}}\left( \eta \right) - r\varepsilon \Delta T}}{{\sigma \sqrt {\Delta T} }}$ ， ${d_4} = {d_3} - \sigma \sqrt {\Delta T} $ 。不妨令 ${W_1} = $ $= \Phi \left( {{d_2}} \right) + \displaystyle\frac{{{e^{r\Delta T}}}}{\eta }\Phi \left( { - {d_1}} \right)$ ， ${W_2} = \left( {1 - \varepsilon } \right)\Phi \left( { - {d_2}} \right) + {\eta ^{R - 1}}\left( {1\! - \displaystyle\frac{1}{{\sigma \sqrt {\Delta T} }}} \right)\Phi \left( { - {d_3}} \right) + {\eta ^R}{e^{r\Delta T}}\left( {1 - \displaystyle\frac{\varepsilon }{{\sigma \sqrt {\Delta T} }}} \right)\Phi \left( {{d_4}} \right)$ ，则式（3）和式（10）可分别简化为：

${y_1} = r - \frac{1}{{\Delta T}}{\rm{Ln}}\left( {{W_1}} \right)$

(11)

${y_2} = r - \frac{1}{{\Delta T}}{\rm{Ln}}\left( {{W_1} + {W_2}} \right)$

(12)

式（11）和式（12）分别是无兜底预期和有兜底预期下的借款人债务融资成本，其中W₂刻画了兜底预期对借款人债务融资成本的潜在影响，借款人的风险状态（η和σ）通过W₂间接影响兜底预期下其债务融资成本。

1. 当W₂<0时，有y₂>y₁。当存在中国式兜底预期时，借款人的债务融资成本被“高估”（y₂>y₁）的边界条件是W₂<0。

2. 当W₂>0时，有y₂<y₁。当存在中国式兜底预期时，借款人的债务融资成本被“低估”（y₂<y₁）的边界条件是W₂>0。

可见，在W₂<0或W₂>0的情形下，若能显性求解η或σ的边界条件或变动区间，则能观测不同风险状态借款人（高风险借款人的η或σ较高，低风险借款人的η或σ较低）的W₂符号，进而推断其债务融资成本是否被“高估”或“低估”。遗憾的是，当W₂<0或W₂>0时，我们难以显性求解η或σ的边界条件或变动区间。甚于此，我们在近似逼近现实的状态下，^⑪在借款人风险特征（η和σ）的宽幅变动范围内测试其融资成本的差异及变动趋势，进而观察借款人的风险状态与其债务估值的结构性关系。数值计算结果表明，在中国式兜底预期下，高风险借款人的债务融资成本倾向于被“低估”，而低风险借款人的债务融资成本则被“高估”。

四、数值计算及敏感性分析

（一）计算示例。数值计算需要设定关键参数{r，σ²，η，ΔT}的初值及其变动区间（其他变量可视为有关参数的函数）。关键参数的初值设定情况及其现实考量如下：第一，市场无风险利率r，设其与长期国债的到期收益率相当（约3.5%）；第二，借款人债务杠杆η的初值为62%（工业部门资产负债率的长期水平约60%，相应的债务杠杆约62%）；^⑫第三，借款人资产波动性σ的初值为10%；第四，债务期限ΔT标准化为1。鉴于债务杠杆和资产波动性分别反映了借款人的财务杠杆和风险承担倾向，分析两者对债务融资成本的边际影响，有助于推断借款人的风险特征与其债务融资成本的结构性关系，故下文在相当宽广的参数空间内做敏感性测试：当借款人的债务杠杆η∈[0.45，0.75]（Step=0.05）和资产波动性σ∈[5%，50%]（Step=5%）分别在上述区间变动时，它们对借款人债务融资成本的潜在影响，这里η和σ的取值涵盖了绝大多数可能的合理情景。

在上述初值设定下，表1给出了有关变量的递次计算过程及结果。由表1可知，在无兜底预期下，借款人的债务融资成本为3.50%，其与市场无风险利率相当，隐含具备“η=0.62和σ=10%”风险特征的借款人的信用风险溢价极低，可将其视为低风险借款人的参照基准；当存在中国式兜底预期时，低风险借款人（η=0.62和σ=10%）的债务融资成本从3.5%跃升至35.81%。

（二）无兜底预期下的借款人债务融资成本。当借款人的债务杠杆（η∈[0.45，0.75]，Step=0.05）和资产波动性（σ∈[5%，50%]，Step=5%）分别在上述区间变动时，表2报告了无兜底预期下借款人债务融资成本的变动状况。不难发现，给定借款人的债务杠杆，其资产波动性越大，债务融资成本通常越高；给定借款人的资产波动性，其债务杠杆越大，债务融资成本通常越高，这与市场正常的风险定价原则一致。^⑬

（三）兜底预期下的借款人债务融资成本。当借款人的债务杠杆（η∈[0.45，0.75]，Step=0.05）和资产波动性（σ∈[5%，50%]，Step=5%）分别在上述区间变动时，表3报告了兜底预期下借款人债务融资成本的变动状况。对比分析表2和表3的数值关系及变动趋势，可得如下规律：

1. 当借款人的资产波动性在特定边界以内变动时（如σ≤20%，隐含借款人的风险承担倾向相对较弱），无论是否存在中国式兜底预期，借款人的债务融资成本均为正，且兜底预期下的债务融资成本大于无兜底预期时。可见，对低风险借款人而言，兜底预期下的债务融资成本倾向于被“高估”。

2. 当借款人的资产波动性在特定边界以外变动时（如σ>20%，隐含借款人的风险承担倾向相对较强），无兜底预期下的借款人债务融资成本大于零，而兜底预期下的债务融资成本小于零。当存在中国式兜底预期时，债权人向高风险借款人（如σ>20%）索取的信用风险补偿小于零，隐含债权人不仅不要求高风险借款人付息，甚至还向其间接提供本金补贴。

3. 当借款人的财务杠杆给定时，若借款人的资产波动性在特定边界以内变动（如σ≤20%），随着资产波动性的提高，其债务融资成本呈上升态势，似乎低风险借款人的风险承担倾向越强，其债务融资成本越倾向于被“高估”；若借款人的资产波动性在特定边界以外变动（如σ>20%），随着资产波动性的提高，其债务融资成本呈下降态势，似乎高风险借款人的风险承担倾向越强，其债务融资成本越倾向于被“低估”。

（四）中国式兜底预期与资本误配。上文推演总体上表明：第一，当存在中国式兜底预期时，债权人倾向于“高估”低风险借款人的信用风险溢价，低风险借款人的债务融资成本（或市场“无风险”资金价格及预期）被抬升；高风险借款人的信用风险溢价则倾向于被“低估”，高风险部门、行业或项目的融资成本通常被拉低。这便形成了结构分化的债务估值体系。第二，当借款人的财务杠杆给定时，低风险借款人的风险承担倾向越强，其债务融资成本越倾向于被“高估”；而高风险借款人的风险承担倾向越强，其债务融资成本越倾向于被“低估”。即低风险借款人的风险承担与其债务融资成本正相关，而高风险借款人的风险承担与其债务融资成本负相关，债权人明显增强了高风险借款人的风险承担倾向。

在中国式兜底预期下，债权人对高风险借款人的“风险定价不足”拉低了高风险部门、行业或项目的融资成本，增强了高风险借款人的风险承担倾向；债权人对低风险借款人的“风险定价过度”则间接抬升了市场“无风险”资金价格及预期，可能诱使社会资本提高对“低风险”投资的回报目标及预期。从这个意义上讲，中国式兜底预期恶化了债务融资市场的逆向选择问题，可能会引致广泛的资本误配。在中国式兜底预期下，债务融资成本被“低估”刺激了高风险借款人的潜在资金需求，而低风险借款人的债务融资成本被“高估”诱使社会资本提高投资目标及期望，更多的资金流向有兜底预期的高风险部门、行业或项目（当存在中国式兜底预期时，高风险部门、行业或项目近似于“无风险”；但无论如何，高风险借款人的名义融资成本普遍高于低风险借款人），从而引致广泛的资本误配。

在中国式兜底预期下，债务融资市场上述扭曲的风险定价机制有助于解释中国经济金融中广泛存在的资本误配现象，这与已有文献的观察视角明显不同。部分文献研究了国内资本误配的关键诱因，如要素价格扭曲（陈永伟和胡伟民，2011）、所有制歧视（张庆君，2016）、行政干预（邢志平和靳来群，2016）、政治周期（周黎安等，2013）、房价绑架（陈斌开等，2015）等。与之不同的是，本文认为中国式兜底预期恶化了债务融资市场的逆向选择，诱导了社会资本的误配。

五、结论与启示

（一）主要结论

在债券市场的早期发展阶段，制度环境和债权保障机制等不尽完善，中国式兜底预期或有助于保护投资者的利益，维护金融市场的稳定，推动相关行业的发展，但也可能引致有关主体的道德风险，扭曲市场正常的风险定价机制，降低社会资本的配置效率。此属对中国式兜底预期总体影响的感性认知。为了理论上揭示中国式兜底预期对不同风险状态借款人债务估值的结构性影响，本文对兜底预期下的借款人债务融资成本进行了定价解析，并对其估值“偏离”状况进行了数值计算及比较静态分析，得到了以下合乎逻辑的推断：

第一，中国式兜底预期恶化了债务融资市场的逆向选择，诱发了结构分化的债务估值体系。在中国式兜底预期下，低风险借款人的信用风险溢价倾向于被“高估”，进而推升其债务融资成本；高风险借款人的信用风险溢价则倾向于被“低估”，进而拉低高风险行业、部门或项目的债务融资成本。债权人对高风险和低风险借款人的估值偏离及定价差异形成了结构分化的债务估值体系。

第二，中国式兜底预期可能引致了广泛的资本误配。在中国式兜底预期下，债务融资成本被“低估”刺激了高风险借款人的潜在资金需求，而低风险借款人的债务融资成本被“高估”也诱使社会资本提高投资目标及期望，更多的资金流向有兜底预期的高风险部门、行业或项目。这一扭曲的风险定价机制有助于解释经济金融中广泛存在的资本误配现象。

（二）政策启示

弱化中国式兜底预期是缓释其负面影响的关键，这要视中国式兜底预期的具体形态进行相应的设计及讨论。

1. 增强金融机构对地方政府债务的融资约束是弱化中央政府隐性担保预期影响的合意手段。在中国现有的政治体系和经济结构安排下，中央政府对地方政府的隐性救助预期是不可打破的“金科铁律”。弱化中央政府隐性担保预期的影响，不仅要约束地方政府的债务融资模式、融资规模以及融资冲动，更要切实增强金融机构的融资约束。从央行角度看，可提出考虑各地区负债状况及偿债能力的“合意信贷指导”。与以前的合意信贷控制机制不同（央行根据各地区的信贷增速是否超出其正常经济需要等，制定各地区的合意信贷规模，金融机构对各地区的增量信贷供给不得超过合意信贷规模），合意信贷指导非指令性计划，且考虑了地方政府的负债状况及偿债能力。从银监会角度看，可要求银行在按内部评级分类计算相关资本要求时进行额外的调节。银监会可对地方政府债务风险进行评估，将其划分为高风险组、中等风险组和低风险组，分别提出递减的资本调节系数，以引导合意的信贷供给和约束融资冲动。

2. 弱化或切断地方政府与融资平台的各种隐性联系，明确融资平台的企业属性。应切实将地方政府的投融资功能从融资平台剥离，明确融资平台的借款主体和偿债主体的市场地位，明确其企业债务属性（而非地方政府的或有债务），向市场释放无兜底的清晰信号，增强市场的风险意识和定价弹性。

3. 坚决打破信托业的刚性兑付神话，禁止银行业无底线的兜底活动。信托业无疑是中国刚性兑付的“重灾区”。在银行主导的银信合作业务中，银行借信托通道向其表内客户间接提供类信贷资金支持，双方的权利义务由抽屉式协议约定，不清晰的责任边界增强了投资者的或有代偿预期，也是投资者“强求”信托兜底的正当理由。监管部门有必要限制信托业的被动通道角色，坚决打破其刚性兑付神话。对银行理财产品而言，监管部门应充分落实“备案制”管理，要求银行明确报告各项理财业务的投资范围和具体对象，严格基于所投底层资产计提拨备和进行资本管理，回归“代客理财”的本质，禁止银行无底线的兜底活动。

4. 鼓励市场化机构或业务在职责边界清晰的情形下打破刚性兑付。P2P等市场化机构或业务要逐步纳入监管框架，并对其资金投向进行分类监管（如对常规性项目和超大项目分别实行“备案制”和“核准制”管理），明确P2P平台的信息中介角色，并在统一的监管平台下披露P2P平台的资金募集和投向信息。P2P平台的资金投向应清晰，所投项目应结构简单，且不得嵌套复杂产品或隐性承诺等，投资者应承诺具备风险自知和承受能力。在职责边界清晰的情形下，应鼓励P2P平台等市场化机构或业务打破刚性兑付。

① 基于借款项目的刚性兑付在房地产信托、融资平台融资类信托、银行非保本理财中相当流行。

② 即资金需求方。

③ 对企业债、公司债、私募债、中票等风险债券而言，投资者在运用利率债模型进行估值外，还考虑其信用风险因素。

④ 限于篇幅，引言和第二部分删减了部分文献。

⑤ 详见2015年9月24日《中国经济网》的报道。

⑥ 受篇幅限制，文中未给出式（2）的推导过程，需要的读者可与作者联系。

⑦ 此属结构化信用风险模型的经典内容。

⑧ 即 $ {\widetilde {{V_T}} = {D_T} \displaystyle\frac{{{V_T}}}{{\mathop {\min }\limits_{\rm{\tau }} \left( {{V_\tau }} \right)}} > {D_T}}$ 。

⑨ 推导过程略，需要的读者可与作者联系。

⑩ $ {{y_2} = {\rm{Ln}}\left( {{D_T}/{D_{2t}}} \right)/\Delta T}$ 。

⑪ 参数初值与实际情况尽可能相符。

⑫ $ {\eta = \displaystyle\frac{{{D_T}}}{{{V_t}}} \approx \displaystyle\frac{{{D_t}}}{{{V_t}}} {e^{r\Delta T}}}$ ，相关数据估算参阅许友传（2017）。

⑬ 即借款人的风险越高，其债务融资成本越高。