一、问题的提出

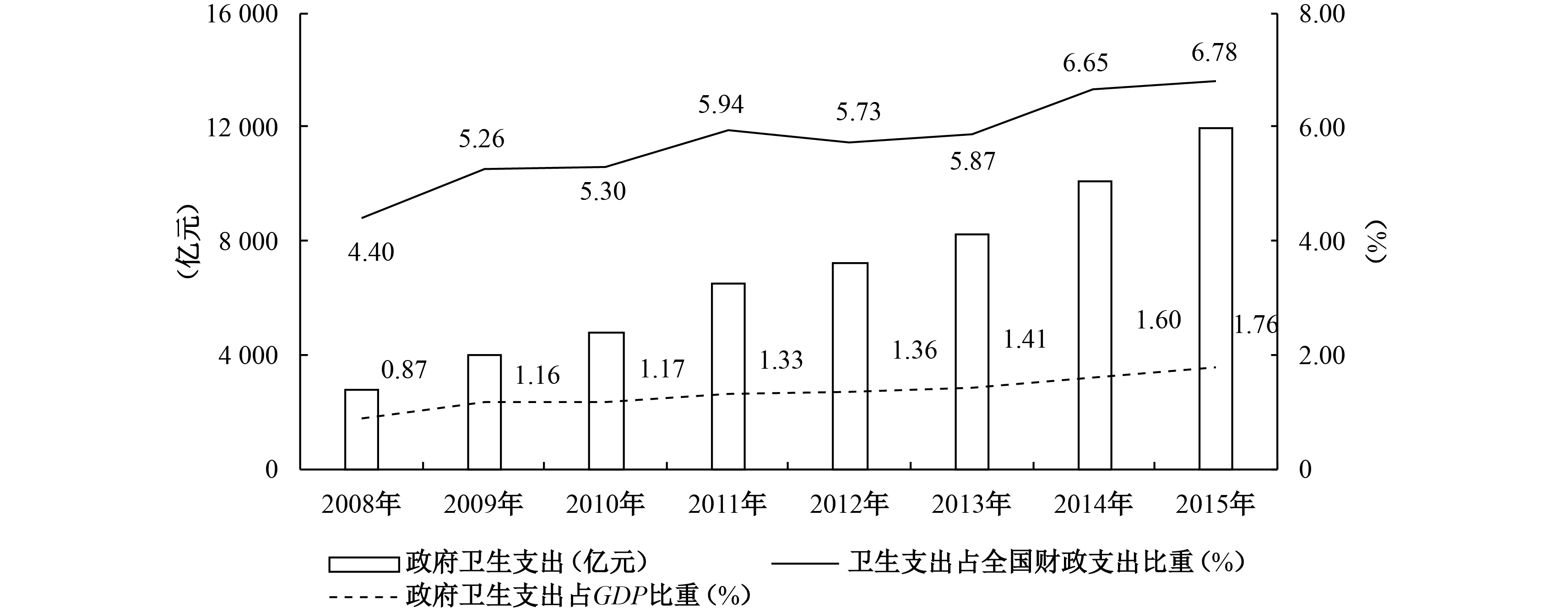
伴随着我国政府财政支出功能定位由“生产型财政”向“民生财政”的不断转变，近年来学者们基于不同的视角和方法针对政府卫生支出效率（Gupta和Verhoeven，2001；Greene，2004）、卫生支出或服务均等化（王晓洁，2009；冯海波和陈旭佳，2009；贾俊雪，2011）、最优支出规模（肖海翔等，2011；王萱，2013）及其影响因素（Matteo和Matteo，1998；肖海翔和刘乐帆，2013）等展开深入探究。但既有文献很少关注中国式分权体制下政府卫生支出的策略互动行为。Elhorst和Fréret（2009）采用静态空间Durbin模型证实了法国1992—2000年95个省的福利支出存在显著的标尺竞争效应。Atella等（2014）同样基于空间Durbin模型，证实了意大利的人均公共卫生支出存在空间相关性。这表明，地方政府行为不仅表现为“为增长而竞争”，也可能存在“为福利而竞争”的锦标赛（李郇等，2013）。事实上，随着国家绩效考核指向的不断变化和人民生活水平的不断提升，公众对社会福利的诉求日益强烈，地方政府的行为也会伴随着最优化目标而转变。那么，近年来我国政府卫生支出逐年增长态势是否表明卫生支出也存在“为福利而竞争”的策略性行为？倘若存在，则其占GDP的比例为何徘徊在2%左右（见图1）？显然，深入理解和探讨这一问题有其现实性和必要性。

1994年分税制改革形成的中国式分权结构极大地调动了地方政府的积极性，其引发的地方财政支出竞争行为已被多数学者证实（周黎安，2007；李涛和周业安，2009；郭庆旺和贾俊雪，2009；Caldeira，2012）。不难发现，现有针对财政分权影响地方政府财政支出行为尤其是公共支出行为的研究往往聚焦于省级总量支出指标，由此证明存在公共支出的省际空间外溢效应和竞争关系（郭庆旺和贾俊雪，2009）。而针对某一项公共支出是否存在交互作用展开的研究明显不足（Caldeira，2012）。此外，笼统地使用总量支出无法准确地揭示各项支出的空间关系，也难以探究其背后的经济学逻辑（周亚虹等，2013）。以省级层面讨论财政分权的公众福利促进效应，忽视省区内部城市间的资源禀赋、发展阶段及制度环境等空间异质性，往往会导致结果偏误。事实上，目前我国98%以上的政府卫生支出主要依赖于中央以下地方政府财政，其中省级以下政府在我国政府财政职能划分中承担了制定政策与标准的主要监督职能（张曙霄等，2012）。倘若假定中央政府向地方政府实施财政分权对所有地区卫生支出增长的作用相同，这一同质性显然不符合现实，因而在地市级层面研究某一项支出的策略性行为更切合实际。此外，城市层级政府也存在财政收支层面上拥有空间策略互动竞争的动机，孕育了财政分权的空间策略性竞争行为（张曙霄等，2012）。有鉴于此，从城市层级研究政府卫生支出空间行为、财政分权及地市级政府间财政分权空间策略互动行为影响政府卫生支出的微观机理，具有重要的理论及现实价值。

基于上述学术和政策背景，本文开展如下研究工作：首先，在理论研究上，考虑有限资源约束下的福利最大化决策，拓展一个“自上而下”的竞争模型，作为地市级政府间政府卫生支出相互影响的理论框架。其次，在研究方法上，利用动态空间Durbin模型解决政府卫生支出变化的“路径依赖”特征和缓解“内生性”问题，综合考虑了政府卫生支出的时间、空间和时空滞后效应，从而使研究结论更为准确。第三，在研究数据上，基于283个地级城市2007—2013年统计数据的应用，以使本文可以更微观、准确地刻画地级市政府的相互竞争行为。最后，在研究视角上，研究政府卫生支出是否存在空间策略互动行为，并深入挖掘财政分权的空间策略性竞争对政府卫生支出的短期和长期影响，进而使本文的研究结论更具现实价值。

二、理论模型

本文根据竞争模型（Besley和Case，1995；Caldeira，2012），假设某个省份存在两个地级市，分别命名为地区A与地区B。它们之间存在异质性并主要体现在GDP、人口规模、卫生基础状况等经济社会方面。设定地区A与地区B所隶属的省级政府作为社会计划者，行为目标是最大化所属地区居民的福利水平。由于某种福利水平如卫生福利状况的改善很可能会降低其他方面的福利，整体考虑将更加接近最优化状况。为此，首先需要考虑省级政府对地区A与地区B各种政府行为福利水平的权衡取舍。

假设居民卫生福利状况 $W$ ，取决于该地区政府的卫生支出额 $Q$ ，设定 $W = f\left( Q \right)$ 。根据实际状况，满足 $f'\left( Q \right) > 0$ 且 $f''\left( Q \right) < 0$ 。居民在卫生之外的福利状况 ${W^ - }$ 取决于地方政府其他方面的财政支出额 ${Q^ - }$ ，同样有 ${W^ - } = g\left( {{Q^ - }} \right)$ ，且 $g'\left( {{Q^ - }} \right) > 0$ ， $g''\left( {{Q^ - }} \right) < 0$ 。其中 $Q$ 与 ${Q^ - }$ 关系满足 $R = Q + {Q^ - }$ ，R表示地区可支配总的财政资金。对总福利函数而言，假定为卫生福利与其他福利简单加总，也即：

$W + {W^ - } = f\left( Q \right) + g\left( {{Q^ - }} \right) = f\left( Q \right) + g\left( {R - Q} \right)$

(1)

式（1）关于卫生支出 $Q$ 的一阶导数为 $f'\left( Q \right) - g'\left( {{Q^ - }} \right)$ 。

由于式（1）的二阶导数满足：

$f''\left( Q \right) + g''\left( {{Q^ - }} \right) < 0$

(2)

因此，式（1）取最大值时卫生支出 $Q$ 应该有：

$f'\left( Q \right) = g'\left( {{Q^ - }} \right)$

(3)

以上函数 $f( \bullet )$ 与 $g\left( \bullet \right)$ 取决于居民效用等因素，而地级政府能够决定的是卫生支出额 $Q$ 。如果某个地区在卫生支出及其他方面的财政支出能够实现 $f'\left( Q \right) = g'\left( {{Q^ - }} \right)$ ，那么该政府官员就实现了在约束条件下所能达到的居民最大福利水平，倘若上级政府（即省级政府）具有完全的信息，能够察觉下级（即地市级政府）行为的最优化决策并据此确定官员留任与否。那么，可以看出地区A与B之间的卫生支出不存在竞争。

考虑转移支付的支出决策。地方政府可支配的总财政资金R主要包括两个部分：财税收入tY和上级政府的转移支付TR，其中：t代表税率，f表示当地产出水平如GDP总量。那么，财政收入 $R = tY + TR$ 。基于以上有关卫生支出总量的讨论，设定 $Q = \lambda R$ ， $\lambda $ 为卫生支出占财政收入的比率（0≤ $\lambda $ ≤1），同样 ${Q^ - }{\text{ = }}\left( {1 - \lambda } \right)R$ 。因此，最优化的卫生支出比率应该满足：

$\frac{{\partial f}}{{\partial \lambda }} + \frac{{\partial g}}{{\partial \lambda }} = 0 \Rightarrow Rf'\left( {\lambda R} \right) - Rg'\left[ {\left( {1 - \lambda } \right)R} \right] = 0 \Rightarrow f'\left( {\lambda R} \right) = g'\left[ {\left( {1 - \lambda } \right)R} \right]$

(4)

根据式（4），任意地区确定其各自的卫生支出所占财政收入的最优比率，并且彼此独立。对所确定的最优比率 $\lambda $ ，卫生支出总额为 $Q = \lambda R = \lambda \left( {tY + TR} \right)$ 。可以看出，对最优的卫生支出占财政收入的比率，取决于当地经济社会环境的异质性，比如GDP总量、税率和上级政府的转移支付等，与其他地区不相关。对已确定的最优卫生支出比率，更优越的经济发展状况和更丰厚的上级政府转移支付都对应着更高的卫生支出水平。

对地区A，最优化的卫生支出比率应该满足：

$f'\left( {{\lambda _A}{R_A}} \right) = g'\left[ {\left( {1 - {\lambda _A}} \right){R_A}} \right]$

(5)

同样地区B满足：

$f'\left( {{\lambda _B}{R_B}} \right) = g'\left[ {\left( {1 - {\lambda _B}} \right){R_B}} \right]$

(6)

如果 $f'\left( {{\lambda _A}{R_A}} \right) = g'\left[ {\left( {1 - {\lambda _A}} \right){R_A}} \right] > f'\left( {{\lambda _B}{R_B}} \right) = g'\left[ {\left( {1 - {\lambda _B}} \right){R_B}} \right]$ ，上级政府最优决策是将更多的转移支付投向地区A。根据函数 $f( \bullet )$ 与 $g\left( \bullet \right)$ 的二阶导数的特性，地区A不断增加的转移支付会降低与地区B的边际福利收益差距。反之，上级政府会将更多的转移支付投向地区B。这也说明为何中央财政会向落后地区倾斜，其中原因就是这些地区财政拨款的边际福利收益相对较大。

倘若上级政府能察觉下级政府是否按照既定约束做出最大化居民福利的决策，此为最确切的竞争尺度。现实中往往存在极大的信息不对称问题，首先居民福利函数难以确定，且下级政府行为的边际福利效益更难以衡量，以致上级政府难以甚至根本无法判断下级政府是否已选择最优化决策。

当设定上级政府根据下级政府在各种行为上的财政投入来确定努力程度时，上级政府不会只关注下级政府的某一行为如教育、科技或者卫生支出等，依然会对各种行为支出进行权衡。对下级政府卫生支出 $Q$ 与其他财政支出 ${Q^ - }$ 来说，上级政府的关注程度分别用一个系数来刻画，设为 $x$ 与 ${x^ - }$ ，从而上级政府衡量下级政府行为努力的基本式为 $xQ + {x^ - }{Q^ - }$ 。不过，该式存在很大的局限性，如果 $x$ > ${x^ - }$ 的话，下级政府无疑会将所有财政投入到卫生支出中。反之，政府不会在卫生方面投入任何财政资金。因此，上级政府对下级政府的所有财政支出存在最低性要求 ${Q_0}$ 与 $Q_0^ - $ ，这是下级政府投入的最低红线。如此判断的话，上级政府判断下级政府的努力方程应该是：

$N = \left\{ \begin{aligned}& xQ + {x^ - }{Q^ - } , Q > {Q_0} {\text{且}} {Q^ - } > Q_0^ - \\&\;\;\;\;\;\;\;\; 0,\;\;\;\;\;\;\;\;\;\; {\text{其他情况}}\end{aligned} \right.$

(7)

当 $x$ 大于 ${x^ - }$ 时，下级政府会选择在卫生支出行为方面按照上级政府最低要求 $Q_0^ - $ 投入资源，而将剩余的财政资金全部投入到卫生支出中。反之，下级政府在卫生方面投入最低要求的财政资金。式（7）仅考虑了上级政府对下级政府的权衡，下级政府将所有精力用于上级政府对其努力的判断上。尽管这在中国自上而下的行政体制下具有一定的参考意义，不过中国政府官员是民众的公仆，他们行为的最终衡量标准应该是人民群众的满意程度。鉴此，下级政府还应该考虑民众对财政支出效果的满意程度。同时，上级政府在考察下级政府政绩和考虑下级政府财政收入分配的合理性时，人民群众的满意度的确占据着非常重要的地位。当上级政府对卫生支出具有更高关注度时，下级政府会将更多的财政资金用于卫生事业。不过，民众对各项公共事业的均衡化需求会相对弱化下级政府的这种行为选择。

由于 $N = xQ + {x^ - }{Q^ - } = \left( {x - {x^ - }} \right)Q + {x^ - }R$ ，为了体现民众的意志，上级政府修正下级政府努力的衡量标准为：

$N = \left\{ \begin{aligned}& \left( {x - {x^ - }} \right)Q + {x^ - }R - {\mathop{\rm sgn}} \left( {x - {x^ - }} \right) \cdot z{Q^2} ,\;\;Q > {Q_0} {\text{且}} {Q^ - } > Q_0^ - \\& \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{其他情况}}\end{aligned} \right.$

(8)

其中： ${\mathop{\rm sgn}} \left( \bullet \right)$ 是符号函数。

当 $x > {x^ - }$ 时，

$N{\rm{ = }}\left( {x - {x^ - }} \right)Q + {x^ - }R{\rm{ - }}z{Q^2}$

(9)

当 $x < {x^ - }$ 时，

$N{\rm{ = }}\left( {x - {x^ - }} \right)Q + {x^ - }R + z{Q^2}$

(10)

因此，卫生财政支出的极值为：

$Q = \frac{{\left| {x - {x^ - }} \right|}}{{2z}}$

(11)

当 $x > {x^ - }$ 时，卫生支出 $Q = \displaystyle\frac{{x - {x^ - }}}{{2z}}$ ，下级政府所体现的努力程度是最大化的。

当 $x < {x^ - }$ 时，卫生支出 $Q = \displaystyle\frac{{{x^ - } - x}}{{2z}}$ ，下级政府所体现的努力程度是最小化的。

为了简化起见，下文仅论述 $x > {x^ - }$ 时的情形。以上分析中，依然看出地区A与地区B的决策是相互独立的。同样假定上级政府是按照地级市政府决策独自权衡的，事实上，上级政府对所覆盖的地区，会潜意识地比较它们各自的财政投入状况。

当政府比较关注地级市政府卫生支出情况时，地区A的卫生最优支出应为：

${Q_A} = \frac{{x - {x^ - }}}{{2{z_A}}}$

(12)

地区B的卫生最优支出应为：

${Q_B} = \frac{{x - {x^ - }}}{{2{z_B}}}$

(13)

由于 $x$ 、 ${x^ - }$ 取决于同一上级政府对财政支出的偏好情况，因此各地区间具有同样的参数取值。

对地区A，如果 ${Q_A} > {Q_B}$ 的话，那么地区A将按照上级政府考察努力的最优化方式确定卫生的财政资金支出。当 ${Q_A} < {Q_B}$ 时，上级政府倾向于依据地区间卫生支出的差异来判断努力程度，那么地区A很可能会违背原先的最优化决策，选择扩大卫生支出来降低与地区B所存在的差异。可见，同一省区不同地市级政府可能存在卫生支出的空间策略互动行为。

值得指出的是，改革开放以来，中国凭借人口、土地等红利实现了经济高速增长。但这种以牺牲环境为代价的高速增长也对人们的健康造成了严重影响。随着民众健康意识的越来越强，对政府医疗服务供给的诉求日益高涨。2008年“民生财政”一词被政府首次应用于官方文件中，2009年中共中央、国务院发布的新一轮医疗卫生体制改革重点并将改革成效列入政府绩效考核范畴。因此，在国家财政和绩效考核方向逐步转向“民生指标”的背景下，一方面，同一省份内城市财政分权程度的提升会激发地方政府会通过提高当地医疗卫生服务供给增加民众满意度获取晋升筹码的政治激励。另一方面，财政分权会带来医疗卫生服务供给增加的同时，在现有体制框架下中国式分权同样孕育了地方政府竞争，而且这一竞争不仅体现在政府卫生支出上，还会体现在教育等其他支出方面（周亚虹等，2013）。事实上，在财政支出权利日益扩大的背景下，财政分权的空间策略性强度也会越大。由于不同城市的资源禀赋、经济发展水平、区位条件和制度环境等诸多因素存在着空间异质性，加之政绩考核指标逐步的多元化和“民生”化，为成功把握住政治晋升锦标赛激励机遇，辖区官员可能会综合权衡做出最有利于自身的决策。倘若同一省区的临近城市在政府卫生支出处于较强优势时，本地区官员会依据“邻居”城市的情况和投入的边际效益，可能会把精力放在其他诸如教育、科技等公共支出上来弥补劣势，借助财政转移支付等公共池渠道挤占卫生支出。根据理论分析提出如下两个假说。

假说1：在中国式分权制度框架下，同一省区内地市级政府卫生支出行为存在策略互动行为，一地区制定本辖区的卫生支出决策时会考虑到邻近地区的反应。

假说2：在现有财政体制安排下，财政分权对地方政府的公共支出具有推动效应，但地市级政府间财政分权的空间策略性竞争可能成为对政府卫生支出的约束因素。

三、研究设计

（一）计量模型

空间计量模型为准确刻画政府医疗卫生支出方面的空间策略互动行为提供了一个很好的工具。值得指出的是，以往应用于考察政府竞争行为的静态空间滞后模型（SAR）、静态空间滞后误差模型（SAC）（周亚虹等，2013）往往难以获得无偏估计。LeSage和Pace（2009）的研究指出空间Durbin模型（SDM）才是产生无偏估计的唯一模型。因此，空间Durbin模型成为了刻画政府公共支出空间交互行为的理想模型（Elhorst和Fréret，2009；Atella等，2014）。遗憾的是，上述文献忽视了空间变量如福利支出变化的“路径依赖”特征。从计量经济学角度看，静态空间计量模型未考虑到由联立性和遗漏变量导致的内生性问题，故通过取被解释变量滞后一期项来构建动态空间面板模型有其必要性。Caldeira（2012）纳入被解释变量的滞后一期，基于动态空间滞后模型考察了中国地方政府公共支出的空间行为。然而，Elhorst（2012）指出，变量的空间依赖关系不仅体现在当期地区间的相关影响，而且可能来自其他地区先前行为的影响。因此，针对本文的核心变量人均政府卫生支出可能还存在时间上的动态依赖性。为同时解决上述问题并缓解内生性偏误，本文拓展现有研究，将政府卫生支出的时间滞后效应、空间滞后效应和时空滞后效应纳入统一的分析框架中，借鉴Elhorst等（2016）提出的动态空间Durbin模型来模拟不同个体间的互动影响。设定如下动态空间广义嵌套模型：

${Y_{it}} = \tau {Y_{i,t{\rm{ - 1}}}}{\rm{ + }}\rho \sum\limits_{j = 1}^N {{W_{ij}}} {Y_{jt}}{\rm{ + }}\varphi \sum\limits_{j = 1}^N {{W_{ij}}} {Y_{j,t{\rm{ - }}1}} + \beta {X_{it}} + \theta \sum\limits_{j = 1}^N {{W_{ij}}} {X_{jt}} + {\alpha _i} + {\nu _t} + {\varepsilon _{it}}$

(14)

其中： ${Y_{it}}$ 代表被解释变量，本文特指第 $i$ 个城市第 $t$ 年的政府卫生支出 $R{G_{it}}$ ， ${X_{it}}$ 表示财政分权及控制变量， ${\alpha _i}$ 、 ${\nu _t}$ 、 ${\varepsilon _{it}}$ 分别代表城市和年份的固定效应以及随机扰动项。 ${W_{ij}}$ 表示空间权重矩阵，用来描述样本期各城市的空间关联结构。 $\tau $ 表示时间滞后系数，反映前一期政府卫生支出对本期的影响； $\rho $ 表示空间滞后系数，用来捕捉政府卫生支出政策的策略反应强度，如果 $\rho $ >0且显著，说明地级市政府在公共卫生支出上存在相互模仿的策略互动，反映出地方政府卫生支出决策表现为“策略互补”；反之，表现为“策略替代”； $\varphi $ 表示时空滞后系数。在模型的估计上，借鉴Lee和Yu（2010）提出的纠偏极大似然估计（BCQML）方法估计动态空间面板模型。

依据第二部分的理论模型可知，策略互动往往发生在同一省区内不同地市级政府之间。因此，本文设定所有空间权重矩阵 $W$ 的基础判断依据为两个城市是否属于同一省区。由于空间相互作用及空间效应大小、符号和显著性水平对空间权重矩阵的选取较为敏感（Elhorst和Halleck Vega，2017），借鉴周亚虹等（2013）、Halleck Vega和Elhorst（2015）的思路，本文依据地理空间、经济空间和社会空间等赋值标准构造逆距离的连续型空间权重矩阵作为比较，以刻画同一上级不同地市级政府之间的空间关联结构。具体构造如下：第一类是逆距离的地理空间权重矩阵W_geo。^①设定 ${d_{ij}}$ 为城市 $i$ 和城市 $j$ 间的地理距离，若两城市属于同一省区，则 ${W_{geo}} = 1/d_{ij}^\gamma $ ，否则取值为0。其中，地理距离依据地级市行政单位的经纬度数据计算而成。第二类是逆距离的经济社会空间权重矩阵。采用经济、社会两个赋值因素来构建空间权重矩阵 $W$ ，若城市 $i$ 和 $j$ 属于同一省区，则 $W = 1/{\left| {{X_i} - {X_j}} \right|^\gamma }$ ，否则取值为0。其中， ${X_i}$ 表示城市 $i$ 或 $j$ 样本期内人均实际GDP、人口密度、医疗技术人员和医疗机构的平均值，本文分别以符号 ${W_{grp}}$ 、 ${W_{pop}}$ 、 ${W_{jsry}}$ 和 ${W_{jgs}}$ 来表示相应的空间权重矩阵。需要指出的是，采用地区医疗技术人员数和医疗机构数作为赋值因素构建出社会空间权重矩阵，主要刻画出因社会基础资源空间差异所形成的空间关联结构。上述公式中的 $\gamma $ 表示空间衰减参数，本文取2。最后，针对上述五种空间权重矩阵进行行标准化。

（二）变量定义

1. 因变量。采用城市人均政府卫生支出，并取自然对数。

2. 自变量。采用财政分权度。财政分权程度的指标选择一直争议较大。为消除人口规模及转移支付的影响，本文借鉴傅勇（2010）、贾俊雪和应世为（2016）的做法来以地级市人均财政支出占总财政支出（中央政府本级、省级本级和地级市人均预算内财政支出总和）的比重来表征。

3. 控制变量。依据现有文献及数据可得性，选取人口密度、产业结构、经济发展水平、基础设施、环境质量等经济社会因素。其中，产业结构为第一产业增加值占GDP的份额；人均实际GDP用于捕捉经济发展水平的影响；以公路里程数与土地面积之比来反映城市基础设施水平。需要指出的是，环境质量对政府卫生支出规模的影响体现为两个方面：其一，环境质量下降通过影响当地居民的健康水平，从而会提高居民对卫生公共服务的需求；其二，环境质量提高改善居民健康福利从而减少公共卫生支出规模。本文采用全局主成分分析法（PCA），将全市工业废水排放量（万吨）、SO₂排放量（吨）、工业烟尘排放量（吨）以及城市建成区绿化覆盖率（%）四个反映环境的指标进行信息整合来衡量城市环境质量。具体做法为：首先对上述四个环境质量指标进行正向和逆向标准化处理，进而基于全局主成分分析法得到环境质量综合指数，其值越大，说明环境质量越好。

（三）数据来源

基础数据来源于《中国区域经济统计年鉴》（2008—2014年）、《中国城市统计年鉴》（2008—2014年，考虑到《2007年政府收支分类科目》[财预（2006）401号]对各项政府支出功能进行重新分类，因此，本文选取的数据观测期为2007年至2013年（T=7），样本截面为中国283个地级市，总样本数为1 981个。所有以货币为单位的变量，均采用各城市其所属省份CPI指数进行平减化处理，基期为2007年。为减少异方差，货币变量如政府人均卫生支出和经济发展水平分别取自然对数。表1 汇报了主要变量的基本描述性统计。

四、实证分析结果及其解释

回归之前，我们采用控制了相关因素后的全局Moran’s I指数展开空间相关性预检验，估测样本期间内政府卫生支出在地理、经济、社会空间上均表现出的相关性。结果显示，在 ${W_{geo}}$ 、 ${W_{grp}}$ 、 ${W_{pop}}$ 、 ${W_{jsry}}$ 和 ${W_{jgs}}$ 五种权重矩阵下的全局Moran’s I值分别为0.642、0.674、0.638、0.611和0.632，且均通过了1%的显著性水平检验，初步判断地市级政府卫生支出具有显著的空间相关性。那么，其呈现怎样的特征，有待后续计量的进一步严格检验。

（一）不同空间权重矩阵下地方政府卫生支出反应方程的CQML回归结果分析

在实证分析前，为捕捉不可观测的地区异质性和宏观经济因素的共同冲击，我们基于五种权重矩阵来检验空间效应和时间效应的存在性。LR检验表明同时存在上述两种效应；根据Elhorst等（2016）的做法，经Wald-spatial-lag检验和Wald-spatial-error检验显示动态空间Durbin模型无法退化至空间滞后模型（SAR）和空间误差模型（SEM），证实了采用包含被解释变量内生交互项（W×Y）和解释变量外生交互项（W×X）的空间Durbin模型的必要性（LeSage和 Pace，2009）。^②因此，接下来的估计在控制空间固定效应和时间固定效应框架下展开。为进行比较分析，我们选择最小二乘法（OLS）作为参照系，表2同时汇报了OLS模型、静态空间Durbin模型和动态空间Durbin模型的估计结果。

对比发现，在校正了空间相关性导致的估算偏差以及充分考虑到时间滞后效应和时空滞后效应后，各系数符号、显著性水平及其系数大小更符合理论预期，凸显了采用动态空间Durbin模型估计的优势。同时表2所有动态模型中系数 $\tau $ + $\varphi $ + $\rho $ <1，显示出模型的稳健性。因此，接下来的分析主要围绕动态空间Durbin模型的估计结果展开。首先，从空间维度上看，空间滞后系数（ $\rho $ ）在五种权重矩阵设定下均在1%的水平上显著为正。这表明，同一省区的地市级政府卫生支出决策确实存在显著的策略互动行为且主要采取互补性策略。反映出近年来，同一上级管辖的不同地市级政府间，在国家绩效考核方向逐步转向“民生指标”下，孕育了政府公共卫生支出的竞争，与本文的理论假说1形成了呼应。这意味着，对某一城市的政府官员而言，倘若处于同一省区对手选择提高政府卫生支出，那么该城市政府官员的最优策略也是提高政府卫生支出，达到“高水平”的均衡状态，这有力地解释了近年来我国政府卫生支出绝对额持续提升的客观现象。估计结果还表明，同一省区内本城市政府卫生支出程度与地理、经济、医疗基础水平相近城市的卫生支出水平密切相关。从策略互动强度来看，相较于医疗基础水平以及经济距离相近地区，地理距离邻近城市的策略互动强度更为突出。以表2地理距离权重矩阵下空间效应为例，其系数为0.546，即省内邻近城市加权平均的人均政府卫生支出水平每提高1%，会带来本城市的政府卫生支出水平提高0.546个百分点。因此，通过政府公共卫生支出等非生产性支出以改善医疗卫生服务供给，必须充分释放地市级政府在公共卫生支出方面的激励效应，设置科学的绩效考核指标体系重塑竞争规则，从“宏观经济绩效”向“微观福利绩效”转变中，引导政府官员展开卫生服务供给的“趋优竞争”, 逐渐实现政府在卫生领域责任的回归。接下来，从时间维度上看，政府卫生支出的时间滞后系数（ $\tau $ ）在五种空间权重矩阵情形下均在1%的水平上显著为正。这表明，政府卫生支出变化具有典型的路径依赖特征，即前期人均政府卫生支出处于较高水平，则当期人均政府卫生支出规模将可能继续走高，形成一个良性的自我强化过程，从而表现为“惯性效应”。最后，从时空双维度的视角可知，政府卫生支出的时空滞后系数（ $\varphi $ ）在五种空间权重矩阵情形下为正，但仅在社会空间权重距离下显著，表明省内公共医疗卫生基础水平相近的邻近城市上一期较高的政府卫生支出会促使本城市当期的政府卫生支出的提升。这主要归因于邻近地区政府卫生支出对本地区的“示范效应”，即面对邻近地区尤其是公共基础卫生医疗水平与本地区相近的周边地区更好的公共卫生供给和更高的居民医疗满意度，往往容易获得上级部门的认可，本地区政府出于居民舆论压力、官员政绩考核谋求晋升机会，可能将其视为“典型”并随后学习模仿邻近地区的做法进而通过增加本地区政府卫生投入提高卫生绩效。

财政分权度也是本文关注的变量。表2结果显示财政分权变量的系数在五种空间权重情形下的系数均为正数，且均通过了1%的显著性水平检验。说明上级政府将更多财政支出权限下放至下一级地级市政府对促进城市政府卫生支出有着一定的推动效应。究其原因，可能在于2007年党的十七大报告明确将改善民生为主的社会建设纳入国家发展战略。2008年3月，全国人大审议的《关于2007年中央和地方预算执行情况与2008年中央和地方预算草案的报告》中首次使用了“民生财政”一词，此后中央的政策目标到支出安排越来越体现出“民生财政”的导向。2009年中共中央、国务院开展新一轮医疗卫生体制改革，目标是逐步实现人人享有基本医疗卫生服务，有关医疗卫生体制改革成效被各级政府纳入政绩考核范畴。由此可见，在城市财政分权程度不断增强、政府财政由“建设财政”逐步向“民生财政”转变、政府医疗卫生体制改革成效纳入政绩考核的背景下，地方政府医疗卫生供给得到了一定程度上的重视和提升，中国城市政府卫生支出显示出逐年递增的态势。该结论为当前转变政府职能、依托简政放权和深入推进医疗卫生供给侧改革等改善公共服务供需矛盾、提高经济发展质量提供了一个科学决策的经验证据。根据表2的估计结果我们可以得到如下几点认识：产业结构的系数在五种空间权重矩阵下至少在10%的水平上显著为负，表明经济发展水平相对落后地方往往居民疾病率也相对较高。因此，政府具有较大公共卫生支出的压力和责任。经济发展水平对人均政府卫生支出的影响系数在1%的水平上显著为正，这反映出地市级地方政府的卫生投入高度依赖于其经济发展水平，经济越发达地区的居民从地方政府公共医疗服务中获益最大；人口密度、基础设施和环境质量变量的系数在五种空间权重矩阵下有正有负，但这一作用不具有统计显著性，由于该指标不是本文考察的重点，限于篇幅，在此不再赘述。

（二）财政分权的空间溢出效应检验

当存在空间溢出效应时，某因素的变化不仅会导致本地区政府卫生支出的变化，而且会通过系列反馈作用影响邻近地区的政府卫生支出，也即存在策略互动。根据表2结果，地理距离权重下政府卫生支出的空间关联程度明显优于其他权重矩阵下的估计结果，反映出地理区位邻近地区的政府卫生支出规模大的地区对周边地区产生了较大的空间影响力。在信息不对称条件下，同一省区上级政府考核下级政府，更有可能针对地理区位邻近地区地方官员在改善卫生供给上的努力程度及绩效展开比较，进而决定是否提拔或留任。因此，本文基于表2地理距离权重矩阵下动态空间Durbin模型估计结果显示，W×财政分权变量的系数估计为−2.261，且在1%的水平上显著，初步说明城市财政分权水平在空间上存在明显的负相关性，是否存在地方政府竞争扭曲政府公共卫生支出呢？为此，本文进一步从短长期角度分解出各因素对政府卫生支出的直接效应和间接效应。有关空间溢出效应的存在性可根据间接效应的显著水平展开判定（Elhorst，2012)。根据Elhorst（2012）、Elhorst等（2016）的思路，我们对式（14），将间接效应从时间维度上分为短期效应和长期效应，分别反映各因素对政府卫生支出的短期即时效应和考虑时间滞后效应的长期影响。上述效应可通过求 $N$ 个个体因变量对第 $k$ 个自变量的偏导数组成矩阵，进而计算矩阵非对角线元素行和平均值，具体公式为：

${\text{短期间接效应}} = {[(1 - \tau )I - \rho W]^{ - 1}}[{\beta _k}{I_N} + {\theta _k}W]\overline {^{rs}} $

(15)

${\text{长期间接效应}} = {[(1 - \tau )I - (\rho + \varphi )W]^{ - 1}}[{\beta _k}{I_N} + {\theta _k}W]\overline {^{rs}} $

(16)

其中： $I$ 为单位矩阵， $\overline {rs} $ 表示测算矩阵非对角线元素行和平均值的运算符，其他符号变量与式（14）变量含义相同。

表3显示，除了环境质量外，其他指标均存在长期效应且其效应（系数绝对值）均大于短期效应，从而表明各因素对政府卫生支出具有更为深远的长期影响。本文重点考察政府间财政分权的空间策略互动行为在短期内和长期内对政府卫生支出的影响，可以看到，无论在短期还是长期条件下，财政分权对政府卫生支出的间接效应均为负，显示出财政分权的空间策略性行为属于“策略替代”且城市间存在长期博弈特征，这说明控制城市其他条件下，地市级政府间财政分权的空间策略互动强度的增加并不利于城市公共卫生福利的供给，证实了本文的理论假说2。需要说明的是，尽管前文的估计显示，财政分权虽然对政府卫生支出具有推动效应，但在中国式分权体制下，其空间策略性竞争反而抑制了政府卫生支出，这或许构成了我国政府卫生支出占GDP比重徘徊在2%左右背后的制度与经济学的重要成因之一。

（三）稳健性检验

1. 基于区域异质性的稳健性检验。考虑到城市样本的空间异质性特征，本文结合地理距离空间权重矩阵及采用人均财政支出指标计算的财政分权度展开地区分组回归，结果呈现于表4第1—3列中。从时间维度上看，政府卫生支出的“惯性效应”在东部地区体现最为明显，其次为中部，西部排最末。从空间维度上看，政府卫生支出的“竞争效应”表现为中部地区>东部地区>西部地区。从时空双维度上看，东部地区和中部地区的系数显著为负，而西部地区显著为正，究其原因，通过统计2007−2013年东、中、西部地区的人均政府医疗卫生支出年平均规模，如图2所示。结果发现，东、中、西部地区人均政府医疗卫生支出年均规模几乎一致，西部地区略高。显然，对经济相对落后的西部地区而言，增加人均政府卫生支出越有可能获取政治晋升和留任的优势。因此，其更有可能根据上期邻近地区的政府卫生支出做出正向反应；较高经济发展水平的东部和中部地区人均寿命较高，居民健康福利较高，因此医疗卫生支出的边际效益相对较低，辖区官员为了晋升可能会从其他途径寻找竞争优势。比如同一省区的A城市上一期医疗卫生支出很高，B城市政府官员可能会认为通过医疗卫生支出竞争难以取得优势，因而可能会把精力放在其他诸如教育、科技等公共支出，削弱了政府卫生支出的正向激励。从财政分权变量的系数来看，财政分权对政府卫生支出具有显著的推动效应，其影响力度与经济发展水平密切相关，从估计系数来看，东部>中部>西部，证实了前文所得出的财政分权显著地促进了政府卫生支出规模提升的结论。从财政分权的空间溢出效应来看，均表现为“策略替代”，但西部地区不显著。

2. 基于不同卫生服务供给指标的稳健性检验。医疗服务供给不仅体现为投入层面，还体现为产出层面。因此，本文进一步从产出角度采用每万人拥有医疗机构病床数以及每万人拥有卫生技术人员数作为政府卫生服务供给程度进行稳健性回归，结果见表4第4和第5列。从结果来看，核心变量与前文的估计结果基本一致。

3. 基于不同财政分权度指标的稳健性检验。依据前文考虑中央本级、省级本级和地级市本级三级政府支出思路来测度人均财政收入的分权指标和以总量规模作为财政分权稳健性指标展开重新估计，结果分别呈现于表4第6和第7列中。从以财政收入分权作为财政分权代理变量和以总量度量财政分权度的估计结果可知，所有核心指标在系数大小、符号和显著性水平上与前文保持了较好的一致性，进一步证实了本文结论的稳健性。

（四）财政分权对政府卫生支出竞争影响程度的进一步考察

前述我们已经验证了地市级政府存在着竞争行为，财政分权及其空间策略性竞争均会影响到政府卫生支出，且存在区域异质性。那么，财政分权又是否会影响到地市级政府卫生供给的策略互动效果呢？因此，本文将纳入财政分权与政府卫生服务供给滞后项（W×政府卫生供给）的交叉项基于地理距离空间权重矩阵进行重新估计，结果呈现于表5中。由表5可知，政府卫生支出空间滞后项的系数始终显著为正，而财政分权与空间滞后项的系数显著为负，这表明，财政分权确实会缓解政府卫生服务供给的空间策略互动强度，这与Caldeira（2012）关于财政分权削弱了公共支出策略互动的结论类似。显然，面对财权上收、事权留置，“为晋升”所支配的地级市政府往往在公共支出的水平和结构上存在“此消彼长”的策略互动行为，进一步佐证了前文财政分权存在空间策略互动的结论。在此背景下，现阶段深化财税体制改革与医疗卫生供给侧改革应当协调、协同推进。

五、主要结论及启示

本文在构建地方政府卫生支出策略互动理论模型的基础上，应用动态空间Durbin模型和2007−2013年中国283个城市面板数据对分权体制下政府卫生支出竞争行为进行了经验检验，同时揭示出财政分权及其空间策略性竞争对政府卫生支出的影响。主要结论与启示如下：

（1）在当前中国式分权体制下，我国同一省区内地市级政府卫生支出决策确实存在显著的互补型策略互动行为，反映出倘若同一省区内相邻地市级政府提高医疗卫生供给水平，那么本城市政府也会相应提高政府卫生供给水平，达到“高水平”均衡。为此，中央政府应增加公共医疗服务、人民健康状况等发展成果和社会治理的绩效考核指标并赋予其更大的权重，将共享发展理念纳入地方政府竞争目标函数中。发挥竞争机制积极引导地方政府展开卫生服务供给的高质量发展，加速实现公共卫生服务的均等化进程。对比地理距离、经济距离和社会距离三类空间权重矩阵设定下竞争效应的大小可以发现，地理相邻地区出于竞争的策略互动强度更为突出。基于政府卫生支出在时间单维度、空间单维度和时空双维度上分别表现为惯性效应、标杆效应和示范效应的演变特征，因而推进医疗卫生供给侧改革必须坚持常抓不懈、树立标杆和示范引领。

（2）研究还发现，财政分权可以有效地促进政府卫生服务供给，但无论是短期还是长期条件下，城市政府间财政分权的空间策略性竞争对政府卫生支出具有显著的抑制作用，其主要原因在于财政公共支出竞争结构的变化，较好地解释了政府卫生支出比重一直徘徊在2%左右的原因。事实上，本文的理论分析和经验证据也反映出，“为晋升”所支配的地市级政府往往在公共支出的水平和结构上存在“此消彼长”的策略互动行为。在当前地方政府竞争模式下，加入任何一种诸如教育、医疗等激励指标，都可能让地方政府展开竞争，但由于信息不对称，很难保证这些用于激励官员的指标与社会福利最大化相一致（陆铭，2017）。因此，中央政府在市场化的改革取向中，适度增加区域公共事务的权利和责任，一方面考虑设置诸如公共服务满意度综合考核指标实现社会整体福利最大化；另一方面，因地制宜地设置偏向公共医疗服务供给数量和质量方面的绩效考核指标解决医疗卫生供给不充分的问题。

① 基于地理距离考察范围内任何两地区间的相关性，相关强度随距离增大而加速减弱，服从地理学第一定律。

② 限于篇幅，本文未报告详细的检验结果，欢迎读者索要。