一、引　言

2008年全球金融危机之后，制定和实施扩张性财政政策已然成为各国预防和化解经济危机和外部风险的基本共识。根据传统凯恩斯主义的有效需求理论，扩张性财政政策运用（主要是支出扩张）通过乘数效应（Multiplier Effect）能够刺激国内有效需求，促进实际产出的提高。从各国的政策实践来看，财政支出扩张在一定程度上也确实缓解了货币金融部门的疲软，为全球经济的企稳回升提供了政策性保障（Blanchard和Leigh，2013；Agnello等，2016）。然而自2008年以来，希腊、意大利等南欧国家在财政支出大幅增加的情况下，国民经济却未呈现回暖趋势。由此，寻找乘数效应背后的影响因素随之成为学者们研究的一个新焦点。研究者很快发现了一个典型事实：希腊、意大利等南欧国家在面临超额支出的同时，往往还具有过度举债的动机（Hürtgen和Rühmkorf，2014；Nickel和Tudyka，2014）。所以直觉上，政府债务应该是影响财政支出乘数效应的关键因素。那么我们不禁产生这样的疑问：随着一国政府债务的不断积累，财政支出的乘数效应真的会减弱吗？倘若如此，那么为了遏制经济下行，一国政府又应当如何评估政府债务的适度水平呢？在后危机时代的全球经济背景下，对以上问题的解答具有重要的理论价值和现实意义。

无论是传统凯恩斯主义还是新凯恩斯主义理论，都从需求冲击的理论角度充分论证了财政支出对实际产出的乘数效应（Gali等，2007；Ramey，2011；Eggertsson，2011）。在实证测度方面，西方学者大多采用发达国家的样本数据，运用结构向量自回归（SVAR）方法考察财政支出的乘数效应。Perotti（2007）采用SVAR方法对美国、加拿大、澳大利亚和英国的财政支出乘数进行了估计，发现四国的财政支出乘数存在−2.3到3.7的较大跨度。Mountford和Uhlig（2009）利用美国的季度数据进行的实证检验发现，短期内美国的财政支出乘数约为0.65，但长期内财政支出乘数将转为负值。Cogan等（2010）的模拟结果显示，美国的财政支出乘数在2009年第一季度快速跃至1.03，随即逐步衰减至0.4。Cimadomo和Bénassy-Quéré（2012）测算了英国和德国财政支出的产出弹性，发现德国的财政支出乘数约为0.69，而英国的财政支出乘数为0.28，并且两国的财政支出乘数都趋于减弱。上述研究表明，学者们对财政支出乘数的估计存在着不确定性，尤其是近期研究发现，财政支出的乘数效应会呈现减弱甚至是反转的情况。

引致财政支出乘数变动的一个关键因素是居民对未来财政政策预期的调整（Ramey，2011；Corsetti等，2012；Zubairy，2014），而政府债务作为赤字融资的重要手段，会直接影响财政政策的预期效应。Bi（2012）认为，“财政极限”（Fiscal Limit）是政府偿还债务的最大能力，即代表未来所有财政盈余的当期贴现值。在政府债务不断积累的情况下，宏观经济运行的不确定性随之加大，违约风险溢价（Default Risk Premia）逐步提高。政府债务水平越高，负债率触及“财政极限”的可能性就越大，居民对未来财政政策调整的预期愈发强烈，使得宏观经济运行的稳定性变得越差。Baum等（2013）认为，即便政府的实际债务水平并未达到或超过“财政极限”，整个经济系统的动态性质也会因为财政极限的存在而发生改变，财政支出乘数等反映宏观经济波动的特征也将出现不同程度的变动。

在理论层面，政府债务可能通过减少私人消费和私人投资引致财政支出乘数效应的弱化。一方面，根据标准的真实经济周期（RBC）模型，随着政府债务水平的提高，居民预期到政府在未来会通过提高税率以应对不断增加的支出。这意味着，居民未来收入和永久收入的当期贴现值都会减少，财政支出增加将会产生负的财富效应，进而挤出私人消费（Perotti，1999；Beetsma，2008）。同时，政府债务的积累会激发居民强烈的预防性储蓄动机（Leeper等，2013；Hürtgen和Rühmkorf，2014）。预防性储蓄的增加会抑制私人消费和国内有效需求，不利于实际产出的提高；另一方面，政府债务水平的提高使得该国的违约风险溢价大幅提升，推动国内利率水平的提升，进而挤出私人投资（Kim和Roubini，2008；Cogan等，2010；王仕进和刘杰，2017）。因此，随着政府债务水平的提高，财政支出对私人消费和私人投资的挤出将部分或完全抵消实际产出的增加，财政支出的乘数效应将趋于减弱。在经验层面，仅有少数学者佐证了这一理论逻辑。Giavazzi和Pagano（1996）采用19个OECD国家的样本数据发现，当一国政府债务占GDP的比重较低时，私人部门不会充分考虑未来政府的财政调整状况。财政支出规模的扩张和债务风险溢价的降低会降低市场利率，增加私人部门储蓄的机会成本，进而提高了私人部门的财富，刺激了私人消费，财政政策即具有“凯恩斯效应”。而当一国政府债务占GDP的比重较高时，未来财政调整所引发的收入和转移支付的变化会改变居民对永久收入的预期，财政支出的增加会抑制私人消费，财政政策就具有“非凯恩斯效应”。Kirchner等（2010）对8个欧元区国家进行实证考察后发现，政府债务是导致长期财政支出乘数减弱的关键因素。Nickel和Tudyka（2014）基于17个欧盟国家的实证研究表明，低债务国家的财政支出乘数显著为正，而高债务国家的财政支出乘数反转为负值。然而上述经验研究存在以下三点局限性：（1）研究对象仅包含发达经济体，那么是否与发达经济体的典型事实相一致，其他类型经济体的政府债务也会导致财政支出的乘数效应趋弱呢？已有研究并未给出普适性解答；（2）研究方法大多采用线性回归范式，无法有效评估政府债务的适度水平。倘若财政支出的乘数效应确实趋于减弱，那么如何评估政府债务的适度水平就显得至关重要。然而已有线性研究并未给出明确答案；（3）财政支出和实际产出间存在着显著的内生性问题，^①这一问题会使得财政支出乘数效应的检测失真。但上述研究都未考虑这一问题，这可能是因为在跨国样本中，解决内生性问题会相对困难。

①例如经济危机会导致实际产出下降，进而增加财政支出。

本文尝试在一个更具普遍意义的跨国样本中，实证考察政府债务对财政支出乘数效应的影响。与现有研究相比，本文的主要贡献在于：（1）在跨国样本中克服了财政支出的内生性问题。本文引入国防支出作为财政支出的有效工具变量，利用两阶段最小二乘法（2SLS）对包括发达经济体、新兴市场和发展中经济体在内的150个国家（地区）的面板数据进行估计，得到了与理论研究一致的经验证据；（2）有效评估了政府债务的适度水平。在已有线性研究的基础上，本文采用面板平滑转移（PSTR）模型进一步检验了政府债务的非线性作用。实证结果显示，当政府债务占GDP的比重达到88%的阈值后，财政支出的乘数效应将会呈现由正变负的逆向转换；（3）研究结论能为探讨中国的经济现状提供重要依据。国内学者已对中国财政支出的乘数效应（储德银和黄文正，2010；王国静和田国强，2014）及其影响因素（简志宏等，2011；李永友，2012）进行了理论或实证探索，但相关研究均未涉及政府债务这一关键要素。本文将跨国数据的检验结果与中国具体国情相结合，有助于合理评估中国政府债务的适度水平，稳定中央政府对财政政策的预期。

二、一个简单的理论模型

我们首先通过求解一个简单的均衡模型来得到财政支出乘数的闭式解，从理论上分析政府债务对财政支出乘数的影响，讨论其内在的逻辑联系。沿袭传统凯恩斯主义的逻辑范式，假定在一个封闭经济中，短期内价格水平具有刚性。根据国民收入恒等式，一国实际产出可以表示为：

$Y = c[Y - T(Y)] + I(i) + G$

(1)

其中：Y表示实际产出；c表示边际消费倾向，c<1；T表示税收收入， $dT/dY = {T_Y} < 1$ ；I表示私人投资，i为投资利率， ${\rm{dI}}/di = {I_i} < 0$ ；G为财政支出。

借鉴Hürtgen和Rühmkorf（2014）的研究，假设一国政府存在债务违约风险，以 $\pi $ 表示政府债务违约的概率。我们不失一般性地假定，在债务价值比（Loan-to-Value Ratio）为0的情况下，政府债务违约的概率 $\pi $ 将被外生决定。对风险中性的投资者而言，依据非权衡定理（No-Trade Condition），政府债务的风险调整（Risk-Adjusted）利率r与无风险利率 $\rho $ 之间存在以下关系：

$r(1 - \pi ) - \pi = \rho $

(2)

对式（2）进一步变形得到：

$1 + r = (1 + \rho )/(1 - \pi )$

(3)

其中：由于 $\partial r/\partial \pi {\rm{ = }}(1 + \rho )/{\left( {1 - \pi } \right)^2} > 0$ ， ${\partial ^2}r/{\partial ^2}\pi = - [2\left( {1 + \rho } \right)]/{\left( {1 - \pi } \right)^3} < 0$ ，因此 $r{\rm{ = }}r(\pi )$ 是一个凸的增函数。借鉴Mendoza和Yue（2012）的假定，政府多依据自身的财政赤字状况，选择积累债务为赤字融资。随着超额赤字和过度举债倾向的增强，政府债务的可持续性将逐步下降，债务违约风险则相应提高。基于此，我们可以将债务违约的概率 $\pi $ 定义为政府债务和财政赤字的增函数：

$\pi = F(D,DEF)$

(4)

其中：D代表政府债务水平； $DEF{\rm{ = }}G - T(Y)$ 代表财政赤字规模； $\partial \pi /\partial D = {F_1}(\cdot) > 0$ ， $\partial \pi /\partial DEF = {F_2}(\cdot) > 0$ 。一国在面临超额赤字的同时，往往具有过度举债的动机。在财政赤字规模较高的情况下，过度举债引致债务违约的可能性会大幅提高，即满足 ${\partial ^2}\pi /\partial D\partial DEF = {F_{12}}(\cdot) > 0$ ，这样的假设显然是合乎现实的（Bi，2012；Baum等，2013）。

在不完全信息条件下，投资者一般会使用主权风险作为投资风险的代理（Remolona等，2008；Borensztein等，2013）。尤其是当一国的主权信用评级被降级时，对投资者而言，资本的平均投入成本将会提高（Brooks等，2004）。因此，我们可以将私人部门的投资利率i表示为政府债务利率r的增函数：

$i{\rm{ = }}i(r),\;\;di/dr = {i_r} > 0$

(5)

根据式（3）−（5），可以得到如下关系式：

$i = i(r(F(D,DEF))) = \psi (D,DEF)$

(6)

其中： ${\psi _1} > 0$ ， ${\psi _2} > 0$ ， ${\psi _{12}} > 0$ 。当政府增加财政支出（dG>0）时，财政赤字相应恶化。假定一国财政赤字的增加完全由政府债务进行融资，即dDEF=D。政府债务的变动dD即等于二阶的财政赤字变动，在计算过程中我们可以将其忽略不计。

根据以上分析，对式（1）进行全微分处理，并结合式（6）可以得到：

$dY = c[1 - {T_Y}]dY + {I_i}{\psi _2}(dG - {T_Y}dY) + dG$

(7)

将 $\mu $ 定义为财政支出乘数，可以得到：

$\mu {\rm{ = }}{{dY}}/{{dG}} =({{1 + {I_i}{\psi _2}}})/{{[1 - c(1 - {T_Y}) + {T_Y}{I_i}{\psi _2}}}]$

(8)

其中：财政支出乘数的大小取决于私人投资对利率的敏感程度I_i以及利率对财政赤字的敏感程度 ${\psi _2}$ 。当 $c < - {I_i}{\psi _2}$ 时， $\mu < 1$ ；当 $c {\text{≥}} - {I_i}{\psi _2}$ 时， $\mu {\text{≥}} 1$ 。显然，一国边际储蓄倾向（1−c）会直接影响财政支出乘数的大小，这在一定程度上支持了Hürtgen和Rühmkorf（2014）等学者关于预防性储蓄动机的推断。更为重要的是，我们发现，政府债务是影响财政支出乘数的关键因素。根据式（8），可以得到：

${{d\mu }}/{{dD}}{\rm{ = }}{{(c - 1)({T_Y} - 1){I_i}{\psi _{12}}}}/{{{{\left[ {1 - c(1 - {T_Y}) + {T_Y}{I_i}{\psi _{12}}} \right]}^2}}}$

(9)

由于 ${\psi _{12}} > 0$ ，则 $d\mu /dD < 0$ ，表明政府债务水平的提高会导致财政支出的乘数效应趋于减弱。显然，在给定财政支出变动的情况下，政府债务水平的提高会推动国内利率的上升，挤出私人投资，这就部分抵消了财政支出的乘数效应。上述理论分析非常简明地刻画了政府债务对财政支出乘数的影响，但需要指出的是，我们仅构建了一个封闭经济下的局部均衡模型，而更为一般化的途径是将外部经济也引入该理论框架中。这里我们主要考虑到以下两点因素：一是如果对模型施加更为复杂的假设，例如纳入开放经济条件，那么政府债务必然会通过利率变动影响实际汇率和净出口，这使得关于影响机制的探讨变得更为复杂和困难。然而本文的理论基点在于刻画政府债务对财政支出乘数效应的影响，并没有明确揭示政府债务的影响机制（在后文的经验分析中也并未探讨），由此我们未对理论模型作进一步拓展；二是根据Ilzetzki等（2013）、Born等（2013）的研究结论，相对于开放经济环境，封闭经济中的财政支出乘数更为显著。因此，这里我们仅构建一个简单的理论框架，为接下来的经验分析提供研究基础。

三、计量模型、变量与数据说明

（一）基准模型设定与变量选取。根据本文的数据结构，由于非平衡面板数据并不影响计算离差形式的组内估计量，因而不会影响固定效应模型的估计（陈强，2014）。为此本文选择最小虚拟变量二乘法（LSDV）进行参数估计，在加入国家与时间双固定效应的情况下，有效降低非平衡面板数据的测量偏误。本文的基准模型设定如下：

$gdp{p_{it}} = {\alpha _0} + {\beta _1}f{e_{it}} + {\beta _2}deb{t_{it}} + {\beta _3}f{e_{it}} \times deb{t_{it}}{\rm{ + }}\theta {Z_{it}} + {\lambda _t} + {\mu _i} + {\varepsilon _{it}}$

(10)

其中：i和t分别代表国家和时间（以年度表示）。 $gdp{p_{it}}$ 为实际产出变量， $f{e_{it}}$ 为财政支出变量； $deb{t_{it}}$ 为政府债务变量，反映一国的政府债务水平； $f{e_{it}} \times deb{t_{it}}$ 为财政支出与政府债务的交互项，是本文的核心解释变量，用来验证政府债务对财政支出乘数效应的影响； ${Z_{it}}$ 为其他控制变量，包括通货膨胀、实际利率、人口增长率、人力资本、制度质量等。 ${\lambda _t}$ 代表时间固定效应， ${\mu _i}$ 代表不可观测的国家固定效应， ${\varepsilon _{it}}$ 为随机误差项。主要变量的选取依据和度量方法如下：

1. 财政支出（fe）和实际产出（gdpp）。财政支出是政府调控经济的重要工具之一。如果政府能够发挥财政支出的“自动稳定器”功能，将有助于平抑经济的周期性波动。对财政支出变量，本文选取2010年固定美元计价的人均政府消费来衡量。其原因在于相较于政府投资，政府消费能够更加准确地反映财政支出的周期性特征（Lamo等，2008；Beetsma等，2008）；对实际产出变量，本文采用2010年固定美元计价的人均实际GDP来衡量。此外，考虑到经济周期波动的内生性影响，本文选择国防支出（military）作为财政支出的工具变量，以减轻经济周期波动的潜在影响。

2. 政府债务（debt）。由于各国的经济体量存在较大差异，因而使用政府债务的绝对指标缺乏量化涵义，为此我们采用政府债务占GDP的比重来衡量一国政府债务的相对规模，由此考察政府债务的边际影响。但鉴于Giavazzi等（2000）、Nickel和Tudyka（2014）的研究结论，政府债务对财政支出乘数的影响可能是非线性的，后文将进一步讨论政府债务的非线性作用。与已有研究不同的是，我们并未沿用外生界定政府债务阈值的计量方法，^①而是采用新近发展的非线性检验方法，根据数据本身的特点内生地判断政府债务的阈值，并以此评估一国政府债务的适度水平。

①Giavazzi 等（2000）将70% 的政府债务占比作为区分高债务国家和低债务国家的阈值，Nickel 和Tudyka（2014）则将这一比例提高至90%。

3. 其他控制变量。除上述指标外，本文进一步选择通货膨胀（inf）、实际利率（rir）、基础设施质量（tel）、人口增长率（pop）、金融发展水平（fd）、人力资本（hum）和制度质量（pol）作为控制变量。已有研究表明，实际利率的提高（Gale和Orzag，2003；Kumar和Baldacci，2010）、通货膨胀的加剧（Cochrane，2011；Barro，2013）和人口数量的增长（Becker等，1999；Coale和Hoover，2015）会显著抑制实际产出的增加，而基础设施的完善（Straub等，2008；Pereira和Andraz，2013）、金融发展水平的提高（Levine，1997；Hassan等，2011）、人力资本的积累（Barro，2001；Fleisher等，2010）会显著促进实际产出的增加。除了以上经济因素，制度质量也是驱动实际产出波动的重要因素，但现有研究尚未形成一致的经验结论（Gerring等，2005；Acemoglu等，2008）。鉴于此，本文选取实际利率、通货膨胀率和人口增长率分别衡量本国利率、物价和人口数量的变动；选取每百人拥有的电话数衡量基础设施质量，^②采用私人信贷占GDP的比重衡量金融发展水平；借鉴程宇丹和龚六堂（2014），采用各国的中学入学率来度量人力资本；采用民主自由程度评估一国的制度质量，变量取值为[1，7]，数值越小表示民主自由程度越高，制度质量越优，反之亦然。

②其他表示基础设施质量的指标，如道路（公路、铁路）里程、港口建设等，数据缺失严重，本文并未选用。

借鉴Born等（2013）、Nickel和Tudyka（2014）的研究，本文对基准模型中的实际产出、财政支出、政府债务、基础设施质量、金融发展水平、人力资本等变量均进行对数化处理，而对通货膨胀率、人口增长率等可能为负的变量以及制度质量等离散变量，则未进行对数化处理。

（二）数据说明与统计特征。本文选取150个国家（地区）的非平衡面板数据，样本既包括发达经济体，也包括崛起中的新兴市场经济体及其他发展中经济体。这些经济体的财政支出、政府债务数据来源于IMF的世界经济展望（WEO）数据库；实际产出、通货膨胀、实际利率、基础设施质量、人口增长率、金融发展水平以及人力资本的相关数据，均来源于世界银行的世界经济发展指标（WDI）数据库；制度质量数据来源于Freedom House数据库。基于数据的可获取性，样本选取的时间维度为2000-2014年。表1和表2显示了主要变量的统计特征。

由表1可见，实际产出变量的最小值与最大值之间存在较大差异。例如丹麦、瑞典等北欧国家具有较高的人均GDP，是全球实际产出最高的区域，而非洲绝大多数国家则较为贫穷；对财政支出变量，不同类型的经济体具有财政支出扩张的一致倾向。但受次贷危机和欧债危机的影响，发达经济体运用扩张性财政政策的力度不断增强，财政支出规模要远高于发展中经济体（见表2）；政府债务变量相对广泛地分布在[−0.536，6.672]区间。尽管债务高企在一定程度上是世界各国为应对危机而加大杠杆的必然结果，但发达国家由于复苏艰难，往往具有更强烈的过度举债倾向；对通货膨胀率变量，可以看到样本中存在明显的异常值，变量的最大值高达324.997%。为了避免异常值的潜在影响，本文采用Winsor方法，在5%的概率下修正通货膨胀率的异常值。

四、计量检验与结果分析

（一）基准模型回归结果。对式（10）进行LSDV估计，以控制国家的个体差异性和时间趋势效应。估计结果如表3所示。

表3回归结果显示，列（1）−（3）中的财政支出变量均在1%的水平下显著为正，表明财政支出具有显著的乘数效应，这与传统凯恩斯主义的理论预期相吻合。其中，列（1）反映了在没有政府债务的影响下，财政支出对实际产出的直接影响。结果显示，财政支出与实际产出之间存在显著的正向关联，财政支出的产出弹性约为0.206%；列（2）是在引入政府债务的情况下，对式（10）进行估计的结果，反映了财政支出与政府债务交互项的间接影响。结果显示，随着政府债务水平的提高，财政支出的乘数效应会趋于减弱，这与理论模型的结论一致；列（3）将控制变量纳入回归方程，结果发现交互项的系数符号和显著性水平并未发生改变。具体而言，在给定财政支出的情况下，政府债务每增加1个单位，财政支出的乘数效应将减少0.020个单位。因此，表3的回归结果支持了前文的理论预期。

通货膨胀变量、实际利率变量和人口增长率变量均显著为负，而金融发展水平变量显著为正，这与已有研究结论相吻合，表明实际利率的提高、通货膨胀的加剧和人口数量的增长是抑制实际产出增加的重要因素，而金融发展水平的提高是促进实际产出增加的关键动因；基础设施变量和人力资本变量并未通过显著性检验。这可能是由于相比道路里程、港口建设等代理指标，人均电话数无法体现基础设施质量的内涵，而中学教育不足以为社会提供充裕的熟练劳动生产力，因此作为人力资本要素的代理效用相对有限；制度质量变量仅在10%的水平下显著为负，且估计系数较小，表明民主程度对实际产出的抑制作用相对有限，这与Acemoglu等（2008）的结论相一致。

（二）国防支出的引入：工具变量回归结果。根据凯恩斯的宏观调控理论，财政支出和实际产出间存在着显著的内生性问题。在给定“财政自动稳定器”的条件下，政府在经济衰退时会增加财政支出，在经济繁荣时则会减少财政支出。因此，实际产出的变动会直接影响财政支出规模（Beetsma和Giuliodori，2010；Aghion等，2014）。考虑到经济周期波动的内生性影响，本文采用工具变量对式（10）进行两阶段最小二乘法（2SLS）估计，以消除基准回归结果中可能存在的估计偏倚。在采用工具变量之前有必要检验财政支出变量是否存在内生性问题，由表4可见，C统计量在1%的显著水平下拒绝了“所有解释变量均为外生”的判断，表明财政支出变量确实存在内生性。

对工具变量的选择，一般而言需满足以下两个条件：首先，该工具变量本身应该是外生的；其次，该工具变量与内生变量之间存在较强的相关性。借鉴Barro（1981）、Ramey和Shapiro（1998）的理论思想，本文选取国防支出变量military作为财政支出的工具变量，选取依据在于：（1）国防支出变量能够满足外生性条件。一方面，国防支出作为国防安全产品及劳务的非生产性投资，往往具有外生的“自主性支出”特征（Barro，1981）。政府增加国防支出并非是出于直接的经济诉求，而大多是出于政治、军事或人口的诉求等，基本上不受经济周期波动的影响。此外，囿于战争的稀发性，国防支出也不会转化为战争力直接影响国民经济。因此，采用国防支出作为工具变量能够有效消除财政支出与产出之间的双向因果关系；另一方面，Ramey和Shapiro（1998）指出，由于存在自动稳定效应，财政支出的影响效应受制于周期性因素。国防支出的变动中不包含自动稳定效应，即剔除了财政支出变动中的周期性因素，因而有助于识别去周期的财政支出效应；（2）国防支出变量与财政支出变量之间本身就存在很强的相关性。国防支出项目中的武器装备采购费、活动与维持性经费、军事人员经费和研究费用等，都直接反映在各国的财政预算安排中。以美国为例，根据2000−2015年的《美国国防预算报告》，美国的国防支出额逐年攀升，国防支出占财政总支出的平均比重约为18.3%。近期研究也表明，美国财政支出的周期性波动在很大程度上是受国防支出的影响（Ramey，2011；Walker，2013）。由此，本文选择国防支出变量能够较好地满足工具变量的基本条件。

本文采用2010年固定美元计价的实际国防支出（取对数）来衡量国防支出变量，数据来源于世界银行WDI数据库。由于内生变量存在于基准回归模型的交互项中，我们采用新交互项 $military \times debt$ 作为原交互项 $fe \times debt$ 的工具变量。为了确认工具变量的有效性，我们对工具变量进行了弱识别检验和识别不足检验。其中，弱识别检验采用Kleibergen-Paap（2006）的F统计量，原假设是工具变量与内生变量弱相关，若拒绝弱相关的原假设，则表明工具变量与内生变量具有强相关性；识别不足检验采用Kleibergen-Paap（2006）的LM统计量，若拒绝识别不足检验的原假设，则表明工具变量外生。表4的检验结果表明，Kleibergen-Paap（2006）的F统计量远大于Stock-Yogo弱识别检验的10%临界值，因此拒绝了工具变量弱识别的原假设。Kleibergen-Paap（2006）的LM统计量也在1%的显著水平下拒绝了“工具变量识别不足”的原假设。因此，本文选取的工具变量不仅是严格外生的，还与内生变量高度相关，是有效的强工具变量。

由表4列（1）−（3）可见，在对财政支出变量的内生性进行有效处理后，fe的系数值较基准回归模型有所提高，但系数符号并未发生改变，表明财政支出增加会促进实际产出的提高，即存在显著的乘数效应。列（2）−（3）中的交互项回归系数显示，随着政府债务水平的提高，财政支出的乘数效应趋于减弱。政府债务每增加1个单位，财政支出的乘数效应将减少0.063个单位。可以看出，对内生性问题进行处理后，并没有显著改变表3中解释变量系数的符号方向和显著性水平。但是在进行内生性处理之后，fe和 $fe \times debt$ 的系数值均显著增大。这说明在控制内生性后，财政支出对实际产出的影响作用体现得更为明显，而政府债务对财政支出乘数效应的抑制作用也更为显著。这也进一步验证了本文的理论预期。

（三）稳健性检验。

1. 区分经济体类型。相对于发展中经济体，以OECD为代表的发达经济体往往具有更强烈的超额支出和过度举债倾向（Baldacci等，2011；郭步超和王博，2014）。^①为了检验财政支出的乘数效应与经济体类型之间的具体关系，并对比发达经济体与发展中经济体的效应差异，本文采用LSDV和2SLS方法对OECD成员和非OECD成员样本进行估计，回归结果如表5所示。

①发达经济体的民主自由程度普遍较高，选民更容易产生“财政幻觉”（fiscal illusion），即在主观上放大了征税带来的“税负痛苦”，进而促使政府增加财政支出，并通过举债来筹集资金（Buchanan，2014）。

由表5可见，随着政府债务水平的提高，财政支出的乘数效应在发达经济体和发展中经济体的回归样本中均呈现减弱趋势，这与表3和表4的回归结果相一致。但值得注意的是，两类样本的回归结果也存在以下两方面的差异：第一，与发展中经济体不同，发达经济体的制度质量变量显著为正，而人口增长变量变得不显著，这表明发达经济体的经济增长更倚重制度因素，而发展中经济体则更依赖要素禀赋；第二，政府债务的抑制作用在发达经济体中相对较强。这是由于发达经济体的政府债务水平普遍较高（见表2）。根据2015年IMF的《财政监测报告》，发达经济体的政府债务占比由2007年的71.4%提升至2014年的104.6%，年均增长率达到6.6%。其中，欧盟国家的政府债务率在2010年高达84.0%，已经突破了《稳定与增长公约》（SGP）规定的60%警戒线。因此，在总体联动趋势一致的情况下，发达经济体较高的政府债务水平将会引致较强的乘数衰减效应。

2. 财政支出功能的影响。Barro（1990）等经典研究发现，相对于福利性支出，生产性支出更有利于促进经济增长。如果一国政府债务的积累源于生产性支出，那么生产性支出在促进经济增长的同时，也能够弥补本国债务。根据前文的经验判断，政府债务的减少将会进一步刺激经济增长；而如果一国政府债务的积累源于福利性支出，那么福利性支出则对经济增长的贡献较为有限。^①鉴于此，本文从财政支出功能的角度进一步揭示政府债务对财政支出乘数效应的影响。囿于数据的可获取性，我们选取公共教育支出占财政支出的比例（edu）替代式（10）中的财政支出变量。通常意义上，生产性支出主要体现在城市道路、高速公路等基础建设方面的支出，而福利性支出则体现在“科教文卫”和社会保障方面的支出（傅勇，2010），因此公共教育支出的占比在一定程度上也能够反映出财政支出功能的偏向。教育支出占比数据来源于世界银行WDI数据库，采用LSDV方法进行估计，回归结果见表6。

①感谢匿名审稿人提出的宝贵建议。

由表6可见，列（2）−（3）中edu的回归系数在1%的水平下显著为负，表明福利性支出功能的强化（即生产性支出功能的弱化）会抑制实际产出的提高，这与Barro（1990）的研究结论相一致。交互项 $edu \times debt$ 的回归系数在1%的水平下显著为正，表明随着政府债务水平的提高，福利性支出功能的强化对实际产出的抑制作用会趋于减弱。这亦意味，政府债务的积累可能主要源于生产性支出，因而在一定程度上能够冲销福利性支出偏向的不利影响。^①

①囿于数据所限，我们只能从财政支出偏向角度间接反映政府债务的源泉，具体机制仍需后续做进一步研究。

3. 半参数估计方法。前文的回归结果显示，财政支出的乘数效应会随政府债务水平的提高而呈现逐步减弱的趋势。为进一步检验这种关系的存在，本文采用半参数估计方法对2000−2014年的总体样本进行回归分析。由于前文的参数估计方法对模型中debt分布的假定较强，可能导致相应的统计推断存在“设定误差”（Specification Errors）。尽管非参数估计方法不对模型中的变量分布作具体设定，却可能面临“维度的诅咒”（Robinson，1988）。因此，本文选择半参数估计作为非参数估计和参数估计的一种折中手段，既假定部分解释变量对被解释变量的影响是未知的，又降低了对样本维度的要求。本文构建的半参数模型如式（11）所示，其中参数部分为线性函数，而非参数部分 $f(deb{t_{it}})$ 为未知函数。回归结果见表7。

$gdp{p_{it}} = {\beta _1}f{e_{it}} + {\beta _2}f(deb{t_{it}}) + {\beta _3}f{e_{it}} \times deb{t_{it}}{\rm{ + }}\theta {Z_{it}} + {\lambda _t} + {\mu _i} + {\varepsilon _{it}}$

(11)

表7列（1）−（2）是使用Robinson（1988）的差分估计量进行半参数估计的结果，但鉴于差分估计量未能考虑个体和时间效应，我们采用Baltagi和Li（2002）构建的序列估计量对半参数双固定效应模型进行估计，^②结果见列（3）−（4）。我们发现，在控制国家和时间效应的情况下，半参数回归结果与前文的参数回归结果一致，核心变量 $fe \times debt$ 的系数值仍然显著为负。随着一国政府债务水平的提高，财政支出的乘数效应趋于减弱。政府债务水平每提高1个单位，乘数效应将减少0.011个单位。因此，对设定误差问题的处理并没有改变本文的基本结论，半参数估计的结果也进一步支持了前文的经验判断。

②Baltagi 和Li（2002）的序列估计量是采用B-spline 样条进行估计。

五、进一步讨论：非线性特征及中国现状分析

前文的交互项检验方法假定政府债务对财政支出乘数效应的影响是单调递增或递减的，这种线性检验的计量方法有效揭示了政府债务的边际影响。但是政府债务的作用可能并非是简单的线性影响，而会呈现非线性特征（Giavazzi等，2000；Nickel和Tudyka，2014）。那么我们不禁产生这样的疑问：是否存在一个政府债务阈值，一旦超过了这一阈值，财政支出的乘数效应就会产生显著的差异呢？这意味着，如果能够有效评估政府债务的适度水平，就有可能缓解甚至是消除财政支出扩张所带来的经济下行风险。已有研究并未对这一问题给出明确答案，为此本文在线性研究的基础上，对前文的交互项检验方法进行改进，采用非线性检验方法进一步考察政府债务的非线性作用。有别于目前研究广泛采用的面板门限模型，本文采用面板平滑转移（PSTR）模型进行非线性检验，具有以下三点优势：第一，Hansen（1999）的面板门限模型假定变量系数是离散型跳跃，并不能准确反映估计系数的连续型趋势。尤其是考虑到政府债务的变动通常会引起私人部门的连续性反应，而非阶段性反应（Hürtgen和Rühmkorf，2014），我们采用连续型的非线性估计方法会更为合适；第二，尽管可以设置更多的门限值来平滑政府债务变量的离散型跳跃，但更多的门限值也意味着每阶段门限回归中更少的样本量，而我们采用的连续型估计方法能利用全样本进行估计，最大程度地减少了样本量的损失；第三，Hansen（1999）的面板门限模型只能处理平衡面板数据，采用面板平滑转移模型能够有效克服非平衡面板数据的测度问题，保证了样本的信息量。基于此，本文选择González等（2005）提出的面板平滑转移模型对政府债务的非线性作用做进一步讨论。

（一）非线性模型设定与估计。参照González等（2005），本文构建的非线性PSTR模型如下：^①

$gdp{p_{it}} = {\beta _{11}}f{e_{it}} + \sum\limits_{k = 1}^n {(\beta _{21}^kf{e_{it}})} {\rm{ }}{f_k}(deb{t_{it}};{\rm{ }}\gamma ,{\rm{ }}c) + \theta {Z_{it}}{\rm{ + }}{\lambda _t}{\rm{ + }}{\mu _i}{\rm{ + }}{\varepsilon _{it}}$

(12)

①González 等（2005）的初始设定只包含个体固定效应，本文进一步引入了时间固定效应。

其中： ${f_k}(deb{t_{it}};{\rm{ }}\gamma ,{\rm{ }}c)$ 为关于转换变量 $deb{t_{it}}$ 的连续函数；k为转换函数的个数； $\gamma $ 为平滑参数，反映不同区制间的转换速度；c为转换函数的m维位置参数。转换函数 ${f_k}(deb{t_{it}};{\rm{ }}\gamma ,{\rm{ }}c)$ 遵循如下的Logistic函数形式：

${f_k}(deb{t_{it}};{\rm{ }}\gamma ,{\rm{ }}c) = {[1 + \exp ( - {\gamma ^k}\prod\limits_{j = 1}^m {(deb{t_{it}} - c_m^k)} )]^{ - 1}}{\rm{ }},\gamma > 0$

(13)

式（13）表明，当 $\gamma \to 0$ 或 $deb{t_{it}} = c$ 时， ${f_k}(deb{t_{it}};{\rm{ }}\gamma ,{\rm{ }}c) = 0.5$ ，PSTR模型即转换为线性的LSDV模型；而当 $\gamma \to + \infty $ 时，转换函数将在位置参数c附近直接跳跃，此时PSTR模型将转换为Hansen（1999）的面板门限模型。因此，线性LSDV模型与面板门限模型均可视为PSTR模型的特殊形式。在此基础上，可以进一步估计财政支出乘数的大小：

${\psi _{it}} = \frac{{\partial gdp{p_{it}}}}{{\partial f{e_{it}}}} = {\beta _{11}} + \sum\limits_{k = 1}^n {\beta _{21}^k} {\rm{ }}{f_k}(deb{t_{it}};{\rm{ }}\gamma ,{\rm{ }}c) + \sum\limits_{k = 1}^n {\beta _{21}^k} \frac{{\partial {f_k}(deb{t_{it}};{\rm{ }}\gamma ,{\rm{ }}c)}}{{\partial f{e_{it}}}}$

(14)

由式（14）可知，PSTR模型对财政支出乘数的测度分为两部分：线性弹性系数与加权转换后非线性弹性系数的加总。在对PSTR模型进行估计之前，有必要确定转换函数的个数k和位置参数的个数m。为此，我们采用F统计值、LM统计值和pseudo-LRT统计值来考察转换函数的最优个数，检验结果见表8。线性检验显示，在5%的显著水平下，三类统计值均显著拒绝了模型为线性的原假设（k=0），表明政府债务与财政支出乘数之间存在显著的非线性关系。非线性残余检验显示，在10%的显著水平下，三类统计值均不能拒绝原假设（k=1），表明PSTR模型的最优转换函数个数为1。进而根据AIC和BIC准则来判定最优位置参数（见表9），最终选定转换函数与位置参数的最优组合为（k=1；m=1）。

在最优模型选择的基础上，本文采取均值差分法与前向均值差分法去除时间效应和个体效应，然后采用格点搜索法（Grid）选取PSTR模型中 $\gamma $ 和c的初始参数值，运用非线性最小二乘法（NLLS）对式（12）进行参数估计。估计结果见表10。

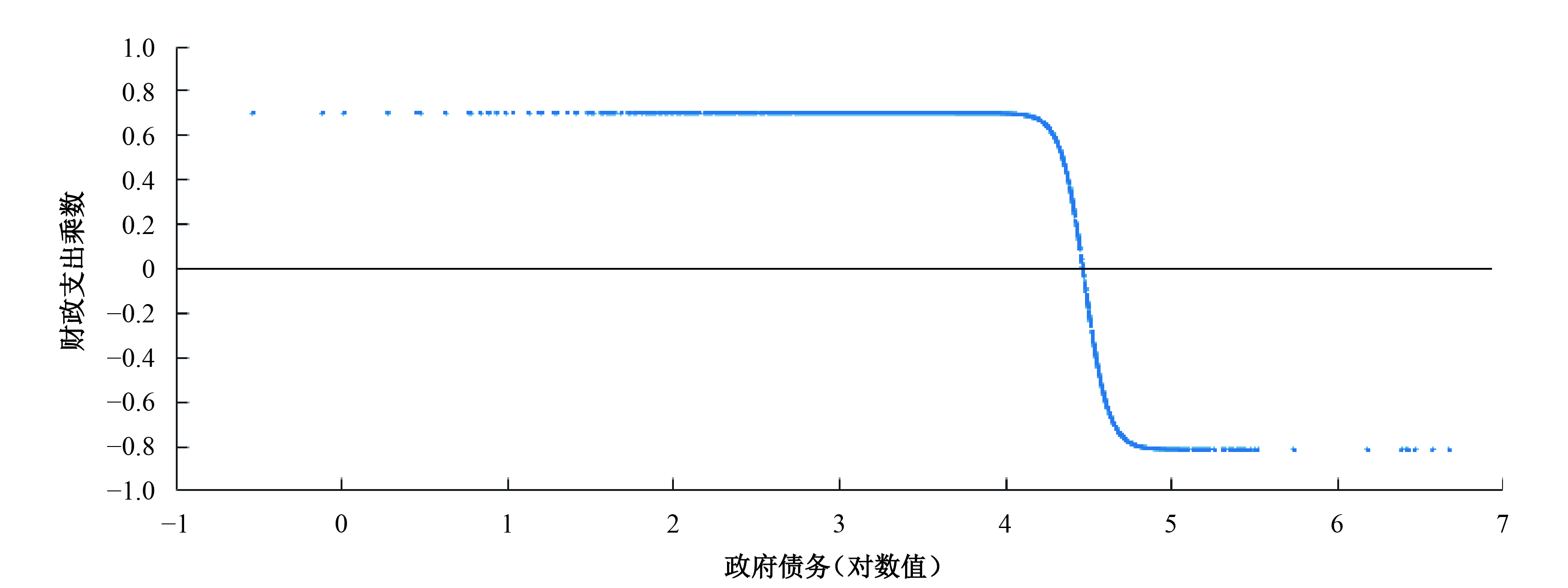
由表10列（1）−（3）可见，政府债务对财政支出乘数存在显著的非线性影响。列（1）是未纳入控制变量的估计结果；列（2）是基于González等（2005）的设定，在纳入控制变量的情况下对个体固定效应进行均值化处理的结果；列（3）则在González等（2005）的模型基础上，进一步引入了时间固定效应并进行均值化处理。我们发现，当政府债务占GDP的比重低于88%（e^4.475）时，财政支出乘数随政府债务水平的提高而逐步增强，边际效应为0.701，表明低债务国家的财政支出具有增长刚性特征；而当政府债务占GDP的比重超过88%的阈值后，随着政府债务水平的提高，财政支出的乘数效应迅速减弱，最终弹性水平稳定在−0.814（0.701−1.515），表明高债务国家的财政支出具有逆向抑制特征。此外，平滑参数的估计值为14.144，表明模型在高低体制间实现了非常快速的转换。为了更加直观地呈现政府债务的非线性影响，我们测算了150个国家（地区）2000−2014年的政府债务均值，并根据式（14），绘制了政府债务与财政支出乘数之间的非线性关系图（见图1）。

由图1可见，随着政府债务水平的提高，财政支出的乘数效应由正转负，表明在政府债务水平较高的国家，财政支出扩张将会抑制实际产出的提高，即财政政策具有“非凯恩斯效应”，这与Giavazzi和Pagano（1996）的研究结论相符。当政府债务达到4.475的阈值，财政支出乘数会在低债务国家和高债务国家之间发生非常迅速的转换。这意味着，各国政府应当审慎评估政府债务的适度水平，尤其是在政府债务突破阈值之后，需要适度调控财政支出扩张的强度和速度。

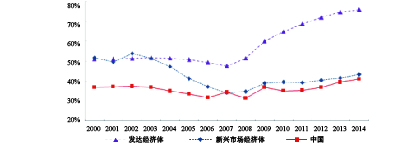
（二）中国现状分析。根据跨国数据的非线性回归结果可以判断，高债务国家的财政支出乘数要明显弱于低债务国家。那么，中国的财政支出乘数又是否与经验研究的判断相符呢？由图2可见，中国政府债务占GDP的比重要明显低于发达经济体均值和其他新兴经济体的均值水平，仅在2007年超过新兴经济体的平均水平。2000−2013年中国政府债务占GDP的比重均低于40%，2014年才达到41.12%的债务率。显然，中国的政府债务水平不仅远低于发达经济体，而且未达到新兴经济体的均值水平，目前尚未达到财政支出乘数效应产生差异的阈值。因此，与美国、希腊等高债务水平国家相比，中国政府债务水平处于较低的状态。根据非线性结论的推断，中国的财政支出会呈现较强的乘数效应。

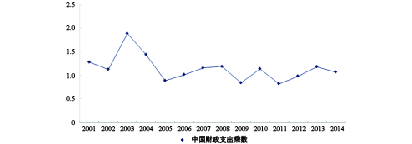
图3显示了中国财政支出乘数的变化趋势。^①可以看出，随着中国政府举债压力的日益增强，财政支出的乘数效应会趋于减弱，这与前文的线性研究结论相符。虽然总体趋势在减弱，但中国的财政支出乘数仍相对较高，年均达到1.228，这正如非线性检验所预期的，中国财政支出的乘数效应要显著强于美国（0.773）、希腊（0.426）等高债务国家。根据凯恩斯的宏观调控理论，理想的相机抉择财政政策应呈现逆周期性，但中国的财政政策却呈现显著的顺周期特征（方红生和张军，2009；付敏杰，2014），这似乎与IMF在2015年《财政监测报告》中提出的“避免顺周期财政政策”的建议存在明显矛盾。然而以上分析结论证实了中国顺周期财政政策运用的有效性。对中国这样的低债务国家，在经济繁荣（衰退）时，中央政府采取增加（减少）财政支出的顺周期财政政策，将会进一步提高（减少）实际产出，顺周期财政政策的可持续性因而得到强化；但对美国、希腊等高债务国家而言，采取顺周期的财政政策则可能加剧经济运行的不稳定性。例如在经济繁荣时采取增加财政支出的扩张性财政政策，将会抑制实际产出的提高，降低顺周期财政政策的有效性。与低债务国家不同，高债务国家只有采取逆周期的财政政策才能避免经济波动的风险。

①根据财政支出乘数的定义Δgdpp/Δfe，初步测算了中国财政支出乘数的大小。

六、结论与政策意涵

在已有关于财政支出乘数效应的文献中，政府债务的角色非常重要但存在诸多未解的疑问。例如：是否与发达经济体的典型事实相一致，其他类型经济体的政府债务也会显著影响财政支出的乘数效应？倘若是，一国政府又应当如何评估政府债务的适度水平呢？针对上述问题，本文首先构建一个简单的局部均衡模型，从理论上分析了政府债务对财政支出乘数的影响；然后采用包括发达经济体、新兴市场和发展中经济体在内的150个国家（地区）2000−2014年的跨国面板数据，利用最小虚拟变量二乘法（LSDV）实证考察了政府债务对财政支出乘数效应的影响。为了克服模型中潜在的内生性问题，引入国防支出作为财政支出的有效工具变量，采用两阶段最小二乘法（2SLS）证明了政府债务是影响财政支出乘数效应的重要因素。在线性研究的基础上，本文进一步采用面板平滑转移（PSTR）模型检验了政府债务的非线性作用，在跨国样本中有效测度了政府债务的适度水平。本文对已有研究中存在的疑问进行了解答：（1）跨国经验结果支持了理论分析的预期，即随着政府债务水平的提高，财政支出的乘数效应会趋于减弱。尤其是在克服内生性问题之后，这一结论仍然成立；（2）政府债务会对财政支出乘数产生显著的非线性影响。当政府债务占GDP的比重突破88%的阈值后，财政支出乘数会在低债务国家和高债务国家之间发生由正变负的逆向转换，并且转换的速度非常快；（3）对中国这样的低债务国家，顺周期的财政政策运用是非常有效的。而对美国、希腊等已经处于高债务水平的国家，则采取逆周期的财政政策才能避免潜在的经济波动风险。

本文研究结论的政策含义为。（1）本文将跨国数据的检验结果与中国具体国情相结合，有助于合理评估中国政府债务的适度水平，稳定中央政府对财政政策的预期。根据财政部公布的2016年财政预算草案，2016年底中国政府债务总额将超过29万亿元，占GDP的比重仅为40%左右，尚未达到财政支出乘数开始减弱的拐点。根据本文的研究结论，对中国这样的低债务国家，扩张性财政政策是驱动经济上行的有力工具，证实了中国顺周期财政政策运用的有效性。尤其是在当前中国“供给侧结构性改革”的战略背景下，扩张性财政政策在中国经济转型过程中仍将持续。由此可以预期，在政府债务水平保持稳定的情况下，中国的实际产出仍将保持较大规模的提高。但需要注意的是，尽管当前中国的政府债务水平偏低，但潜在的政府隐性负债数额巨大，蕴藏的风险不容小觑。因此，中央政府应当全面评估政府债务的实际规模，并将其控制在适度范围内，有利于充分发挥顺周期财政政策的可持续性；（2）对美国、希腊等高债务水平的国家，则应当采取逆周期的财政政策，充分发挥“财政自动稳定器”的功能。与低债务国家不同，高债务国家的顺周期财政政策并非是最优决策，甚至还会威胁到国内经济的稳定。例如，2013年美国参众两院通过了“财政悬崖”议案，试图通过长期内的减赤计划来缓解财政赤字日益膨胀的风险。但结合本文的研究推断，我们认为，在经济下行阶段采取这种减赤政策可能会严重影响美国甚至全球经济复苏的进程。高债务国家的政府应当采取逆周期的调节机制，在经济繁荣（衰退）阶段，减少（增加）财政支出，充分发挥财政支出的“自动稳定器”功能，以巩固宏观经济运行的稳定性和可持续性。最后需要说明的是，本文从理论和经验层面证明了政府债务是影响财政支出乘数效应的重要因素，但囿于研究视角和篇幅所限，我们并没有没有明确揭示政府债务的影响机制。政府债务可能通过减少私人消费（如预防性储蓄动机）和私人投资（如利率提高）引致财政支出乘数效应的减弱，如何从经验上探讨这些影响机制是我们后续进一步研究的方向。