文章信息
 | 财经研究 2018年44卷第1期 |
- 黄秀路, 葛鹏飞,
- Huang Xiulu, Ge Pengfei.
- 债权激励降低了银行系统性风险吗?
- Do debt-based incentives lower bank systemic risks?
- 财经研究, 2018, 44(1): 47-60
- Journal of Finance and Economics, 2018, 44(1): 47-60.
-
文章历史
- 收稿日期:2017-09-14

2018第44卷第1期
2. 西北大学 中国西部经济发展研究中心,陕西 西安 710127;
3. 西北大学 经济管理学院,陕西 西安 710127
2. Center for Studies of China Western Economic Development,Northwest University,Xi’an 710127,China;
3. School of Economics and Management,Northwest University,Xi’an 710127,China
一、引 言
2008年爆发的国际金融危机显现出银行业的不稳定性。正如前美联储主席Bernanke(2009)指出,为提高经营业绩,银行实施以股权激励为主的凸性薪酬激励制度,促使高管追求短期经营行为,从事过度风险活动,最终导致银行损失和金融体系不稳定。不合理的高管薪酬激励方案被认为是引发金融危机的深层根源(Bebchuk和Spamann,2010)。为此,美国、英国以及欧盟等都纷纷出台银行高管薪酬的改革方案,其中一项重要措施就是对高管薪酬实施延期支付、奖金追讨等债权激励。中国银监会也于2010年2月发布《商业银行稳健薪酬监管指引》,明确要求商业银行应制定高管绩效薪酬延期追索、扣回规定等债权激励,目的在于将风险成本、风险抵扣与薪酬挂钩,从而真正发挥薪酬机制对风险防控的约束作用。截至2015年底,实施该制度的银行已有65家,包括4家国有商业银行、8家股份制商业银行、45家城市商业银行以及8家农村商业银行。债权激励是指在高管薪酬中设置类似债务性质的部分,其本质属于企业对高管的负债,也被称为内部债务,以激励性的养老金和延期支付的薪酬为主要形式,具有“未受保护”的特征,即一旦企业破产,求偿权将次于债权人(Edmans和Liu,2011)。
已有关于债权激励效应的研究主要围绕个体银行的风险承担展开,研究对冲决断、支付政策、盈余管理、信贷配置等行为(Belkhir和Boubaker,2013;Srivastav等,2014;Dhole等,2016;何靖,2016)。然而,随着现代金融业的发展,银行间的关联程度不断增强且日趋复杂;银行个体层面的风险会通过风险溢出和传染来加剧系统性风险,进而引发金融危机。结合IMF、FSB和BIS对系统性风险的认知,银行系统性风险是指可能导致银行体系部分或全部受到损害,进而引起大范围金融服务紊乱,并给实体经济造成严重影响的风险。银行系统性风险的管理问题正在成为国内外学术界研究和政府审慎监管的重点。因此,从银行系统性风险的角度讨论债权激励的实施效果显得很有意义。那么,高管债权激励降低了银行的系统性风险吗?高管债权激励通过哪些渠道影响银行系统性风险?这些问题对于监管部门设计银行薪酬方案、推进薪酬制度改革、严防系统性风险具有重要的意义。
本文以中国上市银行为样本,探讨了高管债权激励对银行系统性风险的影响状况和作用渠道。本文的边际贡献在于:第一,首次研究了高管债权激励与银行系统性风险的关系,为优化薪酬制度设计提供了支撑;第二,从期限错配、非利息收入和衍生金融工具视角出发,全面考察了高管债权激励对银行系统性风险的影响渠道,为薪酬改革拓展了方向。
二、文献回顾与研究假说
(一) 高管债权激励与银行系统性风险
公司的代理成本源自股东与债权人以及股东与高管的利益冲突(Jensen和Meckling,1976)。债权人取得公司现金流的固定收益,希望公司违约风险越低越好。而股东只取得公司现金流的剩余收益,仅负有限责任。为谋求利益最大化,股东会以债权人利益为代价,选择高风险的投资项目。同时,为确保高管与其利益一致,股东会设计现金及期权类凸性薪酬激励方案,诱使高管更激进且易于冒险(Ross,2004)。期权激励促使银行高管减少现金持有、增加短期债务融资,进而加重资产负债错配和流动性风险,最终导致银行危机(Chava和Purnanandam,2010)。薪酬激励的凸性越大,高管越不关注下行风险,破产风险就会急剧上升(Gormley等,2013)。期权激励会诱使高管承担过多风险,从而增大银行系统性风险(Kim等,2016)。因此,高管薪酬激励方案应同时兼顾股东与债权人以及股东与高管之间的两类代理问题(John和John,1993)。
Edmans和Liu(2011)直接提出了高管债权激励,即在高管薪酬中设置内部债务,如激励性的养老金和延期支付的薪酬,目的在于促使高管与债权人利益一致,缓解股东与高管的利益冲突,抑制高管风险承担行为。一系列的研究证实债权激励的积极作用。Anantharaman等(2013)认为,债权人将内部债务看成可以抑制高管风险承担行为的薪酬激励。Bennett等(2015)得出,债权激励会促使高管与债权人利益一致,从而降低银行违约风险。银行内部债务水平不仅与其下行风险呈负向关系(Tung和Wang,2012),而且在高管持有内部债务较多的银行,其资产比较优质,银行风险较低(何靖,2016;朱波等,2017)。
现有研究的局限在于,没有进一步探讨高管债权激励对银行系统性风险的影响。Levine(2004)指出,银行能迅速将资产的风险成份转移到非金融行业,并且轻易地隐藏问题,从而金融机构的过度风险承担会影响债权人、存款人和纳税人,甚至整个金融体系。高管风险承担行为提高了银行间资产组合的关联程度,导致银行联合失败或危机的概率上升,其实质在于增加银行系统性风险,而非个体风险(Armstrong和Vashishtha,2011)。因此,本文提出以下假说:
假说1:在控制其他因素的情况下,高管债权激励有助于降低银行系统性风险。
(二) 高管债权激励对银行系统性风险的作用渠道
高管债权激励是相对股权(或期权)激励而言的,对于高管股权激励对银行系统性风险的影响途径,现有研究主要围绕期限错配、非利息收入以及衍生金融工具等三个方面展开(张雪兰等,2014;Kim等,2016)。因此,本文也从这三个角度探讨高管债权激励对银行系统性风险的作用渠道。
1. 银行计息资产和负债在重新定价日或者到期日上的期限错配可能造成违约行为。这是因为:一方面,期限错配程度越高,银行对银行间借贷的依赖性越强,银行之间的业务关联程度的提高会增大共同风险暴露程度,加速风险在银行体系内的传染,系统性风险也就随之上升(Allen等,2012);另一方面,在市场流动性不足的情形下,期限错配问题极有可能迫使债务银行折价抛售非流动性资产,甚至引发存款人和其他股东的大量挤兑行为,此类坏消息在银行体系内流转,最终导致系统性风险大幅增加(Kim等,2016)。凸性薪酬激励方案会显著影响银行资产负债期限错配程度(Brockman等,2010),从而导致银行系统性风险上升。但在债权激励下,高管与债权人的利益更加一致,从而倾向于采取风险程度较小的保守政策,如较低的杠杆率(Cassell等,2012)、较高的现金持有水平(Liu等,2014)以及较少的负债(Brisker和Wang,2017),这些都有利于降低银行资产负债期限错配程度和流动性风险。综上分析,本文认为期限错配是高管债权激励影响银行系统性风险的一种渠道,据此提出以下假说:
假说2a:在控制其他因素的情况下,高管债权激励有助于降低资产负债错配程度,进而起到降低银行系统性风险的作用。
2. 学术界关于非利息收入对银行风险的影响存在两类不同的看法。一类认为,非利息收入比利息收入来源稳定,可以在稳定银行收益的同时降低银行风险(Smith等,2003);另一类则认为,非利息收入会提高银行运营杠杆,加大银行收益的波动程度(DeYoung和Roland,2001)。就中国的实际情况而言,银行业非利息收入业务起步晚、起点低、基础差、总量小、对利润的总体贡献度低,而且非利息收入主要依靠手续费及佣金收入,波动性较小;另外,非利息收入对中国宏观经济状况的依赖程度较低,发展非利息收入业务可以减少经济周期性变动对银行经营收入的冲击,进而降低银行系统性风险(张晓玫和毛亚琪,2014)。实行高管债权激励会提高中国银行非利息收入占比,达到风险分散效果。据此,本文提出以下假说:
假说2b:在控制其他因素的情况下,高管债权激励可通过增加非利息收入,起到降低银行系统性风险的作用。
3. 衍生金融工具具有高风险和高杠杆的特征。自20世纪90年代以来,全球几乎每一场金融风暴都与衍生金融工具有关。银行介入衍生金融工具交易,不仅会增大银行的违约风险,还会加大银行间资产负债的关联程度,从而提高银行业的联合违约风险,形成一损俱损的多米诺式系统性金融危机(Battiston等,2012)。期权激励会促使高管从事较多的衍生金融工具交易,在内部关联和风险外溢的驱动下,导致银行系统性风险上升(Kim等,2016);另外,期权激励产生的泡沫资产会挤出安全资产和正常风险资产,进一步加剧高管的过度冒险倾向。考虑到债权激励下高管会更像债权人,倾向于做出风险程度较低的决策,我们借鉴逆向论证方法,提出以下假说:
假说2c:在控制其他因素的情况下,高管债权激励有助于减弱衍生金融工具使用倾向,进而起到降低银行系统性风险的作用。
三、研究设计
(一) 银行系统性风险测度
1. 测度方法。系统性风险的测量方法主要分为三类:第一类是基于资产负债关联的网络分析法,它以银行间的双边资产负债为出发点,考察银行网络体系中单个或多个银行遭受随机事件冲击时所导致的银行破产数量、破产损失以及易受传染程度(方意,2016)。第二类是基于资产负债表和金融市场数据的结构法(CCA方法),它将权益看作以资产为标的物、负债为执行价格的看涨期权,通过期权定价公式和伊藤引理来考察银行体系的系统性风险(Gray和Jobst,2010)。第三类是基于金融市场传染的简式法,它利用银行资产收益的尾部依赖关系,考察银行之间或银行对整个银行体系的风险外溢程度,主要包括CoVaR方法和MES方法(Acharya等,2010;Adrian和Brunnermeier,2016)。网络分析法难以获得银行之间的实际双边资产负债数据,一般利用最大熵原理间接估计,结论会存在较大的误差。CCA方法则衡量整个银行体系的系统性风险时序特征,不能直接甄别单个银行的风险贡献状况。相比而言,简式法使用金融市场数据,具有前瞻性和时效性特征,能直接计算单个银行的风险外溢值。因此,本文基于简式法中的CoVaR方法来测度银行的系统性风险。
CoVaR方法测度在特定的概率水平下,当一家银行遭受随机事件冲击时,其他个体银行或整个银行体系可能遭受的最大损失,即它是一个基于“条件”概念下的VaR值(Adrian和Brunnermeier,2016)。基于CoVaR方法,可以定义个体银行i对整个银行体系的系统性风险溢出效应:当个体银行i所处的状况从常态变化为极端情形时,整个银行体系的CoVaR值变化,即ΔCoVaR。这一风险溢出度ΔCoVaR可作为个体银行i系统性风险的代理变量。
| $\begin{array}{l}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. \begin{array}{l}VaR_t^i(q) = \hat \alpha _q^i + \sum\limits_k {\hat \gamma _{k,q}^i{M_{k,t - 1}}} \\CoVaR_t^i(q) = \hat \alpha _q^{system|i} + \hat \beta _q^{system|i}VaR_t^i(q) + \sum\limits_k {\hat \gamma _{k,q}^{system|i}{M_{k,t - 1}}} \end{array} \right\} \Rightarrow \\\Delta CoVaR_t^i(q) = CoVaR_t^i(q) - CoVaR_t^i(50\% ) = \hat \beta _q^{system|i}\left( {VaR_t^i(q) - VaR_t^i(50\% )} \right)\end{array}$ | (1) |
本文取q=1%,借鉴Adrian和Brunnermeier(2016)选取状态变量Mt:(1)沪深300指数回报率,反映宏观金融市场整体状况;(2)沪深300指数回报波动率,刻画金融系统波动情况;(3)短期流动性价差,衡量市场的流动性风险;(4)无风险收益率变动,描述基准利率情况;(5)国债收益率曲线斜率,反映市场期限结构;(6)信用价差,刻画市场的信用风险;(7)房地产行业价差。此外,银行系统收益率用Wind银行业指数收益率来表示。
2. 测度结果分析。本文选取了14家银行,样本区间为2008−2015年。数据源自Wind数据库、CSMAR数据库和RESSET数据库。值得注意的是,ΔCoVaR为负值,且绝对值越大,银行的系统性风险越高。
根据测算结果,各银行系统性风险呈现以下特点:第一,在2008年金融危机和2015年股灾爆发的年份,各银行系统性风险ΔCoVaR均显著高于2009−2014年的均值。另外,2008年金融危机时期的系统性风险显著高于2015年股灾时期的均值。第二,无论在危机时期还是平稳阶段,各上市银行系统性风险均表现出稳定的差异性。整体而言,工商银行、浦发银行、招商银行、建设银行和兴业银行等规模较大的国有银行和股份制银行系统性风险较高,而宁波银行、南京银行等规模较小的城市商业银行系统性风险较低。
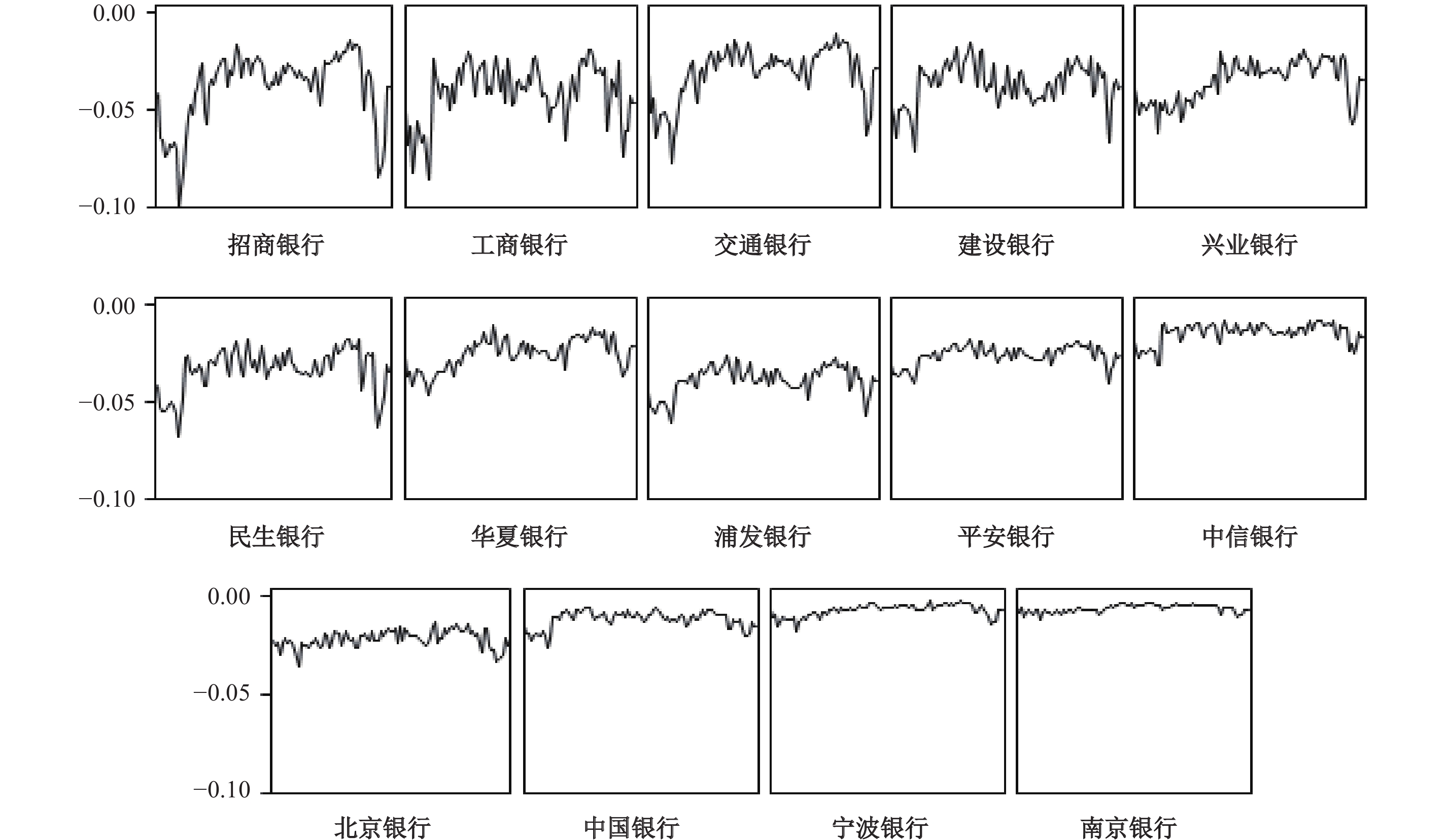
本文还从波动性视角分析了各上市银行的系统性风险,图1给出了各上市银行系统性风险随时间的波动情况。直观上,系统性风险的波动性在银行之间表现出显著的个体异质性特征,招商银行的波动性最为剧烈,而南京银行最为平稳。根据各银行系统性风险的波动情况,大致分为强波动性(招商银行、工商银行、交通银行、建设银行和兴业银行)、弱波动性(民生银行、华夏银行、浦发银行、平安银行和中信银行)和平稳波动性(北京银行、中国银行、宁波银行和南京银行)。基本上,对于波动性强的银行,平均系统性风险较高;对于波动性平稳的银行,平均系统性风险较低。不过也有例外,浦发银行的平均系统性风险较高,但其波动性却较平稳。
|
| 图 1 中国上市银行系统性风险的波动分析 |
(二) 模型构建
1. 基准模型。本文研究的核心在于检验高管债权激励对银行系统性风险的影响情况。为此,构建非观测效应面板数据模型如下:
| $\Delta CoVa{R_{it}} = {\alpha _0} + {\alpha _1}Deferre{d_{it}} + {\alpha _2}Control{s_{it}} + {\xi _i} + {\varphi _t} + {\varepsilon _{it}}$ | (2) |
其中,被解释变量ΔCoVaR为银行系统性风险,解释变量Deferred为高管债权激励(Deferred_L或Deferred_D)。控制变量Controls包括银行规模(Bank_Size)、净资产收益率(ROE)、杠杆率(LEV)、贷款增速(Loan_G)、贷款拨备率(LPR)、董事会规模(Board_Size)以及经济周期(GDP_G)。我们最关注的是系数α1,它表示债权激励对银行系统性风险的影响。考虑到ΔCoVaR为负数,根据研究假设,预期α1为正。
2. 渠道分析。借鉴张雪兰等(2014)的做法,构建渠道效应模型,进一步探讨债权激励对银行系统性风险的影响渠道。
| $Channe{l_{it}} = {\beta _0} + {\beta _1}Deferre{d_{it}} + {\beta _2}Control{s_{it}} + {\eta _i} + {\psi _t} + {u_{it}}$ | (3) |
| $\Delta CoVa{R_{it}} = {\gamma _0} + {\gamma _1}Deferre{d_{it}} + {\gamma _2}Channe{l_{it}} + {\gamma _3}Control{s_{it}} + {\mu _i} + {\phi _t} + {v_{it}}$ | (4) |
其中,渠道变量Channel为期限错配变量(Mat_Mis)、非利息收入变量(NII、NFII和NOII)和衍生金融工具变量(Der、Der_Ex、Der_In和Der_Ot)中的一种。在式(3)中回归系数显著的前提下,式(4)是对式(2)的具体分解,它把债权激励对银行系统性风险的作用分解为直接效应和通过渠道变量的间接效应两种。我们将式(3)和式(4)联立来识别这两种效应。
| $\Delta CoVa{R_{it}} = ({\gamma _0} + {\gamma _2}{\beta _0}) + ({\gamma _1} + {\gamma _2}{\beta _1})Deferre{d_{it}} + ({\gamma _3} + {\gamma _2}{\beta _2})Control{s_{it}} + {\xi _i} + {\varphi _t} + {\varepsilon _{it}}$ | (5) |
观察式(2)和式(5)可知,高管债权激励对银行系统性风险的总效应为α1=γ1+γ2β1,其中直接效应是γ1,通过渠道变量发挥作用的间接效应是γ2β1。根据研究假设,预期γ1为正,而β1和γ2的符号则随渠道变量的不同而不同。对于期限错配和衍生金融工具渠道,预期β1和γ2同时为负;而对于非利息收入渠道,预期β1和γ2同时为正。
(三) 变量定义
1. 核心解释变量。债权激励是本文研究的核心解释变量,现有文献集中于欧美发达国家,以高管薪酬中债权激励与股权激励的比值来度量。其中,债权激励指高管养老金的精算现值和延期支付的薪酬,而股权激励指高管持有的股权和期权的价值(Bennett等,2015)。目前,中国普遍没有执行养老金激励制度,并且大部分银行也没有采用相关的股票期权激励,现金和持股仍然是高管薪酬激励的最主要手段(何靖,2016)。鉴于此,在当前研究的基础上并结合中国银行业的实际情况,本文采用会计年度末延期支付的高管薪酬结余总和与已支付的高管现金薪酬加上持股收益之比,对高管债权激励进行度量。该比例越大,表明债权激励程度越大。考虑到估计所得数据可能存在误差,我们还构建了银行实施债权激励的虚拟变量。如果银行从第t年起实行高管薪酬延期支付制度,那么从这一年起该变量值为1,之前年份为0。
2. 渠道变量。第一,期限错配,用重新定价日或到期日1年内计息资产扣除相应期限计息负债的差额绝对值与银行总资产之比来衡量(斯文,2014)。第二,非利息收入,用非利息收入与总营业收入之比来衡量(张晓玫和毛亚琪,2014),并进一步分解为手续费及佣金收入、其他非利息收入。第三,衍生金融工具,用衍生金融工具的合约名义本金与总资产的比值来衡量(斯文,2014),并考虑了外汇类、利率类、权益和其他类的差异性。
3. 控制变量。除了我们重点研究的高管债权激励外,其他因素也会对银行系统性风险造成影响。借鉴张晓玫和毛亚琪(2014)以及何靖(2016)等,我们控制了以下变量:(1)银行规模,用银行总资产的自然对数值表示;(2)净资产收益率,用加权平均净资产收益率表示;(3)杠杆率,用权益资本与总资产的比率表示;(4)贷款增速,用贷款总额的增长率表示;(5)贷款拨备率,用贷款损失准备与贷款总额之比表示;(6)董事会规模,用董事人数表示;(7)经济周期,使用全国GDP增长率(对国有银行和股份制银行)或地区GDP增长率(对城市商业银行)表示。
(四) 描述性统计
本文使用的数据为中国上市银行2008−2015年的面板数据。所用财务数据源于CSMAR数据库和RESSET数据库,高管债权激励变量与渠道变量的数据则来源于各上市银行年报,由作者手工整理。GDP数据源于中经网统计数据库、国家及各地区统计局。描述性统计见表1。
| 变量 | 均值 | 标准差 | 最小值 | 25%分位数 | 中位数 | 75%分位数 | 最大值 |
| ΔCoVaR | −0.0269 | 0.0139 | −0.0693 | −0.0364 | −0.0266 | −0.0157 | −0.0049 |
| Deferred_D | 0.6518 | 0.4786 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 |
| Deferred_L | 0.4025 | 0.3756 | 0.0000 | 0.0000 | 0.4991 | 0.6856 | 1.5417 |
| Mat_Mis | 0.0700 | 0.0558 | 0.0006 | 0.0301 | 0.0555 | 0.0976 | 0.2779 |
| NII | 0.1862 | 0.0713 | 0.0135 | 0.1322 | 0.1791 | 0.2338 | 0.3896 |
| NFII | 0.1493 | 0.0599 | 0.0110 | 0.1016 | 0.1431 | 0.1979 | 0.3316 |
| NOII | 0.0371 | 0.0292 | −0.0035 | 0.0154 | 0.0306 | 0.0470 | 0.1263 |
| Der | 0.4053 | 0.5176 | 0.0000 | 0.1291 | 0.2387 | 0.4980 | 3.7119 |
| Der_Ex | 0.2321 | 0.2139 | 0.0000 | 0.0816 | 0.1652 | 0.3363 | 1.0899 |
| Der_In | 0.1661 | 0.3313 | 0.0000 | 0.0250 | 0.0621 | 0.1623 | 2.5388 |
| Der_Ot | 0.0071 | 0.0374 | −0.3361 | 0.0000 | 0.0017 | 0.0120 | 0.1149 |
四、实证结果分析
(一) 债权激励能降低银行系统性风险吗?
考虑到本文的样本数据为多期平衡面板数据,且Hausman检验的Wald统计值在5%的水平上显著,因此我们利用固定效应模型来估计式(2)。表2报告了式(2)的估计结果,①其中模型1和模型2以连续型债权激励为核心解释变量,模型3和模型4以债权激励虚拟变量为核心解释变量。可以看出,无论是否加入控制变量,债权激励变量(Deferred_D或Deferred_L)的系数均在1%水平上显著为正,说明银行实施高管债权激励制度可以显著降低系统性风险,并且激励程度越大,系统性风险越低。根据模型2和模型4,在其他因素保持不变的条件下,如果银行实行高管债权激励制度,系统性风险将降低0.82%;激励程度每增加10%,系统性风险将降低0.096%。由此,假说1得到证实。我们可以从以下两方面解释债权激励对银行系统性风险的负向作用:一方面,根据《商业银行稳健薪酬监管指引》,高管债权激励方案设计的初衷在于将高管的薪酬水平与风险成本调整后的经营业绩相适应。由于银行的风险暴露有一定的期限,这样做可以避免“成绩都在这届高管手中,风险却留给下一任来处理”,从而有效降低过度风险承担所引致的破产风险及风险溢出等。另一方面,以延期支付的高管薪酬表示的高管债权激励,本质是高管持有“内部债务”,能够减轻委托−代理的利益冲突,抑制高管的过度冒险行为(Tung和Wang,2012)。
①限于篇幅,表中仅报告了核心变量结果,感兴趣的读者可向作者索取。
| 模型1 | 模型2 | 模型3 | 模型4 | |
| ΔCoVaR | ΔCoVaR | ΔCoVaR | ΔCoVaR | |
| Deferred_L | 0.0091***(3.384) | 0.0096***(3.2510) | ||
| Deferred_D | 0.0062***(3.0754) | 0.0082***(3.3398) | ||
| Controls | 未控制 | 控制 | 未控制 | 控制 |
| F值 | 11.4514*** | 2.0991** | 9.4580*** | 2.1767** |
| Hausman | 8.16*** | 43.47*** | 5.50** | 61.87*** |
| 注:括号内为t值,***、**和*分别表示在1%、5%和10%的水平上显著。下表同。 | ||||
(二) 债权激励通过何种途径降低银行系统性风险?
1. 期限错配。表3报告了以期限错配程度为渠道变量的估计结果。从中可以看出,无论是否加入控制变量,债权激励(Deferred_L或Deferred_D)对银行系统性风险的直接作用均显著为正。这说明实施高管债权激励制度能直接降低银行系统性风险,与我们的预期一致。对于渠道变量的间接作用,首先观察到,无论是否加入控制变量,期限错配程度对债权激励变量(Deferred_L或Deferred_D)的回归系数均在5%的水平上显著为负。也就是说,实施债权激励制度有助于降低银行资产负债期限错配程度,并且债权激励越大,错配程度越低。再来看期限错配程度对银行系统性风险的影响,无论是否加入控制变量,期限错配程度的回归系数均显著为负,说明期限错配程度越低,银行系统性风险越低。因此,银行资产负债期限错配的渠道效应是存在的,债权激励制度的实施会通过影响银行的资产负债期限错配来间接降低系统性风险,假说2a得到证实。
| 模型5 | 模型6 | 模型7 | 模型8 | |||||
| Mat_Mis | ΔCoVaR | Mat_Mis | ΔCoVaR | Mat_Mis | ΔCoVaR | Mat_Mis | ΔCoVaR | |
| Deferred_L | −0.0492*** (−2.6986) |
0.0065** (2.4892) |
−0.0403** (−2.0489) |
0.0072** (2.5911) |
||||
| Deferred_D | −0.0461*** (−3.5002) |
0.0037* (1.8658) |
−0.0366** (−2.2395) |
0.0061** (2.6024) |
||||
| Mat_Mis | −0.0523*** (−3.7247) |
−0.0579*** (−3.9609) |
−0.0524*** (−3.5996) |
−0.0571*** (−3.8920) |
||||
| Controls | 未控制 | 未控制 | 控制 | 控制 | 未控制 | 未控制 | 控制 | 控制 |
| R2 | 0.0698 | 0.2185 | 0.1516 | 0.2835 | 0.1121 | 0.1972 | 0.1589 | 0.2840 |
| F值 | 7.2825*** | 13.4222*** | 2.0105* | 3.9136*** | 12.2515*** | 11.7904*** | 2.1256** | 3.9220*** |
从数值角度分析,模型8表明,在其他因素保持不变的情况下,银行实行债权激励制度会使系统性风险直接降低0.61%,同时使资产负债期限错配程度降低3.66%,这又会间接导致系统性风险进一步降低0.21%(0.0366×0.0571×100%=0.21%)。可见,实行高管债权激励制度的直接效应是0.61%,在总效应中占比74.39%;间接效应是0.21%,在总效应中占比25.61%。就模型6而言,在其他因素保持不变的条件下,债权激励每增加10%,银行系统性风险会直接降低0.072%,同时会使资产负债期限错配程度降低0.403%,进而导致系统性风险间接降低0.024%。因此,直接效应和间接效应在总效应中的占比分别是75%和25%。总而言之,高管的债权激励对银行系统性风险的直接效应要大于基于期限错配渠道的间接效应,两种效应的比例约为3:1。
2. 非利息收入。表4报告了以非利息收入为渠道变量的估计结果。总体而言,首先,无论是否加入控制变量,银行系统性风险对债权激励变量(Deferred_L或Deferred_D)的直接回归系数均在5%的水平上显著为正,说明债权激励可以降低系统性风险。其次,非利息收入对债权激励变量(Deferred_L或Deferred_D)的回归系数均在1%的水平上显著为正,银行系统性风险对非利息收入的回归系数也显著为正。这说明实施债权激励会通过增加非利息收入来降低银行的系统性风险,即存在非利息收入的渠道效应,假说2b得到证实。从数值角度解读,以模型10为例,在其他变量不变时,债权激励每增加10%,银行系统性风险会直接降低0.074%,同时会使非利息收入增加0.465%,从而导致系统性风险间接降低0.022%。因此,债权激励对银行系统性风险的直接效应是0.074%,在总效应中占比约77%;通过非利息收入产生作用的间接效应是0.022%,在总效应中占比约23%,两种效应的比例约为3.35:1。
| 模型9 | 模型10 | 模型11 | 模型12 | |||||
| NII | ΔCoVaR | NII | ΔCoVaR | NII | ΔCoVaR | NII | ΔCoVaR | |
| Deferred_L | 0.0757*** (4.4583) |
0.0074** (2.5235) |
0.0465*** (3.1048) |
0.0074** (2.4447) |
||||
| Deferred_D | 0.0686*** (5.7681) |
0.0047** (2.0276) |
0.0418*** (3.3852) |
0.0063** (2.4684) |
||||
| NII | 0.0222* (1.7926) |
0.0468** (2.3106) |
0.0214* (1.7545) |
0.0452** (2.2156) |
||||
| Controls | 未控制 | 未控制 | 控制 | 控制 | 未控制 | 未控制 | 控制 | 控制 |
| R2 | 0.1701 | 0.1233 | 0.4952 | 0.2049 | 0.2554 | 0.1035 | 0.5042 | 0.2059 |
| F值 | 19.8763*** | 6.7508*** | 11.0345*** | 2.5491** | 33.2713*** | 5.5438*** | 11.4417*** | 2.5644** |
考虑到中国银行业的非利息收入主要是由手续费及佣金收入和其他非利息收入两部分组成的,本文进一步分别考察了以手续费及佣金收入为渠道变量的渠道效应(见表5)和以其他非利息收入为渠道变量的渠道效应(见表6)。就手续费及佣金收入而言,无论是否加入控制变量,银行系统性风险对债权激励(Deferred_L或Deferred_D)的直接回归系数均在5%的水平上显著为正,证明存在直接效应;手续费及佣金收入对债权激励变量(Deferred_L或Deferred_D)的回归系数都在1%的水平上显著为正,银行系统性风险对手续费及佣金收入的回归系数在10%的水平上显著为正。这说明债权激励会通过增加银行手续费及佣金收入来间接降低系统性风险,证明佣金及手续费收入的渠道效应是存在的。
| 模型13 | 模型14 | 模型15 | 模型16 | |||||
| NFII | ΔCoVaR | NFII | ΔCoVaR | NFII | ΔCoVaR | NFII | ΔCoVaR | |
| Deferred_L | 0.0816*** (5.1884) |
0.0071** (2.3474) |
0.0615*** (4.2211) |
0.0068** (2.1599) |
||||
| Deferred_D | 0.0622*** (5.3986) |
0.0045* (1.9846) |
0.0427*** (3.4108) |
0.0062** (2.4383) |
||||
| NFII | 0.0245* (1.7209) |
0.0446** (2.1367) |
0.0266* (1.7193) |
0.0463** (2.3013) |
||||
| Controls | 未控制 | 未控制 | 控制 | 控制 | 未控制 | 未控制 | 控制 | 控制 |
| R2 | 0.2172 | 0.1240 | 0.4726 | 0.1981 | 0.2310 | 0.1102 | 0.44056 | 0.2092 |
| F值 | 26.9191*** | 6.7953*** | 10.0797*** | 2.4471** | 29.1454*** | 5.9470*** | 8.8562*** | 2.6157*** |
| 模型17 | 模型18 | 模型19 | 模型20 | |||||
| NOII | ΔCoVaR | NOII | ΔCoVaR | NOII | ΔCoVaR | NOII | ΔCoVaR | |
| Deferred_L | −0.0063
(−0.8895) |
0.0091*** (3.3744) |
−0.0155** (−2.1528) |
0.0099*** (3.2628) |
||||
| Deferred_D | 0.0061
(1.1757) |
0.0063*** (3.0932) |
−0.0016
(−0.2566) |
0.0082*** (3.3161) |
||||
| NOII | 0.0089
(0.2290) |
0.0208
(0.4788) |
−0.0173
(−0.4403) |
−0.0068
(−0.1601) |
||||
| Controls | 未控制 | 未控制 | 控制 | 控制 | 未控制 | 未控制 | 控制 | 控制 |
| R2 | 0.0810 | 0.1061 | 0.1905 | 0.1594 | 0.0414 | 0.0907 | 0.1494 | 0.1624 |
| F值 | 1.9712* | 5.6960*** | 2.6476** | 1.8754* | 1.8322* | 4.7866*** | 1.9767* | 1.9168* |
对于其他非利息收入,银行系统性风险对债权激励变量(Deferred_L或Deferred_D)的回归系数均显著为正,表明存在直接效应。然而,其他非利息收入对债权激励变量的回归系数以及银行系统性风险对其他非利息收入的回归系数都不显著,表明其他非利息收入的渠道效应是不存在的。综上分析,非利息收入的渠道效应实际上来自手续费及佣金收入的渠道效应。可能的解释为:一方面,其他非利息收入在银行非利息收入中的占比小,业务品种少、种类单一,对银行风险的分散能力有限;另一方面,中国商业银行的存款替代效应比较小,而手续费及佣金收入是银行非利息收入最主要的构成部分,占比高达80%以上,因此增加这部分收入可以确保银行收入稳定,进而起到降低银行系统性风险的作用。DeYoung等(2013)指出,银行的手续费及佣金收入来源比较稳定,能够在宏观经济波动时期减缓冲击的影响,降低银行系统性风险;而其他非利息收入要么既不提高也不降低银行系统性风险,要么在危机时期加速银行破产。
3. 衍生金融工具。表7报告了以衍生金融工具为渠道变量的估计结果。考虑到中国衍生金融工具主要包括外汇类、利率类、权益类及其他衍生金融工具,本文分别考察了以这几类衍生金融工具为渠道变量的渠道效应;由于它们的估计结果与表7一致,限于篇幅,这里不再一一报告。从表7可以看到,银行系统性风险对高管债权激励(Deferred_L或Deferred_D)的回归系数显著为正,表明债权激励可以直接降低银行系统性风险。然而,任何衍生金融工具变量对债权激励变量(Deferred_L或Deferred_D)的回归系数以及银行系统性风险对衍生金融工具变量的回归系数都不显著,表明衍生金融工具的渠道效应是不存在的。这可能是由中国衍生金融工具市场起步较晚、市场发展程度较低以及市场参与主体不成熟导致的。2005年5月,中国人民银行发布《全国银行间债券市场债券远期交易管理规定》,中国衍生金融工具市场正式恢复发展。尽管近年来中国衍生金融工具市场的规模和交易品种不断扩大,但是与国际市场相比,一方面,中国外汇类与利率类衍生金融工具完全在场外市场进行交易,场内市场尚未开展;另一方面,市场参与主体主要不是生产经营者和机构投资者,而多为个体投资者,投机现象严重(李勇和韩雪,2015)。另外,中国银行业金融机构对衍生金融工具交易的态度一向相当谨慎,对衍生金融工具的介入程度与发达国家银行相比要低,这可能是导致衍生金融工具渠道效应不显著的又一主要原因(张雪兰等,2014)。2011年1月,银监会重新修订了《金融机构衍生产品交易业务管理暂行办法》,明确规定在营销与交易时,银行业金融机构应当首先选择基础的、简单的、自身具备定价估值能力的衍生产品。这一系列规定进一步强化了银行业对衍生金融工具谨慎的交易态度,使得衍生金融工具的渠道效应不显著。
| 模型21 | 模型22 | 模型23 | 模型24 | |||||
| Der | ΔCoVaR | Der | ΔCoVaR | Der | ΔCoVaR | Der | ΔCoVaR | |
| Deferred_L | 0.1051
(0.6000) |
0.0092*** (3.4104) |
0.0915
(0.4877) |
0.0097*** (3.2766) |
||||
| Deferred_D | 0.0967
(0.7473) |
0.0063*** (3.1126) |
0.2157
(1.3934) |
0.0086*** (3.4631) |
||||
| Der | −0.0011
(−0.6881) |
−0.0012
(−0.7404) |
−0.0011
(−0.7114) |
−0.0018
(−1.0736) |
||||
| Controls | 未控制 | 未控制 | 控制 | 控制 | 未控制 | 未控制 | 控制 | 控制 |
| R2 | 0.0037 | 0.1100 | 0.1043 | 0.1624 | 0.0057 | 0.0936 | 0.1209 | 0.1728 |
| F值 | 0.3600 | 5.9314*** | 1.3098 | 1.9174* | 0.5585 | 4.9579*** | 1.5469 | 2.0662** |
(三) 稳健性检验
为确保本文实证结果的可靠性,我们进一步从以下四个方面构建了稳健性检验:①第一,风险指标重塑。根据Acharya等(2010)提出的MES方法,首先获得银行体系收益率最差的5%的天数,然后计算银行i在这些天的平均收益率,得到
①限于篇幅,稳健性检验结果未报告,感兴趣的读者可向作者索取。
所有回归结果都符合预期,支持了上文的实证结论,即高管债权激励降低了银行系统性风险,其传染渠道主要是期限错配和非利息收入,而衍生金融工具渠道并未呈现出预期的作用效果。
五、结论与启示
不合理的高管薪酬激励方案是导致银行系统性风险不断积累、最终引发金融危机的深层原因。本文基于2008−2015年中国14家上市银行的数据,考察了高管债权激励对银行系统性风险的影响情况及内在影响渠道。本文主要有以下研究结论:第一,高管债权激励对银行系统性风险有着显著的抑制作用,实施债权激励制度有助于增强高管对银行风险的防范意识。债权激励方案能够有效缓解委托代理冲突,减少高管过度冒险行为。第二,债权激励主要通过降低银行资产负债期限错配程度和增加银行非利息收入(尤其是手续费及佣金收入)来降低银行系统性风险。一方面,降低期限错配会抑制流动性风险和违约风险,减弱银行间关联和风险传染;另一方面,增加非利息收入会加强收入稳定性,缓解系统性冲击的影响。第三,衍生金融工具的渠道效应不显著,可能是由中国衍生金融工具市场起步晚、银行业金融机构过于谨慎而介入程度不深所导致的。此外,一系列稳健性检验,如MES方法替代CoVaR方法对银行系统性风险重新测算、同时性偏误检验、潜在内生性检验、样本量扩充等,均证实了本文结论的有效性。
本文的研究结论为监管部门推动银行业薪酬的债权激励、优化审慎监管方向提供了经验支持,具有较强的政策含义。第一,加强对银行以高管薪酬延期支付为手段的债权激励实施的监管。目前,大部分银行延期支付的高管绩效薪酬比例为50%、期限为3年,仅达到《商业银行稳健薪酬监管指引》的最低要求,并且银行对高管薪酬水平、结构以及延付等信息披露也不详尽。第二,重视逆周期宏观审慎监管,抑制期限错配。长期追踪银行的期限错配情况,正确识别因经济结构、银行运营或薪酬激励等不同因素所导致的期限错配,以便采取针对性的措施来深化银行改革。第三,关注非利息收入业务范围对银行系统性风险的影响。中国银行业非利息收入业务尚处于发展初期,发展非利息收入业务在一定程度上有助于缓和外部冲击的影响,但仍需关注银行对所涉业务的风险管理能力,以维护金融体系的稳定。
随着中国高管期权激励制度的逐渐完善,债权激励制度应该如何设计和优化?在推动高管薪酬延期支付的同时,要鼓励银行实行更加多样化的债权激励方案。当前,中国高管期权激励制度尚不完善,银行业仍然普遍采用“基本薪酬+绩效薪酬”的薪酬机制,参与考核的绩效也多为短期的,长期激励明显不足,由此产生严重的“长计划短安排”现象。2016年以来,国企员工股权激励试点工作正式开展,未来银行业的薪酬设计也将更偏重于股票期权、限制性股票计划等长期激励机制。这虽在一定程度上促使高管自身利益与银行长远利益相一致,但仍然无法根除其作为凸性激励方案可能造成的高管冒进问题。为此,可考虑设计激励性的养老金制度来制衡。根据Edmans和Liu(2011)的研究,债权激励措施包含激励性的养老金制度和延期支付的绩效薪酬,两者是互补的,区别在延期支付的期限上。一般来说,养老金需等到高管离退休后方可领取,这有助于高管职业生命周期与风险持续时期保持一致,从而抑制高管的过度冒险行为。目前,中国的养老金制度更多是作为一种保障性的员工福利,实行专人专户制度,并没有列入公司破产清算范畴,这直接导致高管冒进与其离退休后获得的养老金数目没有关联。因此,为充分发挥债权激励对高管风险行为的约束作用,银行可考虑在保障高管基本养老需求的基础上,进一步设立附带追索与扣回等条款的激励性养老金制度来补充高管薪酬延期支付制度。
| [1] | 方意. 系统性风险的传染渠道与度量研究−兼论宏观审慎政策实施[J]. 管理世界, 2016(8): 32–57. |
| [2] | 何靖. 延付高管薪酬对银行风险承担的政策效应——基于银行盈余管理动机视角的PSM-DID分析[J]. 中国工业经济, 2016(11): 126–143. |
| [3] | 李勇, 韩雪. 关于推进国内衍生品市场规范发展的思考[J]. 中央财经大学学报, 2015(2): 46–50. |
| [4] | 斯文. 我国商业银行使用利率衍生品的动因研究——基于资产负债期限错配视角的经验证据[J]. 南方经济, 2014(2): 42–56. |
| [5] | 张晓玫, 毛亚琪. 我国上市商业银行系统性风险与非利息收入研究——基于LRMES方法的创新探讨[J]. 国际金融研究, 2014(11): 23–35. |
| [6] | 张雪兰, 卢齐阳, 鲁臻. 银行高管薪酬与系统性风险——基于中国上市银行(2007~2013)的实证研究[J]. 财贸经济, 2014(11): 42–54. |
| [7] | 朱波, 杨文华, 刘聪瑞. 中国高管债权激励对银行风险的影响机制[J]. 财经科学, 2017(2): 1–11. |
| [8] | Acharya V V, Pedersen L H, Philippon T, et al. Measuring systemic risk[R]. NYU Working Paper, 2010. |
| [9] | Adrian T, Brunnermeier M K. CoVaR[J]. American Economic Review, 2016, 106(7): 1705–1741. DOI:10.1257/aer.20120555 |
| [10] | Allen F, Babus A, Carletti E. Asset commonality, debt maturity and systemic risk[J]. Journal of Financial Economics, 2012, 104(3): 519–534. DOI:10.1016/j.jfineco.2011.07.003 |
| [11] | Anantharaman D, Fang V W, Gong G. Inside debt and the design of corporate debt contracts[J]. Management Science, 2013, 60(5): 1260–1280. |
| [12] | Armstrong C S, Vashishtha R. Executive stock options, differential risk-taking incentives, and firm value[J]. Journal of Financial Economics, 2011, 104(1): 70–88. |
| [13] | Battiston S, Gatti D D, Gallegati M. Liaisons dangereuses: Increasing connectivity, risk sharing, and systemic risk[J]. Journal of Economic Dynamics & Control, 2012, 36(8): 1121–1141. |
| [14] | Bebchuk L A, Spamann H. Regulating bankers’ pay[J]. Georgetown Law Journal, 2010, 98(2): 247–287. |
| [15] | Belkhir M, Boubaker S. CEO inside debt and hedging decisions: Lessons from the U.S. banking industry[J]. Journal of International Financial Markets Institutions & Money, 2013, 24(2): 223–246. |
| [16] | Bennett R L, Güntay L, Unal H. Inside debt, bank default risk, and performance during the crisis[J]. Journal of Financial Intermediation, 2015, 24(4): 487–513. DOI:10.1016/j.jfi.2014.11.006 |
| [17] | Bernanke B S. Lessons of the financial crisis for banking supervision: A speech at the Federal Reserve Bank of Chicago Conference on Bank Structure and Competition, Chicago, Illinois (via satellite): May 7, 2009[J]. Hospitals, 2009, 20(6): 137–155. |
| [18] | Brisker E R, Wang W. CEO’s inside debt and dynamics of capital structure[J]. Financial Management, 2017, 46(3): 655–685. DOI:10.1111/fima.2017.46.issue-3 |
| [19] | Brockman P, Martin X, Unlu E. Executive compensation and the maturity structure of corporate debt[J]. The Journal of Finance, 2010, 65(3): 1123–1161. DOI:10.1111/j.1540-6261.2010.01563.x |
| [20] | Cassell C A, Huang S X, Sanchez J M. Seeking safety: The relation between CEO inside debt holdings and the riskiness of firm investment and financial policies[J]. Journal of Financial Economics, 2012, 103(3): 588–610. DOI:10.1016/j.jfineco.2011.10.008 |
| [21] | Chava S, Purnanandam A. CEOs versus CFOs: Incentives and corporate policies[J]. Journal of Financial Economics, 2010, 97(2): 263–278. DOI:10.1016/j.jfineco.2010.03.018 |
| [22] | DeYoung R, Roland K P. Product mix and earnings volatility at commercial banks: Evidence from a degree of total leverage model[J]. Journal of Financial Intermediation, 2001, 10(1): 54–84. DOI:10.1006/jfin.2000.0305 |
| [23] | DeYoung R, Peng E Y, Yan M. Executive compensation and business policy choices at U.S. commercial banks[J]. Journal of Financial and Quantitative Analysis, 2013, 48(1): 165–196. DOI:10.1017/S0022109012000646 |
| [24] | Dhole S, Manchiraju H, Suk I. CEO inside debt and earnings management[J]. Journal of Accounting, Auditing & Finance, 2016, 31(4): 515–550. |
| [25] | Edmans A, Liu Q. Inside debt[J]. Review of Finance, 2011, 15(1): 75–102. DOI:10.1093/rof/rfq008 |
| [26] | Gormley T A, Matsa D A, Milbourn T. CEO compensation and corporate risk: Evidence from a natural experiment[J]. Journal of Accounting and Economics, 2013, 56(2-3): 79–101. DOI:10.1016/j.jacceco.2013.08.001 |
| [27] | Gray D F, Jobst A A. Systemic contingent claim analysis—A model approach to systemic risk[R]. IMF Working Paper, 2010. |
| [28] | Jensen M C, Meckling W H. Theory of the firm: Managerial behavior, agency costs and ownership structure[J]. Journal of Financial Economics, 1976, 3(4): 305–360. DOI:10.1016/0304-405X(76)90026-X |
| [29] | John T A, John K. Top-management compensation and capital structure[J]. Journal of Finance, 1993, 48(3): 949–974. DOI:10.1111/j.1540-6261.1993.tb04026.x |
| [30] | Kim J-B, Li L, Ma M L Z. CEO option compensation and systemic risk in the banking industry[J]. Asia-Pacific Journal of Accounting & Economics, 2016, 23(2): 131–160. |
| [31] | Levine R. The corporate governance of banks: A concise discussion of concepts and evidence[R]. Policy Research Working Paper, 2004. |
| [32] | Liu Y, Mauer D C, Zhang Y. Firm cash holdings and CEO inside debt[J]. Journal of Banking & Finance, 2014, 42: 83–100. |
| [33] | Ross S A. Compensation, incentives, and the duality of risk aversion and riskiness[J]. Journal of Finance, 2004, 59(1): 207–225. DOI:10.1111/j.1540-6261.2004.00631.x |
| [34] | Smith R, Staikouras C, Wood G. Non-interest income and total income stability[R]. Bank of England Working Paper, 2003. |
| [35] | Srivastav A, Armitage S, Hagendorff J. CEO inside debt holdings and risk-shifting: Evidence from bank payout policies[J]. Journal of Banking & Finance, 2014, 47(1): 41–53. |
| [36] | Tung F, Wang X. Bank CEOs, inside debt compensation, and the global financial crisis[R]. Boston University School of Law Working Paper, 2013. |
 2018, Vol. 44
2018, Vol. 44


