文章信息
 | 财经研究 2018年44卷第1期 |
- 蒋传海, 杨万中, 朱蓓,
- Jiang Chuanhai, Yang Wanzhong, Zhu Bei.
- 消费者寻求多样化、拥塞效应和厂商歧视定价竞争
- Consumer variety-seeking, congestion effect and firm discriminatory pricing competition
- 财经研究, 2018, 44(1): 100-112
- Journal of Finance and Economics, 2018, 44(1): 100-112.
-
文章历史
- 收稿日期:2017-07-13

2018第44卷第1期
2. 常州工学院 经济与管理学院,江苏 常州 213032
2. School of Economics and Management, Changzhou Institute of Technology, Changzhou 213032, China
一、引 言
在一些行业中,如航空业、旅游业和餐饮业等,我们发现一些外部因素与市场环境有关,如消费者具有寻求多样化(Variety Seeking)购买的倾向,并且不喜欢因消费人数太多而产生的拥塞。Seetharaman 和 Che(2009)认为,寻求多样化购买的消费者重复购买某一种产品会产生效用损失,并把这种损失称为滞留成本(staying costs);拥塞也会导致消费者降低对厂商产品的评价,给消费者带来效用损失,这种损失称为拥塞效应(Congestion)。尽管两者都会给消费者带来效用损失,但还是存在显著的不同,前者是在消费者重复购买时产生效用损失,而后者会在每一期产生,而且消费者人数越多,效用损失越大,因此拥塞效应也被看成是一种网络负外部性(Palma和Proost,2006;Ahlin和Ahlin,2013)。
在这些行业中,我们还可以观察到竞争的寡头厂商根据这些重要的特征使用很多不同于传统的模式进行价格竞争,如餐饮业中一些企业提供的折扣券、航空业的常旅客计划,以及一些行业广泛使用的会员卡模式等。这些定价模式有一个共同的特点,即寡头厂商使用一些手段可以记录并了解消费者购买信息的全部过程,并根据了解的历史信息把消费者分成不同的群体,然后对不同的群体制定不同的价格,这种定价模式称之为基于消费者购买历史的歧视性定价。本文的目的就是引入价格竞争分析范式,结合滞留成本和拥塞效应构建动态价格竞争博弈模型,研究相互竞争的企业使用基于消费者购买历史的歧视性定价策略的本质特征和内在机制,及其对经济效率的影响,我们还进一步讨论了滞留成本和拥塞效应对寡头厂商定价机制选择的影响问题。本文的研究结果不仅可以有效解释在一些行业中广泛存在的一系列重要的经济现象,帮助厂商比较准确地选择营销策略,而且可以有效地帮助反垄断和竞争政策确定对于这种歧视定价的基本态度,因此对于厂商营销决策和竞争政策选择具有重要的现实意义。
消费者行为是营销学研究的重要领域,而消费者寻求多样化购买则是四种重要的消费者行为之一,很早就有一些学者对其开展系统研究。在总结和归纳一些重要研究文献的基础上,Jeuland(1978)和McAlister(1982)分别提出理论来解释消费者寻求多样化购买的行为。虽然这两种理论解释存在显著的不同,但有一个一致的重要特征,就是对消费者来说,重复消费同一种产品会产生效用损失,发生滞留成本。在McAlister(1982)理论解释的基础上,Seetharaman和Che(2009)基于Hotelling空间差异化模型,引入价格竞争理论研究消费者寻求多样化购买对于企业价格竞争的影响。研究发现消费者寻求多样化购买会缓和厂商每一期的价格竞争,形成厂商之间的“默契合谋”,厂商利润也会得到显著的增加。在Seetharaman和Che(2009)研究的基础上,杨渭文和蒋传海(2008)引入基于消费者购买历史的歧视定价策略,进一步研究了消费者寻求多样化购买对于企业价格竞争的影响,发现厂商对消费者进行歧视定价,对于重复购买的消费者给予价格优惠,而对新客户群体索取较高的价格。蒋传海和唐丁祥(2011)则在Jeuland(1978)理论解释的基础上研究了寡头厂商的定价竞争问题,包括统一定价和基于消费者购买历史的歧视定价,也获得了一些重要的研究结果。Chen(1997)、Fudenberg和Tirole(2000)、蒋传海(2010)等学者的文献则基于转移成本研究了寡头厂商的歧视性定价行为。Acquisti和Varian(2005)则是研究了垄断厂商基于消费者购买历史进行歧视性定价,发现尽管歧视性定价是可行的,但这种定价方式对厂商不是最优的。本文的研究进一步丰富和深化了相关领域的研究。
另外一些文献则对拥塞效应的影响展开了研究。Kohlberg(1983)把拥塞效应引入定位竞争的Hotelling模型,主要研究了厂商数量变化时均衡的存在性问题,发现厂商的市场份额是其定位的连续函数,当厂商数大于两个时,竞争均衡并不存在。Pallma和Leruth(1989)在拥塞效应存在的条件下分析了产能和价格竞争问题,研究表明,垄断者倾向于提供更少拥挤的产品,而寡头厂商通过减少产能而减少竞争。胡一竑等(2012)针对拥塞服务业,研究了寡头服务厂商的能力竞争问题。分析结果表明,消费者厌恶拥挤使得任何服务商不可能独占市场。消费者厌恶拥挤的程度越大,服务能力大的服务商所占的优势越大。Ahlin和Ahlin(2013)在 Hotelling模型的基础上引入拥塞效应研究产品差异程度选择问题,他们把拥塞效应看成是网络负外部性,研究发现拥塞效应越大,厂商选择的差异化程度越小。
已有文献基本上都是研究消费者寻求多样化或拥塞效应单个因素对于消费者购买决策和厂商定价的影响。与已有文献相比,本文有三个方面的不同:一,本文结合消费者寻求多样化(滞留成本)和拥塞效应两种因素,重点研究寡头厂商如何使用基于消费者购买历史的歧视定价进行竞争,揭示出定价的本质特征,为现实经济中广泛存在的一些经济现象提供解释;二,在本文的研究中,我们也把拥塞效应视为网络负外部性,但引入Katz和Shapiro(1985)研究网络外部性问题时提出的实现预期①(Fulfilled Expectation)概念,在实现预期均衡下比较和分析社会福利,为竞争政策的选择奠定了基础;三,进一步讨论了寡头厂商的定价机制选择问题。
①实现预期是指消费者对当期市场规模形成预期并在当期实现,对自己未来的市场规模和价格也能形成正确的预期,因此实现预期本质上就是理性预期的一种形式。
二、基本模型
本文聚焦存在滞留成本和拥塞效应的行业,重点研究竞争的寡头厂商使用折扣券、常旅客计划和会员卡等基于消费者购买历史的歧视性定价模式。针对消费者寻求多样化购买,我们采用Jeuland(1978)的理论解释,并视拥塞效应为网络负外部性。
假设市场上有两个厂商A和B,以零边际成本(为了后文分析计算的方便)生产同质产品,不存在固定成本。寻求多样化购买的每个消费者对于产品的保留效用为V,假设V充分大;①消费者数量是连续的,其总量标准化为1。消费者具有如下一些重要的特征:(i)基于Jeuland(1978)的理论解释,消费者寻求多样化购买的程度存在差异,因此具有不同的滞留成本;(ii)消费者对于产品的评价会随着用户的增加而降低,即存在拥塞效应。
①这样假设可以保证在每一期,消费者具有单位需求并且市场被完全覆盖,因此厂商间进行真实的竞争。
在基本模型中,假设寡头厂商使用基于消费者购买历史的歧视定价模式进行竞争。在两期动态博弈竞争模型中,假设在模型的第一期,两个厂商进行线性价格竞争并获得相应的市场份额,价格记为
为对上述基本模型进行社会福利分析,我们需要分析寡头厂商每一期都进行统一定价竞争的情形,并作为比较基准。在基准的两期动态竞争模型中,在每一期两个厂商都进行统一定价竞争,两期都厌恶拥塞的消费者仍然在实现预期的条件下根据厂商的定价做出购买决策。
为了分析在滞留成本和拥塞效应同时存在的情况下,寡头厂商的定价机制选择问题,我们进一步拓展上述博弈模型,建立一个三阶段博弈分析模型。关于博弈的顺序我们将在后文中详细叙述。另外,假设厂商和消费者的贴现因子相等都为
基于基本模型的分析需要从描述消费者的效用函数开始。为了描述消费者的效用函数,假设拥塞效应参数为k(为了保证均衡中纯战略解的存在,假设
在第一期,消费者从厂商A购买获得的效用记为
| ${U_{1A}}({p_{1A}},{N_{1A}}) = V - {p_{1A}} - k{N_{1A}},{U_{1B}}({p_{1B}},{N_{1B}}) = V - {p_{1B}} - k{N_{1B}}$ | (1) |
其中,
在每一期,消费者的购买决策将是选择使其效用最大化的产品,因此他在第二期应该根据预期的市场规模和滞留成本的大小选择使其效用最大化的产品,他在第一期应该选择使其贴现效用最大化的产品,即:
| ${U_i}({p_{1i}},{N_{1i}}) = {U_{1i}}({p_{1i}},{N_{1i}}) + \delta E\left[ {U_{2i}^j,{p_{1A}},{p_{1B}}} \right]$ | (2) |
这里
在统一定价和定价策略选择的分析中,消费者的效用函数及购买决策也相应地适用。
三、基于消费者购买历史的歧视定价竞争
这部分集中研究寡头厂商使用基于消费者购买历史的歧视性定价模式,刻画寡头厂商可以进行歧视定价的本质特征,并且可以很好地解释折扣券、常旅客计划等经济现象。
按照动态博弈分析的逆向归纳法,我们从分析第二期的歧视定价均衡开始。
(一)第二期歧视定价均衡。求解第二期的歧视定价均衡,先需求出每个寡头厂商的市场需求量。对于第一期从厂商A购买产品的消费者,其第二期从厂商A购买或从厂商B购买的无差异条件是:
在实现预期的条件下,消费者预期的市场规模
根据以上所求消费者的数量,厂商A和厂商B第二期的利润分别为:
| ${\pi _{2A}} = {p_{2A}}{d_{AA}} + {\tilde p_{2A}}{d_{BA}} = {p_{2A}}\frac{{{{\tilde p}_{2B}} - {p_{2A}} + k({N_{2B}} - {N_{2A}})}}{\theta }{N_{1A}} + {\tilde p_{2A}}(1 - \frac{{{{\tilde p}_{2A}} - {p_{2B}} - k({N_{2B}} - {N_{2A}})}}{\theta })(1 - {N_{1A}})$ | (3) |
| ${\pi _{2B}} = {p_{2B}}{d_{BB}} + {\tilde p_{2B}}{d_{AB}} = {p_{2B}}\frac{{{{\tilde p}_{2A}} - {p_{2B}} - k({N_{2B}} - {N_{2A}})}}{\theta }(1 - {N_{1A}}) + {\tilde p_{2B}}(1 - \frac{{{{\tilde p}_{2B}} - {p_{2A}} + k({N_{2B}} - {N_{2A}})}}{\theta }){N_{1A}}。$ | (4) |
厂商i会选择歧视定价
| ${p_{2A}} = {p_{2B}} = \frac{1}{3}\theta + k,{\tilde p_{2A}} = {\tilde p_{2B}} = \frac{2}{3}\theta + k$ | (5) |
而且容易验证最优化二阶条件也满足。
从(5)式可以看到,第一,第二期的定价与第一期的市场份额无关;第二,每个厂商对于重复购买的消费者给予价格折扣,而对新顾客要价较高;第三,如果消费者没有寻求多样化购买倾向,即
命题1:在博弈的第二期,寡头厂商之间竞争存在唯一的歧视定价纳什均衡
上述第二期均衡结果不仅可以解释现实经济中厂商的定价行为,而且可以深刻地揭示滞留成本和拥塞效应对于厂商定价的影响。第一,每个厂商对于重复购买的消费者给予价格折扣,而对新顾客索取较高的价格。这可以很好地解释为什么在一些行业中,厂商使用折扣券、常旅客计划和会员卡等定价模式,通过给予价格折扣弥补重复购买消费者的效用损失,吸引一些老顾客不发生转移。其次,随着滞留成本效应
为了求解第一期的均衡,需要计算厂商第二期的利润,因为第一期的决策与第二期的利润有关。在第二期均衡价格下,可以很容易得到第二期重复从厂商A购买的消费者数量
| ${\pi _{2A}} = {N_{1A}}(\frac{\theta }{3} + k)[\frac{1}{3} - \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}] + (1 - {N_{1A}})(\frac{{2\theta }}{3} + k)[\frac{2}{3} - \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}]$ | (6) |
| ${\pi _{2B}} = (1 - {N_{1A}})(\frac{\theta }{3} + k)[\frac{1}{3} + \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}] + {N_{1A}}(\frac{{2\theta }}{3} + k)[\frac{2}{3} + \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}]$ | (7) |
(二)第一期的定价竞争分析。在分析厂商第一期的定价竞争之前,必须分析第一期消费者的购买决策,进而求出每个寡头厂商第一期的市场需求数量。第一期的消费者购买决策比较复杂,他在决策时不但要对第一期的市场规模形成正确预期并在当期实现,而且还要对第二期的定价和市场规模形成正确预期,并且预期的市场规模当期实现。理性的消费者需要对购买每一家厂商的两期总收益进行比较,然后才能进行第一期的购买决策。
如果一个消费者在第一期购买厂商A的产品,并且他在第二期的滞留成本为s,只有当
| ${U_A}({p_{1A}},{N_{1A}}) = V - {p_{1A}} - k{N_{1A}} + \delta E\left[ {U_{2A}^j,{p_{1A}},{p_{1B}}} \right],$ | (8) |
其中
| ${U_B}({p_{1B}},{N_{1B}}) = V - {p_{1B}} - k(1 - {N_{1A}}) + \delta E\left[ {U_{2B}^j,{p_{1A}},{p_{1B}}} \right]$ | (9) |
其中
这里
| ${p_{1A}} - {p_{1B}} - k(1 - 2{N_{1A}}) - \delta \frac{{\theta k(1 - 2{N_{1A}})}}{{9(\theta + 2k)}} = 0$ | (10) |
把第一期消费者数量
| $2(k + \frac{{\delta \theta k}}{{9(\theta + 2k)}})\frac{{\partial {N_{1A}}}}{{\partial {p_{1A}}}} + 1 = 0,2(k + \frac{{\delta \theta k}}{{9(\theta + 2k)}})\frac{{\partial {N_{1A}}}}{{\partial {p_{1B}}}} - 1 = 0$ | (11) |
下面分析厂商第一期的定价竞争问题。在实现预期的约束下,两个厂商A和B将选择价格最大化两期贴现总利润。厂商A和B的两期贴现总利润分别为:
| ${\pi _A} = {\pi _{1A}} + \delta {\pi _{2A}} = {p_{1A}}{N_{1A}} + \delta \left( {{N_{1A}}(\frac{\theta }{3} + k)[\frac{1}{3} - \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}] + (1 - {N_{1A}})(\frac{{2\theta }}{3} + k)[\frac{2}{3} - \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}]} \right)$ | (12) |
| ${\pi _B} \!=\! {\pi _{1B}} \!+\! \delta {\pi _{2B}} \!=\! {p_{1B}}(1 \!-\! {N_{1A}}) \!+\! \delta \left( {(1 \!-\! {N_{1A}})(\frac{\theta }{3} + k)[\frac{1}{3} + \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}] + {N_{1A}}(\frac{{2\theta }}{3} + k)[\frac{2}{3} + \frac{{k(1 - 2{N_{1A}})}}{{3(\theta + 2k)}}]} \right)$ | (13) |
由最优化一阶条件:
| ${p_{1A}} = {p_{1B}} = \frac{{\theta \delta }}{3} + k + \frac{{k\theta \delta }}{{9(\theta + 2k)}}$ | (14) |
把上述价格分别带入(10)式和各自的两期总利润,可以得到
命题2:在第一期市场存在唯一的价格均衡解
通过简单计算可以知道,第一期定价关于两个市场因素满足
通过两阶段的分析结果可以看到:第一,尽管企业进行同质产品的价格竞争,但由于滞留成本和拥塞效应的存在,每一期的定价都高于边际成本,滞留成本和拥塞效应成为寡头厂商市场力量的来源;第二,消费者寻求多样化购买导致消费者的评价产生差异,使厂商使用基于消费者购买历史歧视定价成为可能,并且每个厂商在第二期对重复购买的消费者给予价格折扣;第三,从两期价格竞争结果来看,拥塞效应和滞留成本效应都会弱化厂商的价格竞争,导致厂商之间“默契合谋”。
四、比较基准−统一定价下的均衡结果分析
这一部分我们主要讨论厂商在每一期都进行统一定价(uniform pricing)竞争的情形,博弈的过程如第二部分所述。这种情形不仅可以作为寡头厂商使用基于消费者购买历史进行歧视定价的经济效率的比较基准,而且其本身也具有重要的经济含义。
我们依然使用逆向归纳法分析此两期动态博弈。首先分析第二期两个厂商使用统一定价进行竞争的均衡价格,由于拥塞效应仍然被视为网络负外部性,因此我们继续在实现预期的约束下进行分析。在消费者实现预期的约束下,假设厂商A、B在第一期竞争后的市场规模分别为
(一)第二期的定价均衡结果分析。在统一定价下,我们令
从后面的分析中可以看到第二期两个厂商的竞争均衡存在两种情形,分别对应于第一期市场份额
| $p_{2A}^{u*} = \frac{{\theta (2 - \alpha )}}{{3\alpha }} + k,p_{2B}^{u*} = \frac{{\theta (1 + \alpha )}}{{3\alpha }} + k$ | (15) |
这时厂商A在第二期市场份额
| $p_{2A}^{u*} = \frac{{\theta (2 - \alpha )}}{{3(1 - \alpha )}} + k,p_{2B}^{u*} = \frac{{\theta (1 + \alpha )}}{{3(1 - \alpha )}} + k$ | (16) |
综合(15)和(16)可以求出在统一定价时,第二期博弈唯一的纳什均衡:
| $p_{2A}^{u*} = \left\{ {\begin{aligned}{\displaystyle\frac{{\theta (2 - \alpha )}}{{3\alpha }} + k\;\quad \alpha {\text{≥}} \displaystyle\frac{1}{2}}\\{\displaystyle\frac{{\theta (2 - \alpha )}}{{3(1 - \alpha )}} + k\;\quad \alpha < \displaystyle\frac{1}{2}}\end{aligned}} \right.,p_{2B}^{u*} = \left\{ {\begin{aligned}{\displaystyle\frac{{\theta (1 + \alpha )}}{{3\alpha }} + k\;\quad \alpha {\text{≥}} \displaystyle\frac{1}{2}}\\{\displaystyle\frac{{\theta (1 + \alpha )}}{{3(1 - \alpha )}} + k\;\quad \alpha < \displaystyle\frac{1}{2}}\end{aligned}} \right.$ | (17) |
命题3:两期统一定价博弈的第二期存在由(17)式给出的唯一纳什均衡解,厂商A、B的均衡利润分别为:
| $\pi _{2A}^{u*} = \left\{ {\begin{array}{*{20}{c}}{{{[\displaystyle\frac{{\theta (2 - \alpha )}}{{3\alpha }} + k\;]}^2}\displaystyle\frac{\alpha }{{\theta + 2k\alpha }}\quad \;\;\;\;\;\;\;\;\;\;\;\alpha {\text{≥}} \displaystyle\frac{1}{2}}\\{{{[\displaystyle\frac{{\theta (2 - \alpha )}}{{3(1 - \alpha )}} + k]}^2}\displaystyle\frac{{1 - \alpha }}{{\theta + 2k(1 - \alpha )}}\;\quad {\kern 1pt} \!\!\quad \alpha < \displaystyle\frac{1}{2}}\end{array}} \right.,\pi _{2B}^{u*} = \left\{ {\begin{array}{*{20}{c}}{{{[\displaystyle\frac{{\theta (1 + \alpha )}}{{3\alpha }} + k\;]}^2}\displaystyle\frac{\alpha }{{\theta + 2k\alpha }}\quad \;\;\;\;\;\;\;\;\;\;\;\alpha {\text{≥}} \displaystyle\frac{1}{2}}\\{{{[\displaystyle\frac{{\theta (1 + \alpha )}}{{3(1 - \alpha )}} + k]}^2}\displaystyle\frac{{1 - \alpha }}{{\theta + 2k(1 - \alpha )}}\;{\kern 1pt} \,\,\,\quad \alpha < \displaystyle\frac{1}{2}}\end{array}} \right.$ |
从(17)式可以看到,两期统一定价博弈第二期的均衡价格与厂商第一期所获得的市场份额有关,这与歧视定价策略下均衡结果具有显著的差异。从两厂商的利润表达式可以看出,具有较小市场份额的厂商利润较大;当
(二)第一期的均衡定价。令
在统一定价的情况下,两个厂商第二期的利润函数在
下面的命题说明可以找到满足
命题4:在统一定价竞争下,
①命题4 的证明在未出版的论文中有展示,如读者需要,作者可提供。
根据命题3和命题4,可以归纳出以下命题。
命题5:在统一定价竞争下,存在子博弈精炼纳什均衡解:每个厂商第一期定价为
以统一定价的均衡结果为比较基准,通过比较可以发现,基于消费者购买历史歧视定价下的两期均衡价格相应地低于统一定价下的两期均衡价格,厂商均衡利润也低于统一定价下的厂商均衡利润。通过计算可以看出,与统一定价下的社会福利相比,歧视定价下重复购买的消费者较多,福利损失也较大,因此歧视定价下的社会福利低于统一定价下社会福利。对消费者来说,虽然歧视性定价导致较多的消费者滞留,损失一部分消费者效用,但由于厂商定价较低,使得消费者又获得了较多的剩余,最终使得消费者的剩余更高。
但要注意的是,尽管两个厂商第二期的利润函数
五、定价模式的均衡选择
如果厂商可以在基于消费者购买历史的歧视定价和统一定价两种定价模式之间进行选择,那么它们将选择哪一种定价模式呢?为了分析这个问题,我们建立三期动态博弈,三期博弈的顺序如下:(1)第0期厂商同时决定选择哪一种定价模式,并在第二期使用该定价模式;(2)第1期两个厂商同时选择价格,消费者根据厂商的定价选择从其中一家购买产品;(3)第2期厂商按照第0期选择的定价模式进行定价竞争,消费者决定从哪个厂商处购买产品。
在厂商第0期确定定价模式后,后续博弈存在四个子博弈,分别是:(1)两个厂商同时选择统一定价的子博弈;(2)厂商A选择基于消费者购买历史的歧视定价,厂商B选择统一定价的子博弈;(3)厂商A选择统一定价,厂商B选择基于消费者购买历史的歧视定价的子博弈;(4)厂商A、B同时选择基于消费者购买历史的歧视定价的子博弈。
在第一个子博弈中,它们达成协调子博弈精炼解,两个厂商第一期的定价为
在以下公式中,各符号具有与前面相同的含义,并且消费者对于市场规模具有实现预期。类似前面的分析可得:厂商A和厂商B在第二期的利润分别为:
| $\begin{aligned}{\pi _{2A}} = & \alpha \frac{{{p_{2B}} - {p_{2A}} + k(1 - 2\beta )}}{\theta }{p_{2A}} + (1 - \alpha )\frac{{\theta - {{\tilde p}_{2A}} + {p_{2B}} + k(1 - 2\beta )}}{\theta }{\tilde p_{2A}}\\{\pi _{2B}} =& \frac{{\alpha (\theta + {p_{2A}}) + (1 - \alpha ){{\tilde p}_{2A}} - {p_{2B}} + k}}{{\theta + 2k}}{p_{2B}}\end{aligned}$ | (18) |
由一阶条件为:
| ${p_{2A}} = \frac{{\theta (1 + \alpha )}}{6} + k,{\tilde p_{2A}} = \frac{{\theta (4 + \alpha )}}{6} + k,{p_{2B}} = \frac{{\theta (1 + \alpha )}}{3} + k$ | (19) |
由此可得到两个厂商第二期利润函数分别为:
| $\begin{aligned}{\pi _{2A}} = & \alpha [\frac{{\theta (1 + \alpha )}}{6} + k][\frac{{1 + \alpha }}{6} - \frac{{(1 - 2\alpha )k}}{{3(\theta + 2k)}}] + (1 - \alpha )[\frac{{\theta (4 + \alpha )}}{6} + k][\frac{{4 + \alpha }}{6} + \frac{{(1 - 2\alpha )k}}{{3(\theta + 2k)}}]\\ {\pi _{2B}} = & [\frac{1}{2} - \frac{{\theta (1 - 2\alpha )}}{{6(\theta + 2k)}}][\frac{{(1 + \alpha )}}{3}\theta + k]\end{aligned}$ | (20) |
虽然上面已经求出第二期的均衡解,我们还需求解厂商A在第一期的定价。类似于前面的分析可知,两个厂商在第一期的价格关系为:
| ${p_{1A}} - {p_{1B}} = k(1 - 2\alpha ) + \frac{{\delta \theta }}{4} + \frac{{\delta \theta (1 - 2\alpha )k}}{{6(\theta + 2k)}}$ | (21) |
由于厂商B在第一期对产品的定价为
①这是因为当k=0 时,${\tilde \pi _A} = \frac{{5\delta \theta }}{4} > \pi _A^u = \frac{{5\delta \theta }}{6}$,而${\tilde \pi _A}$和$\pi _A^u$关于k 连续,所以存在k >0,当k ≤k0时有${\tilde \pi _A}$>$\pi _A^u$。
其次分析第二类情况:厂商A使用基于消费者购买历史的歧视定价模式,并在第一期定价
根据对称性,第三个子博弈完全类似于第二个子博弈的分析。
在第四个子博弈中,企业A、B都在第二期使用基于消费者购买历史的歧视定价,由前面分析可知均衡时两个厂商的利润分别为
根据以上分析,第0期厂商的定价模式选择博弈的结果总结为如下:
命题6:如果厂商可以在基于消费者购买历史的歧视定价和统一定价两种定价模式之间进行选择,那么当消费者的拥塞效应k相对于滞留成本效应
消费者的拥塞效应k相对于滞留成本效应
命题6的结果与Acquisti和Varian (2005)的结论有显著的差异。存在差异主要是由于垄断厂商选择歧视性定价导致高估值的消费者可以通过模仿低估值的消费者进行选择,从而导致厂商利润损失,因此厂商选择统一定价。在本文寡头厂商竞争的市场环境下,如果厂商A选择统一定价,那么竞争对手B选择基于消费者购买历史的歧视性定价不仅能吸引厂商A的一部分消费者转移购买,而且还能吸引自己的老客户重复购买,从而导致厂商A利润受损。因此所有的厂商最后都选择基于消费者购买历史的歧视性定价,陷入“囚徒困境”。
六、数值算例
为了更清楚比较厂商不同定价机制的均衡结果,在这里通过一个数值算例给予说明。
由于相对拥塞效应,滞留成本效应对消费者的消费行为会产生更大的影响,因而对厂商的价格竞争也会产生更大的影响,所以在这里主要分析滞留成本效应
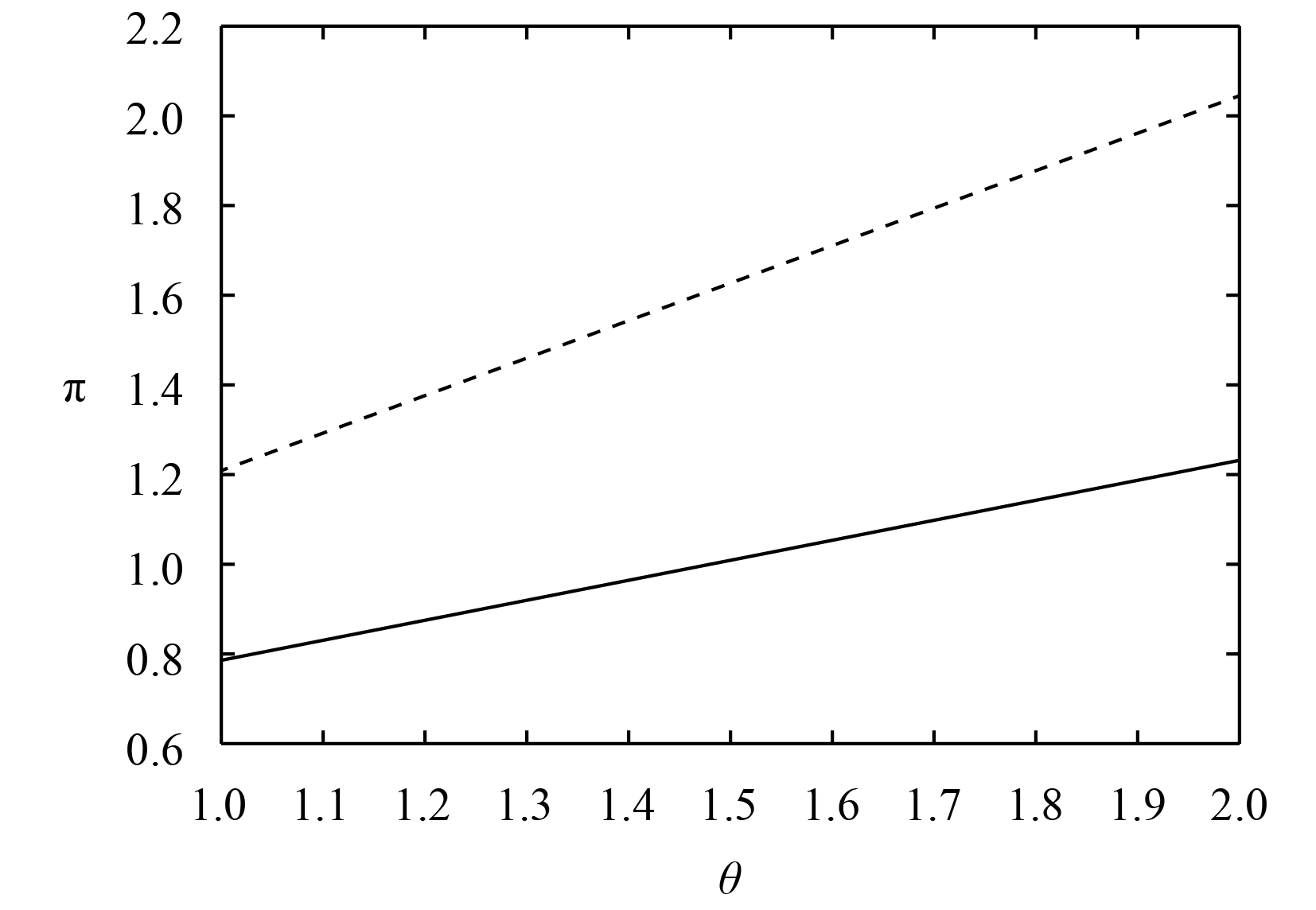
|
| 图 1 厂商均衡利润 |
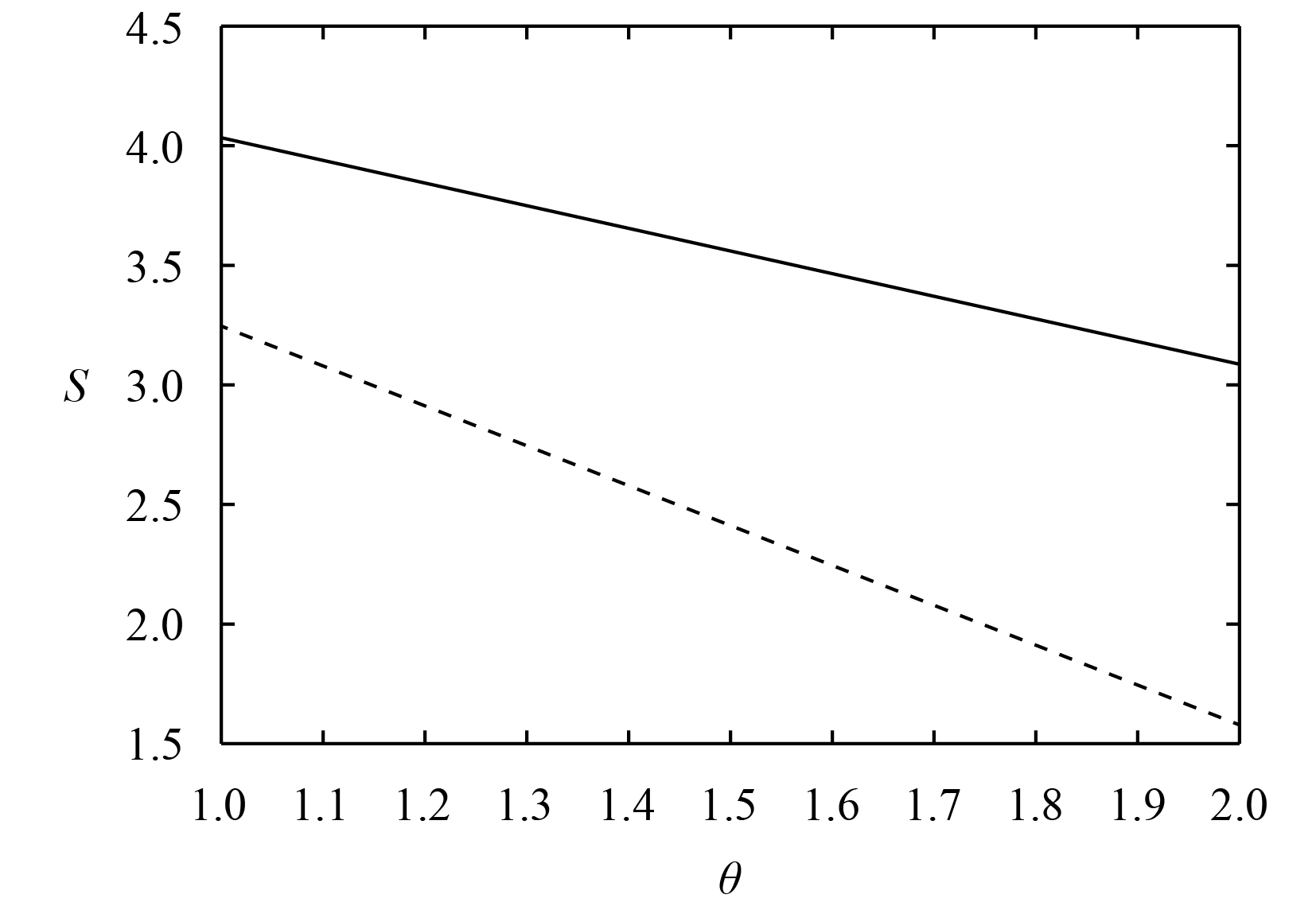
|
| 图 2 均衡消费者剩余 |
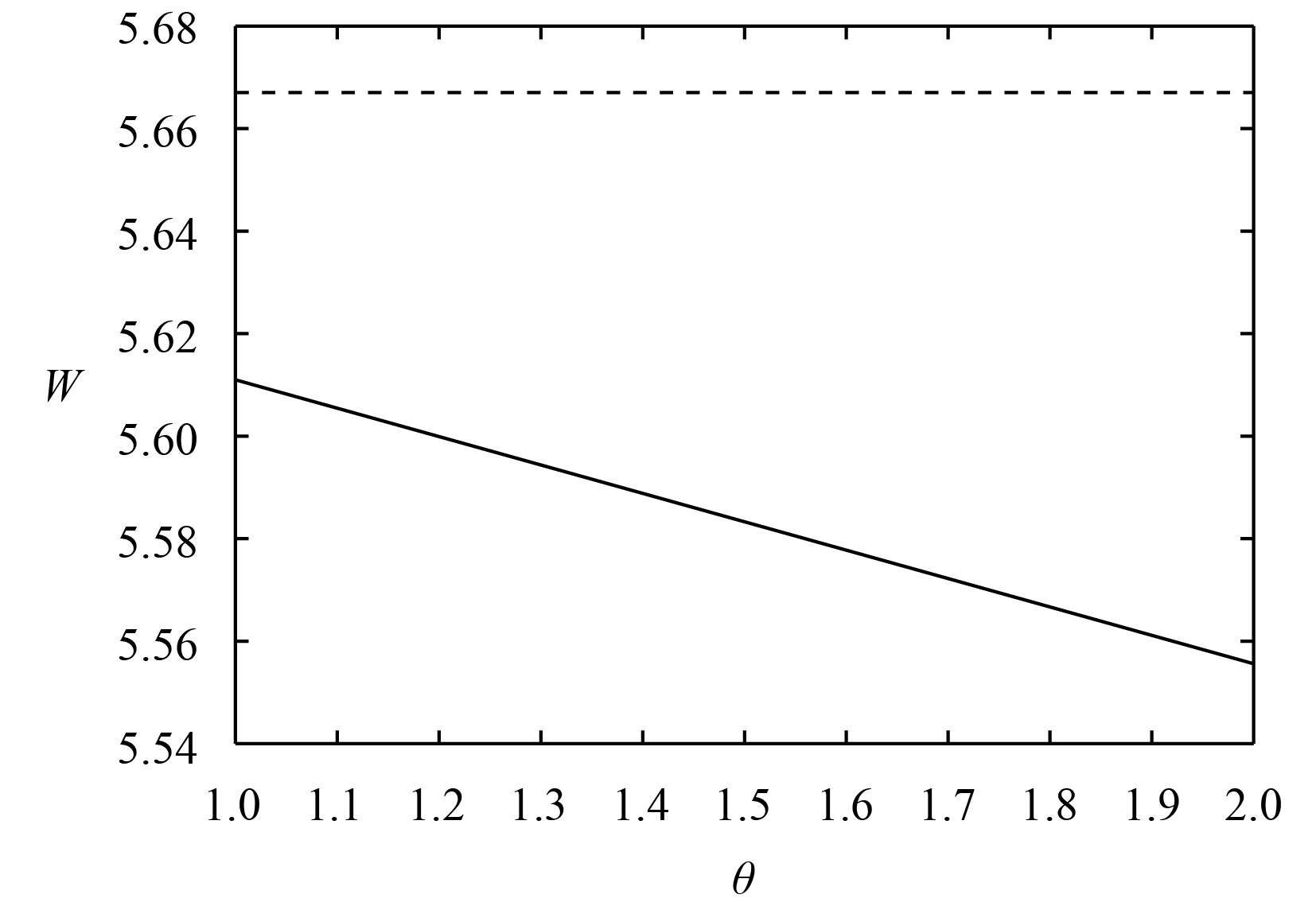
|
| 图 3 均衡社会总福利 |
从图1-3可以看出,厂商的利润随着消费者滞留成本效应
七、结 论
在一些行业中,消费者寻求多样化购买和拥塞效应共同存在,相互竞争的寡头厂商使用诸如折扣券、常旅客计划和会员卡等基于消费者购买历史的歧视性定价模式进行竞争。我们构建了动态博弈模型,主要研究消费者寻求多样化购买和拥塞效应这两种市场环境因素对于厂商歧视定价和社会福利的影响。研究发现,这两种市场环境因素都可以导致厂商的市场势力,但是厂商可以实施歧视定价的根本原因在于消费者寻求多样化。拥塞效应并不会导致厂商对消费者进行歧视定价。但是拥塞效应可以抑制厂商吸引消费者数量增加的降价行为,弱化厂商之间的竞争,导致寡头厂商之间的“默契合谋”。实际上这两种市场环境因素都会弱化市场两期价格竞争。与统一定价相比,歧视定价下的两期均衡价格均低于统一定价下的两期均衡价格,歧视定价下的厂商均衡利润和社会福利也分别低于统一定价下的厂商均衡利润和社会福利。进一步的定价策略选择表明,两个厂商都选择基于消费者购买历史的歧视定价策略是均衡结果,较低的利润会导致两个厂商都陷入“囚徒困境”的境地。
本文的研究结果不仅可以让我们深刻理解消费者寻求多样化购买和拥塞效应对于厂商市场力量的影响,而且可以很好地解释现实经济中广泛存在的许多现象,如折扣券、常旅客计划和会员卡等营销手段。这对于厂商如何选择营销策略具有重要的启示。厂商不仅可以使用传统的营销策略应对消费者的寻求多样化购买行为,而且也要顺应时代的发展,利用信息化技术记录消费者的历史购买信息,以有效地区分消费者群体,实施新型的歧视定价,如基于消费者购买历史的歧视定价,使得自己在竞争中处于有利地位,获得竞争优势。针对拥塞效应,厂商可以利用消费者对于拥塞的厌恶,适当提高产品价格,降低消费者的需求,减少拥塞,也能使自己获得更大的利益。
价格歧视是反垄断法和竞争政策非常关注的企业市场行为,因为企业通过价格歧视既可能榨取更多的消费者剩余,也可能排除和限制竞争。特别对于具有市场支配地位的企业,反垄断当局更加关注这类企业的歧视定价行为。美国的《克莱顿法》和欧盟反垄断法都在市场支配地位滥用条款中列入了价格歧视的行为,需要强调的是他们只惩罚滥用市场支配地位的价格歧视行为,而不惩罚创造市场支配地位的各种行为,包括价格歧视。我国的反垄断法也是这样,其第十七条“禁止具有市场支配地位的经营者从事下列滥用市场支配地位的行为”中的第六款规定:没有正当理由,对条件相同的交易相对人在交易价格等交易条件上实行差别待遇。可见我国反垄断法的这一条款和欧美反垄断法相关条款精神一致,反对滥用市场支配地位的价格歧视行为,但是如果存在正当理由,也可以使用。
针对本文研究的基于消费者购买历史的歧视性定价模式而言,我们将在总福利标准下对其进行考察。在本文的研究中,歧视定价导致社会总福利下降,按照总福利标准,这种歧视定价模式应该被禁止。但这种情况是由于模型的假设和特定参数值决定的,因此在实践中是否禁止还需仔细分析。竞争政策主要关注滥用市场支配地位的价格歧视行为,而在同时存在消费者寻求多样化购买和拥塞效应的行业一般都是竞争非常充分的行业,几乎不存在具有市场支配地位的,而且企业采取这样的定价行为也比较有利于消费者,因此在实践中我们也可以看到反垄断当局较少关注企业采取这样的行为。社会福利的损失主要来自消费者寻求多样化本身,而要了解消费者本身的这种信息非常困难,存在大量的信息成本问题,即使能禁止,执法成本也会非常高。基于这些原因,我们认为针对竞争性比较充分的行业,竞争政策的选择应该放任企业采用此类定价策略,不应过多地干预;只有在确认采用这种定价模式的企业具有市场支配地位时,反垄断当局才要谨慎地予以对待。
| [1] | 胡一竑, 张建同, 朱道立. 考虑消费者偏好的寡头服务商竞争研究[J]. 系统工程学报, 2012(3): 311–319. |
| [2] | 蒋传海. 网络效应、转移成本和竞争性价格歧视[J]. 经济研究, 2010(9): 55–66. |
| [3] | 蒋传海, 唐丁祥. 厂商动态竞争性差别定价和竞争优势实现[J]. 管理科学学报, 2012(2): 48–57. |
| [4] | Acquisti A, Varian H R. Conditioning prices on purchase history[J]. Marketing Science, 2005, 24(3): 367–381. DOI:10.1287/mksc.1040.0103 |
| [5] | Ahlin C, Ahlin P D. Product differentiation under congestion or snobbery:Hotelling was right[J]. Economic Inquiry, 2013, 51(3): 1750–1763. DOI:10.1111/ecin.2013.51.issue-3 |
| [6] | Chen Y. Paying customers to switch[J]. Journal of Economics and Management Strategy, 1997, 6(4): 877–897. DOI:10.1162/105864097567291 |
| [7] | Fudenberg D, Tirole J. Customer poaching and brand switching[J]. RAND Journal of Economics, 2000, 31(4): 634–657. DOI:10.2307/2696352 |
| [8] | Jeuland A P. Brand preference over time: A partially deterministic operationalization of the notion of variety seeking[A]. Jain S(Ed.). AMA research frontiers in marketing: dialogues and directions[C]. Chicago: American Marketing Association, 1978. |
| [9] | Klemperer P. The competitiveness of markets with switching costs[J]. RAND Journal of Economics, 1987, 18(1): 138–150. DOI:10.2307/2555540 |
| [10] | Kohlberg E. Equilibrium store locations when consumers minimize travel time plus waiting time[J]. Economics Letters, 1983, 11(3): 211–216. DOI:10.1016/0165-1765(83)90137-4 |
| [11] | Palma A D, Leruth L. Congestion and game in capacity:A duopoly analysis in the presence of network externalities[J]. Annales d’Economie et de Statistique, 1989(15/16): 389–407. |
| [12] | Seetharaman P B, Che H. Price competition in markets with consumer variety seeking[J]. Marketing Science, 2009, 28(3): 516–525. DOI:10.1287/mksc.1080.0434 |
 2018, Vol. 44
2018, Vol. 44


