文章信息
 | 财经研究 2017年43卷第10期 |
- 徐国祥, 郭建娜.
- Xu Guoxiang, Guo Jianna.
- 金融稳定目标下中国货币政策规则研究
- Research on chinese monetary policy rules under the target of financial stability
- 财经研究, 2017, 43(10): 18-30
- Journal of Finance and Economics, 2017, 43(10): 18-30.
-
文章历史
- 收稿日期:2017-04-01

2017第43卷第10期
2. 上海财经大学 统计与管理学院,上海 200433
2. School of Statistics and Management, Shanghai University of Finance and Economics, Shanghai 200433, China
一、引言
货币政策的制定和实施应趋向规则化已是学者的基本共识。在货币政策规则中,泰勒规则通过关注通货膨胀率和产出两个目标变量来调整利率,这一规则得到了广泛的认可。早期,物价稳定与金融稳定普遍被认为是一致的,货币政策规则关注了物价稳定,不需再关注金融稳定(Bernanke和Mishkin,1997)。但近年来,多次金融危机是在低通胀环境下发生的,说明传统的基于物价稳定目标的货币政策规则已不能满足新形势下稳定经济和金融的要求。理论上,货币政策会通过多种途径影响金融稳定,其实施过程最终也会影响金融稳定(马勇,2016)。实际中,基于宏观审慎框架维护金融稳定还处于初级阶段,效果有待检验,且不易实施,在维护金融稳定方面还需要货币政策的支持。因此,维护金融稳定可以从货币政策入手(弗里德曼和施瓦茨,2009),货币政策规则应添加金融稳定目标。国内有部分学者认为,我国的货币政策需关注或在实践中已经关注了金融稳定目标,如马勇(2013)、郭红兵和杜金岷(2014) 等。
将金融稳定加入货币政策目标中要面对两个问题:一是金融稳定以怎样的形式加入货币政策规则中;二是什么形式的泰勒规则模型更适用。关于前者,当前学者认为相对于单一的金融类指标,将一个能够表示金融稳定情况的综合性指数直接纳入泰勒规则中更合适;关于后者,相对于线性模型,非线性模型更符合现实情况。①由于货币政策效果的非对称性②(肖本华,2012) 以及央行对目标变量反应的非线性特点,非线性泰勒规则更能充分地解释货币政策。但我国当前的研究表明,没有关注金融稳定目标的泰勒规则并不具有非线性特征,不管是高通胀还是低通胀环境下,货币政策调控的效果都被认为是一样的。这也是我国以物价稳定为目标的传统货币政策规则进行宏观调控时存在的一个问题。本文发现将金融稳定纳入货币政策规则后,这个问题得到了改善。将金融稳定纳入货币政策目标的研究具有重要的现实意义:一方面,解决了物价稳定与金融稳定在新形势下不一致的问题,有利于改善传统的物价稳定和产出目标无法维护金融稳定的情况;另一方面,可以利用金融稳定与货币政策间的关系为货币政策的制定和实施提供理论指导,有利于我国货币政策实施的规则化。
① 在线性模型中,不管经济环境如何,货币政策目标变量的增加或减少对利率的影响是相同的;而在非线性模型中,在不同的经济环境下,货币政策目标变量的增加或减少对利率的影响是不同的。
② 一般地,货币政策的非对称效应表现为,在经济紧缩阶段扩张性货币政策的加速作用小于在经济扩张阶段紧缩性货币政策的减速作用。
基于当前经济的实际情况,需将金融稳定目标加入货币政策规则中。本文基于泰勒规则,主要研究了金融稳定目标下中国货币政策规则的特征。研究发现:(1) 将金融稳定以指数的形式加入泰勒规则中,金融稳定和产出在货币政策中可以平稳地传导,但通货膨胀在货币政策中的传导不平稳,我国的货币政策依然是不稳定的。(2) 只包含产出和通货膨胀两个传统货币政策目标时,泰勒规则不具有非线性特征;引入金融稳定目标后,泰勒规则具有符合现实要求的非线性特征,且若以不包含金融稳定目标的泰勒规则进行宏观调控,调控力度会被低估。(3) 泰勒规则的非线性特征表明,在高通胀条件下,金融稳定对利率有显著的影响,此时央行会增加对金融稳定目标的关注,高通胀条件下产出缺口的扩大对利率的影响比低通胀条件下要大,利率需对通货紧缩做出更大的反应。(4) 我国在货币政策的调控中显著关注了金融稳定目标,并逐渐趋于按照含有金融稳定目标的泰勒规则进行操作,因此将金融稳定目标加入货币政策规则中的研究内容和结论是有效的。
本文的创新主要体现在:第一,使用中国金融稳定指数(CFSI)作为金融稳定的衡量指标加入货币政策目标中。与研究中常用单一金融指标或是衡量货币环境宽松程度的金融状况指数、金融形势指数等不同,CFSI由多指标合成,能够反映金融系统稳定性综合、平均、动态的变化,且CFSI是紧扣金融稳定内涵构建的既能准确反映我国金融稳定情况又对通货膨胀和产出有预测能力的指数。第二,发现了含有金融稳定目标的货币政策规则具有未包含金融稳定目标时所不具有的非线性特点。例如,在高通胀条件下,金融稳定程度会显著影响利率,产出缺口的扩大对利率的影响比低通胀条件下要大,这可以为不同的经济环境下货币政策的实施提供更有针对性的指导。
二、研究回顾
关于金融稳定在货币政策中的角色主要有两种观点。传统的观点认为中央银行将目标定为物价稳定和产出稳定是最优的,物价稳定是金融稳定的充分条件(Bernanke,2002;Posen,2006)。另一种观点认为物价稳定并不一定导致金融稳定。在2008年之前,世界经济进入了空前繁荣的时期,高增长和低通胀是这一时期最显著的特征。此时,以物价稳定为目标的货币政策框架使货币当局对物价稳定时的经济繁荣过分乐观,从而忽视了潜在的风险积累,无形中纵容了金融的不稳定现象(Schinasi,2003;封北麟和王贵民,2006)。近年来,以盯住通货膨胀和产出两个目标的泰勒规则进行宏观调控已不足以确保金融稳定。在2008年之前第一种观点被普遍接受,2008年金融危机让学者对当时货币政策的适用性产生了怀疑,开始认为央行的损失函数除了通货膨胀率和产出缺口外,还应包括能够反映金融稳定程度的某种指标(Woodford,2012)。当前,将金融稳定作为另一新目标成为主流观点,这样金融稳定情况对货币政策的影响是直接且清楚的,持这种观点的主要有Roubini(2006)、Woodford(2012) 等。黄佳和朱建武(2007) 研究发现,我国以货币稳定为目标的货币政策确实没能实现金融稳定,货币政策需要关注衡量金融稳定的变量,如银行信贷和房价等。
当前,将金融稳定目标纳入货币政策框架的研究方法主要是将金融稳定指标纳入泰勒规则,构建泰勒规则的扩展模型。Benjamin(2014) 提出可以将代表金融稳定情况的指标直接纳入泰勒规则,这样的指标可以是某个目标资产价格变量或者金融变量,也可以是由相关的多个变量合成的指数,指数相对于单个变量的优点在于允许央行可以对金融不平衡有更广泛的反应,且这样的考虑也更接近实际情况。Castro(2011) 也认为,将多个指标赋权合成一个综合指数是更好的方法,原因在于央行可能并不总是关注某种资产价格或某个金融变量,将相关指标合成指数可以更好地涵盖央行在金融市场上关注的目标。万光彩等(2015) 认为,构建“广义价格指数”是货币政策关注金融稳定的主要方式,这被称作“古德哈特”建议,“广义价格指数”已先后采用了货币状况指数、金融状况指数、金融稳定状况指数等。Baxa等(2013) 将金融稳定以指数形式纳入泰勒规则,结果表明在面对较高的金融压力时,央行通常实施降低利率的政策。Albulescu等(2013) 从金融市场、银行和外部约束三个维度构建相应的不稳定子指数,并将它们纳入泰勒规则来评价欧洲中央银行货币政策的表现。结果显示,不稳定指数的引入改善了泰勒规则,在2005-2009年,不稳定指数对利率变动的贡献高达54%。
20世纪90年代至21世纪初,美联储、英格兰银行、日本银行、欧洲中央银行等的政策执行符合泰勒规则,这些国家迎来了经济和金融繁荣发展的一段时期。关于泰勒规则在我国的应用有三点一致的结论:第一,泰勒规则在全球范围内得到广泛认可和使用,对央行的货币操作具有重要的指导意义;第二,泰勒规则可以描述我国的利率走势,有一定的适用性;第三,泰勒规则在我国是不稳定的规则,主要是利率对通货膨胀的反应不稳定,应推进利率改革,促进货币政策操作的规则化。相关文献主要有谢平和罗雄(2002)、张屹山和张代强(2007)、刘金全和张小宇(2012)、袁野(2014) 等。鉴于此,本文使用泰勒规则来研究加入金融稳定目标的货币政策规则。
最初的泰勒规则是线性模型,如果央行参考该规则进行宏观调控,不管经济环境如何,提高或降低利率的幅度是相同的,这实际上承认了货币政策的作用是对称的。确实,在20世纪20年代之前,货币政策的作用被认为是相对稳定的。直至大萧条时期,紧缩性的货币政策有效,而扩张性的货币政策无效,出现了货币政策的非对称效应,即在不同的经济环境下货币政策效果会不同,则线性的泰勒规则不再适合刻画货币政策。此外,线性的泰勒规则是央行在线性约束条件下二次标准目标损失函数的最优政策,而现实中央行对货币政策目标变量变化有非对称偏好(周波,2014)。因此,新形势下有效的货币政策规则应具有非线性特点(肖本华,2012)。基于国外市场的研究表明,金融稳定目标的引入可以改善泰勒规则的特性,使其具有非线性特点。如Castro(2011) 认为泰勒规则可以引入衡量金融市场环境宽松程度的金融状况指数,并发现欧洲、英国央行的货币政策规则具有非线性特点。国内现有研究表明,我国的货币政策考虑了金融市场的情况(郭红兵和杜金岷,2014;高洁超和孟士清,2015);在泰勒规则中,我国利率对金融变量有反应(刁节文等,2011;卞志村等,2012);在考虑了金融指标后,泰勒规则具有非线性特点(刁节文和章虎,2012;郭红兵和杜金岷,2014)。
综上所述,货币政策规则需在通货膨胀和产出缺口两个传统目标的基础上增加金融稳定目标,金融稳定目标的引入可以改善泰勒规则的性质,使其具有非线性特征。我国的相关研究主要存在以下问题:第一,关于金融稳定在货币政策反应函数中的形式,国内较多地使用单一价格指标或是构建衡量货币环境宽松程度的金融状况指数、金融形势指数等作为金融稳定的代理指标。这种方法不能直接准确地衡量我国的金融稳定情况,不免对金融稳定和货币政策关系的研究有所影响。第二,目前国内对未包含金融稳定目标的货币政策规则研究表明,在不同的经济环境下,产出或通货膨胀的变化对利率的影响效果是相同的。这与现实不符,若按照此规则进行宏观调控,会低估货币政策的效果,产生不良的后果。将金融稳定目标纳入货币政策反应函数后,货币政策的目标变量在不同经济阶段的变化是否引起利率不同程度的变化,我国货币政策制定中是否关注了金融稳定,这些都还需研究和验证。本文对这些问题进行了全面研究,结果表明加入金融稳定目标的泰勒规则可以为货币当局进行更有效地宏观调控提供良好的参考。
三、将中国金融稳定指数纳入货币政策规则的扩展模型
前瞻性货币政策反应函数为:
| $r_t^* = {r^*} + \beta \left( {E\left[ {{\pi _{t + i}}{\rm{|}}{\Omega _t}} \right] - \pi _{t + i}^*} \right) + \gamma E\left[ {{y_{t + j}}{\rm{|}}{\Omega _t}} \right]$ | (1) |
其中,rt*表示t期的目标利率,r*表示均衡名义利率,πt+i表示t+i期的通货膨胀率,πt+i*表示通胀目标,yt+j表示t+j期的产出缺口,Ωt表示央行在t期制定利率时可获得的信息集,i(j)表示领先信息集的期数。
一般认为,央行倾向于缓慢地将利率调整至目标值,其中一阶的利率平滑行为如下:
| ${r_t} = \rho {r_{t - 1}} + \left( {1 - \rho } \right)r_t^*$ | (2) |
其中,rt表示t期的名义利率,ρ∈[0, 1]为利率平滑系数,反映了利率的平滑程度。
将式(2) 代入式(1) 中,并消去不可观测的前瞻性变量,可得基础的泰勒规则线性模型:
| ${r_t} = \left( {1 - \rho } \right)\left[ {{r^*} + \beta \left( {{\pi _{t + i}} - \pi _{t + i}^*} \right) + \gamma {y_{t + j}}} \right] + \rho {r_{t - 1}}$ | (3) |
本文将衡量我国金融稳定情况的CFSI纳入模型,得到扩展的泰勒规则。在此,cfsit+k并不直接进入货币政策反应函数,而是作为利率偏离目标利率的一个影响因素,这样更合理(Baxa等,2013)。扩展的泰勒规则为:
| ${r_t} = \left( {1 - \rho } \right)\left[ {{r^*} + \beta \left( {{\pi _{t + i}} - \pi _{t + i}^*} \right) + \gamma {y_{t + j}}} \right] + \delta cfs{i_{t + k}} + \rho {r_{t - 1}} + {\varepsilon _t}$ | (4) |
令α0=(1-ρ)(r*-βπt+i*),α1=(1-ρ)β,α2=(1-ρ)γ,α3=δ,则式(4) 可写为:
| ${r_t} = {\alpha _0} + {\alpha _1}{\pi _{t + i}} + {\alpha _2}{y_{t + j}} + {\alpha _3}cfs{i_{t + k}} + \rho {r_{t - 1}} + {\varepsilon _t}$ | (5) |
我们使用平滑转换模型(STR模型)来刻画扩展的泰勒规则,此模型允许内生变量进行平滑转换,也可以得到央行进行政策调整的时点。将扩展的泰勒规则用标准的STR模型描述如下:
| ${r_t} = \psi \prime {z_t} + \theta \prime {z_t}G\left( {\eta ,{\rm{ }}c,{\rm{ }}{s_t}} \right) + {\varepsilon _t},{\rm{ }}t = 1, \ldots ,{\rm{ }}T,{\varepsilon _t} \sim i.i.d.N\left( {0,{\rm{ }}{\sigma ^2}} \right)$ | (6) |
其中,zt=(1, rt-1, πt+i, yt+j, cfsit+k)′为解释变量向量,ψt=(ψ0,ψ1, …, ψ4)′和θ=(θ0, θ1, ..., θ4)′分别为变量线性部分和非线性部分的系数向量,G(η, c, st)为转换函数,st为转换变量,η为斜率参数,表示平滑转换的速度,c为位置参数,表示转换发生的位置。当st→-∞时, G(η, c, st)→0;当st→+∞时, G(η, c, st)→1。转换变量可以是解释变量中的一个或是几个的线性组合。一般地,转换函数的形式为:
| $G\left( {\eta ,{\rm{ }}c,{\rm{ }}{s_t}} \right) = {\left( {1 + {\rm{exp}}\left\{ { - \eta \prod\limits_{k = 1}^K {\left( {{s_t} - {c_k}} \right)} } \right\}} \right)^{ - 1}},\eta > 0$ | (7) |
当K=1,式(7) 为Logistic STR或LSTR1模型;当K=2时,式(7) 为LSTR2模型。
我们利用状态空间模型,研究我国的货币政策规则中是否关注了金融稳定目标,以及通货膨胀、产出缺口和金融稳定三个目标变量对利率的影响随时间变化的情况。根据Baxa等(2013),在式(5) 的基础上构建具有时变特征的泰勒规则扩展模型。
| $\begin{array}{l} {r_t} = {\alpha _{0,{\rm{ }}t}} + {\alpha _{1,{\rm{ }}t}}{\pi _{t + i}} + {\alpha _{2,{\rm{ }}t}}{y_{t + j}} + {\alpha _{3,{\rm{ }}t}}cfs{i_{t + k}} + {\rho _t}{r_{t - 1}} + {\varepsilon _t}\\ {\alpha _{m,{\rm{ }}t}} = {\alpha _{m,{\rm{ }}t - 1}} + {\theta _{m,{\rm{ }}t}},{\rm{ }}{\theta _{m,{\rm{ }}t}} \sim i.i.d.N\left( {0,{\rm{ }}\sigma _{{\theta _m}}^2} \right),m = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3\\ {\rho _t} = {\rho _{t - 1}} + {\theta _{4,{\rm{ }}t}},{\theta _{4,{\rm{ }}t}} \sim i.i.d.N\left( {0,{\rm{ }}\sigma _{{\theta _4}}^2} \right) \end{array}$ | (8) |
四、我国金融稳定与货币政策规则的关系
(一) 中国金融稳定指数对通货膨胀和产出的预测能力
中国金融稳定指数的构建指标主要包括:存贷款利率差、证券化率、国内信贷/GDP、商业银行不良贷款率、存贷款比率、股票市盈率、实际有效汇率指数、通货膨胀率、商品房销售价格、财政赤字/GDP以及M2/GDP,我们使用结构向量自回归赋权法编制2003年第二季度至2016年第一季度的CFSI。数据来源主要是万得数据库、国际清算银行和中国经济数据库。指标的选择依据和CFSI的编制过程详见徐国祥等(2017)。
将金融稳定指数纳入货币政策反应函数,成为货币政策操作目标变量的一个前提条件是,其对产出有较好的预测能力且包含了未来通货膨胀的信息(Castro,2011)。
1.格兰杰因果检验。由表 1可知,CFSI是通货膨胀率的因,通货膨胀率不是CFSI的因,说明CFSI对通货膨胀有预测能力(戴国强和张建华,2009)。同样地,CFSI是产出的因,产出不是CFSI的因,说明CFSI对产出有预测能力。
|
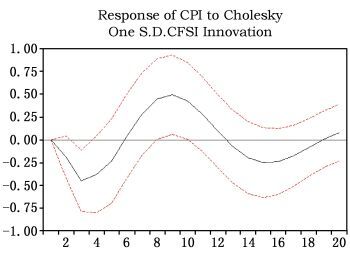
| 图 1 通货膨胀率对CFSI的脉冲响应 |
| 被解释变量:CPI | |||||||
| 领先期数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| CFSI | -22.39 | -20.28 | -13.78 | -3.91 | 6.19 | 13.40 | 17.04 |
| P值 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0953 | 0.0001 | 0.0000 |
| 被解释变量:GDP | |||||||
| 领先期数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| CFSI | -4089.32 | 765.26 | 5061.98 | 6919.90 | 7789.17 | 6738.06 | 4712.51 |
| P值 | 0.0607 | 0.7303 | 0.0190 | 0.0010 | 0.0001 | 0.0013 | 0.0296 |
2.脉冲响应分析。我们分别建立CFSI与通货膨胀率、CFSI与GDP的双变量VAR模型,结果见图 1和图 2。可以看到,CFSI的一个冲击后,通货膨胀率在第3期达到最小值,在第9期达到最大值,GDP在第6期达到最大值。

|
| 图 2 GDP对CFSI的脉冲响应 |
3.循环方程法的预测能力分析。我们使用循环方程法(Celine等,2004) 对CFSI的预测能力进行了分析。
| $CP{I_t} = \alpha + \beta CFS{I_{t - k}} + {\varepsilon _t},GD{P_t} = \alpha \prime + \beta \prime CFS{I_{t - k}} + \varepsilon {\prime _t}$ | (9) |
一般地,k取0,1,...,6。回归结果见表 2。在10%的显著性水平上,领先6期以内的CFSI连续地显著影响通货膨胀率,领先2至6期的CFSI连续地显著影响GDP,说明CFSI对通货膨胀率和产出的影响在中长期较大。
综上所述,本文构建的CFSI对通货膨胀率和产出有一定的预测能力,可作为新的货币政策目标引入泰勒规则。
(二) 加入金融稳定目标的泰勒规则非线性特征
名义利率的季度值计算如下:
| $r = \left( {{r_1}{f_1} + {r_2}{f_2} + {r_3}{f_3}} \right)/\sum\limits_{i = 1}^3 {\left| {{f_i}} \right|} $ | (10) |
其中,ri为当季各月的7天银行间同业拆借加权平均利率,fi为对应的银行间同业拆借成交金额。
产出缺口的计算公式为:
| ${\rm{产出缺口 = }}\left( {{\rm{实际产出}} - {\rm{潜在产出}}} \right)/{\rm{潜在产出}} \times 100\% $ | (11) |
以2003年1月份为基期,由月度环比CPI数据可得到当月CPI,然后通过简单平均得到季度CPI,最后转化为以2003年第一季度为基期的当期CPI。由名义GDP除以当期CPI并经季节调整后得到实际GDP,潜在GDP由实际GDP经H-P滤波法得到。平稳性检验结果显示,产出缺口和CFSI是平稳序列,通货膨胀率和利率是I(1) 序列。另外,通货膨胀率和利率在5%的显著性水平上至少存在一个协整关系。
我们使用JMulTi软件进行STR建模。在实证中,根据经验,式(6) 中i=j=0。①非线性检验结果显示,r(t)、r(t-1)、π(t)和y(t)之间不存在非线性关系,r(t)、r(t-1)、π(t)、y(t)和cfsi(t)之间存在非线性关系。这说明在我国,不含金融稳定目标的泰勒规则呈现线性的特点,将金融稳定加入货币政策目标改善了泰勒规则的性质,呈现出非线性特征。这与当前的研究结论和理论是一致的。也就是说,在基于通货膨胀和产出两个传统目标的泰勒规则中,不管当前的通货膨胀情况如何,通货膨胀率(或产出)的提高或降低对利率的影响程度是相同的;而在加入金融稳定目标后的泰勒规则中,当经济条件是高通胀或低通胀时,金融稳定(通货膨胀率或产出)的提高或降低对利率的影响程度是不同的。建模的主要结果见表 3。
| 模型1 | 模型2 | 模型3 | |||||
| 估计值 | P值 | 估计值 | P值 | 估计值 | P值 | ||
| 线性部分 | cons | 0.8603 | 0.0002 | 1.2264 | 0.0002 | 1.7263 | 0.0032 |
| r(t-1) | 0.5864 | 0.0000 | 0.4722 | 0.0005 | 0.2884 | 0.0408 | |
| π(t) | 0.0137 | 0.0353 | 0.0180 | 0.0228 | 0.0333 | 0.3320 | |
| y(t) | 0.1742 | 0.0141 | 0.1609 | 0.0112 | 0.0207 | 0.8167 | |
| cfsi(t) | -1.8781 | 0.0946 | -3.5494 | 0.1183 | |||
| 非线性部分 | cons | -1.1913 | 0.4369 | ||||
| π(t) | 0.0170 | 0.6930 | |||||
| y(t) | 0.4288 | 0.0681 | |||||
| cfsi(t) | 1.4597 | 0.6975 | |||||
| Gamma | 10.0597 | 0.5034 | |||||
| C1 | 22.0121 | 0.0000 | |||||
| Adj. R2 | 0.7512 | 0.7727 | 0.8531 | ||||
| 模型4 | 模型5 | 模型6 | |||||
| 估计值 | P值 | 估计值 | P值 | 估计值 | P值 | ||
| 线性部分 | cons | 4.8999 | 0.0659 | 1.1784 | 0.0002 | 1.0748 | 0.0004 |
| r(t-1) | 0.2082 | 0.1783 | 0.4847 | 0.0003 | 0.3288 | 0.0137 | |
| π(t) | -0.0072 | 0.9484 | 0.0172 | 0.0309 | 0.0736 | 0.0059 | |
| y(t) | -0.6630 | 0.0284 | 0.1682 | 0.0145 | 0.1254 | 0.0679 | |
| cfsi(t-1) | -9.9720 | 0.1488 | -1.4754 | 0.0801 | |||
| 非线性部分 | cons | -5.1370 | 0.1867 | -0.1628 | 0.7966 | ||
| π(t) | 0.0804 | 0.5685 | -0.0357 | 0.1595 | |||
| y(t) | 1.2504 | 0.0093 | 0.2682 | 0.0312 | |||
| cfsi(t-1) | 9.2376 | 0.3028 | -2.3469 | 0.0891 | |||
| Gamma | 1.9282 | 0.0738 | 15.4711 | 0.3890 | |||
| C1 | 11.1765 | 0.7827 | 20.6617 | 0.0000 | |||
| C2 | 11.1765 | 0.7827 | |||||
| Adj. R2 | 0.8575 | 0.7555 | 0.8471 | ||||
| 注:模型1的回归方程为rt=α0+α1πt+α2yt+ρrt-1+εt,工具变量为r(t-1)、π(t-1) 和y(t-1)。模型2的回归方程为rt=α0+α1πt+α2yt+α3cfsit+ρrt-1+εt,工具变量为r(t-1)、π(t-1)、y(t-1) 和cfsi(t-1)。模型3为LSTR1模型,将cfsi(t)引入线性及非线性部分。模型4为LSTR2模型,将cfsi(t-1) 引入线性及非线性部分。模型5的回归方程为rt=α0+α1πt+α2yt+α3cfsit-1+ρrt-1+εt,工具变量为r(t-1)、π(t-1)、y(t-1) 和cfsi(t-1)。模型6为LSTR1模型,将cfsi(t-1) 引入非线性部分。Gamma为STR中转换函数的斜率参数,C1和C2为位置参数。模型1、模型2和模型5使用GMM估计法。模型3、模型4和模型6中转换变量为π(t),不考虑利率平滑效应随转换变量的变化而变化,使用网格搜索法寻找初始值。模型2可作为模型3的对比模型,模型5可作为模型6的对比模型。 | |||||||
① k的取值在实证中确定。
当不包含金融稳定目标时,泰勒规则是线性模型,估计结果见模型1。加入金融稳定目标后,扩展的泰勒规则是非线性模型,结果见模型3。前三个模型中①金融稳定系数为负,其他变量系数皆为正,这符合经济意义,且通货膨胀在货币政策中的传导是不稳定的,产出缺口和金融稳定在货币政策中的传导是稳定的。通货膨胀率的系数小于1,这意味着当通货膨胀率上升时,名义利率的上升不足以抵消通胀率的上升,导致实际利率下降,需求扩张,经过传导通货膨胀升高加剧,说明线性模型下中国货币政策是不稳定的。假设其他变量不变,当产出缺口提高时,由于其反应系数大于0,实际利率上升,抑制总需求,从而抑制产出缺口的扩大,反之亦然,使得总产出一直保持在潜在产出附近。在模型2及模型3的线性部分,CFSI的反应系数皆为负,当金融稳定程度提高时,实际利率下降,从而刺激总需求,通胀提高。本文构建CFSI时通货膨胀与CFSI负相关,则CFSI进一步降低。因此,当CFSI的反应系数为负时,基于本文构建的CFSI,其在泰勒规则中的传导是稳定的。综上所述,通货膨胀率的上升或下降经过货币政策传导会被进一步扩大或缩小,金融稳定或产出的变化经过货币政策传导会被抵消,趋于平衡。
① 此处,模型3指其线性部分。
模型3中cfsi(t)不够显著。为此,考虑改进模型,先将cfsi(t)只引入非线性部分,cfsi(t)依然不够显著;②接着,将cfsi(t-1) 引入模型,估计结果见模型4,此时多个变量不显著,且系数不符合经济学意义;进一步将cfsi(t-1) 只引入非线性部分,估计结果见模型6。模型6中金融稳定变量显著,其他变量也几乎都显著,且拟合优度相对于模型3并未下降很多,各变量的系数都符合经济学意义。
② 受篇幅所限,模型结果未列入表 4。
模型6中,转换变量的阈值为20.6617。这表明当通货膨胀率③小于21%时,转换函数趋于0或等于0,非线性关系不明显;当通货膨胀率大于21%时,转换函数趋于1或等于1,非线性部分影响力显现。转换函数的斜率为15.4711,表明状态的转换速率较快。
③ 通货膨胀率以2003年第一季度为基期,以此阈值为标准,下文中高通胀指通货膨胀率高于此值,低通胀指通货膨胀率低于此值。
从模型6中可以看到,随着转换变量通货膨胀率的变化,CFSI对利率的影响具有非线性特点。具体地,当经济处于低通胀或通货紧缩时,央行调整利率时关注的主要目标是通货膨胀和产出,而并不关注金融稳定;当经济处于高通胀时,央行在制定货币政策时会显著地关注金融稳定,CFSI每提高0.01,名义利率下降约0.0235。这表明相对于低通胀,在高通胀环境下,央行更加需要关注金融稳定。这与理论相符,高通胀环境更易带来经济和金融的不稳定,从而更需增加对金融稳定目标的关注。此外,非线性模型6中的效应高于线性模型5,表明线性的货币政策规则会低估金融稳定对货币政策的影响程度。
模型1中通货膨胀率的系数为0.0137,即在不考虑金融稳定目标的基础泰勒规则中,通货膨胀率每提高1%,名义利率上升0.0137。在考虑了金融稳定目标后,通货膨胀对利率具有非线性影响。模型6的结果显示,当经济处于低通胀时,通货膨胀率每提高1%,名义利率上升0.0736;而在高通胀环境下,通货膨胀率每提高1%,名义利率上升0.0379。这表明货币政策需对低通胀做出更大的反应。此外,非线性模型中的效应均大于三个线性模型,线性的货币政策规则低估了通货膨胀对货币政策的影响。
模型1中产出缺口的系数为0.1742,即在不考虑金融稳定目标的基础泰勒规则中,产出缺口每提高1%,名义利率上升0.1742。在考虑了金融稳定目标后,随着转换变量通货膨胀率的变化,产出缺口对利率的影响具有非线性特点。模型6的结果显示,当经济处于低通胀或通货紧缩时,产出缺口每提高1%,名义利率上升0.1254;而当经济处于高通胀时,产出缺口每提高1%,名义利率上升约0.3936。这表明在高通胀环境下,利率对产出缺口扩大的反应更大。此外,线性的货币政策规则低估(高估)了高(低)通胀下产出缺口扩大对利率的影响。
模型6中通货膨胀率、产出缺口和CFSI的系数情况见图 3。

|
| 图 3 模型6中通货膨胀率、产出缺口和CFSI的系数 |
转换函数在2003年第二季度至2007年第四季度数值趋近0或为0,通货膨胀率和产出缺口的系数较小,金融稳定的系数为0。此阶段,我国的货币政策并没有很好地按规则施行,也没有显著地关注金融稳定目标。从2008年第一季度到2010年第四季度,转换函数数值在0和1之间,金融稳定的系数显著为负,对利率的影响较大。这一期间爆发了美国金融危机,中国为应对金融危机而频繁地调整短期利率以稳定物价,促进经济增长。特别地,在2008年第三季度至2009年第一季度,短期平均利率连续下调,改善了金融系统的稳定情况。在2011年第一季度至2016年第一季度,转换函数的值为1,各变量的系数趋于稳定,货币政策的调整趋于规则化。此外,从图 3中可以看到,产出缺口的系数高于通货膨胀率的系数,说明在政策调整中,对产出情况的关注大于通货膨胀。一方面,面对经济中众多的不确定因素,特别在2008年的金融危机中,央行往往更倾向于从全局出发重视调控经济,而不是首先稳定物价;另一方面,我国物价基本处于比较合理的一个区间,虽然货币政策的首要目标是稳定物价,但往往有各种货币政策工具可以加以调控(高洁超和孟士清,2015),利率的调整能较快地影响经济和金融,这也是产出系数一直高于通货膨胀率系数的一个原因。再者,由于我国利率的调整对产出的反应具有稳定性,对通货膨胀率的反应则不具有稳定性,对产出目标的关注程度高于通货膨胀率目标也有一定的合理性。
(三) 加入金融稳定目标的泰勒规则时变特征
我们进一步研究我国货币政策规则在2003年第二季度至2016年第一季度的变化,据此也可验证其是否显著地关注了金融稳定目标,即纳入金融稳定的货币政策规则研究的有效性。我们对状态空间模型式(8) 进行估计,①使用EViews 8。信号方程为:
① 一般地,取i=j=k=0。
| $r = c\left( 1 \right) + p1 \times r\left( { - 1} \right) + p2 \times \pi + p3 \times y + p4 \times cfsi + \left[ {var = exp\left( {c\left( 2 \right)} \right)} \right]$ | (12) |
状态方程为:
| $p1 = p1\left( { - 1} \right),p2 = p2\left( { - 1} \right),p3 = p3\left( { - 1} \right),p4 = p4\left( { - 1} \right)$ | (13) |
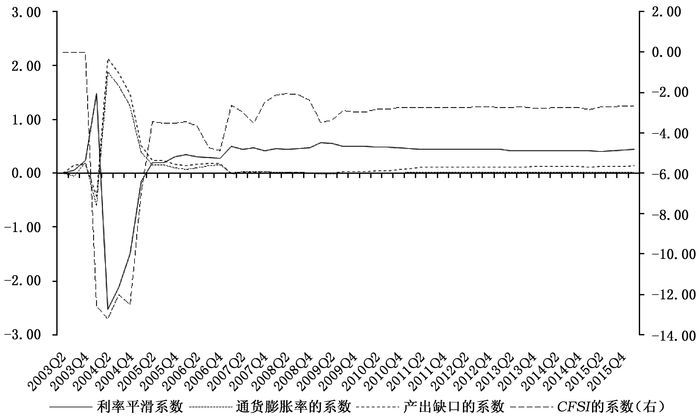
状态空间模型中各系数均显著,①表明我国货币政策调控关注了金融稳定,且具有明显的时变特征。各变量的时变系数情况见图 4。
|
| 图 4 状态空间模型中各变量的时变系数 |
① 受篇幅限制,估计结果未列出,如有需要可联系作者。
整体上,三个目标变量的系数和利率平滑系数皆存在明显的时变特点。其中,从2003年第二季度到2005年第二季度,各变量系数的变化幅度较大,利率平滑系数在此区间出现小于0的情况,CFSI的系数也出现绝对值偏大的负值。这可能是因为此阶段我国的金融市场不完善,货币政策也未很好地按照泰勒规则调整。此后,在扩展的泰勒规则中,各变量的时变系数逐渐趋于合理和稳定。从长期来看,名义利率在面对各变量变化的压力时,调整趋于规则化,央行的政策调控基本符合扩展的泰勒规则。
CFSI的系数依然为负,其绝对值经历了从较大值逐渐下降并趋于稳定的过程。从中可以看出,金融稳定对利率的影响逐渐平稳化,近年来稳定在-2.7附近。通货膨胀的系数大部分依然大于0且小于1,说明一直以来名义利率对通胀的反应不足。产出缺口的系数基本大于0,从长期来看,产出缺口的时变系数具有缓慢上升的趋势,表明相对于通货膨胀,央行更倾向于关注产出,这与图 3的结果一致。
五、结论、启示与展望
金融稳定影响着一国经济的稳定,维护金融稳定的最终目的是促进经济的健康发展。货币政策规则是央行制定货币政策、调控金融系统和经济的重要参考。传统的货币政策规则只关注通货膨胀和产出,容易让人错误地认为物价稳定时的金融过度繁荣是经济利好的象征,于是潜在的风险积累助长了金融不稳定的发生甚至金融危机的爆发。而将金融稳定作为新目标加入货币政策规则中,可以更有效地防范风险。未考虑金融稳定目标的货币政策规则显示,不管经济处于高通胀还是低通胀条件下,货币政策的调整程度是相同的。这并不符合当前新形势下的情况,而且若按照此规则进行宏观调控会低估货币政策的效果。本文研究发现,在经济处于高通胀时,央行增加了对金融稳定目标的关注,且产出缺口的扩大对利率的影响比低通胀条件下要大。作为研究的前提,金融稳定的测算是当前研究的一个热点和难点。相对于使用单一的金融变量作为代理指标,本文构建了由多个指标合成的中国金融稳定指数来衡量我国金融系统的稳定情况。之后将中国金融稳定指数纳入泰勒规则构建了包含金融稳定目标的泰勒规则扩展模型,并研究了扩展模型的非线性特征和系数的时变特征。本文主要得到以下结论:
第一,在我国,若不关注金融稳定目标,通胀或产出对利率的影响是一定的,即在不同的经济环境下,我国货币政策的调整程度是相同的。将金融稳定加入货币政策目标后,货币政策规则表明,宏观经济环境不同时,各个目标变量的变化对利率的影响程度会不同。如果忽略了金融稳定目标进行宏观调控,金融稳定、通货膨胀率以及高通胀下产出缺口对利率的影响程度会被低估。
第二,不管是否考虑金融稳定目标,通货膨胀率在我国货币政策中的传导皆是不稳定的,而金融稳定和产出在货币政策中的传导则是稳定的。即通货膨胀率的上升或下降经过货币政策传导会被进一步扩大或缩小,金融稳定或产出的变化经过货币政策传导会被抵消,趋于平衡。将金融稳定纳入货币政策目标后,在不同的通货膨胀条件下,金融稳定、通货膨胀率和产出的变化对利率有不同的影响。
第三,在低通胀环境下,央行主要关注通货膨胀目标和产出目标,没有显著地关注金融稳定目标;而在高通胀环境下,金融稳定程度对利率有显著较大的影响,央行在调整利率时会考虑金融稳定目标。另外,在高通胀环境下,产出缺口的扩大对利率的影响比低通胀条件下要大,货币政策需对通货紧缩做出更大的反应。
第四,我国货币政策的制定显著关注了金融稳定,并逐渐趋于按照含有金融稳定的泰勒规则进行操作,说明将金融稳定目标纳入货币政策规则的研究内容和结果是有效的。
基于本文的研究结果,我们得到以下的政策启示:
第一,加快推进利率的市场化,创造泰勒规则的应用环境。我国货币政策主要依靠的是改变基础货币的数量,利率的调节机制十分有限。由于基础货币本身并不是一个可控的工具,美国等一些发达国家只使用了很短的一段时间就转向了利率规则。但如果利率没有市场化,货币政策就不能有效地影响利率。可以在局部地区试点形成经验,对各项利率有序地进行市场化,打通利率的传导渠道,提高货币政策有效性。
第二,关注金融稳定目标,货币政策的实施趋向规则化。根据研究结果,央行可以关注金融稳定,尤其是在高通胀环境下。同时,需避免较高的通货膨胀经不稳定传导被进一步扩大。推进供给侧改革,调整产出结构,发挥低通胀下产出缺口对经济发展的有利影响。宏观调控中合理地关注通货膨胀、产出和金融稳定三个目标,推动货币政策规则化。
第三,构建能够反映我国金融稳定情况的指数。鉴于金融稳定指数既能够综合反映我国金融稳定情况,又可以成为货币政策的新目标,可以考虑构建并定期发布此指数。这样不仅可为金融监管部门和投资者把握我国金融稳定情况提供参考,还有利于货币政策规则的应用。
将金融稳定加入货币政策目标后,与通货膨胀、产出构成了目标体系,这就涉及目标间的权重问题,本文未详细研究货币政策目标间权重的分配问题。此外,盯住金融稳定的主要目的是对金融不稳定进行预警,当金融系统出现较大不稳定时,通过货币政策的逆向操作化解风险。因此,如何根据指标或指数的偏离情况实施不同的货币政策,需要进一步的研究和探索。
| [1] | 卞志村, 孙慧智, 曹媛媛. 金融形势指数与货币政策反应函数在中国的实证检验[J]. 金融研究, 2012(8): 44–55. |
| [2] | 戴国强, 张建华. 中国金融状况指数对货币政策传导作用研究[J]. 财经研究, 2009(7): 52–62. |
| [3] | 刁节文, 章虎. 基于金融形势指数对我国货币政策效果非线性的实证研究[J]. 金融研究, 2012(4): 32–44. |
| [4] | 刁节文, 章虎, 李木子. 中国金融形势指数及其在货币政策中的检验[J]. 山西财经大学学报, 2011(7): 49–56. |
| [5] | 封北麟, 王贵民. 金融状况指数FCI与货币政策反应函数经验研究[J]. 财经研究, 2006(12): 53–64. DOI:10.3969/j.issn.1001-9952.2006.12.006 |
| [6] | 高洁超, 孟士清. 中国非线性审慎利率规则的实证研究[J]. 南京审计学院学报, 2015(6): 95–104. |
| [7] | 郭红兵, 杜金岷. 中国货币政策关注金融稳定吗?——纳入FSCI的货币政策反应函数的实证检验[J]. 广东财经大学学报, 2014(5): 4–13. |
| [8] | 黄佳, 朱建武. 基于金融稳定的货币政策框架修正研究[J]. 财经研究, 2007(4): 96–106. |
| [9] | 刘金全, 张小宇. 时变参数"泰勒规则"在我国货币政策操作中的实证研究[J]. 管理世界, 2012(7): 20–28. |
| [10] | 马勇. 基于金融稳定的货币政策框架:理论与实证分析[J]. 国际金融研究, 2013(11): 4–15. |
| [11] | 马勇. 金融稳定与宏观审慎理论框架及在中国的应用[M]. 北京: 中国金融出版社, 2016. |
| [12] | 米尔顿·弗里德曼, 安娜·雅各布森·施瓦茨. 美国货币史: 1967-1960[M]. 巴曙松等, 译. 北京: 北京大学出版社, 2009. |
| [13] | 万光彩, 张霆, 卫松涛. 基于金融稳定视角的货币政策与宏观审慎政策演进[J]. 东北农业大学学报(社会科学版), 2015(5): 31–37. |
| [14] | 肖本华. 货币政策规则——行为经济学范式[M]. 上海: 上海财经大学出版社, 2012. |
| [15] | 谢平, 罗雄. 泰勒规则及其在中国货币政策中的检验[J]. 经济研究, 2002(3): 3–12. |
| [16] | 徐国祥, 郭建娜, 陈燃萍. 中国金融稳定指数的构建及其领先能力分析[J]. 统计与信息论坛, 2017(4): 3–9. |
| [17] | 袁野. 时变参数的货币政策规则及其对利率期限结构的动态影响——基于资产价格波动、汇率因素对Taylor规则的修正[J]. 中央财经大学学报, 2014(5): 40–46. |
| [18] | 张屹山, 张代强. 前瞻性货币政策反应函数在我国货币政策中的检验[J]. 经济研究, 2007(3): 20–32. |
| [19] | 周波. 我国非线性货币政策规则研究[J]. 财经问题研究, 2014(1): 53–59. |
| [20] | Albulescu C T, Goyeau D, Pepin D. Financial instability and ECB monetary policy[J]. Economics Bulletin, 2013, 33(1): 388–400. |
| [21] | Baxa J, Horvath R, Vasicek B. Time-varying monetary policy rules and financial stress:Does financial instability matter for monetary policy?[J]. Journal of Financial Stability, 2013, 9(1): 117–138. DOI:10.1016/j.jfs.2011.10.002 |
| [22] | Benjamin K. The Taylor rule and financial stability-A literature review with application for the Eurozone[J]. Magks Papers on Economics, 2014, 65(2): 159–192. |
| [23] | Bernanke B S. Asset-price "bubbles" and monetary policy[R]. Working Paper, 2002. |
| [24] | Bernanke B S, Mishkin F S. Inflation targeting:A new framework for monetary policy?[J]. Journal of Economic Perspectives, 1997, 11(2): 97–116. DOI:10.1257/jep.11.2.97 |
| [25] | Castro V. Can central banks' monetary policy be described by a linear (augmented) Taylor rule or by a nonlinear rule?[J]. Journal of Financial Stability, 2011, 7(4): 228–246. DOI:10.1016/j.jfs.2010.06.002 |
| [26] | Celine G, Graham C, Liu Y. Financial conditions indexes for Canada[R]. Bank of Canada Working Paper No.22, 2004. |
| [27] | Posen A S. Why central banks should not burst bubbles[J]. International Finance, 2006, 9(1): 109–124. DOI:10.1111/infi.2006.9.issue-1 |
| [28] | Roubini N. Why central banks should burst bubbles[J]. International Finance, 2006, 9(1): 87–107. DOI:10.1111/infi.2006.9.issue-1 |
| [29] | Schinasi G J. Responsibility of central banks for stability in financial markets[R]. IMF Working Paper WP/03/121, 2003. |
| [30] | Woodford M. Inflation targeting and financial stability[R]. NBER Working Paper No.17967, 2012. |
 2017, Vol. 43
2017, Vol. 43



