文章信息
 | 财经研究 2017年43卷第8期 |
- 丁从明, 谢凤璘, 雷雨.
- Ding Congming, Xie Fenglin, Lei Yu.
- 什么都涨,工资不涨?——价格刚性下通货膨胀对劳动收入比重的影响
- Rising prices, stable wages: a study on the influence of inflation on labor income share under price rigidity
- 财经研究, 2017, 43(8): 56-68
- Journal of Finance and Economics, 2017, 43(8): 56-68.
-
文章历史
- 收稿日期:2016-10-26

2017第43卷第8期
2. 重庆大学 公共经济与公共政策研究中心,重庆 400044
2. Public Economy and Policy Research Center, Chongqing University, Chongqing 400044, China
一、引言
“什么都在涨,就是工资没有涨”这一简单逻辑表明物价水平与劳动工资之间并不存在一一对应关系。劳动力市场工资形成机制的刚性意味着通货膨胀在短期内可以降低实际工资,从而促进就业,并带来劳动收入比重的提高。本文中,我们借鉴Calvo(1983) 的随机定价模型,构建了一个通货膨胀率—劳动收入比重的理论模型,研究通货膨胀这一短期经济波动因素对劳动收入比重的影响。
现有研究强调引起劳动收入比重下降的长期成因。研究主要包括四个方面的因素。(1) 产业结构:强调劳动密集型产业在整个产业结构中的相对萎缩,导致劳动收入份额的下降。白重恩和钱震杰(2009) 将中国劳动收入比重的变动分解为产业内效应和产业间效应,研究结果支持上述设想。Arpaia等(2009) 以及Bassanini和Manfredi(2014) 利用欧盟的数据也证实了产业结构是收入报酬变化的重要因素。(2) 技术进步:技术进步的非中性导致对不同要素的利用密度不一样,从而导致不同要素的收入份额的变迁。Acemoglu(2003) 强调偏向型技术进步的内生性,Mahony等(2014) 认为劳动收入比重的下降是长期趋势,而这一下降主要由资本利用型技术进步所导致。而丁从明等(2013) 验证了“拿来主义”的技术引进方式对劳动收入比重的不利影响。(3) 非竞争性市场:在非竞争性劳动力市场下,劳资双方的议价能力的差异导致不同要素所有者的收入份额的差异。McDonald和Solow(1981) 提出的有效谈判模型认为工人的谈判能力越低,工资越接近工人的边际产出,劳动收入比重越低。Judzik和Sala(2013) 从就业与工资视角出发,发现工会密度降低进而侵蚀劳动力收入比重。马磊(2015) 强调中国工会组织力量薄弱对劳动收入比重的不利影响。(4) 全球化:这一理论强调全球化通过改变劳动市场竞争条件,进而影响劳动收入比重。Buchele和Christiansen(2007) 强调美国在1950-2005年间劳动收入比重下降的主要因素是全球化。Hung和Hammett(2016) 指出全球化并不总是导致劳动份额下降。但在测算期内,全球化导致美国制造业部门的劳动份额降低3%-6%,总劳动份额至少降低20%-36%。
整体而言,上述文献强调结构性、制度性或技术等长期因素对劳动收入比重的影响,显然,这些研究具有高度的合理性。本文强调在注重长期基本面因素的同时,不能忽视短期的周期性因素对劳动收入份额的影响。Gali和Gertler(1999) 将劳动收入比重作为边际成本的代理变量,利用新菲利普斯曲线(New-Keynesian Phillips Curve,NKPC)解释通货膨胀机制的合意性。Batin等(2000) 使用基于成本调整模型的NKPC,捕捉英国的劳动收入比重与通货膨胀的关系。与上述强调劳动收入比重对通货膨胀率影响的研究不同,本文强调通货膨胀对劳动收入比重的影响。通过构建一个带有价格刚性的理论模型,本文发现短期内适度的通货膨胀可以改善劳动收入比重。为验证上述假说,本文选择Hoover和Perez(1999) 提出的“从一般到特殊”的动态计量方法。计量结果表明:适度通货膨胀率短期内可以提高劳动收入比重。短期内通货膨胀每增加1%,将导致劳动收入比重增加0.05%,短期内通货膨胀率从样本均值处的5.3%增加到6.3%,对应劳动收入比重将从均值的49.4%增加到49.86%左右。长期中估计效应将从0.05%下降到0.03%。考虑到劳动收入比重=工资×(就业/产出),文章进一步将通货膨胀对劳动收入比重的影响转化为工资效应、就业效应和产业效应,利用省级面板数据,证实了短期内通货膨胀降低了实际工资水平,带来就业增加和劳动收入比重的提升。当然,本文的研究结论并不意味着长期中为了促进劳动收入比重的提高,可以大规模刺激通货膨胀率。因为一方面,长期中就业效应将会因为工资上升而逐步消失;另一方面,较高的通货膨胀将改变企业定价决策(丁从明,2010),增加企业定价的弹性。
文章结构安排如下:第二部分是文章的理论部分;第三部分阐述数据来源以及计量方法;第四部分分析实证检验结果并验证传导机制;最后是研究结论。
二、理论与方法说明
(一) 理论框架
这里,我们通过建立一个价格刚性的调整模型来说明通货膨胀与劳动收入比重之间的关联。基本设想如下:价格水平上升,企业实际工资下降,就业增加,劳动者名义报酬增加,企业产出虽然也会增加,但是在不完全竞争市场上,产业增加幅度没有就业增加幅度高,从而导致劳动收入比重可能因为通货膨胀的提高而增加。根据Calvo(1983) 的随机定价理论,可以将市场价格表示为:
| ${p_t} = \theta {p_{t - 1}} + \left( {1 - \theta } \right)p_t^*$ | (1) |
其中:pt表示价格水平Pt的自然对数,式(1) 表示的市场价格由两类价格加权而成,一类是惰性的价格制定者,他们使用上一年的价格pt-1,其比例为θ;另一类是企业按照其目标价格制定本年度的价格水平,此类企业比例为1-θ,其意愿新价格为pt*,新制定的价格符合新凯恩斯主义的加成定价原则:
| $p_t^* = \left( {{W_t}/MP{L_t}} \right)\left[ {1/(1 - \left| {1/\varepsilon } \right|)} \right]$ | (2) |
其中:Wt表示名义工资水平,MPLt表示劳动的边际产出,而ε为不完全竞争市场的企业需求的价格弹性,ε为负数。为了将劳动收入比重与价格联系起来,我们使用规模报酬不变的Cobb-Douglas生产函数Yt=AtKtαLt1-α,其中劳动边际产出为:
| $MP{L_t} = \left( {1 - \alpha } \right){A_t}K_t^\alpha L_t^{ - \alpha }$ | (3) |
将式(3) 代入式(2),并利用劳动收入比例公式St=WtLt/PtYt,得到:
| $p_t^* = \frac{{W{L_t}_t}}{{\left( {1 - \alpha } \right){A_t}K_t^\alpha L_t^{1 - \alpha }}}\left( {\frac{1}{{1 - \left| {1/\varepsilon } \right|}}} \right) = \frac{1}{{\left( {1 - \alpha } \right)}}\left( {\frac{1}{{1 - \left| {1/\varepsilon } \right|}}} \right){S_t}{P_t}$ | (4) |
对式(4) 两边取对数,并计小写符号,得到:
| $p_t^* = \varphi + {s_t} + {p_t}$ | (5) |
其中:参数
| ${s_t} = - \varphi + \left[ {\theta /\left( {1 - \theta } \right)} \right]{\pi _t}$ | (6) |
其中:πt=pt-pt-1,表示通货膨胀率。根据式(6) 可以对通货膨胀率与劳动收入比重的关系做如下假说。
假说:考虑成本加成定价和企业价格制定的刚性,通货膨胀率和劳动收入比重之间可能存在稳定的正向关系。
(二) 研究方法
本文使用以Hendry(1995) 为代表的动态建模方法进行计量分析。在Favero(2001) 归纳的三种经济计量模型①中,向量自回归模型对数据量的要求极高,自由度损失过大,且不适用于政策研究;跨时最优方法以微观数据集为基础,而本文使用的宏观数据时序较短,样本空间难以满足模型对待估参数的要求(康继军等,2012),因此本文采用动态建模方法。
① Favero(2001) 将经济计量模型分为三类,分别为:动态建模、向量自回归、跨时最优。
Hendry(1995) 强调,计量模型应该遵从“一般”到“简单”的路径,用序贯约化将模型简化为变量和参数都很少的简约型模型。同时,由于实际经济数据往往是“非均衡过程”的结果,建模时应该使用数据的动态非均衡过程来逼近经济理论的长期均衡状态,“从一般到特殊”模型就能够模拟此过程。随着协整理论和误差修正模型的广泛应用,该方法被大量应用于现实问题,其逐步简单集约化的处理流程使模型设计过程有据可循(康继军等,2012)。建立“从一般到特殊”动态模型的基本流程如下(伍戈,2009;Doornik和Hendry,2013):
(1) 对需要研究的变量进行单位根检验,考察各变量的平稳性。
(2) 对所有变量进行协整分析,明确各变量之间是否具有长期均衡关系,如果存在协整关系,则使用三类统计值检验协整向量中各变量的弱外生性、②显著性③和平稳性。④
② 如果变量不受长期均衡偏差的影响,即协整关系前面的调整系数αi等于0,则该变量是弱外生变量。给定变量的外生性检验其实就是检验矩阵相应的行是否为0,若为0,那么协整关系中的不均衡就不会反馈到相应的变量中。有效的外生性使得对协整向量的分析可以在单方程中进行,而不会损失有用的信息。检验过程中建立VEC模型,在协整约束中施加A(k,r)=0约束(k表示协整中第k个方程,r表示方程中的第r个协整系数)。A(2,1)=0表示第2个方程的第1个协整系数等于0。
③ 显著性检验χ2值实质上是验证协整向量β中相应的系数是否可以设定为0,如果检验结果是稳定的,则表明协整关系中各变量的系数均显著地不为0。B(r,k)=0表示第r个协整方程的第k个变量的系数等于0。譬如B(2,1)=0表示第2个协整方程的第1个变量的系数设定为0。
④ 该统计值检验这样一个约束条件:协整向量中除某指定变量为1之外,其他变量均为0。例如,变量1具有平稳性的原假设即表明协整向量为(1 0 0 0 0)。该检验的前提条件是存在一个协整向量。该检验实际就是检验变量的平稳性,在单位根检验中已经有所涉及,但是利用更多信息进行检验,比单位根检验更具有解释力。
(3) 求取长期均衡模型的误差修正项ecm。协整关系表达变量之间的长期均衡关系,将长期均衡模型中的误差项看作均衡误差,加入到待估模型中,可以用长期静态模型弥补短期动态模型的不足,这样能使模型既体现短期状态又体现长期状态,并描述短期不均衡向长期均衡状态调整的过程(伍戈,2009)。
(4) 通过对“一般模型”①的贯序约化不断精简模型,得到一个包含误差修正项的短期均衡模型。具体做法:对“一般模型”回归,通过判断解释变量是否显著为0,决定该解释变量是否继续留在模型中,剔除不显著为0的变量再回归,不断循环上述过程直至得到统计意义上显著的模型为止。
① Hendry认为,最一般的模型是自回归分布滞后模型(Autoregressive Distributed Lag Modeling,ADLM)。本文也使用这种方法,因其复杂且非无意义,因此仅给出“简化模型”,未给出完整的ADL“一般模型”形式。
三、数据分析
(一) 数据说明
本文数据采集主要来源1978-2014年我国除港澳台外31个省、市、直辖市的时间序列数据,数据主要来源于《中国统计年鉴》、《China’s National Income,1952-1995》(Hsueh等,1999)、《中国城市统计年鉴》。文章选择变量说明如下。
劳动收入比重:按收入法计算的劳动者报酬占收入法GDP的比重,鉴于连续性和国际统计口径一致性等问题,本文使用省际收入法估算劳动收入比重,取其对数,用lnl表示。
通货膨胀:以1978年的CPI为基期计算1978-2014年的通货膨胀率,用lnf表示。
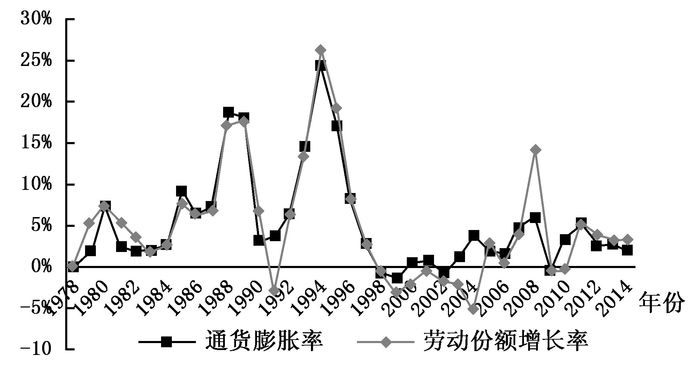
图 1显示了观测期内劳动收入比重增长率②与通货膨胀率的堆积折线。由图 1可见,2004年以前,两者几乎趋势变化近乎一致,2004年存在较大出入,但其后变动又一次亦步亦趋。查阅统计年鉴可以发现,2004年劳动报酬的统计口径发生了较大改变。白重恩和钱震杰(2009) 也发现,由于统计口径和方法的变化,2004年劳动收入比重下降幅度占到1995-2004年间降幅的59%。
|
| 图 1 1978-2014年中国劳动份额增长率与通货膨胀率堆积折线 数据来源:《中国统计年鉴》、《China’s National Income,1952-1995》 |
② 事实上,劳动收入比重与通货膨胀率的堆积折线图的同步性也非常明显,但两者绝对值相差太大,所以将劳动收入比重取增长率进行比较。
产业结构:白重恩、钱震杰(2009) 将1978年以来的劳动收入比重分解为产业影响和结构影响,发现劳动收入比重从农业部门向非农业部门、工业部门的转移是影响劳动收入比重的中坚力量。本文使用第二产业增加值占GDP比重(%)表示产业结构,用lnd表示。
人力资本:人力资本是衡量劳动力存量的指标,对劳动收入比重具有重大影响。Diwan(2000) 用人均受教育年限来代表人力资本,罗长远和张军(2009) 用每万人中的大学生人数代表人力资本,张全红(2010) 用6岁以上人均受教育年限代表人力资本。本文用每万人中大学生数代表人力资本,取其自然对数,用lnm表示。
对外开放:根据Stolper-Samuelson定理,具有劳动力比较优势的国家,通过出口劳动密集型产品,收入会向劳动者倾斜,这说明对外开放对劳动收入比重可能存在极大影响。本文选用进出口总额占GDP的比重(%)代表对外开放,取对数用lno表示。
技术进步:由于微观层面技术进步和技术改造难以用一个指标刻画,目前研究多使用代理变量进行替代。鉴于数据可得性,本文采用罗长远和张军(2009) 的方法核算技术进步,用当年实际GDP比从业人员(%),取其分子的自然对数,用lnt表示,这一指标也代表了劳动生产率的改善程度。
虚拟变量:为了刻画2004年统计口径变化对劳动收入比重的影响,我们在动态模型中加入虚拟变量dut,2004年以前取0,2004年以后年份取1。
根据理论假设和对各变量的处理给出初始的理论模型为:
| $\ln {l_t} = f(\ln {f_t},\ln {d_t},\ln {m_t},\ln {o_t},\ln {t_t})$ | (7) |
(二) 统计分析
数据平稳性检验,首先利用ADF(Augented Dickey-Fuller Test)对各变量进行单位根检验,为减小变量的波动幅度,避免异方差,各变量均经过取对数处理。本文从四阶滞后期的回归开始,用最小赤池信息原则确定单位根阶数,检验结果见表 1。从检验结果看,Δlnl、Δlnf、Δlnd、Δlnm、Δlno和Δlnt均在1%的显著性水平下,拒绝了存在单位根的原假设,即各变量均为一阶单整过程I(1)。
| 原假设 | 变量 | |||||
| lnl | lnf | lnd | lnm | lno | lnt | |
| I(0) | -0.416 (-2.63) |
-0.474 (-2.65) |
-0.508 (-2.51) |
-1.956 (-4.24) |
-1.249 (-4.24) |
-0.360 (-3.63) |
| I(1) |
-6.027***
(-2.63) |
-10.831***
(-4.25) |
-4.715***
(-2.63) |
-2.731***
(-2.63) |
-5.389***
(-4.24) |
-2.845***
(-2.63) |
| 注:***表示在1%的显著性水平上显著。 | ||||||
协整关系检验。本文采用向量自回归系统的Johansen检验进行协整检验,由于VAR(Vector Auto Regression)模型中最佳滞后期的选定会极大地影响Johansen检验的效力,因此首先判定最佳滞后期。我们从含有lnl、lnf、lnd、lnm、lno和lnt的四阶VAR开始(含截距和虚拟变量),逐步简化到一阶VAR。表 2的舒尔茨准则(Schwartz Criterion,SC)表明,无约束VAR模型的最佳滞后阶期为3。
| 滞后阶数 | 无约束参数的数目 | 对数-似然值 | 舒尔茨准则(SC) |
| VAR(4) | 156 | — | — |
| VAR(3) | 120 | 472.26 | -15.33 |
| VAR(2) | 84 | 387.85 | -13.63 |
| VAR(1) | 48 | 331.25 | -13.62 |
资料来源:《中国统计年鉴》、《China’s National Income,1952-1995》、《中国城市统计年鉴》。
基于VAR模型的协整检验是对无约束VAR模型进行协整约束后得到的VAR模型,其滞后阶数是对无约束VAR一阶差分后的滞后期,因此协整检验的阶数应为无约束VAR滞后期减1,即协整检验的滞后阶数为2。
表 3显示了对该四阶VAR实施Johansen协整检验的标准统计结果。最大特征值λmax和迹特征值λtrace显著地拒绝了不存在协整关系的原假设,并显示变量间存在五个协整关系。表 3同时显示了标准化的特征向量和调整系数,通常以矩阵β'和α表示,β'的第一行是估计的协整向量。矩阵α中的第一列系数测度了协整关系中的(滞后)不均衡对VAR变量的反馈效应。特别地,0.007是对劳动收入比重方程的反馈系数,系数为正表示滞后的劳动收入比重对现期劳动收入比重具有促进作用,数值很小说明其调整过程十分缓慢。
| 特征值 原假设 | 0.998459 r=0 | 0.951747 r≤1 | 0.895030 r≤2 | 0.831590 r≤3 | 0.513039 r≤4 | 0.014078 r≤5 |
| λtrace | 471.100*** | 137.397*** | 157.382*** | 82.998*** | 24.214** | 0.468 |
| λmax | 213.684*** | 100.033*** | 74.385*** | 58.785*** | 23.746*** | 0.468 |
| 标准化的特征向量β′ | ||||||
| 变量 | lnl | lnf | lnd | lnm | lno | lnt |
| -126.6375 | 0.911698 | -19.46350 | -4.753732 | -13.50751 | 2.557838 | |
| 42.18314 | 18.47766 | 61.01591 | 20.26030 | -42.23447 | -18.75756 | |
| 57.75481 | -13.67013 | -25.07097 | -12.21007 | 34.21306 | 13.40670 | |
| 41.81298 | -11.63181 | -48.90021 | -4.986521 | 21.95851 | 7.563549 | |
| -15.56673 | 10.81472 | 4.705978 | 9.344942 | -16.31392 | -11.93673 | |
| 26.48288 | 1.525015 | 65.74076 | 7.015449 | 6.061683 | -7.513245 | |
| 标准化的调整系数矩阵α | ||||||
| Δlnl | 0.007296 | -0.010459 | -0.011979 | -0.002640 | -0.006358 | 0.000141 |
| Δlnf | -0.001116 | 0.020384 | 0.014277 | 0.058618 | -0.006881 | -0.000707 |
| Δlnd | -0.002898 | -0.005202 | 0.004823 | 0.005184 | 0.007105 | 0.000563 |
| Δlnm | 0.010353 | 0.034670 | 0.030323 | -0.014267 | -0.024804 | 0.000365 |
| Δlno | -0.001929 | 0.036612 | -0.017811 | 0.046359 | 0.010455 | 0.003601 |
| Δlnt | 0.018614 | 0.010734 | 0.014464 | 0.024592 | 0.011912 | -0.000202 |
| 弱外生性检验的统计值 | ||||||
| lnl | lnf | lnd | lnm | lno | lnt | |
| χ2(5) | 61.588*** | 58.665*** | 32.446*** | 51.250*** | 41.192*** | 57.953*** |
| 显著性检验的统计值 | ||||||
| lnl | lnf | lnd | lnm | lno | lnt | |
| χ2(5) | 193.747*** | 82.202*** | 102.353*** | 97.686*** | 122.547*** | 86.284*** |
| 稳定性检验的统计值 | ||||||
| lnl | lnf | lnd | lnm | lno | lnt | |
| χ2(1) | 18.664*** | 6.760*** | 29.362*** | 24.577*** | 1.720* | 7.236*** |
| 注:(1) 该向量自回归包括lnl、lnf、lnd、lnm、lno和lnt的二阶滞后变量、常数项和虚拟变量。估计的区间为:1978-2014年;(2) 统计值λtrace和λmax是用来分别检验协整关系的Johansen迹特征值和最大特征值。原假设为协整关系中秩r的个数。例如,如果拒绝了原假设r=0,那么也就是证明至少有一个协整向量;(3) 对弱外生性、显著性和平稳性的检验都是基于r=5的假设。它们分别服从χ2(5)、χ2(5) 和χ2(1) 的分布;(4) 表中***表示在1%的显著性水平下拒绝原假设。 | ||||||
表 3最后部分列出了三类统计值:一是检验协整向量中变量的弱外生性;二是检验协整向量中变量的显著性;三是检验各变量的平稳性。这些统计值都是直接运用Johansen和Juselius的方法,对α或β施加相应线性约束的检验而得到的。对给定变量的外生性检验其实就是检验矩阵相应的行是否为0,能够解决建模过程中存在的内生性问题(康继军等,2012)。如果该行的值为0,那么协整关系中的不均衡就不会反馈到相应的变量中去。如表 3所示,所有变量都变现出了外生性,有效的外生性使得对协整向量的分析可以在单方程中进行,而不会损失有用的信息。
表 3中倒数第二部分列出了协整向量中对各变量显著性检验的χ2统计值。该检验实质上是验证β中相应的系数是否可以设定为0。lnl、lnf、lnd、lnm、lno和lnt都十分显著。表 3的最后一部分列出了检验各变量平稳性的多元统计值。具体来说,该统计值检验这样一个约束条件:协整向量中除某指定变量为1之外,其他变量均为0。例如,劳动收入比重具有平稳性的原假设即表明协整向量为(1 0 0 0 0 0)'。该检验的前提条件是存在一个协整向量。检验的结果表明各变量都以小于0.01%的p值拒绝了平稳性。①通过引入多元统计量和更大的信息集,该统计量比表 1的单变量平稳性检验更具有解释力。
① 由于时间序列本身具有较强的相关性,检验时比较严格,因此以1%的显著性水平判断显著性和弱外生性。
四、一般到特殊的计量建模
(一) 模型的建立
以式(7) 为基础构建一个3阶滞后的ADL模型作为一般化模型,通过PcGive软件求取ADL模型的长期均衡关系为:
| $\begin{array}{l} \ln {l_t} = \mathop {5.20}\limits_{\left( {13.68} \right)} + \mathop {0.03}\limits_{(3.03)} \ln {f_t} - \mathop {0.24}\limits_{( - 2.18)} \ln {d_t} - \mathop {0.05}\limits_{( - 2.63)} \ln mt - \mathop {0.12}\limits_{( - 4.14)} \ln {o_t} - \mathop {0.003}\limits_{( - 0.17)} \ln {t_t}\\ T = 37,{R^2} = 0.90,{{\bar R}^2} = 0.89,DW = 1.76,\hat \sigma = 1.67\% ,RSS = 0.023 \end{array}$ | (8) |
由长期均衡关系模型推导出长期趋势项ECM为:
| $ec{m_t} = - 5.20 + \ln {l_t} - 0.03\ln {f_t} + 0.24\ln {d_t} + 0.05\ln {m_t} + 0.12\ln {o_t} + 0.003\ln {t_t}$ | (9) |
式(8) 表示各解释变量对劳动收入比重的长期影响,可见,通货膨胀率在长期内对劳动收入比重有正作用,通货膨胀率每增加1 %,劳动收入比重上升0.03%,估计系数显著为正。而产业结构的改善、人力资本的提高、对外开放的深化、技术进步的推进则促使劳动收入比重下降,但技术进步指标并不显著。
式(9) 表示变量长期均衡模型的残差与变量之间的关系。如果ECM为平稳时间序列I(0),则可以利用ECM将各变量从I(1) 空间转换到I(0) 空间。本文对ECM模型的单位根检验结果表明:ECM序列在1%显著性水平下拒绝原假设,为平稳时间序列I(0)。
在三阶滞后的ADL模型中加入ECM滞后一阶项作为动态调整项,利用PcGive软件中的“自由策略”对一般模型进行逐步约化,降维处理后得到简化模型。含有ECM的短期模型为:
| $\begin{array}{l} \ln {l_t} = - \mathop {0.74}\limits_{\left( { - 0.48} \right)} + \mathop {0.97}\limits_{(8.82)} \ln {l_{t - 1}} + \mathop {0.05}\limits_{(2.38)} \ln {f_{t - 1}} + \mathop {0.21}\limits_{(1.31)} \ln {d_{t - 2}} + {\rm{ }}\mathop {0.09}\limits_{(1.84)} \ln {m_{t - 1}} - \mathop {0.07}\limits_{( - 2.33)} \ln {m_{t - 3}}\\ \quad \quad - \mathop {0.11}\limits_{( - 3.67)} \ln {o_t} + \mathop {0.17}\limits_{(2.83)} \ln {t_{t - 1}} - \mathop {0.22}\limits_{( - 3.72)} \ln {t_{t - 2}} + \mathop {0.05}\limits_{\left( {2.14} \right)} d{u_t} - \mathop {0.71}\limits_{\left( { - 2.20} \right)} ec{m_{t - 1}}\\ T = 37,{R^2}0.96,{{\bar R}^2} = 0.95,DW = 2.24,\hat \sigma = 0.7\% ,RSS = 0.017 \end{array}$ | (10) |
式(10) 中既包含了劳动收入比重与各解释变量间的长期关系,也包含了短期动态关系。ECM项估计系数显著为负,长期趋势项即误差修正项对模型具有反向调节作用,有助于短期内的不稳定状态回到长期均衡状态,从长期趋势项系数绝对值的大小可以看出模型从短期动态状态回归到长期均衡状态的速度较快,长期趋势项对短期均衡状态的调节力度很大。由模型可知劳动份额具有一定的惯性,这由模型中出现劳动份额滞后一阶项体现。模型的各项基本统计检验良好,参见附录1。
(二) 模型的经济解释
(1) 长期关系分析。模型(8) 及模型(9) 的误差修正项表明了变量的长期关系。结合模型(8) 进一步发现,在长期稳定的发展状态下,通货膨胀对劳动收入比重的影响是积极的,通货膨胀率每增长1%,劳动份额上升0.03%。利用样本期间平均通货膨胀率为5.3%和劳动收入比重的均值为49.4%,简单计算显示:通货膨胀率从5.3%增加到6.3%(增加18.8%),对应劳动收入比重将从49.4%上升到49.68%左右,这个估计效应虽然并不是特别大,但也比较符合预期。模型(10) 中长期均衡项ecmt-1的系数为-0.71,符合误差修正机制,显示短期的暂时背离可以为负反馈修正机制调整,其值为0.71,调整速度约为一年零五个月(1/0.71≈1.41年)。
模型(8) 还显示,长期内产业结构、对外开放、人力资本和技术进步对劳动收入比重的影响都为负数,但是技术进步指标估计系数并不显著。产业结构(二产比重)每增长1%,劳动收入比重下降0.24%,这一估计与白重恩和钱震杰(2009) 等人的估计结果完全一致。而对外开放每提高1%,劳动收入比重下降0.12%,开放导致劳动收入比重下降说明对外开放规模扩大主要使资本受益,这与地方政府激烈竞争弱化劳动力谈判能力有关(罗长远和张军,2009)。
(2) 短期关系分析。短期均衡模型中劳动收入比重惯性系数为0.97,可以看出本期劳动收入比重惯性极大。式(10) 中通货膨胀估计系数为0.05,即短期内通货膨胀率每增加1%,将导致劳动收入比重增加0.05%,同样计算显示,短期内通货膨胀率从5.3%增加到6.3%,对应劳动收入比重将从49.4%增加到49.86%左右,效应较长期效应大。这一点与理论分析完全一致。短期内,工资价格刚性导致实际工资下降,从而导致劳动收入比重较大幅度的增加。长期中,随着价格刚性的逐步减缓,通货膨胀对劳动收入比重的效应也从0.05%下降到0.03%左右。
(三) 传导机制检验
模型(10) 的计量结果证实了通货膨胀率对劳动收入比重具有稳定的促进作用。我们进一步对内在的传导机制进行检验。①根据劳动收入比重的定义,可以将通货膨胀对劳动收入比重的影响表达如下:
| $S\left( p \right) = W\left( p \right) \times N\left( p \right)/Y(p)$ | (11) |
① 此处感谢审稿人提出的宝贵意见,当然文责自负。
其中:S代表劳动收入比重;W代表单个劳动者的实际劳动报酬,即单个劳动者的实际工资;N代表劳动者数量;Y代表实际总产出。显然,上述三个变量都是通货膨胀率p的函数,对式(11) 取自然对数可得:
| $L{\rm{n}}S\left( p \right) = L{\rm{n}}W\left( p \right) + L{\rm{n}}N\left( p \right) - L{\rm{n}}Y(p)$ | (12) |
将式(12) 对通货膨胀率p取导数,可以将通货膨胀率对劳动收入的边际影响效应分解为如下工资效应、就业效应和产出效应:
| $dS\left( p \right)/dp = {\chi _1}\left( {dW/dp} \right) + {\chi _2}\left( {dN/dp} \right) + {\chi _3}(dY/dp)$ | (13) |
其中:χ1=L/W,χ2=L/N,χ3=-L/Y,式(13) 意味通货膨胀对劳动收入的效应可以分解为三种效应,也即:通货膨胀的劳动收入分配效应=工资效应+就业效应+产出效应。根据长期劳动合同论(Fischer,1975等)以及交错调整工资理论(Taylor,1980等),我们预期通货膨胀的工资效应为负;菲利普斯曲线证实失业率与通货膨胀率之间存在此消彼长的关系,所以预期就业效应为正;根据传统凯恩斯主义“产出—物价”曲线,预期产出效应为负。①综上所述,本文预期就业效应为正,工资和产出效应为负。结合前文通货膨胀率对劳动收入比重有促进作用的结论,可以得出以下推论。
① 产出项的系数χ3为负,因此通货膨胀的产出效应为负。
推论:通货膨胀率提高劳动收入比重的主要原因在于,通货膨胀的就业效应超过其工资效应和产出效应的合力。
表 4验证了通货膨胀影响劳动收入比重的三种机制:工资、就业和产出。表 4使用1993-2014年剔除重庆、西藏后的30个省、市、自治区的面板数据,除通货膨胀率用百分数表示外,其他变量均用对数表示,被解释变量分别对应平均实际工资水平、就业人数和实际产出水平指标。其他控制变量包括:产业结构、人力资本、对外开放和技术进步,其统计方法及指标与前文所述一致。因为存在被解释变量的动态效应,我们在模型中加入了被解释变量的滞后项。考虑三种效应的相互关联,以及避免计量的联立内生性导致的估计偏误,实证研究中,我们采用系统广义矩估计法(SYS-GMM),该方法通过大量使用差分和水平变量作为工具变量,一方面避免了单方程估计中的内生偏误;另一方面,也可以较为有效地缓解联立偏误问题,从而得到一致有效的估计量。
| 解释变量 | 工资 | 就业 | 产出 | |||
| W-1 | W-2 | L-1 | L-2 | Y-1 | Y-2 | |
| 被解释变量滞后 | 0.897*** | 0.900*** | 0.968*** | 0.964*** | 0.959*** | 0.947*** |
| (149.00) | (115.52) | (126.33) | (178.42) | (379.13) | (363.69) | |
| 通货膨胀 | -0.081*** | -0.129*** | 0.186*** | 0.212*** | -0.034*** | -0.061*** |
| (-17.13) | (-11.17) | (8.21) | (7.42) | (-7.55) | (-5.07) | |
| 其他解释变量 | Y | Y | Y | Y | Y | Y |
| cons | 0.008 | 0.008 | 0.189*** | 0.176*** | -0.178*** | -0.204*** |
| (0.08) | (0.07) | (2.78) | (3.12) | (-5.88) | (-3.66) | |
| m1 | 0.003 | 0.003 | 0.004 | 0.004 | 0.01 | 0.01 |
| m2 | 0.865 | 0.832 | 0.546 | 0.536 | 0.371 | 0.354 |
| sargan | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| N | 630 | 630 | 630 | 630 | 630 | 630 |
数据来源:历年《中国统计年鉴》。(1)W-1、W-2分别代表工资滞后一期、滞后两期作为被解释变量加入模型中,同行符号的意义与此类似;(2) 其他解释变量仅为当期变量,无滞后项;(3)m1、m2表示Arellano Bond序列自相关检验,sargan表示过度识别检验,其数值都是p值,N表示样本数量;(4)***表示在1%的显著性水平下显著。
计量结果显示:通货膨胀对工资和产出的影响均显著为负,对就业的影响显著为正。具体而言,就业效应的变化幅度最大,通货膨胀率每提高一个百分点,就业效应就提高0.19%-0.21%;工资效应和产出效应下降幅度较小,分别为0.08%-0.13%和0.03%-0.06%,其中工资效应下降幅度较大一些;综合而言,就业效应超出工资效应与产出效应的合力0.02%-0.07%,结合模型(10) 的计量结果可以验证推论:三种效应的合力为正,就业效应的影响最大,占据主导地位。
五、结论
考虑劳动力市场工资形成机制的制度化、非市场化等一系列特征,工资无法与价格形成同步波动,工资的刚性可能带来短期劳动收入比重的调整。本文尝试从这一短期经济波动视角探索劳动收入比重波动的原因。我们在理论上证实了通货膨胀对劳动收入比重的影响稳定为正。为验证此观点,本文利用“从一般到特殊”的建模方法对通货膨胀与劳动收入比重的关系进行了实证研究,本文研究发现:适度的通货膨胀对劳动收入比重具有积极影响。短期内通货膨胀率每增长1%,劳动份额上升0.05%。利用样本期间平均通货膨胀率为5.3%,劳动收入比重的均值为49.4%,简单计算显示:通货膨胀率从5.3%增加到6.3%(增加18.8%),对应劳动收入比重将从49.4%上升到49.68%左右。长期中估计效应从0.05%下降到0.03%;误差修正系数为0.71,说明长期趋势项对短期劳动收入比重变动具有重大调节作用,调整速度约为一年零五个月(1/0.71≈1.41年)。
本文为收入分配理论提供了有益的短期研究视角。初次分配中的劳动收入比重很大程度上受制于制度、技术等长期因素。本文认为在注重长期技术性等因素的同时,需要重视短期的周期性因素对劳动收入份额的影响。尤其是考虑到工资与物价波动不同步的情况下,给定短期实际工资的刚性,适当的通货膨胀有可能通过显著促进就业而提高劳动收入比重。受制于劳动力市场价格形成机制的非市场化,工资调整的短期刚性可能是中国劳动收入比重下降的重要因素之一。增加工资形成机制的灵活性,避免劳动力市场调整的滞后(叶正茂和王仕进,2014),从而让劳动收入比重调整回归到经济长期基本面决定的轨道上,这是长期收入分配调整的关键。
需要强调的是,本文研究结论并不意味着长期中为了提升劳动收入比重,短期中需要提升或大幅度提升通货膨胀。本文的研究结论具有严格的限制,即短期中在工资调整具有刚性的情况下,通货膨胀的上升将会导致实际工资的下降和就业的增加,在不完全竞争市场中,上述就业效应将超越产出效应和工资效应,导致劳动收入比重的上升。长期中随着工资刚性的逐步消失,劳动收入比重的长期影响将逐步下降。其次,短期内较高的通货膨胀率可能会使本文的研究结论失效,正如丁从明(2010) 强调,更高的通货膨胀将导致企业定价策略发生变化,从而不再满足通货膨胀与劳动收入比重的正向关系。更严格的证明在本文中并没有涉及,这是本文研究不足之处和未来进一步研究的方向。
附录:模型的统计属性
附表 1给出了正文模型(10) 的一些假设检验,模型通过了主要的稳定性假设检验,且模型的拟合程度很高(R2=0.95),可初步判断模型具有稳定性,能够较好地模拟劳动收入比重的变化规律。
| 假设检验 | 零假设(H0) | 检验结果([]内为概率值) | 结论 |
| 自相关检验 | 无自相关 | F(1, 22)=0.003[0.9538] | 无自相关 |
| 自回归条件异方差检验 | 无异方差 | F(1, 31)=0.615[0.4388] | 无异方差 |
| 正态性检验 | 正态分布 | χ2(2)=0.574[0.7505] | 正态分布 |
| 回归模式识别检验 | 回归设定正确 | F(1, 22)=2.914[0.1019] | 回归设定正确 |
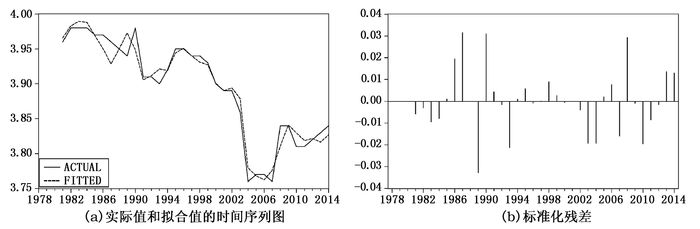
为了进一步分析模型的稳定性,本文对式(10) 的统计属性进行了深入分析。附图 1给出了样本区间内简化模型的基本图形分析,包括实际值和拟合值的时间序列图和标准化的残差。(a)图显示拟合线与实际值线重合程度很高。经标准差σ标准化的残差图显示仅有少量的异常值,标准化残差仅在区间[-0.04, +0.04]之内波动说明异常程度很低。
|
| 附图 1 劳动收入比重的基本形状 |
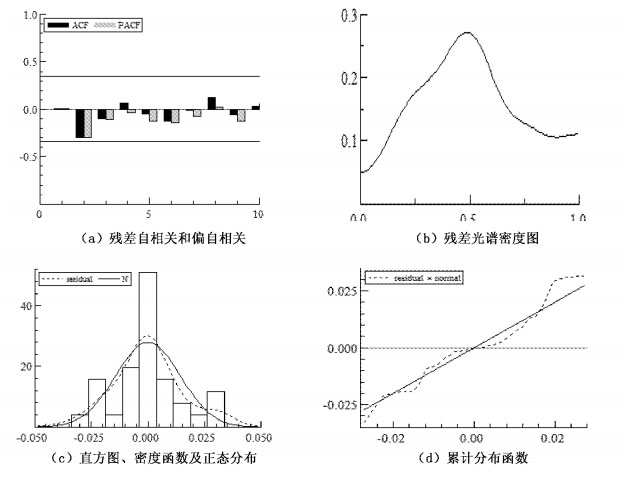
附图 2给出了模型(10) 的一系列残差分析图:残差自相关和偏自相关、残差光谱密度图、直方图、密度函数及正态分布、累计分布函数(分位数或QQ图,Quantile-Quantile Plot)。其中,(a)图描绘了连续的滞后残差之间的自相关性和偏自相关关系(图中±0.5的两条横线代表了95%的置信度水平),图中所有柱状没有超过横线而且短小,趋近于0,非常近似于白噪声序列,说明自相关和偏自相关不明显。(b)图是对自相关系数加权求和得到的序列,横轴已经被π标准化,因此横轴区间为[0, 1],光谱图将时间序列分解为不同振幅和频率的成分(伍戈,2009)。图中曲线虽然中间有突起,但相对比较扁平,仅在0.05-0.25之间波动,残差自相关不明显。从(c)图可以直观地观察到残差序列的正态分布特性,说明模型在总体上是合意的。(d)图中的对角线代表了正态分布的情况,是假设该序列为连续性正态分布时的累积分布线,类似于洛伦兹曲线中的均等线。残差紧紧围绕正态线波动说明残差序列较平稳,但是图形右方表现出的不吻合情况,说明部分异常值的存在。
|
| 附图 2 残差分析 |
| [1] | 白重恩, 钱震杰. 国民收入的要素分配——统计数据背后的故事[J]. 经济研究, 2009(3): 27–41. |
| [2] | 丁从明, 陈仲常. 价格波动与资源配置效率研究[J]. 统计研究, 2010(6): 22–28. |
| [3] | 丁从明, 刘明. 技术选择与劳动收入比重变迁的理论与实证研究[J]. 中国人口·资源与环境, 2013(7): 129–135. |
| [4] | 康继军, 傅蕴英, 张宗益. 中国经济转型与货币需求[J]. 经济学(季刊), 2012(2): 461–488. |
| [5] | 罗长远, 张军. 劳动收入占比下降的经济学解释[J]. 管理世界, 2009(5): 25–35. |
| [6] | 马磊. 为什么发达国家劳动收入份额下降?——基于纳什谈判理论的解释[J]. 世界经济研究, 2015(5): 60–68. |
| [7] | 伍戈. 中国的货币需求与资产替代:1994-2008[J]. 经济研究, 2009(3): 53–67. |
| [8] | 叶正茂, 王仕进. 劳动市场摩擦、工资刚性与中国的通货膨胀持续性——基于不同工资竞价模型的动态分析[J]. 财经研究, 2014(10): 32–45. |
| [9] | Acemoglu D. Labor and capital-augmenting technical change[J]. Journal of the European Economic Association, 2003, 1(1): 1–37. DOI:10.1162/154247603322256756 |
| [10] | Arpaia A, Perez E H, Pichelmann K. Understanding labour income share dynamics in Europe[J]. European Economy-Economic Papers, 2009, 379(2): 1–51. |
| [11] | Bassanini A, Manfredi T. Capital's grabbing hand? A cross-industry analysis of the decline of the labor share in OECD countries[J]. Eurasian Business Review, 2014, 4(1): 3–30. |
| [12] | Batini N, Jackson B, Nickell S. Inflation dynamics and the labour share in the UK[R]. Discussion Paper, 2000. |
| [13] | Buchele R, Christiansen J. Globalization and the declining share of labor income in the United States[R]. The 28th International Working Party on Labor Market Segmentation, France, 2007. |
| [14] | Calvo G A. Staggered prices in a utility-maximizing framework[J]. Journal of Monetary Economics, 1983, 12(3): 383–398. DOI:10.1016/0304-3932(83)90060-0 |
| [15] | Diwan L. Labor shares and globalization[R]. Working Paper, 2000. |
| [16] | Favero C A. Applied macroeconometrics[M]. Oxford: 2001. |
| [17] | Fischer S. Long-term contracts, rational expectations, and the optimal money supply rule[J]. Journal of Political Economy, 1975, 85(1): 191–205. |
| [18] | Gali J, Gertler M. Inflation dynamics: A structural econometric analysis[J]. Journal of Monetary Economics, 1999, 44(2): 195–222. DOI:10.1016/S0304-3932(99)00023-9 |
| [19] | Hendry D F. Dynamic econometrics[M]. Oxford: 1995. |
| [20] | Hoover K D, Perez S J. Data mining reconsidered: Encompassing and the general-to-specific approach to specification search[J]. Econometrics Journal, 1999, 2(2): 167–191. DOI:10.1111/ectj.1999.2.issue-2 |
| [21] | Hung J H, Hammett P. Globalization and the labor share in the United States[J]. Eastern Economic Journal, 2016, 42(2): 193–214. DOI:10.1057/eej.2014.50 |
| [22] | Judzik D, Sala H. Productivity, deunionization and trade: Wage effects and labour share implications[J]. International Labour Review, 2013, 152(2): 205–236. DOI:10.1111/j.1564-913X.2013.00178.x |
| [23] | Mahony M, Vecchi M, Venturini F. The long-run decline in labor share: Technology versus Institutions [R]. Working Paper, 2014. |
| [24] | Mcdonald I M, Solow R M. Wage bargaining and employment[J]. The American Economic Review, 1981, 71(5): 896–908. |
| [25] | Taylor J B. Aggregate dynamics and staggered contracts[J]. Journal of Political Economy, 1980, 88(1): 1–23. DOI:10.1086/260845 |
 2017, Vol. 43
2017, Vol. 43


