文章信息
 | 财经研究 2017年43卷第7期 |
- 田娇, 王擎.
- Tian Jiao, Wang Qing.
- 系统性风险防范与多重金融政策搭配——基于DSGE模型的逆周期监管效应分析
- Systemic risk prevention and multiple financial policy coordination:analysis of countercyclical regulatory effect based on dsge model
- 财经研究, 2017, 43(7): 57-69
- Journal of Finance and Economics, 2017, 43(7): 57-69.
-
文章历史
- 收稿日期:2017-02-21

2017第43卷第7期
2. 西南财经大学 中国金融研究中心,四川 成都 611130
2. Chinese Finance Research Institute, Southwestern University of Finance and Economics, Chengdu 611130, China
一、引言
2008年全球金融危机发生后,系统性风险开始受到关注。G20财长和欧洲央行行长Trichet(2010) 将系统性风险定义为一种影响广泛的破坏金融体系功能,以致经济增长和福利受到实质损害的金融失稳现象。近年来,面对经济波动加大、金融风险不断上升的事实,我国央行、银监会等金融监管部门相继提出坚决守住不发生系统性金融风险的底线,这更是被国家主席在2017年4月的中共中央政治局会议上所强调。降低危机发生的可能性是宏观审慎时代银行监管政策的目标之一,而2008年金融危机暴露出微观审慎的资本监管政策无力兼顾宏观审慎性。作为补救和改革措施,巴塞尔协议Ⅲ于2010年9月面世,要求提高银行核心一级资本充足率,并要求计提一定比例的防护缓冲资本和逆周期准备资本。我国银监会亦很快跟进,从2013年1月1日起开始实施《商业银行资本管理办法(试行)》。巴塞尔协议Ⅲ增加了逆周期监管思想,试图以此来提升资本约束对系统性风险的防范作用。从改进监管政策的角度看,至少有两大途径可以探索:一是假定其他政策不变,考察资本监管政策的改变对系统性风险和宏观经济波动的影响;二是假定资本监管政策不变,考察其他的多重金融监管政策如何对资本监管政策的宏观经济效应产生影响。
现有文献大多孤立地以银行资本监管政策作为探讨对象。比如,毛捷和金雪军(2007) 构建了包含违约风险和系统性风险的银行贷款定价模型,发现在巴塞尔资本协议Ⅱ的内部评级法下,资本金约束会引起系统性风险与贷款利率的反向联动,增大银行失败的风险。Dib(2010a)建立了一个包含银行部门的DSGE模型,发现银行间市场和银行资本市场的金融摩擦放大了冲击响应,但是资本监管要求会减弱总冲击的实际影响,进而降低宏观经济波动。Repullo和Suarez(2013) 在世代交叠模型下比较了巴塞尔协议Ⅰ、Ⅱ、Ⅲ,发现不同资本要求所产生的顺周期程度对银行风险的影响不同。高国华(2013) 构建了一个包含同质金融体系的DSGE框架,讨论了提高监管资本要求以及实施逆周期资本监管等产生的宏观经济效应和社会福利效应。这些研究实际上假定其他政策不变。但现实经济金融体系中往往有多重的监管政策,这些政策在作用于特定监管对象时,可能对系统性风险产生不一致的影响。比如,Acharya(2003) 发现在全球统一的资本充足要求下,跨国银行由于面临各个国家的救助措施或政府宽容度不同而产生失稳溢出效应,系统性风险增加。朱民(2010) 则指出,巴塞尔协议Ⅲ在各个国家实施的时间不同步,协议中资本金的标的及其质量、流动性以及杠杆率等各类指标对不同规模的银行等金融机构的监管力度不一致,都可能导致世界范围内的监管套利。
国内的新近研究开始探讨多重政策对金融风险的影响。江曙霞和何建勇(2011) 基于C-C模型的研究表明,在BaselⅠ和BaselⅡ的资本要求下,信贷风险和存贷比约束具有双重强化银行资本顺周期性的特征。李静婷和孟繁旺(2012) 实证研究了巴塞尔协议Ⅲ的指标在信贷增长、流动性比率、杠杆比率中的作用,发现多重政策下资本充足率要求并不是一个良好的控制银行风险传染的监管工具。马勇和陈雨露(2013) 基于DSGE模型考察了货币政策、信贷政策和金融监管政策(盯住社会融资规模以调节银行资本)等,认为宏观审慎政策的协调搭配需要避免“政策冲突”和“政策叠加”问题。可见,仅通过银行监管中的某一政策达到“公平竞争环境”,而忽视与其他监管政策的一致性,将有可能破坏银行体系的稳定性。就防范系统性风险而言,当银行存在风险转移动机时,如果监管只是针对单个银行风险而忽视其行为的负外部性,系统性风险就会被放大。这意味着多重政策之间存在最优搭配或取舍的问题,即如何统筹才能有利于巴塞尔协议Ⅲ宏观审慎性监管理念的实施。
回到现实来看,由于银行的特殊性,监管部门对银行业施加了严于其他行业的各种金融政策。然而,无论是与国际接轨的资本充足要求,还是我国特有的存贷比约束存贷比约束①,均未考虑银行之间的交互影响可能会引起负外部性。为了维持银行系统的稳定,政府还会通过“隐性担保”②对银行间市场上出现的违约风险予以事后保障。可见,金融监管是一项包含多重制度安排的系统工程,这些政策相互影响、共同作用于特定的监管对象。这些举措从不同方面保障银行的正常运行,具有微观审慎性。但当经济金融体系遭遇冲击时,多重金融政策的实施真的能像监管部门所期望的那样,协同资本监管政策来防范系统性风险?中国特有的流动性风险管理是否会影响资本监管缓释系统性金融风险的效果?
① 指贷款余额与存款余额比例不得超过75%,这一政策自1995年5月开始实施至2015年9月已长达20余年,该指标从2015年10月起由法定监管指标转为流动性监测指标。本文的研究主要基于1998-2013年的数据,设定有存贷比约束的模型能够反映经济金融现实,参数校准亦更为准确合理。
② 隐性担保是指政府对企业的经营损失和失败提供不言自明的担保,形式包括直接注资、资产剥离等。
基于这样的疑问,本文在资本监管要求下研究了如何协调其他金融政策以增强逆周期监管效应,进而抑制银行系统性风险。基于DSGE模型的研究结果表明:在资本约束条件下,中国特有的存贷比约束会通过银行间市场加大系统性金融风险和经济波动;取消政府在银行间市场的隐性担保这一流动性干预措施,使正常的违约机制显性化,将有利于抑制系统性金融风险的发生和扩大。本文的主要贡献在于:(1) 以弱化资本监管的顺周期性为视角,考察了资本监管政策与中国特有的微观金融政策在防范系统性风险方面的一致性;(2) 多重金融政策探析的对象是存贷比约束和政府隐性担保等带有行政保护色彩的流动性风险管理措施,这类政策的存废取舍具有金融市场化改革的意义;(3) 构建的DSGE模型将研究内容纳入统一框架下,形成更为贴近现实的有机结合,使研究结果能更为确切地反映、模拟和预测现实。
二、模型构建
本文模型包括居民、银行、企业和广义政府。居民部门分为资金紧缺的借款居民和资金充裕的储蓄居民,以体现居民异质性。银行的多样化体现在银行间市场的地位和资本充足情况不同,将其分为资金净拆出银行(资本充足)和资金净拆入银行(资本紧缺)。净拆出银行是指在银行间拆借市场中资金拆出大于资金拆入的银行,较为典型的是四大国有商业银行。净拆入银行是指在银行间拆借市场中资金拆入大于资金拆出的银行,较为典型的是一些经营策略较为激进的股份制银行和城商行等。银行间市场是连接银行体系资金流动性的重要渠道,也是系统性风险传导的必经路径之一。鉴于本文主要考察金融监管政策及金融风险防范,对企业部门的模型设定较为简洁,广义政府涵盖了政府部门和中央银行的职能。
(一) 居民
1.借款居民(资金紧缺方)
借款居民在t期以工资率wt提供劳动ntB,闲暇为1-ntB。为满足t期消费CtB,该类居民以利率rtB向银行申请消费贷款本息μtB,获得实际可用本金μtB/(1+rtB)。t期住房Ht-1的使用成本(租金率或视为分期付款)为rtSH,该类居民以利率rtH向银行申请住房贷款本息μtH,获得实际可用本金μtH/(1+rtH)以满足住房需求。居民的贷款行为存在违约可能,消费贷款偿还率为υtB,住房贷款偿还率为υtH。参照Suh(2012),借款居民的目标函数为:
| $ \mathop {{\rm{max}}}\limits_{\left\{ {C_t^B{\rm{, }}{H_t}{\rm{, }}n_t^B{\rm{, }}\mu _t^B{\rm{, }}\mu _t^H} \right\}} {{\rm{E}}_0}\left\{ {\sum\limits_{t = 0}^\infty {\beta _B^t} \left[{\gamma {\rm{log(}}C_t^B{\rm{)}} + {\rm{(}}1{\rm{-}}\gamma \varepsilon _t^\gamma {\rm{)log(}}{H_t}{\rm{)}} + \phi {\rm{log(}}1{\rm{-}}n_t^B{\rm{)}}} \right]} \right\} $ | (1) |
预算约束为:
| $ \begin{array}{l} C_t^B + r_t^{SH}{H_{t{\rm{- }}1}} + \upsilon _t^B\frac{{\mu _{t{\rm{- }}1}^B}}{{{\pi _t}}} + \upsilon _t^H\frac{{\mu _{t{\rm{- }}1}^H}}{{{\pi _t}}} + \frac{{{\theta ^B}}}{2}{\left[{{\rm{(}}1{\rm{-}}\upsilon _t^B{\rm{)}}\frac{{\mu _{t{\rm{-}}1}^B}}{{{\pi _t}}}} \right]^2}\\ \; + \frac{{{\theta ^H}}}{2}{\left[{{\rm{(}}1{\rm{-}}\upsilon _t^H{\rm{)}}\frac{{\mu _{t{\rm{-}}1}^H}}{{{\pi _t}}}} \right]^2} \le {w_t}n_t^B + \frac{{\mu _t^B}}{{1 + r_t^B}} + \frac{{\mu _t^H}}{{1 + r_t^H}} + \tau {T_t} \end{array} $ | (2) |
其中,βB是折现率,γ和ϕ反映居民对各类物品的效用偏好,θB和θH是惩罚系数,τ是借款居民在居民中的人口占比。εtγ反映住房偏好冲击,遵循式(3)。预算约束中,πt是通货膨胀率,Tt是政府对居民的转移支付,按人口比例在借款居民和储蓄居民中分配。借鉴Lin(2012) 的做法,以(1-υti)μit-1/πt2(i∈B, H)表示贷款违约对借款居民的非线性惩罚,违约率或贷款规模越高,边际惩罚越重。贷款违约冲击遵循式(4)。预算约束说明居民当期的消费、住房支出、对上期借款的实际还款额以及违约惩罚之和不能超过当期劳动收入、当期借款本金以及政府转移支付之和。
| $ {\rm{log}}(\varepsilon _t^\gamma ) = (1 - {\rho _\gamma }){\rm{log}}(\varepsilon _o^\gamma ) + {\rho _\gamma }{\rm{log}}(\varepsilon _{t - 1}^\gamma ) + \varepsilon _t^\gamma ,\varepsilon _t^\gamma \sim (0,\sigma _\xi ^2) $ | (3) |
| $ {\rm{log}}(\upsilon _t^B) = (1 - {\rho _B}){\rm{log}}(\upsilon _o^B) + {\rho _\gamma }{\rm{log}}(\upsilon _{t - 1}^B) + \varepsilon _t^B,\varepsilon _t^B \sim (0,\sigma _B^2) $ | (4) |
2.储蓄居民(资金富余方)
储蓄居民在t期以工资率wt提供劳动ntS,闲暇为1-ntS,以房屋租金率rtSH获得房产Ht-1收入。应有ntS≤ntB,即在工资水平无差异的情况下,富人的劳动收入占比小于穷人。该类居民资金富余,除了t期消费CtS,以利率rtS提供存款本金DtS,还投资房地产ItH,同时接受政府转移支付(1-τ)T。储蓄居民的目标函数为:
| $ \mathop {{\rm{max}}}\limits_{\left\{ {C_t^S{\rm{, }}{H_t}{\rm{, }}n_t^S{\rm{, }}D_t^S} \right\}} {{\rm{E}}_0}\left\{ {\sum\limits_{t = 0}^\infty {\beta _S^t} \left[{\gamma {\rm{log(}}C_t^S{\rm{)}} + {\rm{(}}1{\rm{-}}\gamma \varepsilon _t^\gamma {\rm{)log(}}{H_t}{\rm{)}} + \phi {\rm{log(}}1{\rm{-}}n_t^S{\rm{)}}} \right]} \right\} $ | (5) |
预算约束为:
| $ C_t^S + D_t^S + I_t^H \le {w_t}n_t^S + \frac{{D_{t{\rm{-}}1}^S}}{{{\pi _t}}}\left( {1 + r_t^S} \right) + \frac{{{\rm{(}}1 + r_t^{SH}{\rm{-}}{\delta _H}{\rm{)}}{H_{t{\rm{-}}1}}}}{{{\pi _t}}} + (1 - \tau ){T_t} $ | (6) |
住房积累方程为:
| $ {H_t} = (1-{\delta _H}){H_{t-1}} + I_t^H $ | (7) |
其中,βS是折现率,且βS>βB,即富人的消费更平滑,比穷人更具耐心。上标S表示储蓄居民,其他变量含义与借款居民相同。计算房产收益时,假定房产租售比在均衡状态时为常量,所以租金率的高低实际上反映了房价的高低。预算约束说明储蓄居民当期的消费、存款以及房产投资之和不能超过当期劳动收入、上期存款本息、上期房产投资收益以及政府转移支付之和。
(二) 银行
1.资金净拆出银行(资金充足方)
借鉴Lin(2012) 的做法,资金净拆出银行以全民所有的形式存在,即获得的利润以股利分配的形式消费CtL。以利率rtF向企业提供贷款本金μtF,存在违约可能,偿还率为υtF。以利率rtI在银行间市场拆出资金本金μtM,存在违约可能,交易对手偿还率为υtI。以利率rtS从居民部门吸收存款本息DtL,以贴现利率rtC向央行贴现获得本息μtC,根据中国银行业的实际情况,假定这两个市场不存在违约。银行资本充足率为ktL,监管要求为ko,则资本缓冲为ktL-ko。资金净拆出银行的目标函数为:
| $ \mathop {{\rm{max}}}\limits_{\left\{ {C_t^L{\rm{, }}\mu _t^F{\rm{, }}D_t^L{\rm{, }}\mu _t^C{\rm{, }}\mu _t^M} \right\}} {{\rm{E}}_0}\left\{ {\sum\limits_{t = 0}^\infty {\beta _L^t} \left[{\frac{{{{{\rm{(}}C_t^L{\rm{)}}}^{1{\rm{-}}\sigma }}}}{{1{\rm{-}}\sigma }} + \eta {\rm{log(}}k_t^L{\rm{-}}{k^o}{\rm{)}}} \right]} \right\} $ | (8) |
资金流约束为:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;C_t^L + \mu _t^F + \mu _t^M + \frac{{D_{t{\rm{-}}1}^L}}{{{\pi _t}}} + \frac{{\mu _{t{\rm{-}}1}^C}}{{{\pi _t}}} \le }\\ {\upsilon _t^F\frac{{\mu _{t{\rm{-}}1}^F{\rm{(}}1 + r_{t{\rm{ - }}1}^F{\rm{)}}}}{{{\pi _t}}} + \upsilon _t^I\frac{{\mu _{t{\rm{ - }}1}^M{\rm{(}}1 + r_t^I{\rm{)}}}}{{{\pi _t}}} + \frac{{D_t^L}}{{1 + r_t^S}} + \frac{{\mu _t^C}}{{1 + r_t^C}}} \end{array} $ | (9) |
存贷比约束为:
| $ \mu _t^F \le {\varphi ^L}\left[{D_t^L/\left( {1 + r_t^S} \right)} \right] $ | (10) |
其中,βL是折现率,σ是消费的风险厌恶系数,η反映对资本缓冲的偏好,φL是反映流动性的存贷比上限。资金流约束条件说明当期消费、提供的企业贷款额、在银行间市场拆出的资金、支付上期居民存款本息以及返还上期央行贴现之和不能超过收到的企业对上期借款的实际还款、银行间市场对上期拆出资金的实际还款以及本期向央行贴现之和。加入存贷比约束可反映中国特有的现实情况,使模型更加贴近实际。
资本充足率按式(11) 定义。EtL为银行权益,ωti为风险权重,μti为各种资产,i∈{F, M}。值得一提的是,当期银行权益为上期权益加上当期银行的净收入变动。净收入变动等于贷款和银行间市场的利息收入减去客户存款、央行贴现的利息支出以及股利分配后的余值(见式(12))。该式反映出为满足资本监管要求,银行可能采取降低资本金的分子策略,也可能采取缩小企业贷款和银行间市场资金拆出规模的分母策略。前者使银行股东或投资者收益下降,后者将减少金融对实体经济的支持。
| $ k_t^L = \frac{{E_t^L}}{{\omega _t^F\mu _t^F + \omega _t^M\mu _t^M}} $ | (11) |
| $ \begin{array}{l} E_t^L = \frac{{E_{t{\rm{-}}1}^L}}{{{\pi _t}}} + \frac{{\mu _{t{\rm{-}}1}^F}}{{{\pi _t}}}\left( {\upsilon _t^F + \left( {1 + r_{t{\rm{-}}1}^F} \right) - 1} \right) + \frac{{\mu _{t{\rm{ - }}1}^M}}{{{\pi _t}}}\left( {\upsilon _t^I\left( {1 + r_{t{\rm{ - }}1}^I} \right) - 1} \right)\\ \;\;\;\;\;\;\;\; - \frac{{D_{t{\rm{ - }}1}^L}}{{{\pi _t}{\rm{(}}1 + r_{t{\rm{ - }}1}^S{\rm{)}}}}r_{t{\rm{ - }}1}^S - \frac{{\mu _{t{\rm{ - }}1}^C}}{{{\pi _t}{\rm{(}}1 + r_{t{\rm{ - }}1}^C{\rm{)}}}}r_{t{\rm{ - }}1}^C - C_t^L \end{array} $ | (12) |
2.资金净拆入银行(资金紧缺方)
资金净拆入银行获得的利润以股利分配的形式消费CtD。以利率rtB向居民提供消费贷款本金μtR,偿还率为υtB。以利率rtH提供住房贷款本金μtN,交易对手偿还率为υtH。以利率rtS从居民部门吸收存款本息DtD,以利率rtI在银行间市场拆入资金本息μtI,偿还率为υtI。银行资本充足率为ktD,所以资本缓冲为ktD-ko。资金净拆入银行的目标函数为:
| $ \mathop {{\rm{max}}}\limits_{\left\{ {C_t^D{\rm{, }}D_t^D{\rm{, }}\mu _t^I{\rm{, }}\mu _t^R{\rm{, }}\mu _t^N{\rm{, }}\upsilon _t^I} \right\}} {{\rm{E}}_{\rm{0}}}\left\{ {\sum\limits_{t = 0}^\infty {\beta _D^t} \left[{\frac{{{{{\rm{(}}C_t^D{\rm{)}}}^{1{\rm{-}}\sigma }}}}{{1{\rm{-}}\sigma }} + \eta {\rm{log(}}k_t^D{\rm{-}}{k^o}{\rm{)}}} \right]} \right\} $ | (13) |
资金流约束为:
| $ \begin{array}{*{20}{l}} {C_t^D + \mu _t^R + \mu _t^N + \frac{{D_{t{\rm{- }}1}^D}}{{{\pi _t}}} + \upsilon _t^I\frac{{\mu _{t{\rm{- }}1}^I}}{{{\pi _t}}} + \frac{{{\theta ^I}}}{2}{{\left[{{\rm{(}}1{\rm{-}}\upsilon _t^I{\rm{)}}\frac{{\mu _{t{\rm{-}}1}^I}}{{{\pi _t}}}} \right]}^2}}\\ { \le \frac{{D_t^D}}{{1 + r_t^S}} + \frac{{\mu _t^I}}{{{\rm{(}}1 + r_t^I{\rm{)}}}} + \upsilon _t^B\frac{{\mu _{t{\rm{ -}}1}^R{\rm{(}}1 + r_{t{\rm{ -}}1}^B{\rm{)}}}}{{{\pi _t}}} + \upsilon _t^H\frac{{\mu _{t{\rm{ -}}1}^N{\rm{(}}1 + r_{t{\rm{ - }}1}^H{\rm{)}}}}{{{\pi _t}}}} \end{array} $ | (14) |
存贷比约束为:
| $ \mu _t^R + \mu _t^N \le {\varphi ^D}\left[{D_t^D/\left( {1 + r_t^S} \right)} \right] $ | (15) |
其中,βD是折现率,资金充足的银行更易平滑未来的股利分配和资本充足率,所以βD < βL。资金流约束条件说明当期消费、提供的消费贷款和住房贷款、支付上期居民存款本息、支付上期银行间市场拆入资金以及银行间市场违约惩罚之和不能超过收到的本期居民存款、本期银行间市场拆入资金、居民对上期消费贷款的实际偿还以及居民对上期住房贷款的实际偿还之和。
资本充足率按式(16) 定义。EtD为银行权益,ωti为风险权重,μti为各种资产,i∈{R, N}。同样地,当期银行权益为上期权益加上当期银行的净收入变动。净收入变动等于各类贷款的利息收入减去客户存款和银行间市场拆入资金的利息支出、违约惩罚以及股利分配后的余值(见式(17))。该式同样反映出为满足资本监管要求,资金净拆入银行除了可以采取分子策略或分母策略外,还可以在银行间市场提高违约率(1-υtI)来提升银行权益进而维持资本充足率。①同时,资金净拆出银行的权益资本将因υtI而下降(见式(12)),该类银行将采取上述类似行为以维持资本充足水平。由此可见,在资本监管资本约束和银行间市场流动性不足的触发机制下,整个银行业将采取惜贷等措施,进而影响实体经济。
① 虽然违约惩罚可能降低银行权益,但对违约惩罚系数θl施以很小的百分比约束,使违约率的上升对银行权益的影响方向不会因此发生扭转。从现实的违约惩罚机制看,惩罚通常为违约金额的一定比例,假定条件与之符合。
| $ k_t^D = \frac{{E_t^D}}{{\omega _t^R\mu _t^R + \omega _t^N\mu _t^N}} $ | (16) |
| $ \begin{array}{l} E_t^D = \frac{{E_{t{\rm{- }}1}^D}}{{{\pi _t}}} + \frac{{\mu _{t{\rm{- }}1}^R}}{{{\pi _t}}}\left( {\upsilon _t^B + \left( {1 + r_{t{\rm{- }}1}^B} \right) - 1} \right) + \frac{{\mu _{t{\rm{ - }}1}^N}}{{{\pi _t}}}\left( {\upsilon _t^H\left( {1 + r_{t{\rm{ - }}1}^H} \right) - 1} \right) - C_t^D\\ \;\;\;\;\;\;\;\;\; - \frac{{D_{t{\rm{ - }}1}^D}}{{{\pi _t}{\rm{(}}1 + r_{t{\rm{ - }}1}^S{\rm{)}}}}r_{t{\rm{ - }}1}^S - \frac{{\mu _{t{\rm{ - }}1}^L}}{{{\pi _t}{\rm{(}}1 + r_{t{\rm{ - }}1}^I{\rm{)}}}}\left( {\upsilon _t^I\left( {1 + r_{t{\rm{ - }}1}^I} \right) - 1} \right) - \frac{{{\theta ^I}}}{2}{\left[{{\rm{(}}1{\rm{-}}\upsilon _t^I{\rm{)}}\frac{{\mu _{t{\rm{-}}1}^I}}{{{\pi _t}}}} \right]^2} \end{array} $ | (17) |
(三) 企业
本文假设企业部门只有一种产出且处于完全竞争均衡,所得利润为全民所有并用于消费。企业以工资率wt雇佣劳动力nt,利用上期末实物资本Kt-1,生产物品Yt。将生产所得卖出Qt,其余用于全民消费CtF、补充实物资本、缴纳贷款违约惩罚等。企业以利率rtF向银行申请贷款本息μtP,存在违约可能,偿还率为υtF。企业的目标函数为:
| $ \mathop {{\rm{max}}}\limits_{\left\{ {{n_t}{\rm{, }}{K_t}{\rm{, }}{Q_t}{\rm{, }}\mu _t^P} \right\}} {{\rm{E}}_{\rm{0}}}\left\{ {\sum\limits_{t = 0}^\infty {\beta _F^t} \left[{{\rm{log(}}C_t^F{\rm{)}}} \right]} \right\} $ | (18) |
资源约束为:
| $ {Y_t} = C_t^F + I_t^K + {Q_t} + \frac{{{\theta ^F}}}{2}{\left[{{\rm{(}}1{\rm{-}}\upsilon _t^F{\rm{)}}\frac{{\mu _{t{\rm{-}}1}^P}}{{{\pi _t}}}} \right]^2} $ | (19) |
生产函数为:
| $ {Y_t} = {A_t}K_{t{\rm{-}}1}^\alpha n_t^{1{\rm{-}}\alpha } $ | (20) |
资本积累方程为:
| $ {K_t} = (1-{\delta _K}){K_{t-1}} + I_t^K $ | (21) |
预算约束为:
| $ {w_t}{n_t} + \upsilon _t^F\frac{{\mu _{t{\rm{-}}1}^P}}{{{\pi _t}}} \le {Q_t} + \frac{{\mu _t^P}}{{1 + r_t^F}} $ | (22) |
其中,βF是贴现率,δK是资本折旧率。生产函数中全要素生产率冲击遵循式(23)。预算约束表明企业当期的劳动力成本和贷款实际偿还额之和不能超过当期产品出售收入和贷款之和。企业贷款违约冲击遵循式(24)。
| $ {\rm{log}}({A_t}) = (1 - {\rho _A}){\rm{log}}({A_o}) + {\rho _A}{\rm{log}}({A_{t - 1}}) + \varepsilon _t^A,\varepsilon _t^A \sim (0,\sigma _A^2) $ | (23) |
| $ {\rm{log}}(\upsilon _t^F) = (1 - {\rho _F}){\rm{log}}(\upsilon _o^F) + {\rho _F}{\rm{log}}(\upsilon _{t - 1}^F) + \varepsilon _t^F,\varepsilon _t^F \sim (0,\sigma _F^2) $ | (24) |
(四) 政府
本文的广义政府兼具央行的职能。本文假定无生产缺口,且利率没有盯住通胀水平。式(25) 反映了外生利率rtC的冲击。转移支付Tt来源于政府的铸币税收入,即式(26)。Mt是货币供应量,其增长率gt的外生冲击反映货币政策,即式(27)。
| $ r_t^C = \left( {1-{\rho _C}} \right)r_o^C + {\rho _C}r_{t{\rm{-}}1}^C + \varepsilon _t^C, \;\;\varepsilon _t^C \sim \left( {0, \sigma _C^2} \right) $ | (25) |
| $ {T_t} = \frac{{{M_{t{\rm{-}}1}}r_{t{\rm{-}}1}^C}}{{{\pi _t}}}, \frac{{{M_t}}}{{{M_{t{\rm{-}}1}}}} = {g_t}, {T_t} \le {M_t} - \frac{{{M_{t{\rm{ - }}1}}}}{{{\pi _t}}} $ | (26) |
| $ {\rm{log}}({g_t}) = (1-{\rho _g}){\rm{log}}({g_o}) + {\rho _g}{\rm{log}}({g_{t-1}}) + \varepsilon _t^g, \varepsilon _t^g \sim (0, \sigma _g^2) $ | (27) |
三、模型求解
首先是定义均衡。本文的模型经济由效用函数、生产函数、违约惩罚函数、贴现参数、现金先行参数、折旧参数以及各种利率和违约概率等法则构成。在此框架下,一个含有违约机制和银行体系的经济体货币均衡是指,各类经济主体根据宏观经济变量做出理性预期,在满足约束条件下做出各种决策,使目标函数最大化,同时市场出清。市场出清指各个子市场供求相等,如劳动力市场满足nt=(ntB)τ(ntS)1-τ。
参数校准是DSGE模型求解的关键,大致分为几种情况:根据经济中的实际数据赋值;根据已有文献惯例赋值;根据本文模型的稳态方程估计(结合实际数据);根据模型公式估计。本文综合运用以上几种赋值方法,得到相应的参数值,具体见表 1。①
① 本文参数校准采用王擎和田娇(2016) 的数据。由于模型设定与其一致,限于篇幅,本文将不对参数做更多的分析,具体解释请参见王擎和田娇(2016)。
| 参数含义 | 参数符号 | 参数值 | 所用指标 | 数据来源 | 校准依据 | 类型 |
| 货币供应增长率 | go | 1 | 货币供应增长率 | 王君斌和王文甫(2010) | 已有文献惯例 | 稳态值 |
| 全要素生产率 | Ao | 1 | 全要素生产率 | |||
| 通货膨胀率 | π | 1.0075 | GDP平减指数 | 国家统计局网站 | 经济中的实际数据 | |
| 住房租金率 | rSH | 0.0189 | 租售比、房地产销售价格指数、房地产租赁价格指数 | RESSET数据库、中经网统计数据库、中国指数研究院 | ||
| 央行基准利率 | roC | 0.0068 | 季度国债回购利率 | RESSET数据库 | ||
| 银行间市场拆借利率 | rI | 0.0072 | 季度银行间7天拆借利率 | 中经网统计数据库 | ||
| 银行间市场偿还率 | υI | 0.9975 | 银行间市场违约率 | Dib(2010b) | ||
| 消费贷款偿还率 | υoB | 0.9874 | 季度信用卡透支贷款不良贷款率 | 中国银监会《中国银行业运行报告》 | ||
| 住房贷款偿还率 | υoH | 0.9969 | 季度住房贷款不良贷款率 | |||
| 企业贷款偿还率 | υoF | 0.975 | 分行业部门贷款不良贷款率 | 中国经济与社会发展统计数据库 | ||
| 净拆出银行资本充足率 | kL | 0.1289 | 122家国内商业银行资本充足率 | Bankscope数据库 | ||
| 净拆入银行资本充足率 | kD | 0.0918 | ||||
| 资本充足率 | k | 0.098 | 银行业核心资本充足率 | 中国银监会网站 | ||
| 储蓄居民折现率 | βS | 0.9946 | 金融机构人民币存款3个月定期利率均值rS | RESSET数据库 | 参数 | |
| 借款居民折现率 | βB | 0.9860 | 消费贷款利率、金融机构人民币1年及以下短期贷款利率均值rB | |||
| 企业折现率 | βF | 0.9922 | 国债票面利率 | |||
| 资金充足银行折现率 | βL | 0.9933 | 再贴现利率均值 | 稳态方程 | ||
| 资金紧缺银行折现率 | βD | 0.9929 | 银行间市场利率均值rI | |||
| 消费偏好 | γ | 0.97 | 住房均值、借款居民消费均值 | |||
| 闲暇偏好 | φ | 2.3 | 借款居民就业、消费均值 | |||
| 消费贷款违约惩罚系数 | θB | 0.57 | 人均消费贷款本金μR | |||
| 企业贷款违约惩罚系数 | θF | 17.47 | 人均企业贷款本金μF | |||
| 住房贷款违约惩罚系数 | θH | 8.45 | 人均消费贷款本金μN | |||
| 银行拆借违约惩罚系数 | θI | 32.83 | 人均银行间拆出资金本金μM | |||
| 资本缓冲偏好 | η | 0.006 | 银行股利分配CD、银行资本充足率kD、风险权重ωR和ωN | |||
| 房贷利率 | rH | 0.0108 | 五年以上住房公积金贷款利率 | RESSET数据库 | 稳态值 | |
| 消费贷款利率 | rB | 0.0142 | 金融机构人民币1年及以下短期贷款基准利率 | |||
| 企业贷款利率 | rF | 0.0077 | 各期国债票面利率均值 | |||
| 就业 | n | 0.5691 | 就业人员占人口比重 | 中经网统计数据库 | ||
| 实物资本折旧率 | δK | 0.025 | 实物资本折旧率 | 单豪杰(2008) | 已有文献惯例 | 参数 |
| 住房折旧率 | δH | 0.0125 | 住房折旧率 | 骆永民和伍文中(2012) | ||
| 借款居民劳动份额 | τ | 0.3 | 可支配收入占比、耐用品消费用户数占比 | 中国经济与社会发展统计数据库、中经网统计数据库 | ||
| 实物资本份额 | α | 0.47 | 生产函数估计,GDP、就业人数、实物资本 | 中国经济社会发展统计数据库 | ||
| 银行风险厌恶系数 | σ | 5.42 | 银行消费跨期替代率倒数,银行收益、股利分配、支付职工现金 | RESSET数据库 | ||
| 资本监管要求 | ko | 0.04 | 核心资本充足率要求 | 中国银监会规定 | 实际数 | |
| 技术进步冲击: 一阶自相关系数 | ρA | 0.91 | GDP、新增固定资产(用于计算实物资本)、就业人数 | 中经网统计数据库 | 模型公式估计 | 参数 |
| 回归残差标准差 | σA | 0.000944 | ||||
| 住房需求冲击: 一阶自相关系数 | ργ | 0.98 | 房地产销售价格指数季度增长率 | |||
| 回归残差标准差 | σξ | 0.035859 | ||||
| 货币供应冲击: 一阶自相关系数 | ρg | 0.91 | M2货币供应量环比增速 | |||
| 回归残差标准差 | σg | 0.001423 | ||||
| 基准利率冲击: 一阶自相关系数 | ρC | 0.99 | 三个月期央票利率(公开市场操作,发行参考收益率) | RESSET数据库 | ||
| 回归残差标准差 | σC | 0.000059 | ||||
| 消费贷款违约冲击: 一阶自相关系数 | ρB | 0.95 | 消费贷款不良贷款率 | 中国银监会《中国银行业运行报告》 | ||
| 回归残差标准差 | σB | 0.000053 | ||||
| 企业贷款违约冲击: 一阶自相关系数 | ρF | 0.91 | 企业贷款不良贷款率 | |||
| 回归残差标准差 | σF | 0.000517 |
四、不同经济周期下资本监管的宏观审慎缺失
大量文献(Blum和Hellwig,1995) 研究表明,资本监管存在顺周期性,即在资本约束下,银行资本通过对银行信贷等经营活动的影响,在宏观经济波动时会助推高涨或加剧衰退。这部分将探析经济处于不同运行周期时,经济体遭受六类不同外生冲击后的脉冲响应,以考察在多重金融政策约束下,资本监管顺周期性的“顽固性”。这六类外生冲击包括:经济处于下行期或衰退时企业贷款违约率上升、消费贷款违约率上升、全要素生产率下降、货币供应增加,以及经济处于上行期或过热时基准利率上升、住房需求下降。
(一) 经济处于下行期或衰退时
经济金融领域不同类型的外生冲击作用于经济体的初始途径有所不同。比如,当消费贷款违约率上升时,提供消费贷款和住房贷款业务的净拆入银行将及时调整资产组合,降低住房贷款利率rtH以促使住房贷款μtN增加;经济下行时,政府可能实施宽松的货币政策以刺激经济,使得货币增速gt加大,基准利率rtC随之下降;当企业贷款违约率上升时,提供企业贷款业务的净拆出银行将上调企业贷款利率rtF以反映风险溢价,从而企业贷款规模μtF下降;当全要素生产率下降时,根据生产函数,实体经济yt将下滑。
但无论遭受的外生冲击最初作用于哪个领域,资本监管约束均在统一的系统性风险传递机制下体现出顺周期性。这是因为受到资本监管约束的银行体系会进一步紧缩贷款以满足监管要求(见图 1)。具体而言,为缓解经济体遭受负向冲击的影响,央行会下调基准利率rtC。消费贷款利率rtB、住房贷款利率rtH等商业贷款利率随之下降,进而消费贷款μtR和住房贷款μtN增加。在风险加权资产构成的资本充足率计算方法下,提供消费贷款和住房贷款业务的净拆入银行的资本充足率ktD因为贷款规模上升而出现较大幅度的下降。为满足资本监管要求,净拆入银行在银行间市场的违约风险-υtI加大,进而银行间市场拆借利率rtI上升以反映风险溢价。由于银行间市场违约风险加大和利率上升释放出经济金融风险上升和资金紧张的信号,净拆出银行会提高企业贷款利率rtF,从而缩减企业贷款μtF。这使投资itK和资本形成kt相继减少,进而实体经济yt持续下滑。经济衰退使就业需求nt下降,在买方市场条件下,均衡时的就业水平下降。可见,在经济下行时,资本监管要求助推了经济下行趋势,缺乏宏观审慎性。

|
| 图 1 资本监管约束下的系统性风险传递 |
(二) 经济处于上行期或过热时
资本监管要求在经济上行期亦体现出顺周期性。当经济处于上行期或过热时,政府可能采取紧缩的货币政策以抑制经济高涨,具体的政策工具是调高基准利率rtC。当房地产过热时,政府将实施从严的房地产政策以调节房地产行业,使其回到正常的发展轨迹。这意味着居民的住房偏好-εtγ下降,从而住房贷款μtN减少。这些变化与图 1所示的方向相反,在同样的系统性风险传递机制作用下,助推了经济上行趋势。
五、多重金融政策取舍下的逆周期调节
从上述分析可以看到,无论在经济周期的哪个阶段、发生怎样的外生冲击,资本监管均存在强烈的顺周期性。另外,长期以来,中国的经济金融政策除了对银行业实施国际范式的资本监管外,还存在诸多行政保护。随着金融深化改革的不断推进,大量的金融政策面临着存废取舍,典型的便是放开存贷比约束和允许银行间市场违约。这部分将从多重监管政策的协调匹配视角,分析应如何对这些带有行政保护色彩的流动性风险管理措施进行取舍,以减缓资本监管的顺周期性,进而抑制系统性风险。
(一) 干预个体银行流动性的存贷比约束
我国实施存贷比要求的初衷是管理银行的流动性风险。随着国内金融市场的发展,存贷比要求暴露出干扰信贷统计、加剧存款竞争等弊端,监管层最终于2015年取消了存贷比要求,仅作为参考指标。这一举措是否会加剧资本监管的顺周期性?本文对基准模型放开存贷比约束进行了考察,即μtF≤φL[DtL/(1+rtS)]和μtR+μtN≤φD[DtD/(1+rtS)]不再成立。这意味着银行有了更大的业务调整度,但这种便利是否有益于防范系统性风险还不能一概而论。
仍以发生六大外生冲击做脉冲响应,与存贷比要求下的基准模型相比,取消存贷比要求后出现了以下三种情况(见图 2):(1) 当处于下行期或衰退时,经济体遭遇来自信贷行业的负向外生冲击,实际产出等指标下降幅度加大,整个经济金融体系的波动幅度增大。这里的信贷行业主要指企业贷款和消费贷款。以消费贷款违约上升为例,房地产投资及其资本积累的波动方向改变且波动幅度加大。这说明取消存贷比约束后,当面临来自金融业内部的外生冲击时,有了更大业务调整度的净拆入银行进行了积极的资产组合调整。银行追求收益、规避风险的自利行为使微观金融风险溢出至实体经济,形成更大的系统性风险。(2) 当处于下行期或衰退时,经济体遭遇技术进步下降或货币供给增加的外生冲击,整个经济金融体系的波动幅度减小,经济金融发展平稳。可见,当经济体遭遇的外生冲击来自非金融行业时,银行业通过利用存贷比约束取消所带来的业务调整便利,积极应对非金融领域的负面影响,风险缓释直接作用于经济金融体系,减缓了经济波动。(3) 当处于上行期或过热时,经济体遭遇来自政策层面的外生冲击,整个经济金融体系的波动趋势发生反转,实际产出、房产投资等下降,同时波动幅度减小,起到了抑制经济波动的作用。面对经济过热,政府可能实施价格型的紧缩货币政策,即调高基准利率。政府也可能实施从严的房地产政策以应对房地产过热,使居民的住房偏好-εtγ下降。放开存贷比约束后,这些政策措施通过银行业务调整,对经济有一定的降温效果。
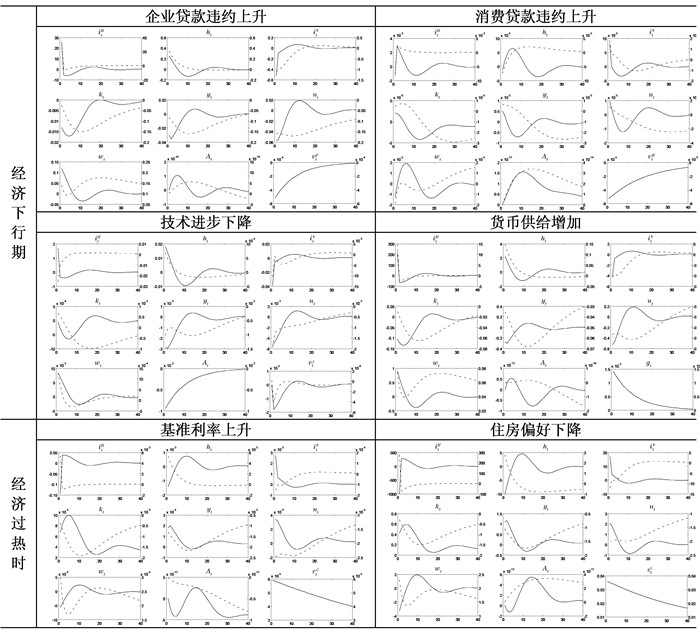
|
| 图 2 存贷比约束政策存废的脉冲响应对比 注:图中实线为基准模型,对应左纵轴;虚线为取消存贷比约束后的比较模型,对应右纵轴。 |
可见,在部分外生冲击下,取消存贷比约束体现出减缓监管资本顺周期性的逆周期调节效应。存贷比监管本身并不随着经济形势进行逆周期调整,不同类型的外生冲击所产生的风险传递前期机制不同,成为其是否具有调节效应的关键。当外生冲击来自金融业之外时,取消存贷比约束有助于提高监管资本下的系统性风险防范功能。
(二) 保护银行间流动性的政府隐性担保
银行间市场为资金融通提供了便利性和流动性,其与金融稳定之间存在十分紧密的关系。我国统一的同业拆借市场自1996年运行以来,逐渐发展成为国内金融市场乃至金融体系的重要组成部分。由于同业业务不需缴纳存款准备金、不受存贷比约束,银行业存在监管套利的动机,增加了潜在风险。2013年6月20日,上海银行间隔夜利率大幅飙升超过500个基点,达到13.44%,7天利率达到11.00%,均创下历史新高,银行间市场暴露出明显的流动性不足。尽管如此,鉴于银行间市场在金融体系中的重要性,监管部门并未完全放开银行间市场的流动性风险,通过央行和大型商业银行的流动性救助等政府隐性担保,这次流动性不足最终并未发展出现市场化的正常违约。那么,以政府的隐性担保替代显性的市场违约机制,是否有助于缓解资本监管的顺周期性?我们在基准模型的基础上设定银行间市场在政府隐性担保下不存在违约现象,即偿还率υtI≡1。
仍以发生六大外生冲击做脉冲响应,得到的结果较为一致。①无论经济处于哪个时期、发生何种冲击,与存在银行间市场违约可能的基准模型相比,资本监管和政府隐性担保双重约束使整个经济金融体系遭遇更大的波动,经济下行(或过热)时实际产出等下降(或上升)幅度加大。可见,当银行体系遭受不利的外生冲击时,若银行间市场存在政府隐性担保,资本监管的顺周期性会加大。这说明政府的隐性担保可能阻止了银行间市场正常的违约机制。虽然这会在短期内对市场参与者产生保护作用,但金融风险在微观层面未得到及时释放,加大了风险的积累和滚雪球效应,进而无法抑制系统性风险波及实体经济。
① 限于篇幅,文中未给出银行间市场是否存在违约的脉冲响应对比图,如感兴趣可向作者索取。
六、结论与政策启示
早期的资本监管要求旨在降低银行个体的金融风险。但大量的实证研究发现,资本监管在防范系统性金融风险时存在顺周期性,即资本要求作为微观审慎的监管工具缺乏宏观审慎性。本文在此背景下,结合中国当前不断深化的金融改革,考察了银行资本监管与流动性干预之间是否存在“政策叠加”或“政策冲突”,以此探析中国对银行体系特有的流动性干预方式是否有助于缓解资本监管要求的顺周期性。本文基于DSGE模型的研究表明:只有当经济体遭遇非金融领域的外生冲击时,取消存贷比约束才有助于弱化资本监管的顺周期性;取消政府隐性担保而使银行间拆借市场正常的违约机制显性化,在经济体遭遇各类外生冲击时,均有利于抑制系统性金融风险的发生和扩大,起到逆周期调节作用。
可见,从多重金融政策搭配来抑制国内系统性金融风险的角度讲,在现行资本监管约束下,对银行体系的流动性干预去行政化是有效的措施,且取消银行间市场的政府隐性担保比取消银行存贷比约束更为稳健。因此,应建立监管部门之间政策协调方面的决策机制,加强系统性风险的分析与防范。事实上,2013年8月设立的由中国人民银行牵头的金融监管协调部际联席会议制度,就是为了维护金融稳定和协调防范化解系统性金融风险。该联席会议通过信息共享来提升系统性风险管理水平,在解决“政策叠加”问题方面是新的尝试,但并未打破原有监管体制。可考虑在适当时候进一步构建目标一致的多重政策联合决策机制,为旨在防范系统性风险的资本监管搭配相融的政策工具组合。
| [1] | 单豪杰. 中国资本存量k的再估算:1952~2006年[J]. 数量经济技术经济研究, 2008(10): 17–31. |
| [2] | 高国华. 基于系统性风险的银行资本监管及其宏观经济效应[D]. 上海: 上海交通大学博士学位论文, 2013. |
| [3] | 江曙霞, 何建勇. 银行资本、银行信贷与宏观经济波动——基于C-C模型的影响机理分析的拓展研究[J]. 金融研究, 2011(5): 100–112. |
| [4] | 李静婷, 孟繁旺. 宏观审慎监管对传染性银行风险的控制作用研究[J]. 北京工商大学学报(社会科学版), 2012(3): 87–94. |
| [5] | 骆永民, 伍文中. 房产税改革与房价变动的宏观经济效应——基于DSGE模型的数值模拟分析[J]. 金融研究, 2012(5): 1–14. |
| [6] | 马勇, 陈雨露. 宏观审慎政策的协调与搭配:基于中国的模拟分析[J]. 金融研究, 2013(8): 57–69. |
| [7] | 毛捷, 金雪军. 巴塞尔新资本协议与银行贷款定价——一个基于信贷市场系统性风险的模型[J]. 经济科学, 2007(5): 54–65. |
| [8] | 王君斌, 王文甫. 非完全竞争市场、技术冲击和中国劳动就业——动态新凯恩斯主义视角[J]. 管理世界, 2010(1): 23–35. |
| [9] | 王擎, 田娇. 银行资本监管与系统性金融风险传递——基于DSGE模型的分析[J]. 中国社会科学, 2016(3): 99–122. |
| [10] | 朱民. 危机后的全球金融格局十大变化[J]. 国际金融研究, 2010(1): 16–22. |
| [11] | Acharya V V. Is the international convergence of capital adequacy regulation desirable?[J]. Journal of Finance, 2003, 58(6): 2745–2781. DOI:10.1046/j.1540-6261.2003.00621.x |
| [12] | Blum J, Hellwig M. The macroeconomic implications of capital adequacy requirements for banks[J]. European Economic Review, 1995, 39(3-4): 739–749. DOI:10.1016/0014-2921(94)00081-A |
| [13] | Dib A. Capital requirement and financial frictions in banking:Macroeconomic implications[R]. Working Paper, Bank of Canada, 2010a. |
| [14] | Dib A. Banks, credit market frictions, and business cycles[R]. Working Paper, Bank of Canada, 2010b. |
| [15] | Lin L. Rating systems and procyclicality:An evaluation in a DSGE framework[R]. AEA 2013 Annual Meeting Papers, 2012. |
| [16] | Repullo R, Suarez J. The procyclical effects of bank capital regulation[J]. Review of Financial Studies, 2013, 26(2): 452–490. DOI:10.1093/rfs/hhs118 |
| [17] | Suh H. Macroprudential policy:Its effects and relationship to monetary policy[R]. FRB of Philadelphia Working Paper No.12-28, 2012. |
| [18] | Trichet J-C. Keynote address by Jean-Claude Trichet[J]. CESifo Forum, 2010(3): 8–11. |
 2017, Vol. 43
2017, Vol. 43


