一、引言

在经济周期的下行阶段，银行的资产质量趋于恶化，信贷资产的违约概率等信用风险要素倾向于上升，进而导致了其监管资本要求被动上升(Heid, 2007; Lee等, 2011)。然而，此时银行通常难以进行增量的资本补充，进而被迫削减信贷供给，加速了宏观经济的衰退进程，监管资本要求的此“顺周期”效应曾引起文献广泛的讨论(Koopman等, 2005; Jokipii和Milne, 2008)。与之对照鲜明的是，人们对不稳健的贷款损失准备(简称LLP)管理可能引致的顺周期性却知之甚少。当银行基于历史信息进行后顾性的信用风险评估时，其将在经济周期的上行阶段乐观估计抵押品价值和借款人的还款能力，并给予较低的违约风险评估和计提较少的LLP，进而释放更多的信贷供给；随着经济周期下行阶段的演化，借款人的资产质量恶化，银行不得不计提较多的LLP，进而被动压缩信贷供给，加速了宏观经济的衰退进程，使得非自由裁量的LLP呈现周期变动的特点(Borio等, 2001; Laeven和Majnoni, 2003)。为了降低LLP顺周期性的潜在不利影响，FSF (2009) 和BCBS (2010) 等机构主张对LLP进行动态和前瞻性管理。在相关研究中，Laeven和Majnoni (2003) 建议从平均意义上满足LLP的最低监管要求。Bouvatier和Lepetit (2012) 认为在经济周期的上行阶段，专项准备(针对已实现信贷损失或风险计提的准备)相对较低，银行可择机建立前瞻性准备(信贷组合预期损失与专项准备之差)；而在经济周期的下行阶段，前期累积的前瞻性准备可用于核销问题贷款，以抵补专项准备的逆周期变动，进而降低总准备的顺周期变动。然而，有适当理论基础、可经验估计的前瞻性LLP方法的缺少，限制了该宏观审慎政策工具的使用空间及其政策效果，本文希望对此进行有益地探索与补充。

理论上来讲，动态和前瞻性LLP要体现以下精神：银行须在经济周期内对信用风险进行动态评估，适时微调LLP的计提标准，而非在信贷资产风险分类和计提指引下对LLP进行静态的即期估计；银行须进行跨周期的信用风险评估，同时平滑地计提LLP。从建模的视角来看，可从以下视角反映该诉求：首先，借款人信用风险要素的测度必须是动态时变的，且其“偿付标的”呈现出周期变化的特点。在信用风险的结构化模型中，文献假设借款人的违约行动由其资产价值的随机运动驱动，同时在资不抵债边界下进行违约刻画，然而，其盯住的偿债标的是借款人的资产价值，是非周期和非平稳的，有关风险测度不仅难以估计，亦不能体现借款人风险要素周期变动的倾向。而本文将借款人的资产增速(或资产价值的相对变化)作为观测变量，并设其服从均值回复特征的随机过程，基于资产价值和资产增速间的近似函数关系，间接推导了资产价值的动态随机运动规律，再在结构化模型框架内对借款人的风险要素及其拨备要求进行了刻画。其次，对LLP的估计必须是前瞻性的。本文在借款人下个周期内的目标资产负债率(或预测的资产负债率)和融资成本约束下，对其下个周期内各时点上的风险要素及其拨备要求进行动态的递推估计，并将其平均趋势作为前瞻性LLP的测度安排或参照基准。

本文的边际贡献体现在两个方面：第一，给出了一种有理论基础、可经验估计的动态和前瞻性LLP方法。信用风险的结构化模型假设借款人的违约行动由其资产价值的随机运动驱动，然而，资产价值具有不易观测性、非周期性和非平稳性等特征，这极大地限制了其实际应用。与之不同的是，本文的研究对象是借款人的资产增速，具有周期性和平稳性等特征，使之不仅契合前瞻LLP管理的内在要求，而且有助于模型的经验估计和实施推广。此外，模型还能敏感测试借款人的目标杠杆(或预期杠杆)和融资成本对前瞻性拨备要求的潜在影响，并为LLP管理的适度性提供研判视角。第二，基于工业部门1993-2013年的资产负债等数据，经验估计了该部门及其子行业的未来信用风险及前瞻性拨备要求，同时基于银发〔2002〕98号和银监发〔2010〕98号的有关规定估算了监管要求的前瞻性准备成分和银行实提的前瞻性准备成分，并根据它们理论映射的借款人目标杠杆和融资成本组合状态研判了其适当性。本文深入揭示了不同杠杆和融资成本约束下的工业部门信用风险及其演变趋势，回答了银行体系和监管要求的前瞻性拨备管理是否适当等热点问题。

需要强调的是，本文与自由裁量LLP管理文献明显不同。LLP被视为银行会计中最大的自由裁量应计项目，通过对问题贷款形成时间和潜在规模的选择性识别与管理，银行能将之用于特定目的或需要。历史文献曾对LLP的自由裁量成分(或自由裁量的LLP)，如盈余管理(Cornett等, 2009; Balboa等, 2013)、资本管理(Ahmed等, 1999; Beatty等, 2002)、信号管理(Kanagaretnam等, 2005; Elnahass等, 2013) 等进行了丰富的研究。然而，对非自由裁量的LLP而言，更多关注其顺周期的存在性及其潜在影响(如Jokipii和Milne, 2008; Bouvatier和Lepetit, 2012)。由于易估计的前瞻性LLP方法供给不足，故部分国家的监管当局采取了简化的权宜安排(如Chan-Lau, 2012; Wezel等, 2012)，本文对前瞻性LLP计提方法及其计提标准的定量测度等是对已有文献的重要补充。

二、模型

(一)模型结构。模型的基本想法是：假设借款人的资产增速服从具有均值回复特征的随机过程，再基于资产价值和资产增速之间的近似函数关系，间接推导资产价值的动态随机运动规律，然后在结构化信用风险模型框架内对借款人的信用风险要素和LLP要求(或预期损失)进行测度。假设借款人的资产增速r_t(t≤T)服从如下Ornstein-Uhlenbeck过程：

其中，θ为资产增速的长期水平或趋势，k为资产增速向长期趋势的收敛速度，β为资产增速的波动性，标准维纳过程dW_t~N(0, t)。式(1) 的随机过程隐含：当资产增速低于长期水平时，大于零的漂移项(drift)将其向上拉升；当资产增速大于长期水平时，小于零的漂移项将其向下拉动，从而使之具有均值回复特征，这能体现资产增速的周期运动倾向。由Back (2010) 和Shreve(2010) 等可知，借款人资产增速的动态过程是：

这里，r_T表示T时点的资产增速，ΔT=T-t，且r_T服从期望u_r=E[r_T]=θ+(r_t-θ)e^-kΔT和方差$\sigma _r^2 = Var\left[ {{r_T}} \right] = \frac{{{\beta ^2}}}{{2k}}\left( {1 - {e^{ - 2k\Delta T}}} \right)$的正态分布。假设借款人在t和T时点的资产价值分别为V_t和V_T，则其在ΔT内的资产增速r_T=(V_T-V_t)/V_t，由泰勒级数展开可知：${\rm{Ln}}\left( {\frac{{{V_T}}}{{{V_t}}}} \right) = {\rm{Ln}}\left( {1 + {r_T}} \right) = {r_T} + \frac{{r_T^2}}{{2!}} + \cdots + \frac{{r_T^n}}{{n!}} + 0\left( {r_T^{n + 1}} \right)$，在r_T非足够小的情形下，可取二阶项逼近上式，则借款人资产价值的动态运动规律为：

基于式(2) 易证，r_T²服从如下的随机运动过程：

且r_T²~N(u_r²+σ_r², 4u_r²σ_r²)，则E[r_T+r_T²/2]=u_r+(u_r²+σ_r²)/2和Var[r_T+r_T²/2]=σ_r²(1+u_r)²。不妨令x=r_T+r_T²/2，由式(2) 和式(4) 知，它服从期望μ=u_r+(u_r²+σ_r²)/2和方差σ²=σ_r²(1+u_r)²的正态分布。设借款人T时点的待偿债务价值为D_T，将V_T=V_te^x代入违约概率PD_T=P(V_T＜D_T)有：

这里，Φ·表示标准正态累积分布函数，则借款人的动态违约损失率LGD_t为：^①

① 推导过程略，需要的读者可与作者联系。

单位贷款暴露在T时点的预期损失及其拨备要求LLP_T为：

其中，$LG{D_T} = P{D_T} - \frac{{{V_t}}}{{{D_T}}}{e^{\mu + \frac{{\sigma 2}}{2}}} \cdot \mathit{\Phi }\left( {\frac{{{\rm{Ln}}\left( {{D_T}/{V_t}} \right) - \left( {\mu + {\sigma ^2}} \right)}}{\sigma }} \right),P{D_T} = \mathit{\Phi }\left[ {\frac{{{\rm{Ln}}\left( {{D_T}/{V_t}} \right) - \mu }}{\sigma }} \right],$$\mu = {u_r} + \left( {u_r^2 + \sigma _r^2} \right)/2,{\sigma ^2} = \sigma _r^2{\left( {1 + {u_r}} \right)^2},{u_r} = \theta + \left( {{r_t} - \theta } \right){e^{ - k\Delta T}},\sigma _r^2 = \left( {{\beta ^2}/2k} \right)(1 - {e^{ - 2k\Delta T}})$。

(二)模型估计。给定当前信息集Ω_T0={r_t, t≤T₀}，结合式(5) 和式(6) 可知，借款人在未来T₀+i(i=1, 2, …, T)时点的违约概率PD_T0+i和违约损失率LGD_T0+i分别为：

我们需要基于当前信息集Ω_T0，估计借款人在下个周期内的{LLP_T0+i}(i=1, 2, …, T)，并将其平均趋势作为前瞻性LLP的参照基准，这里T表示资产增速的周期。为此，需要解决以下两个问题：① 识别资产增速的周期(有关内容请见第三部分)；② 估计借款人在下个周期内的{LLP_T0+i}(i=1, 2, …, T)及其平均趋势。

在估计{LLP_T0+i}(i=1, 2, …, T)时，需要估计或设定以下参数：① 基于资产增速的历史序列{r_t, t≤T₀}估计其特征参数θ、k和β，进而估算μ和σ²；② 设定T₀+i时点的待偿债务价值和当前资产价值的比例D_T0+i/V_T0。不妨设借款人在下个周期内的平均负债成本为y，则T₀时点贴现后的资产负债率α_i是：α_i=D_T0+ie^-yi/V_T0或D_T0+i/V_T0=α_ie^yi，这里，α_i表示借款人在T₀+i(i=1, 2, …, T)时点的目标杠杆(或预期杠杆)水平。因此，在给定信息集或参数集Ω_T0={r_T0, (θ, k, β), (α_i, y)}的条件下，可得如下公式：

其中，μ=u_r+(u_r²+σ_r²)/2，σ²=σ_r²(1+u_r)²，u_r=θ+(r_T0-θ)e^-ki，σ_r²=(β²/2k)(1-e^-2ki)，(i=1, 2, …, T)。特别地，当借款人在下个周期内的目标杠杆水平为常数α时，表示无论其未来T₀+i(i=1, 2, …, T)时点的待偿债务价值如何变化，贴现后的资产负债比率都保持了相对的稳定性，不妨称之为“目标资产负债率”或“目标杠杆”。

由式(10) 至式(12) 可知，μ和σ²是u_r和σ_r²的函数，而u_r和σ_r²是当前时点的资产增速r_T0，资产增速的特征参数θ、k、β，以及时间i((i=1, 2, …, T))的时变函数。在当前信息集{r_t, t≤T₀}下，当前时点的资产增速r_T0已知，且可基于{r_t, t≤T₀}估计资产增速的动态特征参数θ，k和β。也即，在设定(或估算)借款人T₀+i时点的目标杠杆和融资成本组合(α_i, y)的情形下，仅须基于其资产增速的历史序列{r_t, t≤T₀}就能估计μ和σ²，再将其代入式(10) 至式(12)，可得借款人在T₀+i时点的LLP要求。

资产增速的特征参数可根据{r_t, t≤T₀}估计。由式(2) 知，当时间下标T取t+1时有：${r_{t + 1}} = \theta \left( {1 - {e^{ - k}}} \right) + \left( {{e^{ - k}}} \right) \cdot {r_t} + \beta \int\limits_t^{t + 1} {{e^{ - k\left( {t + 1 - u} \right)}}} d{W_u}$，不妨令β₁=θ(1-e^-k)，β₂=e^-k和$\varepsilon = \beta \int\limits_t^{t + 1} {{e^{ - k\left( {t + 1 - u} \right)}}} d{W_u}$，易证σ_ε²=Var(ε)=(β²/2k)(1-e^-2k)，则其等价于r_t+1=β₁+β₂·r_t+ε_t，ε_t~N(0，σ_ε²)，基于参数关系体系β₁=θ(1-e^-k)，β₂=e^-k和σ_ε²=(β²/2k)(1-e^-2k)，获得$\hat k = - {\rm{Ln}}\left( {{{\hat \beta }_2}} \right),\hat \theta = \frac{{{{\hat \beta }_1}}}{{\left( {1 - {{\hat \beta }_2}} \right)}},\hat \beta = \sqrt {\frac{{ - 2\sigma _\varepsilon ^2{\rm{Ln}}\left( {{{\hat \beta }_2}} \right)}}{{1 - \hat \beta _2^2}}} $，以及μ和σ²的估计量，再将有关参数代入式(10) 至式(12)，将获得{LLP_T0+i}(i=1, 2, …, T)的估计。

本文将使用简单平均和加权平均两种方法估算{LLP_T0+i}(i=1, 2, …, T)的平均趋势：

这里，式(14) 是对{LLP_T0+i}(i=1, 2, …, T)的加权平均，且平滑参数λ∈(0, 1) 越趋向于1，近期数据的影响越大，不妨借鉴Risk-Metric对平滑参数的设定标准，假设λ为0.94。

模型还能敏感测试借款人的目标杠杆和融资成本组合对前瞻性LLP的影响。易证$\frac{{\partial LL{P_{{T_0} + i}}}}{{\partial {\alpha _i}}} > 0$和$\frac{{\partial LL{P_{{T_0} + i}}}}{{\partial y}} > 0$，^①表示“前瞻性LLP是借款人目标杠杆和融资成本的单增函数”，这隐含“若特定前瞻性准备水平理论映射的借款人目标杠杆和融资成本均高于其实际情况，则该前瞻性准备水平能够覆盖借款人的未来信用风险”。

① 证明过程略，需要的读者可与作者联系。

三、工业部门的信用风险与前瞻性拨备要求

模型实施前需要明确借款人的类型，这取决于管理诉求和数据支持等。从“自下而上”的风险管理视角来看，银行可基于单个借款人的资产负债状况，进行前瞻性的LLP管理，但其对微观主体资产负债表信息的要求较高，如资产增速的时间跨度要足够长，且具有明显的周期变动趋势等。从“自上而下”的风险管理视角来看，银行总部或监管当局关心的是“基于全社会或特定部门(行业)的资产负债状况及其演变趋势，对其未来信用风险及前瞻性拨备要求进行研判”。然而，并无社会各部门(如政府部门、居民部门、企业部门、金融部门)资产负债表的长期与可靠性统计。李扬等(2012a，2012b)曾编制了国家资产负债表，但其数据仅涵盖1996-2012年，马骏等(2012) 的情况与之相似。较短的数据期间、谨慎的数据推断、非一致接受的判定标准等，使之不适于估计有关部门资产增速的周期和动态特征，从而给前瞻性LLP管理提出了特殊挑战。

根据李扬等(2012a)的估计，中国全社会杠杆率已由1996年的113 %上升至2012年的215 %，且各部门杠杆率呈较快上升趋势。从分部门情况来看，企业部门的杠杆上升较快，杠杆水平最高，其杠杆水平及演变趋势对行业信用风险的前瞻性影响是被严重关切的问题。然而，并无企业部门资产负债表的长期和可靠的统计。我们对CSMAR、WIND、iFinD、CEIC和《中国工业经济数据库》等数据库的大范围检索发现“国有工业企业及非国有规模以上工业企业(简称‘工业部门’)”的资产负债表信息的时间跨度较长，其等距时间序列可追溯至1992年。鉴于工业企业在企业部门中的重要地位，以及数据可得性等，不妨以工业部门为例，审视其未来信用风险状况及前瞻性拨备要求。

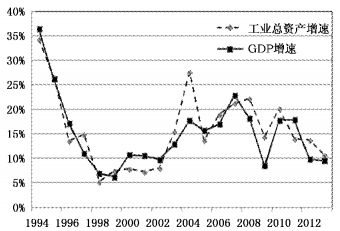
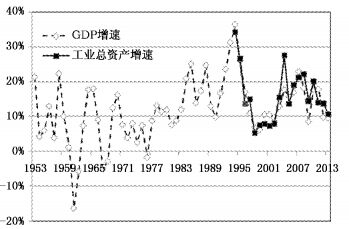
(一)周期识别。图 1报告了1993-2013年工业部门总资产增速和GDP增速的时序规律。工业部门的总资产增速有明显的周期性趋势，且与GDP增速保持了较强的同步性。从1953-2013年的更长时间维度来看，两者的运动趋势和周期特征似乎更加一致(见图 2)。也就是说，当工业部门总资产增速时序非足够长时(如未包含多个周期)，若周期识别方法无法显著估计其周期特征，则可从长时跨度的GDP增速中近似推断前者的周期特征。

图 1 工业部门总资产增速和GDP增速(1994-2013)

图选项

图 2 工业部门总资产增速和GDP增速(1953-2013)

图选项

由时间序列理论可知，当工业部门的总资产增速r_t服从AR(2) 过程r_t=cons_+φ₁r_t-1+φ₂r_t-2+e_t时，其自相关函数ρ_k将满足Yule-Walker方程ρ_k=φ₁ρ_k-1+φ₂ρ_k-2。当Yule-Walker方程的特征函数1-φ₁x+φ₂x²有复根时(如φ₁²+4φ₂＜0)，其k阶自相关函数${\rho _k} = {\left( {\sqrt { - \phi 2} } \right)^k}\frac{{sin\left( {\mathit{\Theta }k + \mathit{\Phi }} \right)}}{{sin{\rm{ }}(\mathit{\Phi })}}$，其中Θ和Φ是方程组$cos\left( \mathit{\Theta } \right) = \frac{{{\varphi _1}}}{{2\sqrt { - {\varphi _2}} }}$和$tan(\mathit{\Phi }) = \frac{{1 - {\varphi _2}}}{{1 + {\varphi _2}}}$的解。在复数特征根情形下，ρ_k是阻尼因子$\sqrt { - {\varphi _2}} $、频率Θ和项位Φ的正弦波动曲线，其中$T = 2\pi /\mathit{\Theta }(\mathit{\Theta } = arcos\left( {\frac{{{\varphi _1}}}{{2\sqrt { - {\varphi _2}} }}} \right))$是AR(2) 过程的准周期(Cryer和Chan, 2008)。基于上述周期识别方法，我们对1994-2013年工业部门总资产增速的AR(2) 的拟合表明，参数φ₁在10 %的显著性水平显著，但参数φ₂不显著，这可能与相对较短的数据区间有关(当原始序列未包括多个周期时，计量模型可能无法显著识别其周期特征)。鉴于工业部门总资产增速和GDP增速的运动规律和周期特征相似，不妨从更长时间维度的GDP增速中间接推断工业部门总资产增速的周期。我们对1953-2013年的GDP增速进行了AR(2) 拟合，发现参数φ₁和φ₂均显著，其周期T是8.74年；同理，对改革开放后(1979-2013年)GDP增速的AR(2) 拟合表明φ₁和φ₂均显著，且显著性水平有所上升，其周期T是8.21年。有鉴于此，下文将工业部门总资产增速的周期视为8年。

(二)前瞻性LLP估计。在对工业部门总资产增速时序进行1阶滞后的MLE估计后，能获得参数β₁、β₂和σ_ε²的估计值，再基于参数之间的关系体系，获得总资产增速的特征参数k，θ和β的估计(请见表 1)。表 1揭示：模型总体显著，且有关参数均在1 %的显著性水平下显著，其中工业部门总资产增速的长期水平为14 %，其95%的置信区间是(9%, 19%)；总资产增速的波动性为8%，其95%的置信区间是(6%, 10%)；总资产增速向长期趋势的修正速度为0.80，其95%的置信区间是(0.16, 1.43)。

在前述参数估计和当前(2013年)资产增速的基础上，可获得各目标杠杆和融资成本组合(α, y)，工业部门在下个周期内的动态违约概率PD_T0+i、违约损失率LGD_T0+i和贷款损失拨备LLP_T0+i(T₀=2013, i=1, …, 8) 的估计，以及工业部门负债的前瞻性拨备要求。

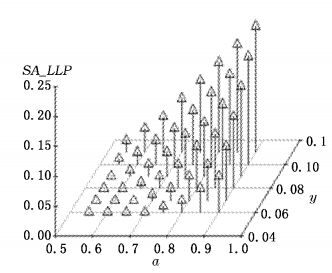
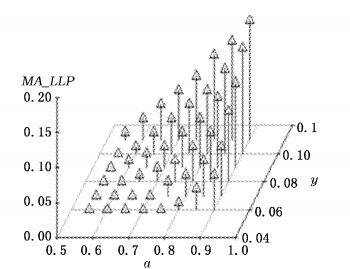
图 3和图 4给出了当工业部门的目标杠杆和融资成本分别在55 %-90 %(Step=5 %)和7 %-11 %(Step=1 %)区间变动时，其SA_LLP和MA_LLP的三维结构。显然，随着目标杠杆或融资成本的上升，工业部门的前瞻性LLP要求(包括SA_LLP或MA_LLP)均呈非线性上升趋势。融资成本和前瞻性LLP的单增关系表明，“融资贵”在提高银行名义收益的同时，亦提高了信贷组合的信用风险及其前瞻性拨备要求。问题是，工业部门实际的杠杆水平和融资成本如何呢？若掌握了这两方面信息，将能相对准确地推断其理论上的信用风险状况和前瞻性拨备要求。对工业部门2002-2013年资产负债率的统计表明，其均值和标准差分别是57.87 %和0.55 %，其95 %的置信区间是(57.58 %, 58.15 %)，部门杠杆在不同年度间的分布相当稳定，其年度取值介于55 %-60 %之间。然而，尚无估算工业部门融资成本的合理数据支撑和外部条件。从全社会最主要的资金获得途径——贷款的成本及其变动趋势中或能近似推断工业部门的总体负债成本状况。譬如，2008年第4季度-2013年第3季度的RMB贷款的加权平均利率约6.53 %，若按照季度新增贷款对有关利率进行加权，则2013年新增贷款的加权平均利率约为7 %，故保守推测工业部门的总体负债成本处于6 %-8 %。模型估计表明：当工业企业的目标杠杆和融资成本分别在55 %-60 %和6 %-8 %区间变动时，其前瞻性LLP要求将不超过0.06 %。也就是说，在目标杠杆相对稳定和当前融资成本约束下，工业部门理论上的信用风险及其前瞻性拨备要求处于较低水平，其当前负债成本并没有“贵”到危及行业实质性违约的程度。

图 3 (α, y)组合下的SA_LLP

图选项

图 4 (α, y)组合下的MA_LLP

图选项

(三)预期杠杆对前瞻性LLP的影响。前文在估计前瞻性LLP时，假设工业部门在下个周期内的资产负债水平保持了相对稳定性(或目标杠杆是常数)，似与社会各部门“加杠杆”的基本认知不一致。为了反映工业部门加杠杆的倾向，本节将对工业部门资产负债率的历史序列进行函数拟合，动态预测其在下个周期内的变动趋势，并将其视为相应时点的目标资产负债率。

基于工业各行业2000-2013年间的资产负债数据，我们根据《国民经济行业分类》(GB/T4754-2011) 的行业分类和编码规则，对各行业的资产和负债数据进行了合并汇总，并将其分成采矿业、制造业、电热水气的生产和供应业(包括电力、热力、燃气及水的生产和供应业)。分别对工业各行业的资产负债率进行了线性函数、指数函数、对数函数、多项式函数和幂函数的拟合，其中因变量是行业资产负债率，自变量是时间(当时间取2000-2013年时，自变量分别赋值1-14)。将各种函数均转换成线性模型，对各行业分别进行了上述函数形态的线性拟合，并根据其R²来研判模型的拟合优度(估计结果见表 2)。在五种常见的函数类型中，多项式函数的拟合效果最优，故据此动态预测工业各行业在下个周期内的目标资产负债率(当时间取2014-2021年时，自变量分别赋值15-22)。对工业部门而言，其资产负债率是关于时间的凹函数，且在下个周期内有上升趋势，但从子行业资产负债率的预测结果来看，存在明显的结构性背离。在工业部门内部，采矿业和电热水气业的资产负债水平呈上行趋势，但制造业的预期杠杆有下降态势(图略)。

在对工业各行业资产负债率进行如上预测后，若设其下个周期内的平均融资成本为7%(保守推测工业部门的总体负债成本处于6%-8%)，则可估计其未来的信用风险状况及前瞻性拨备要求(见表 3)。表 3揭示：当行业预期的杠杆水平趋于上升时，其信用风险和前瞻性拨备要求均相应提高。对工业部门而言，动态预测的杠杆水平对前瞻性LLP几乎没有“总体性”影响，但从分行业情况来看，电热水气业的前瞻性风险偏高，其移动平均和简单平均的前瞻性LLP分别高达4.21%和5.56%，而制造业的前瞻性风险较低。由此可见，工业部门的“总体性”信用风险和前瞻性拨备要求处于较低水平，但存在不容忽视的“结构性”风险，对电热(准)公益性行业和资源开采型工业而言，预期杠杆的较快上升，可能显著放大了其未来信用风险和前瞻性拨备要求。

四、模型应用

(一)监管规定的前瞻性准备成分及其适度性。从2002年开始，央行要求商业银行在贷款分类的基础上，进行贷款损失确认和拨备计提。《贷款损失准备计提指引》(银发〔2002〕98号)规定“商业银行应在贷款风险分类的基础上，合理估计贷款可能发生的损失，及时计提一般准备和专项准备”。银发〔2002〕98号文规定“一般准备年末余额不低于年末贷款余额的1 %”，“商业银行可参照以下比例按季计提专项准备：对于关注类贷款，计提比例为2 %；对于次级类贷款，计提比例为25 %；对于可疑类贷款，计提比例为50 %；对于损失类贷款，计提比例为100 %”。由于LLP的非自由裁量成分用于覆盖组合未来的预期损失，它是针对未实现风险或损失计提的准备，故与一般准备相当。在对信贷资产进行五级分类的情形下，正常类贷款和关注类贷款属于尚未形成风险或损失的资产，银行须为之计提一般准备，其与前瞻性准备成分相当。

然而，在2013年之前，监管当局只公布银行体系的不良贷款总量与结构，以及行业的总体损失拨备状况，我们无法获悉正常类贷款和关注类贷款的结构性信息，从而难以核算银行体系的一般准备计提要求(或监管规定的前瞻性准备成分)。自2014年开始，银监会开始披露银行体系贷款的五级分类情况。如截止2014年3月末，银行体系的正常类贷款和关注类贷款分别是599 670亿和15 553亿，则正常贷款为630 776亿，按监管规定计提的一般准备是6 307.76亿，一般准备占正常贷款的比例是1.03 %。同理，可分别计算2014年第二季末和第三季末的一般准备占正常贷款的比例，该指标值均为1.03 %。

当工业企业的目标杠杆和融资成本分别在55 %-80 %(Step=5 %)和6 %-10 %(Step=1 %)区间变动时，1.03 %的前瞻性LLP水平理论映射的借款人目标杠杆和融资成本组合(α_i, y)状况详见表 4。譬如，若借款人的融资成本为6 %，唯当目标杠杆在75 %-80 %的区间变动时，其前瞻性LLP要求将介于0.42 %-1.36 %(1.03 %∈0.42 %, 1.36 %)；若借款人的融资成本为7 %，唯当目标杠杆在70 %-75 %的区间变动时，其前瞻性LLP要求将介于0.50 %-1.52 %(1.03 %∈0.50 %, 1.52 %)；……；若借款人的融资成本为10 %，唯当目标杠杆在55 %-60 %的区间内变动时，其前瞻性LLP要求将介于0.43 %-1.49 %(1.03 %∈0.43 %, 1.49 %)。因此，银发〔2002〕98号文规定的前瞻性准备理论映射的目标杠杆和融资成本均高于工业部门可能所处的区间(α_i∈55 %, 60 %且y∈6 %, 8 %)，这隐含“监管所规定的前瞻性准备能够满足工业部门信用风险的管理需要”。

表 4 监管规定的前瞻性准备成分映射的目标杠杆和融资成本组合状况

	MA_LLP					SA_LLP
αi\y	6%	7%	8%	9%	10%	6%	7%	8%	9%	10%
0.55				0.05%	0.43%				0.07%	0.59%
0.60				0.51%	1.49%				0.69%	2.02%
0.65			0.53%	1.59%				0.72%	2.14%
0.70		0.50%	1.59%				0.67%	2.14%
0.75	0.42%	1.52%				0.57%	2.03%
0.80	1.36%					1.81%

表选项

(二)银行体系实提的前瞻性准备成分及其适度性。面对2008年金融危机的冲击，银行业金融机构积极响应政府号召，进行了大规模快速的信贷投放，消耗了行业大量的资本基础。在综合考量行业信贷增速、风险演变和宏观经济金融形势等因素后，银监会适时提出了逆周期的宏观审慎监管思路，主张对LLP进行前瞻性管理，并相机提高了银行体系的总体拨备要求。《关于加强当前重点风险防范工作的通知》(银监发〔2010〕98号)要求“商业银行贷款损失准备金占贷款余额的比例原则上不低于2.5%，贷款损失准备金占不良贷款的比例原则上不低于150%，且两者按孰高要求执行，该计划于2011年施行，其中系统重要性银行须在2012年底达标，非系统重要性银行于2016年达标”。银监发〔2010〕98号文中的“拨贷比”相当于商业银行的总准备要求，它是银行体系当前存量贷款损失准备的管控底线。鉴于监管当局未曾披露银行体系的一般准备情况，不妨基于银发〔2002〕98号文的规定，近似估算银行体系专项准备的计提状况(专项准备=次级类贷款×25%+可疑类贷款×50%+损失类贷款×100%)，再将其从总准备中扣减，即可获得银行体系一般准备(或银行体系实提的前瞻性准备成分)的近似估计(见表 5)。

表 5的测算表明：截止2013年末，银行体系实提的前瞻性准备占贷款余额的比例约为2.37%，其理论映射的借款人目标杠杆和融资成本组合状况见表 6，它们均高于工业部门可能所处的区间(α_i∈55%, 60%且y∈6%, 8%)，这意味着“银行体系实提的前瞻性准备能够满足工业部门信用风险的管理需要”。

表 6 银行体系实提的前瞻性准备映射的目标杠杆和融资成本组合状况

	MA_LLP						SA_LLP
αi\y	6%	7%	8%	9%	10%	11%	6%	7%	8%	9%	10%	11%
0.55						1.32%						1.79%
0.60					1.49%	2.85%					2.02%	3.81%
0.65				1.59%	3.04%					2.14%	4.05%
0.70			1.59%	3.14%					2.14%	4.16%
0.75		1.52%	3.14%					2.03%	4.14%
0.80	1.36%	3.03%					1.81%	3.99%
0.85	2.84%						3.72%

表选项

五、结语

(一)主要结论与启示。本文在对借款人的资产增速进行均值回复随机过程刻画后，基于资产价值和资产增速之间的近似函数关系，间接推导了借款人资产价值的分布规律，并在结构化模型框架内给出了其信用风险要素及其前瞻性拨备要求的计算公式。与结构化信用风险模型的常见处理方法不同，本文将借款人的资产增速作为理论建模的出发点，因其周期性特征与前瞻LLP的管理理念相契合，其平稳性特征有助于模型的经验估计与推广。

本文还以工业部门为例，近似识别了其资产增速的周期特征，估计了其动态特征参数、信用风险要素和前瞻性拨备要求。研究表明，当工业部门的目标杠杆和融资成本分别在55 %-60 %和6 %-8 %区间变动时(此属工业部门可能所处的区间)，其前瞻性LLP要求将不超过0.06 %。也就是说，在目标杠杆相对稳定和当前融资成本约束下，工业部门理论上的信用风险及其前瞻性拨备要求处于较低水平，其当前负债成本并未“贵”到危及行业实质性违约的程度。尽管工业部门的“总体性”信用风险较低，但存在明显的“结构性”差异，对电热(准)公益性行业和资源开采型行业而言，预期杠杆的较快上升可能显著放大其未来信用风险及前瞻性拨备要求。

本文为LLP管理的适度性提供了研判视角。模型推导表明，前瞻性LLP是借款人的目标杠杆及其融资成本的单增函数，这意味着“若监管规定的前瞻性准备成分(或银行体系实提的前瞻性准备成分)理论映射的借款人目标杠杆和融资成本均高于其实际情况，则相关准备要求能够覆盖借款人的未来信用风险或满足工业部门前瞻性信用风险的管理需要”。基于银发〔2002〕98号文和银监发〔2010〕98号文的规定，我们分别估算了监管规定的前瞻性准备成分和银行体系实提的前瞻性准备成分，发现这两种前瞻性准备成分理论映射的借款人目标杠杆和融资成本组合均高于工业部门可能所处的区间，表明其能够满足工业部门前瞻性信用风险的管理需要。

(二)有待思考的问题。若有各部门或行业在较长时期内的资产负债表数据，将能前瞻性地估计其未来信用风险和拨备要求，这种精细化的LLP管理不仅更加逼近现实，还能满足银行微观风险定价的需要。有必要强调的是，本文是在当前有限信息集约束下，对借款人在下个周期内的信用风险要素及其LLP要求进行了动态推演和估计，但理论上来讲，随着预测时期的推延，其不确定性可能增强。若在信贷风险评估和LLP管理时，考虑了太长时期内的不确定预期，可能会模糊LLP管理和资本管理(或预期损失和非预期损失)的数量边界(Banque de France, 2001;许友传, 2011)。给定LLP管理和资本管理之间的紧密关系，稳健的LLP管理应被视为资本监管的组成(Banque de France, 2001; Cavallo和Majnoni, 2001)，若考虑了信用风险在太长时间维度内的不确定预期，可能将部分资本缓冲调整到LLP之中，这是理论建模时有待思考的问题。另外，本文在结构化模型框架内刻画了借款人的信用风险要素及其前瞻性拨备要求，该风险测度取决于资产对债务的总体覆盖能力，仅刻画了借款人的总体信用风险状况，不能考虑债务结构的优先清偿顺序对信用风险的可能影响，以及流动性管理不当可能引致的“结构性”偿付风险。