文章信息
 | 财经研究 2017年43卷第6期 |
- 石晓军, 闫竹.
- Shi Xiaojun, Yan Zhu.
- 城镇化一定能促进寿险业发展吗?——基于人类发展指数的异质性分析
- Must urbanization promote the development of life insurance industry? heterogeneity analysis based on human development index
- 财经研究, 2017, 43(6): 105-117
- Journal of Finance and Economics, 2017, 43(6): 105-117.
-
文章历史
- 收稿日期:2017-01-20

2017第43卷第6期
一、 引言
城镇化会对一国寿险业发展产生重大影响。城镇化一方面会带来交易成本的降低、资源、人才和产业的聚集等多种效应,促进经济的发展;另一方面也会使城镇人口暴露于更大的健康与生命风险之中:传染性疾病更容易爆发;因污染、高强度工作导致慢性疾病患病率增加;因人口高密度导致的暴力、犯罪和交通事故风险造成的人身伤亡。城镇化也会增强人们对人力资本的保护意识。随着城镇化带来的收入增长,人们的支付能力也会相应地提高。在与人力资本风险抵御相关的金融服务中,寿险是对冲人力资本风险(特别是死亡风险)的基础性金融工具(Campbell, 1980;Pliska和Ye, 2006)。故而,研究城镇化对寿险需求的影响是一个基础性问题,对正处于城镇化进程中的发展中国家来说具有现实意义。
然而,文献中关于城镇化影响寿险需求的证据并不一致。一些文献认为城镇化能够提高寿险需求。Zelizer(1978) 认为,大规模城市化是19世纪中期美国寿险业繁荣发展的重要原因。城市化带来了家庭结构、功能的深刻变化,减少了对社会网络等非正式风险分担机制的依赖。这样,城市家庭需要用正式的风险保障机制来替代原来的非正式风险保障网,因而对寿险这类正式风险保障就会产生相应的需求。Outreville(1996) 发现,在发展中国家,农业人口占比的减少可以促进人均寿险保费收入的提高,原因是农业面临气候等自然条件与农产品价格波动的双重风险,收入的高不确定性大大降低了家庭对寿险的需求。Huang和Gao(2003) 基于中国这一新兴经济体的研究发现城镇化与寿险增长显著正相关,认为城镇化过程中子女数量的减少使得父母需要为退休自我积蓄。近年来,以中国城镇化为背景的中文文献比较一致地认为中国的城镇化促进了寿险业的发展(如徐志峰、温剑波,2013;杜菲,2013;杨汇潮、江生忠,2014;臧志谊等,2015;许闲等,2016)。
一些文献也给出了城镇化不能促进寿险需求的证据。Beck和Webb(2003) 检验了68个国家寿险消费的影响因素,发现城镇化水平与寿险需求之间并没有显著的正向关系。Sen(2008) 对亚洲12个经济体的寿险市场进行了分析,发现城镇化水平虽然显著解释了国家间的寿险深度、寿险密度的差异,但发现城镇化减少了寿险需求。可能的解释是,在这些亚洲经济体中,劳动力的城乡转移反而使得城市中贫困人口占比提高了。
本文认为,文献中关于城镇化是否促进寿险需求的证据之所以存在矛盾,是因为并没有对城镇化模式做出区分。本文区别于以往文献的主要理论贡献是,对全球不同国家的城镇化进行异质性处理,而不是将其视为全球统一的同质过程。具体方法上,采用联合国人类发展指数(Human Development Index, HDI)作为度量人的发展的综合指标,以是否能够促进HDI的提高为标准,将各国的城镇化分为两类:一是提供配套设施等的Ⅰ型城镇化,这类城镇化能够有效配套教育与培训、医疗、就业、保障等基础设施,从而有助于促进人的发展;二是仅转移人口而无配套设施等的Ⅱ型城镇化,此类城镇化模式不能有效促进人的发展。在上述分类基础上,本文扩展了Campbell(1980) 的经典寿险需求模型,将不同类型城镇化对人力资本积累的影响纳入分析框架,给出本文的核心可检验假设,即只有Ⅰ型城镇化才能促进寿险业需求。
本文研究发现,(1) 城镇化总体上提升了寿险深度,在全球水平上城镇化对寿险深度的促进作用为2.3%。(2) 验证两类城镇化对寿险业发展的不同影响,发现Ⅰ型城镇化对寿险深度的提高作用比Ⅱ型城镇化高出31.2%,而Ⅱ型城镇化并不能促进寿险需求。(3) 中介机制检验进一步表明,城镇化作用于寿险业发展的经济学机理,是通过促进人力资本积累,提高了人力资本风险保障的需求。(4) 发挥城镇化对寿险的促进作用存在最佳时机,即寿险业在城镇化过程的增长呈现S形规律,存在一个加速发展的黄金阶段。
本文的主要贡献有两点。首先,在概念上,首次提出了用人类发展指数将城镇化分为Ⅰ型和Ⅱ型的方法。这有助于实现“促进人的发展”的城镇化、“钢筋水泥”的城镇化等抽象概念的可操作化,使得“促进人的发展”的城镇化由一个抽象的概念变得可度量,为相关的实证研究提供一个新的思路。其次,在方法上,首次针对寿险业发展特点构造了高次模型,用以刻画寿险业在城镇化高速进程中加速发展的轨迹,从而突破了以往文献采用简单线性模型的设定不能体现寿险业发展阶段性规律的局限性;体现了作为现代服务业的寿险业的“双平台”特点,是对寿险业与经济发展之间关系的文献的一个贡献,为寿险业发展的政策制定提供了理论依据,尤其是对发展中国家寿险业发展具有重要的政策启示。
二、 理论模型与检验假设
以往的文献对城镇化模式的分类,总体上可以归纳为伴随和未伴随经济增长的城镇化,学者们对这一区别提供了多方面解释,内容包括公共部门管理能力、民生保障体系、城市人口结构等,这些涉及城市建设和发展的因素都直接影响着“人”的城镇化的质量。据此,我们将世界范围内的城镇化主要分成两类。Ⅱ型城镇化仅仅将人口转移到城镇,但教育与培训、医疗、就业、保障等配套机制没有得到相应的发展,是一种“钢筋水泥”的城镇化,对人的发展、人力资本水平提升并无显著作用,反而会使一部分贫困人口愈加贫困。与此形成对比的是以“促进人的发展”为目标的Ⅰ型城镇化,这类城镇化会按照规划稳定地提供促进人的发展的配套设施,能够促进人力资本水平的快速提高。
Ⅰ型、Ⅱ型城镇化对人力资本的累积和价值形成的影响是不同的,故而人力资本存量可以看成是城镇化的函数。我们将寿险看成是人力资本的保障机制。沿着这一逻辑链条,容易推知Ⅰ型、Ⅱ型城镇化对寿险业发展的影响也是不同的。从人力资本作为城镇化的函数这个基点出发,通过扩展Campbell(1980) 的经典寿险保险需求模型,来探讨不同类型的城镇化对寿险需求的影响。Campbell(1980) 从人力资本不确定性角度对人寿保险的经济功能和需求进行了研究。对众多初始资本水平并不高的家庭及个人来说,人力资本的未来不确定性相比于资本收入更受重视,而人寿保险则是对人力资本收入的未来不确定进行规避的机制安排。Campbell(1980) 设定的家庭效用是消费效用V[]与遗产动机效用B[]之和,在最大化家庭效用的基础上选择最优的寿险保障水平有:
| $ \begin{array}{l} \mathop {{\rm{Max}}}\limits_{{\rm{INS}}} \left[{1-{q_x}\Delta t} \right]V\left[{{W_x}{ + _R}{H_x}-\left( {INS} \right){q_x}\left( {1 + \lambda } \right)\Delta t} \right]\\ + \left[{{q_x}\Delta t} \right]B\left\{ {{W_x} + \left( {INS} \right)\left[{1-{q_x}\left( {1 + \lambda } \right)\Delta t} \right]} \right\} \end{array} $ | (1) |
其中:qx为x岁的人在下一时段的即时死亡概率;Δt为时间区间;V[]是家庭消费效用;Wx为家庭财富水平;RHx为未来人力资本价值折现值;INS是寿险需求水平;λ是保费的附加费率。须注意,如前所述,人力资本价值的积累受城镇化的影响,因而是城镇化Ur的函数:
| $ _R{H_x} = F\left( {{U_r}} \right) $ | (2) |
其中:Ur为城镇化水平,F(·)为函数形式。F(Ur)的增减性根据城镇化对人的发展的影响确定:若城镇化促进了人的发展,F(Ur)为递增函数;反之为递减函数(与实证结果一致)。
Campbell(1980) 通过对Wx+RHx泰勒级数展开,并对保险需求求解一阶导数,得出最优保险水平INS为:
| $ INS{ = _R}{H_x}- \left( {1 + \lambda- k} \right)/kR\left[{{W_x}{ + _R}{H_x}} \right] $ | (3) |
将式(2) 代入式(3) 中,包含城镇化影响的人寿保险需求为:
| $ INS = F\left( {{U_r}} \right) + \left[{\left( {1 + \lambda-k} \right)/k} \right]\left[{1/A\left( {F\left( {{U_r}} \right)} \right)} \right] $ | (4) |
其中:A(F(Ur))=-V″(Wx+F(Ur))/V′(Wx+F(Ur))×[(Wx+F(Ur))]表示财富水平为Wx+F(Ur)时的Pratt-Arrow相对风险厌恶程度;k=B/V是遗产动机强度系数,值域[0, 1],k值越大,表示经济个体的遗产动机越强。
式(4) 表明,在给定其他参数不变时,城镇化对寿险业的影响取决于A(F(Ur))和F(Ur)的分布状况。基于一般情形,假定经济个体是绝对风险厌恶不变型(CARA)或绝对风险厌恶递减型(DARA)。Ⅰ型城镇化意味着DARA的F′(Ur)>0、A′(F(Ur)) < 0,CARA的F′(Ur)>0、A′(F(Ur))=0,从而INS′(Ur)>0。因此Ⅰ型城镇化能够激发寿险业需求。相反,在Ⅱ型城镇化中,DARA的F′(Ur)≤0、A′(F(Ur))≥0,CARA的F′(Ur)≤0、A′(F(Ur))=0,从而INS′(Ur)≤0,Ⅱ型城镇化不能带动寿险需求。
基于以上理论模型的分析得到本文的核心检验假设如下所示。
H: Ⅰ型城镇化(“促进人的发展”的城镇化)对寿险业的发展具有促进作用,而Ⅱ型城镇化(“钢筋水泥”式城镇化)对寿险业的发展没有促进作用。
三、 实证模型
(一)实证模型设定。第一步,首先区分两种城镇化。建模的思路是用一个国家“人的发展”对城镇化回归。为减少可能的反向因果关系影响,本文采用工具变量的两阶段最小二乘法进行估计,模型设定如下:
| $ HD{I_i} = {a_i} + {b_i}UR{B_i} + {c_i}CTR{L_i} + {\varepsilon _i} $ | (5) |
| $ UR{B_i} = {\beta _{i1}} + {\beta _{i2}}UR{B_{i\left( {-1} \right)}} + {\beta _{i3}}FO{R_i} + {\beta _{i4}}LAN{D_i} + {\zeta _i} $ | (6) |
其中:HDIi是第i个国家各年的人类发展指数,作为各个国家“人的发展”程度的衡量指标;URBi是第i个国家各年的城镇化水平;CTRLi是控制变量,选取各国医疗支出水平;①URBi(-1)是第i个国家城镇化水平的滞后一期;FORi表示森林面积;LANDi是土地面积;ai、bi、ci和βi·均为待估计系数。式(5) 和式(6) 是分国家估计,并未使用固定效应。
① 按照Ranis等(2000),经济发展中公共教育、医疗支出等因素会显著促进人类发展。为避免共线性而过多地损失样本国家,本文没有将GDP作为独立变量加入式(5) 中。
本文将城镇化水平滞后一期、森林面积和土地面积作为城镇化变量的工具变量,以减少可能的反向因果关系的影响。上一期城镇化水平可能影响当期人的发展,但当年人的发展不可能对去年的城镇化产生作用;城镇化进程一般具有连续性,Gallup等(1999) 的实证结果表明以前的人口聚集密度与当期的城镇化水平显著正相关;因此城镇化滞后期是当期城镇化水平的强有效工具变量。Gallup等(1999) 也指出,地理因素如地理位置、气候条件等是影响经济增长和人口聚集的重要因素,其中稻米种植面积、适耕土地显著促进人口聚集,而沙漠、极地区域等因素与人口聚集显著负相关。Kumar和Kober(2012) 在探讨城镇化对全要素生产率的影响时,也采用了多种地理位置指标作为城镇化水平的工具变量。本文沿用他们的思想,选取土地面积、森林面积作为工具变量。这两者是完全外生给定的自然、地理属性,对人的发展的直接作用并不明显;作为地理特征,它们也会通过影响人口的聚集,对城镇化进程产生重要影响。根据式(5),对不同国家的城镇化与人的发展之间的关系进行检验,如果两者之间有显著正向关系,则归为Ⅰ型城镇化;否则,就是Ⅱ型城镇化。
现有研究寿险业增长影响因素的文献,对回归模型的设定没有考虑服务业发展的阶段性特点。根据Eichengreen和Gupta(2013) 对经济增长和服务业发展关系的研究,服务业的发展具有两阶段特点:在第一阶段,人均收入较低时,服务业减速增长;在人均收入较高的第二阶段,服务业加速增长。传统服务业的经济份额随经济增长不断降低,混合型服务业的经济份额减速增长,而现代服务业的发展趋势呈加速增长。
保险业是现代服务业的重要组成部分,需要考虑寿险业增长的特点,经济增长与寿险业发展不是简单的线性关系。本文检验核心假设的高次模型具有两个特点:一是基于Eichengreen和Gupta(2013) 的服务业四次方程式模型,可以对寿险业的发展规律进行分析;二是采用对比分析,可以清晰地比较两类不同城镇化对寿险业的影响。基本实证模型如式(7):
| $ \begin{array}{l} INS{U_{it}} = {\alpha _0} + {\alpha _1}GDPP{C_{it}} + {\alpha _2}GDPPC_{it}^2 + {\alpha _3}GDPPC_{it}^3 + {\alpha _4}GDPPC_{it}^4\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; + {\alpha _5}UR{B_{it}} + {\alpha _6}{D_i} + {\alpha _7}UR{B_{it}}{D_i} + \sum\limits_{j = 8}^k {{\alpha _j}Contro{l_{it}}} + {\xi _{it}} \end{array} $ | (7) |
其中:INSUit是第i个国家在第t年的寿险保费深度;GDPPCit表示人均GDP对数,GDPPCitn表示人均GDP的高次阶;URBit是城市人口占比,代表各国城镇化水平。Di是根据式(5) 和式(7) 确定的虚拟变量:Di=1,代表Ⅰ型城镇化国家;Di=0,代表Ⅱ型城镇化国家。URBitDi交叉项用来衡量Ⅰ型城镇化的影响。Controlit表示其他控制变量。如果假设成立,那么交叉项URBitDi的系数α7应该显著为正,这意味着在控制其他因素后,Ⅰ型城镇化能够显著促进寿险业发展。如果系数α5不显著或为显著的负数,则Ⅱ型城镇化对寿险业发展没有促进作用。这一对比能够检验城镇化与寿险业发展的因果关系。
我们对式(7) 的内生性问题进行了一定处理。首先,在城市经济学国际主流文献中,早期城市的兴起和发展得益于工业化和经济聚集效应,而城镇化是驱动第三产业发展的重要动因,罕有文献讨论保险业发展对城镇化进程的影响。其次,本文对式(7) 的估计包含了固定效应,用以控制个体不随时间变化的遗漏变量可能引起的内生性。本文也根据以往文献在模型中加入了控制变量,尽量缓解由随时间变化变量引发的内生性问题。最后,我们使用OLS及差分GMM检验,对城镇化与寿险业可能存在的反向关系进行了检验。就本文国家层面的样本而言,寿险业对城镇化进程的推动作用并不明显。
(二)变量设计。
1.寿险业发展、城镇化测量。以往学者较多使用保险深度和保险密度分析保险业发展。保险深度(保费收入/GDP)强调经济发展中保险行业的重要性,保险密度(保费收入/人口数量)强调一个国家人均保费支出水平。相对于经济发展的行业发展指标更加直观,保险深度指标更适合于分析寿险业发展规律,沿用Enz(2000)、Beck和Webb(2003) 以及Sen(2008) 的实证研究,本文采用保险深度指标。需要指出的是,人口城镇化本质上是一种发展型的城镇化,而不是成熟的城市体系形成之后的高级形态的城镇化。本文采用城镇化人口占总人口的比例衡量城镇化水平,这一指标沿用Beck和Webb(2003)、Huang和Gao(2003) 以及Sen(2008) 的设定。
2.人的发展的衡量。本文将“人的发展”定义为人们经济、教育及健康状况的改善。人的发展衡量指标来源于联合国开发计划署发布的人类发展指数HDI。2010年以前,HDI是根据收入、教育和健康这三个子指标的算术平均计算而来。UNDP在2010年修正了部分子指标的构成因素,并将算术平均改为几何平均。本文采用的HDI数据来源于UNDP公布的更新过的数据,因此数据一致性得以保证。
上述人类发展衡量指标或许有局限性。根据Pinar等(2013),UNDP公布的HDI指标的构造没有考虑其子指标不同构成因素之间的依赖性,而且,算术平均赋予三个子指标同等的权重,这与人类发展不同维度的隐含权重不一致。Pinar等(2013) 采用随机占优方法计算出最佳权重,教育指标应被赋予最大的权重即0.7117,而GDP指标和预期寿命指标的随机占优权重分别为0.1645和0.1238。本文采用Pinar等(2013) 对HDI指标的修正计算作为稳健性检验数据。子指标的构成因子数据都来源于UNDP网站。
3.控制变量。除经济因素(本文选取2005年美元不变价人均GDP对数表示)之外,人口、社会文化、制度和结构等因素也会对寿险增长产生影响。Lewis(1989) 从生命效用最大化角度,证实了被保险人的其他家庭成员对寿险的需求,被保险人的家庭人口结构是寿险需求的重要影响因素。Truett和Truett(1990)、Browne和Kim(1993) 显示抚养率和寿险需求具有显著正向关系。本文选取人口增长率(PG)、少儿抚养率(YDR)、老人抚养率(ODR)作为人口因素控制变量。以往文献显示,期望寿命(LE)和婴儿死亡率(IMR)也影响寿险需求。社会/文化因素中具有代表性的是教育,本文依据Beck和Webb(2003) 的方法,用高等教育入学率(TER)作为控制变量。Outreville(1996)、Beck和Webb(2003) 都证实了金融发展和寿险市场的正向关系。本文依据Qutreville(1996) 的做法,采用(M2/GDP)作为金融发展深度(FD)的代理变量。
(三)样本选择说明。本文样本包括1990-2012年151个国家的数据,数据来源于World Bank数据库和UNDP数据库。为保证数据的一致性,本文根据以下原则进行筛选:(1) 以UNDP数据库中有HDI数据的国家为基准,剔除World Development Indicators(WDI)数据库中没有HDI数据的国家,然后进一步去除样本中没有城镇化或寿险深度数据的国家;(2) 从UNDP数据库中可以获得的HDI数据只有8年,因此对模型(5)、(6) 进行回归时,仅采用2005-2012年间的数据。World Bank的Global Financial Development(GFD)数据库中只包含1990年之后各个国家的寿险保费深度数据,因此本文模型(7) 的回归样本期间为1990-2012年。表 1给出了本文主要变量的描述性统计和数据来源。
| 变量 | 观测数量 | 均值 | 标准差 | 最小值 | 最大值 | 数据来源 | |
| 全样本 | INSU(%) | 2 496 | 1.357 | 2.109 | 0 | 15.784 | Global Financial Development |
| HDI | 1 189 | 0.671 | 0.177 | 0.258 | 0.955 | United Nations Development Program | |
| D | 3 473 | 0.861 | 0.346 | 0 | 1 | 作者计算 | |
| URB(%) | 3 473 | 54.476 | 23.092 | 5.416 | 98.891 | World Development Indicators | |
| GDPPC(ln化) | 3 362 | 8.022 | 1.631 | 4.717 | 11.382 | ||
| PG(%) | 3 464 | 1.528 | 1.583 | -7.597 | 17.483 | ||
| ODR(%) | 3 447 | 11.436 | 7.013 | 0.390 | 39.043 | ||
| YDR(%) | 3 447 | 53.676 | 23.837 | 15.495 | 115.042 | ||
| LE(年) | 3 435 | 67.337 | 10.306 | 26.764 | 83.096 | ||
| IMR(‰) | 3 473 | 37.091 | 34.419 | 1.700 | 158.100 | ||
| TER(%) | 2 349 | 29.565 | 23.939 | 0 | 101.759 | ||
| FD(%) | 3 211 | 57.325 | 54.543 | 0.831 | 669.880 | ||
| 中低收入国家子样本 | INSU(%) | 1 556 | 0.699 | 1.579 | 0 | 15.784 | Global Financial Development |
| HDI | 776 | 0.577 | 0.144 | 0.258 | 0.793 | United Nations Development Program | |
| D | 2 277 | 0.919 | 0.273 | 0 | 1 | 作者计算 | |
| URB(%) | 2 277 | 44.309 | 19.177 | 5.416 | 87.360 | World Development Indicators | |
| GDPPC(ln化) | 2 195 | 7.068 | 1.060 | 4.717 | 9.080 | ||
| PG(%) | 2 275 | 1.760 | 1.273 | -7.597 | 11.181 | ||
| ODR(%) | 2 254 | 8.215 | 3.884 | 3.976 | 28.012 | ||
| YDR(%) | 2 254 | 64.810 | 20.893 | 19.278 | 115.042 | ||
| LE(年) | 2 249 | 62.997 | 9.655 | 26.764 | 79.846 | ||
| IMR(‰) | 2 277 | 51.212 | 33.646 | 4 | 158.100 | ||
| TER(%) | 1 395 | 17.649 | 16.397 | 0 | 91.452 | ||
| FD(%) | 2 139 | 43.894 | 31.262 | 0.831 | 247.824 | ||
四、 实证分析
(一)模型设定检验。
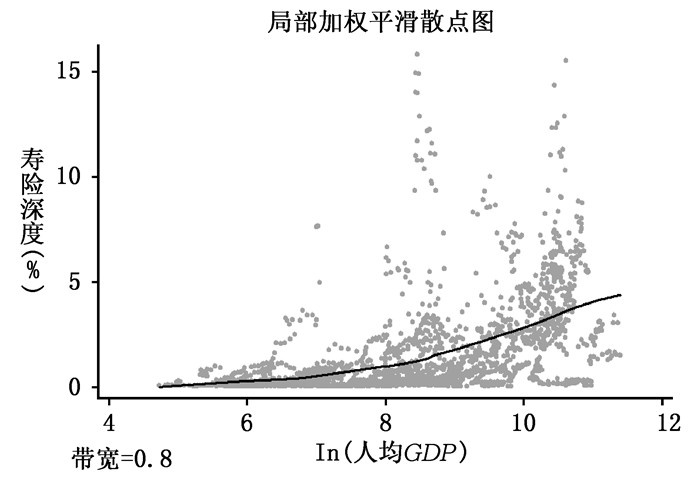
1.寿险业两阶段特点图解。Eichengreen和Gupta(2013) 采用四次模型拟合经济增长和服务业发展关系,经过实证检验发现服务业发展具有两阶段特点。寿险业是典型的现代服务业,需要考虑寿险业增长是否也具有两阶段的特点。从人均GDP对数与寿险深度的散点关系图(图 1)可以看出,经济增长与寿险深度之间是非线性相关的,有一定程度的高阶关系,以往文献中采用的简单线性模型可能并不能准确展现寿险业发展的特点。因此本文沿用Eichengreen和Gupta(2013) 的方法,对寿险增长的设定采用四次模型。
|
| 图 1 人均GDP对数与寿险深度关系 |
2.工具变量检验。模型(5)、(6) 的估计使用了工具变量,有必要对工具变量URBi(-1)、FORi、LANDi的有效性进行检验(表 2第[2]和第[5]列)。工具变量不可识别检验(K-P秩Wald LM统计量)显示可以在1%显著水平上拒绝原假设,工具变量与内生变量相关;弱工具变量检验(K-P秩Wald F统计量)表明工具变量与内生性变量有较强的相关性;被解释变量为调整HDI的过度识别检验(Hansen J统计量)显示P值显著大于10%,不能拒绝原假设,说明工具变量与扰动项无关,为外生工具变量。由于被解释变量为HDI的Hansen检验显示工具变量并非严格外生,因此本文根据Conley等(2012) 提出的UCI方法重新进行了两阶段最小二乘估计。根据Conley等(2012) 的思想,如果工具变量完全外生,那么在原模型(OLS)中加入工具变量作为控制变量,则该控制变量的系数γ严格为零;如果不严格为零,说明该工具变量具有一定内生性。根据OLS回归的系数设定工具变量的内生程度,假定URBi(-1)、FORi和LANDi取值区间分别为[-0.05,0]、[0, 0]和[0, 0],在95%置信水平下的置信区间如表 2第[3]和[6]列所示。OLS、2SLS和UCI的估计结果具有一致性,内生变量URB的OLS、2SLS的回归系数均位于置信区间内。
| 解释变量 | 原HDI | 调整HDI | ||||
| OLS[1] | 2SLS[2] | UCI[3] | OLS[4] | 2SLS[5] | UCI[6] | |
| URB | 0.030*** [7.03] |
0.006*** [35.93] |
[0.005, 0.056] | 0.022*** [4.22] |
0.005*** [32.16] |
[0.005, 0.056] |
| L.URB | -0.022*** [-5.15] |
-0.013*** [-2.58] |
||||
| FOR | -0.000*** [-5.17] |
-0.000*** [-5.14] |
||||
| LAND | 0.000*** [-0.46] |
0.000*** [-0.80] |
||||
| CTRL | 0.001*** [3.19] |
0.013*** [10.97] |
[0.010, 0.016] | 0.002*** [3.48] |
0.017*** [13.48] |
[0.014, 0.020] |
| 截距项 | 0.385 [1.09] |
0.273*** [23.53] |
[0.227, 0.296] | 0.506 [1.16] |
0.213*** [17.54] |
[0.167, 0.237] |
| K-P秩Wald LM (P值) |
497.035 [0.0000] |
498.202 [0.0000] |
||||
| K-P秩Wald F | 2.7e+06 | 2.7e+06 | ||||
| Hansen J | 13.304 | 4.126 | ||||
| (P值) | [0.0013] | [0.1270] | ||||
| 固定效应 | 是 | 否 | 否 | 是 | 否 | 否 |
| N | 1 211 | 1 211 | 1 211 | 1 203 | 1 203 | 1 203 |
| R-sq | 0.539 | 0.603 | 0.473 | 0.564 | ||
| 注(1):模型(5)、(6) 的估计是分国家估计,在使用两阶段最小二乘估计时并未使用固定效应。 | ||||||
最后,对模型(5)、(6) 进行检验,结果显示,在具有有效数据的151个国家中,130个国家的城镇化对人的发展具有显著的正向影响,11个国家具有显著的负向影响,10个国家的影响不显著。表明不同的城镇化模式对人的发展具有不同的影响。
3.固定效应检验。对模型(7) 进行豪斯曼检验,以区分是采用固定效应还是随机效应模型。采用Stata12.0运算,得到P值为0.0000,因此拒绝原假设,采用固定效应模型。
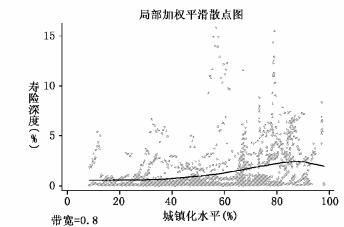
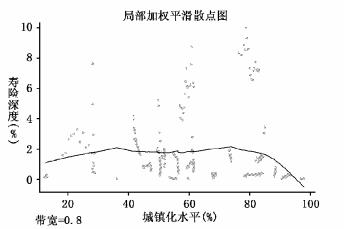
4.两类城镇化中寿险业发展轨迹。首先将两类国家的城镇化和寿险业发展的散点平滑图进行了对比。由图 2、图 3可见,Ⅰ型、Ⅱ型城镇化与寿险业之间的关系明显不同。Ⅰ型城镇化与寿险业发展具有明显的正向关系,寿险业发展轨迹在此类城镇化过程中呈“S型”曲线,具有先增速增长、后减速增长的特点,大致与寿险和经济增长之间的关系一致(Enz(2000) 提出的“S型”曲线)。这意味着,寿险业在城镇化加速发展期间存在一个加速发展的“黄金阶段”。但在城镇化没有促进人的发展的国家,寿险业发展与城镇化之间的关系大致呈“一”字形。这说明,城镇化呈Ⅱ型发展的国家,由于不注重人的发展,导致城镇化进程没有发挥推动人力资本积累的有效作用,最终导致强调人的价值的寿险业发展动力不足。
|
| 图 2 城镇化水平与寿险保费深度关系(Ⅰ型城镇化) |
|
| 图 3 城镇化水平与寿险保费深度关系(Ⅱ型的城镇化) |
(二)结果分析。
1.不同城镇化模式对寿险业发展的影响。模型(7) 的回归结果如表 3所示。第[2]列是混合样本模型的估计结果,即不区分不同类型的城镇化。在考虑了寿险增长的阶段性特点后,城镇化的系数显著为正。也就是说,在全球意义上,城镇化对寿险业的促进作用为2.3%。第[3]列是本文实证主要结果。Ⅰ型和Ⅱ型城镇化对寿险业的作用出现了分离均衡。首先,城镇化与Ⅰ型城镇化哑变量交叉项的系数显著为正且数值很大,为31.2%。这表明,Ⅰ型城镇化对寿险业的促进作用比Ⅱ型城镇化的作用要高出31.2%。这个证据给出了城镇化对寿险业促进作用的部分因果关系的解释。相反,模型[3]中城镇化变量的系数却显著为负且数值很大,为-28.8%。这个系数估计的是D=0时,也就是Ⅱ型城镇化反而会降低寿险业的发展。综合来看,模型(7) 的回归结果验证了本文提出的核心假设。
| 解释变量 | 全样本 | 中低收入国家子样本 | ||||
| [1] | [2] | [3] | [4] | [5] | [6] | |
| URB×D | 0.312*** [6.60] |
0.094** [2.19] |
||||
| URB | 0.049*** [8.58] |
0.023*** [3.34] |
-0.288*** [-6.25] |
0.034*** [7.30] |
0.012** [2.10] |
-0.074* [-1.83] |
| GDPPC | -13.322 [-1.05] |
-54.895*** [-2.60] |
-45.654 [-1.63] |
-110.087*** [-2.88] |
||
| GDPPC2 | 3.23 [1.32] |
11.752*** [2.95] |
9.839 [1.61] |
23.180*** [2.85] |
||
| GDPPC3 | -0.333 [-1.63] |
-1.098*** [-3.34] |
-0.92 [-1.57] |
-2.146*** [-2.82] |
||
| GDPPC4 | 0.013** [2.02] |
0.038*** [3.80] |
0.032 [1.53] |
0.074*** [2.79] |
||
| PG | -0.038 [-1.30] |
-0.191*** [-5.40] |
||||
| ODR | 0.055*** [2.59] |
0.029 [1.13] |
||||
| YDR | 0.005 [0.92] |
0.010** [2.34] |
||||
| LE | -0.105*** [-4.21] |
-0.072*** [-4.07] |
||||
| IMR | -0.019*** [-3.27] |
-0.011*** [-2.94] |
||||
| TER | 0.007** [2.22] |
0.001 [0.15] |
||||
| FD | 0.001 [1.13] |
0.010*** [6.40] |
||||
| 截距项 | -1.437*** [-4.41] |
17.776 [0.73] |
102.234** [2.45] |
-0.857*** [-4.02] |
76.432 [1.61] |
197.171*** [2.94] |
| 固定效应 | 是 | 是 | 是 | 是 | 是 | 是 |
| N | 2 496 | 2 435 | 1 658 | 1 556 | 1 504 | 932 |
| R-sq | 0.03 | 0.116 | 0.191 | 0.035 | 0.065 | 0.235 |
| 注:(1) 被解释变量均为寿险深度(%);(2)*、**和***分别表示在10%、5%和1%水平上显著。 | ||||||
考虑到发达国家的城镇化可能已经发展到了一个高的平台上,而中低收入的发展中国家的城镇化可能更具有动态性。因而,只用中低收入国家的子样本来检验本文的核心假设可以得到更强的证据。中低收入国家的选择主要依据WB数据库的分类。估计结果见表 3的[4]列至[6]列。可以看到,中低收入国家子样本估计的结果与全样本一致。对中低收入的发展中国家而言,不同类型的城镇化对寿险业发展的作用也出现了分离均衡。Ⅰ型城镇化对寿险业的促进作用比Ⅱ型的作用要显著地高出9.4%,而Ⅱ型城镇化会降低寿险业的发展,降低的幅度高达-7.4%。本文提出的核心假设得到进一步的验证。
2.城镇化促进寿险业发展的经济学机制。模型(7) 的回归结果证实了本文的核心假设,也即只有Ⅰ型城镇化才能显著地促进寿险业发展。下面我们检验其背后的经济学机制。根据本文的理论模型,假设人力资本积累是Ⅰ型城镇化促进寿险业发展的经济学机制。也即如果有证据支持全球范围内Ⅰ型城镇化通过促进人力资本的积累进而推动寿险业的发展,那么我们提出的经济学机制假设就得到验证。
检验方法采用Baron和Kenny(1986)、Zhao等(2010) 提出的中介变量检验法。在控制和不控制人力资本的情况下,比较Ⅰ型城镇化对寿险业发展的影响程度是否发生变化。如果在控制人力资本的情况下Ⅰ型城镇化对寿险业发展的解释力下降,而且人力资本的系数显著为正,就给出了证据表明Ⅰ型城镇化至少是部分通过了人力资本的累积进而促进寿险业的发展。
我们采用平均受教育年限(MYS)表示人力资本水平。受数据限制,并非所有年份都有平均受教育年限的数据,因此,在用中介法检验时,我们统一使用有平均受教育年限数据的样本进行估计和比较。表 4给出了控制人力资本水平前后回归结果的对比。由表 4可见,城镇化以及城镇化与Ⅰ型城镇化哑变量的交互项对寿险业发展的解释力都随着人力资本的控制而显著地减少了,而且人力资本的系数显著为正。这充分表明了人力资本的积累是Ⅰ型城镇化促进寿险业发展的一个“中介”途径。
| 解释变量 | [1] | [2] |
| URB×D | 0.451***[3.99] | 0.341***[2.99] |
| URB | -0.414***[-3.74] | -0.324***[-2.93] |
| MYS | 0.408***[4.46] | |
| GDP高次项 | 是 | 是 |
| 其他控制变量 | 是 | 是 |
| 固定效应 | 是 | 是 |
| N | 736 | 736 |
| Rsq | 0.157 | 0.185 |
| 注:(1) 两列回归的被解释变量均为寿险深度(%);MYS为平均受教育年限,数据来源于UNDP网站;回归均控制了人均GDP水平的一次到四次项以及核心检验中的其他控制变量。(2) 为便于机制检验的比较,对样本量作一致性处理。由于来自UNDP的MYS数据量少于WDI数据库中的其他数据,未加入人力资本因素的回归的样本量与加入人力资本水平的回归的样本量不一致,样本量的显著差异将降低机制检验效果。故在进行机制检验前根据MYS数据的观测值进行样本缩减,以保证两个回归样本量的一致性。(3)*、**和***分别表示在10%、5%和1%水平上显著。表 5同。 | ||
| 解释变量 | OLS | 2SLS |
| [1] | [2] | |
| URB | 0.125***[14.48] | 0.124***[10.65] |
| GDPPC | 1.705***[13.74] | 0.688***[4.60] |
| EDUE | 0.073***[3.38] | 0.021[1.22] |
| 截距项 | -13.632***[-15.78] | -4.758***[-4.33] |
| 固定效应 | 是 | 是 |
| N | 851 | 614 |
| R-sq | 0.585 | 0.352 |
| 注:[1]、[2]列被解释变量为平均受教育年限(MYS),数据来源于UNDP网站。 | ||
进一步地,我们检验Ⅰ型城镇化是否真的对人力资本累积有促进作用。控制经济发展水平(用人均GDP来表示)和政府在教育上的投入。OLS结果如表 5中的第[1]列所示。由表 5可见,城镇化的系数显著为正。
城镇化与人力资本之间可能存在双向的因果关系,为了减少可能存在的双向因果关系对估计结果的影响,本文也用2SLS对城镇化与人力资本积累的关系进行了检验。与模型(5)、(6) 的设定一致,采取城镇化滞后一期(L.URB)、森林面积(FOR)和土地面积(LAND)作为城镇化的工具变量。①2SLS回归结果如表 5中的第[2]列所示。在用工具变量控制了可能的双向因果关系后,城镇化的系数仍然显著为正,与OLS的估计结果并无太大差异。
① EDUE为政府教育支出占GDP的比例(%),数据来自WDI数据库;L.URB、FOR和LAND分别为城镇化滞后一期、森林面积(千平方千米)和土地面积(千平方千米),与城镇化类型分类所依据的模型(5)、(6) 中所用控制变量保持一致。
综合表 4和表 5的结果,我们理论模型中关于Ⅰ型城镇化通过促进人力资本的积累进而促进寿险业发展的经济学机制假设得到有力的支持证据。
3.稳健性检验。本文采用三种方法进行稳健性检验。首先,采用Pinar等(2013) 的方法重新构建HDI。对模型(5)、(6) 重新进行检验,回归结果与原结果大致类似:在具有有效数据的151个国家中,共有127个国家表现出正相关性,10个国家显示出负相关性,14个国家显示无明显关系。模型(7) 的回归结果如表 6所示。与核心检验结果相类似。
| 解释变量 | 全样本 | 中低收入国家子样本 | ||||
| [1] | [2] | [3] | [4] | [5] | [6] | |
| URB×D | 0.106***[4.42] | 0.039**[2.33] | ||||
| URB | 0.049***[8.58] | 0.023***[3.34] | -0.083***[-3.58] | 0.034***[7.30] | 0.012**[2.10] | -0.02[-1.25] |
| GDPPC | -13.322[-1.05] | -45.906**[-2.15] | -45.654[-1.63] | -95.167**[-2.46] | ||
| GDPPC2 | 3.23[1.32] | 9.821**[2.44] | 9.839[1.61] | 20.155**[2.45] | ||
| GDPPC3 | -0.333[-1.63] | -0.917***[-2.76] | -0.92[-1.57] | -1.878**[-2.44] | ||
| GDPPC4 | 0.013**[2.02] | 0.032***[3.14] | 0.032[1.53] | 0.065**[2.43] | ||
| PG | -0.041[-1.41] | -0.178***[-5.02] | ||||
| ODR | 0.054**[2.54] | 0.033[1.26] | ||||
| YDR | -0.002[-0.42] | 0.005[1.16] | ||||
| LE | -0.100***[-3.97] | -0.070***[-3.95] | ||||
| IMR | -0.017***[-2.88] | -0.010**[-2.57] | ||||
| TER | 0.007**[2.18] | -0.001[-0.25] | ||||
| FD | 0.001[0.50] | 0.010***[6.52] | ||||
| 截距项 | -1.437***[-4.41] | 17.776[0.73] | 85.149**[2.02] | -0.857***[-4.02] | 76.432[1.61] | 170.112**[2.50] |
| 固定效应 | 是 | 是 | 是 | 是 | 是 | 是 |
| N | 2 496 | 2 435 | 1 658 | 1 556 | 1 504 | 932 |
| R-sq | 0.03 | 0.116 | 0.178 | 0.035 | 0.065 | 0.236 |
| 注:(1) 被解释变量均为寿险深度(%);(2)*、**和***分别表示在10%、5%和1%水平上显著。 | ||||||
其次,为减少异常值的影响,本文分别去掉城镇化水平最高、城镇化水平最低各10%的国家,对全样本和中低收入国家子样本做进一步检验(结果略),结果也显著支持本文的核心假设。
最后,为检验寿险业的阶段性发展特点,本文使用的是高阶回归模型,不同于以往文献的普通线性回归。但为检验的稳健性起见,本文也使用普通线性回归模型进行检验(结果略),结果同样支持本文的核心假设。
五、 结论、启示及展望
文章基于现有文献关于城镇化是否促进寿险业发展研究结论尚不一致的现实背景,从能否促进HDI的提高区分不同城镇化类型的视角,根据全球151个国家1990-2012年的面板数据,进行了系统的实证研究,给出了显著而稳健的经验证据支持。结果表明:只有促进人们经济、教育和健康状况改善的城镇化,才能推动寿险业的快速发展;而仅仅是农村人口向城镇转移、而没有相应配套的基础设施和制度的Ⅱ型城镇化,并不会带来寿险业的繁荣和发展。借助服务业增长的高次项实证模型,文章描述了寿险业在Ⅰ型城镇化推进增长中呈现S形轨迹。在经济意义上,也证实了城镇化促进寿险业发展的关键机制是促进了人力资本的提高和累积。
上述结论对我国目前推动以人为核心的新型城镇化、促进寿险业发展具有一定启示意义。(1) 人的发展是新型城镇化的重要内容之一,应加大农业转移人口的职业教育和培训项目投入,实现基本医疗和养老公共服务的均等化,完善劳动力市场制度以推动人力资本收益的实现。(2) 在城镇化加速发展期,寿险业也会有一个加速发展的黄金阶段,在越过加速阶段之后,会进入漫长的平台期,即“S”的平缓的“尾巴”。这对正处于城镇化进程中的中国有着明确的政策含义。寿险业需要把握人口新型城镇化的机遇,立足于对人的价值的保障之本,在产品结构调整升级上深耕细作,最终实现寿险业的飞跃发展。
最后,本文还存在一些可拓展之处。虽然本文从宏观层面对城镇化影响寿险业发展提供了一致的解释,但城镇化进程会带来经济、社会甚至文化方面的变化,对人及家庭的影响是多方面的,例如风险态度、环境问题和社会网络的变化都有可能对寿险需求产生不一样的影响,需要从微观角度进行多方面的、更深入细致的探讨,这也是未来研究可以突破的方向。
| [1] | 杜菲. 城镇化率与保险密度正相关[N]. 中国保险报, 2013-7-29(6). |
| [2] | 许闲, 丁墨海, 王丹阳. 城镇化进程和保险业发展的互动机制研究[J]. 保险研究, 2016(3): 18–31. |
| [3] | 徐志峰, 温剑波. 保险业参与城镇化发展的思考[J]. 保险研究, 2013(6): 68–75. |
| [4] | 杨汇潮, 江生忠. 城镇化促进保险业发展研究——基于面板数据[J]. 保险研究, 2014(8): 82–92. |
| [5] | 臧志谊, 景鹏, 李正. 城镇化与保险业发展的耦合协调关系及表现[J]. 保险研究, 2015(3): 3–12. |
| [6] | Conley T G, Hansen C B, Rossi P E. Plausibly exogenous[J]. Review of Economics and Statistics, 2012, 94(1): 260–272. DOI:10.1162/REST_a_00139 |
| [7] | Dercon S, Hill R V, Clarke D, et al. Offering rainfall insurance to informal insurance groups:Evidence from a field experiment in Ethiopia[J]. Journal of Development Economics, 2014, 106: 132–143. DOI:10.1016/j.jdeveco.2013.09.006 |
| [8] | Eichengreen B, Gupta P. The two waves of service-sector growth[J]. Oxford Economic Papers, 2013, 65(235): 96–123. |
| [9] | Glaeser E L. A world of cities:The causes and consequences of urbanization in poorer countries[J]. Journal of the European Economic Association, 2014, 12(5): 1154–1199. DOI:10.1111/jeea.12100 |
| [10] | Gollin D, Jedwab R, Vollrath D. Urbanization with and without industrialization[J]. Journal of Economic Growth, 2016, 21(1): 35–70. DOI:10.1007/s10887-015-9121-4 |
| [11] | Janvry A D, Dequiedt V, Sadoulet E. The demand for insurance against common shocks[J]. Journal of Development Economics, 2014, 106: 227–238. DOI:10.1016/j.jdeveco.2013.10.001 |
| [12] | Jedwab R, Vollrath D. The mortality transition, malthusian dynamics, and the rise of poor mega-cities, [R]. Working Paper, 2015. |
| [13] | Jedwab R, Christiaensen L, Gindelsky M. Demography, urbanization and development:Rural push, urban pull and…urban push?[J]. Journal of Urban Economics, 2017, 98: 6–16. DOI:10.1016/j.jue.2015.09.002 |
| [14] | Kumar A, Kober B. Urbanization, human capital, and cross-country productivity differences[J]. Economics Letters, 2012, 117(1): 14–17. DOI:10.1016/j.econlet.2012.04.072 |
| [15] | Pinar M, Stengos T, Topaloglou N. Measuring human development:A stochastic dominance approach[J]. Journal of Economic Growth, 2013, 18(1): 69–108. DOI:10.1007/s10887-012-9083-8 |
| [16] | Shi X, Wang H-J, Xing C. The role of life insurance in an emerging economy:Human capital protection, assets allocation and social interaction[J]. Journal of Banking和Finance, 2015, 50: 19–33. |
 2017, Vol. 43
2017, Vol. 43


