文章信息
 | 财经研究 2017年43卷第4期 |
- 靳卫东, 宫杰婧, 尹义龙.
- Jin Weidong, Gong Jiejing, Yin Yilong.
- 我国人口的社会结构失衡:理论机制与经验事实
- Social Structure Imbalance of Chinese Population: Theoretical Mechanism and Empirical Analysis
- 财经研究, 2017, 43(4): 17-30
- Journal of Finance and Economics, 2017, 43(4): 17-30.
-
文章历史
- 收稿日期:2016-07-28

2017第43卷第4期
2. 山东财经大学 计算机科学与技术学院,山东 济南 250000
2. School of Computer Science & Technology, Shandong University of Finance and Economics, Ji'nan 250000, China
一、 引言
人口再生产与物质资料再生产是社会生产过程的两个方面,必须保持良好的协调关系。长期以来,我国计划生育政策为控制人口过快增长、保持两种再生产的协调发展做出了突出贡献;但是,严格的生育管制也带来了生育率水平的持续下降。根据四次全国人口普查数据,1981年我国总和生育率为2.63,1990年降低为2.31,2000年进一步变为1.22,而2010年总和生育率仅为1.18,已远远低于生育更替水平。根据发达国家的经验,生育率持续下降在导致人口增长困难的同时,还会产生人口结构失衡,包括人口的自然结构失衡 (如年龄结构和性别结构失衡),以及人口的社会结构失衡 (如城乡结构、地区结构、民族结构和素质结构失衡);①并且,人口结构失衡一定会逐步上升为人口问题的核心内容,成为社会经济健康发展的主要障碍 (郭志刚,2010)。因此,分析生育率变化的决定因素,认识人口结构失衡的形成与发展,是我国人口学研究所面临的紧迫任务 (尹文耀等,2013;易富贤,2015)。
①随着生育率水平的持续下降,我国已经发生了严重的人口社会结构失衡。在城乡结构方面,城乡出生率之比由2000年的1:1.23降低为2010年的1:1.51;在地区结构方面,东西部地区出生率之比由2000年的1:1.32变为2010年的1:1.20;在民族结构方面,少数民族人口占比从1990年的8.00%上升到2000年的8.40%,2010年更是达到了8.50%。鉴于我国地区之间、城乡之间和民族之间的教育发展差距,这些人口结构失衡也会产生人口的逆淘汰效应 (尹银和邬沧萍,2013),导致人口的素质结构失衡。
目前,研究我国人口结构失衡的文献还比较少,仅有的少数研究也主要是分析人口的自然结构失衡,而对于人口的社会结构失衡则鲜有涉及。此类研究通常是将人口结构失衡归因于计划生育政策,主要是从经济学、社会学和法学的角度论证人口年龄结构和性别结构失衡所产生的劳动力供给短缺、人口老龄化以及犯罪率上升等问题,并将调整生育政策视为解决问题的关键 (吕程,2011;陆旸和蔡昉,2014;谭远发和宋寅书,2015)。不过,很多发达国家没有实施计划生育政策,同样也存在人口结构问题。这就说明生育政策只是决定人口结构失衡的一个而非唯一的要素,我国人口结构研究还需要进行教育、经济和文化等非政策因素的人口功能分析。另外,随着“双独二孩”、“单独二孩”和“全面二孩”等一系列生育政策改革,我国的人口结构失衡并无明显改善。这都充分反映了我国人口结构研究的不足,也凸显了基于非政策因素开展人口社会结构研究的紧迫性和必要性。
人口发展是一个复杂过程,是政治、经济、文化、社会和心理等多种因素综合作用的结果。因此,在短期内生育政策也许能够对人口发展产生显著影响,但是长期而言,其他非政策因素的作用必将占据主导地位。例如,教育就对人口发展具有重要的长期影响。一方面,很多非政策因素 (包括经济、文化和心理等) 的影响都不同程度地与教育有关 (张爱婷和杜跃平,2006;周长洪,2015);另一方面,教育还可以通过提高妇女就业机会、增加生育知识、推迟初婚初育年龄等途径直接产生“节育”效果。甚至有研究指出,教育的人口功能可以解释近年来我国生育率变化的大部分内容 (易富贤,2015)。
因此,针对现有研究的不足,本文借鉴教育资源稀释理论,使用数理模型论证我国人口发展规律及其所决定的人口社会结构失衡,并基于全国人口普查县级数据为之提供经验证据的支持。研究结果表明,教育的人口抑制效应以及人口转变对教育发展的影响,有可能在教育与生育率之间形成一种相互作用机制,使人口发展呈现出“Z”形变化趋势。结合我国业已存在的城乡之间、地区之间和民族之间的教育发展差距,这种人口发展规律必然会造成人口的城乡结构、地区结构、民族结构和素质结构失衡,产生人口安全问题。
二、 已有研究的评述
一般认为,教育对人口发展具有重要影响。教育程度越低,居民越偏向于追求子女数量而较少关注子女质量,由此就容易产生“越生越穷、越穷越生”的高生育陷阱 (董泽芳,2009);相反,如果居民受教育水平很高,那么社会、经济和文化因素又可能使人口发展滑入低生育陷阱 (Lutz等,2006)。基于大量实证研究,教育资源稀释理论阐述了教育与生育率之间的这种复杂关系 (Blake,1981;Downey,1995)。它认为,在教育资源有限的条件下,子女数量的增多会稀释每个子女所获得的教育资源量,从而会降低他们的平均受教育水平,因此父母必须在子女数量与质量之间做出权衡,通过适度压缩子女数量来换取其质量提升,以达到家庭效用的最大化。这就是教育的人口抑制效应。显然,如果父母受教育水平很低,并不关心子女质量,这种人口抑制效应就会很小;同样,如果父母受教育水平很高,拥有丰富的教育资源,那么子女不必为教育资源展开竞争,教育的人口抑制效应也会很小 (Downey,1995;张月云和谢宇,2015)。由此可见,随着父母受教育水平的提高,教育与生育率之间应该是一种“Z”形变化关系,即在中等教育水平上教育的人口抑制效应最大,教育与生育率之间显著负相关,而在较高和较低的教育水平上,教育的人口抑制效应都很小,教育对生育率变化基本没有显著影响。①
①与此类似,Varvarigos (2013) 通过构建数理模型也分析了教育与生育率之间的这种三阶段变化关系,并提出了人口发展的“N”形变化规律。
近年来,随着教育和经济的发展,我国生育率持续下滑,教育与生育率之间的负向变化关系十分显著。另外,有研究表明,这种负向变化关系存在一个教育“门槛”(即初中教育),当低于或者高于这个“门槛”时,教育的人口抑制效应都会明显减小 (王军和王广州,2013;侯佳伟等,2014)。这似乎印证了上述关于人口发展规律的描述。
一方面,我国西部少数民族地区,特别是西部少数民族农村地区的人均受教育水平很低,明显低于上述教育“门槛”(王美艳和Hannum,2012;郑长德,2014),而这些地区的生育率却较高,显著高于全国平均水平 (严维青,2013),甚至有些地区深陷“越生越穷、越穷越生”的高生育陷阱 (赵鸿娟和陈梅,2006;江承凤等,2014);另一方面,某些东部和东北地区的教育水平较高而生育率却很低 (尹文耀等,2013),甚至有学者认为一些地区业已陷入了低生育陷阱 (尹文耀等,2013)。因此,这两种相悖的生育现象正好符合上述“Z”形变化规律的高低两端特征,似乎也为教育资源稀释理论及其所描述的人口发展规律提供了直接的经验证据。
那么,结合我国城乡之间和地区之间的教育发展差距,以及少数民族聚居于西部农村地区的空间分布特征,“Z”形人口发展规律必然导致人口的城乡结构、地区结构、民族结构和素质结构失衡问题,产生严重的人口安全问题。这基本可以解释目前我国人口发展的社会结构失衡问题。不过,如前文所述,教育的人口抑制效应与社会、经济、文化和心理等多种因素相关,并不必然要符合教育资源稀释理论的机制分析,而高生育陷阱和低生育陷阱并存的相悖现象也可以被很多其他逻辑自洽的理论所解释。因此,关于教育资源稀释理论及其所决定的人口发展规律和人口社会结构失衡,还需要进行更为充分的经验事实分析。
综上所述,本文试图在以下三个方面做出贡献:第一,参照教育资源稀释理论,建立教育和生育决策模型。这有利于分析教育与生育率之间的复杂关系,在一个理论框架下解释高生育陷阱和低生育陷阱并存的相悖现象,并由此总结人口发展规律,论证人口社会结构失衡现象及其形成机制。第二,使用县级人口普查数据,以西部少数民族地区和东部低生育地区为研究对象,实证检验教育与生育率之间的复杂关系。县级政府是实施教育、经济和生育政策的重要主体,其内部在教育、经济、文化和人口结构等方面具有很大的均质性,因此不同于现有的大量省级数据分析,本文使用县级数据能够充分反映教育与生育率之间的相互作用关系。另外,之所以选择上述两类地区作为研究对象,主要是因为它们的教育和生育行为具有“Z”形变化规律的高低两端特征,同时受生育政策的影响也较小。第三,采用工具变量法分析教育的人口功能。根据教育资源稀释理论,教育与生育率之间存在内生性,因此不同于现有文献中大量使用的统计描述和简单线性回归,本文采用工具变量法,可以有效地避免估计偏误。
三、 人口发展规律与人口社会结构失衡的理论分析
参照教育资源稀释理论,在教育的人口抑制效应以外,教育与生育率之间还有可能存在一种相互作用机制。由此,在中等教育水平上,教育程度下降或者生育率的短期上升都会导致生育率的持续上升,最终人口发展将达到“Z”形变化趋势的顶端;相反,如果教育程度上升或者生育率的短期下降,这个机制又会导致生育率的不断下降,最终使人口发展达到“Z”形变化趋势的低端。因此,中等教育水平是教育与生育率组合的非均衡点,在此生育率既有向上攀升的可能,也有向下滑落的趋势,从而不同类型的居民将分别向“Z”形变化趋势的高低两端集聚,形成高生育陷阱和低生育陷阱并存的相悖现象,造成人口结构失衡。参照Varvarigos (2013) 的研究,为了分析教育与生育率之间的这种复杂关系,本文构建了一个教育和生育决策模型。
(一) 有关教育和生育行为的假设
生育子女是严格意义上的家庭行为,生育决策都是以家庭为单位进行的。按照教育资源稀释理论,家庭生育决策受到教育资源限制,需要在子女数量与质量之间加以权衡。假设一个典型家庭生育的子女数量为nt,那么每个子女的受教育水平可以表示为教育资源投入的函数,也即:
| $ {{e}_{t}}=\frac{{{x}_{t-1}}}{{{n}_{t}}}+{{g}_{t}} $ |
其中,gt表示政府的教育财政投入;xt-1(=λt-1It-1) 表示教育资源量,它是家庭经济收入It-1的函数,λt-1是家庭教育投入系数,决定于家庭决策主体——父母对子女教育的重视程度,且0 < λt-1 < 1;①根据已有研究,λt-1是父母受教育水平的函数,即λt-1=p(et-1),其中,et-1表示父母受教育水平,et-1≥0,p′e>0。
①本文将父母抽象为除子女以外的所有家庭成员,包括父亲和母亲以及祖父和祖母、外公和外婆等。
为了简化分析,假设家庭经济收入等于父母受教育水平,即It-1=et-1,家庭效用是子女数量与质量的函数,也即:
| $ {{U}_{t-1}}={{n}_{t}}e_{t}^{{{\alpha }_{t}}} $ |
其中,αt表示子女质量 (即子女受教育水平) 对家庭效用的贡献系数,显然αt≥0。根据前文分析,αt同样反映了家庭对子女教育的重视程度。因此,类似于λt-1=p(et-1),αt也是家庭决策主体——父母受教育水平的函数,即αt=q(et-1),q′e>0(侯佳伟等,2014;周长洪,2015)。
(二) 人口发展的“Z”形变化趋势
根据上述假设,家庭生育决策受到效用函数约束,也即:
| $ {{U}_{t-1}}={{n}_{t}}e_{t}^{{{\alpha }_{t}}}={{n}_{t}}{{(\frac{{{x}_{t-1}}}{{{n}_{t}}}+{{g}_{t}})}^{{{\alpha }_{t}}}}={{n}_{t}}{{(\frac{{{\lambda }_{t-1}}{{e}_{t-1}}}{{{n}_{t}}}+{{g}_{t}})}^{{{\alpha }_{t}}}} $ |
要使家庭效用最大化,必有:
| $ \frac{\partial {{U}_{t-1}}}{\partial {{n}_{t}}}={{(\frac{{{\lambda }_{t-1}}{{e}_{t-1}}}{{{n}_{t}}}+{{g}_{t}})}^{{{\alpha }_{t}}-1}}(\frac{{{\lambda }_{t-1}}{{e}_{t-1}}+{{n}_{t}}{{g}_{t}}-{{\lambda }_{t-1}}{{\alpha }_{t}}{{e}_{t-1}}}{{{n}_{t}}})=0 $ |
由于
| $ {{n}_{t}}=\frac{{{\lambda }_{t-1}}\left( {{\alpha }_{t}}-1 \right){{e}_{t-1}}}{{{g}_{t}}} $ |
将λt-1=p(et-1) 带入上式,可得:
| $ {{n}_{t}}=\frac{p\left( {{e}_{t-1}} \right)\left( {{\alpha }_{t}}-1 \right){{e}_{t-1}}}{{{g}_{t}}} $ |
由此可得,父母受教育水平与家庭生育子女数量的函数关系为:
| $ \frac{\partial {{n}_{t}}}{\partial {{e}_{t-1}}}=\frac{({{\alpha }_{t}}-1)}{{{g}_{t}}}[p\prime ({{e}_{t-1}}){{e}_{t-1}}+p({{e}_{t-1}})] $ |
由于0 < λt-1=p(et-1) < 1,et-1≥0,p′e>0,进而可得:
| $ p'({{e}_{t-1}}){{e}_{t-1}}+p({{e}_{t-1}})>0 $ |
因此,根据αt的取值范围不同,家庭生育可能存在以下三种情况:
1.当父母受教育水平较低,只关注子女数量而不关心子女质量时,子女质量 (即子女受教育水平) 对家庭效应的影响极小 (αt→0),而家庭的教育投入系数也较低 (λt-1=p(et-1)→0)。这时有:
| $ \frac{\partial {{n}_{t}}}{\partial {{e}_{t-1}}}\approx-\frac{p'({{e}_{t-1}}){{e}_{t-1}}}{{{g}_{t}}}<0 $ |
如前文所述,我国教育的人口抑制效应存在一个教育“门槛”,当父母受教育水平et-1低于初中阶段教育时,人口抑制效应会很小,而且很不显著 (侯佳伟等,2014)。这时,小幅提升家庭决策主体——父母的受教育水平,也很难改变他们对子女教育的重视程度,即p′(et-1) 很小 (Varvarigos,2013)。另外,目前我国的政府承担了义务教育经费投入的主要责任,所以教育财政投入gt较大 (靳卫东,2014,2015)。因此,上述ənt/əet-1应该是一个很小的负值,此时教育对生育率的影响很小,人口发展处于高生育率和低教育水平阶段。
2.当父母受教育水平逐步提高,开始重视子女质量时,子女质量 (即子女受教育水平) 对家庭效应的影响增加,即αt∈(0, 1),则有:
| $ \frac{\partial {{n}_{t}}}{\partial {{e}_{t-1}}}=\frac{({{\alpha }_{t}}-1)}{{{g}_{t}}}[p'({{e}_{t-1}}){{e}_{t-1}}+p({{e}_{t-1}})]<0 $ |
家庭将在子女数量与质量之间进行权衡,即通过降低子女数量来换取子女质量的提升。因此,随着家庭决策主体——父母受教育水平的提高,家庭生育开始受到显著抑制。
3.当父母受教育水平很高,子女质量 (即子女受教育水平) 对家庭效应的影响进一步增加时,即αt→1,必有:
| $ \mathop {\lim }\limits_{{a_t} \to 1} {\mkern 1mu} \frac{{\partial {n_t}}}{{\partial {e_{t - 1}}}} = 0 $ |
这说明,如果家庭决策主体——父母的受教育水平很高,家庭特别重视子女质量,并且由于高教育水平所带来的家庭经济收入很高,教育资源丰富,子女不必再为教育资源展开竞争,那么教育对生育率的影响将重新变得很小。此时,子女数量将被限定在一个较低水平,人口发展处于低生育率和高教育水平阶段。
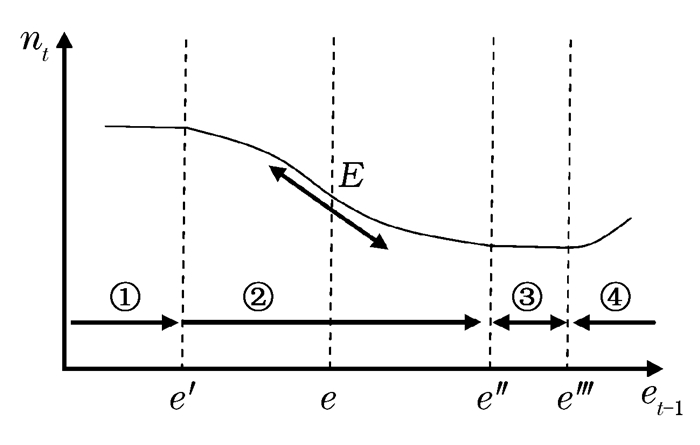
综上所述,家庭决策主体——父母的受教育水平对家庭生育的影响分为不同阶段。如图 1所示,横轴表示父母受教育水平,纵轴表示家庭生育子女的数量,①、②、③和④分别表示人口发展的四个阶段。E是阶段②上的一个非均衡点,它既有向下滑落的趋势,又有向上攀升的可能。在第一阶段:e < e′,ənt/əet-1是极小的负值,即教育对生育率的影响很小;在第二阶段:e′ < e < e″,ənt/əet-1 < 0,即教育与生育率显著负相关;在第三阶段:e″ < e,
(三) 人口社会结构失衡现象
1.高生育陷阱。如前文所述,我国西部少数民族地区仍然存在“越生越穷、越穷越生”的高生育陷阱。这时,子女受教育函数是:
| $ {{e}_{t}}=\frac{{{x}_{t-1}}}{{{n}_{t}}}+{{g}_{t}} $ |
假设父母受教育水平为e*,如图 1所示,一个外生冲击使生育率上升或者使父母受教育水平下降,那么每个子女所获教育资源就会减少,即xt-1/nt降低。如果教育财政投入gt不变,则子女受教育水平et会下降,这将导致αt+1(=q(et)) 降低,那么在第二代子女数量不变的条件下,第二代子女质量所产生的家庭效用Ut会减小。因此,按照教育资源稀释理论,家庭第二代父母将对其子女的数量与质量重新进行权衡,这必然会增加第二代子女的生育数量。①
①按照出生顺序,本文将家庭子女划分为第一代、第二代和第三代等;那么,按照这种划分,第一代子女就是第二代子女的父母 (简称第二代父母),第二代子女就是第三代子女的父母 (简称第三代父母),以此类推。
另外,如果et下降,家庭第二代父母的经济收入It会降低,同时其对第二代子女的教育投资意愿λt也会下降,那么教育资源总量将减少。而上述第二代子女数量的增加,又稀释了这些有限的教育资源,因此会进一步恶化第二代子女的受教育状况,导致et+1更大幅度的降低,也即:
| $ {{e}_{t+1}}\downarrow \downarrow =\frac{p({{e}_{t}}\downarrow ){{e}_{t}}\downarrow }{{{n}_{t+1}}\uparrow }+\overline{{{g}_{t+1}}} $ |
上式中,↓表示下降,↓↓表示更大幅度的下降,↑表示上升。同理可得,第三代父母受教育水平的降低,又会引起第三代子女的数量上升和质量下降,由此就产生了一个生育率不断攀升而教育程度不断下降的循环,最终使人口发展进入图 1中的第一阶段。这时,由于父母受教育水平很低,而教育的人口抑制效应又极小,因此生育率将被长期锁定在较高水平,形成高生育陷阱。因此,本文提出如下假设:
假设1:图 1中的第一阶段是一个相对稳定的人口发展状态,此时教育水平很低而教育的人口抑制效应也很小,生育率将被长期锁定在较高水平。
2.低生育陷阱。在图 1中人口发展的第二阶段,如果外生冲击导致父母受教育水平上升或者生育率下降,那么λt-1(=p(et-1))、αt(=q(et-1)) 以及It-1(=et-1) 都会增加,而nt会减少。在教育财政投入gt不变的情况下,此时et(=xt-1/nt+gt) 将上升,即子女受教育水平将提高。同理,子女受教育水平et提高以及子女数量nt减少,又会提高第二代子女及其后代的受教育水平,并降低他们的生育率。这样,教育与生育率之间相互作用,将使人口发展最终进入图 1中的第三阶段。另外,根据前文分析,此时父母受教育水平和家庭经济收入都很高,家庭教育资源丰富,子女不必再为教育资源展开竞争,所以教育的人口抑制效应会变小,生育率将被长期锁定在较低水平,形成低生育陷阱。因此,本文提出如下假设:
假设2:图 1中的第三阶段是一个相对稳定的人口发展状态,此时教育水平很高而教育的人口抑制效应很小,生育率将被长期锁定在较低水平。
因此,根据我国城乡之间、地区之间和民族之间的教育和经济发展差距,这高低两种生育陷阱并存的相悖现象,必然会导致人口的社会结构失衡,包括城乡结构、地区结构、民族结构和素质结构失衡。
(四) 人口社会结构失衡的形成机制
如前文分析,在图 1中的第二阶段,所有的教育与生育率组合都处于非均衡状态,它们既有向上攀升的可能,也有向下滑落的趋势。那么,参照教育资源稀释理论,所有家庭最终将被分为两类,分别向人口发展“Z”形变化趋势的高低两端集聚,产生两种生育均衡:一种是低教育水平和高生育率的均衡,即高生育陷阱;另一种是高教育水平和低生育率的均衡,即低生育陷阱。由此,本文提出如下假设:
假设3:图 1中的第二阶段是人口发展的非均衡状态,在此所有家庭将分化为两类,分别向第一和第三阶段集聚,从而产生了人口的社会结构失衡。
另外,应该指出的是,在前文分析中,关于子女质量对家庭效用的影响系数αt,本文只讨论了三种情况,即αt→0、αt→1以及αt∈(0, 1)。假如在很高的教育水平上,αt进一步增加,即αt>1,则一定有:
| $ \frac{\partial {{n}_{t}}}{\partial {{e}_{t-1}}}=\frac{({{\alpha }_{t}}-1)}{{{g}_{t}}}[p'({{e}_{t-1}}){{e}_{t-1}}+p({{e}_{t-1}})]>0 $ |
因此,随着家庭决策主体——父母受教育水平的提高,教育与生育率之间也有可能出现正相关关系,由此人口社会结构失衡将得以自行缓解。也就是说,本文所提出的“Z”形人口发展规律,很可能只是对人口发展规律的阶段性描述,据此并不足以判断低生育陷阱就是人口发展的未来趋势。而且,近年来一些欧洲国家生育率水平的持续回升也为这种情况提供了经验上的证据 (石人炳,2010;靳永爱,2014)。因此,教育与生育率之间的关系更应该被描述为一种尾部上翘的“Z”形变化曲线,如图 1中人口发展的四阶段划分。由此,本文提出如下假设:
假设4:在图 1中的第四阶段,随着教育水平的持续提高,生育率也有可能增加,从而可以在一定程度上缓解人口社会结构失衡。
不过,我国教育与经济发展的总体水平还比较低,尚未进入人口发展的高级阶段,所以上述尾部上翘的“Z”形变化规律将很难在我国人口发展实践中获得全面而充分的经验证据支持。正因为如此,本文选择西部少数民族地区和东部低生育地区作为研究对象,主要是为了验证“Z”形人口发展规律 (即图 1中的前三阶段) 以及由此所决定的人口社会结构失衡。
四、 人口发展规律与人口社会结构失衡的实证检验
(一) 研究方法、变量选择和数据说明
1.研究方法。首先,为了检验教育的人口抑制效应,本文采用最小二乘估计方法,估计方程为:
| $ {{R}_{ij}}=\delta +\alpha ed{{u}_{ij}}+\rho {{X}_{rij}}+{{\mu }_{rij}} $ | (1) |
其中,Rij是生育率,eduij是受教育水平,Xrij是所有影响生育率的向量,μrij是随机残差项,δ是截距项,α是教育对生育率的影响系数。如果教育具有人口抑制效应,α将显著为负值。
其次,如前文所述,教育与生育率之间存在相互作用机制,为了解决由此产生的内生性问题,本文采用工具变量法重新估计上述方程,也即:
| $ \left\{ \begin{align} & {{R}_{ij}}=\delta +\alpha ed{{u}_{ij}}+\rho {{X}_{rij}}+{{\mu }_{rij}} \\ & ed{{u}_{ij}}=\lambda +\beta tec{{h}_{ij}}+\sigma {{X}_{rij}}+{{\mu }_{eij}} \\ \end{align} \right. $ | (2) |
其中,techij是教育发展的工具变量,λ是截距项,μeij是随机残差项。相对于城镇,农村地区普遍实施了相对宽松的计划生育政策,因此为了消除生育政策的影响,精确检验教育与生育率之间的关系,本文只选择了农村地区县级样本。由于农村居民的受教育水平既可以影响农业生产技术和劳动力在产业之间的流动,又可以决定文化变迁和对外开放度,因此本文选取了两个指标来反映这两个方面因素的变化,即人均农业机械总动力与第一、二产业从业人员比的交互项以及每万户居民的电话数,并以此作为教育发展的工具变量。这两个工具变量受生育率的影响较小,基本上可以通过针对工具变量的各种检验,包括不可识别检验、弱工具变量检验、过度识别检验和外生性检验等。①
①人均农业机械总动力与第一、二产业从业人员比的交互项=(农业机械总动力/第一产业从业人员数)×(第一产业从业人员数/第二产业从业人员数)=农业机械总动力/第二产业从业人员数。这一交互项和每万户居民的电话数,显然不受生育率变化的显著影响,所以在估计方程式 (1) 中不存在互为因果关系所产生的内生性问题。不过,大量研究表明,经济发展可以作用于生育率变化,而上述两项指标显然都与经济发展相关,由此也可能产生内生性问题。本文认为,首先,经济发展是一个综合概念,它包括了收入增加、教育发展和生活质量提高等多方面内容,可以影响养育子女的生活费用、教育投入、人均预期寿命和婴幼儿死亡率等,从而能够作用于生育率的变化。可是,随着我国经济发展,养育子女的生活费用占比相对减少,而医疗条件的改善又大幅度降低了婴幼儿死亡率,提高了人均预期寿命,所以很多地区人口再生产已经转变为高出生、低死亡与高增长的人口发展类型 (即高生育陷阱),甚至有些地区已转变为低出生、低死亡和低增长的人口发展类型 (即低生育陷阱)(蒋正华,1988)。这时,生育意愿是决定生育率变化的主因,经济发展与生育率的因果关系将很有限 (李仲生,2008)。因此,上述两项指标也许与经济发展高度相关,但经济发展与生育率之间的相对独立性仍然可以保证它们作为工具变量的合理性和有效性。其次,在表 1中,经济发展作为控制变量被引入估计方程,并没有改变教育的人口抑制效应,而且其估计结果也很不显著。这再次说明,经济发展对生育率的影响有限,仅有的影响也主要是通过教育而发挥作用,所以上述两项指标可以作为教育发展的工具变量。最后,上述两项指标也通过了针对工具变量的各种检验。此处,为了简化分析,本文没有列出有关工具变量的检验结果,有需要的读者可以直接向作者索取。
| 估计 方程 | 西部少数民族农村地区 | 东部农村地区 | ||||||
| 受教育年限 | 经济发展 | 民族虚 拟变量 | 样本区间 | 受教育年限 | 经济发展 | 地区虚 拟变量 | 样本区间 | |
| (1) | -1.385***(0.32) | 少数民族 人口占比 达到85% 以上的县 级样本 | -2.165***(0.68) | 第一 分位段 | ||||
| (2) | -1.415***(0.32) | 0.282(0.55) | -2.142***(0.68) | -0.248(0.29) | ||||
| (3) | -1.486***(0.30) | + | -1.278*(0.73) | + | ||||
| (4) | -1.469***(0.30) | -0.339(0.30) | + | -1.154(0.74) | -0.393*(0.24) | + | ||
| (5) | -0.700(0.52) | 少数民族 人口占比 达到95% 以上的县 级样本 | -3.487(2.67) | 第四 分位段 | ||||
| (6) | -0.675(0.52) | -0.298(0.41) | -2.438(1.58) | -0.512(0.64) | ||||
| (7) | -0.747(0.53) | + | -0.386(1.02) | + | ||||
| (8) | -0.739(0.53) | -0.193(0.47) | + | -0.471(1.01) | -0.061(0.30) | + | ||
| 注:“+”代表加入了民族、地区虚拟变量;为了简化分析,此处以及后文中都没有列出最小二乘估计结果;同时,表中没有列出截距项和其他控制变量的回归结果,也省略了东部农村地区中第二、三分位段样本的估计结果。显然,东部农村经济发展的影响普遍不显著,这说明它是通过教育来发挥人口功能的。 | ||||||||
根据前文分析,人口发展存在“Z”形变化趋势,那么可以预期:第一,当居民受教育水平较低时,其生育率水平较高,而生育率受教育的影响很不显著,即|α|很小;第二,随着居民受教育水平的提高,生育率开始持续下降,两者的负相关关系却变得十分显著,即|α|较大;第三,当居民受教育水平较高时,生育率极低,其与教育的关系重新变得很不显著,即|α|很小。
最后,为了检验教育与生育率之间的相互作用,本文实证分析了人口转变对教育发展的影响,从而为人口社会结构失衡的形成机制提供经验证据的支持。本文借鉴尹银和邬沧萍 (2013) 的研究,使用每万人中的中学在校生数 (Midsch) 作为被解释变量,估计方程为:
| $ Midsc{{h}_{ij}}=\omega +\gamma {{R}_{ij}}+\tau {{X}_{eij}}+{{\mu }_{mij}} $ | (3) |
如果人口转变对教育发展的影响很大,那么γ为负且很显著;否则,就说明人口转变对教育发展的影响并不存在。
2.变量选择。受限于数据资料的可得性,本文使用出生率作为生育率变化的衡量指标,并且选择人均受教育年限作为解释变量,由此分析教育的人口抑制效应。同时,考虑到大量文献将经济发展作为生育率变化的主要影响因素 (尹文耀等,2013),本文在估计方程 (1) 中又引入经济发展作为控制变量,并选择人均第一产业增加值作为经济发展的衡量指标,其中,人均第一产业增加值=第一产业增加值/第一产业从业人员数。如前文所述,目前经济发展与生育率变化的关系并不紧密,仅有的影响也主要是通过教育而发挥作用,所以预期经济发展的估计结果很不显著。另外,教育财政投入也是影响教育及其人口抑制效应的重要方面,而根据相关研究,我国的教育财政投入与地方经济发展之间存在显著的正相关关系 (靳卫东,2014,2015),所以此处使用经济发展作为控制变量,也在一定程度上反映了教育财政投入的人口功能。
一般认为,在生育政策以外,生育行为主要决定于生育意愿,而生育意愿不仅受到教育和经济发展的影响,还决定于其他很多因素,如宗教、文化、风俗习惯、人口结构和婴幼儿死亡率等 (张天路,1990)。因此,在估计方程 (1) 中,本文还引入了一些其他控制变量。
首先,是民族虚拟变量。与汉族相比,少数民族的计划生育工作有两个突出特点:一是在时间上都晚于汉族,二是在要求上都实行“适当放宽”政策 (张天路,1990;易富贤,2015)。为了反映这种政策实施差异对生育率变化的影响,本文在西部少数民族教育的人口抑制效应分析中,引入了民族虚拟变量。其实,各民族的传统文化和风俗习惯对生育率的影响,都可以通过民族虚拟变量得以体现。并且,鉴于宗教对人口发展的重要影响,以及我国宗教信仰普遍具有的鲜明民族特征,民族虚拟变量也反映了宗教信仰的人口功能。
其次,是人口结构变量。人口结构对生育率有直接影响 (江承凤等,2014),但本文使用出生率作为被解释变量,并没有考虑人口转变的结构因素,特别是没有考虑育龄妇女占比的影响。因此,本文在估计方程中引入育龄妇女的人口占比作为控制变量。
再次,是医疗卫生条件变量。从总体上看,随着经济发展和医疗条件的改善,死亡率已不再是决定我国生育率变化的主要因素。但是,考虑到西部少数民族地区和东部的农村地区经济发展相对滞后,本文仍然将医院和卫生院床位数作为控制变量,以反映医疗卫生条件对生育率的影响。
最后,地理环境 (赵鸿娟和陈梅,2006)、区域政策 (王美艳和Hannum,2012)、婚姻与生育文化 (闫玉和马学礼,2014) 等因素也会对人口转变产生一定作用,因此本文还引入了这方面的控制变量,如山区县和贫困县虚拟变量以及女性离婚率。
另外,在检验人口转变对教育发展的影响时,除了出生率和每万人中的中学在校生数作为解释变量和被解释变量以外,本文在估计方程 (3) 中也引入了一些影响教育发展的因素作为控制变量,如经济发展、人均财政支出、乡村人口占比以及贫困县和山区县的虚拟变量等 (靳卫东,2014,2015)。
3.数据说明。首先,本文选择西部少数民族农村地区县级样本来检验高生育陷阱。根据已有研究,大多数少数民族地区的生育率明显高于全国平均值,而实际生育率又低于政策生育水平 (易富贤,2015)。这主要是因为,受限于历史、地理和文化等因素,西部少数民族地区的教育和经济发展相对滞后,同时又实行了相对宽松的计划生育政策 (张天路,1990)。因此,选择西部少数民族农村地区作为研究对象,可以有效地避免生育政策的影响,以检验教育的人口功能及其所产生的高生育现象。
并且,为了尽量消除有可能存在的生育政策限制,本文选择少数民族人口占比较大的县级样本作为研究对象,其中剔除了县级以上城市及市区样本,同时还剔除了非西部地区的少数民族县级样本以及广西壮族自治区的县级样本。这是因为:一方面,由于地理上相连,环境上相近,西部不同民族之间的教育和人口问题存在共性,但与非西部地区少数民族的差异较大 (黄荣清,2009);另一方面,与其他少数民族地区不同,广西壮族自治区实施了较为严格的计划生育政策,其实际生育率受生育政策的影响较大 (易富贤,2015)。由此,本文共得到西部少数民族农村地区县级样本124个。
其次,本文选择具有较低生育水平的东部农村地区样本来检验低生育陷阱。近年来,由于强调依法行政,计划生育工作的许多强制性措施不再被使用,而更多地依靠“柔性”手段 (尹文耀等,2013)。因此,即使是在生育率明显高于政策生育水平的地区,生育率下降的主要动因也是经济和教育发展,生育政策的影响日趋减小。不过,为了尽量避免生育政策所可能产生的影响,以单独分析教育的人口功能,本文仍然选择了生育率较低而生育政策相对宽松的东部农村地区作为研究对象。这样,参照尹文耀等 (2013) 的研究,以生育率低于1.25并且大大低于政策生育水平为标准,①剔除县级以上城市及市区样本,本文共得到东部地区县级样本160个。
①从1984年开始,我国在大多数农村地区实施“一孩半”生育政策,即第一个孩子为男孩的家庭不得再生,而第一个孩子为女孩的农户在间隔四五年后允许生育第二胎,所以农村地区的政策生育水平应该为1.5。另外,一些学者也实际测算了各地的政策生育水平 (尹文耀等,2013)。根据政策生育水平,考虑到上述县级样本仍然包含了部分城镇人口,本文以生育率低于1.25为标准,共选择了低生育县级样本160个。
最后,对两类县级样本的统计分析表明,我国西部少数民族农村地区的人均受教育年限较低,特别是在少数民族人口占比大于95%的县域内,人均受教育年限仅为5.5年,基本上处于初中教育阶段的低端。与之相比,东部农村地区的人均受教育水平较高,特别是在第四分位段县级样本中,人均受教育年限达到了8.13年,基本上处于初中教育阶段的顶端。②根据前文分析,初中教育是影响生育率变化的关键阶段,初中以上及以下教育的人口抑制效应都很小。因此,按照教育资源稀释理论及其所决定的人口发展规律,上述两类地区很可能会存在高生育陷阱和低生育陷阱。这也是本文选择这两类地区来研究人口社会结构失衡的主要原因。
②我国义务教育法规定的义务教育年限为九年,义务教育学制是以“六三制”(即小学六年制、中学三年制) 为主,但是也有少数地区实行八年制义务教育,即小学五年制、中学三年制。因此,本文据此判断,8.13年和5.5年分别处于初中教育阶段的高低两端。
以上数据资料的来源是2000年和2010年的《中国人口普查资料》《中国人口普查分县资料》以及历年的《中国县 (市) 社会经济统计年鉴》和《中国统计年鉴》。
(二) 对高生育陷阱的检验
1.高生育陷阱的现象验证。采用少数民族人口占比达到85%以上的西部农村县级样本,使用最小二乘法的估计结果表明,经济发展的人口功能并不明显,而教育的影响十分显著。这验证了工具变量选择的有效性,说明在西部少数民族农村地区,经济发展对生育率的影响主要是通过教育发挥作用,教育是抑制人口增长的关键 (张爱婷和杜跃平,2006;Varvarigos,2013)。同样,在表 1中,使用工具变量法的估计结果也表明,教育的人口抑制效应显著且稳定,而经济发展的作用很小。另外,与最小二乘估计相比,在工具变量法的估计结果中,教育的人口抑制效应普遍增加。这表明遗漏变量的影响超过生育率变化对教育的影响,因此教育的人口功能在工具变量回归中更大。总之,教育确实具有显著的人口抑制效应。
相反,如表 1所示,如果选择少数民族人口占比达到95%以上的西部农村县级样本为研究对象,使用工具变量法,并且加入山区县、贫困县和民族虚拟变量,教育的人口抑制效应就变得很小,且很不显著。结合统计分析结果可知,①因为在少数民族人口占比较高的地区,教育和经济发展更为落后,所以类似于图 1中人口发展的第一阶段,教育的人口抑制效应变得很小。那么,这类地区应该是属于高生育、低教育和低经济发展的人口发展模式 (张天路,1990;郑真真和吴要武,2005),已经陷入了高生育陷阱。
①为了简化分析,本文没有详列西部少数民族农村地区和东部农村地区县级样本的统计分析结果。
因此,综合上述两组样本的分析结果,我们基本上验证了假设1,初步证明了“Z”形人口发展规律的第一阶段,即当教育水平很低时,教育的人口抑制效应很小,人口发展被锁定在高生育状态。在这里,按照前文分析,要进一步认识高生育陷阱的形成机制,还需要检验人口转变对教育发展的影响,以判断教育与生育率之间是否存在相互作用。
2.检验高生育陷阱的形成机制。为了验证教育与生育率之间的相互作用及其所决定的高生育陷阱,参照尹银和邬沧萍 (2013) 的研究,本文分析了人口转变对教育发展的影响。以每万人中的中学在校生数为被解释变量,以出生率为解释变量,同时选择教育发展的其他影响因素作为控制变量,估计结果如表 2所示。
| 估计 方程 | 西部少数民族农村地区 | 东部农村地区 | ||||||
| 出生率 | 经济发展 | 民族虚 拟变量 | 样本区间 | 出生率 | 经济发展 | 地区虚 拟变量 | 样本区间 | |
| (1) | -0.114***(0.02) | -0.123(0.12) | 少数民族 人口占比 达到85% 以上的县 级样本 | -0.009(0.03) | 0.192(0.28) | 第一分位段 | ||
| (2) | -0.104***(0.02) | -0.094(0.13) | + | -0.001(0.03) | -0.052(0.36) | + | ||
| (3) | -0.125***(0.02) | -0.954**(0.40) | 少数民族 人口占比 达到95% 以上的县 级样本 | 0.114***(0.04) | 0.647***(0.21) | 第四分位段 | ||
| (4) | -0.123***(0.03) | -0.759*(0.44) | + | 0.087*(0.05) | 0.560***(0.18) | + | ||
| 注:“+”代表加入了民族、地区虚拟变量;出生率取千分值,并对每万人中的中学在校生数和人均财政支出分别取对数,以缩小量纲对估计结果的不利影响;在东部农村地区中,为了简化分析,本文没有列出第二、三分位段样本的估计结果。 | ||||||||
在少数民族人口占比达到85%以上的西部农村县级样本中,最小二乘法的估计结果显示,出生率显著降低了中学在校生数,所以子女数量增长对教育发展的影响明显。Hausman-Taylor面板数据估计结果 (1) 和 (2) 也显示,①生育率对教育的负向影响仍然十分显著。这说明子女之间存在明显的教育资源竞争,所以结合教育的人口抑制效应,教育与生育率之间的相互作用机制确实可以导致生育率不断攀升而进入高生育陷阱,由此就验证了假设3。
①为了充分利用面板数据的信息,同时考虑到不随时间变化的山区县、贫困县和民族虚拟变量,本文在此处以及后文中分析人口转变对教育发展的影响都采用了Hausman-Taylor估计,其原理是利用解释变量的信息产生工具变量,用工具变量来解决内生性问题 (Hausman和Taylor,1981;宋小宁等,2015)。
另外,在少数民族人口占比达到95%以上的西部农村县级样本中,子女之间显然也存在教育资源竞争。但是,按照表 1中的估计结果可知,此处教育的人口抑制效应很小。因此,这再次验证了假设1,说明此处教育与生育率之间的相互作用机制并不存在,生育率有可能被长期锁定在较高水平,从而形成了高生育陷阱。
(三) 对低生育陷阱的检验
1.低生育陷阱的现象验证。由于东部地区内部存在巨大的经济发展差距,所以按照2000年和2010年人均GDP的四分位点,本文将东部地区样本由低到高分为四组。这样,以出生率为被解释变量,以人均受教育年限和经济发展为解释变量,同时引入其他控制变量,估计结果如表 1所示。
估计结果表明,随着经济发展和教育水平的提高,教育的人口抑制效应具有明显的下降趋势,即|-1.154|>|-0.471|。特别是在第四分位段中,教育的人口抑制效应很小,而且很不显著。根据统计分析结果,第四分位段样本的平均受教育年限为8.13年,处于初中教育阶段的顶端。因此,这验证了已有研究关于教育“门槛”的描述和假设2,即此处教育的人口抑制效应很小,基本上类似于图 1中人口发展的第三阶段,生育率被长期锁定在较低水平,陷入了低生育陷阱。
2.检验低生育陷阱的形成机制。在表 2中,两组东部地区样本的回归结果表明,出生率对中学在校生数的负向影响很小,甚至在第四分位段中显著为正。这说明在相对发达的东部农村地区,教育资源充裕而生育水平较低,所以子女之间不必为教育资源展开竞争,人口转变对教育发展的影响很小。这再次验证了假设2,同时也表明此处教育与生育率之间确实存在正相关关系,从而可以在一定程度上证明假设4。
(四) 稳健性检验
本文主要是从调整样本区间、替换衡量指标以及使用其他计量分析方法三个方面来检验了上述实证分析结果的稳健性。具体内容包括:第一,选择少数民族人口占比达到80%和90%以上的西部农村县级样本为研究对象,对比验证高生育陷阱;按照2000年和2010年的人均GDP水平,将东部农村地区县级样本分为两组,对比检验低生育陷阱。第二,用妇女平均受教育年限、人均住房面积的对数值和总和生育率来分别反映教育发展、经济发展和生育率变化,以检验教育的人口抑制效应;以男女人均受教育年限之比为被解释变量,以出生率为解释变量,检验人口转变对教育发展的影响。第三,针对人口发展规律的非线性特征,使用静态面板门槛模型进行稳健性检验。②这些研究都没有改变前文实证分析的主要结论。
②为了简化分析,本文没有列出稳健性检验结果,有需要的读者可以直接向作者索取。
因此,综合西部少数民族地区和东部地区县级样本的实证分析结果可知,“Z”形人口发展规律基本上可以得到经验证据的支持,而高生育陷阱和低生育陷阱的形成机制也能够获得事实验证。那么,结合我国城乡之间、地区之间和民族之间的教育发展差距,人口社会结构失衡就是一种必然的趋势。
五、 结论与启示
近年来的人口社会结构失衡是我国社会经济发展所面临的重大挑战,认识其成因与发展成为人口学研究的重要任务。基于教育资源稀释理论,本文通过数理模型分析了教育与生育率之间的相互作用,提出了人口发展的“Z”形变化规律,即在中等教育水平上教育与生育率变化显著负相关,而在较高和较低教育水平上两者并无明显关联。那么,根据我国城乡之间和地区之间的教育发展差距,以及少数民族聚居于西部农村地区的空间分布特征,这种“Z”形人口发展规律必然会使不同居民分化为两类,分别向生育率的高低两端集聚。这就解释了高生育陷阱与低生育陷阱并存的相悖现象,阐明了我国人口的城乡、地区、民族和素质结构失衡的形成机制。
基于全国人口普查县级数据,本文使用工具变量法和Hausman-Taylor估计方法,检验了上述人口发展规律及其所决定的人口社会结构失衡,结果表明:第一,在西部少数民族农村地区,随着少数民族人口占比的增加,教育与生育率从显著负相关逐步转变为没有显著关联。那么,结合少数民族的高生育水平,这说明教育与生育率之间的相互作用确实使某些少数民族地区陷入高生育陷阱,由此就验证了“Z”形人口发展规律的第一、二阶段。第二,在东部农村地区,随着经济和教育发展,教育的人口抑制效应明显降低,而教育与生育率之间的相互作用关系一直都不显著。结合东部地区的低生育水平,这说明某些地区已经滑入了低生育陷阱,由此就证明了“Z”形人口发展规律的第三阶段。第三,综合两类地区的实证分析结果,“Z”形人口发展规律基本可以得到事实验证,所以人口社会结构失衡就成为一种必然的趋势。
综上可知,放宽生育管制也许能够促进人口数量增长,但是却很难改变教育的人口功能,所以并不能有效缓解人口社会结构失衡。其中的政策启示是:第一,要增加针对农村、西部和少数民族地区的教育投入,进一步普及九年义务教育,以保证落后地区居民的受教育水平全部跨越中等教育门槛 (即初中教育),使教育与生育率有可能进入相互作用的良性循环;第二,在普及九年义务教育的同时,要不断提高国民受教育水平,以保证所有居民进入教育与生育率变化的良性循环,实现经济和教育的可持续发展;第三,适应于教育和经济的持续发展,要尽快出台生育激励措施,以避免某些地区陷入有可能出现的低生育陷阱。
最后,应该指出的是,本文只研究了教育的人口功能及其所决定的人口发展规律和人口社会结构失衡,而人口发展的影响因素很多,因此要判断我国人口的未来发展,仍然需要相关研究结合其他影响因素提供更多的经验证据。
| [1] | 郭志刚. 中国的低生育率与被忽略的人口风险[J]. 国际经济评论, 2010(6): 112–126. |
| [2] | 侯佳伟, 黄四林, 辛自强, 等. 中国人口生育意愿变迁:1980-2011[J]. 中国社会科学, 2014(4): 78–97. |
| [3] | 靳卫东. 农村义务教育经费保障机制改革的成效评价[J]. 统计研究, 2014(12): 61–68. |
| [4] | 靳永爱. 低生育率陷阱:理论、事实与启示[J]. 人口研究, 2014(1): 3–17. |
| [5] | 石人炳. 低生育率陷阱:是事实还是神话?[J]. 人口研究, 2010(2): 107–112. |
| [6] | 王军, 王广州. 中国育龄人群的生育意愿及其影响估计[J]. 中国人口科学, 2013(4): 26–35. |
| [7] | 易富贤. 从少数民族生育率看停止从严控制人口政策的急迫性[J]. 人口与社会, 2015(2): 19–32. |
| [8] | 尹文耀, 姚引妹, 李芬. 生育水平评估与生育政策调整——基于中国大陆分省生育水平现状的分析[J]. 中国社会科学, 2013(6): 109–128. |
| [9] | 张天路. 谈谈少数民族地区传统观念的更新与人口素质提高的有关问题[J]. 人口与经济, 1990(6): 36–39. |
| [10] | 郑真真, 吴要武. 人口变动对教育发展的影响[J]. 北京大学教育评论, 2005(2): 84–89. |
| [11] | 周长洪. 经济社会发展与生育率变动关系的量化分析[J]. 人口研究, 2015(2): 40–47. |
| [12] | Lutz W, Skirbekk V, Testa M R. The low-fertility trap hypothesis:Forces that may lead to further postponement and fewer births in Europe[J]. Vienna Yearbook of Population Research, 2006, 4: 167–192. |
| [13] | Varvarigos D. A theory of demographic transition and fertility rebound in the process of economic development[R]. University of Leicester Working Paper No. 13/19, 2013. |
 2017, Vol. 43
2017, Vol. 43