文章信息
 | 财经研究 2017年43卷第4期 |
- 马文涛.
- Ma Wentao.
- 预期形成机制的选择、宏观政策搭配与通胀预期管理
- The Selection of the Formation Mechanism of Expectation, the Mix of Macro-policy and the Management of Inflation Expectation
- 财经研究, 2017, 43(4): 4-16, 封三
- Journal of Finance and Economics, 2017, 43(4): 4-16, 封三.
-
文章历史
- 收稿日期:2016-08-09

2017第43卷第4期
一、 引言
当前,随着发达经济体的政府债务高企和名义利率趋近零,甚至转换为负值,不仅各国宏观政策调控空间逐步收窄,协调难度增大,而且调控绩效急剧下降,尤其是在步入负利率时代之后,支撑传统宏观政策调控的理论逐步失效,增加了未来宏观调控的不确定性,这使预期管理,尤其是通胀预期管理成为当前政策制定者关注的重点。就我国而言,鉴于近些年来关于宏观调控绩效下降的论断此起彼伏 (陈彦斌等,2015),政府也开始注重预期管理,在数次中央经济工作会议中强调宏观政策要保持“可预期性”,要注重“引导社会心理预期”。事实上,大量研究表明,在复杂多变的经济形势下预期管理往往成为各国宏观调控的重点所在 (Eggertsson和Woodford, 2003)。
尽管预期管理,尤其是通胀预期管理在当前经济形势下的重要性已得到充分认识,然而,对如何管理预期,尤其是通胀预期却未在学术界与政策制定者中达成一致。一种观点认为,在非常时刻必有非常之举,在“新常态”下宏观政策制定者不应纠结于传统宏观政策工具的樊篱,而应该跨越传统界限,寻找新工具实施预期管理 (Woodford, 2012)。在这种逻辑下,发达经济体针对次债危机不仅采取以大规模“有毒资产”购买为特征的量化宽松政策,还实施了以维持利率低水平为特征的前瞻性引导策略,试图以此塑造公众对未来宏观政策的预期 (Plosser, 2013),甚至跨越传统理论边界,采取负利率政策。另一种观点更强调了传统宏观政策工具的积极作用,尤其突出预期形成机制变动在摆脱通货紧缩中的重要性 (García-Schmidt和Woodford, 2015;等)。相比较而言,基于前一种观点的预期管理固然有助于在短期内稳定宏观经济,抑制通缩预期。然而,可能因公众难以基于非常规宏观政策形成准确预期而在长期内加剧经济波动;与之不同,基于后一种观点的预期管理因借助公众对过往宏观调控所形成的稳定预期,并注意预期形成机制对宏观调控所构成的约束,从而强化传统宏观政策工具的调控效果,尤其能有效管理通胀预期。从现实看,前一种观点的负面效应逐步显现,而基于后一种观点的预期管理才是切实可行的宏观调控策略。本文正是沿着后一种观点并结合中国现实,探讨预期形成机制对宏观政策搭配及其通胀预期管理的影响。
本文以Christiano等 (2005) 提出的经典动态随机一般均衡模型为基本框架,结合中国宏观政策特征和公众预期形成的特点,一方面同时引入价格型与数量型工具信息的混合货币政策指标以及公共资本的积累过程,凸显宏观政策对经济供求的影响;另一方面,通过归纳现有文献,筛选学习型预期表征公众预期并以此为基础,既从理论层面推导实现预期稳定时宏观政策搭配所必须满足的理论条件,还采用数值模拟方法揭示这种政策搭配的特征。
二、 文献综述
纵观现有文献,预期形成机制对宏观调控及其通胀预期影响的研究主要集中于以分布滞后式预期为代表的静态预期、理性预期、学习型预期等预期形成机制。静态预期方面,Lahiri (1976) 通过研究静态预期对费雪效应的影响发现,在这种预期形成机制下公众预期调整迟缓,作为货币政策中介指标的名义利率不能完全反映通胀预期变化,Frenkel (1975a、b) 探究了静态预期对数量型货币政策调控的影响发现,在这种静态预期作用下货币供给的增加不会导致通胀预期的迅速增加,只有当货币供给增速加快时,通胀预期才逐渐上升。Velde (2004) 对20世纪70年代“滞胀”历史进行研究后指出,在宏观经济波动较大时静态预期与基于实际统计调查所得的公众预期相距甚远,会对宏观调控造成误导,引发宏观政策频繁变动。理性预期研究方面,Lucas (1976)、Sargent和Wallace (1976) 等强调,在理性预期下预期形成机制与宏观政策范式之间的关系属于“一币两面”:一方面预期形成过程严重依赖宏观政策所传递的信息,一旦宏观政策范式改变,预期形成机制必随之改变,否则可能形成与现实相背离的预期;另一方面宏观政策有效性又在很大程度依赖于在特定预期形成机制下能否被很好预期。更有意思的是,在理性预期下通胀预期能及时跟随宏观政策变化,使宏观政策能无成本地降低通胀,甚至能制造经济繁荣 (Mankiw, 2000等)。与静态预期和理性预期相比,学习型预期既不像静态预期那样机械,也不像理性预期那样要求公众有强大信息处理能力,使这种预期形成机制有广泛适应性和很强灵活性 (Mackowiak和Wiederholt, 2010),能很好解释宏观政策演变和通胀预期历史轨迹,这既包括20世纪80年代美国由高通胀时代转入大稳健时代的经历 (Sargent等,2006),也包括Paul Volcker的反通胀时期 (Curto, 2007),还包括20世纪80年代拉美高通胀时期 (Cogley等,2008),甚至影响低利率时代财政政策以及以前瞻性引导为代表的非常规货币政策的有效性 (Cochrane, 2015;等等)。同时,Eusepi和Preston (2011) 以及Klaus和Woodford (2012) 等均证明,学习型预期要求宏观政策必须提高反通胀立场,才能确保通胀预期稳定在政策目标的范围内。
国内相关探讨从中国特有转轨经济体制特征出发,寻找契合实际的预期形成机制 (李拉亚, 1991、1995;薛万祥, 1995),基于新凯恩斯菲利普斯曲线框架分析了适应性预期 (范从来, 2000;王少平等, 2001;高铁梅等, 2003)、理性预期 (陈彦斌, 2008)、兼具适应性预期和理性预期的混合型预期 (杨继生, 2009)、学习型预期 (徐亚平, 2009、2011)、粘性预期 (李颖等, 2010) 等形成机制对通胀演变和宏观调控的影响。少量基于DSGE模型的研究探讨了预期形成机制与宏观政策之间的相互影响机制 (张佐敏, 2013;卞志村和高洁超, 2014)。
综合来看,现有研究在预期形成机制对宏观政策及其通胀预期管理的影响方面做出了积极探索,但是存在以下不足:(1) 理论上,预期形成机制对宏观政策及其通胀预期管理的影响不仅局限于货币政策,还包括财政政策,而且不仅体现于宏观政策对通胀预期的反应上,还与宏观政策对其他政策目标的反应力度相关。然而,现有文献更关注货币政策及其对单一政策目标的反应。(2) 与发达经济体相比,我国宏观调控不仅综合运用价格型与数量型货币政策工具,还通过引导财政支出投向基础设施领域,使宏观政策能同时影响总供给和总需求 (郭长林,2016)。然而,现有相关文献却忽视上述具有中国特色的因素。
三、 DSGE模型构建:含混合型货币政策工具和财政支出的总供给效应
借鉴Christiano等 (2005),建立包含价格型与数量型货币政策工具加权方式形成的混合型货币政策工具以及兼顾总需求与总供给效应的财政支出的动态随机一般均衡模型。
1.家庭。所有家庭构成测度为1的连续统,第j个家庭的效用是:
| $ \begin{align} & {{E}_{0}}\sum\limits_{t=0}^{\infty }{{{\beta }^{t}}}U({{C}_{j,t}},{{H}_{j,t}},{{M}_{j,t}}/{{P}_{t}})={{E}_{0}}\sum\limits_{t=0}^{\infty }{{{\beta }^{t}}}{{\varepsilon }_{c,t}}\{\text{ln}({{C}_{j,t}}-h{{C}_{j,t-1}}) \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -{{\theta }_{1}}{{({{H}_{j,t}})}^{1+{{\eta }_{h}}}}/(1+{{\eta }_{h}})+{{\theta }_{2}}\text{ln}({{M}_{j,t}}/{{P}_{t}})\} \\ \end{align} $ | (1) |
其中:β为折现因子,Ci, t为消费, h为消费惯性,Hi, t为劳动供给,Mj, t为货币,εc, t为偏好冲击,ηh为劳动供给弹性的倒数,θ1与θ2分别为劳动与货币效用的贡献。资本利率vj, t将资本Kj, t转换为有效资本Kj, t:Kj, t=vj, tKj, t-1。资本Kj, t的积累方程:Kj, t=(1-δ)Kj, t-1+εi, t[1-S(Ij, t/Ij, t-1)]Ij, t,δ为折旧率,S(·) 为调整成本,稳态时其二阶导数ηk>0,εi, t为投资冲击,Ij, t为投资。预算约束为:
| $ \begin{array}{l} {C_{j,t}} + {I_{j,t}} + \left( {{B_{j,t}}/{P_t}} \right) + \left( {{M_{j,t}}/{P_t}} \right) + {T_{j,t}} + k\left( {{v_t}} \right){{\bar K}_{j,t - 1}} \le \left( {{W_{j,t}}{H_{j,t}}/{P_t}} \right) + {\mathit{\Omega }_{j,t}} + {\mathit{\Psi }_{j,t}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + ({R_{n,t - 1}}{B_{j,t - 1}}/{P_t})\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + ({M_{j,t - 1}}/{P_t})\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + ({R_{k,t}}{v_t}{{\bar K}_{j,t - 1}}/{P_t}) \end{array} $ | (2) |
其中:Bj, t为政府债券,Tj, t为税收,k(vt) 为物质资本生产成本且其曲率ηv>0。Wj, t为工资,Ωj, t为状态依赖证券;Ψj, t为中间品净利润,Rn, t-1为名义利率,Rk, t为资本收益率。一阶条件有:
消费:
| $ {\lambda _t} = {\varepsilon _{c,t}}/({C_t} - h{C_{t - 1}}) - \beta h{\varepsilon _{c,t + 1}}/({C_{t + 1}} - h{C_t}) $ | (3) |
债券:
| $ {\lambda _t}/{P_t} = \beta {\lambda _{t + 1}}{R_{n,t}}/{P_{t + 1}} $ | (4) |
投资:
| $ 1={{\varepsilon }_{i,t}}{{Q}_{t}}\{1-S({{I}_{t}}/{{I}_{t-1}})-{{I}_{t}}S'/{{I}_{t-1}}\}+\beta {{\varepsilon }_{i,t+1}}{{Q}_{t+1}}{{({{I}_{t+1}}/{{I}_{t}})}^{2}}S'{{\lambda }_{t+1}}/{{\lambda }_{t}} $ | (5) |
资本量:
| $ {Q_t} = (\beta {\lambda _{t + 1}}/{\lambda _t})[{r_{k,t + 1}}{\nu _{t + 1}} - \kappa ({\nu _{t + 1}}) + {Q_{t + 1}}\left( {1 - \delta } \right)] $ | (6) |
资本利用率:
| $ {r_{k,t}} - \kappa ' ({\nu _t}) = 0 $ | (7) |
货币余额:
| $ {\varepsilon _{c,t}}{({M_t}/{P_t})^{ - 1}} - {\lambda _t}(1 - R_{n,t}^{ - 1}) = 0 $ | (8) |
其中:πt+1=Pt+1/Pt,rk, t=Rk, t/Pt,λt为边际效用,Qt为资本价格。家庭提供劳动的目标函数为:
| $ {\rm{Ma}}{{\rm{x}}_{W_{j,t}^*}}{E_t}\{ \sum\limits_{t = 0}^\infty {{{\left( {\beta \mu } \right)}^s}} [(\lambda t + s/{P_{t + s}})W_{j,t}^*{H_{j,t + s}}{F_{t,t + s}} - {\varepsilon _{c,t + s}}{({H_{j,t + s}})^{1 + {\eta _h}}}/(1 + {\eta _h})]\} $ | (9) |
其中:μ为每期不设定最优工资的概率,Hj, t为劳动力供给,εW, t为工资加成率。求解最优工资:
| $ \begin{array}{l} W_{j,t}^*:{\left( {W_t^*} \right)^{\frac{{\varepsilon W,t + s\;\eta h + 1}}{{\varepsilon W,t + s - 1}}}} = \sum\limits_{t = 0}^\infty {{{\left( {\beta \mu } \right)}^s}} \left\{ {{\varepsilon _{c,t + s}}{\varepsilon _{W,t + s}}{{\left[ {{L_{t + s}}{{({F_{t,t + s}}/{W_{t + s}})}^{\frac{{ - \varepsilon W,t + s}}{{\varepsilon W,t + s - 1}}}}} \right]}^{\eta h + 1}}/\left( {{\varepsilon _{W,t + s}} - 1} \right)} \right\}/\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{t = 0}^\infty {{{\left( {\beta \mu } \right)}^s}} \left\{ {{L_{t + s}}{{({F_{t,t + s}}/{W_{t + s}})}^{\frac{{ - \varepsilon W,t + s}}{{\varepsilon W,t + s - 1}}}}/\left( {{\varepsilon _{W,t + s}} - 1} \right)\left[ {{F_{t,t + s}}{\lambda _{t + s}}/{P_{t + s}}} \right]} \right\} \end{array} $ | (10) |
依据总工资Wt定义式,可得:
| $ {{W}_{t}}={{[\mu {{({{g}_{y}}{{({{\pi }_{t-1}})}^{{{\sigma }_{w}}}}{{(\pi _{t}^{*})}^{1-{{\sigma }_{w}}}}{{W}_{t-1}})}^{1/(1-{{\varepsilon }_{W,t}})}}+\left( 1-\mu \right){{(W_{t}^{*})}^{1/(1-{{\varepsilon }_{W,t}})}}]}^{1-{{\varepsilon }_{W,t}}}} $ | (11) |
2.最终产品生产者。在最终产品市场中产品生产者的生产函数为:
| $ {Y_t} = {[{\int_0^1 {{Y_{i,t}}} ^{1/{\varepsilon _{p,t}}}}di]^{{\varepsilon _{p,t}}}} $ | (12) |
其中:εp, t为价格加成比率,衡量中间品市场竞争程度。依据最终产品生产者的目标函数得到最优中间品需求为:
| $ {Y_{i,t}}:{Y_{i,t}} = {({P_{i,t}}/{P_t})^{ - {\varepsilon _{p,t}}/\left( {{\varepsilon _{p,t}} - 1} \right)}}{Y_t} $ | (13) |
最优总体价格Pt为:
| $ {P_t} = {[{\int_0^1 {({P_{i,t}})} ^{1/({\varepsilon _{p,t}} - 1)}}di]^{({\varepsilon _{p,t}} - 1)}} $ | (14) |
3.中间品厂商。在垄断竞争的中间品市场中企业生产函数为:
| $ {Y_{i,t}} = {\rm{Max}}\{ {({A_t})^{1 - {\alpha _G} - {\alpha _K}}}{({L_{i,t}})^{1 - {\alpha _K}}}{({K_{G,t}})^{{\alpha _G}}}{({K_{i,t}})^{{\alpha _K}}} - {A_t}F,0\} $ | (15) |
其中:αk和αG分别为私人资本和公共资本的产出弹性。At为技术,F≠0为固定成本。KG, t为生产性公共资本,演化方程为:KG, t=(1-δG)KG, t-1+ςtGt,δG为折旧率,ςt为公共财政支出占比且为外生变量。(15) 式表明,公共资本不具排他性,生产者都能享受相同公共资本,且中间品厂商有垄断权力。为保证 (15) 式生产函数的合理性,必须满足:αG+αK < 1。
生产者的最优化决策分两步:第一步,成本最小化:
| $ {\rm{Min}}{W_t}{L_{i,t}} + {R_{k,t}}{K_{i,t}} $ | (16) |
最优劳动力需求:
| $ {W_t} = {\xi _t}(1 - {\alpha _K}){({A_t})^{1 - {\alpha _G} - {\alpha _K}}}{({K_{G,t}})^{{\alpha _G}}}{({K_{i,t}}/{L_{i,t}})^{{\alpha _K}}} $ | (17) |
最优资本需求:
| $ {R_{k,t}} = {\xi _t}{\alpha _K}{({K_{G,t}})^{{\alpha _G}}}{({A_t})^{1 - {\alpha _G} - {\alpha _K}}}{({L_{i,t}}/{K_{i,t}})^{1 - {\alpha _K}}} $ | (18) |
ξt为名义边际成本MCi, t。化简 (17) 式和 (18) 式有 (19) 式:
| $ {\xi _t} = {[{R_{k,t}}/{\alpha _K}]^{{\alpha _K}}}{({A_t})^{\left( {{\alpha _G} + {\alpha _K} - 1} \right)}}{[{W_t}/(1 - {\alpha _K})]^{1 - {\alpha _K}}}/{({K_{G,t}})^{{\alpha _G}}} $ | (19) |
第二步,收益流的折现值最大化:
| $ {\rm{Ma}}{{\rm{x}}_{P_{i,t}^*}}\;\sum\limits_{t = 0}^\infty {{{(\beta \Phi )}^s}} {E_t}[({\lambda _{t + s}}/{\lambda _t})\left[ {({P_{i,t + s}} - M{C_{t + s}})/{P_{t + s}}]{Y_{i,t + s}}} \right] $ | (20) |
其中:Ф为每期不调价概率。最优价格Pt*满足:
| $ \begin{array}{l} P_t^* = \sum\limits_{t = 0}^\infty {{{(\beta \Phi )}^s}} {E_t}\left[ {\frac{{{\lambda _{t + s}}}}{{{\lambda _t}}}\frac{{{\varepsilon _{p,t + s}}}}{{{\varepsilon _{p,t + s}} - 1}}\frac{{M{C_{t + s}}}}{{{P_{t + s}}}}{{\left( {\frac{{{\Delta _{t,t + s}}}}{{{P_{t + s}}}}} \right)}^{ - {\varepsilon _{p,t + s}}/\left( {{\varepsilon _{p,t + s}} - 1} \right)}}{Y_{t + s}}} \right]\\ \;\;\;\;\;\;\;/\sum\limits_{s = 0}^\infty {{{(\beta \Phi )}^s}} {E_t}\left[ {\frac{{{\lambda _{t + s}}}}{{{\lambda _t}}}\left( {\frac{1}{{{\varepsilon _{p,t + s}} - 1}}} \right){{\left( {\frac{{{\Delta _{t,t + s}}}}{{{P_{t + s}}}}} \right)}^{ - 1/\left( {{\varepsilon _{p,t + s}} - 1} \right)}}{Y_{t + s}}} \right] \end{array} $ | (21) |
依据 (14) 式总体价格指数可得:
| $ {P_t} = {[\Phi {({P_{t - 1}}{({\pi _{t - 1}})^{{\sigma _P}}}{(\pi _t^*)^{1 - {\sigma _P}}})^{1/\left( {{\varepsilon _{p,t}} - 1} \right)}} + (1 - \Phi ){(P_t^*)^{1/\left( {{\varepsilon _{p,t}} - 1} \right)}}]^{\left( {{\varepsilon _{p,t}} - 1} \right)}} $ | (22) |
4.政府。借鉴胡永刚和郭长林 (2013) 的做法,设定财政政策规则有:
| $ \begin{array}{l} {\rm{ln}}({G_t}/G) = {\rho _G}{\rm{ln}}({G_{t - 1}}/G) - (1 - {\rho _G})\{ {\lambda _{G,\pi }}{\rm{ln}}({\pi _{t - 1}}/\pi _t^*)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { + {\lambda _{G,\pi }}{\rm{ln}}({Y_{t - 1}}/Y_{t - 1}^*)} \right\} + {\lambda _{Z,t}}{e_{Z,t}} + {\rm{ln}}({\varepsilon _{g,t}}) \end{array} $ | (23) |
其中:Yt*为总产出趋势,等于去趋势后的均衡产出与技术乘积。从开放经济视角看,模型的“财政支出”不仅含传统意义上的财政支出,还包括净出口。据此借鉴Slobodyan和Wouters (2008),引入对技术冲击的反应系数λz, t来体现这种影响。货币政策方面,鉴于人民银行综合运用价格型与数量型工具,借鉴栗亮和刘元春 (2014) 的做法,通过加权利率和货币供给增速的方式,构建混合货币政策工具:
| $ \begin{array}{l} {\rm{ln}}({{\rm X}_t}/X) = {\lambda _M}{\rm{ln}}({X_{t - 1}}/X) + (1 - {\lambda _M})\{ {\lambda _{M,\pi }}{\rm{ln}}({E_t}{\pi _{t + 1}}/\pi _t^*)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {\lambda _{M,Y*}}{\rm{ln}}({Y_t}/Y_t^*)\} + {\rm{ln}}{\varepsilon _{M,t}} \end{array} $ | (24) |
其中:Xt为混合货币政策工具:Xt=(1/ωt)ζ(Rn, t)1-ζ,ωt=Mt/Mt-1,πt*为通胀目标,ζ为权重,代表我国宏观政策转型,尤其是货币政策转型的影响,可视为我国货币政策调控方式的表征。
5.总体资源约束。
| $ {Y_t} = {C_t} + {G_t} + {I_t} + \kappa ({\nu _t}){{\bar K}_{t - 1}} $ | (25) |
6.外生冲击过程。本文包括9种外生冲击。除通胀目标冲击外,其余外生冲击均为AR(1) 过程。通胀目标冲击为:
| $ \begin{array}{l} {\rm{Ln}}(\pi _t^*) = (1 - {\rho _{{\pi ^*}}}){\rm{Ln}}\left( \pi \right) + {\rho _{{\pi ^*}}}{\rm{Ln}}(\pi _{t - 1}^*) + {\phi _Z}{e_{z,t}} + {\phi _i}{e_{i,t}} + {\phi _c}{e_{c,t}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; + {\phi _w}{e_{w,t}} + {\phi _p}{e_{p,t}} + \phi {e_{g,t}} + {\phi _{ς}}{e_{ς,t}} + {e_{\pi ,t}} \end{array} $ | (26) |
上述过程借鉴Ireland (2007) 的做法,体现通胀目标调整的内生性。具体地,中央银行调整通胀目标时有两种倾向:一是逆周期调整,即通胀目标的调整方向与不同外生冲击下的通胀变动相反,当正向需求冲击 (偏好冲击、投资冲击、政府支出冲击) 和加成冲击会推高通胀时,降低通胀目标;而当正向技术冲击降低通胀时,提高通胀目标即ϕZ>0。公共财政支出部分增加时,会扩大总供给,抑制通胀,但是,此时提高通胀目标,即ϕs>0,而ϕi、ϕc、ϕw、ϕp和ϕg均小于0。另一种是顺周期调整。
四、 学习型预期的理论刻画与说明
借鉴Slobodyan和Wouters (2012) 的思想,以前瞻性变量为基础,将其表示为对应滞后变量的线性组合,以此表征预期形成机制。具体构造过程如下:
首先,将线性化DSGE模型写为:
| $ {A_0}[{y_{t - 1}}{\Delta _{t - 1}}]' + {A_1}[{y_t}\;\;\;{\Delta _t}]' + {A_2}{E_t}{y_{t + 1}} + {B_0}{\varepsilon _t} = 0 $ | (27) |
其中:yt和Δt分别为内外生变量。在满足Blanchard和Kahn (1980) 条件下 (27) 式的解为:
| $ [{y_t}\;\;{\Delta _t}]' = \Omega + T[{y_{t - 1}}\;\;\;{\Delta _{t - 1}}]' + R{\varepsilon _t}\;\;\;其中\Omega ,{\rm{T}}和{\rm{R}}为系数矩阵。 $ | (28) |
其次,公众在预期形成过程中设定前瞻性变量为滞后1期的前瞻性变量的线性函数:ytf=XtTβt0+ut,βt0为系数矩阵,ut为观测误差向量。采用卡尔曼滤波法更新系数矩阵,设定系数矩阵满足:vec(βt-β0)=F×vec(βt-1-β0)+vt,vec为向量运算符号,F为对角矩阵且主对角元素ρ≤1,vt为服从正态分布的残差项且方差与协方差矩阵为V。
再次,采用卡尔曼滤波法更新系数:
| $ {{\beta }_{t|t}}={{\beta }_{t|t-1}}+{{P}_{t|t-1}}{{X}_{t-1}}[\sum +]X_{t-1}^{T}{{P}_{t|t-1}}{{X}_{t-1}}{{]}^{-1}}(y_{t}^{f}-X_{t-1}^{T}{{\beta }_{t|t-1}}) $ | (29) |
| $ {\beta _{t + 1|t}} - {\beta _0} = F({\beta _{t|t}} - {\beta _0}) $ | (30) |
| $ {P_{t|t}} = {P_{t|t - 1}} - {P_{t|t - 1}}{X_{t - 1}}{[\sum + X_{t - 1}^T{P_{t|t - 1}}{X_{t - 1}}]^{ - 1}}X_{t - 1}^T{P_{t|t - 1}} $ | (31) |
| $ {P_{t + 1|t}} = F\;\;{P_{t|t}}{F^T} + V $ | (32) |
其中:∑为观测误差ut的方差与协方差矩阵,Pt为βt的方差与协方差矩阵。每期将系数估计值βt|t-1代入预期形成机制,得到前瞻变量预期Etyt+1f,再将其引入 (27) 式,得到线性系统有:
| $ [{y_t}\;\;{\Delta _t}]' = {\Omega _t} + {T_t}[{y_{t - 1}}\;\;{\Delta _{t - 1}}]' + {R_t}{\varepsilon _t} $ | (33) |
最后,在定量刻画学习预期之前,对系数矩阵的卡尔曼滤波法赋予初始值,即对系数矩阵β1|0=β0、方差与协方差矩阵P1|0和Σ以及观测误差的方差与协方差矩阵V赋值。假定在初始取值下学习预期等价于理性预期。在观测误差ut满足同方差情形下用最小二乘估计法得到系数初始值,计算观测误差向量ut的方差与协方差矩阵,求解系数的方差与协方差矩阵的初始信念P1|0以及随机冲击vt的方差与协方差矩阵V。
五、 DSGE模型估计与预期形成机制的选择
(一) 数据说明。分析区间为1992年第1季度到2014年第4季度。数据自国家统计局网站和CEIC数据库。选取居民消费者价格指数代表通胀并以其定基比表征GDP平减指数。用社会零售品消费总额、固定资产投资以及城镇就业人数分别代表名义消费、投资和就业。利用城镇单位就业人员劳动报酬的季度累计值除以就业人数,得到名义工资,分别以广义货币供给同比和一年期存款基准利率分别代表数量型与价格型货币政策工具。上述数据均经过季节性调整。
(二) 结构性参数的校准与贝叶斯估计。在模型参数中,私人资本的折旧率δ取0.025,取1992年到2014年政府消费占GDP比重均值0.14,其余参数采用贝叶斯估计,先验分布说明为:(1) 消费惯性h、价格与工资的调整概率 (μ, Φ)、价格与工资的指数化程度 (σp, σw)、政策平滑因子λM、资本的产出弹性αk、折现因子β、资本利用率参数ϕv、预期到冲击间的跨期相关系数ρEM、生产性公共资本的产出弹性αG、混合货币政策工具的权重均衡值ζ、公共资本的折旧率δG、财政支出中用于形成公共物质资本的部分均衡值ς、通胀目标以及外生冲击的AR(1) 系数均介于0到1,选取Beta分布为先验分布。消费惯性h取值必介于0到1。刘斌 (2008) 通过贝叶斯估计得到的事后均值为0.65,定为先验均值。价格粘性概率Ф和工资粘性概率μ代表价格或工资粘性的强度。Zhang(2009) 通过GMM估计得到取值分别为0.84和0.6,刘斌 (2008) 通过贝叶斯估计得到后验均值分别为0.85和0.6,两组结果接近。据此确定Ф=0.85和μ=0.6为先验均值。价格与工资的指数化程度 (σp, σw) 均位于[0,1],故设先验均值为0.5。资本利用率成本函数的曲率ηv为资本利用率弹性ϕv的函数:ηv=(1-ϕv)/ϕv>0。故合理的先验均值ϕv为0.5。依据国内文献对资本产出弹性αk的取值 (李成等, 2011等),定αk先验均值为0.5。由于生产性公共资本的产出弹性αG与资本产出弹性αk必须小于1,结合αk先验均值可知,αG必须小于0.5,由此设定αG先验均值为0.25,接近郭长林 (2016) 的估计。混合货币政策工具的权重均衡值ζ同栗亮和刘元春 (2014) 一样取先验均值为0.5。就公共资本折旧率δG而言,金戈 (2012) 结合我国实际测算为9.2%,郭长林 (2016) 将先验均值定为9%并通过贝叶斯估计得到后验均值0.0824。结合上述三组取值,确定δG的先验均值为8.81%,推算公共财政支出占比均衡值ς为0.1914。宏观政策规则通过GMM估计获取,见表 1,将估计值确定为先验均值。
| 参数 | λM | λM,π | λM, Y | 可决系数 | D.W.值 | Hansen过度识别检验 |
| 货币政策工具 | 0.2412[1.94] | 0.1878[1.51] | 0.3809[1.92] | 0.65 | 1.75 | 10.08(0.54) |
| 参数 | ρG | λG,π | λG, Y | 可决系数 | D.W.值 | Hansen过度识别检验 |
| 财政政策 | 0.3628[3.41] | -2.96[-3.38] | 0.9858[2.20] | 0.17 | 1.20 | 4.16(0.12) |
| 注:混合货币政策工具估计时,取权重为0.5,这也是时变权重ζt的先验均值。 | ||||||
依据均衡条件:ω=Zπ和β=ω/Rn可知,折现因子β、均衡技术增长率Z以及均衡通胀π和均衡利率Rn等存在关联。利用GDP季度环比增速均值确定Z。1992年第1季度到2014年第4季度实际GDP环比增速的均值为1.027,确定均衡增长率Z=1.027。取通胀均值π为1.0144,得ω=1.0378。我国利率体系包括官方管制利率和市场化利率,因此确定Rn需结合两方面信息,取两者均值代表模型的名义利率即均衡利率Rn为1.0464。由此可得β=0.9918。大量研究认为,通胀目标有很高的持续性 (Del Negro和Eusepi, 2010),将其持续性系数ρπ*的先验均值定为0.95。外生冲击持续参数介于0到1,故先验均值定为0.5。
(2) 均衡技术增长率Z,均衡通胀π,均衡名义利率Rn,通胀预期和产出增长率反应系数 (λπ、λGY),资本调整成本弹性ηk,价格加成比率εp,工资加成比率εw,劳动供给弹性的倒数ηh,中央银行的通货膨胀目标对外生冲击的反应系数 (ϕZ、ϕi、ϕc、ϕg、ϕw、ϕp和ϕς),先验分布定为Gamma分布。ηk为资本边际成本函数S’(gy) 在投资增速等于Z时的导数,取值大于0即投资增速越高,边际生产成本越大。刘斌 (2008) 通过贝叶斯估计得到的事后均值为2.09。由此确定ηk的先验均值为2。价格加成比率εp和工资加成比率εw分别反映垄断竞争市场中的垄断市场能力,须大于1,结合Justinano和Primiceri (2013) 和Sala等 (2010),设1.15为εp、εw两者的先验均值。就劳动供给弹性的倒数ηh而言,王君斌和王文甫 (2010) 认为在我国定为3较合理,故取3为先验均值。此外,固定成本与实际产出之比F/Y=εp-1,说明固定资产与产出之比与加成比率正相关;投资占比i/y=αk[Z-(1-δ)]/[Z/β-(1-δ)]。将前述参数先验均值代入得i/y=0.42,接近从1992年到2014年投资与GDP之比均值40%,表明其他校准值合理。
通货膨胀目标对外生冲击的反应系数的校准借鉴Ireland (2007) 的做法,通过多次估计尝试,将先验均值设定为0.01。借鉴Slobodyan和Wouters (2008、2012) 的思路,λz, t的先验均值确定为0.5,方差为0.25。现有文献通常将外生冲击标准差的先验概率分布定为逆伽玛分布 (inv-Gamma),本文亦如此。设标准差的先验均值为0.01。通过不断估计与尝试,获取先验均值与标准差。
(三) 基于学习型预期形成机制下对DSGE模型的评估与预测。既包括对观测变量预测能力的评估,也包括对非观测变量预测能力的评估。在图 1中,实线段为实际值,带圈的实线为预测值,虚线为95%的预测置信区间。可见,模型不仅对产出增长率、消费增长率、投资增长率、工资增长率、通货膨胀、货币供给增速和利率等观测变量的预测值与实际变量保持了相对一致走势,而且对以股票价格为代表这种资产价格缺口保持了较好的预测能力。同时,由于模型估计时主要采用了反映经济基本面的数据,模型对资产价格缺口变动的良好预测表明,尽管我国资产价格可能存在泡沫,但是经济基本面在主导资产价格方面发挥了积极作用,即我国资产市场可能存在“理性泡沫”(沈哲, 2013;等等)。在理性泡沫下公众预期未来能以更高价格出售资产,从而导致其愿意支付比基本面价值更高的价格购买资产,以便未来获得资本利得,并产生资产价格对基本面的偏离,并且理性泡沫不影响预期收益率。这可能正是模型所预测的资产价格与实际资产价格保持一致的关键。同时,这也印证了国外研究学习机制对资产价格动态的观点 (Burnside等, 2015):公众学习机制提供以股票价格为代表的资产价格脱离基本面价格的重要途径。整体而言,在本文所选择的这种学习型预期形成机制下模型能对我国宏观经济提供较好的预测。
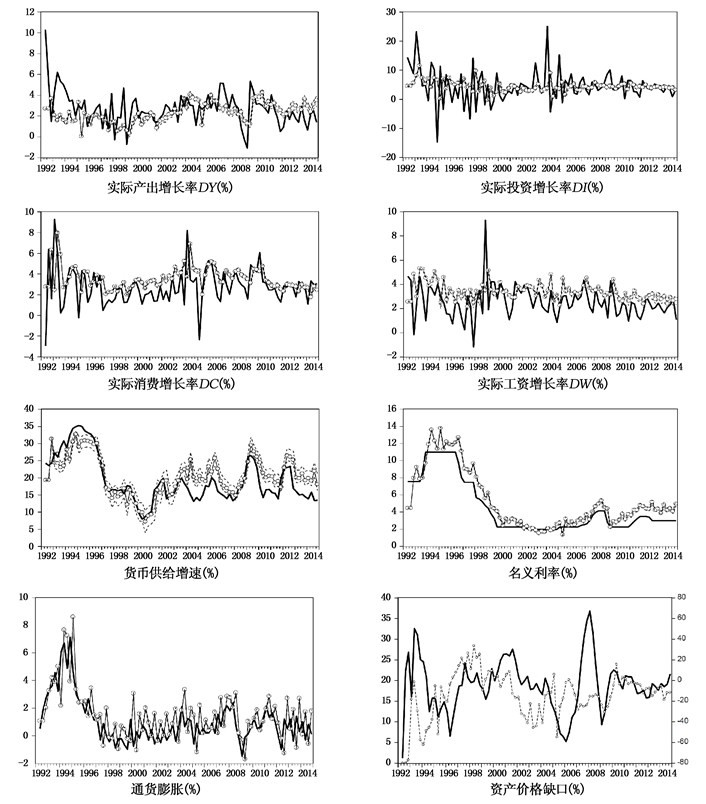
|
| 注:模型预测值为带圈的虚线段 (左轴),而实际值为粗实线段 (右轴) |
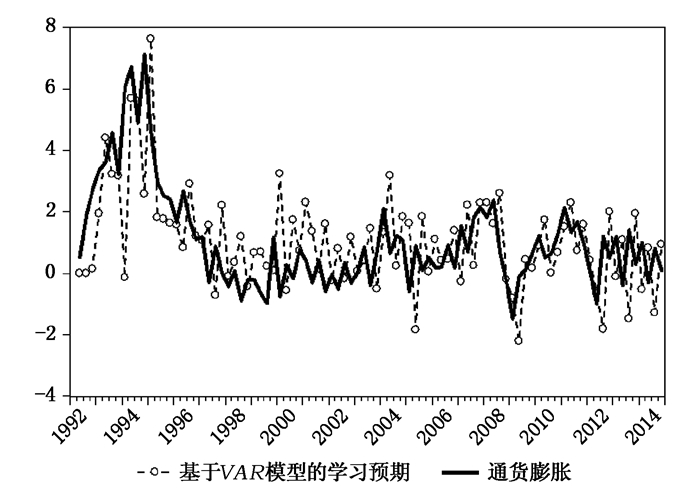
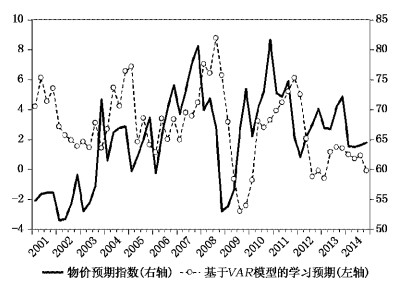
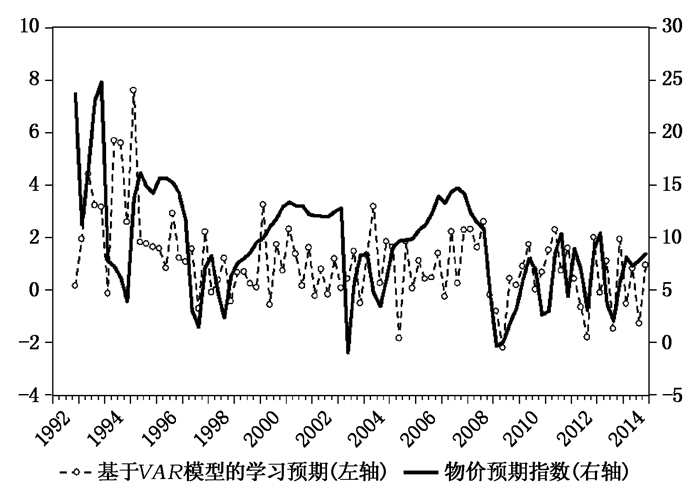
(四) 基于学习型预期与实际通胀及其通胀预期指标的对比分析。由图 2可见,基于多变量学习规则的预期与实际通胀保持相似走势,但是不完全一致。在部分时间内高于实际通胀,另一部分时间内低于通胀,而且这种高估与低估不随经济形势而立即逆转,反而持续一段时间,体现出通胀预期调整的持续性 (Fuhrer, 2015),如20世纪90年代通胀预期对实际通胀的高估一直持续到亚洲金融危机之后。同时,随着经济市场化进程的稳步推进,基于学习型预期对实际通胀的高估与低估所持续的时间缩短,由早期持续数年之久到现在仅持续几个季度。进一步,将这种学习预期与中国人民银行所公布的物价预期指数、国家统计统计局所公布的消费者预期指数对比。由图 3和图 4可见,这种预期与上述官方所发布的指数保持相似,乃至一致走势,进一步证实了本文所选的预期形成机制的合理性。
六、 学习型预期约束下货币政策与财政政策搭配特点及其对通胀预期管理的影响分析
(一) 在简化模型下预期稳定时货币政策与财政政策搭配的理论条件。假设:(A) 消费惯性h=0;(B) 产出等于消费和政府购买之和;(C) 劳动力市场完全竞争;(D) 资本利用率和公共资本折旧率均为1;(E) 价格指数化程度σp=0;(F) 政策平滑系数均为0;(G) 固定投资成本F=0,aK=0。将上述假设代入模型最优化条件得到由欧拉方程、菲利普斯曲线和货币政策规则所组成的线性系统并进行矩阵运算得到:
| $ {E_t}{N_{t + 1}} = - {\Pi _1}{N_t} $ | (34) |
其中:Nt=
| $ \left| {\begin{array}{*{20}{c}} {\lambda + \zeta \vartheta {R_n}/({R_n} - 1)}&{{\lambda _{M,{Y^*}}} - {\lambda _{M,x}}\vartheta \nu /(1 - {g_y})}&{{\lambda _{M,\pi }}/\beta \vartheta }&{ - {\lambda _{M,\pi }}{\lambda _{G,Y}}\chi \vartheta /\beta (1 - {g_y})}&{ - {\lambda _{M,x}}{\lambda _{G,\pi }}\chi \vartheta /\beta (1 - {g_y})}\\ {\zeta {R_n}\vartheta (1 - {g_y})/({R_n} - 1)}&{\lambda - \nu ({\lambda _{M,x}}\vartheta - 1) + \vartheta (1 - {g_y}){\lambda _{M,{Y^*}}} - {g_y}{\lambda _{G,Y}} + 1}&{({\lambda _{M,x}}\vartheta - 1)(1 - {g_y})/\beta - {g_y}{\lambda _{G,x}}}&{{g_y}{\lambda _{G,Y}} - ({\lambda _{M,x}}\vartheta - 1)\chi {\lambda _{G,Y}}/\beta }&{{g_y}{\lambda _{G,\pi }} - ({\lambda _{M,\pi }}\vartheta - 1)\chi {\lambda _{G,\pi }}/\beta }\\ 0&{\nu /(1 - {g_y})}&{\lambda + \left( {1/\beta } \right)}&{{\lambda _{G,Y}}\chi /\beta (1 - {g_y})}&{{\lambda _{G,\pi }}\chi /\beta (1 - {g_y})}\\ 0&l&0&\lambda &0\\ 0&0&l&0&\lambda \end{array}} \right| = 0 $ | (35) |
其中:λ为特征根,ϑ=(Rn-1)/[ζ(2-Rn)-(1-Rn)],χ=[αG(ηh+1)(1-gy)+gy>],ν=(1-Φ)[ηh(1-gy)+1]/(Φβ)。
依据学习型预期定义,要保证预期稳定,要求前瞻变量
| $ \begin{array}{l} {\lambda ^2} + \{ 1/\beta - \nu ({\lambda _{M,\pi }}\vartheta - 1) + \vartheta (1 - {g_y}){\lambda _{M,Y*}} - {g_y}{\lambda _{G,Y}} + 1\} \lambda \\ + [1 + \vartheta (1 - {g_y}){\lambda _{M,Y*}} - {g_y}{\lambda _{G,Y}}]/\beta - \nu {g_y}{\lambda _{G,\pi }}/(1 - {g_y}) = 0 \end{array} $ | (36) |
依据Blanchard-Kahn条件,(36) 式必有两个绝对值大于1的根。依据韦达定理可知,满足如下必要条件之一时公众预期能稳定:
| $ {A_0} + {A_1}{\lambda _{M,Y*}} + {A_2}{\lambda _{G,Y}} + {A_3}{\lambda _{G,\pi }} - {\lambda _{M,\pi }} > 0 $ | (37) |
| $ 1/\vartheta - {A_3}{\lambda _{G,\pi }} - {A_1}{\lambda _{M,Y*}} - {A_2}{\lambda _{G,Y}} - {\lambda _{M,\pi }} < 0 $ | (38) |
| $ \left\{ \begin{array}{l} {A_0} + {A_1}{\lambda _{M,Y*}} + {A_2}{\lambda _{G,Y}} + {A_3}{\lambda _{G,\pi }} - {\lambda _{M,\pi }} < 0\\ 1/\vartheta - {A_3}{\lambda _{G,\pi }} - {A_1}{\lambda _{M,Y*}} - {A_2}{\lambda _{G,Y}} - {\lambda _{M,\pi }} > 0 \end{array} \right. $ | (39) |
其中:A0=[1+2(β+1)/(νβ)]/ ϑ>0,A1=(1-gy)(β+1)/(νβ)>0,A2=-gy(β+1)/(νϑβ) < 0,A3=-gy/[ϑ(1-gy)] < 0。
上述条件表明,在学习型预期下公众预期稳定要求货币政策与财政政策必须采用特定搭配方式。同时,这种搭配方式与经济基本面因素以及货币政策调控方式有关。进一步,在公众预期稳定性要求下宏观政策特定搭配方式体现为,在给定宏观政策对产出反应力度下,上述理论条件规定了宏观政策对通胀预期反应力度的变动轨迹。同样地,在给定宏观政策对通胀预期反应力度下,上述理论条件也制约了宏观政策对产出的反应力度。进而通过观察发现,上述搭配条件实质上界定了宏观政策规则中反应系数的临界值。就 (37) 式而言,给定宏观政策对产出的反应系数,为保证预期稳定,财政政策对通胀的反应系数越大,货币政策对通胀预期反应系数的临界值就越小,对 (38) 式而言,当财政政策对通胀反应系数越大时,货币政策对通胀预期反应系数的临界值恰好与 (37) 式相反。在 (39) 式中,当财政政策对通胀反应系数变化时,货币政策对通胀预期反应系数的临界值介于上述两种情况之间。同理,当给定宏观政策对通胀的反应系数时,当货币政策对产出的反应系数越大时,只有财政政策对产出反应系数的临界值越小才能保证预期稳定。得到命题1:
命题1:在给定宏观政策对产出反应系数,要实现公众预期稳定,货币政策对通胀预期的反应系数与财政政策的反应系数临界值变动方向既可能一致,也可能相反;而在给定通胀预期或通胀反应系数下,货币政策和财政政策对产出反应系数临界值的变动方向相反。
可见,上述命题一方面在应对产出方面要求货币政策与财政政策保持“一松一紧”搭配,而如果考虑通胀预期稳定,要求货币政策与财政政策改变这种搭配,转换为“双松”或“双紧”搭配模式。这可视为对传统货币政策与财政政策搭配模式的重要拓展。
(二) 在复杂模型下对预期稳定时货币政策与财政政策搭配特征的数值模拟分析。前述理论命题是基于简化的模型,是否适合本文所构造的复杂模型还需验证。同时,鉴于我国货币政策调控的复杂性和财政支出的生产性特征,在考察宏观政策搭配方式时,分析混合货币政策工具中货币增速权重ζ和公共资本产出弹性αG的影响。本文的参数模拟结果与命题一致,货币政策和财政政策对通胀或通胀预期反应系数的临界值正向变动,而货币政策和财政政策对产出反应系数的临界值反向变动,如理论条件 (37) 式至 (39) 式那样,货币政策调控方式参数ζ对上述临界值产生影响,而公共资本的产出弹性αG对上述临界值未产生影响。
具体来看,随着货币政策调控方式参数ζ的增大,确保公众预期稳定的通胀预期或通胀反应系数临界值组合范围不断增大,而产出反应系数临界值组合不存在类似现象。这表明,与价格型工具相比,以数量型工具为主的货币政策调控更易确保预期稳定,体现出价格型货币政策工具比数量型货币政策工具对通胀变化更敏感,能更好控制通货膨胀及其预期的攀升 (马文涛,2011)。这在一定程度上既可以解释为何在市场化改革持续多年之后以数量型工具为主的货币政策对通胀预期管理的绩效不高 (熊海芳、王志强,2012等),经济一旦遭遇巨大冲击,通胀及其预期陡升陡降;也能解释在利率市场化持续推进且深入的背景下以数量型工具为主的货币政策调控绩效下降的现象 (陈彦斌等,2015)。与数量型货币政策工具相比,价格型工具不仅能更好地控制通胀,还有更高的透明度,更有效地向市场传达政策意图 (Calvo和Vegh, 1999),在引导公众预期方面,尤其是在通胀预期方面有更高的效率。
正是因为价格型工具的上述特征加上学习型预期形成机制的作用,货币政策调控越来越依赖价格型工具时,不仅货币政策与财政政策在应对通胀或通胀预期时应采取“双松”或“双紧”的搭配模式且在应对产出方面也呈现上述模式。从表面上看,上述发现似乎违背了一般经济直觉。因为从宏观政策制定者角度看,为降低决策失误并提高调控绩效,其不仅应提前采取措施预防决策失误的负面影响,也要在宏观调控背离经济形势时采取适当措施予以纠正,货币政策与财政政策所采取的“一松一紧”的搭配模式恰好将两种政策调控风险予以对冲,有助于实现最优宏观调控绩效,避免政策调整过度、引发经济不稳定。然而,在上述直觉背后往往被忽视的是,上述搭配模式所需要的是公众的理性预期,能及时准确评判宏观调控绩效的结果。同时,宏观政策主要借助于总需求影响经济。
正如模型所展示的,上述条件在我国不完全成立。但是,这并不是说,我国公众预期绝非是非理性的,而要强调的是在本文学习型预期下公众会相对有效地利用信息,不会系统高估或低估实际通胀,而与实际通胀保持一致趋势 (李昊和王少平,2011;王雅炯,2012)。同时,我国宏观政策传导不仅依赖总需求渠道,也依赖总供给渠道 (彭方平、连玉君, 2010;郭长林,2016)。上述条件使得宏观政策调控能同时从总需求面和总供给面对宏观经济产生影响,客观上构成了宏观政策采取“双松”或“双紧”搭配模式的基础所在。毕竟与宏观政策仅能对总需求产生影响不同,宏观政策能从供求两端“发力”能更精确地锁定政策目标。这种对政策目标的“精确锁定”显然更有助于公众形成稳定预期,尤其是通胀预期。另一方面,在这种学习型预期下公众的通胀预期不像理性预期那样,能及时跟随经济形势变化,反而是呈现很强持续性,在一定时期内引发通胀预期与实际通胀的持续偏离。此时,尽管货币政策与财政政策维持“一松一紧”的调控模式能很好对冲经济形势所产生的风险,但是不能稳定公众预期,相反可能因宏观政策在管理公众预期方面的过度保守或立场不坚定而增强这种预期变化的持续性,产生公众预期与宏观经济形势变化的完全背离,违背稳定公众预期的初衷。显而易见,在本文学习型预期作用下货币政策与财政政策选择“双松”或“双紧”的搭配模式能增强宏观政策的“历史依赖性”(Woodford, 2003),体现宏观政策制定者维护政策目标的决心,能向公众传达更明确的政策信号,使政策制定者维护政策目标的承诺更可信。当货币政策调控逐步由数量型转向价格型时,宏观政策透明度提高并进一步增强政策的可预期性。这在客观上要求货币政策不仅要与财政政策在应对通胀及其预期方面保持“双松”或“双紧”搭配模式,而且与财政政策在应对产出方面也保持这种模式。否则,一方面是政策透明度的提高,而另一方面是宏观政策在应对通胀预期和产出时反应方向的不一致,会引发预期混乱,大大降低政策可信度,从而影响宏观调控绩效。进一步,不仅从宏观政策理论看,还是从宏观调控实践看,货币政策与财政政策所采取的“双松”或“双紧”搭配模式也与宏观政策在面对传统的产出与通胀目标时所面临的“稳增长”与“反通胀”之间的抉择存在关联 (Benanke, 2004;Levin和Taylor, 2010)。依据Mishkin (2007、2008) 的观点,“稳增长”与“反通胀”不仅有矛盾面,而且有相互统一、相互增强的一面。具体表现为,一方面反通胀与稳增长之间的有效抉择能增强宏观政策尤其是货币政策的稳定性,促成公众形成稳定通胀预期;另一方面,通胀预期稳定为宏观政策面临反通胀与稳增长之间的抉择时创造适度空间,使宏观政策在追求短期内经济稳定时,不用担心因通胀偏离目标而导致未来通胀高企,也就是说,稳定通胀预期强化了宏观政策的反通胀立场,铸造了预期形成的稳固名义瞄。从这个角度看,货币政策与财政政策所采取的这种“双松”或“双紧”的搭配模式恰好为公众的预期形成提供了一个明确且清晰的名义锚,不仅能在外部经济形势恶化时应对通胀及其预期的正向或负向冲击,实现公众预期的稳定,还能确保宏观政策在稳增长与反通胀之间实现有效平衡,“巩固”这种名义锚。
历史上,我国宏观政策先后经历了1998年到2003年的“积极财政政策”搭配“扩张型货币政策”、2004年到2006年的“双稳健”、2008年到2010年的“适度宽松货币政策”搭配“积极财政政策”以及2011年以来的“积极财政政策”搭配“稳健货币政策”。尽管货币政策与财政政策的搭配在各个时期表述不一样,但是,仔细察看各时期的《货币政策报告》发现,上述政策搭配在本质上均是“双松”或“双紧”模式。更重要的是,在这种搭配模式下我国宏观经济呈现平稳化态势 (马文涛和魏福成, 2011),进一步佐证了这种宏观政策搭配的合理性。同时,自20世纪90年代确立社会主义市场经济体制以来,我国宏观政策转型稳步推进,先是在1998年确立以货币供给量为核心的间接调控体系,近年来则加快利率市场化进程,而我国经济的市场化由早期的商品市场扩展到当前的要素市场,取得显著进展,其间经济结构发生了明显变化,促使公众通过持续的学习机制不断更新对宏观经济的预期 (李成等,2011),而这种宏观政策搭配正是这样一种市场经济结构大变迁所引发形成的公众学习机制下实现的,正好体现了本文所选择的这种学习型预期形成机制对宏观政策搭配的重要性。
七、 结论与政策含义
本文基于经典动态随机一般均衡模型,结合我国宏观调控的特点,探讨了学习型预期对宏观政策搭配及其通胀预期管理的影响。研究发现:(1) 在学习型预期作用下模型不仅能刻画通胀预期与实际通胀之间的趋势一致性与持续偏离,还能反映人民银行所公布的物价预期指数和国家统计统计局所公布的消费者预期指数变化。(2) 为确保公众预期稳定,货币政策与财政政策搭配不仅受各自对产出和通胀反应力度与反应方向的影响,还受劳动力市场、产品市场的消费偏好等基本面因素的影响。更重要的是,受到预期形成机制的显著制约。随着货币政策调控模式由以数量型工具为主转变为以价格型工具为主,只有当货币政策对通胀或通胀预期的敏感度提高时,才能实现对公众预期的管理与引导。与此同时,货币政策与财政政策的搭配也不应固守传统上的“一松一紧”模式,而是应在利率市场化不断深入且宏观政策不断转型的背景下及时由“一松一紧”搭配模式转变为“双松”或“双紧”搭配模式。这种搭配一方面借助于宏观政策从供需两端精确“发力”,体现宏观政策制定者维护政策目标的决心,向公众传达明确且清晰的政策信号,为公众预期形成提供唯一名义锚;另一方面通过宏观政策在稳增长与反通胀之间的有效平衡,“巩固”这种名义锚,体现政策制定者维护政策目标的高可信度,提高政策的可预期性,促使公众形成与政策意图一致且稳定的预期。
依据以上结论,在当前国际经济形势下,宏观政策调控应逐步放弃“大水漫灌式”刺激,转而实现“精确制导式”的定向调控。这种定向调控不仅要求宏观政策积极“挽救”总需求的“萎靡”,还要求宏观政策能从总供给面出发,与总需求的变化相配合,精确锁定政策目标。通过宏观政策的合理搭配,尤其是货币政策与财政政策应采取“双松”或“双紧”的搭配,向公众释放明晰的政策信号和可信的政策承诺,引导并塑造公众预期。不仅让预期管理成为宏观调控的重要手段,还要让公众预期成为宏观政策传导的重要渠道。一方面,宏观政策调控不仅要关注经济数据的“起伏”,更要通过统计调查手段,获取公众对经济形势感受的信息,并加强与公众沟通,向公众解释“过去的宏观政策何以那样,今天的宏观政策又何以这样”,增强公众对宏观调控的理解。另一方面,要进一步加大经济体制改革力度,着力疏通宏观政策传导机制并适时调整货币政策与财政政策的搭配形式。在保证宏观政策搭配稳定的同时,不可忽视灵活性与可操作性,着力扩大政策调控空间,使宏观政策与市场价格信号相配合,实现公众预期的逐步稳定和经济的平稳增长。
| [1] | 卞志村, 高洁超. 适应性学习、宏观经济预期与最优货币政策[J]. 经济研究, 2014(4): 32–46. |
| [2] | 郭长林. 被遗忘的总供给:财政政策扩张一定会导致通货膨胀吗?[J]. 经济研究, 2016(2): 30–41. |
| [3] | 胡永刚, 郭长林. 财政政策规则、预期与居民消费[J]. 经济研究, 2013(3): 96–107. |
| [4] | 栗亮, 刘元春. 经济波动的变异与中国宏观经济政策框架的重构[J]. 管理世界, 2014(12): 38–50. |
| [5] | 沈哲. 中国新股异常现象的行为解释[J]. 统计研究, 2013(5): 63–70. |
| [6] | Bianchi F, Ilut C. Monetary/Fiscal policy mix and agents beliefs[R]. Working Paper, 2015. |
| [7] | Burnside C, Eichenbaum M, Rebelo S. Understanding booms and busts in housing markets[R]. Working Paper, 2015. |
| [8] | Cochrane J H. Do higher interest rates raise or lower inflation[R]. Working Paper, 2015. |
| [9] | Fuhrer J. Expectations as a source of macroeconomic persistence:An exploration of firms' and households' expectation formation[R]. Working Paper, 2015. |
| [10] | García-Schmidt M, Woodford M. Are low interest rates deflationary? A paradox of perfect-foresight analysis[R]. NBER Working Papers No.21614, 2015. |
 2017, Vol. 43
2017, Vol. 43