文章信息
 | 财经研究 2016年42卷第12期 |
- 何雄浪, 姜泽林.
- He Xionglang, Jiang Zelin.
- 自然资源禀赋与经济增长:资源诅咒还是资源福音?——基于劳动力结构的一个理论与实证分析框架
- Natural Resource Endowments and Economic Growth: Resources Curse or Resources Blessing? A Theoretical and Empirical Analysis Framework Based on Labor Structure
- 财经研究, 2016, 42(12): 27-38
- Journal of Finance and Economics, 2016, 42(12): 27-38.
-
文章历史
- 收稿日期:2016-08-12

2016第42卷第12期
对“资源诅咒”与“资源福音”命题的剖析发端于对“荷兰病”(Dutch disease)问题的思考。“荷兰病”指的是资源贸易活动导致国内制造业衰退的现象,这种现象吸引了大量的学者进行研究。Corden和Neary (1982)最早提出了“荷兰病”模型,在Matsuyama (1992)模型的基础上,Sachs和Warner (1995)发展了动态的“荷兰病”内生增长模型,该模型对“荷兰病”作了经典的诠释,认为自然资源部门贸易规模的扩大会导致进入制造业部门的资本和劳动规模减小,出口自然资源产品带来外汇收入的增加使得本币升值,再次打压了制造业的竞争力,在制造业部门具有“干中学”的假设条件下,这种“荷兰病”就妨碍了经济增长。实质上,“荷兰病”就是自然资源禀赋与经济增长之间的悖论关系问题,即为“资源诅咒”问题(Auty,1994)。Sachs和Warner (1995)的研究引起了学者们的广泛关注,使得“资源诅咒”的研究工作相继展开。
人类的生产过程就是对自然资源开发的过程,自然资源的开发利用与劳动投入和配置存在着紧密的联系,从劳动、劳动力的角度探析“资源诅咒”问题能切中“资源诅咒”命题的本质。搜集国内外相关资料,可以发现从劳动力的角度分析“资源诅咒”问题的文献屈指可数,虽然有文献从人力资本角度予以阐述,如Gylfason (2001)、谢波和陈仲常(2011)及杨莉莉和邵帅(2014)等,但是由于人力资本具有资本属性,而劳动力包含有劳动属性,二者显然存在差异,因此,这些研究并未深入到劳动力的领地。进一步地,由于劳动力本身是一个抽象的概念,我们需要从更为细致的视角刻画“资源诅咒”的发生机制,其中劳动力结构隶属于劳动力的范畴,能较多维地反映劳动力的属性,从劳动力结构的角度入手分析核心命题,具备代表性。所谓劳动力结构,它着重指参与生产的劳动力存在异质性,特别强调劳动力在教育背景、劳动技能和产业间的分布等方面的差异性。
为了探究劳动力结构如何对“资源诅咒”效应施加影响,本文拟采用理论与实证分析两类方法,双管齐下。首先,建立一个包含自然资源存量和劳动力结构因素的经济增长理论模型,通过均衡分析和平衡增长路径分析,首次在考虑劳动力结构异质性的条件下,阐明劳动力在制造业部门和自然资源开发部门的配置关系以及劳动力的技能差异两个方面对“资源诅咒”发生机制的作用。接着,采用计量实证对理论进行递进性佐证,并通过实证分析对我国区域层面上是否存在“资源诅咒”现象进行深刻的探讨。最后,基于劳动力结构的视域,结合我国区域发展实际,分析“资源诅咒”现象为何在经济发展水平不同的地区存在异质性,并提出有针对性的政策建议。
二、 理论模型分析1.基本结构。鉴于许多文献中的经济增长模型没有纳入自然资源这一重要要素,为了弥合这一缺陷,本文将其引入到新古典增长模型中试图解决“资源福音”与“资源诅咒”的悖论问题。假设一个经济体由制造业部门、自然资源开发部门组成,制造业部门由最终产品生产部门、中间产品生产部门两个子部门构成。为了体现劳动力技能的差异性以及其对经济体产出的影响,本文将劳动力分为熟练工人和非熟练工人两大类,从而从另外一个角度,根据劳动力的熟练程度,也可以将制造业部门分为运用熟练的劳动力生产部门和运用非熟练的劳动力生产部门两个子部门。在运用熟练的劳动力生产部门(我们不妨称之为第1生产部门),代表性企业运用熟练的劳动力和中间产品来生产最终产品,其生产函数为:
| ${Y_{1t}} = LS_t^\alpha \int_0^{{M_t}} {x_i^\beta di} $ | (1) |
其中:下标t表示时间,Y1表示第1生产部门的最终产出,LS表示第1生产部门有效的劳动力投入总量,系数α、β分别表示要素的产出弹性,范围在0到1之间(α+β>1),M表示第1生产部门的技术知识的总体存量,xi表示中间产品i投入的数量。第1生产部门投入的有效劳动总量LS可表示为:
| $L{S_t} = {A_{1t}}{L_{1t}}$ | (2) |
其中:A1表示第1生产部门的中间投入品生产率参数,L1表示第1生产部门的劳动力投入总量。类似地,在运用非熟练的劳动力生产部门(我们不妨称之为第2生产部门),代表性企业的生产函数可设为:
| ${Y_{2t}} = LB_t^\alpha \int_0^{M_t^*} {x_i^{*\beta }di} $ | (3) |
其中:Y2为第2生产部门的最终产出,LB表示第2生产部门投入的有效劳动力总量,xi*对应为中间产品i的投入数量,M*为第2生产部门的技术知识的总体存量。同样,第2生产部门投入的有效劳动力总量LB可表示为:
| $L{B_t} = {A_{2t}}{L_{2t}}$ | (4) |
其中:A2表示第2生产部门的中间投入品生产率参数,L2表示第2生产部门的劳动力投入总量。第1、第2生产部门投入的中间产品总量可分别设为Xt和Xt*,则
在劳动力的分层时期,熟练的劳动力由新部门(第1生产部门)雇用,非熟练的劳动力则在一般性技术部门(第2生产部门)工作,制造业部门的最终产出为Y,它是第1生产部门和第2生产部门产出的总和,即Y=Y1+Y2。现在假设第1、第2生产部门不同种类的中间产品的数量都相同(稍后可以看到在生产均衡时确实如此),则有xi=x=X/M,xi*=x*=X*/M*,分别代入式(1)、式(3),则制造业部门生产最终产品的总的生产函数可表示为:
| ${Y_t} = LSj_t^\alpha M_t^{1 - \beta }X_t^\beta + LB_t^\alpha M_t^{*1 - \beta }X_t^{*\beta }$ | (5) |
制造业部门、自然资源开发部门两部门使用的劳动力总量为Lt,假设Lt保持不变,即Lt=L,则根据劳动力市场的出清条件有:
| ${L_t} = {L_{1t}} + {L_{2t}} + {n_t} = \frac{{L{S_t}}}{{{A_{1t}}}} + \frac{{L{B_t}}}{{{A_{2t}}}} + {n_t} = L$ | (6) |
其中:n表示自然资源开发部门使用的劳动力数量,n=θL,θ∈(0, 1)。对消费者而言,需要按照最优化其效用方式确定消费路径,假设c代表人均消费的时间路径,以一个无限生存的代表性消费者为例,其生命效用为
在自然资源开发部门,生产函数采用一般的固定替代弹性(CES)生产函数形式:
| ${O_t} = {\left[ {\eta n_t^\xi + \left( {1 - \eta } \right)\chi _t^\xi } \right]^{\frac{\omega }{\xi }}}$ | (7) |
其中:Ot表示在t时期自然资源开发部门(包括采矿业、资源初级加工业、以资源消耗为主的高耗能工业等)开发自然资源得到的资源型产品的总产出,χ(χ>0)为自然资源要素的投入量,即自然资源要素的投入价值。①可以证明,η越大(0 < η < 1),自然资源开发部门的劳动产出弹性越大,劳动的收入分配比重等于劳动的产出弹性,因此,η在一定程度上反映了自然资源开发部门的劳动产出弹性的大小,也在一定程度上反映了劳动收入所占的比重。类似地,1-η在一定程度上反映了自然资源要素的产出弹性的大小,也在一定程度上反映了自然资源要素所有者所获得的收入占总收入的比重,也可以这么讲,1-η在一定程度上反映了自然资源开发部门对自然资源要素的依赖程度。0 < ξ < 1,其中1/(1-ξ)为自然资源开发部门的劳动力与资源要素之间的替代弹性。ω表示自然资源开发部门生产的规模报酬递增程度(ω>0)。
①显然,自然资源有不同的种类,不同种类的自然资源难以在量上进行加总,因此,资源要素的投入量我们可以用资源要素的投入价值来衡量。这样的改变只是意味着资源要素投入量的衡量标准发生了变化,并不会对我们研究得出的结论产生实质性的影响。
自然资源开发部门需要对资源开发活动予以投资,投资量受资源和劳动力的影响,因此可设t时期的投资量为I(Ot, nt)。t时期资源型产品的总产值变化轨迹可表示为:
| ${{\dot E}_t} = - {\chi _t} + I\left( {{O_t},{n_t}} \right)$ | (8) |
其中:Et表示t期资源型产品的产值,即Et=PO(t)Ot;PO表示资源型产品的市场价格;PO(t)表示t期资源型产品的市场价格。
2.均衡分析。(1) 最终产品生产部门。设WLB是第1生产部门工人的工资,WLS是第2生产部门工人的工资,pi、pi*分别表示第1生产部门、第2生产部门的中间产品的价格。生产部门处于完全竞争的市场状态,不妨假设最终产品的市场价格P=1,第1生产部门与第2生产部门生产最终产品获得的利润π可表示为:
| $\pi = Y - \left( {{W_{LB}}LB + {W_{LS}}LS} \right) - \left( {\int_0^{{M^*}} {p_i^*x_i^{*\beta }di} + \int_0^M {{p_i}x_i^\beta di} } \right)$ | (9) |
在生产均衡的条件下,我们有
| ${W_{LS}} = \alpha L{S^{\alpha - 1}}\int_0^M {x_i^\beta di,{W_{LB}} = \alpha L{B^{\alpha - 1}}\int_0^{{M^*}} {x_i^{*\beta }di} } $ | (10) |
| ${x_i} = {\left( {\frac{{\beta L{S^\alpha }}}{{{p_i}}}} \right)^{\frac{1}{{1 - \beta }}}},x_i^* = {\left( {\frac{{\beta L{B^\alpha }}}{{p_i^*}}} \right)^{\frac{1}{{1 - \beta }}}}$ | (11) |
(2) 中间产品生产部门。在完全竞争的市场条件下,每一种中间产品的价格等于其边际产品价值,从而根据(1)式和(3)式,我们不难得到:
| ${p_i} = \beta L{S^\alpha }x_i^{\beta - 1},{p_i} = \beta L{B^\alpha }x_i^{*\beta - 1}$ | (12) |
每一种中间产品都由其厂商垄断进行生产,在给定一比一技术的条件下,垄断者的收益就是价格乘以数量,而成本就等于产出。用π和π*分别表示第1生产部门和第2生产部门中间产品生产企业的利润,则它们可以表示为:
| ${\pi _i} = {p_i}{x_i} - {x_i},\pi _i^* = p_i^*x_i^* - x_i^*$ | (13) |
在中间产品生产企业的生产均衡条件下,可以得到第1生产部门和第2生产部门生产的第i种中间产品的数量:
| ${x_i} = {\beta ^{\frac{2}{{1 - \beta }}}}L{S^{\frac{\alpha }{{1 - \beta }}}},x_i^* = {\beta ^{\frac{2}{{1 - \beta }}}}L{B^{\frac{\alpha }{{1 - \beta }}}}$ | (14) |
因此,生产均衡时企业生产的中间产品的数量与产品的种类无关,则有X=Mx,X*=M*x*,据此(5)式可以重新整理为:
| $Y = {\beta ^{\frac{2}{{1 - \beta }}}}L{S^{\frac{\alpha }{{1 - \beta }}}},x_i^* = {\beta ^{\frac{2}{{1 - \beta }}}}L{B^{\frac{\alpha }{{1 - \beta }}}}$ | (15) |
另外,将(14)式代入(10),可推得熟练工人和非熟练工人的工资之比为:
| $\frac{{{W_{LS}}}}{{{W_{LB}}}} = \frac{{ML{S^{\alpha - 1}}}}{{{M^*}L{B^{\alpha - 1}}}}\frac{{L{S^{\frac{{\alpha \beta }}{{1 - \beta }}}}}}{{L{B^{\frac{{\alpha \beta }}{{1 - \beta }}}}}} = \left( {\frac{M}{{{M^*}}}} \right){\left( {\frac{{LS}}{{LB}}} \right)^{\frac{{\alpha + \beta - 1}}{{1 - \beta }}}} = \left( {\frac{M}{{{M^*}}}} \right){\left( {\frac{{{A_1}{L_1}}}{{{A_2}{L_2}}}} \right)^{\frac{{\alpha + \beta - 1}}{{1 - \beta }}}}$ | (16) |
(3) 自然资源开发部门。资源型产品生产商的利润
| ${W_O} = \eta \omega {P_O}^{1 - \frac{\xi }{\omega }}{n^{\xi - 1}}$ | (17) |
假设劳动力充分流动的结果使得制造业部门、资源开发部门具有相等的工资水平,即有WLS=WLB=WO,进一步可得自然资源开发部门产品的市场定价:
| ${P_{O}} = M\alpha L{S^{\frac{{\alpha + \beta - 1}}{{1 - \beta }}}}{\beta ^{\frac{{2\beta }}{{1 - \beta }}}}/\eta \omega {O^{1 - \frac{\xi }{\omega }}}{n^{\xi - 1}}$ | (18) |
由于资源投资力度越大,则资源的消耗速率越大,另外在资源丰裕的情况下,一般对应着较强的资源再生能力,能减缓资源消耗的速率,因此,我们可以假设资源消耗速率γ与I呈正比,与O呈反比,则有γ=γ(I(O, n)/O)。又因为γ=∂χ/∂O,从而χ也是O与n的函数,即有χ=χ(I(O, n)/O),投入的自然资源要素价值同样与投资量呈正向关系,与资源型产品的产出呈反向关系。
3.平衡增长路径。消费者效用达到最大的汉密尔顿方程为:
| $\begin{array}{c} H = {e^{ - \rho t}}u\left( c \right) + {\mu _A}\left[ {{\beta ^{\frac{{2\beta }}{{1 - \beta }}}}\left( {ML{S^{\frac{\alpha }{{1 - \beta }}}} + {M^*}L{B^{\frac{\alpha }{{1 - \beta }}}}} \right) + O - C} \right]\\ + {\mu _B}\left( { - \chi + I'} \right) + {\mu _C}\left[ {\left( {1 - \theta } \right)L - \frac{{LS}}{{{A_1}}} - \frac{{LB}}{{{A_2}}}} \right] \end{array}$ | (19) |
μA、μB和μC为描述相关变量之间关系的系数。由一阶条件:∂H/∂C=0,∂H/∂O=-μ·A,∂H/∂L=0,∂H/∂LS=0,∂H/∂LB=0,经整理后分别可得如下(20)式至(24)式:
| $\frac{{{{\dot \mu }_A}}}{{{\mu _A}}} = - \rho - \varepsilon \frac{{\dot c}}{c}$ | (20) |
| $ - {\dot \mu _A} = {\mu _A} - \left[ {\gamma \left( {I - {I_O}} \right)/{O^2} + {I_O}} \right]{\mu _B}$ | (21) |
| ${\mu _B}\left( { - \theta {\chi _L}{I_L} + \theta {I_L}} \right) = \left( {\theta - 1} \right){\mu _C}$ | (22) |
| ${\mu _C} = \left[ {\alpha /\left( {1 - \beta } \right)} \right]{\beta ^{\frac{{2\beta }}{{1 - \beta }}}}L{S^{\frac{\alpha }{{1 - \beta }} - 1}}M{A_1}{\mu _A}$ | (23) |
| ${\mu _C} = \left[ {\alpha /\left( {1 - \beta } \right)} \right]{\beta ^{\frac{{2\beta }}{{1 - \beta }}}}L{B^{\frac{\alpha }{{1 - \beta }} - 1}}{M^*}{A_2}{\mu _A}$ | (24) |
其中:I是I(O, θL)的简写形式,IO表示I(O, θL)对O求一阶偏导数,IL表示I(O, θL)对L求一阶偏导数,χL表示χ(I(O, θL)/O)对L求一阶偏导数,χL一定程度上体现了资源生产中劳动的边际产出能力。结合(22)式、(23)式可以推得:
| ${\mu _b} = \frac{{\left( {1 - \theta } \right)\Delta {\mu _A}}}{{\theta {I_L}{\chi _L} - \theta {I_L}}}$ | (25) |
其中:
| $gc = \frac{{\dot c}}{c} = \left\{ {{O^2} - \frac{{\left( {1 - \theta } \right)\Delta }}{{\theta {I_L}{\chi _L} - \theta {I_L}}}\left[ {\gamma \left( {I - {I_O}} \right) + {I_O}{O^2}} \right] - \rho {O^2}} \right\}/\varepsilon {O^2}$ | (26) |
因为总的产出R是制造业部门和自然资源开发部门的产出之和,制造业部门的产出和自然资源开发部门的产出之间是线性关系,因此在稳态下有gC=gR=gY=gO,gR、gY和gO分别表示总产出增长率、制造业部门产出增长率和自然资源开发部门产出增长率,因此,经济体的产出增长率为:
| $g = \left\{ {{O^2} - \frac{{\left( {1 - \theta } \right)\Delta }}{{\theta {I_L}{\chi _L} - \theta {I_L}}}\left[ {\gamma \left( {I - {I_O}} \right) + {I_O}{O^2}} \right] - \rho {O^2}} \right\}/\varepsilon {O^2}$ | (27) |
根据(27)式,我们有:
| $\frac{{\partial g}}{{\partial O}} = g'\left( O \right) = 2\left( {1 - \theta } \right)\Delta \gamma \left( {I - {I_O}} \right)/\varepsilon \theta \left( {{I_L}{\chi _L} - {I_L}} \right){O^3} = \nabla /{O^3}$ | (28) |
其中:
1.计量模型的设定。为了考察自然资源丰裕度对经济增长的影响,结合上述理论模型的经济含义,本文建立如下基本计量模型:
| ${G_{it}} = C + {a_1}N{R_{it}} + {a_2}Q{F_{it}} + {A_3}ED{U_{it}} + d{U_{it}} + {\varepsilon _{it}}$ | (a) |
其中:下标i表示地区,t表示年份,G表示经济增长率,NR表示自然资源丰裕度,QF是劳动力数量结构的衡量指标,EDU是劳动力质量的衡量指标,U是控制变量集合,C是常数,ε是随机误差项,a1、a2、a3、d和后面公式的a4、a5均表示变量的系数值。
观察上述理论模型中(27)式可知,劳动力结构与自然资源丰裕度的结合形态会对经济增长产生显著的影响,因此在计量模型里面我们考虑两者形成的交叉项对经济增长的作用,于是便形成了另外两个基本的计量模型,即模型(b)与模型(c)。模型(b)考虑的是劳动力数量结构指标与自然资源丰裕度结合形成的交叉项对经济增长产生的影响,模型(c)考虑的是劳动力质量指标与自然资源丰裕度结合形成的交叉项对经济增长产生的影响。
| ${G_{it}} = C + {a_1}N{R_{it}} + {a_2}Q{F_{it}} + {a_3}ED{U_{it}} + {a_4}Q{F_{it}}N{R_{it}} + d{U_{it}} + {\varepsilon _{it}}$ | (b) |
| ${G_{it}} = C + {a_1}N{R_{it}} + {a_2}Q{F_{it}} + {a_3}ED{U_{it}} + {a_5}ED{U_{it}}N{R_{it}} + d{U_{it}} + {\varepsilon _{it}}$ | (c) |
2.变量的说明及数据来源。自然资源丰裕度(NR)的衡量方法较多,考虑到数据的可得性,与Sachs和Warner (1999)、邵帅和齐中英(2009)等的衡量方法类似,本文采用自然资源开发行业工业产值(煤炭、石油、天然气三大行业的产值之和)占工业总产值的比重来度量自然资源丰裕度。经济增长率(G)即为与上年相比的实际国内生产总值增长率。在上述理论模型的建立过程中,我们讨论的是自然资源开发部门和制造业部门的劳动力构成对经济增长的影响,为了与理论模型相耦合对应,劳动力结构的数量指标(QF)用资源开发部门和制造业部门劳动力的数量比例关系来描述,即采用煤炭、石油、天然气三大行业从业人员人数除以制造业从业人员人数的值来表示QF。劳动力结构的质量指标(EDU)描述的是从业人员的技能和素质等,按照一般做法,我们用从业人员的平均受教育年限为代理变量来加以衡量。
本文的控制变量集合包括了市场开放度、财政支持力度、交通设施状况、期初的国内生产总值等4个控制指标。市场开放度(OPE)用进出口贸易额占GDP的比重来衡量,财政支持力度(FS)用财政支出占GDP的比重来衡量,交通设施状况(TR)用每万人拥有的公路里程来衡量,期初的国内生产总值考虑的是对数形式。另外,还有一个工具变量指标(NF),该指标表示的是各个地区煤炭、石油、天然气三大自然资源开发行业的企业个数之和。研究样本为1994年至2012年中国大陆30个省、直辖市、自治区(重庆的数据并入四川省作为一个截面单位),实证分析的各种数据来源于中经网统计数据库等。
3.变量的描述性统计分析。各个变量的描述性统计如表 1所示。
| 变量 | 样本数 | 单位 | 均值 | 标准差 | 最小值 | 最大值 |
| G | 570 | % | 11.5936 | 5.4820 | 3.800 | 23.8000 |
| NR | 570 | % | 8.4743 | 2.4874 | 0.0011 | 94.6700 |
| QF | 570 | % | 22.3553 | 19.4957 | 0.0246 | 128.8669 |
| EDU | 570 | 年 | 7.9852 | 1.17821 | 3.8600 | 11.8693 |
| OPE | 570 | % | 3.9865 | 4.1203 | 0.0014 | 24.2543 |
| FS | 570 | % | 17.9884 | 14.2814 | 4.9171 | 129.1443 |
| TR | 570 | 公里/万人 | 25.7928 | 29.0492 | 2.8649 | 211.9498 |
| lnGDP | 570 | 亿元 | 0.3697 | 1.5893 | 0.0020 | 8.8381 |
| NF | 570 | 个 | 223.1039 | 320.4051 | 0 | 2111 |
4.面板的单位根检验。在进行实证研究前,本文首先对被解释变量和主要的解释变量进行单位根检验,采用的是HT检验方法(Harris和Tzavalis,1999)。检验结果表明G和NR同阶单整,劳动力数量结构指标QF和劳动力质量指标EDU一阶单整,因而可以进行后面的计量分析。
| 变量 | Z | P | 结论 |
| G | -6.7134 | 0.0000 | 平稳 |
| NR | -24.3791 | 0.0000 | 平稳 |
| QF | 0.8979 | 0.8154 | 非平稳 |
| EDU | 3.3421 | 0.9996 | 非平稳 |
| D.G | -30.6163 | 0.0000 | 平稳 |
| D.NR | -42.7770 | 0.0000 | 平稳 |
| D.QF | -35.8672 | 0.0000 | 平稳 |
| D.EDU | -37.8232 | 0.0000 | 平稳 |
| 注:此处变量前加D.表示对变量取一阶差分。 | |||
5.计量结果分析。本文采用了混合回归分析、工具变量两阶段最小二乘法以及面板分位数回归分析方法三种实证分析方法来剖析“资源福音”和“资源诅咒”命题。
(1) 总体混合回归分析。首先我们对样本数据进行豪斯曼检验来确定样本数据服从固定效应还是随机效应,豪斯曼检验值为20.31,伴随概率为0.0265,故认为固定效应优于随机效应,针对混合回归和固定效应的优劣比较,我们运用了LSDV(虚拟变量最小二乘法)方法进行检验,检验结果表明在30个省、市、自治区中仅有8个个体的虚拟变量显著(10%的显著性水平内),因此我们采用混合回归方法进行估计。为方便作计量结果的比较分析,我们构设了9个计量模型,这9个计量模型均是在模型(a)、模型(b)和模型(c)的基础上衍生、展开的。9个计量模型的回归结果如表 3所示:
| 变量 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| NR | -0.223** (-2.50) | -0.029** (-2.46) | -0.010 -0.62) | 0.002 0.14) | -0.202** (-2.42) | -0.227** (-2.48) | -0.352*** (-3.77) | -0.482*** (-6.24) | -0.328*** (-3.50) |
| QF | 0.003 0.44) | 0.0008 0.087) | 0.023** (2.29) | -0.005 -0.66) | 0.0126** (1.28) | -0.020*** (-3.48) | |||
| QFNR | -0.0004 -1.12) | -0.001*** (-2.71) | -0.001*** (-3.45) | -0.002*** (-3.92) | -0.002*** (-3.92) | ||||
| EDU | 0.475*** (5.27) | 0.544*** (5.84) | 0.350*** (3.28) | 0.324*** (2.87) | 0.263*** (2.42) | 0.318*** (2.85) | |||
| EDUNR | 0.022** (2.13) | 0.026*** (2.19) | 0.047*** (3.11) | 0.065*** (6.24) | 0.045*** (3.58) | ||||
| OPE | 0.068** (2.66) | 0.067** (1.90) | 0.071*** (2.73) | 0.074*** (2.91) | 0.062*** (2.48) | 0.058*** (2.26) | 0.052*** (2.09) | 0.056*** (2.20) | 0.062*** (2.46) |
| FS | -0.067*** (-4.41) | -0.053*** (-3.57) | -0.069** (-4.51) | -0.058** (-3.86) | -0.049*** (-3.26) | -0.047*** (-3.10) | -0.045*** (-3.28) | -0.050*** (-3.29) | -0.049*** (-3.28) |
| TR | 0.049*** (6.53) | 0.049*** (6.67) | 0.050*** (6.59) | 0.050*** (6.89) | 0.045*** (5.92) | 0.045*** (5.92) | 0.041*** (5.43) | 0.039*** (5.14) | 0.042*** (5.60) |
| lnGDP | 0.184*** (2.91) | 0.270*** (4.23) | 0.181*** (2.87) | 0.276*** (4.35) | 0.272*** (4.29) | 0.273*** (4.29) | 0.282*** (4.47) | 0.250*** (4.04) | 0.285*** (4.53) |
| C | 11.372*** (50.27) | 7.305*** (9.06) | 11.238*** (41.87) | 6.408*** (7.38) | 8.390** (9.06) | 8.670** (8.52) | 9.052*** (9.66) | 11.081*** (42.46) | 8.304*** (8.23) |
| R2 | 0.10 | 0.15 | 0.11 | 0.16 | 0.15 | 0.15 | 0.17 | 0.16 | 0.18 |
| F | 12.97 | 13.65 | 9.43 | 13.00 | 14.38 | 12.62 | 14.31 | 13.68 | 13.22 |
| obs | 570 | 570 | 570 | 570 | 570 | 570 | 570 | 570 | 570 |
| 注:解释变量括号外数字表示系数,括号内数字表示t检验统计量。*、**和***分别表示通过10%、5%和1%的显著性检验。下表同。 | |||||||||
上述计量模型表明,除了模型(4)NR的系数为正值但不显著外,其他8个计量模型NR的系数均为负值,并且都显著。因此,我们可以认为“资源诅咒”现象总体上是存在的。另外,EDU的系数均为正值,都在1%的水平下显著。这说明,劳动者素质的提高能显著促进经济的增长。市场开放度、基础设施的变动与经济增长的变动也是显著的正相关的关系。这说明区域间联系的加强,交通等基础设施的深入发展,也能够有力地促进区域经济增长。FS的系数均为负值,并且都显著。因此,地方政府干预经济力度的增大,对区域经济增长会带来负面影响。lnGDP的系数符号都显著为正。这说明,我国区域增长不存在收敛现象,我国区域发展差距有扩大的趋势。QF的变动对经济增长的影响方向不能确定。因此,资源开发部门和制造业部门劳动力的比例值变大是增加还是降低“资源诅咒”的影响,在混合回归条件下结论不明朗,其可能原因为在模型中QF系数总体上并不显著,其自身可能存在一定的内生性,因此针对此问题,后文采取了一定的方法予以解决。
对比模型(1)与模型(2)、模型(3)与模型(4),我们发现,加入EDU后,“资源诅咒”效应在降低。因此,劳动者素质的提高能弱化“资源诅咒”效应,甚至有可能使这种效应发生逆转,将“资源诅咒”效应转变为“资源福音”效应。QFNR交叉项系数的符号为负,而EDUNR交叉项系数的符号始终显著为正值,这也说明解决“资源诅咒”问题的“杀手锏”是劳动者素质的提高,资源开发部门劳动力数量增加的作用有限。
(2) 工具变量的两阶段最小二乘法(2sls)估计。在总体混合回归分析中,模型(2)、模型(3)、模型(6)中QF的系数不显著,我们怀疑劳动力数量结构指标存在内生性,可能对一些模型中自然资源丰裕度的系数产生了干扰,从而影响了计量分析结果,因此有必要为劳动力数量结构指标寻找工具变量。此处我们将各个地区自然资源开发行业中的企业个数作为劳动力数量结构指标的工具变量,使用这个工具变量的考虑在于劳动力数量结构指标与自然资源开发行业的从业人数有关,而区域该行业从业人数与行业中的企业个数有关,并且企业个数与经济增长率之间并没有直接的关系,因此遵循这个逻辑及工具变量条件,本文将自然资源开发行业中的企业个数NF作为QF的工具变量,采用工具变量模型进行两阶段最小二乘法(2sls)估计,估计结果如表 4所示。
| 变量 | (1) | (2) | (3) | (4) |
| NR | -0.073** (-3.38) | -0.062** (-2.70) | 0.243(0.18) | 0.208** (1.86) |
| QF | 0.045** (2.44) | 0.122*** (2.69) | 0.049** (2.09) | 0.123** (2.92) |
| QFNR | -0.004** (-5.69) | -0.004** (-3.76) | ||
| EDU | 0.510*** (5.46) | 0.263*(1.03) | 0.584*** (3.72) | 0.606*** (3.66) |
| EDUNR | 0.126(0.64) | 0.033** (2.29) | ||
| OPE | 0.094*** (2.99) | 0.100** (4.48) | 0.099*** (3.17) | 0.112*** (3.36) |
| FS | -0.006** (-3.90) | -0.057** (-3.47) | -0.064** (-3.15) | -0.072** (-3.89) |
| TR | 0.048*** (6.25) | 0.047*** (6.17) | 0.052*** (6.08) | 0.050*** (5.73) |
| lnGDP | 0.270*** (4.14) | 0.319*** (4.88) | 0.269*** (4.09) | 0.299*** (4.40) |
| C | 6.498*** (7.27) | 8.915*** (8.69) | 5.810*** (3.73) | 4.425** (2.36) |
| R2 | 0.10 | 0.13 | 0.10 | 0.12 |
| F | 13.65 | 14.11 | 12.15 | 11.73 |
| LM | 87.24 | 78.05 | 71.06 | 38.50 |
| wald | 96.94 | 88.84 | 79.89 | 40.56 |
| obs | 570 | 570 | 570 | 570 |
由此可见,得到的估计结果相对于混合回归估计结果更加显著,实证分析结果显示:第一,EDU、OPE、TR和lnGDP的变动与经济增长的变动方向一致,FS的变动与经济增长的变动方向相反,这与前面得到的结论一致;第二,QF的变动与经济增长的变动方向一致,这说明,自然资源开发部门劳动力数量的增加能在一定程度上促进经济增长。因此,我国省际范围内并不存在“荷兰病”现象,即劳动力向资源行业的适度转移不会“架空”制造业,不会抑制整体经济的增长。但是,EDU的系数值显示,劳动力素质的提高更能显著地促进经济增长,劳动力的数量与质量相比,在经济增长中所起的作用不可同日而语,毕竟劳动力的数量增加有限,而劳动力质量的增加潜力大得多;第三,模型(1)至模型(4)的NR的系数逐渐由负变为正,这说明随着自然资源开发部门劳动力投入数量的增加,劳动者素质的提高,会在一定程度上扭转“资源诅咒”的负面效应,甚至还会将“资源诅咒”转化为“资源福音”。对比模型(1)与模型(2),QFNR交叉项的引入在一定程度上降低了“资源诅咒”的负面效应,模型(1)与模型(3)对比说明,EDUNR交叉项的引入将自然资源对经济增长的消极作用转变为促进经济增长的“福音”,这也说明避免“资源诅咒”问题的发生,使丰裕的自然资源成为地区发展的“福音”,关键在于劳动者素质的提高,而自然资源开发部门劳动力数量增加所起的作用有限。
(3) 自然资源丰裕度等要素对经济增长的分位数回归分析。无论是总体混合回归分析,还是工具变量的两阶段最小二乘法估计,实质上都是均值回归,我们有必要进一步刻画整个条件分布下解释变量尤其是核心解释变量和经济增长率之间的动态关系,为此我们采用面板分位数回归方法作进一步的分析,得到的结果如图 1至图 8所示。

|
| 图 1 NR的分位数回归系数变化 |
|
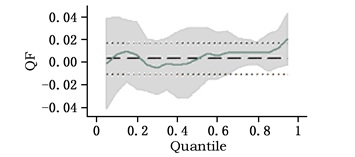
| 图 2 QF的分位数回归系数变化 |

|
| 图 3 EDU的分位数回归系数变化 |
|
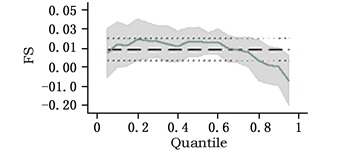
| 图 4 FS的分位数回归系数变化 |
|
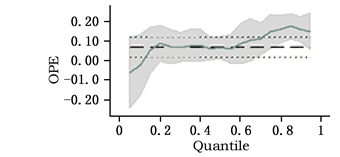
| 图 5 OPE的分位数回归系数变化 |
|
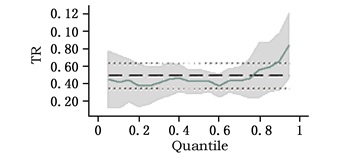
| 图 6 TR的分位数回归系数变化 |

|
| 图 7 lnGDP的分位数回归系数变化 |
|
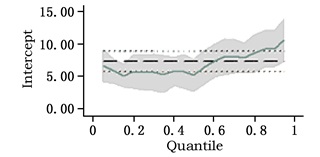
| 图 8 常数C的分位数回归系数变化 |
图 1表明,在不考虑交叉项的情况下,NR的系数为负数,从而再次支撑了“资源诅咒”命题。在0-70%的分位数内自然资源丰裕度的系数变化轨迹较为明显,并且基本上随着分位数的增加而降低,在70%-100%的分位数内NR的系数变化不明显,也就是说经济较为落后的地区“资源诅咒”效应较为显著,且不同地区存在较大的差异性,而对经济较发达的省份而言,“资源诅咒”效应比较趋同;由图 2可知,约50%以上的分位数范围内QF的系数均为正数,约20%-50%范围内QF的系数均为负数,在低于约20%分位数范围内QF系数均为正数,那么可以推知对经济发达地区与落后地区而言将劳动力配置到资源密集型行业促进了经济发展水平的提高。因此,我国以东部为主体的发达地区的经济增长,资源密集型行业的发展作出了一定的贡献,而以西部为主体的落后地区的经济增长立足于本地的资源开发也并非是一条不可行的发展道路。由于东、西部的经济发展都在一定程度上依赖自然资源的投入与开发,这对中部地区的经济发展造成了一定的负面影响。因此,资源密集型行业劳动力数量的增加与中部地区的经济增长是一种负相关的关系;从图 3来看,在整个分位数范围内EDU的系数显著为正,这表明无论是针对发达地区,还是落后地区来讲,提高劳动者素质始终是促进经济增长的一个非常重要的手段;图 4至图 7反映了控制变量的分位数回归系数的变化轨迹。图 4显示70%-100%的分位数内财政支持对经济增长有抑制作用,70%以下则无抑制作用。因此,越是经济发达的地区,政府对经济的干预力度越大,对经济增长的损害就越大;相反,政府干预对落后地区来讲,则是一个利好的因素。图 5显示60%-100%的分位数内OPE的系数为正值且较大,则表明经济发达地区市场开放度的提高对其经济增长作出了显著贡献;相反,0-20%的分位数内,OPE的系数为负值,这表明,地区间市场开放度的提高不利于落后地区的发展。因此,我们也就不难理解落后地区的地方政府更倾向于保护本地的市场。在20%-60%的分位数内OPE的系数接近于0,因此,对经济发展水平处于中间水准的一些地区来说,市场开放度在一定范围内的变动对其经济增长来说影响微小。图 6、图 7显示,在整个分位数内TR、lnGDP的分位数回归系数都为正值。因此,无论是对落后地区,还是对发达地区来讲,TR、lnGDP的变动与经济增长的变动方向一致,只不过程度不同而已;图 8反映了其他因素对不同地区经济增长的影响。
四、 简要结论与政策建议本文构建了一个包含自然资源存量和劳动力结构因素的经济增长理论模型,通过均衡分析和平衡增长路径分析,探究劳动力结构如何与资源要素、经济增长率产生内在联系。理论研究发现,在不同限制条件下,自然资源开发部门劳动力数量的增加对经济增长的作用不同,而劳动者素质的提高对缓解“资源诅咒”效应而言始终是一个有利因素。实证研究进一步表明,从总体上讲,我国省域层面的“资源诅咒”现象是存在的,但并非没有逆转的可能,避免“资源诅咒”问题的发生,使丰裕的自然资源成为地区发展的“福音”,关键在于劳动者素质的提高,资源开发部门劳动力数量的增加所起的作用有限;分地区讲,经济落后地区“资源诅咒”效应较为显著,且不同地区存在较大的差异性,而对于经济较发达的省份而言,“资源诅咒”效应比较趋同。对于东部地区与西部地区而言,将劳动力配置到资源密集型行业促进了经济发展水平的提高,而资源密集型行业劳动力数量的增加与中部地区的经济增长是一种负相关的关系。劳动力素质的提高无论对于发达地区还是欠发达地区而言都可以减缓“资源诅咒”效应。
基于本文的研究结论,我们提出如下一些政策建议:第一,建立和完善各地区劳动力培训机制,加强各行业劳动力的交流和互动,提高外溢性技术的吸收能力,特别要着力培育资源密集型行业部门工人的技能和素质,以匹配资源型行业劳动力需求。作为减少产能的一部分措施,我国将在煤炭和钢铁等资源密集型行业进行大裁员,但裁员不是解决问题的根本,解决问题的根本在于着力提升劳动力素质,促进产品优化升级,增强企业的市场竞争力,促进自然资源的合理有效地开发与利用,减少自然资源开发过程中的资源漏损,避免环境污染问题;第二,东部、中部和西部地区的“资源诅咒”的引起缘由具有一定的差异性,因此需要对症下药,有的放矢,要根据各区域内企业属性和资源状况优化劳动力的配置,促进制造业和资源型行业协调联动发展。对于东部与西部而言,要从本地的资源禀赋特征出发,适当引导劳动力向资源密集型行业的转移,对于中部地区而言则需要限制资源密集型行业人员数量的过度膨胀,为劳动力迁向制造业甚至是现代服务业提供渠道;第三,结合当下的以经济结构调整为主线的供给侧改革,我们需要在资源生产、供给层面上下功夫,必须根据区域的自然资源的丰、缺和供需平衡的不同情况以及制度、交通状况等有规律、有原则、有步骤地进行自然资源的利用与开发,提升资源供给端主体的供给质量和效率。并且,适当扩大对落后地区的财政支出,为资源型行业企业进行技术升级和产业转型提供资金支持,改善区域的交通设施条件,降低区域能源矿产的开发、运输成本,为区域间的贸易往来设计不同的制度安排,削减资源密集型行业的垄断势力也是切断“资源诅咒”效应的负面传导途径的辅助力量,这些也应纳入资源开发的规划中去。
| [1] | 邵帅, 齐中英. 资源输出型地区的技术创新与经济增长[J]. 管理科学学报, 2009(6): 23–33. |
| [2] | 谢波, 陈仲常. 自然资源、人力资本异质性与区域经济增长[J]. 人口与经济, 2011(4): 35–44. |
| [3] | 杨莉莉, 邵帅. 人力资本流动与资源诅咒效应:如何实现资源型区域的可持续增长[J]. 财经研究, 2014(11): 44–60. |
| [4] | Auty R M. Industrial policy reform in six large newly industrializing countries:The resource curse thesis[J]. World Development, 1994, 22(1): 11–26. DOI:10.1016/0305-750X(94)90165-1 |
| [5] | Corden W M, Neary J P. Booming sector and de-industrialization in a small open economy[J]. The Economic Journal, 1982, 92(368): 825–848. DOI:10.2307/2232670 |
| [6] | Gylfason T. Natural resources, education, and economic development[J]. European Economic Review, 2001, 45(4-6): 847–859. DOI:10.1016/S0014-2921(01)00127-1 |
| [7] | Harris R D, Tzavalis E. Inference for unit roots in dynamic panels where the time dimension is fixed[J]. Journal of Econometrics, 1999, 91(2): 210–226. |
| [8] | Matsuyama K. Agricultural productivity, comparative advantage, and economic growth[J]. Journal of Economic Theory, 1992, 58(2): 317–334. DOI:10.1016/0022-0531(92)90057-O |
| [9] | Sachs J D, Warner A M. Natural resource abundance and economic growth[R]. NBER Working Paper No. 5398, 1995. |
| [10] | Sachs J D, Warner A M. The big push, natural resource booms and growth[J]. Journal of Development Economics, 1999, 59(1): 43–76. DOI:10.1016/S0304-3878(99)00005-X |
 2016, Vol. 42
2016, Vol. 42


