
2.上海财经大学 财经研究所,上海 200433;
3.上海财经大学 高等研究院,上海 200433
2.Institute of Finance and Economics,Shanghai University of Finance and Economics,Shanghai 200433,China;
3.Institute for Advanced Research,Shanghai University of Finance and Economics,Shanghai 200433,China
近年来中国经济进入“新常态”,《中国制造2025》提出了加快推进实施制造业升级的战略,制造业是工业的主要组成部门,推进制造业升级也即推进工业结构升级,因此,对工业结构升级问题进行考察具有重要的现实意义。供给侧改革是近期热点,那么从供给侧角度考察,是什么因素推动了工业结构的升级,其内在的机制又是什么,本文尝试通过建立理论模型并模拟实际的中国工业结构变化过程,对该问题进行探讨。
在工业化进程中,工业结构升级的趋势呈现一定的规律性。Hoffmann(1958) 指出,随着一国工业化的推进,工业结构中重工业比重逐渐增加,即霍夫曼系数(轻工业净产值与重工业净产值之比) 逐渐下降。Syrquin和Chenery(1989) 在对108个国家1950-1983年的经济数据进行分析后指出,在工业化进程中,工业结构的变化无论国家大小都有许多共同特征:工业化初期产业部门在总产出中所占的份额保持不变,工业化中期产业部门占总产出的份额在工业化初期增加,但随后不再进一步增加,工业化后期产业部门(包括纸业印刷业、基础金属业、金属制品业与机械设备制造业) 占总产出的份额约从3%增加到10%,是工业占总产出份额增加的主要原因。杨智峰等(2014) 分析了1992-2010年中国产业结构的变化,在工业化进程中,工业占GDP的比重上升,同时重工业占工业的比重逐渐增加。干春晖等(2011) 提出了产业结构优化指数和产业结构升级指数,他们用泰尔指数来描述产业结构的合理性,用第三产业产值与第二产业产值之比作为产业结构高级化的度量指数,他们的度量方法是基于古典经济学的经济均衡与各产业部门生产率水平相同的假设。戴魁早(2012和2014) 使用泰尔指数来描述工业结构的合理性,同时使用工业中第三类产业产值与第一、二类产值之比作为工业结构升级的度量,并对中国工业结构变迁的动因进行了实证分析。
国内外相关理论文献主要解释农业、工业和服务业的产出和劳动的变化,大致可分为两类,一类从需求角度进行分析,如Kongsamut等(2001) 认为,产品间需求的收入弹性不同推动产业结构变迁,即随着资本积累和收入增长,需求将由低收入弹性的产品(如食品) 转向高收入弹性的产品(如服务业),从而导致部门间产出和生产要素的比重发生变化。Foellmi 和Zweimüller(2008) 指出,新产品自身收入弹性的变化会导致产业结构变迁,当新产品刚出现时,是收入弹性较高的奢侈品;当它即将淘汰时,是收入弹性较低的必需品。新产品不断引入,导致新产业的扩张和旧产业的萎缩。李尚骜和龚六堂(2012) 内生化了产品的非一致性偏好,解释了中国农业、工业和服务业的产值和劳动份额的变化。
另一类从供给角度进行分析,如Ngai和Pissarides(2007) 认为,部门间TFP(全要素生产率) 增长率的差异会推动产业结构变迁,如果产品间的替代弹性满足一定条件,劳动份额将转移至TFP增长率高的部门。Acemoglu和Guerrieri(2008) 指出,农业、工业和服务业结构的变迁来源于要素禀赋差异和资本深化,资本深化将提高资本密集型部门的相对产出,但会导致资本和劳动从资本密集型部门流出。Alvarez-Cuadrado和Van Long (2011) 认为,部门间资本和劳动的替代弹性不同将会推动产业结构变迁,随着资本的不断积累,替代弹性高的部门的资本份额提高、劳动份额将会下降。Mao和Yao(2010) 考察了开放经济条件下农业、工业和服务业的产值和劳动变化的推动因素。
本文试图从非均衡增长的角度解释中国工业结构升级的动因。首先厘清中国工业结构变化的经验事实,然后建立两部门的中国工业结构变化模型,进行数值模拟,拟合中国工业结构变化的经验事实,并对模型经济的机制进行分析,结合中国经济的实际运行情况,探讨中国工业结构升级的动因和机制。本文与以往文献的不同之处在于以下几个方面:
新古典理论假设生产要素自由流动,竞争均衡的结果是不同部门之间生产要素的边际生产率相同,钱纳里等(1989) 提出的“非均衡增长”是与新古典理论相背离的经济制度的特征,“非均衡增长”属于“次优论”范畴,产业之间生产要素的边际生产率是不同的,而且不收敛。本文基于非均衡增长理论(将工业分为两个边际生产率不同的部门),尝试构建动态随机一般均衡模型并进行数值模拟,对工业结构升级的动因进行理论探讨。此外,本文模型构建的是一个两部门的分析框架,同时基于非均衡增长的理论,将工业分为资本密集型(重工业) 与劳动密集型(轻工业) 两个边际生产率不同的部门,因此本文不考察工业结构合理化或优化,只考察工业结构高度化或工业结构升级的问题。
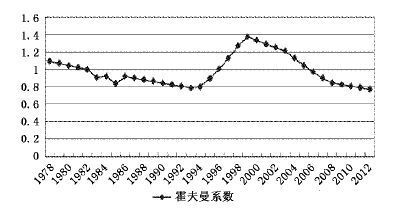
由于理论与实证的对应,我们没有在工业内部再做进一步的细分部门。本文使用中国数据的时间区间为1978-2012年,如果用轻重工业增加值考察该时期的霍夫曼系数(见第二部分图 4) 可知,中国的霍夫曼系数虽有起伏,但主要是从1左右向小于1变化,因此可以得出中国在该时期主要处于重工业化阶段,基于此判断本文将工业分为轻重工业两个部门,这也与《中国统计年鉴》和马克思主义政治经济学对工业的划分一致。同时,霍夫曼系数的变化(先升后降) 实际上也反映了改革开放以来中国跌宕起伏的重工业化过程。
反映中国工业结构变化的模型,既存在增长趋势,也有短期冲击,在建立模型进行数值模拟时,国内外相关文献通常只单独考虑其中的一个方面。本文通过建立两部门的中国工业结构变化模型,采取先消除模型经济的增长趋势,得到一个波动模型,考察短期冲击,然后再还原增长趋势进行数值模拟,这样的处理更为合理准确。
本文得到的主要研究结论是:轻重工业技术进步率的相对变化是中国工业(产出) 结构变化的动因,而重工业相对于轻工业有较高的技术进步率,是中国工业结构升级的动因;重工业技术进步对轻工业产出存在溢出效应;重工业产品消费对轻重工业技术进步率的变化不敏感,而投资和轻工业产品消费对轻重工业技术进步率的变化敏感,重工业技术进步率相对高于轻工业时,投资率呈上升趋势,轻工业产品消费份额逐步下降,同时重工业产出份额呈上升趋势。通过这些分析结论,我们可以解读出相关的政策含义。
二、 中国工业结构变化的经验事实本文使用《中国工业经济统计年鉴》中的重工业增加值数据作为重工业产出,用《中国统计年鉴》中的工业增加值减去重工业增加值后得到的数据作为轻工业产出,①并分别用生产资料价格指数和生活资料价格指数进行平减;使用《中国工业经济统计年鉴》中轻重工业的资产合计作为轻重工业资本,并统一用固定资产投资价格指数进行平减;使用《中国工业经济统计年鉴》中轻重工业的年平均劳动人数作为轻重工业投入生产的劳动。
①《中国统计年鉴》中的工业增加值和《中国工业经济统计年鉴》中的轻重工业增加值之和并不相等,且《中国工业经济统计年鉴》中轻重工业增加值的统计口径发生数次变化,由于重工业有较高的技术进入门槛,因此本文选择《中国工业经济统计年鉴》中的重工业增加值数据作为重工业产出,并用《中国统计年鉴》中的工业增加值减去重工业增加值后得到的数据作为轻工业产出。
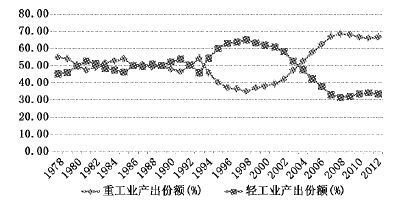
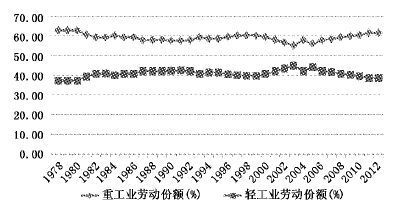
在1978-2012年间中国工业结构发生了深刻的变化,见图 1中国工业中轻重工业产出份额的变化和图 2中国工业中轻重工业劳动份额的变化。
|
| 图 1 中国工业中轻重工业产出份额的变化 |
|
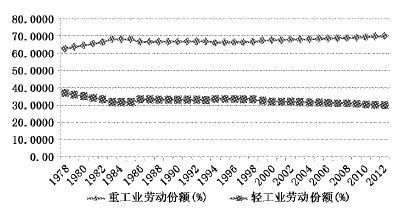
| 图 2 中国工业中轻重工业劳动份额的变化 |
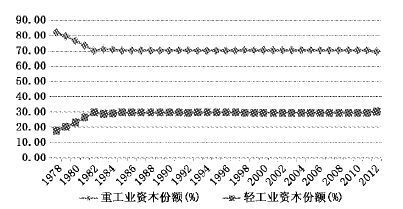
由图 1至图 4可知,中国改革开放以来的工业结构变化呈现以下特点:1.工业中轻重工业的产出份额变化较大,但是劳动和资本份额变化不大、基本保持稳定。轻重工业产出份额尤其在1994年之后变化较大,如1998年轻工业产出份额为65%,达到峰值,重工业产出份额为35%;而2008年轻工业产出份额只有31.47%,重工业产出份额却高达68.53%(见图 1)。然而,轻重工业的劳动和资本份额的变动则基本保持稳定,重工业劳动份额始终远高于轻工业,从1978年到2012年,重工业劳动份额最高为62.75%,最低为55.13%,其变化曲线类似于一条水平线;轻工业劳动份额最高为44.87%,最低为37.25%,其变化曲线同样几乎是一条水平线(见图 2)。重工业资本份额也始终远高于轻工业,从1978年到2012年,重工业资本份额约为70%,其变化曲线虽有起伏但基本类似于一条水平线;轻工业资本份额约为30%,其变化曲线同样虽有起伏但类似一条水平线(见图 3)。2.工业中轻重工业产出份额的变化大致可以分为3个阶段(见图 1):第一阶段为1978年至1994年,轻重工业产出份额基本持平,呈现胶着状态;第二阶段为1995年至1998年,重工业产出份额呈下降趋势,轻工业产出份额呈上升趋势,轻工业产出份额高于重工业产出份额;第三阶段为1999年至2012年,重工业产出份额呈上升趋势,而轻工业产出份额呈下降趋势,该阶段以2004年为界又可分为两个时期:2004年以前,工业中轻工业产出份额仍高于重工业产出份额,但差距不断缩小;2004年及以后,重工业产出份额高于轻工业产出份额,2012年重工业产出份额为66.66%,轻工业产出份额为33.34%。3.霍夫曼系数的变化同样可以分为3个阶段,印证了工业中轻重工业产出份额的变化(或工业结构的变化)(见图 4):第一阶段为1978年至1994年,霍夫曼系数数值在1附近波动,轻重工业产出份额基本持平,工业结构呈现维持状态;第二阶段为1995年至1998年,霍夫曼系数数值呈上升趋势,轻工业产出份额上升且轻工业产出份额高于重工业产出份额,工业结构呈现去工业化趋势;第三阶段为1999年至2012年,霍夫曼系数数值呈下降趋势,工业结构呈现重工业化(或升级) 趋势,重工业产出份额逐渐上升,而轻工业产出份额逐渐下降,该阶段以2004年为界又可分为两个时期:2004年以前,工业中轻工业产出份额仍高于重工业产出份额,但差距不断缩小;2004年及以后,重工业产出份额高于轻工业产出份额,霍夫曼系数数值逐渐趋向小于1。
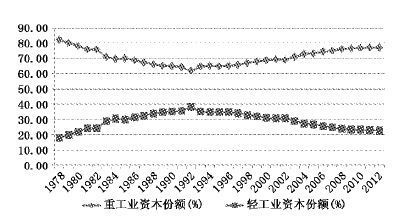
|
| 图 3 中国工业中轻重工业资本份额的变化 |
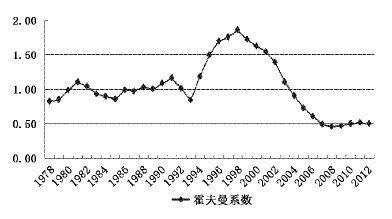
|
| 图 4 中国霍夫曼系数的变化 |
在厘清经验事实的基础上,本文将进一步建立模型以刻画中国工业结构变化的动态过程,分析中国工业结构升级的机制和动因。
三、 中国工业结构变化模型工业内部进行产业分类的方法有很多种,本文遵循中国统计年鉴的方法将工业划分为轻工业和重工业,工业生产存在生产专业化,轻工业产品只能用来消费,重工业产品可以用来消费或者投资,在构建中国工业结构变迁模型时我们将遵循这些设定。
在组织生产时,轻重工业的要素密度是不同的,重工业倾向于资本密集型,而轻工业倾向于劳动密集型。因此,劳动的产出弹性在轻重工业中是不同的,并且资本产出比在轻重工业中也不同。本文在中国工业结构变迁模型中,将工业分为轻工业和重工业,并考虑到劳动和资本在轻重工业中组织生产时的差异。
不仅轻重工业的要素密度不同,技术进步对轻重工业生产的影响也存在差异。相对而言,重工业的技术进步倾向于劳动增进型,因此极大地提高了劳动生产率和劳动的边际报酬;而轻工业的技术进步更倾向于中性的特征,对劳动边际报酬的提高程度远弱于重工业。在模型中设定考虑技术进步的轻重工业生产函数的方式时,我们将引入这种差异。
轻重工业的技术进步率也存在差异,由于轻重工业的技术进步率是动态变化的,因此这种差异也具有动态变化的特征。1978年至2012年,中国技术进步的方式经历了原计划经济体制下低起点的“以创新为主”研发体系的逐步瓦解和向“以模仿为主”研发体系的转变;2012年后又再次处于向“以创新为主”研发体系的转变过程中。因此,轻重工业的技术进步率是动态变化的,其差异也呈现动态变化的特征。本文将在反映中国工业结构变迁的模型中考虑轻重工业技术进步率的动态变化,进行参数校准,并在消去增长趋势的波动模型基础上进行数值模拟。
在研究农业、工业和服务业结构变化的一些文献中,作者认为由于“恩格尔效应”,随着收入的增长,需求将转移至收入弹性高的部门,产品间需求收入弹性的不同是推动产业结构变迁的重要因素。区别于这些文献,本文主要从供给角度考察工业结构变迁,设定代表性家庭对轻重工业产品需求的收入弹性是相同的。
借鉴Dennis和İşcan (2009) 和Echevarria(1997) 的做法,假定经济中包含两个部门:代表性家庭和厂商。代表性家庭最大化其期望终生效用,形成可供租用的轻重工业资本,将其租给轻重工业厂商,并在轻重工业间分配劳动;厂商分为轻工业厂商和重工业厂商,分别生产轻工业产品和重工业产品。轻工业产品只能消费,重工业产品可以进行消费或投资。以下我们分部门来讨论中国工业结构变迁的模型。
(一) 代表性家庭。经济中代表性家庭分配劳动、选择消费轻工业产品和重工业产品,最大化其期望终生效用,也即:
| $Max{{E}_{0}}\sum\limits_{t=0}.{\infty }{{{\beta }.{t}}}[\theta log{{C}_{Lt}}+(1-\theta )log{{C}_{Ht}}$ | (1) |
其中:β∈(0,1)为主观贴现率,CLt为消费的轻工业产品,CHt为消费的重工业产品,θ为消费的轻工业产品在整个消费品中的比重,1-θ为消费的重工业产品在整个消费品中的比重,这里设定消费的轻工业产品和重工业产品有相同的需求收入弹性。代表性家庭所面临的跨期预算约束为:
| ${{C}_{Lt}}\le {{W}_{Lt}}{{n}_{Lt}}+{{R}_{Lt}}{{K}_{Lt}}$ | (2) |
| ${{C}_{Ht}}+{{I}_{t}}\le {{W}_{Ht}}{{n}_{Ht}}+{{R}_{Ht}}{{K}_{Ht}}$ | (3) |
| ${{K}_{Lt+1}}+{{K}_{Ht+1}}=\left( 1-\delta \right)\left( {{K}_{Lt}}+{{K}_{Ht}} \right)+{{I}_{t}}$ | (4) |
(2) 式、(3) 式和(4) 式中,WLt表示供给轻工业厂商的劳动的工资,nLt为投入轻工业生产的劳动,WHt表示供给重工业厂商的劳动的工资,nHt为投入重工业生产的劳动,KLt和KHt分别表示t期代表性家庭租用给轻、重工业厂商的资本,Kt为t期总资本,RLt和RHt分别表示轻、重工业资本的租金率,It为t期投资。劳动标准化为1,也即:
| ${{n}_{Lt}}+{{n}_{Ht}}=1$ | (5) |
因此,劳动不进入代表性家庭的效用函数,只在轻重工业间进行分配,nLt和nHt可以看作是轻重工业劳动在总劳动中的份额。
(二) 厂商。厂商分为轻工业厂商和重工业厂商,分别生产轻工业产品和重工业产品。
1.轻工业厂商。轻工业厂商从代表性家庭租用资本,向代表性家庭雇佣劳动,生产轻工业产品,并进行利润最大化。
| ${{Y}_{Lt}}={{B}_{L}}{{A}_{Lt}}{{\gamma }.{t}}_{L}K_{Lt}.{1-{{\alpha }_{L}}}n_{Lt}.{{{\alpha }_{L}}}$ | (6) |
| $Max{{\pi }_{Lt}}={{Y}_{Lt}}-{{W}_{Lt}}{{n}_{Lt}}-{{R}_{Lt}}{{K}_{Lt}}$ | (7) |
(6) 式和(7) 式中,YLt为轻工业产出,BL为轻工业的效率参数,KLt为投入生产的轻工业资本,nLt为投入轻工业生产的劳动,轻工业的技术进步为中性,技术进步率为γL,ALt为轻工业的确定性技术冲击,αL为投入轻工业生产的劳动的产出弹性,лLt为轻工业厂商的利润。
2.重工业厂商。重工业厂商从代表性家庭租用资本,向代表性家庭雇佣劳动,生产重工业产品,并进行利润最大化。
| ${{Y}_{Ht}}={{B}_{H}}K_{Ht}.{1-{{\alpha }_{H}}}\left( _{Ht}.{A}{{n}_{Ht}} \right){{\alpha }_{H}}$ | (8) |
| $Max~{{\pi }_{Ht}}={{Y}_{Ht}}-{{W}_{Ht}}{{n}_{Ht}}-{{R}_{Ht}}{{K}_{Ht}}$ | (9) |
(8) 式和(9) 式中,YHt为重工业产出,BH为重工业的效率参数,KHt为投入生产的重工业资本,nHt为投入重工业生产的劳动,重工业的技术进步是劳动增进型的,技术进步率为γH,AHt为重工业的确定性技术冲击,αH为投入重工业生产的劳动的产出弹性,лHt为重工业厂商的利润。
(三) 均衡和生产专业化。由于生产专业化,轻工业产品只能消费,重工业产品可以进行消费或投资,可得:
| ${{C}_{Lt}}={{Y}_{Lt}}$ | (10) |
| ${{C}_{Ht}}+{{I}_{t}}={{Y}_{Ht}}$ | (11) |
其中:模型经济包含增长和波动两部分。首先考虑增长部分,模型经济存在部门间非平衡增长的均衡增长路径:重工业部门的产出和消费以γH的速度增长,轻工业部门的产出和消费以γLγH (1-αL) 的速度增长,投资和轻重工业资本以γH的速度增长,轻重工业的劳动份额nLt和nHt保持不变。消除模型经济的增长趋势,得到一个波动模型,该波动模型存在唯一的稳态(推导和求解过程略),稳态值仅依赖于模型的参数,通过参数校准,我们可以将波动模型的稳态值求出。稳态的存在是我们对模型经济进行分析和数值模拟的基础。
四、 参数校准对重工业厂商,使用1992年、1997年、2002年、2007年和2010年的投入产出表中重工业的劳动报酬占增加值的比重,取平均数作为重工业劳动投入的收入份额,即重工业劳动的产出弹性αH=0.248;将重工业的增加值、资本和劳动人数分别除以轻重工业劳动人数之和,得到标准化的重工业人均产出、重工业人均资本和重工业劳动投入,于是有:
| $S{{R}_{Ht}}=log{{Y}_{Ht}}-(1-{{\alpha }_{H}})log{{K}_{Ht}}-{{\alpha }_{H}}log{{n}_{Ht}}$ | (12) |
得到重工业的全要素生产率SRHt。相对于轻工业,重工业有企业、研究机构、学校和政府组成的相对完整的研发体系,有相对较高的技术进步率,1978年至2012年重工业技术进步率的变化体现了中国技术进步方式的转变,即由原计划经济体制下低起点的“以创新为主”方式向“以模仿为主”方式的转变。结合中国经济的发展历程可考察到重工业技术进步率大致有三次较大的波动:(1)1982年“党的十二大”提出了“二十年翻两番”的奋斗目标之后,中国实施了有限度的对外开放,经济开始了1978年以来短暂的第一次扩张,直到1986年由于出现经济过热和大幅通货膨胀,重工业在这一时期延续了原计划经济体制下低起点的“以创新为主”的技术进步方式,由于起点低,重工业的技术进步率相对较高;(2)1992年邓小平发表“南巡谈话”,两年后中国确立了市场经济发展方向,扩大了对外开放,本国重工业面临激烈的市场竞争,但缺乏相应的产业保护政策,因此低起点的“以创新为主”的重工业技术进步方式逐渐瓦解,重工业技术进步率大幅下降,直到1997年左右的亚洲金融危机爆发;(3) 亚洲金融危机后重工业技术进步逐步向“以模仿为主”的方式进行转变,配套出台了一系列鼓励重工业和高科技产业发展的财政、信贷政策和产业振兴措施,通过“走出去,引进来”的政策,重工业逐步建立了“以模仿为主”的技术进步方式,又进入了其技术进步率相对较高的发展时期,直至2007年美国次贷危机波及我国。据此我们建立三个虚拟变量DH1=(1,年份为1983-1985年;0,其他年份)、DH2=(1,年份为1994-1998年;0,其他年份)、DH3=(1,年份为2000-2007年;0,其他年份),做如下(13) 式的回归有:
| $\begin{align} & S{{R}_{Ht}}=log{{B}_{H}}+(log{{\gamma }_{H}})t{{\alpha }_{H}}+{{\beta }_{H1}}\left( {{D}_{H1}}t{{\alpha }_{H}} \right) \\ & +{{\beta }_{H2}}\left( {{D}_{H2}}t{{\alpha }_{H}} \right)+{{\beta }_{H3}}\left( {{D}_{H3}}t{{\alpha }_{H}} \right)+S{{R}_{Ht-1}}+{{\varepsilon }_{Ht}} \\ \end{align}$ | (13) |
其中:t为标准化的时间,εHt为随机误差项,为消除误差自相关,我们加入了被解释变量SRHt的一阶滞后项,估计结果如表 1:
| 模型SRHt | logBH | tαH | DH1tαH | DH2tαH | DH3tαH | SRHt-1 |
| 0.2608 | 0.0202 | 0.0704 | -0.0328 | 0.0083 | 0.7463 | |
| (0.0682)*** | (0.0069)*** | (0.0236)*** | (0.008)*** | (0.0042)** | (0.0633)** | |
| R2=0.9640 | LM(1)=0.2138 | LM(2)=7.0776 | ||||
| 注:括号内的数值为标准差,*、**和***分别表示在10%、5%和1%的显著性水平下显著。 | ||||||
可得重工业生产的效率参数BH=2.7953,各时期重工业的技术进步率依次为1.4293(1983-1985年)、0.9516(1994-1998年)、1.1189(2000-2007年) 和1.0828(其他年份),则校准重工业的长期技术进步率γH =1.0828;重工业的确定性技术冲击AHt =1.32(1983-1985年)、0.8789(1994-1998年) 和1.0333(2000-2007年)。
对轻工业厂商,同样使用1992年、1997年、2002年、2007年和2010年的投入产出表中轻工业的劳动报酬占增加值的比重,取平均数作为轻工业劳动投入的收入份额,即轻工业劳动的产出弹性αL=0.282;将轻工业的增加值、资本和劳动人数分别除以轻重工业劳动人数之和,得到标准化的轻工业人均产出、轻工业人均资本和轻工业劳动投入,于是有如下(14) 式:
| $S{{R}_{Lt}}=log{{Y}_{Lt}}-(1-{{\alpha }_{L}})log{{K}_{Lt}}-{{\alpha }_{L}}log{{n}_{Lt}}$ | (14) |
得到轻工业的全要素生产率SRLt。轻工业以面向市场的企业为研发主体,有相对较低的技术进步率,1978年至2012年轻工业技术进步率大致有3次较大的波动:(1)1982年后中国经济开始了1978年以来短暂的第一次扩张,伴随着重工业技术进步率的大幅增长,轻工业的技术进步率也有所增长,但有起伏;(2)1992年邓小平发表“南巡谈话”,两年后中国确立了市场经济发展方向,扩大了对外开放,轻工业开始大幅增长,进入了其技术进步率相对较高的发展时期,直至1997年左右的亚洲金融危机,由于中国承诺人民币不贬值,结果使得中国的轻工业产品出口下降,被迫收缩;(3)2003年后政府大力扶持重工业和高科技产业发展,轻工业进入了弱发展时期,轻工业技术进步率相对较低。据此我们建立3个虚拟变量DL1=(1,年份为1984年、1986年;0,其他年份)、DL2=(1,年份为1995-1999年;0,其他年份)、DL3=(1,年份为2004-2008年;0,其他年份),做如下(15) 式的回归有:
| $\begin{align} & S{{R}_{Lt}}=log{{B}_{L}}+(log{{\gamma }_{L}})t+{{\beta }_{L1}}\left( {{D}_{L1}}t \right)+{{\beta }_{L2}}\left( {{D}_{L2}}t \right) \\ & +{{\beta }_{L3}}\left( {{D}_{L3}}t \right)+S{{R}_{Lt}}_{(-1)}+{{\varepsilon }_{Lt}} \\ \end{align}$ | (15) |
其中:t与(13) 式相同为标准化的时间,εt为随机误差项,为消除误差自相关,我们加入了被解释变量SRLt的一阶滞后项。同重工业,可得轻工业的效率参数BL=9.2674,各时间段轻工业的技术进步率分别为1.1279(1984年、1986年)、1.1077(1995-1999年)、0.9581(2004-2008年) 和1(其他年份)。则校准轻工业的长期技术进步率γL =1,各时间段轻工业的确定性技术冲击ALt分别为1.1279(1984年、1986年)、1.1077(1995-1999年) 和0.9581(2004-2008年)。
对代表性家庭消费的轻工业产品的比重参数θ,找不到轻重工业产品消费的增加值数据,因此本文使用1992年、1997年、2002年、2007年和2010年的投入产出表中居民消费的轻重工业产品的总产值来计算,得到θ=0.69;对轻重工业资本的折旧率,王益煊和吴优(2003) 分行业对折旧率进行了研究,指出中国各行业机器设备的年折旧率在0.036-0.138之间,Echevarria(1997) 设美国和OECD国家全行业资本的年折旧率为0.08,张军(2002) 设中国全行业资本的年折旧率为0.05。本文只研究工业,中国工业的资本年折旧率应高于中国全行业的资本年折旧率,这里设中国轻重工业资本的年折旧率δ=0.1;对代表性家庭的主观贴现率β,在消去趋势后的模型中对重工业消费品(cHt) 和重工业资本(kHt) 的一阶条件进行整理并在模型稳态附近取值可得:
| ${{\gamma }_{H}}=\beta [\left( 1-{{\alpha }_{H}})/\left( \tfrac{{{k}_{H}}}{{{y}_{H}}} \right)+(1-\delta ) \right]$ | (16) |
在消去趋势后的模型中对代表性家庭消费的轻工业产品(cLt) 和重工业产品(cHt) 的一阶条件以及关于代表性家庭消费的重工业产品(cHt) 的约束条件进行整理,并在模型稳态处附近取值可得:
| $\frac{\left( 1-\theta \right)\left( 1-{{\alpha }_{H}} \right)}{\theta \left( 1-{{\alpha }_{L}} \right)}\frac{{{k}_{L}}}{{{k}_{H}}}=1-\left( {{\gamma }_{H}}+\delta -1 \right)\left( 1+\frac{{{k}_{L}}}{{{k}_{H}}} \right)\frac{{{k}_{H}}}{{{y}_{H}}}$ | (17) |
由(16) 式和(17) 式可知,模型稳态时轻重工业资本比kL/kH决定了重工业资本产出比kH/yH,重工业资本产出比kH/yH决定了β值,实际数据中kL/kH=0.42,取β=0.947。
本模型的参数校准值见表 2。
| 变量 | 校准值 | 含义 |
| θ | 0.69 | 效用函数中轻工业产品的比重 |
| δ | 0.1 | 轻重工业资本的折旧率 |
| β | 0.947 | 代表性家庭的主观贴现率 |
| αH | 0.248 | 重工业劳动的产出弹性 |
| BH | 2.7953 | 重工业生产的效率参数 |
| γH | 1.0828 | 重工业的长期技术进步率 |
| 1.32 | 1983-1985年重工业的技术冲击 | |
| AHt | 0.8789 | 1994-1998年重工业的技术冲击 |
| 1.0333 | 2000-2007年重工业的技术冲击 | |
| αL | 0.282 | 轻工业劳动的产出弹性 |
| BL | 9.2674 | 轻工业生产的效率参数 |
| γL | 1 | 轻工业的长期技术进步率 |
| 1.1279 | 1984年、1986年轻工业的技术冲击 | |
| ALt | 1.1077 | 1995-1999年轻工业的技术冲击 |
| .9581 | 2004-2008年轻工业的技术冲击 |
(一) 数值模拟。本文在进行数值模拟时,把轻重工业技术冲击设定为确定性冲击而非随机性冲击,这是因为一方面通过参数校准可知轻重工业技术进步率呈阶梯形变化;另一方面,随机性冲击不能体现1978-2012年间轻重工业技术进步率的相对变化。
通过参数校准可知,模型经济中轻重工业的长期技术进步率并不相同,且轻重工业均存在技术冲击,但在1978-1982年模型经济的最初5年,轻重工业以长期技术进步率增长,不存在技术冲击。因此,我们在消去趋势后的波动模型基础上进行模拟,轻重工业的技术冲击可以看做是对波动模型的确定性冲击,据此分析波动模型中变量的变化,然后将波动模型中的变量加上增长趋势,还原为模型经济中的变量,据此进行数值模拟。从技术角度看,波动模型对技术冲击的反应是从波动模型的稳态开始的,那么我们就要先确定波动模型的稳态值和初始值,确认波动模型是否一开始就处于稳态。
使用校准的参数和我们对波动模型稳态时各变量的求解公式,可以求解波动模型具体的稳态值,接下来确定波动模型中各变量的初始值:将1978年的轻重工业劳动人数分别除以轻重工业劳动人数之和,得到标准化的轻工业劳动投入的初始值nL0=0.3725,与标准化的重工业劳动投入的初始值nH0 =0.6275;将1978年的轻重工业资本分别除以轻重工业劳动人数之和,得到轻工业人均资本的初始值kL0=1 326.01,与重工业人均资本的初始值kH0=6 061.65;将1978年的轻重工业增加值分别除以轻重工业劳动人数之和,得到轻工业人均产出的初始值yL0=1 449.61,与重工业人均产出的初始值yH0=1 758.62;由于没有轻重工业产品的消费数据,本文根据模型设定即轻工业产品消费等于轻工业人均产值,确定轻工业产品消费cL0=1 326.01,根据波动模型的一阶条件
波动模型的稳态值和初始值见表 3,可以看出波动模型的初始值不等于稳态值,其中重工业的资本和产出高于稳态值,而轻工业的资本和产出低于稳态值,轻重工业产品的消费均低于稳态值,波动模型一开始并不处于稳态。通过参数校准,我们已知在1978-1982年模型经济的最初5年,轻重工业以长期技术进步率增长,不存在技术冲击。因此,这里我们假定在波动模型最初的5年中,经济逐步向稳态转移,在第5年到达稳态,第5年以后轻重工业的技术冲击就可以用波动模型来进行模拟。
| 变量 | 稳态值 | 初始值 | 含义 |
| nL0 | 0.3351 | 0.3725 | 轻工业劳动投入 |
| nH0 | 0.6649 | 0.6275 | 重工业劳动投入 |
| kL0 | 1 772.04 | 1 326.01 | 轻工业人均资本 |
| kH0 | 4 187.81 | 6 061.65 | 重工业人均资本 |
| yL0 | 1 463.70 | 1 449.61 | 轻工业人均产出 |
| yH0 | 1 337.24 | 1 758.62 | 重工业人均产出 |
| cL0 | 1 463.70 | 1 449.61 | 轻工业产品人均消费 |
| cH0 | 266.26 | 181.02 | 重工业产品人均消费 |

|
| 图 5 轻重工业产出份额模拟 |
|
| 图 6 轻重工业劳动份额模拟 |
|
| 图 7 轻重工业资本份额模拟 |
|
| 图 8 霍夫曼系数模拟 |
图 5为模型经济中轻重工业产出份额的动态变化图,图 6为模型经济中轻重工业劳动份额的动态变化图,由图可知:1.在模型经济中,工业中轻重工业的产出份额的变化较大,但是劳动份额和资本份额变化不大、基本保持稳定。轻重工业的产出份额尤其在1994年之后变化较大(见图 5),如1999年轻工业产出份额为58.07%,达到峰值,重工业产出份额为41.93%;2012年重工业产出份额达到约57%,轻工业产出份额只有约43%。然而,轻重工业的劳动份额和资本份额的变动基本保持稳定,重工业劳动份额始终远高于轻工业,从1978年到2012年,重工业劳动份额最高约为70%,最低约为62%;轻工业劳动份额最高为37%,最低为30%,轻重工业劳动份额变化曲线几乎类似于一条水平线(见图 6)。重工业资本份额同样始终远高于轻工业,从1978年到2012年,重工业资本份额约为70%,轻工业资本份额约为30%,轻重工业资本的变化曲线均类似一条水平线(见图 7)。2.在模型经济中,工业中轻重工业产出份额的变化大致可以分为3个阶段:第一阶段为1978年至1994年,轻重工业产出份额基本持平,呈现胶着状态;第二阶段为1995年至1999年,重工业产出份额呈下降趋势,轻工业产出份额呈上升趋势,轻工业产出份额在1995年后均高于重工业产出份额;第三阶段为2000年至2012年,重工业产出份额呈上升趋势,而轻工业产出份额呈下降趋势,该阶段以2005年为界又可分为两个时期:2005年以前,工业中轻工业产出份额仍高于重工业产出份额,但差距不断缩小;2005年以后,重工业产出份额高于轻工业产出份额(见图 5)。由经验事实对比可见:模型经济的轻重工业产出、劳动份额和资本份额变化基本上体现了中国工业结构变迁这一经验事实的特点,只是幅度略有不同。模型经济较好地模拟了1978-2012年的中国工业结构变迁。3.在模型经济中,霍夫曼系数的变化同样可以分为3个阶段,这印证了工业中轻重工业产出份额的变化(或工业结构的变化)(见图 8):第一阶段为1978年至1994年,霍夫曼系数数值在1附近波动,轻重工业的产出份额基本持平,工业结构呈现维持状态;第二阶段为1995年至1998年,霍夫曼系数数值呈上升趋势,轻工业产出份额上升,且轻工业产出份额高于重工业产出份额,工业结构呈现去工业化趋势;第三阶段为1999年至2012年,霍夫曼系数数值呈下降趋势,工业结构呈现重工业化(或升级) 趋势,重工业产出份额逐渐上升,而轻工业产出份额逐渐下降,该阶段以2005年为界又可分为两个时期:2005年以前,工业中轻工业产出份额仍高于重工业产出份额,但差距不断缩小;2005年及以后,重工业产出份额高于轻工业产出份额,霍夫曼系数数值逐渐趋向小于1,只是减小幅度略低于实际经济中的霍夫曼系数。
(二) 从供给侧角度对工业结构变迁的分析。由模型对轻工业劳动(nLt)、重工业劳动(nHt)、轻工业资本(KLt) 和重工业资本(KHt) 的一阶条件可得:
| $\frac{(1-{{\alpha }_{L}})\frac{{{y}_{Lt}}}{{{k}_{Lt}}}}{{{\alpha }_{L}}\frac{{{y}_{Lt}}}{{{n}_{Lt}}}}=\frac{(1-{{\alpha }_{H}})\frac{{{y}_{Ht}}}{{{k}_{Ht}}}}{{{\alpha }_{H}}\frac{{{y}_{Ht}}}{{{n}_{Ht}}}}$ | (18) |
即MRTSLt=MRTSHt,资本和劳动的边际技术替代率在轻重工业间是相等的,这意味着在轻重工业间,资本和劳动的边际生产率虽不相同,但有相同比例的差距。如重工业资本的边际报酬比轻工业高10%,则重工业劳动的工资比轻工业同样高10%。模型经济的这一内在机制与钱纳里等(1989) 和杨智峰(2011) 对轻重工业的实证分析结果一致。对(18) 式我们进一步整理可得:
| $\frac{{{K}_{Ht}}}{{{K}_{Lt}}}/\frac{{{n}_{Ht}}}{{{n}_{Lt}}}=\frac{(1-{{\alpha }_{H}})}{{{\alpha }_{H}}}/\frac{(1-{{\alpha }_{L}})}{{{\alpha }_{L}}}$ | (19) |
如不考虑技术冲击和向稳态的转移,处于均衡增长路径的轻重工业资本以同样的增长速度增长,轻重工业资本比保持不变,而由(19) 式可知,轻重工业资本比与劳动比为定值,因此轻重工业劳动比也保持不变。考虑到技术冲击和资本、劳动向稳态的转移,轻重工业的资本和劳动份额将有小的波动,但基本保持稳定,其变化曲线均类似于一条水平线(见图 6和图 7),由于模型经济的外生冲击只有轻重工业技术进步率的变化,因此,轻重工业技术进步率的变化对轻重工业间劳动份额和资本份额的变化影响不大。
如果模型经济不存在外生冲击,轻重工业的技术进步以其长期的技术进步率增长,则模型经济不能模拟和解释改革开放以来中国实际的轻重工业产出结构的变化和霍夫曼系数的变化。
模型经济存在外生冲击,即轻重工业技术进步率的变化,重工业产出以其技术进步率γH的速度增长,轻工业的技术进步率为γL,而轻工业产出是以γLγH(1-αL) 的速度增长,那么,如果γHαL>γL,则工业中重工业产出份额呈上升趋势;如果γHαL<γL,则工业中重工业产出份额呈下降趋势,而轻工业产出份额呈上升趋势;如果γHαL≈γL,则工业中轻重工业份额呈维持状态。模型经济中轻重工业技术进步率的相对变化见图 9,再参考图 1或图 5,可以看出轻重工业技术进步率和产出份额的相对变化与该分析一致,并且在不同的经济发展阶段,技术进步对工业结构变化的影响并不一致。中国自1978年改革开放至1994年前,重工业技术进步率的绝对值高于轻工业,但重工业技术进步率的相对值与轻工业大致相等(即γHαL≈γL)。因此重工业产出以略高于轻工业的速度增长,重工业产出份额略有波动并缓慢上升,但总体上轻重工业产出份额呈现维持约各占50%的胶着状态;1995-1998年,轻工业技术进步率的绝对值远高于重工业,且重工业的技术进步率为负,这一时期重工业的技术进步率相对低于轻工业的技术进步率(即γHαL<γL),该时期轻工业产出份额呈快速上升趋势,1999年重工业的技术进步率由负转正,但轻工业的技术进步率仍相对略高于重工业,轻工业产出份额略有上升并达到顶点,工业结构呈现轻工业化趋势(或去工业化趋势);2000年后,重工业技术进步率的绝对值远高于轻工业,轻工业的技术进步率逐步下降为0或负,这一时期重工业技术进步率的相对值也高于轻工业(即γHαL>γL),该时期重工业产出份额呈上升趋势,工业结构呈现优化升级趋势。由此可知,轻重工业技术进步率的相对变化是导致中国工业结构变化的原因,重工业相对于轻工业有较高的技术进步率,是中国工业结构升级的动因。

|
| 图 9 模型经济中轻重工业技术进步率的变化 |
为了进一步验证因果关系,我们对轻重工业的技术进步率与霍夫曼系数进行因果关系检验,可得表 4。
| 原假设 | 滞后期 | F统计量 | P值 | 结论 |
| DTECH不是HOFFMAN的格兰杰原因 | 1 | 3.01867 | 0.09224 | 拒绝* |
| HOFFMAN不是DTECH的格兰杰原因 | 0.01445 | 0.90511 | 接受 | |
| TECHL不是HOFFMAN的格兰杰原因 | 1 | 2.02065 | 0.16516 | 接受 |
| HOFFMAN不是TECHL 的格兰杰原因 | 2.07106 | 0.16014 | 接受 | |
| TECHH不是HOFFMAN的格兰杰原因 | 1 | 1.51898 | 0.22704 | 接受 |
| HOFFMAN不是TECHH 的格兰杰原因 | 0.20399 | 0.65466 | 接受 | |
| 注: DTECH为重工业技术进步率与轻工业技术进步率之差,TECHL为轻工业技术进步率,TECHH为重工业技术进步率,***、**和*分别表示1%、 5%和10%的显著性水平。 | ||||
由表 4可知,1.轻重工业技术进步率不是霍夫曼系数的格兰杰原因,而轻重工业技术进步率之差是霍夫曼系数的格兰杰原因,因此进一步验证了轻重工业技术进步率的相对变化是中国工业结构变化的原因; 2.轻重工业技术进步率之差是霍夫曼系数的单向格兰杰原因,而霍夫曼系数不是轻重工业技术进步率以及轻重工业技术进步率之差的格兰杰原因。
因此,从供给侧角度分析,轻重工业技术进步率的相对变化是轻重工业产出结构变化的动因,且重工业相对于轻工业有较高的技术进步率(即γHαL>γL),是工业结构升级的动因。
通过参数校准,我们知道长期中重工业技术进步率的绝对值高于轻工业,这是由轻重工业的行业特性所决定,重工业生产投资品,投资品的技术进步率通常较高,如芯片产业的摩尔定律(当价格不变时,集成电路上可容纳的元器件的数目约每隔18-24个月便会增加一倍,性能也将提升一倍),装备制造业的指数型自我繁殖等,也表现为重工业的行业规模报酬递增现象,重工业技术水平是国民经济整体水平的基础;轻工业生产消费品,消费品一般属低技术范畴,技术进步率通常较低。
模型经济在均衡增长路径上,重工业产出以其技术进步率γH的速度增长,轻工业产出是以γLγH(1-αL) 的速度增长。由此可知,重工业的技术进步率γH是轻工业产出增长率的一个重要因素,提高重工业的技术进步率会相应提高轻工业的产出增长率。因此,重工业技术进步对轻工业产出具有溢出效应。这是因为重工业生产投资品,如机器设备等,轻工业使用重工业生产的投资品组织生产,如果投资品的生产效率提高,则会相应提高轻工业产出。
轻工业产出不仅受到其本身技术进步的影响,而且还受到重工业技术进步的影响。因此,当重工业技术进步率的绝对值高于轻工业(即γH>γL) 时,重工业产出的增长率可能并不高于轻工业产出的增长率,只有当重工业技术进步率的相对值高于轻工业(即γHαL>γL) 时,重工业产出的增长率才高于轻工业产出的增长率,重工业产出份额呈上升趋势,工业结构才呈现升级趋势。
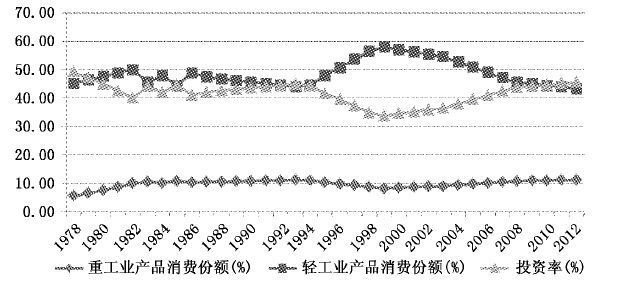
(三) 从需求侧角度对工业结构变迁的分析。对产出的需求分为对轻工业产品的消费(CLt)、对重工业产品的消费(CHt) 和对投资(It) 的需求,模型经济在均衡增长路径上,重工业产品的消费以γH的速度增长,轻工业产品的消费以γLγH(1-αL)的速度增长,投资以γH的速度增长。考虑到技术冲击和向稳态的转移,轻重工业产品的消费和投资存在变化,模型经济中消费结构和投资率的变化见图 10所示。
|
| 图 10 模型经济中消费结构和投资率的变化 |
由图 10可知,重工业产品消费份额略有增长,但基本保持稳定,变化较大的是轻工业产品的消费份额和投资率。与图 9结合起来看,在1994年前轻工业产品的消费份额和投资率呈胶着状态;1995-1998年,轻工业的技术进步率远高于重工业;同时,1999年轻工业的技术进步率仍略高于重工业时,轻工业产品的消费份额快速上升至顶点,而投资率则快速下降至谷底;2000年后,重工业的技术进步率远高于轻工业,轻工业的技术进步率逐步下降为0或负时,投资率呈逐步上升趋势,而轻工业产品的消费份额逐步下降,与此相对应,重工业的产出份额呈上升趋势,工业结构优化升级。由此可见,重工业的产品消费对轻重工业技术进步率的变化不敏感,而投资和轻工业产品的消费对轻重工业技术进步率的变化敏感,重工业技术进步率的相对值高于轻工业时,投资率呈上升趋势,轻工业产品的消费份额逐步下降,同时重工业产品的消费份额保持稳定并略有增长,从而使得重工业的产出份额呈上升趋势。因此,推动工业结构的升级,应适当保持对重工业的投资。
重工业产品的价格相对轻工业产品而言较为昂贵,重工业产品消费份额的增加意味着消费升级,而消费升级则需要整个社会进行较长时间的财富积累,因此当重工业的技术进步率高于轻工业时,重工业产品的消费份额基本稳定并略有上升,而轻工业产品的价格相对低廉;随着居民收入的增长,对轻工业产品的消费增长较快。企业使用重工业产品进行投资、组织生产,重工业技术的快速进步会大大降低企业生产成本,从而使企业增加投资变得更为有利可图,而企业增加投资又使经济中的投资率上升,且投资对重工业技术进步的变化较为敏感。
六、 结 论本文试图从非均衡增长的角度解释中国工业结构升级的动因。首先厘清了中国工业结构变化的经验事实;然后建立两部门的中国工业结构变化模型进行数值模拟,通过拟合中国工业结构变化的经验事实,来对模型经济的机制进行分析;最后结合中国经济的实际运行情况,探讨中国工业结构升级的动因和机制。研究发现:1.从供给侧角度考察,轻重工业技术进步率的相对变化是中国工业产出结构变化的动因,而重工业相对于轻工业有较高的技术进步率,是中国工业结构升级的动因;2.重工业的技术进步对轻工业的产出具有溢出效应;3.重工业产品的消费对轻重工业技术进步率的变化不敏感,而投资和轻工业产品的消费对轻重工业技术进步率的变化敏感,重工业的技术进步率相对高于轻工业(某个幅度) 时,投资率呈上升趋势,轻工业产品的消费份额逐步下降,同时重工业的产出份额呈上升趋势。
基于以上研究结论,本文认为可以在以下几个方面推动中国的工业结构升级:1.政府在推动技术进步方面应将更多的政策支持、人力资源和物质资源等重点配置于重工业,尤其是基础性或者高科技行业,而不是轻工业;推动重工业的发展相对于轻工业会有较高的技术进步率效果,从而有力地推动工业结构的升级和制造业升级。2.建立统一的国内市场,通过税收减免和补贴等措施,鼓励轻工业企业使用本国的重工业产品。3.对使用本国重工业产品进行投资生产的企业,可给予投资税收抵免、退税补贴等政策的鼓励支持。4.从1978年至2012年,中国技术进步的方式完成了由原计划经济体制下低起点的“以创新为主”方式向“以模仿为主”方式的转变;随着经济的快速增长,中国已经成为世界第二大经济体,通过“走出去,引进来”的方式,中国的许多产业部门实现了跨越式的发展,拥有了世界次先进的技术水平,但这种“以模仿为主”的技术进步方式并不能取得最先进的技术从而实现赶超,且由于代价日益高昂业已不能满足中国工业结构升级的要求。因此,需要积极落实“十八届五中全会”精神,把创新摆在经济发展的核心位置,实现技术进步从“以模仿为主”方式向 “以创新为主”方式的再次转变,为技术进步注入创新活力,推动重工业实现较高的技术进步率的发展,从而为进一步推进工业结构升级和制造业升级打下坚实的科技基础。
| [1] | 戴魁早. 中国工业结构变迁的驱动因素: 1985-2010[J]. 当代经济科学 , 2012 (6) : 1–14. |
| [2] | 戴魁早. 中国工业结构的优化与升级: 1985-2010[J]. 数理统计与管理 , 2014 (2) : 296–304. |
| [3] | 干春晖, 郑若谷, 余典范. 中国产业结构变迁对经济增长和波动的影响[J]. 经济研究 , 2011 (5) : 4–16. |
| [4] | 李尚骜, 龚六堂. 非一致性偏好、内生偏好结构与经济结构变迁[J]. 经济研究 , 2012 (7) : 35–47. |
| [5] | (美)钱纳里.H, 鲁宾逊.S, 赛尔奎因.M. 工业化和经济增长的比较研究[M]. 上海: 上海三联书店出版社, 1989 . |
| [6] | 王益煊, 吴优. 中国国有经济固定资本存量初步测算[J]. 统计研究 , 2003 (5) : 40–45. |
| [7] | 杨智峰. 工业化对经济增长的影响分析:1981-2008[J]. 山西财经大学学报 , 2011 (3) : 26–32. |
| [8] | 杨智峰, 陈霜华, 汪伟. 中国产业结构变化的动因分析—基于投入产出模型的实证研究[J]. 财经研究 , 2014 (9) : 38–49. |
| [9] | 张军. 资本形成、工业化与经济增长: 中国的转轨特征[J]. 经济研究 , 2002 (6) : 3–13. |
| [10] | Acemoglu D, Guerrieri V. Capital deepening and non-balanced economic growth[J]. Journal of Political Economy , 2008, 116 (3) : 467–498. DOI:10.1086/589523 |
| [11] | Alvarez-Cuadrado F, Van Long N. Capital-labor substitution, structural change and growth[R]. CIRANO-Scientific Publications 2011s-68,2011. http://cn.bing.com/academic/profile?id=2102239237&encoded=0&v=paper_preview&mkt=zh-cn |
| [12] | Dennis B N, İşcan T B. Engel versus Baumol: Accounting for structural change using two centuries of U.S. data[J]. Explorations in Economic History , 2009, 46 (2) : 186–202. DOI:10.1016/j.eeh.2008.11.003 |
| [13] | Echevarria C. Changes in sectoral composition associated with economic growth[J]. International Economic Review , 1997, 38 (2) : 431–452. DOI:10.2307/2527382 |
| [14] | Foellmi R, Zweimüller J. Structural change, Engel’s consumption cycles and Kaldor’s facts of economic growth[J]. Journal of Monetary Economics , 2008, 55 (7) : 1317–1328. DOI:10.1016/j.jmoneco.2008.09.001 |
| [15] | Hoffmann W G. The growth of industrial economies[J]. Hitotsubashi Journal of Economics , 1970, 11 (1) : 113–116. |
| [16] | Kongsamut P, Rebelo S, Xie D. Beyond balanced growth[J]. The Review of Economic Studies , 2001, 68 (4) : 869–882. DOI:10.1111/1467-937X.00193 |
| [17] | Ngai L R, Pissarides C A. Structural change in a multisector model of growth[J]. American Economic Review , 2007, 97 (1) : 429–443. DOI:10.1257/aer.97.1.429 |
| [18] | Uy T L, Yi K, Zhang J. Structural change in an open economy[J]. . |
 2016, Vol. 42
2016, Vol. 42




